Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3: 409-418 doi:10.4236/jsea.2010.34046 Published Online April 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes JSEA 409 Designing a Fuzzy Expert System to Evaluate Alternatives in Fuzzy Analytic Hierarchy Process Hamed Fazlollahtabar1, Hamid Eslami2, Hamidreza Salmani2 1Mazandaran Univer si t y of Science and Technology, Babol, Iran; 2Science and Research Campus, Islamic Azad University, Member of Young Researchers Club, Tehran, Iran. Email: hamed@ustmb.ac.ir Received June 23rd, 2009; revised July 18th, 2009; accepted July 25th, 2009. ABSTRACT This paper concerns with proposing a fuzzy logic based expert system to breakthrough the problem of alternatives evaluation in Analytic Hierarchy Process (AHP). AHP as a multi criteria decision aid helped decision makers for ana- lyzing and prioritizing the alternatives in a hierarchical structure. During times AHP encountered some problems. Hence, fuzzy analytic hierarchy process (FAHP) and some other extensions of AHP have been configured to solve those problems. Keywords: Multi Criteria Decision Making (MCDM), Analytic Hierarchy Pro ces s (AHP), Expert System 1. Introduction Analytic hierarchy process (AHP) [1] has been widely used as a useful multiple criteria decision making (MCDM) tool or a weight estimation technique in many areas such as selection, evaluation, planning and devel- opment, decision making, forecasting, and so on [2]. The AHP is expressed by a unidirectional hierarchical rela- tionship amongst decision levels. The top element of the hierarchy is the overall goal for the decision model. The hierarchy decomposes to a more specific criterion on a level and each criterion may be related to some subcrite- ria. The AHP separates complex decision problems into elements within a simplified hierarchical system. The AHP usually consists of three stages of problem solving: decomposition, comparative judgments, and synthesis of priority. The decomposition stage aims at the construction of a hierarchical network to represent a de- cision problem, with the top level representing the over- all objectives and the lower levels representing the crite- ria, subcriteria, and alternatives. With comparative judgments, users are requested to set up a comparison matrix at each hierarchy by comparing pairs of criteria or subcriteria. A scale of values ranging from 1 (Equally Preferred) to 9 (Extremely Preferred), is used to express the users preferences. Finally, in the synthesis of priority stage, each comparison matrix is then solved by an ei- genvector method for determining the importance of the criteria and alternative performance. One major advantage of AHP is its applicability to the problems of group decision-making. In a group decision setting, each participant is required to set up the prefer- ence of each alternative by the AHP and the collective views of the participants are used to obtain an average weighting of each alternativ e. The traditional AHP requires crisp judgments. Ho wever, due to the complexity and uncertainty involved in real world decision problems, a decision maker (DM) may sometimes feel more confident to provide fuzzy judgments than crisp comparisons. A number of methods have been developed to handle fuzzy comparison matrices. For ex- ample, Van Laarhoven and Pedrycz [3] suggested a fuzzy logarithmic least squares method (LLSM) to obtain trian- gular fuzzy weights from a triangular fuzzy comparison matrix. Wang et al. [4] presented a modified fuzzy LLSM. Buckley [5] utilized the geometric mean method to calculate fuzzy weights. Chang [6] proposed an extent analysis method, which derives crisp weights for fuzzy comparison matrices. Xu [7] brought forward a fuzzy least squares priority method (LSM). Mikhailov [8] de- veloped a fuzzy preference programming method (PPM), which also derives crisp weights from fuzzy comparison matrices. Csutora and Buckley [9] came up with a Lambda-Max method, which is the direct fuzzification of the well-known kmax method. Among the above approaches, the extent analysis me- thod has been employed in quite a number of applica- tions [10-28] due to its computational simplicity. How- ever, such a method is found unable to derive the true  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process 410 weights from a fuzzy or crisp comparison matrix. The weights determined by th e extent analysis method do not represent the relative importance of decision criteria or alternatives at all. Therefore, it should not be used as a method for estimating priorities from a fuzzy pairwise comparison matrix. The purpose of this paper is to show by examples that the priority vectors determined by the extent analysis method do not represent the relative im- portance of decision criteria or alternatives and that the misapplication of the extent analysis method to fuzzy AHP problems may lead to a wrong decision to be made and some useful decision information such as decision criteria and fuzzy comparison matrices not to be consid- ered. We illustrate these problems to avoid any possible misapplications in the future. Here, we compare the Fuzzy AHP with a proposed expert system and illustrate our proposed expert system in an example. 2. Review of the Extent Analysis Method on Fuzzy AHP A triangular fuzzy number is represented by ~ a , with the membership function , ),,( uml )( ~x a , defined by the expression, mx u mx mx l xm x a)(1 )(1 )( ~ where m is the center, l is the left spread and u is the right spread. For two triangular fuzzy number and the fuzzy operations are defined as follows: ~1 M ),,( 111 uml),,( ~2222 umlM ),,( ~~ 21212121 uummllMM ),,( ~ ~ 21212121 uummllMM ) 1 , 1 , 1 ( ~ ), 1 , 1 , 1 ( ~ 222 1 2 111 1 1lmu M lmu M Consider a triangular fuzzy comparison matrix ex- pressed by nnij MA ) ~ ( ~ )1,1,1(...),,(),,( . . . . . . . . . . . .),,(...)1,1,1(),,( ),,(...),,()1,1,1( 222111 222212121 111121212 nnnnnn nnn nnn umluml umluml umluml where ) 1 , 1 , 1 ( ~ ),,( ~1 jijiji jiijijijijlmu aumla , for i,j = 1,…,n and . ji To calculate a priority vector of the above triangular fuzzy comparison matrix, Chang [9] suggested an extent analysis method, which is summarized as follows. Firstly, sum up each row of the fuzzy comparison ma- trix A ~ by fuzzy arithmetic operations: .,...,1),, ~ , ~ , ~ ( ~ 1111 niumlMRS n j ij n j ij n j ij n j iji Secondly, normalize the above row sums by .,...,1, ~ , ~ , ~ ~ 11 1 11 1 11 1 1 ni l u m m u l RS RS Sn k n j kj n j ij n k n j kj n j ij n k n j kj n j ij n j j i i Thirdly, compute the degree of possibility of ji SS ~ ~ by the following equation: other ijnjiulif lmmu lu mmif ssV ij jjii ji ji ji ,0 ;,...,1,,, )()( ,1 ) ~~ ( where ),,( ~ iiiiumlS and . The defini- tion of possibility degree is shown in Figure 1 . ),,( ~jjjjumlS Fourthly, calculate the degree of possibility of i S ~ over all the other (n - 1) fuzzy numbers by , . 1 ~~ (jSSVji ),...,1), ~~ (min);..., ,,...,1 niSSVijn ji ijnj Finally, define the priority vector T n wwW ),...,( 1 of the fuzzy comparison matrix A ~ as .,...,1, ;,...,1 ~~ ;,...,1 ~ ~ 1 ni kjnjSSV ijnjSSV wn k jk ji i It must be pointed out that the normalization formula is wrong. The correct normalization formula for a set of triangular fuzzy weights should be as follows: )( x i S ~ j S ~ ) ~~ ( ji SSV Figure 1. Definition of the degree of possibility of ) ~ ~ ( j iSSV Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process411 ,, ~ ~ 11 1 ,111 1 1 m m ul l RS RS Sn k n j kj n j ij n ikk n j kj n j ij n j ij n j j i i .,...,1, ,111 1ni lu u n ikk n j kj n j ij n j ij Although Fuzzy AHP solved some of the problems of AHP, but still some problems arises: Problem 1. The extent analysis method may assign a zero weight to a decision criterion or alternative, leading to the criterion or alternative not to be considered in de- cision analysis. Problem 2. The weights determined by the extent analysis method do not represent the relative importance of decision criteria or alternatives and cannot be used as their priorities. Problem 3. The extent analysis method may make a wrong decision and select the worst decision alternative as the best one when it is misused for solving a fuzzy AHP problem. Problem 4. The extent analysis method cannot make full use of all the fuzzy comparison matrices information and may cause some useful fuzzy comparison matrices information to be wasted when it assigns an irrational zero weight to some useful decision criteria or sub-criteria. Therefore, we propose an expert system which func- tions based on fuzzy logic, to improve decision making in uncertainties. 3. Fuzzy Logic Fuzzy Logic (FL) is a problem-solving control system methodology that lends itself to implementation in sys- tems ranging from simple, small, embedded micro- controllers to large, networked, multi-channel PC or workstation-based data acquisition and control systems. It can be implemented in hardware, software, or a combina- tion of both. FL provides a simple way to arrive at a defi- nite conclusion based upon vague, ambiguous, imprecise, noisy, or missing input information. FL’s approach to control problems mimics how a person would make deci- sions, only much faster. FL incorporates a simple, rule-based IF X AND Y THEN Z approach to a solving control problem rather than attempting to model a system mathematically. The FL model is empirically-based, relying on an operator’s experience rather than their technical understanding of the system. FL requires some numerical parameters in order to operate such as what is considered significant error and significant rate-of-change-of-error, but exact values of these numbers are usually not critical unless very respon- sive performance is required in which case empirical tuning would determine them. For example, a simple temperature control system could use a single tempera- ture feedback sensor whose data is subtracted from the command signal to compute “error” and then time- differentiated to yield the error slope or rate-of-change- of-error, hereafter called “error-dot”. Error might have units of degs F and a small error considered to be 2 F while a large error is 5 F. The “error-dot” might then have units of degs/min with a small error-dot being 5 F/min and a large one being 15 F/min. These values don’t h ave to be symmetrical and can be “tweaked” once the system is operating in order to optimize performance. Generally, FL is so forgiving that the system will probably work the first time without any tweaking. FL works as follows: 1) Define the control objectives and criteria: What am I trying to control? What do I have to do to control the system? What kind of response do I need? What are the possible (probable) system failure modes? 2) Determine the input and output relationships and choose a minimum number of variables for input to the FL engine (typically error and rate-of-change-of-error). 3) Using the rule-ba sed structure of FL, break the con- trol problem down into a series of IF X AND/OR Y THEN Z rules that define the desired system output re- sponse for given system input conditions. The number and complexity of rules depends on the number of input parameters that are to be processed and the number fuzzy variables associated with each parameter. If possible, use at least one variable and its time derivative. Although it is possible to use a single, instantaneous error parameter without knowing its rate of change, this cripples the sys- tem’s ability to minimize overshoot for a step inputs. 4) Create FL membership functions that define the meaning (values) of Input/Output terms used in the rules. 5) Create the necessary pre- and post-processing FL routines if implementing in S/W, otherwise program the rules into the FL H/W engine. 6) Test the system, evaluate the results, tune the rules and membership functions, and retest until satisfactory results are obtained. In 1973, Professor Lotfi Zadeh proposed the concept of linguistic or “fuzzy” variables. Think of them as lin- guistic objects or words, rather than numbers. The sensor input is a noun, e.g. “temperature”, “displacement”, “ve- locity”, “flow”, “pressure”, etc. Since error is just the difference, it can be thought of the same way. The fuzzy variables themselves are adjectives that modify the vari- able (e.g. “large positive” error, “small positive” error, “zero” error, “small negative” error, and “large negative” error). As a minimum, one could simply have “positive”, “zero”, and “negative” variables for each of the parame- Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process 412 ters. Additional ranges such as “very large” and “very small” could also be added to extend the responsiveness to exceptional or very nonlinear conditions, but aren’t necessary in a basic system. Here, using fuzzy logic we define some rules that help the student to select the opti- mal department, course and teacher based on his age, average grade and skills. 4. Expert Systems Knowledge-based systems are systems based on the me- thods and techniques of Artificial Intelligence. Their core components are the knowledge base and the inference mechanisms. Some particular types of knowledge-based systems are expert systems, case-based reasoning sys- tems and neural networks. Expert Systems (ES) are computer programs that are derived from a branch of computer science research called Artificial Intelligence (AI). AI’s scientific goal is to understand intelligence by building computer pro- grams that exhibit intelligent behavior. It is concerned with the concepts and methods of symbolic inference, or reasoning, by a computer, and how the knowledge used to make those inferences will be represented inside the machine. Of course, the term intelligence covers many cognitive skills, including the ability to solve problems, learn, and understand language; AI addresses all of those. But most progress to date in AI has been made in the area of prob- lem solving; concepts and methods for building programs that reason about problems rather than calculate a solu- tion. AI programs that achieve expert-level competence in solving problems in task areas by bringing to bear a body of knowledge about specific tasks are called knowl- edge-based or expert systems. Often, the term expert systems is reserved for programs whose knowledge base contains the knowledge used by human experts, in con- trast to knowledge gathered from textbooks or non-experts. More often, the two terms, expert systems (ES) and knowledge-based systems (KBS), are used synonymously. Taken together, they represent the most widespread type of AI application. The area of human intellectual endeavor to be captured in an expert system is called the task domain. Task refers to some goal-oriented, problem-solving activity. Domain refers to the area within which the task is being performed. Typi- cal tasks are diagnosis, planning, scheduling, configura- tion and design. Building an expert system is known as knowledge en- gineering and its practitioners are called knowledge engi- neers. The knowledge engineer must make sure that the computer has all the knowledge needed to solve a prob- lem. The knowledge engineer must choose one or more forms in which to represent the required knowledge as symbol patterns in the memory of the computer, that is, he (or she) must choose a knowledge representation. He must also ensure that the computer can use the knowledge efficiently by selecting from a handful of reasoning me- thods. Every expert system consists of two principal parts: the knowledge base; and the reasoning, or inference, en- gine. The knowledge base of expert systems contains both factual and heuristic knowledge. Factual knowledge is that knowledge of the task domain that is widely shared, typically found in textbooks or journals, and commonly agreed upon by those knowledgeable in the particular field. Today there are two ways to build an expert system. They can be built from scratch, or built using a piece of development software known as a “tool” or a “shell”. Before we discuss these tools, let's briefly discuss what knowledge engineers do. Though different styles and me- thods of knowledge engineering exist, the basic approach is the same: a knowledge engineer interviews and ob- serves a human expert or a group of experts and learns what the experts know, and how they reason with their knowledge. The engineer then translates the knowledge into a computer-usable langua ge, an d desig ns an inference engine, a reasoning structure, that uses the knowledge appropriately. He also determines how to integrate the use of uncertain knowledge in the reasoning process, and what kinds of explanation would be usef ul to the end user. Next, the inference engine and facilities for represent- ing knowledge and for explaining are programmed, and the domain knowledge is entered into the program piece by piece. It may be that the inference engine is not just right; the form of knowledge representation is awkward for the kind of knowledge needed for the task; and the expert might decide the pieces of knowledge are wrong. All these are discovered and modified as the expert sys- tem gradually gains competence. The discovery and accumulation of techniques of ma- chine reasoning and knowledge representation is gener- ally the work of artificial intelligence research. The dis- covery and accumulation of knowledge of a task domain is the province of domain experts. Domain knowledge consists of both formal, textbook knowledge, and expe- riential knowledge—the expertise of the experts. Compared to the wid e variation in domain knowledge, only a small number of AI methods are known that are useful in expert systems. That is, currently there are only a handful of ways in which to re present knowledge, or to make inferences, or to generate explanations. Thus, sys- tems can be built that contain these useful methods without any domain-specific knowledge. Such systems are known as skeletal systems, shells, or simply AI tools. Building expert systems by using shells offers signifi- cant advantages. A system can be built to perform a unique task by entering into a shell all the necessary knowledge about a task domain. The inference engine Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process Copyright © 2010 SciRes JSEA 413 corporate know-how so that it can be widely distributed to other factories, offices or plants of the company. that applies the knowledge to the task at hand is built into the shell. If the pro gram is not v er y co mplica ted and if an expert has had some training in the use of a shell, the expert can enter the knowledge himself. Introduction of new products. A good example of a new product is a pathology advisor sold to clinical pa- thologists in hospitals to assist in the diagnosis of dis- eased tissue. Many commercial shells are available today, ranging in size from shells on PCs, to shells on workstations, to shells on large mainframe computers. They range in price from hundreds to tens of thousands of dollars, and range in complexity from simple, forward-chained, rule-based systems requiring two days of training to those so com- plex that only highly trained knowledge engineers can use them to advantage. They range from general-purpose shells to shells custom-tailored to a class of tasks, such as financial planning or real-time process control. An expert system tool, or shell, is a software develop- ment environment containing the basic components of expert systems. Associated with a shell is a prescribed method for building applications by configuring and in- stantiating these components. Some of the generic com- ponents of a shell are shown in Figure 2 and described below. The core components of expert systems are the knowledge base and the reasoning engine. Knowledge base: A store of factual and heuristic knowledge. An ES tool provid es one or more knowledge representation schemes for expressing knowledge about the application domain. Some tools use both frames (ob- jects) and IF-THEN rules. In PROLOG the knowledge is represented as logical statements. Although shells simplify progr amming, in general they don't help with knowledge acquisition. Knowledge ac- quisition refers to the task of endowing expert systems with knowledge, a task currently performed by knowl- edge engineers. The choice of reasoning method, or a shell, is important, but it isn’t as important as the accu- mulation of high-quality knowledge. The power of an expert system lies in its store of knowledge about the task domain—the more knowledge a system is given, the more competent it becomes. Primarily, the benefits of ESs to end users include: Reasoning engine: Inference mechanisms for ma- nipulating the symbolic information and knowledge in the knowledge base to form a line of reasoning for solv- ing a problem. The inference mechanism can range from simple modus pones backward chaining of IF-THEN rules to case-based reasoning. A speed-up of human professional or semi-professional Knowledge acquisition subsystem: A subsystem to help experts build knowledge bases. Collecting knowl- edge needed to solve problems and build the knowledge base continues to be the biggest bottleneck in building expert systems. work—typically by a factor of ten and sometimes by a factor of a hundred or more. Within companies, major internal cost savings. For small systems, savings are sometimes in the tens or hun- dreds of th ousan ds of do llars; bu t for large syste ms, often in the tens of millions of dollars and as high as hundreds of millions of dollars. These cost savings are a result of quality improvement, a major motivation for employing expert system technology. Explanation subsystem: A subsystem that explains the system’s actions. The explanation can range from how the final or intermediate solutions were arrived at to justifying the need for additional data. User interface: The means of communication with the user. The user interface is generally not a part of the ES technology, and was not given much attention in the past. However, it is now widely accepted that the user inter- face can make a critical difference in the perceived utility of a system regardless of the system’s performance. Improved quality of decision making. In some cases, the quality or correctness of decisions evaluated after the fact show a ten-fold improv ement. Preservation of scarce expertise. ESs are used to pre- serve scarce know-how in organizations, to capture the expertise of individuals who are retiring, and to preserve Figure 2. Basic components of expert system tools  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process 414 5. Comparison between Expert System and Fuzzy AHP Expert system has been applied for ranking [29]. Expert system in comparison with fuzzy AHP has the following advantages: The alternatives are analyzed using quantitative and qualitative criteria without normalization process More than seven alternatives can be processed against AHP which encountered problems in pairwise comparisons [30]. By entrance of new alternatives, the ranking of the alternatives do not change The fuzzy expert system is able to consider a stan- dard in evaluating the alternatives It is possible to apply group decision making of the experts in evaluating the alternatives The capability of sensitivity analysis for all the al- ternatives No limitation for evaluating many criteria The mistakes in computations such as the zero result will not occur in expert system The possibility of evaluating the alternatives using both quantitative and qualitative criteria The possibility of evaluating the alternatives while some information about some criteria are missing The possibility of keeping the same membership during the process of decisio n m a king [31] . In an expert system a membership function is pro- posed for criteria regarding to the experts idea. To pro- pose an expert system the following steps should be tak- en: 1) Determining the objective, alternatives and criteria 2) Identifying the input and output variables 3) Proposing membership functions for input and out- put variables 4) Proposing rules to determine the relations between inputs and outputs 5) Selecting an appropriate inference mechanism 6) Placement of alternatives corresponding to each criteria 7) Extracting the evaluation result by the proposed expert system 8) Sensitivity analysis of evaluated alternatives Net section presents a numerical illustration to indicate the application of the proposed expert system. 6. Numerical Illustrations Here, we illustrate the proposed expert system in priori- tizing four br and s of mobile p hon e. We analyze HAD, IC, TA, HAM as alternatives using the criteria services, power of antenna, prestige, and price. The hierarchy of the model is shown in Figure 3. The linguistic variables for criteria and their corresponded membership functions are as follows (Figures 4-9). Figure 3. The hierarchy of the model Figure 4. The inputs and outp uts Considering the experts the price has a Gaussian membership function with minimum price of 5000 and maximum of 700000. For the power of antenna linguistic triangular fuzzy number (high, medium, low) is considered. Membership Value Figure 5. Price membership function Membership Value Figure 6. The power of antenna membership function Membership Value Figure 7. Services membership function Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process Copyright © 2010 SciRes JSEA 415 5-If services is low Then rating low. 6-If services is high Then rating high. 7-If the_power_of_antenna is high Then rating high. Membership Value 8-If the_power_of_antenna is low Then rating low. 9-If the_power_of_antenna is medium Then rat- ing low. 10-If price is medium Then rating high. 11-If price is very high Then rating low. Figure 8. Prestige membership function 12-If price is low Then rating high. 13-If prestige is very low Then rating low. 1 4-If prestige is medium Then rating me- dium. Membership Value 15-If prestige is very high Then rating high Regarding to the proposed rules of the expert system, we evaluate the alternatives as follows. To facilitate the computations MATLAB package has been applied (Ap- pendix A). TA Price: 200 Services: medium Figure 9. Rating membership function Power of antenna: high Prestige: medium The output of the system which is the evaluation result, is a combined linguistic fuzzy number with a Gaussian membership function for medium and triangular fuzzy membership function for high and low. Output: 0.518 The graphical presentation is shown in Figure 10. IC Price: 15 Regarding to the experts and taking the criteria into considerations, the following rules are derive d: Services: low Power of antenna: high 1-If price is high Then rating medium. Prestige: low 2-If price is very low Then rating low. Output: 0.51 3-If services is high Then rating high. The graphical presentation is shown in Figure 11. 4-If services is medium Then rating low. Figure 10. The rule viewer for TA 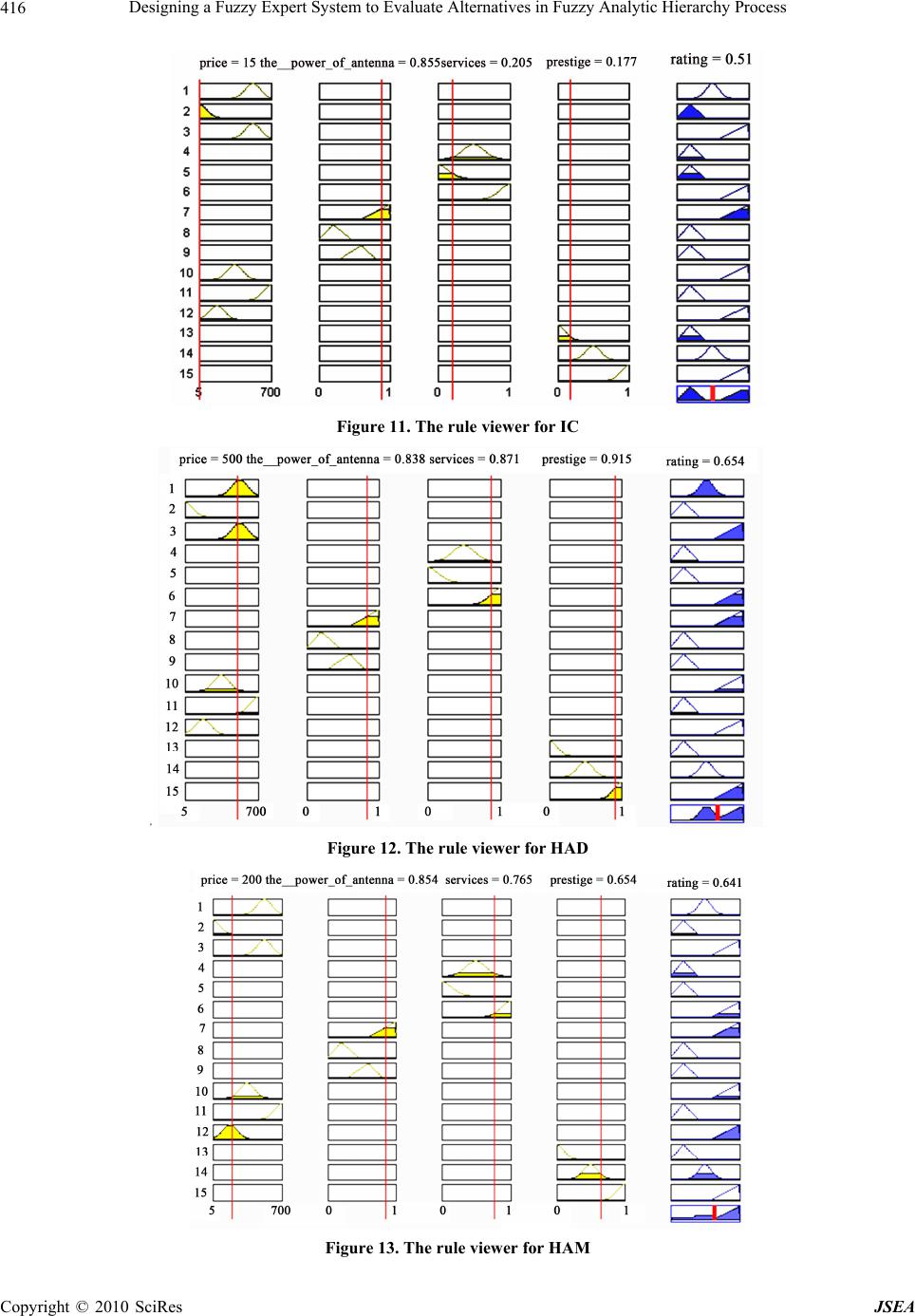 Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process 416 Figure 11. The rule viewer for IC Figure 12. The rule viewer for HAD Figure 13. The rule viewer for HAM Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process417 HAD Price: 500 Services: high Power of antenna: high Prestige: very high Output: 0.654 The graphical presentation is shown in Figure 12. HAM Price: 200 Services: high Power of antenna: high Prestige: high Output: 0.641 The graphical presentation is shown in Figure 13. The ranking indicates the importance degree of each mo- bile brand. 7. Conclusions In this paper, we developed a fuzzy expert system on the basis of rule base fuzzy logic to overcome the problems in AHP and Fuzzy AHP. The advantages of using expert system to prioritize the alternatives in comparison with fuzzy AHP are discussed. To present the validity and effectiveness of the proposed expert system a numerical example is illustrated. REFERENCES [1] T. L. Saaty, “Multicriteria Decision Making: The Ana- lytic Hierarchy Process,” RWS Publications, Pittsburgh, 1988. [2] O. S. Vaidya and S. Kumar, “Analytic Hierarchy Process: An Overview of Applications,” European Journal of Op- erational Research, Vol. 169, 2006, pp. 1-29. [3] P. J. M. Van Laarhoven and W. Pedrycz, “A Fuzzy Ex- tension of Saaty’s Priority Theory,” Fuzzy Sets and Sys- tems, Vol. 11, 1983, pp. 229-241. [4] Y. M. Wang, T. M. S. Elhag and Z. S. Hua, “A Modified Fuzzy Logarithmic Least Squares Method for Fuzzy Ana- lytic Hierarchy Process,” Fuzzy Sets and Systems, Vol. 157, 2006, pp. 3055-3071. [5] J. J. Buckley, “Fuzzy Hierarchical Analysis,” Fuzzy Sets and Systems, Vol. 17, 1985, pp. 233-247. [6] D. Y. Chang, “Applications of the Extent Analysis Me- thod on Fuzzy AHP,” European Journal of Operational Research, Vol. 95, 1996, pp. 649-655. [7] R. Xu, “Fuzzy Least-Squares Priority Method in the Analytic Hierarchy Process,” Fuzzy Sets and Systems, Vol. 112, 2000, pp. 359-404. [8] L. Mikhailov, “Deriving Priorities from Fuzzy Pairwise Comparison Judgments,” Fuzzy Sets and Systems, Vol. 134, 2003, pp. 365-385. [9] R. Csutora, and J. J. Buckley, “Fuzzy Hierarchical Analy- sis: The Lamda-Max Method,” Fuzzy Sets and Systems, Vol. 120, 2001, pp. 181-195. [10] F. T. Bozbura and A. Beskese, “Prioritization of Organ- izational Capital Measurement Indicators Using Fuzzy AHP,” International Journal of Approximate Reasoning, Vol. 44, 2007, pp. 124-147. [11] F. T. Bozbura, A.Beskese and C. Kahraman, “Prioritiza- tion of Human Capital Measurement Indicators Using Fuzzy AHP,” Expert Systems with Applications, Vol. 32, 2007, pp. 1100-1112. [12] C. E. Bozdag, C. Kahraman and D. Ruan, “Fuzzy Group Decision Making for Selection among Computer Inte- grated Manufacturing Systems,” Computers in Industry, Vol. 51, 2003, pp. 13-29. [13] G. Bu¨yu¨ko¨zkan, “Multi-Criteria Decision Making for E-Marketplace Selection,” Internet Research, Vol. 14, No. 2, 2004, pp. 139-154. [14] G. Bu¨yu¨ko¨zkan, T. Ertay, C. Kahraman and D. Ruan, “Determining the Importance Weights for the Design Requirements in the House of Quality Using the Fuzzy Analytic Network Approach,” International Journal of Intelligent Systems, Vol. 19, 2004, pp. 443-461. [15] G. Bu¨yu¨ko¨zkan, C. Kahraman and D. Ruan, “A Fuzzy Multi-Criteria Decision Approach for Software Devel- opment Strategy Selection,” International Journal of General Systems, Vol. 33, 2004, pp. 259-280. [16] F. T. S. Chan and N . Kum ar, “Globa l Supp lier Develo pm ent Considering Risk Factors Using Fuzzy Extended AHP Based Approach,” Omega, Vol. 35, 2007, pp. 417-431. [17] T. Ertay, G. Bu¨yu¨ko¨zkan, C. Kahraman and D. Ruan, “Quality Function Deployment Implementation Based on Analytic Network Process with Linguistic Data: An Ap- plication in Automotive Industry,” Journal of Intelligent and Fuzzy Systems, Vol. 16, 2005, pp. 221-232. [18] Y. C. Erensal, T. O¨ ncan and M. L. Demircan, “Deter- mining Key Capabilities in Technology Management Us- ing Fuzzy Analytic Hierarchy Process: A Case Study of Turkey,” Information Sciences, Vol. 176, 2006, pp. 2755- 2770. [19] C Kahraman, U. Cebeci and D. Ruan, “Multi-Attribute Comparison of Catering Service Companies Using Fuzzy AHP: The Case of Turkey,” International Journal of Production Economics, Vol. 87, 2004, pp. 171-184. [20] C. Kahraman, U. Cebeci and Z. Ulukan, “Multi-Criteria Supplier Selection Using Fuzzy AHP,” Logistics Infor- mation Management, Vol. 16, No. 6, 2003, pp. 382-394. [21] C. Kahraman, T. Ertay, and G. Bu¨yu¨ko¨zkan, “A Fuzzy Optimization Model for QFD Planning Process Using Analytic Network Approach,” European Journal of Op- erational Research, Vol. 171, 2006, pp. 390-411. [22] C. Kahraman, D. Ruan and I. Dogan, “Fuzzy Group De- cision-Making for Facility Location Selection,” Informa- tion Sciences, Vol. 157, 2003, pp. 135-153. [23] O. Kulak and C. Kahraman, “Fuzzy Multi-Attribute Se- lection among Transportation Companies Using Axio- matic Design and Analytic Hierarchy Process,” Informa- tion Sciences, Vol. 170, 2005, pp. 191-210. [24] C. K. Kwong, and H. Bai, “Determining the Importance Copyright © 2010 SciRes JSEA  Designing a Fuzzy E xpert System to Ev al uate Alternati ves in Fuzzy Analyti c Hi e ra r c hy Process Copyright © 2010 SciRes JSEA 418 Weights for the Customer Requirements in QFD Using a Fuzzy AHP with an Extent Analysis Approach,” IIE Transactions, Vol. 35, 2003, pp. 619-626. [25] Y. C. Tang and M. Beynon, “Application and Develop- ment of a Fuzzy Analytic Hierarchy Process within a Capital Investment Study,” Journal of Economics and Management, Vol. 1, 2005, pp. 207-230. [26] E. Tolga, M. L. Demircan and C. Kahraman, “Operating System Selection Using Fuzzy Replacement Analysis and Analytic Hierarchy Process,” International Journal of Production Economics, Vol. 97, 2005, pp. 89-117. [27] F. Tu¨ysu¨ z, and C. Kahraman, “Project Risk Evaluation Using a Fuzzy Analytic Hierarchy Process: An Applica- tion to Information Technology Projects,” International Journal of Intelligent Systems, Vol. 21, No. 6, 2006, pp. 559-584. [28] K. J. Zhu, Y. Jing and D. Y. Chang, “A Discussion on Extent Analysis Method and Application of Fuzzy AHP,” European Journal of Operational Research, Vol. 116, 1999, pp. 450-456. [29] S. Malagoli, C. A. Magni and G. Mastroleo, “The Use of Fuzzy Logic and Expert Systems for Rating and Pricing Firms,” Social Science Research Network, Vol. 33, No. 11, 2007, pp. 77-120. [30] E. Turban, J. E. Aronson and T. P. Liang, “Decision Support Systems and Intelligent Systems,” 7th Edition, Prentice Hall of India, New Delhi, 2007. [31] Y. M. Wang, Y. Luo and Z. Hua, “On the Extent Analysis Method for Fuzzy AHP and its Applications,” European Journal of Operational Research, Vol. 186, 2008, pp. 735-747. Appendix A Here, some useful MATLAB commands to work with the proposed fuzzy in ference system (FIS) which is based on Mamdani are presented: [System] Name='AHP mobile' Type='mamdani' Version=2.0 NumInputs=4 NumOutputs=1 NumRules=15 AndMethod='min' OrMethod='max' ImpMethod='min' AggMethod='max' DefuzzMethod='centroid' |

