J. Biomedical Science and Engineering, 2009, 2, 30-35
Published Online February 2009 in SciRes. http://www.scirp.org/journal/jbise JBiSE
Investigating connectional characteristics of
motor cortex network*
Dong-Mei Hao1, Ming-Ai Li2
1School of Life Science and Bioengineering. 2School of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124,
China. Correspondence should be addressed to Dong-Mei Hao ([e-mail])
Received September 10th, 2008; revised November 12th, 2008; accepted December 11th, 2008
ABSTRACT
To understand the connectivity of cerebral cor-
tex, especially the spatial and temporal pattern
of movement, functional magnetic resonance
imaging (fMRI) during subjects performing finger
key presses was used to extract functional
networks and then investigated their character-
istics. Motor cortex networks were constructed
with activation areas obtained with statistical
analysis as vertexes and correlation coefficients
of fMRI time series as linking strength. The
equivalent non-motor cortex networks were
constructed with certain distance rules. The
graphic and dynamical measures of motor cor-
tex networks and non-motor cortex networks
were calculated, which shows the motor cortex
networks are more compact, having higher sta-
tistical independence and integration than the
non-motor cortex networks. It indicates the
motor cortex networks are more appropriate for
information diffusion.
Keywords: Motor Cortex Network, Connectivity,
Correlation Coefficient, Functional Magnetic
Resonance Imaging (fMRI), Activation Area
1. INTRODUCTION
Neuroanatomical studies have revealed a large number
of connections linking different brain structures. There is
a wealth of information about the patterning and func-
tional impact of connection pathways linking segregated
areas of the cerebral cortex. The brain consists of net-
works of highly interconnected regions, coordinating
major aspects of behaviour. The brain is inherently a
dynamic system, in which the traffic between regions,
during behavior or even at rest, creates and reshapes
continuously complex functional networks of correlated
dynamics [1]. The cerebral motor cortex which is closely
associated with movement is innervated by a number of
anatomical and functional connections.
Over recent years, neurophysiological and neuroi-
maging experiments as well as detailed computer simu-
lations of neuronal networks have contributed to our
understanding of the neural mechanisms generating
functional connectivity. Functional magnetic resonance
imaging (fMRI) is a non-invasive and widely available
technique for mapping brain functions. It is based upon
the blood oxygenation level-dependent (BOLD) effect.
As concerns the motor system, the available functional
imaging studies indicate a mass activation effect within
the hand representation area during finger-tapping or
finger-to-thumb opposition tasks in terms of either a
stepwise or a linear function between movement rate and
hemodynamic response [2].
Some computational approaches such as covariance
structural equation modelling (SEM) aim at inferring
causal relations between brain areas from their pattern of
covariance, by extracting networks of effective connec-
tivity [3]. Dynamic causal modelling (DCM) character-
izes the dynamics of interactions among states of brain
regions with bilinear approximations of intrinsic cou-
pling among neuronal states and the influence of exter-
nal inputs [4]. Granger causality mapping (GCM) ex-
tends the vector autoregressive (VAR) technique to cap-
ture interactions among brain regions, assuming a causal
and dynamic system of linear interactions, driven by
stochastic innovations [5]. A graphical approach linking
the notions of graphical models and Granger causality
has been applied to describe dynamic dependencies in
neural systems [6, 7]. Several principled approaches
such as non-metric multidimensional scaling [8], hierar-
chical analysis [9] and cluster analysis [10] have been
used to derive numerical descriptions of the organization
of the network from neuroanatomical connection data.
Using basic and general concepts from information the-
ory, entropy and mutual information, O. Sporns et al.
have developed a theoretical measure that captures the
interplay of functional segregation and integration within
a given system [11]. A close look at the anatomical and
functional organization of the cerebral cortex provides
important clues for formulating a potential general
mechanism for neural integration.
In this paper we present our current research investi-
gating the connectivity of the motor system, the network
underlying the generation of movement. We propose a
*This work was supported by the National Natural Science Foundation
of China (30670543).
SciRes Copyright © 2009

D. M. Hao et al. / J. Biomedical Science and Engineering 2 (2009) 30-35 31
SciRes Copyright © 2009 JBiSE
method to extract motor networks and non-motor net-
works, as revealed by fMRI when humans perform fin-
ger tasks, and then analyze them in the context of the
current understanding of complex networks.
2. MATERIALS AND METHODS
Considering the multiple processes taking place at dif-
ferent brain regions and interacting with one another in
executing a specific task, extracting brain connectivity
from fMRI data facilitates our understanding of brain
function. The states of activated brain regions are fully
observed as intensity variations of fMRI time-series.
2.1. Data Acquisition
The fMRI data center [12] afforded the fMRI data sub-
mitted by Kathleen Y. Haaland [13]. Fourteen healthy
right-handed volunteers between the ages of 20 and 40
participated in this study. Subjects performed finger key
presses in response to numeric sequences presented
visually on the screen. The index (“1”), middle (“2”),
and ring (“3”) fingers of the right or left hand were
placed on response keys. Two sequence conditions were
used. The simple condition required repetition of one of
three sequences (i.e., 11111, 22222, or 33333) and the
complex condition consisted of heterogeneous sequences
(i.e., 12131, 23231, or 32321). Each 3-sec trial began
with the appearance of a five-digit number sequence
presented vertically on the screen for 2.5 sec, cueing
subjects to immediately perform the sequence as quickly
and accurately as possible. The task paradigm consisted
of ten 12-s epochs alternating between rest and activa-
tion.
Functional MRI was obtained on a 1.5-T General
Electric Signa scanner. Echo-planar (EP) images were
collected using a single-shot, blipped, gradient echo EP
pulse sequence: echo time (TE)=40 msec, data acquisi-
tion time =40 msec, field of view (FOV)=24 cm, resolu-
tion=64×64. Twenty-two contiguous sagittal 6-mm thick
slices provided coverage of the entire brain (voxel size:
3.75×3.75×7mm). Prior to functional imaging, high-
resolution 3-D spoiled gradient-recalled at steady-state
anatomic images were collected: TE =5 msec, repetition
time (TR)=24 msec, 40° flip angle, number of excitations
=1, slice thickness=1.2 mm, FOV=24 cm, resolution=256×
128. Refer to [13] for detail.
2.2. Motor Cortex Network, MCN
fMRI data were analyzed using SPM5 (Welcome De-
partment of Cognitive Neurology, London, UK) and
MATLAB 7 (The Mathworks Inc.) for all subjects. The
first six images of each time series were discarded to
eliminate signal intensity variations arising from pro-
gressive saturation. Echo-planar images were realigned
to the first functional image of each time series to re-
move residual head movement. The functional images of
each subject were coregistered with the mean functional
image from realignment, normalized to MNI (Montreal
Neurological Institute) standard space and spatially
smoothed using a Gaussian filter of 6 mm FWHM. First
level analysis of each individual was conducted;
one-tailed Student t-tests were used to identify brain
regions most responsive for finger key presses. The
maximum intensity projection of the statistical map and
coordinates in MNI space for each maximum were ob-
tained.
We define the maximum intensity voxels (activation
areas) as vertexes of a motor cortex network (MCN).
The activity of voxel x at time t is denoted as V(x, t)
after fMRI pre-processing. We calculate the linear cor-
relation coefficient between any pair of voxels, x1 and x2
as formula (1), where 222 ),(),())(( 〉〈−〉〈= txVtxVxV σ ,
〈
•〉
represents temporal averages. The correlation coefficient
is used as the connection strength or weight between
these two nodes. Therefore MCN is constructed with
motor association cortices as vertexes and their correla-
tion coefficients as linking weights.
))(())((
),(),(),(),(
),(
21
2121
21 xVxV
txVtxVtxVtxV
xxr
σσ
〉〈〉〈−〉〈
= (1)
2.3. Non-motor Cortex Network, Non-MCN
The equivalent non-motor cortex network composes of k
vertexes which were generated randomly in the spatial
coordinates range of cerebral cortex and were far away
from (greater than threshold) any vertex in MCN. Sup-
pose (xn, yn, zn) is a voxel coordinates in non-motor cor-
tex and (xmi , ymi, zmi) is the i voxel coordinates in motor
cortex. For all i (i=1…k), it satisfies the following con-
dition :
thredzzyyxx minminmin >−+−+− 222 )()()( (2)
Therefore non-MCN was constructed with k voxels as
nodes and the correlation coefficients among them ac-
cording to formula (1) as connection strength.
2.4. Measures of the Brain Functional Network
Structural aspects are captured using concepts and
measures provided by graph theory. All structural analy-
ses are performed on the network’s connection matrix,
which provides a complete description of all connections
and pathways between the network’s individual units.
Functional connectivity which is the temporal correla-
tion between remote neurophysiological events can be
reflected by information theory.
z Density [14]
Density is defined as the sum of the ties divided by
the number of possible ties (i.e. the ratio of all tie
strength that is actually present to the number of possible
ties). The density of a network may give us insights into
such phenomena as the speed at which information dif-
fuses among the nodes, and the extent to which nodes
have high levels of communicating capital and /or com-
municating constraint.
z Characteristic path length: lpath
lpath is the global mean of the lengths of the shortest
path linking any pairs of nodes, and can be used to de-
scribe the connectivity of a network.

32 D. M. Hao et al. / J. Biomedical Science and Engineering 2 (2009) 30-35
SciRes Copyright © 2009 JBiSE
z System entropy [11]
The cerebral cortex networks are implemented as dy-
namical system. The neural activities can be described as
a Gaussian multidimensional stationary stochastic proc-
ess. The network units interact with each other and devi-
ate from statistical independence through connections.
The entropy H(X) of a system measures its overall de-
gree of independence. Assuming stationarity, the entropy
of a system X composed of n units is computed as for-
mula (3) with⋅indicating the matrix determinant. COV
is the covariance matrix of the system and can be ob-
tained analytically from the connection matrix
))()2ln((5.0)( XCOVeXH n π = (3)
z Integration I(X) [11]
The integration I(X) measures the overall degree to
which a system deviates from statistical independence.
This measure is derived as the difference between entro-
pies of the individual components of X, considered in-
dependently, and the entropy H(X) of the entire system:
)()()(
1
XHxHXI
n
i
i−= ∑
=
(4)
3. RESULTS
We analyzed the fMRI data of 14 subjects with finger
key presses task. 4 subjects had only one activation area
in the simple condition, 3 subjects had none or only one
activation area in the complex condition. Therefore we
only studied the other 10 subjects in the simple condition
and 11 subjects in the complex condition, and con-
structed a MCN and 50 non-MCNs for each of
them.Figure 1 is an example of SPM showing bilateral
activation of motor cortex of subject 5, in which (a) is
the left hand simple condition and (b) is the left hand
complex condition. It lists all clusters above the chosen
level of significance with details of significance thresh-
olds. Figure 2 shows the motor cortex networks (MCNs)
of the same subject in left hand simple and complex
conditions. A vertex indicates an activation area, a line
indicates a bidirectional connection, and the thicker a
line is, the stronger a connection is. Figure 3 shows the
non-motor cortex networks (non-MCNs) of the left hand
simple and complex conditions for subject 5. A vertex
representing a non-activation area is at least 15mm apart
from the activation area according to experience [15],
and a thicker line also indicates a stronger connection. In
Figure 2 (a) vertex 1, 3, 9, 10 locate in BA10 (Brodmann
Area), vertex 2 in BA6, vertex 4 in BA10, vertex 5, 8 in
BA32, vertex 6, 7 in BA47, vertex 11 in BA7, vertex 12
in BA11, vertex 13 in BA22, vertex 14 in BA18; (b)
vertex 1, 2 locate in BA8, vertex 3, 8 in BA47, vertex 4
in BA11, vertex 6 in BA10, vertex 7 in BA9, vertex 10
in BA46, vertex14 in BA31 using Talairach Client 2.4
(Research Imaging Center, University of Texas Health
Science Center at San Antonio) [16]. We calculated the
average characteristic parameters of 50 non-MCNs and
compared them with the corresponding MCNs for each
subject in the simple and complex conditions, see Figure
4 and Figure 5, in which “*” indicates a MCN and “º”
indicates a non-MCN. We noticed the density (p=0.000),
(a) left hand simple condition (b) left hand complex condition
Figure 1. SPM showing activation of motor cortex
SPMmip [0,0,0]
SPMmip [-26.25,33.75,60]
\
s05_epi_r01_LS
H eigh t thr es ho ldT=4.996301 {P<0.05(FWE)}
Ex ten t thr es ho ld k=0 v ox els
\
s05_epi_r01_LS
Height threshold T=4.920125 {P<0.05(FWE)}
Extent threshold k=0 v oxels
Table shows 3 local maxima more than 8.0mm apart
Height threshold: T = 5
.
00, p = 0.000 (0.050) {p<0.05 (FWE)}
Extent threshold: k = 0 voxels, p = 1.000 (0.050)
Expected voxels per cluster, <k> = 0.381
Expected number of clusters, <c> = 0.13
Expected false discovery rate, <= 0.00
Degrees of freedom = [1.0, 55.0]
FWHM = 10.8 10.0 10.7 mm mm mm; 2.9 2.7 1.8 {voxels};
Volume: 1344516; 15935 voxels; 982.5 resels
Voxel size: 3.8 3.8 6.0 mm mm mm; (resel = 13.65 voxels)
Page 1
Table shows 3 local maxima more than 8.0mm apart
Height threshold: T = 4.92, p = 0.000 (0.050) {p<0.05 (FWE)}
Extent threshold: k = 0 voxels, p = 1.000 (0.050)
Expected voxels per cluster, <k> = 0.409
Expected number of clusters, <c> = 0.12
Expected false discovery rate, <= 0.00
Degrees of freedom = [1.0, 55.0]
FWHM = 10.6 10.2 10.9 mm mm mm; 2.8 2.7 1.8 {voxels};
Volume: 1025747; 12157 voxels; 717.6 resels
Voxel size: 3.8 3.8 6.0 mm mm mm; (resel = 14.00 voxels)

D. M. Hao et al. / J. Biomedical Science and Engineering 2 (2009) 30-35 33
SciRes Copyright © 2009 JBiSE
(a) left hand simple condition (b) left hand complex condition
Figure 2. Cerebral motor cortex networks
(a) left hand simple condition (b) left hand complex condition
Figure 3. Cerebral non-motor cortex networks
characteristic path length (p=0.000), system entropy
(p=0.000) and integration (p< MCNs are all significant
different from those of non-MCNs regardless of the sim-
ple or complex condition. In Figure 6, we compared
some features of MCNs in the simple and complex condi-
tion. “*” indicates a MCN in the simple condition and “º”
indicates a MCN in the complex condition. The density
(p=0.668), characteristic path length (p=0.728), system
entropy (p=0.411) and integration (p=0.243) in the simple
condition have no significant difference from those in the
complex condition.
3. DISCUSSION
As shown in Figure 2 and Figure 3, MCNs have denser
and stronger connections than non-MCNs. In Figure 4 and
Figure 5, the density of MCNs are much larger than that of
non-MCNs and the characteristic path length of MCNs are
much shorter than that of non-MCNs. It indicates the infor-
mation such as motor strategy, spatial-temporal arrangement
and sensorimotor message can diffuse among motor regions
with high speed and high level. The entropy and integration
of MCNs are larger than those of non-MCNs, which indi-
cate MCNs have higher overall degree of statistical inde-
pendence than non-MCNs and at the same time there are
more statistical dependencies among the motor regions. We
can deduce that in our experiment, the simple task and the
complex task are at the same cognitive level and therefore
have similar functional connectivity patterns for healthy
subjects. It is different from other studies [17] in which
complex movement increases activity in regions and in-
volvement of areas. Therefore how to define complexity in
an experiment context is to be considered.
Movement is an essential part of our daily life activi-
ties and the movement handicapped cannot lead produc-
tive independent lives due to inability to control their
activities of daily living. We attempt to understand the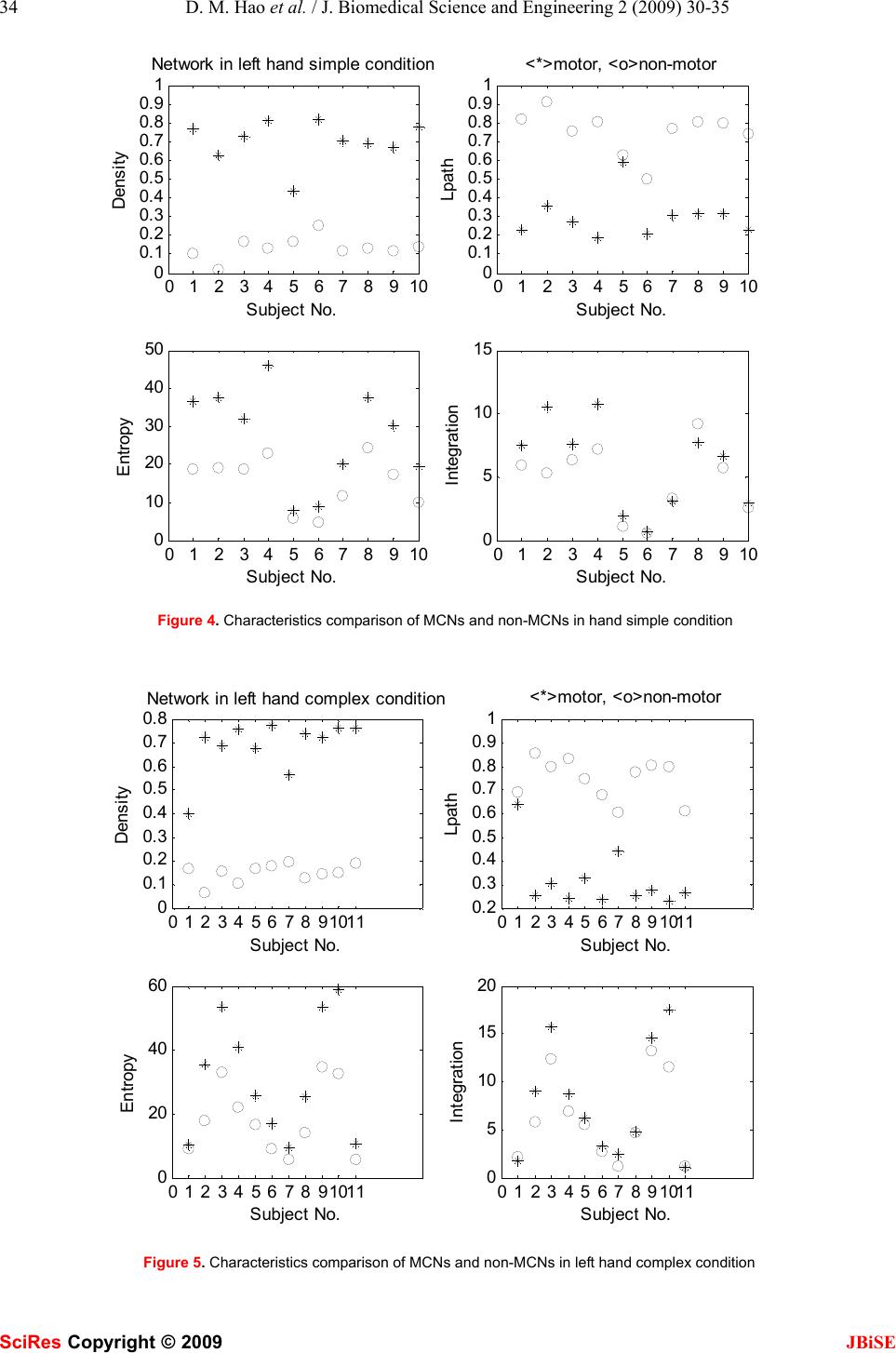

34 D. M. Hao et al. / J. Biomedical Science and Engineering 2 (2009) 30-35
SciRes Copyright © 2009 JBiSE
01 234 567 8910
0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
Densi ty
Subject No.
Network in left hand simple condition
01 23 456 78 910
0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
Lpath
Subject No.
<*>motor, <o>non-motor
01 234 567 8910
0
10
20
30
40
50
Entropy
Subject No.
01 23 456 78 910
0
5
10
15
Integration
Subject No.
Figure 4. Characteristics comparison of MCNs and non-MCNs in hand simple condition
0 123 45 67891011
0
0. 1
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
Dens it y
Subject No.
Network in left hand complex condition
0 1234 56 7891011
0. 2
0. 3
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
Lpath
Subject No.
<*>motor, <o>non-motor
0 123 45 67891011
0
20
40
60
E ntropy
Subject No.
0 1234 56 7891011
0
5
10
15
20
Integration
Subject No.
Figure 5. Characteristics comparison of MCNs and non-MCNs in left hand complex condition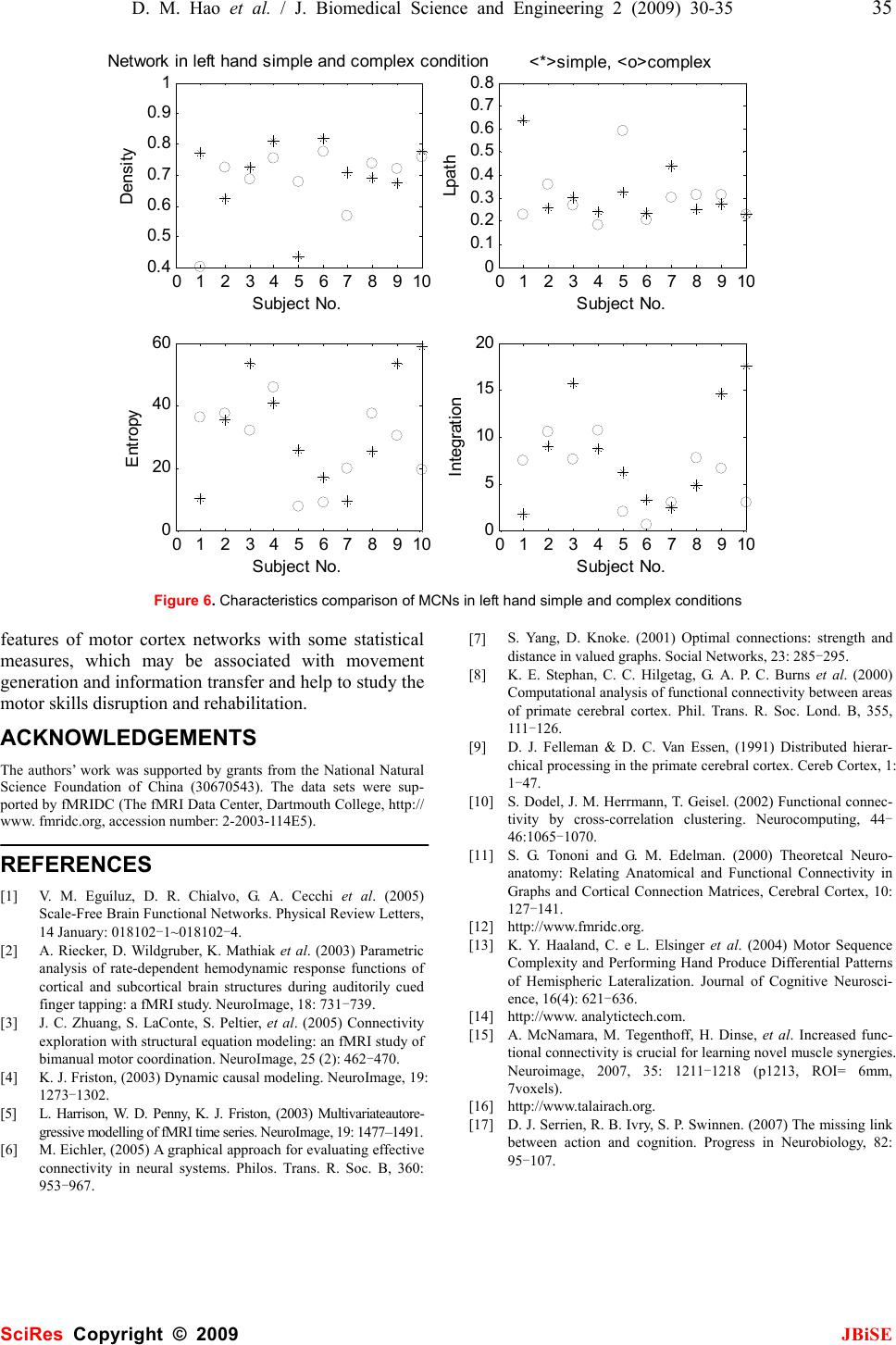

D. M. Hao et al. / J. Biomedical Science and Engineering 2 (2009) 30-35 35
SciRes Copyright © 2009 JBiSE
012345678910
0. 4
0. 5
0. 6
0. 7
0. 8
0. 9
1
Density
Subject No.
Network in left hand simple and complex condition
0123 45678910
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Lpath
Subject No.
<*>simple, <o>complex
012345678910
0
20
40
60
Entropy
Subject No.
0123 45678910
0
5
10
15
20
Integration
Subject No.
Figure 6. Characteristics comparison of MCNs in left hand simple and complex conditions
features of motor cortex networks with some statistical
measures, which may be associated with movement
generation and information transfer and help to study the
motor skills disruption and rehabilitation.
ACKNOWLEDGEMENTS
The authors’ work was supported by grants from the National Natural
Science Foundation of China (30670543). The data sets were sup-
ported by fMRIDC (The fMRI Data Center, Dartmouth College, http://
www. fmridc.org, accession number: 2-2003-114E5).
REFERENCES
[1] V. M. Eguíluz, D. R. Chialvo, G. A. Cecchi et al. (2005)
Scale-Free Brain Functional Networks. Physical Review Letters,
14 January: 018102-1~018102-4.
[2] A. Riecker, D. Wildgruber, K. Mathiak et al. (2003) Parametric
analysis of rate-dependent hemodynamic response functions of
cortical and subcortical brain structures during auditorily cued
finger tapping: a fMRI study. NeuroImage, 18: 731-739.
[3] J. C. Zhuang, S. LaConte, S. Peltier, et al. (2005) Connectivity
exploration with structural equation modeling: an fMRI study of
bimanual motor coordination. NeuroImage, 25 (2): 462-470.
[4] K. J. Friston, (2003) Dynamic causal modeling. NeuroImage, 19:
1273-1302.
[5] L. Harrison, W. D. Penny, K. J. Friston, (2003) Multivariateautore-
gressive modelling of fMRI time series. NeuroImage, 19: 1477–1491.
[6] M. Eichler, (2005) A graphical approach for evaluating effective
connectivity in neural systems. Philos. Trans. R. Soc. B, 360:
953-967.
[7] S. Yang, D. Knoke. (2001) Optimal connections: strength and
distance in valued graphs. Social Networks, 23: 285-295.
[8] K. E. Stephan, C. C. Hilgetag, G. A. P. C. Burns et al. (2000)
Computational analysis of functional connectivity between areas
of primate cerebral cortex. Phil. Trans. R. Soc. Lond. B, 355,
111-126.
[9] D. J. Felleman & D. C. Van Essen, (1991) Distributed hierar-
chical processing in the primate cerebral cortex. Cereb Cortex, 1:
1-47.
[10] S. Dodel, J. M. Herrmann, T. Geisel. (2002) Functional connec-
tivity by cross-correlation clustering. Neurocomputing, 44-
46:1065-1070.
[11] S. G. Tononi and G. M. Edelman. (2000) Theoretcal Neuro-
anatomy: Relating Anatomical and Functional Connectivity in
Graphs and Cortical Connection Matrices, Cerebral Cortex, 10:
127-141.
[12] http://www.fmridc.org.
[13] K. Y. Haaland, C. e L. Elsinger et al. (2004) Motor Sequence
Complexity and Performing Hand Produce Differential Patterns
of Hemispheric Lateralization. Journal of Cognitive Neurosci-
ence, 16(4): 621-636.
[14] http://www. analytictech.com.
[15] A. McNamara, M. Tegenthoff, H. Dinse, et al. Increased func-
tional connectivity is crucial for learning novel muscle synergies.
Neuroimage, 2007, 35: 1211-1218 (p1213, ROI= 6mm,
7voxels).
[16] http://www.talairach.org.
[17] D. J. Serrien, R. B. Ivry, S. P. Swinnen. (2007) The missing link
between action and cognition. Progress in Neurobiology, 82:
95-107.