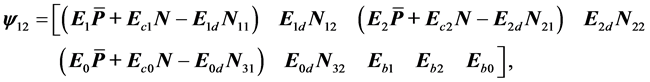Circuits and Systems
Vol.07 No.11(2016), Article ID:70543,25 pages
10.4236/cs.2016.711308
Delay-Dependent Robust H¥ Control for Uncertain 2-D Discrete State Delay Systems Described by the General Model
Arun Kumar Singh, Akshata Tandon, Amit Dhawan
Department of Electronics and Communication Engineering, Motilal Nehru National Institute of Technology, Allahabad, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 8, 2016; Accepted: May 24, 2016; Published: September 13, 2016
ABSTRACT
This paper considers the problem of delay-dependent robust optimal H¥ control for a class of uncertain two-dimensional (2-D) discrete state delay systems described by the general model (GM). The parameter uncertainties are assumed to be norm- bounded. A linear matrix inequality (LMI)-based sufficient condition for the existence of delay-dependent g-suboptimal state feedback robust H¥ controllers which guarantees not only the asymptotic stability of the closed-loop system, but also the H¥ noise attenuation g over all admissible parameter uncertainties is established. Furthermore, a convex optimization problem is formulated to design a delay-de- pendent state feedback robust optimal H¥ controller which minimizes the H¥ noise attenuation g of the closed-loop system. Finally, an illustrative example is provided to demonstrate the effectiveness of the proposed method.
Keywords:
2-D Discrete System, General Model, H¥ Control, Linear Matrix Inequality, State Delays, Uncertain System

1. Introduction
In the past decades, research on two-dimensional (2-D) discrete systems has rapidly increased due to their extensive practical applications in circuits analysis [1] , digital image processing [2] , signal filtering [3] and thermal power engineering [4] , etc. Thus, the study of 2-D systems is an attractive problem and a number of results have been presented in the literature. Among these results the stability analysis of 2-D discrete systems has been given in [5] - [15] . In [5] , the problem of robust stability analysis and stabilization for 2-D discrete uncertain systems described by the Fornasini-Marchesini (FM) second model has been studied and the sufficient conditions for 2-D discrete uncertain systems to be robustly stable have been given in terms of linear matrix inequalities (LMIs). A necessary and sufficient condition for the stability of 2-D discrete systems described by the FM first model has been derived in [13] . The problem of stability for linear discrete 2-D singular general model (GM) has been discussed in [14] and a sufficient condition for the internal stability of the 2-D singular GM has been derived in terms of LMIs. In [15] , the robust stability analysis problem for a class of uncertain 2-D discrete systems described by the FM second model has been studied and sufficient conditions in terms of LMIs have been derived to ensure the robust stability of the uncertain 2-D discrete systems. Lately, the solution to the guaranteed cost control problem for 2-D discrete uncertain systems has been presented by many authors [16] - [22] .
In recent years, the H¥ control problem for 2-D discrete systems has gained a great deal of interest and many important results have been obtained [23] - [26] . A major advantage of H¥ control is that its performance specification takes account of the worst- case performance for system in terms of the system energy gain. This is appropriate for system robustness analysis and robust control with modeling uncertainties and disturbances than other performance specifications, such as the LQ-optimal control specification [23] . In [24] , the solutions for the H¥ control and robust stabilization problems for 2-D systems described by the Roesser model using the 2-D system bounded realness property have been presented. The problem of H¥ static output feedback control for 2-D discrete systems described by the Roesser model and the FM second model has been addressed in [25] . In [26] , the problem of robust H¥ control for uncertain 2-D discrete systems described by the GM via output feedback controllers has been investigated.
Since, delay is encountered in many dynamic systems and is often a source of instability, much attention has been focused on the problem of stability analysis and controller design for 2-D discrete state-delayed systems in the last decades. Presently, the stability results for 2-D discrete state-delayed systems fall in two groups: delay-inde- pendent stability conditions [27] - [35] and delay-dependent ones [36] - [45] . The former refers to the stability conditions which do not depend on delay; the latter contains information on the size of delay. Generally speaking, the delay-dependent stability condition is less conservative especially when the sizes of the delays are small [45] . The problem of stability analysis for 2-D discrete state-delayed systems in the GM has been considered in [33] and sufficient condition for the stability has been derived via Lyapunov approach. In [27] , a solution to the problem of delay-independent H¥ control for 2-D state-delayed systems described by the FM second model has been presented. The problem of robust reliable control for a class of uncertain 2-D discrete switched systems with state delays and actuator faults represented by a model of Roesser type has been studied by [28] . In [35] , the problem of robust guaranteed cost control via memoryless state feedback for uncertain 2-D discrete state-delayed systems described by the FM second model has been considered. Several technical errors that have occurred in the main results of [35] were corrected in [30] . A solution to the guaranteed cost control problem via memory state feedback control laws for a class of uncertain 2-D discrete state-delayed systems described by the FM second model has been presented in [31] . The problem of delay?dependent guaranteed cost control via memoryless state feedback for uncertain 2-D discrete state-delayed systems described by the FM second model has been studied in [43] . In [41] , a delay-range dependent H¥ control and stabilization problem for a class of uncertain 2-D state-delayed systems described by the Roesser model has been proposed. The delay-dependent H¥ control problem via a delay-dependent bounded real lemma for a class of 2-D state-delayed systems described by the FM second model has been addressed in [40] . Recently, the problems of delay- dependent H¥ control for 2-D discrete state-delayed systems described by the FM second model and Roesser model have been considered in [42] [44] , respectively and a delay-dependent optimal state feedback H¥ controller has been obtained for both the models. It may be mentioned here that the criteria presented in [42] [44] do not consider the uncertainty in system parameters. In real-time applications, the parametric uncertainties cannot be ignored as they are the main source of instability and poor system performance. Hence, the delay-dependent robust optimal H¥ control for uncertain 2-D discrete state delay systems is an important and challenging problem. However to the best of authors’ knowledge, the delay-dependent robust optimal H¥ control problem for uncertain 2-D discrete state delay systems represented by the GM which is structurally distinct from FM second model and Roesser model has not been addressed so far in the literature.
This paper, therefore, investigates the problem of delay-dependent robust optimal H¥ control for a class of uncertain 2-D discrete state delay systems described by the GM. The approach adopted in this paper is as follows: We first derive an LMI-based sufficient condition for the existence of delay-dependent g-suboptimal state feedback robust H¥ controllers in terms of feasible solution to a certain LMI. Further, a convex optimization problem with LMI constraints is formulated to design a delay-dependent robust optimal H¥ controller which minimizes the H¥ noise attenuation g of the closed-loop system. The paper is organized as follows. Section 2 formulates the problem of delay- dependent robust H¥ control for a class of uncertain 2-D discrete state delay systems described by the GM and recalls some useful results. In Section 3, a solution to the problem of delay-dependent robust optimal H¥ control is presented. An example illustrating the potential of the proposed technique is given in Section 4.
Notations:
Throughout the paper, the following notations are used: Rn denotes real vector space of dimension n; 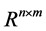 is the set of n ´ m real matrices; the superscript T stands for matrix transposition; 0 denotes null matrix or null vector of appropriate dimension; I is the identity matrix of appropriate dimension; G < 0 stands for the matrix G which is symmetric and negative definite; diag{….} stands for a block diagonal matrix;
is the set of n ´ m real matrices; the superscript T stands for matrix transposition; 0 denotes null matrix or null vector of appropriate dimension; I is the identity matrix of appropriate dimension; G < 0 stands for the matrix G which is symmetric and negative definite; diag{….} stands for a block diagonal matrix;  denotes the Euclidean vector norm. The
denotes the Euclidean vector norm. The 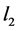 norm of a 2-D signal
norm of a 2-D signal 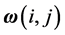 is given by
is given by
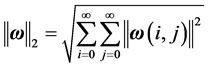 , where
, where 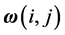 is said to be in
is said to be in  if
if .
.
2. Problem Formulation and Preliminaries
Consider an uncertain 2-D discrete state delay system described by the GM [46] .
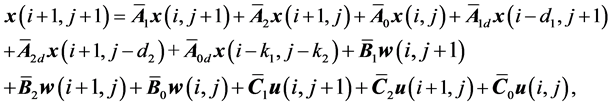 (1a)
(1a)
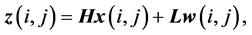 (1b)
(1b)
where
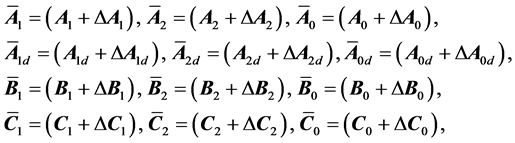 (1c)
(1c)
and 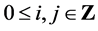 are horizontal and vertical coordinates, respectively,
are horizontal and vertical coordinates, respectively, 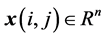 ,
, 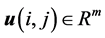 are state and control input, respectively,
are state and control input, respectively, 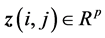 is the controlled output,
is the controlled output, 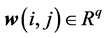 is the noise input with bounded energy i.e., it belongs to
is the noise input with bounded energy i.e., it belongs to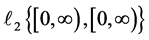 . The matrices
. The matrices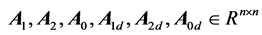 ,
, 




















where






For system (1), suppose a finite set of initial conditions [33] , i.e., there exist positive integers 


Denote 
Definition 1. [42] The system (1) is asymptotically stable if 


Introduce the following state feedback controller

Applying the controller (3) to system (1) will result in the closed-loop system:

where



T o investigate the delay-dependent 


The following well known lemmas are needed in the proof of our main result.
Lemma 1. [42] [44] For any matrices 



where
Lemma 2. [5] Let

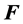




holds for all 



The 
Definition 2. [42] Given a scalar















where
and



In the case when the initial condition is known to be zero, then the 

Using the 2-D Parseval’s theorem [3] , (9) is equivalent to

where 

is the transfer function from the disturbance input 

The objective of this paper is to design a controller of the form (3) such that the closed-loop system (4) is asymptotically stable and the 











3. Main Results
In this section, we first present a delay-dependent approach to solve the 











Theorem 1. The closed-loop system (4), formed by system (1) with the initial condition (2) and state-feedback controller (3), is robustly stable and has a specified 









where












Proof. To prove that the closed-loop system (4) with 

where
and






Along any trajectory of the system (1) with


Applying (5), we get

Now applying Lemma 1, we get the following summation inequalities


and

where
Now, substituting (15)-(18) in (14) yields


Applying Schur complement, it follows from matrix inequality (12) that

Thus, from (19b), it implies that

holds for any delays







Hence, the closed-loop system (4) with 
Next, we establish the 
We consider

where
It follows from inequality (12) that

Summing the inequality (22) over 

Now,


Thus, by using (25) in (23), we get

Since, 







In the following, we will show that the above derived sufficient condition for existence of delay-dependent robust 
Theorem 2. Consider the closed-loop system (4) with the initial condition (2). Given scalars









where







then the closed-loop system (4) with






Proof. It follows from matrix inequality (12) that





Pre-multiplying and post-multiplying both sides of matrix inequality (12) by
and its transpose, respectively, we get

Denoting













where
Using (1d) and (1e), (30) can be expressed as

where


Therefore, using Lemma 2, (31) can be rearranged as

The equivalence of (32) and (27) follows trivially from Schur complements. This completes the proof of Theorem 2.
Theorem 2 provides a parameterized representation of a set of g-suboptimal robust 


which ensures the minimization of 

4. An Illustrative Example
In this section, we present an application example to demonstrate the effectiveness of our proposed result.
Example 1. In this example, we shall illustrate the applicability of Theorem 2 to the control of thermal process in heat exchanger [4] [47] which can be expressed by the partial differential equation with time and space delays:

where 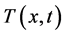













(34) can be expressed in the following form:

where




It is assumed that the surface of the heat exchanger is insulated and the heat flow through it is in steady state condition, then we could take the boundary conditions as


Denote

Next, consider the problem of delay-dependent 













To consider the problem of 

It is also assumed that the above system is subjected to the parameter uncertainties of the form (1c) and (1d) with

Using the MATLAB LMI toolbox [48] [49] , it is found that the optimization problem (33) is feasible for the present example and the optimal solution is given by

and a delay-dependent optimal 

When








5. Conclusion
A solution to delay-dependent robust optimal 


Figure 1. The frequency response
Acknowledgements
The Authors would like to thank the editor and the reviewers for their constructive comments and suggestions.
Cite this paper
Singh, A.K., Tandon, A. and Dhawan, A. (2016) Delay-De- pendent Robust H¥ Control for Uncertain 2-D Discrete State Delay Systems Described by the General Model. Circuits and Systems, 7, 3645-3669. http://dx.doi.org/10.4236/cs.2016.711308
References
- 1. Roesser, R.P. (1975) A Discrete State-Space Model for Linear Image Processing. IEEE Transactions Automatic Control, 20, 1-10.
http://dx.doi.org/10.1109/TAC.1975.1100844 - 2. Bracewell, R.N. (1995) Two-Dimensional Imaging, Signal Processing Series, Prentice-Hall, Englewood Cliffs.
- 3. Lu, W.S. and Antoniou, A. (1992) Two-Dimensional Digital Filters (Electrical Engineering and Electronics). Vol. 80, Marcel Dekker, New York.
- 4. Kaczorek, T. (1985) Two-Dimensional Linear Systems. Vol. 68 of Lecture Notes in Control and Information Sciences, Springer, Berlin.
- 5. Du, C. and Xie, L. (1999) Stability Analysis and Stabilization of Uncertain Two-Dimen- sional Discrete Systems: An LMI Approach. IEEE Transaction Circuits System I, 46, 1371- 1374. http://dx.doi.org/10.1109/81.802835
- 6. Dumistrescu, B. (2008) LMI Stability Tests for the Fornasini-Marchesini Model. IEEE Transactions on Signal Processing, 56, 4091-4095.
http://dx.doi.org/10.1109/TSP.2008.921768 - 7. Hu, G.D. and Liu, M. (2005) Simple Criteria for Stability of Two-Dimensional Linear Systems. IEEE Transactions on Signal Processing, 53, 4720-4723.
http://dx.doi.org/10.1109/TSP.2005.859265 - 8. Kar, H. (2008) Comments on New LMI Condition for the Nonexistence of Overflow Oscillations in 2-D State Space Digital Filters Using Saturation Arithmetic. Digital Signal Processing, 18, 148-150. http://dx.doi.org/10.1016/j.dsp.2007.02.001
- 9. Liu, T. (2008) Stability Analysis of Linear 2-D Systems. Signal Processing, 88, 2078-2084.
http://dx.doi.org/10.1016/j.sigpro.2008.02.007 - 10. Ooba, T. (2000) On Stability Analysis of 2-D Systems Based on 2-D Lyapunov Matrix Inequalities. IEEE Transactions on Circuits and Systems I, 47, 1263-1265.
http://dx.doi.org/10.1109/81.873883 - 11. Singh, V. (2007) New LMI Condition for the Nonexistence of Overflow Oscillations in 2-D State-Space Digital Filters Using Saturation Arithmetic. Digital Signal Processing, 17, 345- 352.
http://dx.doi.org/10.1016/j.dsp.2006.01.003 - 12. Thamvichai, R. and Bose, T. (2002) Stability of 2-D Periodically Shift Variant Filters. IEEE Transactions on Circuits and Systems II, 49, 61-64. http://dx.doi.org/10.1109/82.996060
- 13. Zhou, T. (2006) Stability and Stability Margin for a Two-Dimensional System. IEEE Transactions on Signal Processing, 54, 3483-3488.
http://dx.doi.org/10.1109/TSP.2006.879300 - 14. Zou, Y., Xu, H. and Wang, W. (2008) Stability for Two-Dimensional Singular Discrete Systems Described by General Model. Multidimensional Systems and Signal Processing, 19, 219-229.
http://dx.doi.org/10.1007/s11045-007-0027-y - 15. Wang, Z. and Liu, X. (2003) Robust Stability of Two-Dimensional Uncertain Discrete Systems. IEEE Signal Processing Letters, 10, 133-136.
http://dx.doi.org/10.1109/LSP.2003.810754 - 16. Dhawan, A. and Kar, H. (2007) LMI-Based Criterion for the Robust Guaranteed Cost Control for 2-D Systems Described by the Fornasini-Marchesini Second Model. Signal Processing, 87, 479-488.
http://dx.doi.org/10.1016/j.sigpro.2006.06.002 - 17. Dhawan, A. and Kar, H. (2007) Comment on Robust Optimal Guaranteed Cost Control for 2-D Discrete Systems. IET Control Theory and Application, 1, 1188-1190.
http://dx.doi.org/10.1049/iet-cta:20060327 - 18. Dhawan, A. and Kar, H. (2007) Optimal Guaranteed Cost Control for 2-D Discrete Uncertain Systems: An LMI Approach. Signal Processing, 87, 3075-3085.
http://dx.doi.org/10.1016/j.sigpro.2007.06.001 - 19. Dhawan, A. and Kar, H. (2010) An LMI Approach to Robust Optimal Guaranteed Cost Control of 2-D Discrete Systems Described by the Roesser Model. Signal Processing, 90, 2648-2654.
http://dx.doi.org/10.1016/j.sigpro.2010.03.008 - 20. Dhawan, A. and Kar, H. (2011) An improved LMI-Based Criterion for the Design of Optimal Guaranteed Cost Controller for 2-D Discrete Uncertain Systems. Signal Processing, 91, 1032-1035.
http://dx.doi.org/10.1016/j.sigpro.2010.07.014 - 21. Guan, X., Long, C. and Duan, G. (2001) Robust Optimal Guaranteed Cost Control for 2-D Discrete Systems. IEE Proceedings—Control Theory and Applications, 148, 335-361.
http://dx.doi.org/10.1049/ip-cta:20010596 - 22. Xu, J., Yu, L. and Teng, Y. (2010) Guaranteed Cost Control for Uncertain 2-D Discrete Systems with State Delay in the Roesser Model. Intelligent Control and Information Processing (ICICIP), Dalian, 13-15 August 2010, 680-685.
http://dx.doi.org/10.1109/icicip.2010.5565315 - 23. Xu, J. and Yu, L. (2006) H∞ Control for 2-D Discrete State Delayed Systems. International Journal of Control, Automation, and Systems, 4, 516-523.
- 24. Peng, D., Guan, X. and Long, C. (2008) Delay-Dependent H∞ Control for 2-D State-De- layed Systems. Proceedings of the 17th world congress on the International Federation of Automatic Control, Seoul, 6-11 July 2008, 6004-6009.
- 25. Wang, L.-M., Yu, J.-X., Shi, J. and Gao, F.-R. (2015) Delay-Range Dependent H∞ Control for Uncertain 2-D Delayed Systems. Numerical Algebra Control and Optimization, 5, 11- 23.
http://dx.doi.org/10.3934/naco.2015.5.11 - 26. Xu, J. and Yu, L. (2009) Delay-Dependent H∞ Control for 2-D Discrete State Delay Systems in the Second FM Model. Multidimensional Systems and Signal Processing, 20, 333-349.
http://dx.doi.org/10.1007/s11045-008-0074-z - 27. Xu, J. and Yu, L. (2009) Delay-Dependent Guaranteed Cost Control for Uncertain 2-D Discrete Systems with State Delay in the FM Second Model. Journal of the Franklin Institute, 346, 159-174.
http://dx.doi.org/10.1016/j.jfranklin.2008.08.003 - 28. Xu, J., Nan, Y., Zhang, G., Ou, L. and Ni, H. (2013) Delay-Dependent H∞ Control for Uncertain 2-D Discrete Systems with State-Delay in the Roesser Model. Circuits System & Signal Processing, 32, 1097-1112.
http://dx.doi.org/10.1007/s00034-012-9507-x - 29. Yao, J., Wang, W. and Zou, Y. (2013) The Delay-Range-Dependent Robust Stability Analysis for 2-D State-Delayed Systems with Uncertainty. Multidimensional Systems and Signal Processing, 24, 87-103.
http://dx.doi.org/10.1007/s11045-011-0156-1 - 30. Kurek, J.E. (1985) The General State-Space Model for a Two-Dimensional Linear Digital System. IEEE Transactions on Automatic Control, 30, 1675-1676.
http://dx.doi.org/10.1109/TAC.1985.1103998 - 31. Tandon, A. and Dhawan, A. (2015) Non-Fragile Robust Optimal Guaranteed Cost Control of Uncertain 2-D Discrete State-Delayed Systems. International Journal of Systems Science, 47, 3303-3319.
http://dx.doi.org/10.1080/00207721.2015.1122846 - 32. Boyd, S., Ghaoui, L.E.I., Feron, E. and Balakrishnan, V. (1994) Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970777 - 33. Gahinet, P., Nemirovski, A., Laub, A.J. and Chilali, M. (1995) LMI Toolbox for Use with MATLAB. The Math Works Inc., Natick.
- 34. Paszke, W., Lam, J., Galkowski, K., Xu, S. and Kummert, A. (2006) Delay-Dependent Stability Condition for Uncertain Linear 2-D State-Delayed Systems. 45th IEEE Conference on Decision and Control, San Diego, 13-15 December 2006, 2783-2788.
http://dx.doi.org/10.1109/CDC.2006.377239 - 35. Paszke, W., Lam, J., Galkowski, K., Xu, S. and Kummert, A. (2006) Delay-Dependent Stability of 2D State-Delayed Linear Systems. IEEE International Symposium on Circuits and Systems, Kos, 21-24 May 2006, 2813-2816.
- 36. Feng, Z., Xu, L., Wu, M. and He, Y. (2010) Delay-Dependent Robust Stability and Stabilization of Uncertain Two-Dimensional Discrete Systems with Time-Varying Delays. IET Control Theory and Applications, 10, 1959-1971.
http://dx.doi.org/10.1049/iet-cta.2009.0284 - 37. Chen, S.F. and Fong, I.K. (2007) Delay-Dependent Robust H∞ Filtering for Uncertain 2-D State-Delayed Systems. Signal Processing, 87, 2659-2672.
http://dx.doi.org/10.1016/j.sigpro.2007.04.015 - 38. Ye, S., Wang, W. and Zou, Y. (2009) Robust Guaranteed Cost Control for a Class of Two-Dimensional Discrete Systems with Shift Delays. Multidimensional Systems and Signal Processing, 20, 297-307.
http://dx.doi.org/10.1007/s11045-008-0063-2 - 39. Xu, H., Xu, S. and Lam, J. (2008) Positive Real Control for 2-D Discrete Delayed Systems via Output Feedback Controllers. Journal of Computational and Applied Mathematics, 216, 87-97.
http://dx.doi.org/10.1016/j.cam.2007.04.014 - 40. Xu, H., Guo, L., Zou, Y. and Xu, S. (2007) Stability Analysis for Two-Dimensional Discrete Delayed Systems Described by General Models. IEEE International Conference on Control and Automation, Guangzhou, 30 May-1 June, 924-945.
- 41. Wu, L., Wang, Z., Gao, H. and Wang, C. (2007) H∞ Filtering for Uncertain 2-D Discrete Systems with State Delays. Signal Processing, 87, 2213-2230.
http://dx.doi.org/10.1016/j.sigpro.2007.03.002 - 42. Tiwari, M. and Dhawan, A. (2012b) An LMI Approach to Optimal Guaranteed Cost Control of Uncertain 2-D Discrete Shift-Delayed Systems via Memory State Feedback. Circuits, Systems and Signal Processing, 31, 1745-1764.
http://dx.doi.org/10.1007/s00034-012-9410-5 - 43. Tiwari, M. and Dhawan, A. (2012) Comment on Robust Guaranteed Cost Control for a Class of Two-Dimensional Discrete Systems with Shift-Delays. Multidimensional Systems and Signal Processing, 23, 415-419.
http://dx.doi.org/10.1007/s11045-011-0151-6 - 44. Paszke, W., Lam, J., Galkowski, K., Xu, S. and Lin, Z. (2004) Robust Stability and Stabilization of 2-D Discrete State-Delayed Systems. System Control Letter, 51, 277-291.
http://dx.doi.org/10.1016/j.sysconle.2003.09.003 - 45. Huang, S. and Xiang, Z. (2014) Robust Reliable Control of Uncertain 2-D Discrete Switched Systems with State Delays. Transactions of the Institute of Measurement and Control, 36, 119-130.
http://dx.doi.org/10.1177/0142331213485277 - 46. Xu, J. and Yu, L. (2008) H∞ Control for 2-D Discrete State Delayed Systems in the Second FM Model. Acta Automatica Sinica, 34, 809-813.
http://dx.doi.org/10.3724/SP.J.1004.2008.00809 - 47. Xu, H., Zou, Y., Xu, S. and Guo, L. (2008) Robust H∞ Control for Uncertain Two-Dimen- sional Discrete Systems Described by the General Model via Output Feedback Controllers. International Journal of Control, Automation, and Systems, 6, 785-791.
- 48. Feng, Z. Y., Xu, L. and Anazawa, Y. (2010) Sufficient LMI Conditions for H∞ Static Output Feedback Control of 2-D Systems. 11th Conference on Control, Automation, Robotics and Vision, Singapore, 7-10 December 2010, 57-60.
- 49. Du, C., Xie, L. and Zhang, C. (2001) H∞ Control and Robust Stabilization of Two-Dimen- sional Systems in Roesser Models. Automatica, 37, 205-211.
http://dx.doi.org/10.1016/S0005-1098(00)00155-2