ABSTRACT

Basic set of equations of motion for particles in the case when charge distribution of a particle at rest is spherically symmetric and localized is formulated. Various approximations for interaction forces are derived. The basic approximation is justified by the fact that particle velocities vary little on a time scale (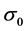~localization radius). Examples of large and small (with respect to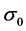) distances between particles are considered. In both cases the slow motion approximation is derived. Apart from calculation of the corrections to the point charge interaction at large distances an approach to the analysis of neutral particles (missing in the point particle theory) containing charged fragments is proposed. In addition, it is shown that at small distances charges of the same sign may attract if their mechanical masses are substantially small.

Keywords:

Extended Charge, Electromagnetic Interaction, Equations of Motion, Classical Electrodynamics, Electromagnetic Mass

1. Introduction

As is well known, classical electrodynamics is intrinsically inconsistent at distances of the order of or less than the “radius” of the electron (see (37.3) in [1] ). In the beginning of the last century it became already possible to cure those inconsistencies by taking into account the theory of extended charges. It is during this time however that quantum “revolution” took place and made this problem no longer relevant as quantum effects “came into a play” already at distances much larger than the electron “radius”. Yet, the divergences that occurred within the point charge approximation were successfully removed by the renormalization methods of quantum field theory. Classical theory was left to (one might say was allowed to) study technically feasible models (charged spheres, capacitors, etc.). Recent researches in this field [2] [3] [4] are worth noticing.

In [5] the author considered this problem in general setup having investigated properties of the field created by an accelerated extended charged particle. Different options for the current vector were considered. In particular, it was assumed that charge distribution of a particle at rest is spherically symmetric. In analyzing interaction of a particle with its own field the field contribution into inertial mass was calculated and the Lorentz-Abraham-Dirac formula for radiation friction was derived more accurately (corrections to the latter as well as conditions for these corrections being comparably small were found). The issue of what makes existence of an extended micro particle charge stable was left aside (according to the author this issue is analogous to the issues of elementary particle stability “causes”).

This work is a follow up of [5] . Its mathematics gets even more cumbersome though that one may wonder if our work makes sense at all. We are pretty sure it does. First of all it is clear that improving the theory to a better perfection is useful from mathematical stand point (to clarify conditions and accuracy of the results provided by the point particle electrodynamics). There are pragmatic reasons too.

1) Currently a combination of relativism along with large acceleration of extended charges can be only observed at microscopic level that is governed by quantum theory. It does not exclude similar phenomena where classical electrodynamics still applies.

2) There are many principles and results of the classical theory that manifest as quantum analogs in one way or another (to name a few, corrections to the potential yield energy spectrum shift, classical trajectory corresponds to the evolution of coordinate mean values with time, etc.). Therefore one cannot exclude the fact that classical phenomena related to a finite size charge may affect quantum ones.

The original system of equations of motion for the extended charge dynamics results from setting the variation of the action to zero while varying particle trajectories (i.e. it is assumed that the field produced by charges is unambiguously defined by their trajectories). This system is relatively simple in its form though hardly applicable in practice making the derivation of the “working” approximations extremely cumbersome. Therefore, to put it clear and short we provide our work with the notations, our analysis scheme and concluding appendix that contains all cumbersome expressions.

2. Notation and Analysis Scheme

1) Vacuum speed of light 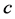is set to 1.

2) Latin letters (except for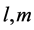) enumerate Minkowski space-time tensor components: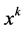?coordinates of a point,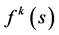―trajectory of the “center” of a

particle,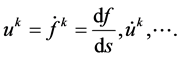―particle velocity, acceleration, etc. 4-vectors. Line element 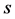is chosen such, that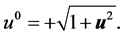

3) Summation over dummy indices is implied. Occasionally we omit tensor index of a vector. For example,. Time component is singled out as follows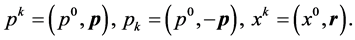

4) Particles and their parameters are enumerated by Greek letters and numbers. A particle is assumed to be arbitrary unless its number is specified.

5) Current density vector of a given particle is defined via integration over the line element:

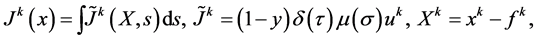(1)

where 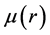is spherically symmetric charge distribution of a particle at rest,

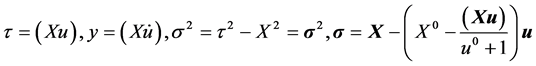(2)

The following shift is implied in integration and. We keep the notation for including when Function is bounded at the origin and localized in such a way, that its “multipoles”

(3)

are finite (at least for in our case).

6) The notation for the following integrals is introduced:

(4)

where in the second integrand. For one has

(5)

Whenever the weight function carries a particle number it is appended explicitly to the associated quantities:. The following functions associated with carry this number as an upper index:

(6)

7) By the order of a charge size is denoted.

8) Derivatives with respect to as well as with respect to parameters are denoted as:

9) Occasionally we omit arguments of a function. In this case a function and its value given at a point specified earlier in the text are denoted by the same symbol. Integration is carried out within infinite limits unless otherwise specified. The multiplicity of an integral is defined by dimensionality of its integrand.

Our analysis is as follows. We derive the original equations and then decompose them with respect to small parameters. The basic parameter is associated with the particle acceleration bound. Namely, the particle velocity is supposed to vary little during the time that light covers distance of the order of. To be specific, suppose that the acceleration is characterized by a certain frequency. We assume

(7)

Suppose is of order of the electron “radius” while is the frequency of a photon interacting with the electron. Inequality (7) breaks down at photon energies being hundreds of the electron self-energies. This implies that (7) rules out very rapid accelerations. Hence, we see (7) is still fulfilled for intermediate accelerations (i.e. not necessary small). By dropping terms of the order of one is said to neglect those velocity derivatives that are of m-th order and higher (i.e., the total order of a given product).

There are two small parameters associated with large and small distances compared to between centers of particles. The fourth parameter is a small velocity of a particle:

We start out by decomposing the original equations with respect to the basic parameter and then derive large and small distance approximations. In both cases we then study their small velocity behavior.

3. Basic System of Equations

Trajectory of the α-th particle is given by functions. Taking an - particle system in some reference frame we can adjust the origins of line elements such that

(8)

(i.e., each can be expressed in terms of a single evolution parameter). From (1, 2) it follows that the current of the α-th particle (we append―index to) has the form

(9)

Equations of motion read

(10)

where is the mechanical mass of the α-th particle, whereas forces are derived from variation of the electro-magnetic part of the action

(11)

here is the gauge potential of the external field, are the potential and the Maxwell tensor of the -th particle correspondingly that satisfy the Lorentz condition and Maxwell equations:

(12)

It follows then the action and its variations are given by

(13)

The variational derivatives are associated with forces. To calculate these derivatives one has to take into account: 1) any variation with respect to is equal to zero; 2) the fact that the Lagrangian depends on accelerations implies that the variations as well as should be equal to zero at the integration boundary.

Therefore, equations (10) cast into

(14)

where is the force the -th particle acts on the α-th one and is the external field force. Explicit expressions for these forces were found in [5] (see (15)). To obtain () it suffices to associate current with the -particle while field-with the one (external). Let us restrict ourselves to the first term resulting from this expression (we omit the second one corresponding to higher order corrections):

(15)

(16)

(recall is given by integral (4), where should be replaced with). We omit the external field below (if present we just add it to the final equations). Note that for sufficiently uniform external field one recovers the usual Lorentz force.

Forces depend in a highly complicated way on particle trajectories and unknown charge distributions (the latter can be more important). This is why equations (14) in general are virtually useless for constructive analysis. Next, we consider the approximations, where this dependence is simplified. Particularly, forces depend on via a few integral characteristics (constants).

4. Limited Accelerations

In order to reduce amount of indices we omit index in identifying a particle and its parameters and take the α-th particle as the first one, whereas is the force created by the field of arbitrary particle (including the first one) acting on the first particle. In final expressions, it suffices to do other way around: by appending an arbitrary particle (and its parameters) while taking the first particle as the α-th.

The field of an accelerated extended charge has been found in [5] . For current (1) it is given by formulae (6, 9) in this paper. Due to localization of the function the integration in this formulae is carried out along region, where is defined by the relation

(17)

For limited accelerations ((7) is fulfilled) we can expand and its derivatives in power series of, e.g.,

(18)

With the aid of expansion (18) and the integration along one can find the potentials with any accuracy. In [5] by dropping 4^th and higher order derivatives the field was found in two cases―in the center of a particle and at distances larger than its “size”. The same accuracy expression for the field at any distance is more involved. We give it here by neglecting 3^rd order velocity derivatives:

(19)

(20)

all functions of are calculated at the point , in particular, in view of (17):

Functions are given in (A.1 ? A.3).

Though we have found the more explicit approximation for the field, integrals (15) still provide one with too big amount of the charge distribution characteristics. For large and small distances between particles the situation simplifies as we show below. In so doing we drop off 2^nd order and higher velocity derivatives.

For a given approximation (see (16) in [5] ), where

(21)

can be called the electromagnetic mass of the first particle. Taking it into account we move on the left in (14) introducing the notation for the full mass of the α-th particle. Correspondingly, any particle but the first one is supposed to be taken as arbitrary in the formulae below.

5. Large Distances

So, let

(22)

In (A.1 - A.3) one has (see (3)). Instead of (20) we now have

(23)

Here (particle charge) and (the electric analog of the momentum of inertia); -same quantities for α-th particle.

In (15) and (17) we make a shift (see (4)), where now

(24)

In (15) we then have. Let us introduce the vector

where is defined in (17) at. Expanding then in powers of and neglecting higher order contribution, we obtain

(25)

Expanding in (23) and taking into account (25) one gets

(26)

Explicit expressions for are given in (A.4 - A.6) while the values of are taken at. which satisfies the equation

(27)

Carrying out integration in and taking into account that odd powers of do not contribute we have

(28)

where, while and are given in (A.7 - A.13). Appending index to an arbitrary particle (including its parameters) in (28), while taking the 1-st particle as the α-th one we obtain the equations of motion

(29)

It is clear that even for the obtained system should be solved numerically (mainly due to implicit form of given in (27)). At small velocities however one can succeed analytically.

Let us denote. Dropping off -terms () we find from Equation (27)

(30)

where (the upper dot denotes differentiation with respect to time). Expanding in (28) we find the three dimensional vector for the force that the field produced by the 2^nd particle acts on the first one:

(31)

(32)

(33)

Changing index 2 to and 1 to in (31 - 33) one finds vector

The obtained results remain valid in case when some of the particles are neutral. For example if then can be determined using (31) from the third term while,―from the second one with the interchange (in these cases the length plays crucial role). Note that if Equation (31) reproduces interaction force of point charges expanded in small velocities. At the same time one needs extended charges to have bounded electromagnetic mass (20).

In case of two equal mass and equal absolute charge particles one has in (29, 31) that. Assuming the center of mass is at rest () and neglecting -terms let us write down the equation for in the following form

(34)

It says that if the inertia mass decreases as the distance between particles decreases (we will see what it implies at small distances).

6. Small Distances

Let us rewrite the condition of small distances in the form

(35)

We do not speculate on to which extent such mutual penetration of particles is possible for it requires understanding of the inner mechanisms that make an extended charge stable. We leave this question aside. Let us however remark that e.g. virtual particle creation (vacuum polarization) hardly escapes from that kind of processes. Under (35) in (20) (taking into account in (15)) we expand it in two parameters 1) in vector is supposed to be small; 2) in solving Equation (17)

(36)

parameter is taken to be small. We neglect?terms and higher. Expanding in results in

(37)

From (36) one obtains (below if not otherwise stated)

(38)

(39)

In (20) we encounter functions of the form, where is some polynomial. Let us introduce the angle belonging to a plane orthogonal to. As and do not depend on this angle and, the integration along and azimuth gives no contribution from odd powers of. For even powers we introduce the notations

(40)

where―are the?independent vectors. In (A14 - A18) the explicit relations for (40) are given. Note, that, where azimuth is the angle between and . In case it makes sense in addition to average with respect to (weighted with). Averaging vectors in (40) yields:

(41)

Substituting (37 ? 39) into (20) one finds from (15)

(42)

Expressions for are given in (A.19 - A.23). As we can see (42) has quite a cumbersome form. This is not a problem for the analysis. The fact that the angle dependence on charge distributions in (42) is expressed via integrals being functions of rather than just constants is a problem:

(43)

where are functions from list (6).

To get reduced to constants let us consider the case of small velocities,. Expanding integrals in (43) in and taking into account (41) one has

(44)

Expressions for are given in first relations (A.24 - A.28) up to order. Let us stress that is a polynomial in and their derivatives depending totally on six constants (hereinafter depend on while denotes (5))

(45)

Equations of motion then take the form

(46)

where―is the 3d vector of the external force acting on the α-th particle while can be restored by appending indices to (44, 45) along the lines of (29). In (46) the dependence on charge distributions is expressed via constants (we have taken into account that in accordance with (5) one has). The amount of constants reduces drastically for specified such that (arguably such an equivalence of distributions takes place for equal absolute values of charges only): constants of type (45) can be expressed (see (A.29, A.30)) via and three positive constants

(47)

If particles can be represented as uniformly charged balls of radius then

(48)

Consider now a system of two equal mass particles in which charges are equal in their absolute values (). Coefficients in (44) now take the form of the second equalities in (A.24 - A.28). The external fields and are supposed to be sufficiently uniform. We are interested in differential equations for (inner motion) and position of the center of mass (motion of the whole system), which are found from (46). Consider the linearized approximation of these equations:

(49)

(50)

For sufficiently large masses there is nothing unexpected about these equations. However if mass is zero or small enough one encounters surprises.

Let In this case processes in which a pair of particles can be created from “nothing” (in vacuum) having zero mechanical masses and opposite charges get “legalized” (no energy conservation breakdown). Equation (49) describes three dimensional linear oscillators. At linearized level the inertial mass in (50) is equal to zero. Motion of the system as a whole at gets highly sensible to the behavior of if corrections to this mass are taken into account.

Another surprise springs out when for. In this case as before (49) remains the equation for an oscillator. In other words, the approach- ing charges of the same sign with sufficiently small mechanical masses switch repulsion to attraction!

It is unlikely to expect this kind of phenomena to be described by equations (49, 50) in the micro world. It seems plausible though that qualitatively they still have some analogs. In the first example, for instance, a small inertial mass of a moving system may correspond to a pair creation supplemented with their rapid drag into a different position. The attraction effect of equal sign charges makes their “merging” to a state of a mass greater than seemingly possible.

7. Conclusion

So, the generalization of electrodynamics to a version of the extended charge one can be considered basically solved. In case of arbitrary distance between particles one could also provide the slow-motion approximation. The author felt redundant not only because of the extremely cumbersome result. What is more important is that the result contains a function of charge distribution, which fails to be expressed as a combination of constants (this means that its analysis demands specifying the form of functions). The ongoing investigations may be aimed at solving the obtained equations as well as at analyzing the other examples of extended charges including those with central symmetry violated and also accounting for the distribution dependence on acceleration (whenever acceleration deforms charge internal structure), etc. The essence of extended charge remains an open issue. The question is whether that extension is a real thing, i.e. analogous to common spread of matter, or the analogy is purely formal (for instance, an “elementary charge” as a field source represents a “smeared” distribution from mathematical stand point).

Cite this paper

Ependiev, M.B. (2017) On the Interaction of Extended Charges in Classical Relativistic Theory. Journal of Mo dern Physics, 8, 654-667. https://doi.org/10.4236/jmp.2017.84044

References

Appendix

To (18, 19):

(A.1)

(A.2)

(A.3)

(see (6)).

To (26):

(A.4)

(A.5)

(A.6)

To (28):

(A.7)

(A.8)

(A.9)

(A.10)

(A.11)

(A.12)

(A.13)

To (40, 41)

(A.14)

(A.15)

(A.16)

(A.17)

(A.18)

To (42):

(A.19)

(A.20)

(A.21)

(A.22)

(A.23)

To (44):

(A.24)

(A.25)

(A.26)

(A.27)

(A.28)

To (45):

(A.29)

(A.30)

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

Or contact jmp@scirp.org