Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60703,6 pages
10.4236/jmp.2015.613194
Electronic Structure of the Cesium Oxide Molecule CsO
Diana Kaeen1, Mahmoud Korek1*, Saleh Nabhan Abdulal2
1Physics Department, Faculty of Science, Beirut Arab University, Beirut, Lebanon
2Physics Department, Lebanese International University, Beirut, Lebanon
Email: *fkorek@yahoo.com, *mahmoud.korek@bau.edu.lb
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 July 2015; accepted 25 October 2015; published 29 October 2015
ABSTRACT
Adiabatic potential energy curves of 12 doublet and quartet lowest spinless electronic states of the molecule CsO have been investigated via ab initio CASSCF and MRCI (doublet and quartet excitations with Davidson correction) calculations. The spectroscopic constants such as vibrational harmonic frequency ωe, the internuclear distance at equilibrium Re, the rotational constant Be, and the electronic transition energy Te of the ground and the excited electronic states have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance. The comparison of these values to those available in the literature shows a good agreement.
Keywords:
ab Initio Calculation, CsO Molecule, Potential Energy Curves, Spectroscopic Constants

1. Introduction
The alkali metal oxides have been the subject of different theoretical and experimental studies in order to specify their electronic ground state. These studies focused on the transition between the 2 electronic states 2Π and 2Σ+ [1] -[3] . This change in ground state symmetry is due to the hole in oxygen that will lead either to a 2Π (LiO and NaO) or to a 2Σ+ (KO, RbO and CsO). The nature of ground state depends on the competing effects. When the terms are attractive, we expect to have 2Π as ground state due to quadrupole interactions while we expect to have 2Σ+ as ground state due to Pauli repulsion. There is a great concern in studying the spectra of this molecule which is shown in different papers written on its ground state 2Π and the first excited state 2Π. Using an ab initio method, Langhoff et al. [4] studied the ground states of alkali oxides and determined the values of spectroscopic constants for the two states 2Σ+ and 2Π. Lindsay et al. [5] demonstrated that CsO had 2Σ+ ground state by using ESR matrix experiments. Allison and Goddard III [2] explained the change in ground state symmetry from LiO (2Π) to CsO (2Σ+). Yamada and Hirota [6] investigated systematically CsO by using microwave and infrared diode laser spectroscopy. The observed spectra showed that the ground state of CsO was 2Σ+. Woodward et al. [7] showed that the ground state of CsO was 2Σ+. It was demonstrated that RbO and CsO had 2Σ+ ground states using ESR experiments [2] [5] which was indicated previously for CsO through reactive scattering experiments [8] . By using a high-level RCCSD(T) ab initio method, Lee et al. [9] calculated the spectroscopic constants of the two lying electronic states 2Σ+ and 2Π.
In the present work 12 low-lying doublet and quartet electronic states of CsO molecule have been investigated by using the ab initio method. The potential energy curves (PECs) together with the transition energy with respect to the minimum energy for the ground state Te, the equilibrium internuclear distance Re, the harmonic frequency ωe, and the rotational constant Be have been obtained for the considered electronic states. Ten electronic states have been investigated here for the first time.
2. Method of Calculations
In the present work we study the low-lying doublet and quartet electronic states of the molecule CsO using state averaged complete active space self consistent field (CASSCF) procedure followed by a multireference configuration interaction (MRDSCI with Davidson correction) treatment for the electron correlation. The entire CASSCF configuration space was used as the reference in the MRDSCI calculations, which were done via the computational chemistry program MOLPRO [10] taking advantage of the graphical user interface GABEDIT [11] . For this purpose five different basis sets were used in our theoretical study for cesium monoxide molecule. In the first basis set the 55 electrons of the cesium atom are considered using a contracted ECP46MWB basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCV5Z basis set for s, p, and d functions. In the second basis set, the 55 electrons of the cesium atom are considered using a contracted ECP46MWB basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the 6-311++G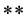 basis set for s, p, and d functions. This basis is developed by optimizing exponents and coefficients at the Möller-Plesset second-order level. It has a triple split in the valence s and p shells together with a single set of uncontracted polarization functions on each atom. In the third basis set, the 55 electrons of the cesium atom are considered using a contracted Hay-Wadt VDZ (n+1) ECP basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCV5Z basis set for s, p, and d functions.
basis set for s, p, and d functions. This basis is developed by optimizing exponents and coefficients at the Möller-Plesset second-order level. It has a triple split in the valence s and p shells together with a single set of uncontracted polarization functions on each atom. In the third basis set, the 55 electrons of the cesium atom are considered using a contracted Hay-Wadt VDZ (n+1) ECP basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCV5Z basis set for s, p, and d functions.
In the fourth basis set the 55 electrons of the cesium atom are considered using a contracted ECP46MWB basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the VDZ basis set for s, p, and d functions. In the fifth basis set, the 55 electrons of the cesium atom are considered using a contracted ECP46MWB basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCVDZ basis set for s, p, and d functions.
Among the 63 electrons explicitly considered for CsO (55 electrons for Cs and 8 for O) 46 inner electrons were frozen in subsequent calculations so that 17 valence electrons were explicitly treated. All computations were performed in the C2v point group. Using the first basis set ECP46MWB, the potential energy curves of 12 low-lying electronic states of the molecule CsO were generated using the MRSDCI for 350 internuclear distances calculations in the range 1.5Å ≤ Re ≤ 5Å in the representation 2s+1Λ(±) where we assumed that, the CsO molecule is mainly ionic around the equilibrium position. These PECs for the different symmetries are given in Figure 1 and Figure 2.
The spectroscopic constant ωe, re, Be, and Te have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance. These values are given in Table 1 with the available values in the literature. The comparison of our results for the constants ωe with those available in literature [3] [4] [6] [9] [12] [13] shows a very good agreement by using the second basis for the states X2Σ+ with the relative difference 2.6% ([4] ) ≤ Δωe/ωe ≤ 4.4% ([9] ); while the best agreement for the state (1)2Π is obtained by using the basis one with the relative difference 4.8% ([12] ) ≤ Δωe/ωe ≤ 6.8% ([4] ). By comparing our calculated values of Re with those found in literature for the 2 electronic states X2Σ+ and (1)2Π, one can find an
Figure 1. Potential energy curves of the lowest doublet electronic states of the molecule CsO using the first basis set.
Figure 2. Potential energy curves of the lowest quartet electronic states of the molecule CsO using the first basis set.
excellent agreement is obtained by using the first, fourth and fifth used basis sets with the relative differences 0.32% ([12] ) ≤ ΔRe/Re ≤ 0.37% ([4] ).
Our calculated values of Te by using basis one are in very good agreement with those given in [4] [6] [9] with the relative differences 1.04% ([6] ) ≤ ΔTe/Te ≤ 6.1% ([9] ). This agreement deteriorates by using third and fifth basis sets. There is no comparison of our calculated values for Be and for the investigated spectroscopic constants of the electronic states (1)4Σ−, (2)2Π, (2)4Σ− since they are given here for the first time. These spectroscopic constants are also absent for other investigated electronic states either because of the crossing or avoiding
Table 1. Spectroscopic constants for the lowest doublet and quartet electronic states of the molecule CsO.
aPresent work using for the 55 electrons of the cesium atom a contracted ECP46MWB basis set for s and p functions, while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCV5Z basis set for s, p, and d functions. bPresent work using for the 55 electrons of the cesium atom a contracted ECP46MWB basis set for s and p functions ,while the oxygen species is treated as a system of 8 electrons by using the 6-311++G basis set for s, p, and d functions. cPresent work using for the 55 electrons of the cesium atom a contracted Hay-Wadt VDZ (n+1) ECP basis set for s and p functions ,while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCV5Z basis set for s, p, and d functions. dPresent work using for the 55 electrons of the cesium atom a contracted ECP46MWB basis set for s and p functions ,while the oxygen species is treated as a system of 8 electrons by using the VDZ basis set for s, p, and d functions. ePresent work using for the 55 electrons of the cesium atom a contracted ECP46MWB basis set for s and p functions ,while the oxygen species is treated as a system of 8 electrons by using the aug-cc-pCVDZ basis set for s, p, and d functions. kRef. [3] , fRef. [4] , gRef. [6] , hRef. [9] , lRef. [12] , iRef. [13] .
*Corresponding author.
3. Conclusion
In the present work, the ab initio investigation for the low-lying doublet and quartet electronic states of the CsO molecule has been performed via CASSCF/MRCI method using five different basis sets. The potential energy curves have been determined along with the spectroscopic constants Te, Re, ωe and the rotational constant Be for these states. The calculation has been done by using 5 different basis sets. The comparison of our results with those obtained theoretically in literature shows a very good accuracy. Ten new electronic states have been investigated in the present work for the first time.
Cite this paper
DianaKaeen,MahmoudKorek,Saleh NabhanAbdulal, (2015) Electronic Structure of the Cesium Oxide Molecule CsO. Journal of Modern Physics,06,1889-1894. doi: 10.4236/jmp.2015.613194
References
- 1. So, S.P. and Richards, W.G. (1975) The Electronic Ground States of Alkali Monoxides. Chemical Physics Letters, 32, 227-230.
http://dx.doi.org/10.1016/0009-2614(75)85109-8 - 2. Allison, J.N. and Goddard III, W.A. (1982) Alkali Oxide Diatomics: Explanation of the Change in Ground State Symmetry from LiO(2Π) CsO(2Σ+). The Journal of Chemical Physics, 77, 4259-4261.
http://dx.doi.org/10.1063/1.444306 - 3. Allison, J.N., Cave, R.J. and Goddard III, W.A. (1984) Alkali Oxides. Analysis of Bonding and Explanation of the Reversal in Ordering of the 2.PI. and 2.SIGMA. States. Journal of Physical Chemistry, 88, 1262-1268.
http://dx.doi.org/10.1021/j150650a049 - 4. Langhoff, S.R., Bauschlicher Jr., C.W. and Partdridge, H. (1986) Theoretical Study of the Diatomic Alkali and Alkaline-Earth Oxides. The Journal of Chemical Physics, 84, 4474-4480.
http://dx.doi.org/10.1063/1.450019 - 5. Lindsay, D.M., Herschbach, D.R. and Kwiram, A.L. (1974) ESR Spectra of Matrix Isolated CsO and RbO Molecules: 2Σ Ground States and Inner Shell Bonding. The Journal of Chemical Physics, 60, 315.
http://dx.doi.org/10.1063/1.1680787 - 6. Yamada, C. and Hirota, E. (1999) The Microwave Spectrum of the Cesium Monoxide CsO radical. The Journal of Chemical Physics, 111, 9587-9592.
http://dx.doi.org/10.1063/1.480291 - 7. Woodward, J.R., Hayden, J.S. and Gole, J.L. (1989) Formation and Characterization of a Low-Lying Electronic State of the Alkali Monoxides LiO…CsO in the Red and Near Infrared. Chemical Physics, 134, 395-419.
http://dx.doi.org/10.1016/0301-0104(89)87171-X - 8. Herm, R.R. and Herschbach, D.R. (1970) Molecular Beam Kinetics: Reactions of Alkali Atoms with NO2 and CH3NO2. The Journal of Chemical Physics, 52, 5783.
http://dx.doi.org/10.1063/1.1672860 - 9. Lee, E.P.F., Lozeille, J., Soldan, P., Daire, S.E., Dyke, J.M. and Wright, T.G. (2001) An ab Initio Study of RbO, CsO and FrO (X2Σ+; A2Π) and their cations (X3Σ-; A3Π). Physical Chemistry Chemical Physics, 3, 4863-4869.
http://dx.doi.org/10.1039/b104835j - 10. Werner, H.J., Knowles, P.J., Lindh, R., Manby, F.R., Schütz, M., Celani, P., Korona, T., Rauhut, G., Amos, R.D., Bernhardsson, A., Berning, A., Cooper, D.L., Deegan, M.J.O., Dobbyn, A.J., Eckert, F., Hampel, C., Hetzer, G., Lloyd, A.W., McNicholas, S.J., Meyer, W., Mura, M.E., Nicklaß, A., Palmieri, P., Pitzer, R., Schumann, U., Stoll, H., Stone, A.J., Tarroni, R. and Thorsteinsson, T. (2009) MOLPRO Is a Package of ab Initio Programs.
- 11. Allouche, A.R. (2011) Gabedit—A Graphical User Interface for Computational Chemistry Softwares. Journal of Computational Chemistry, 32, 174-182.
http://dx.doi.org/10.1002/jcc.21600 - 12. Laskowski, B.C. Langhoff., S.R. and Siegbahn, P.E.M. (1983) Theoretical Determination of the X2Σ+ and A2Π Potentials of CsO Using Relativistic Effective Core Potentials. International Journal of Quantum Chemistry, 23, 483-490.
http://dx.doi.org/10.1002/qua.560230218 - 13. Sarkas, H.W., Kendricks, J.H., Arnold, S.T., Slager, V.L. and Bowen, K.H. (1994) Measurement of the X 2Σ+-A 2Π Splitting in CsO via Photoelectron Spectroscopy of CsO-. The Journal of Chemical Physics, 100, 3358.
http://dx.doi.org/10.1063/1.466428
NOTES

*Corresponding author.




