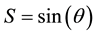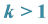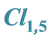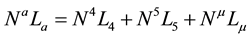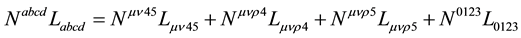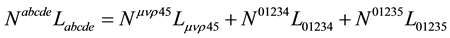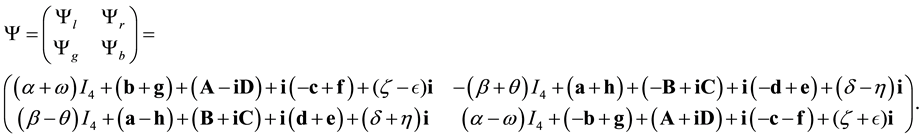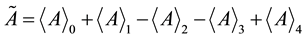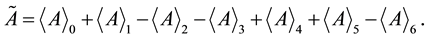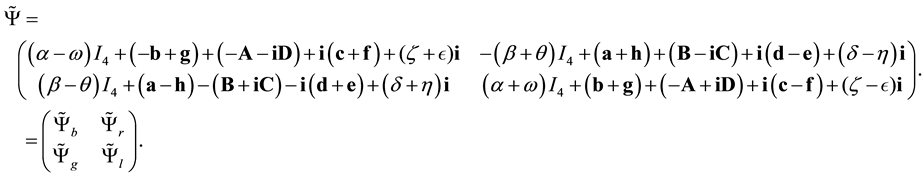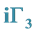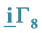Journal of Modern Physics
Vol.05 No.18(2014), Article ID:52750,24 pages
10.4236/jmp.2014.518210
A Wave Equation including Leptons and Quarks for the Standard Model of Quantum Physics in Clifford Algebra
Claude Daviau, Jacques Bertrand
Le Moulin de la Lande, Pouillé-les-Coteaux, France
Email: Claude.Daviau@nordnet.fr, bertrandjacques-m@orange.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 October 2014; revised 27 November 2014; accepted 21 December 2014
ABSTRACT
A wave equation with mass term is studied for all fermionic particles and antiparticles of the first generation: electron and its neutrino, positron and antineutrino, quarks u and d with three states of color and antiquarks
 and
and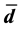 . This wave equation is form invariant under the
. This wave equation is form invariant under the
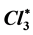 group generalizing the relativistic invariance. It is gauge invariant under the
group generalizing the relativistic invariance. It is gauge invariant under the
 group of the standard model of quantum physics. The wave is a function of space and time with value in the Clifford algebra
group of the standard model of quantum physics. The wave is a function of space and time with value in the Clifford algebra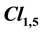 . Then many features of the standard model, charge conjugation, color, left waves, and Lagrangian formalism, are obtained in the frame of the first quantization.
. Then many features of the standard model, charge conjugation, color, left waves, and Lagrangian formalism, are obtained in the frame of the first quantization.
Keywords:
Invariance Group, Dirac Equation, Electromagnetism, Weak Interactions, Strong Interactions, Clifford Algebras

1. Introduction
We use here all notations of “new insights in the standard model of quantum physics in Clifford algebra” [1] . The wave equation for all particles of the first generation is a generalization of the wave equation obtained in 6.7 for the electron and its neutrino. This wave equation has obtained a proper mass term compatible with the gauge invariance in [2] . It is a generalization of the homogeneous nonlinear Dirac equation for the electron alone [3] - [9] .
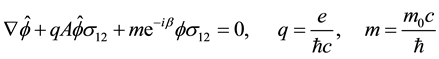 (1.1)
(1.1)
with
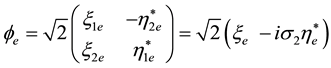 (1.2)
(1.2)
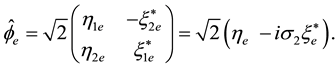 (1.3)
(1.3)
Here
 and
and
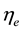 are respectively the right and left Weyl spinors of the electron. The
are respectively the right and left Weyl spinors of the electron. The
 angle is the Yvon- Takabayasi angle satisfying
angle is the Yvon- Takabayasi angle satisfying
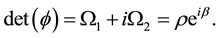 (1.4)
(1.4)
The link with the usual presentation of the standard model is made by the left and right Weyl spinors used for waves of each particle. These right and left waves are parts of the wave with value in .
.
We used previously the same algebra . It is the same algebra, and this explains very well why sub-algebras
. It is the same algebra, and this explains very well why sub-algebras
 and
and
 have been equally used to describe relativistic physics [10] [11] . But the sig- nature of the scalar product cannot be free, this scalar product being linked to the gravitation in the general relativity. It happens that vectors of
have been equally used to describe relativistic physics [10] [11] . But the sig- nature of the scalar product cannot be free, this scalar product being linked to the gravitation in the general relativity. It happens that vectors of



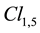

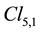




We have noticed, for the electron alone firstly (see [8] 2.4), next for electron + neutrino [2] the double link existing between the wave equation and the Lagrangian density: It is well known that the wave equation may be obtained from the Lagrangian density by the variational calculus. The new link is that the real part of the invariant wave equation is simply
Moreover we generalized the non-linear homogeneous wave equation of the electron, and we got a wave equation with mass term [2] , form invariant under the


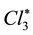

2. From the Lepton Case to the Full Wave
The standard model adds to the leptons (electron


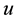
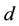


The electro-weak theory [12] needs three spinorial waves in the electron-neutrino case: the right
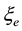
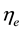



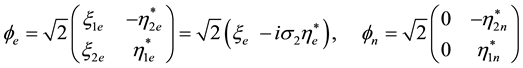

Waves
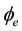
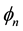


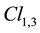


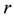
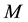
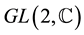
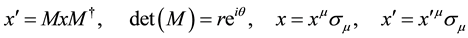

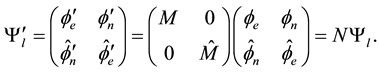
The form (2.3) of the wave is compatible both with the form invariance of the Dirac theory and with the charge conjugation used in the standard model: the wave


We can then think the


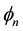



And the antineutrino has only a right wave. The multivector
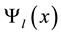


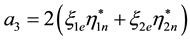
we got

Most of the preceding presentation is easily extended to quarks. For each color


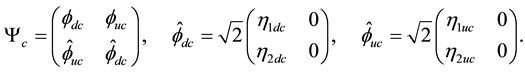
The




The link between the reverse in


The mass term reads

where we use the scalar densities


The covariant derivative

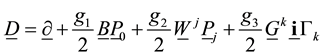


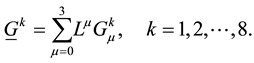
We use two projectors satisfying
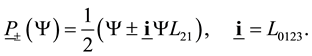
Three operators act on quarks like on leptons:



The fourth operator acts differently on the leptonic and on the quark sector. Using projectors:

we can separate the lepton part

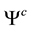
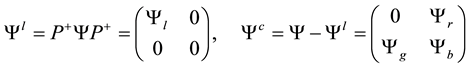
and we get (see [1] (B.4) with
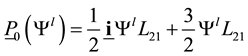

This last relation comes from the non-existence of the right part of the
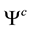
3. Chromodynamics
We start from generators
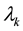
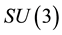
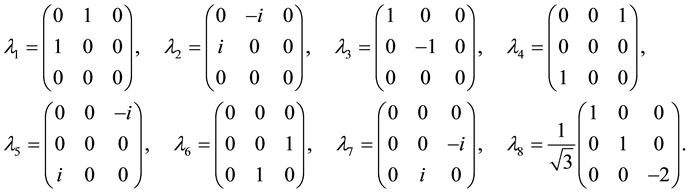
To simplify here notations we use now l, r,

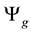
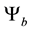
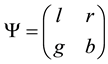
Then (2.1) gives
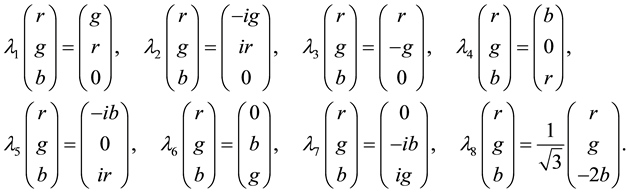
We name

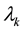
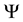
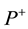

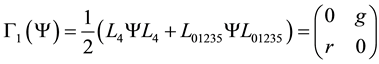
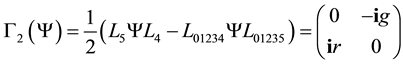

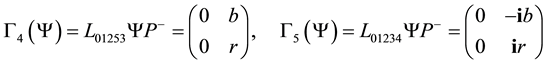
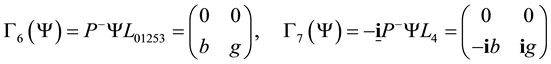
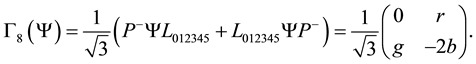
Everywhere the left up term is 0, so all
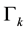

We can extend the covariant derivative of electro-weak interactions in the electron-neutrino case:

to get the covariant derivative of the standard model
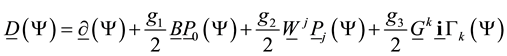
where
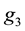
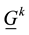
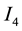

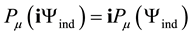
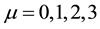
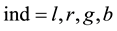
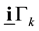
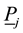
Now we use 12 real numbers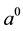

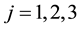
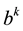
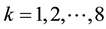
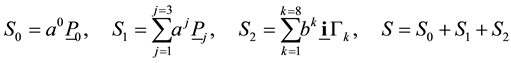
and we get, using exponentiation
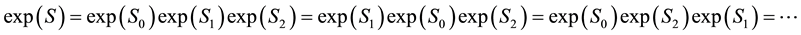
in any order. The set of these operators

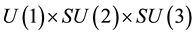

the gauge transformation reads

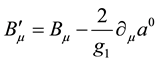
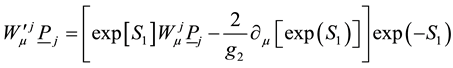

The

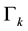
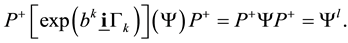
The physical translation is: Leptons do not act by strong interactions. This comes from the structure of the wave itself. It is fully satisfied in experiments. We get then a
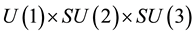
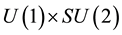
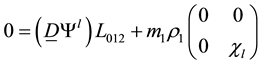
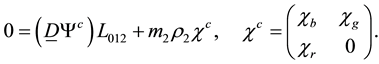
The wave equation (3.19) is equivalent to the wave equation
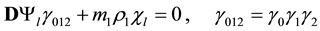
studied in [2] [13] , where
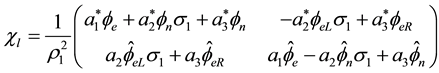
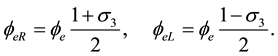
This wave equation is equivalent to the invariant equation:
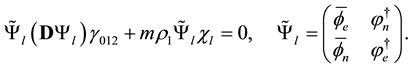
This wave equation is form invariant under the Lorentz dilation

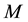
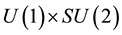
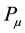
We begin by the double link between wave equation and Lagrangian density that we have remarked firstly in the Dirac equation [8] , next in the lepton case electron + neutrino [1] .
4. Double Link between Wave Equation and Lagrangian Density
The existence of a Lagrangian mechanism in optics and mechanics is known since Fermat and Maupertuis. This principle of minimum is everywhere in quantum mechanics from its beginning, it is the main reason of the hypothesis of a wave linked to the move of any material particle made by L. de Broglie [14] . By the calculus of variations it is always possible to get the wave equation from the Lagrangian density. But another link exists: the Lagrangian density is the real scalar part of the invariant wave equation. This was obtained firstly for the electron alone [8] , next for the pair electron-neutrino [2] where the Lagrangian density reads

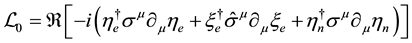

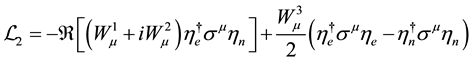
We shall establish the double link now for the wave equation (2.16). It is sufficient to add the property for (3.20). This equation is equivalent to the invariant equation:
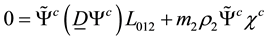
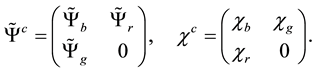
We get from the covariant derivative (2.19) with the operators
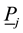

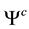

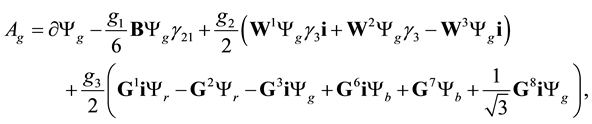


Next we get
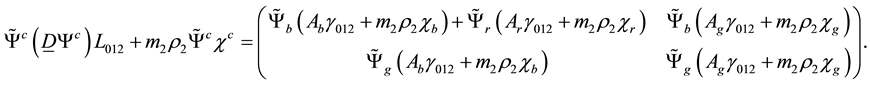
The calculation of the Lagrangian density in the general case is similar to the lepton case. We get

The calculation of

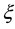
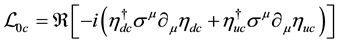

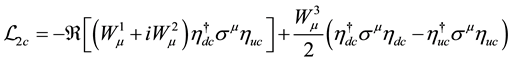
Since three

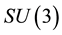
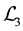
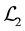
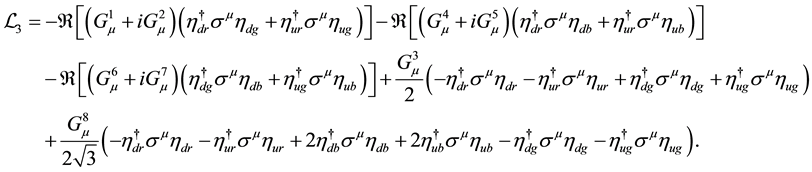
This new link between the wave equation and the Lagrangian density is much stronger than the old one, because it comes from a simple separation of the different parts of a multivector in Clifford algebra. The old link, going from the Lagrangian density to the wave equation, supposes a condition of cancellation at infinity which is dubious in the case of a propagating wave. On the physical point of view, there are no difficulties in the case of a stationary wave. Difficulties begin when propagating waves are studied. Our wave equations, since they are compatible with an oriented time and an oriented space, appear as more general, more physical, than Lagran- gians. These are only particular consequences of the wave equations.
On the mathematical point of view the old link is always available. It is from the Lagrangian density (4.12) and using Lagrange equations that we have obtained the wave equation (2.16).
5. Invariances
5.1. Form Invariance of the Wave Equation
Under the Lorentz dilation

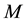
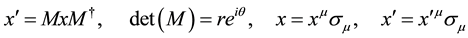


We then let
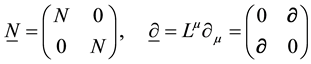
which implies
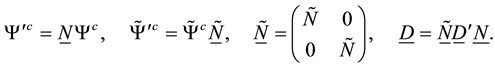
Then we get
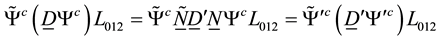
and we shall now study the form invariance of the mass term. All

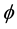
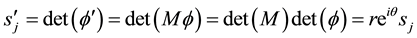
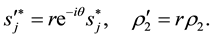
This gives
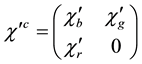
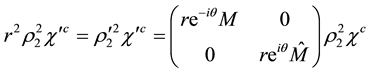

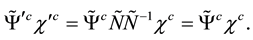
Then the form invariance of the wave equation is equivalent to the condition on the mass term


linked to the existence of the Planck factor [13] .
5.2. Gauge Invariance of the Wave Equation
Since we have previously proved the gauge invariance of the lepton part of the wave equation, it is reason enough to prove the gauge invariance of the quark part of the wave equation.
5.2.1. Gauge Group Generated by
We have here
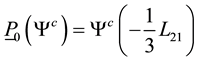

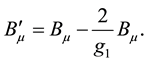
To get the gauge invariance of the wave equation we must get
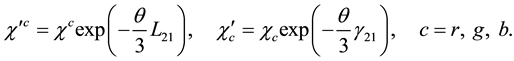
This is satisfied because
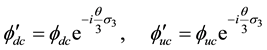
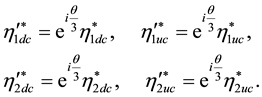
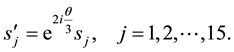
All up terms in the matrix
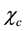
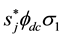
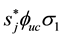
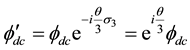
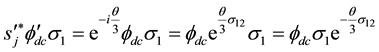
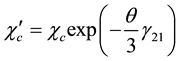
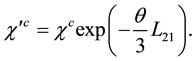
And we finally get

The wave equation with mass term is gauge invariant under the group generated by
5.2.2. Gauge Group Generated by
We have here
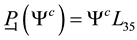

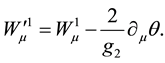
Since
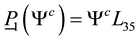
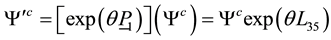

We let
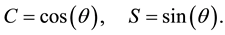
Then (5.31) is equivalent to the system
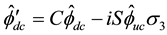
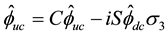
or to the system
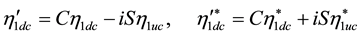
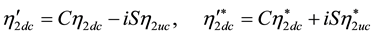
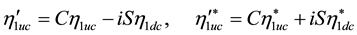
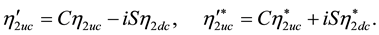
We then get

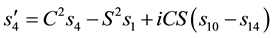
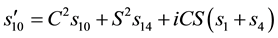

This implies

Similarly, permuting colors, we get
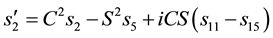
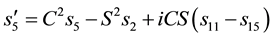
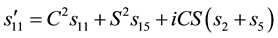
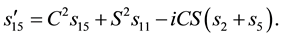
This implies
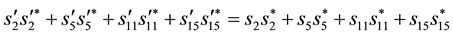
and also
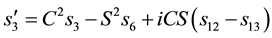
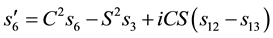
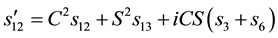

This implies
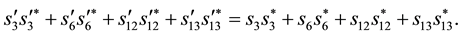
Moreover we get
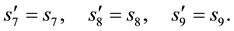
We then get

Next we have
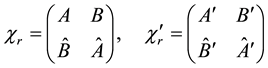
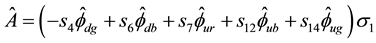
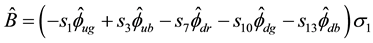
and we get
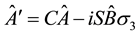

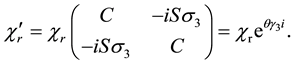
Since we get the same relation for g and b colors we finally get
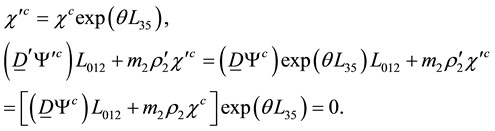
The wave equation with mass term is then gauge invariant under the group generated by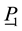
5.2.3. Gauge Group Generated by
We have here

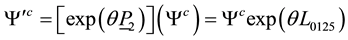
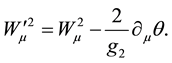
Since

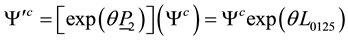
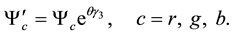
We let

Then (5.67) is equivalent to the system


or to the system

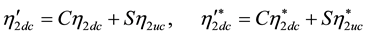
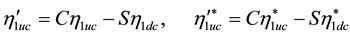
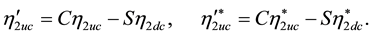
We then get


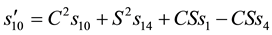
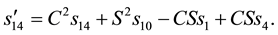
This implies
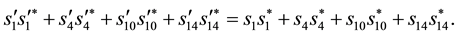
Similarly, permuting colors, we get
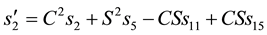
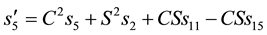
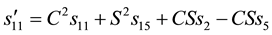

This implies

and also
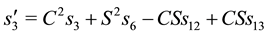
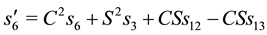
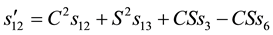
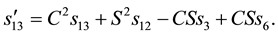
This implies
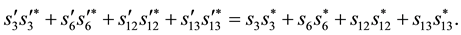
Moreover we get
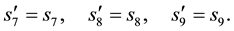
We then get

Next we get with (5.56)
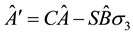
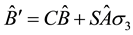
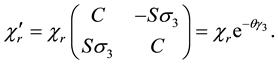
Since we get the same relation for g and b colors we finally get
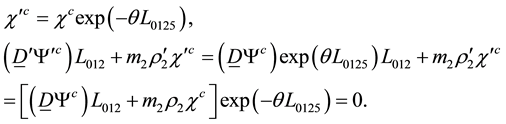
The wave equation with mass term is then gauge invariant under the group generated by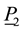
5.2.4. Gauge Group Generated by
We have here
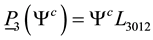
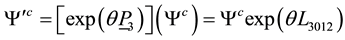

Since
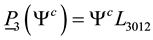
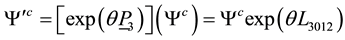

Then (5.97) is equivalent to the system
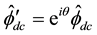
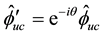
or to the system
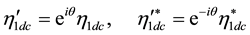
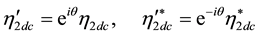
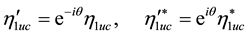

We then get
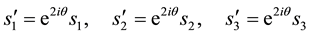
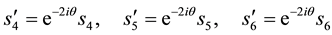
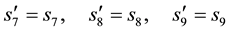

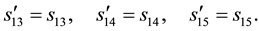
This implies
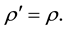
Next we get with (5.56)
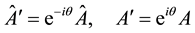


Since we get the same relation for g and b colors we finally get
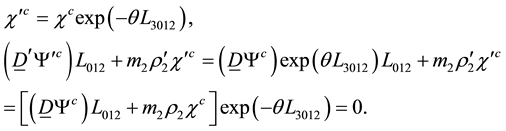
The wave equation with mass term is then gauge invariant under the group generated by
5.2.5. Gauge Group Generated by
We use now the gauge transformation
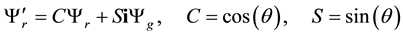
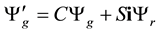
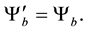
We can then forget here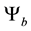

must be equivalent to the system

Using relations (5.117) and (5.118) the system (5.121) is equivalent to (5.120) if and only if
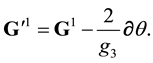
We name
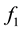

which implies with
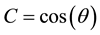
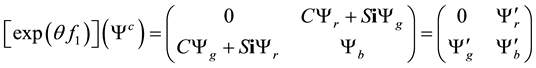

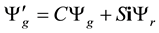
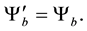
The equality (5.117) is equivalent to the system
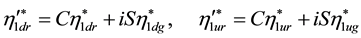
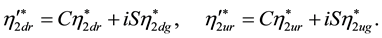
The equality (5.118) is equivalent to the system


This gives for the invariant scalars
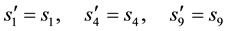




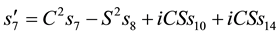
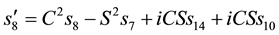
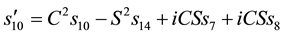
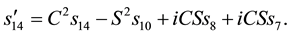
We then get
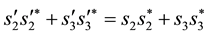
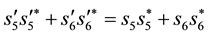
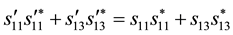
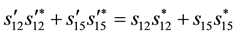


Next we let
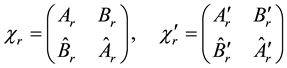
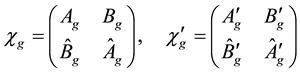
and we get with (B.17) and (B.18)
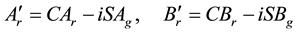
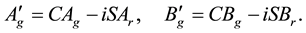
This gives the awaited result

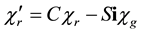
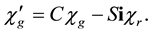
The change of sign of the phase between (5.117) and (5.152) comes from the anticommutation between
5.2.6. Gauge Groups Generated by
We use with
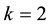
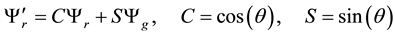

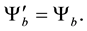
The gauge invariance signifies that the system
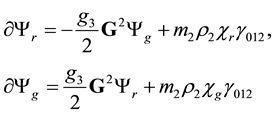
must be equivalent to the system

Using relations (5.154) and (5.155) the system (5.158) is equivalent to (5.157) if and only if
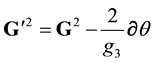
because we get
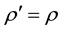
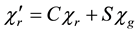

The case
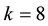
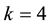

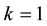
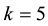
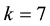

6. Concluding Remarks
From experimental results obtained in the accelerators physicists have built what is now known as the “standard model”. This model is generally thought to be a part of quantum field theory, itself a part of axiomatic quantum mechanics. One of these axioms is that each state describing a physical situation follows a Schrödinger wave equation. Since this wave equation is not relativistic and does not account for the spin 1/2 which is necessary to any fermion, the standard model has evidently not followed the axiom and has used instead a Dirac equation to describe fermions. Our work also starts with the Dirac equation. This wave equation is the linear approximation of our nonlinear homogeneous equation of the electron.
The wave equation presented here is a wave equation for a classical wave, a function of space and time with value into a Clifford algebra. It is not a quantized wave with value into a Hilbertian space of operators. Never- theless and consequently we get most of the aspects of the standard model, for instance the fact that leptons are insensitive to strong interactions. The standard model is much stronger than generally thought. For instance we firstly did not use the link between the wave of the particle and the wave of the antiparticle, but then we needed a greater Clifford algebra and we could not get the necessary link between reversions1 that we used in our wave equation. We also needed the existence of the inverse to build the wave of a system of particles from the waves of its components. And we got two general identities which existed only if all parts of the general wave were left waves, only the electron having also a right wave.
The most important property of the general wave is its form invariance under a group including the covering group of the restricted Lorentz group. Our group does not explain why space and time are oriented, but it respects these orientations. The physical time is then compatible with thermodynamics, and the physical space is compatible with the violation of parity by weak interactions.
The wave accounts for all particles and anti-particles of the first generation. We have also given [2] [8] [9] [13] the reason of the existence of three generations; it is simply the dimension of our physical space. Since the
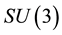
Since the wave equation with mass term is gauge invariant, there is no necessity to use the mechanism of spontaneous symmetry breaking. The scalar boson certainly exists, but it does not explain the masses.
A wave equation is only a beginning. It shall be necessary to study also the boson part of the standard model and the systems of fermions, from this wave equation. A construction of the wave of a system of identical particles is possible and compatible with the Pauli principle [1] [7] .
References
- Daviau, C. and Bertrand, J. (2014) New Insights in the Standard Model of Quantum Physics in Clifford Algebra. JePublie, Pouillé-les-Coteaux. http://hal.archives-ouvertes.fr/hal-00907848
- Daviau, C. and Bertrand, J. (2014) Journal of Modern Physics, 5, 1001-1022. http://dx.doi.org/10.4236/jmp.2014.511102
- Daviau, C. (1993) Equation de Dirac non linéaire. Ph.D. Thesis, Université de Nantes, Nantes.
- Daviau, C. (1997) Advances in Applied Clifford Algebras, 7, 175-194.
- Daviau, C. (2005) Annales de la Fondation Louis de Broglie, 30, 409-428.
- Daviau, C. (2011) L’espace-temps double. JePublie, Pouillé-les-coteaux.
- Daviau, C. (2012) Advances in Applied Clifford Algebras, 22, 611-623. http://dx.doi.org/10.1007/s00006-012-0351-7
- Daviau, C. (2012) Double Space-Time and More. JePublie, Pouillé-les-Coteaux.
- Daviau, C. (2012) Nonlinear Dirac Equation, Magnetic Monopoles and Double Space-Time. CISP, Cambridge.
- Deheuvels, R. (1993) Tenseurs et spineurs. PUF, Paris.
- Hestenes, D. (1986) A Unified Language for Mathematics and Physics and Clifford Algebra and the Interpretation of Quantum Mechanics. In: Chisholm, J.S.R. and Common, A.K., Eds., Clifford Algebras and Their Applications in Mathematics and Physics, Reidel, Dordrecht, 1-23.
- Weinberg, S. (1967) Physical Review Letters, 19, 1264-1266. http://dx.doi.org/10.1103/PhysRevLett.19.1264
- Daviau, C. (2014) Gauge Group of the Standard Model in Cl1,5. ICCA10, Tartu. http://hal.archives-ouvertes.fr/hal-01055145
- de Broglie, L. (1924) Annales de la Fondation Louis de Broglie, 17.
Appendix A. Calculation of the Reverse in
Here indexes
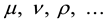

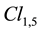
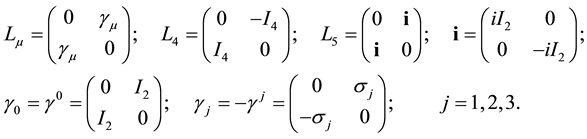
where
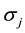

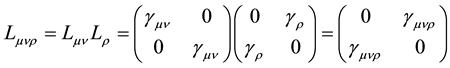

We get also
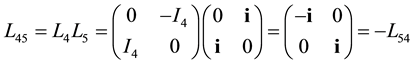
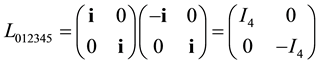
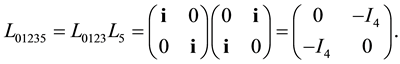
Similarly we get3
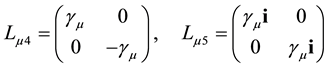
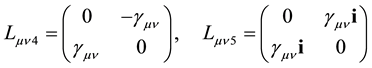

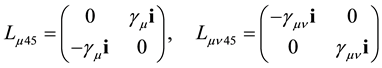

Scalar and pseudo-scalar terms read
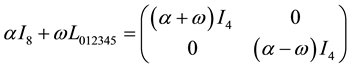
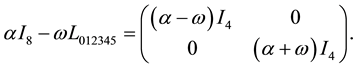
For the calculation of the 1-vector term
we let
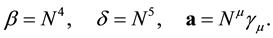
This gives
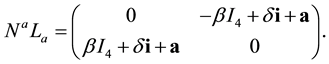
For the calculation of the 2-vector term
we let

This gives

For the calculation of the 3-vector term
we let
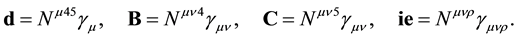
This gives with (A.3) and (A.9)
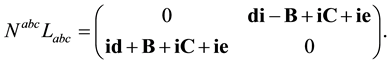
For the calculation of the 4-vector term
we let
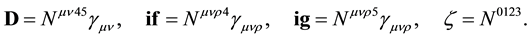
This gives with (A.4) and (A.10)
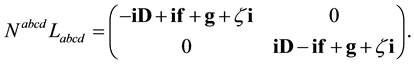
For the calculation of the pseudo-vector term
we let
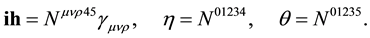
This gives with (A.7) and (A.12)
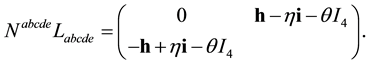
We then get
(A.25)
This implies
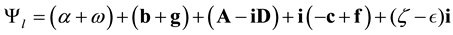
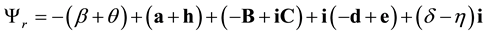
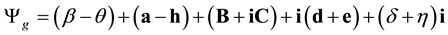
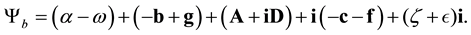
In

is
we must change the sign of bivectors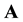
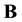
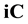

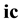
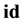
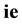
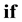
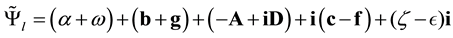


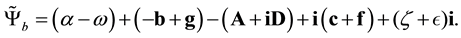
The reverse, in

is
Only terms which change sign, with (A.13), (A.18) and (A.20), are scalars
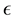
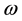
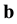
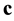
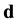

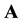
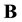
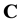
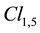
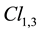
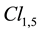
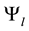

(A.34)
This link between the reversion in

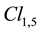
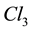
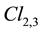
Appendix B. Scalar Densities and

There are
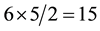
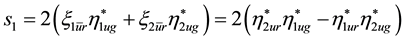

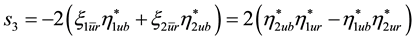

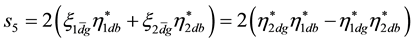
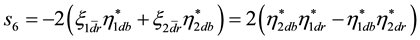
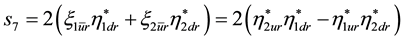
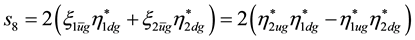
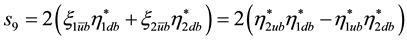

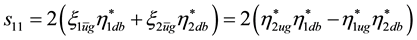

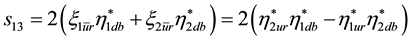


We used in [2]
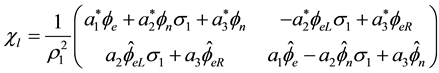
with


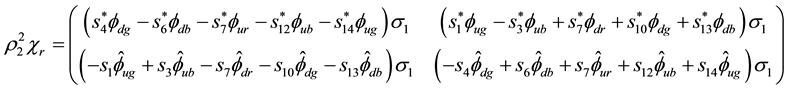
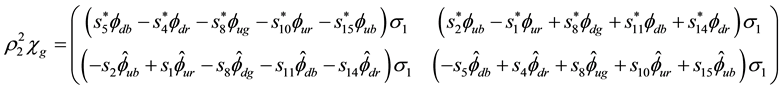

Appendix C. Gauge Invariance, Details
C.1. Gauge Group Generated by
We name
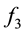

which implies

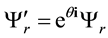
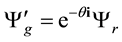

The equality (C.3) is equivalent to
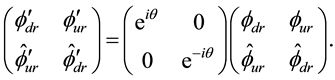
The equality (C.4) is equivalent to
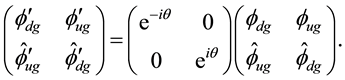
We get




This gives
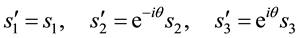


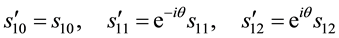
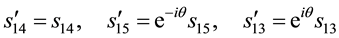
from which we get
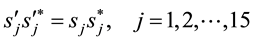
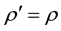
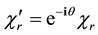
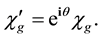
These relations are the awaited ones because
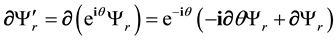
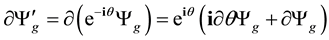

C.2. Gauge Group Generated by
We name
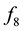

which implies


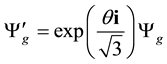
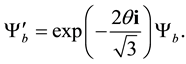
This gives
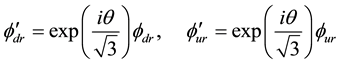
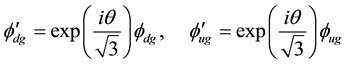
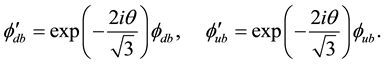
We then get
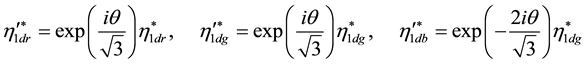

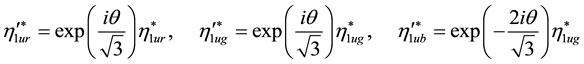
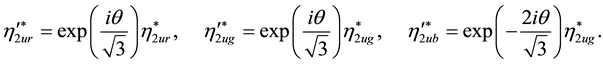
This implies

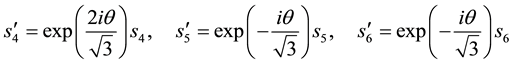
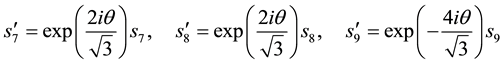
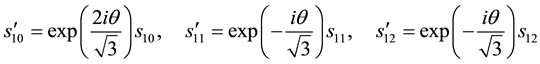

We then get the awaited results
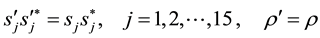
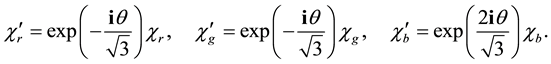 (C.42)
(C.42)
Notes
1The reversion is an anti-isomorphism changing the order of any product (see [1] 1.1). It is specific to each Clifford algebra. The Appendix A explains the link between the reversion in
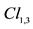
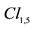
2
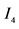
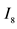
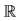

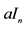

3