ABSTRACT

In this article we show that quantum physics is a straightforward and comprehensive consequence of the model of discrete space-time that we have put forward in [1]. We first introduce the concept of coherent domains and give a proof of the various postulates and principles that form the basis of one-particle quantum systems. Then we consider how spin-statistic theorem and the formalism of second quantization, that are prerequisites for a description of many-particles systems, emerge from the model. Finally the same framework suggests the idea of rigid histories which allows an interpretation of quantum entanglement to be proposed.

Keywords:Quantum Physics Postulates, Decoherence, Entanglement

1. Introduction

In contribution [1] we have put forward a model of discrete space based upon three very general statements: the universe exists; it is not chaotic, and it is not frozen. In this model everything, space, time, fields and particles, has to be reconstructed anew. The first step of this reconstruction, namely the building of space-time, has been carried out in contribution [1] . In the present article we focus our attention on a second step, namely the emergence of the most fundamental description of the physical behaviour of natural phenomena that is quantum physics.

Until the end of the nineteenth century the physicists and more generally the philosophers believed that all natural phenomena could be explained in the framework of classical mechanics. At the beginning of the twentieth century it was realized, however, that classical mechanics was not a convenient tool for small scale (atomic) phenomena. For example, according to classical mechanics, the electrons of an atom must emit electromagnetic waves and immediately fall on the atom nucleus. Therefore, according to classical mechanics, the physical entities called atoms cannot exist despite the numerous proofs of their existence. A new sort of physics, quantum physics, had to be elaborated. It slowly appeared that the quantum theory was based upon three statements called the postulates of the theory. Some physicists prefer the word principle but the two words relate to the same physical reality. Since quantum theory is so efficient at explaining and predicting so many physical phenomena, most physicists do not worry about the physical interpretation of the postulates. Some physicists, however, do not find that this situation is satisfactory and would like to find a physical interpretation to the postulates of quantum theory. This is the purpose of this article. Our physical interpretation of the postulates of quantum theory has made possible thanks to the model of discrete spaces that we put forward in a previous contribution [1] . For sake of completeness and to make this article self contained, a summary of the model of discrete spaces is given in Appendix 1.

The central idea in our way of considering the physical world is that all objects that constitute the universe (particles, field, etc.) are realizations of the structure of space-time itself. Therefore a convenient description of space-time must account for all facets of physics, the quantum theory in particular. In other words, quantum physics must be consubstantial with the structure of space-time. In this article we show that the model of discrete space-time and quantum physics are one and the same thing indeed.

2. Coherent Domains

2.1. Introducing Coherent Domains

Since classical mechanics explains with great precision the behaviour of macroscopic physical bodies and quantum mechanics the behaviour of atomic systems, there is necessarily a boundary where a classical description of physical objects becomes irrelevant and must be replaced by a quantum description. We call this boundary the quantum scale. Here we note a problem: the quantum boundary is not symmetric. Whereas classical mechanics is unable to account for atomic phenomena below the quantum scale, there are many instances of macroscopic situations that cannot be understood without the concepts of quantum mechanics. The electronic properties of metals and semi-conductors, superconductivity, super fluidity, laser emission, Rydberg atoms, etc., are examples of such phenomena.

The model of discrete spaces that forms the basis of the arguments that we develop in this article, and that we intensively use here (Appendix 1) directly gives a physical interpretation to two fundamental aspects of quantum and particles theories: the wave function and the Higgs field.

According to the model of discrete spaces the realizable states of the universe are obtained by minimizing the Lagrangian (Equations (1)-(5) in Appendix 1)

, (1)

where is a set of 4-dimensional matrices, under the constraint

This gives the following eigenvalue equation

, (2)

where is a Lagrange multiplier.

It is unlikely that in Equation (2) represents a physical state of the whole universe because it is unlikely for the coherence of to be preserved everywhere in the universe. Equation (2) must therefore be valid only for a (small) part of the universe wherein keeps its coherence. This part, comprized of 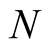world points, is called a coherent domain and, the piece of that belongs to a coherent domain, is called a quantum state. obeys the eigenvalue equation

(3)

with the constraint. is the set of 4-dimensional matrices each associated with a world point of the coherent domain. Since the state in Equation (3) does not depend on we can choose the normalization condition as

. (4)

is a physical entity. It is the set of states of world points belonging to a coherent domain. It must be noted that, because we are dealing with four dimensional objects, the index determines both a time and a position in a four dimensional space. representes the usual wave function of quantum mechanics.

In the same spirit the polarization (see Equations (1)-(4) of Appendix 1) represents a scalar field. It obeys a Landau type free energy and, for four dimendional spaces, its value does not vanish. This corresponds to asymmetric vacuum as assumed for Higgs fields [2] . Moreover, everything disappears, (fields, particles, etc.) if vanishes. seems to have all the properties of a Higgs field and we suggest that the world points polarization is a physical interpretation of Higgs field.

2.2. How Many World Points in a Coherent Domain?

The model of discrete spaces gives a physical meaning to the concept of coherent domains. To determine the number of world points belonging to a given coherent domain we consider the contribution of binary terms to the Lagrangian (Appendix 1 Equation 1-5) of one cosmic bit. On the one hand is connected to the cosmic bits of his own world point through ferromagnetic interactions. This gives rise to a molecular field (where the words molecular field refers to mean field theory). On the other hand is connected to the cosmic bits of the world points “” of the same coherent domain through random interactions. This gives rise to another molecular field. The contribution to is then given by

.

The field is a random Gaussian variable whose distribution is given by

.

Its standard deviation is. The total field is the sum of these contributions:

. The sum of Gaussian variables with standard deviation is a Gaussian variable with standard deviation and the standard deviation of is therefore. In other respects the field is simply given by

.

If the world points are so strongly intertwined that they may be seen as belonging to a single entity, namely a coherent domain. The limit happens when that is when the number of world points neighbours of a world point in a coherent domain is of the order of the number of cosmic bits into this world point.

2.3. On the Size of Coherent Domains

Let us try to give a crude estimate of coherent domain size. A cosmic bit is the smallest physical object one can imagine and the Planck length is the smallest length that can be given a physical meaning. We assume, therefore, that the (non measurable) size of a cosmic bit is.

Furthermore every cosmic bit of a world point is a close neighbour of every cosmic bit of the same world point and, therefore, inside world points, all physical dimensions (space or time) are meaningless concepts. The size of a world point is the scale below which any metrics, the Minkowski metrics in particular, is lost. is also the scale where the distinction between the particles, be they fermions or bosons, disappears and therefore should be the scale where super symmetry theories (Susy) could come play. Hence must of the order of to. For convenience we opt for.

A world point is a four dimensional object and the number of cosmic bits it is made of, is therefore of the order of

The spatial (3-dimensional) size of a coherent domain is then given by

This value must not be taken too strictly since it is very sensitive to the size of a world point. A better way of thinking could be to consider a value of, (the scale where physical phenomena can no more be explained by classical mechanics), say, as an experimental result, and use this value to estimate the size of a world point . We then find which may be interpreted as a boundary between quantum physics and another type of physics that we suggest to call Planck physics.

Classical mechanics, we have said, loses its relevance below the quantum scale and must be replaced by quantum mechanics. Quantum mechanics, however, is not irrelevant above this limit. To understand this point let us consider two identical, slightly overlapping, coherent domains. Their sets of eigenvectors are identical. Let the first coherent domain be in a given eigenstate. This compels the second domain to be in the same eigenstate and this process allows the eigenstates to spread up to macroscopic scales, a process that reminds the technique of analytical continuation.

The effect of a coherent domain that overlaps another, non identical, coherent domain is to destroy the quantum coherence of the later. According to the Zurek terminology the first coherent domain belongs to the environment of the second one. In the present approach of decoherence, space and time are treated on equal footing. This is to be contrasted with the Zurek’s idea of decoherence where time plays a distinctive role [3] . Our understanding of decoherence is, in our opinion, more in the spirit of relativity.

3. One Particle Quantum Systems

This section is devoted to the construction of the basis of one-particle quantum systems. We show below that the postulates of quantum theory are, so to speak, theorems derived from the axioms determined by the proposed model of discrete spaces.

3.1. Introducing a Particle P into Vacuum

First of all the notion of vacuum must be defined. All matrices of a coherent domain devoid of particles are equal to each other and given by

(5)

is the metric matrix of vacuum and is the (dimensionless) speed of light [1] . A coherent domain, comprised of world points, contains one particle if all matrices of the system are all identical to the vacuum matrix except for one world point , called the seed of the particle, where a matrix characterized by the symmetry properties of. The state of the domain housing a particle is given by the following eigenvalue equation

(6)

The eigenvalue equation does not depend on the number of world points in the domain and, therefore, the norm of may be normalized along

.

This normalization condition is written as

.

The parameters are positive numbers and their sum is 1. Therefore they can be interpreted as probabilities: is the probability for world point to be in state. It must be stressed that this is only but an interpretation: itself has no random character.

The mass of particle is given by the eigenvalue: that is by

provided that.

The model of discrete space imposes some properties to one particle quantum systems. These properties are usually expressed in the form of postulates which, therefore, appear as consequences of the model itself.

3.2. First Postulate

The first postulate claims that the states of a quantum system form a complex Hilbert vector space. There are two important points in this statement: on the one hand the states are vectors of a vector space. On the other this space is complex.

Linearity (and therefore the superposition principle) is one of the most central and striking property of quantum mechanics. In the present approach, linearity stems from the quadratic form of the Lagrangian which is a result of limiting to binary interactions. As far as quantum theory is concerned, the influence of fourth order interactions is completely negligible.

is a collection of world points states

that are determined as we have seen, by Equation (6). This equation is linear: that is if and are two eigenstates associated with the same eigenvalue the linear combination

is also an eigenstate of (6) associated with the same eigenvalue. The set of states associated with therefore forms a vector space, and since these vectors are normalized, the set constitutes a Hilbert vector space.

The second statement of the first postulate points out the necessity to use complex vectors. The random matrix and the matrices are, indeed, real-valued and symmetrical. Then the eigenvalues and the eigenstates are real-valued.

The vector space can be made complex-valued by introducing local phase factors, that is, by letting

where the suffix is for complex. This modification does not change the normalization condition since

and transforms the matrix into

a hermitian operator that has exactly the same properties as (in particular the same real eigenvalues), because the eigenvalue equation

becomes

or

.

Transforming the real vector space into a complex vector space therefore has no effect whatsoever as far as physics is concerned: at atomic scale, physics is better expressed in term of complex numbers.

The first postulate writes accordingly:

The states of a quantum system constitute a Hilbert space that is a complex vector space equipped with an inner product that is defined for all its vectors. Let and be two states of a quantum system. These states can be normalized

and the linear superposition

is an allowed state of the quantum system.

3.3. Second Postulate

The second postulate states that the physical quantities that may be measured in a quantum system are given by the eigenvalues of hermitian operators (or observables) that operate in Hilbert spaces.

Besides local symmetries that reflect the symmetry properties of world points and particles, a quantum system may also display global symmetries.

Global symmetries are operations carried out on a quantum system as a whole that leave the physics of the system unchanged. The set of such operations constitutes a finite group that permute the labels ‘’ of world points. We recall that, according to Cayley theorem, any finite group can be considered as a sub-group of a permutation group [4] . One may associate a linear operator to a global symmetry by compelling the operator to remain unchanged under the operations of.

.

The linear operator reflects the physical (symmetry) properties of the system. It may be obtained by projecting the Lagrangian on the trivial representation of.

where is the order of. Let be an eigenvalue of:. is also an eigenvalue of each term of since

and, therefore, is an eigenvalue of itself. We conclude that the set of eigenvalues of is a subset of the set of eigenvalues of. The process can be repeated with a subgroup of. The linear operator associated with is given by

.

The set of eigenvalues of is a subset of. We can consider all possible consecutive subgroups until there is no more subgroup left. We thus obtain a hierarchy of eigenvalues that completely characterize the eigenstates of the system.

Let and be a complete set of eigenvectors and eigenvalues of:

One has

and the closure relation

.

The physical states are normalized

The’s are positive numbers and their sum is 1. They may be considered therefore as probabilities. The average value of in state, computed by using these probabilities, is given by

We thus obtain the second postulate of quantum theory:

To each dynamical variable (a physical concept) there corresponds a linear operator (a mathematical object), or observable, that operates in the Hilbert space. The average value of an operator for a system in state is given by

.

3.4. Third Postulate

According to the third postulate, the dynamics of a quantum system is determined by a Schrödinger equation.

. (7)

To demonstrate this statement we proceed in two steps. We first establish that the eigenvalue Equation (6) is a discrete form of Klein-Gordon equation. Then, in the classical (non relativistic) limit, the Klein-Gordon equation transforms into the Schrödinger equation.

We have already carried out the first step in a previous contribution [1] . For completeness the arguments are repeated in Appendix 2.

The Klein-Gordon equation writes

. (8)

In the non-relativistic limit, where the mass term is much larger than the other terms, the equation may be approximated by

whose solution is

(9)

with

as may be observed by carrying out the derivative of Equation (9) with respect to time. The + sign corresponds to Schrödinger equation (Equation (7)) and we recover the third postulate.

In conclusion, the set of the three postulates of one-particle quantum theory may be seen as consequences of the model of discrete space that we put forward in this essay.

4. Fermions, Bosons and Spin Statistics

Many-particles systems show cooperative phenomena where the spin-statistic theorem plays a central role. This theorem and its formalization by second quantization are introduced along arguments that are, in our opinion, better understood in the framework of the proposed model of discrete than in usual derivations.

4.1. Fermions and Bosons

The symmetry of matrix is determined by a gauge symmetry: The properties of a world point must be insensitive to permutations of the four axes that span the internal spaces of world points, or in other words, it must be insensitive to the operations of the finite group of permutations of four objects. The group has five irreducible representations namely [5] . The representations and their conjugates determine the symmetry of particles. The particles associated with are fermions and those associated with are bosons according to the following argument: The 24 matrices of the irreducible representation may be seen as rotations described by the 2-dimensional representation (SU(2)) of 3-dimensional rotations and one knows that, in this representation, one has which is a specific property of fermions

.

The 24 matrices of the irreducible representation may be seen as rotations described by the 3-dimensional representation of 3-dimensional rotations (SO(3)) and we know that, in this representation, one has which is a specific property of bosons

.

4.2. Spin Statistics

If is a state of a coherent domain containing one particle, the state is the same state whatever.

Let us now introduce a second, identical, particle in the same coherent domain. The state of this second particle is identical to the state of the first particle if. The phase of can be chosen at will but this is not the case for the phase of.

For particles called bosons it is necessary that because a non co linearity of the states would induce an increase of the Lagrangian of all world points and therefore an increase of the Lagrangian of the whole coherent domain. In a system containing identical bosons all phases tend to be equal to each other. This coherent phase manifests itself at a macroscopic level through the special properties of super conductors and super fluids.

The behaviour of particles called fermions is different due to their different symmetry properties. While, for bosons, one has:

the same rotation acting on a fermion changes its sign:

.

Then the Lagrangian is minimized if and the optimal state is a state where the states of the two fermions are opposite and therefore annihilate each other because. Two fermions cannot be in the same state.

Fermions and bosons are usually defined by the symmetry properties of a pair of identical particles under the symmetry group of permutations of two objects. This group has two elements, two classes and two irreducible representations and with the following table of characters (Table 1).

In this approach bosons are defined as particles that transform according to and fermions as particles that transform according to. This way of introducing the particles is not really satisfactory because only pairs of

particles are defined and isolated particles are not given a meaning. A particle is better defined by the symmetry properties of the matrices associated with world points. Bosons are particles whose matrices are left invariant under the transformation of group SO(3) and fermions are particles whose matrices are left invariant under the transformation of group SU(2).

In our opinion this is a better, and more physical, way for an introduction to the Pauli Exclusion Principle and the spin statistics theorem.

4.3. Creation and Annihilation Operators

Let us consider a quantum system containing two identical particles that is a system where two matrices associated with world points and are such that. Two limit situations are possible:

a) and belong to the same coherent domain. The set of matrices of the domain is called and the state of the domain is given by the eigenvalue equation

with the normalization condition.

b) and belong to two disconnected coherent domains. The set of matrices of the system is called and the state of the domain is given by the eigenvalue equation

with the normalization condition.

More generally, with identical particles, one has in the first case and in the second.

There are intermediate situations where the coherent domains more or less overlap. For example the state

represents a set of particles, with particles gathered into one domain and one other particle into a disconnected, but slightly overlapping, domain. For bosons may be any number. For fermions only the values are permitted.

The transition, from the state with all particles belonging to a given coherent domain to the state, represents the creation of one particle in another coherent domain. This transition can be formalized by a creation operator whose effect is to move one particle from a coherent domain into another coherent domain. This operator is defined by

.

The space built up from the states with different occupation numbers is called a Fock space. The representation of the creation operator in the Fock space is given by

.

All other terms vanish. The annihilation operator is the conjugate of. Its elements are therefore written as

.

Then, for bosons,

andthat is

, whence the bosons commutation rule

.

The Fock space of fermions is bi-dimensional. That is

and

or

, whence the fermions anti-commutation rule

.

A new particle emerges by decreasing the overlap between the coherent domains. The creation process therefore amounts to a disconnection between two coherent domains.

5. Non-Locality of Quantum Physics

A consequence of quantum physics is the entanglement phenomenon according to which two particles, once in interaction, remain in interaction for ever. Such behaviour seems to go against the principles of relativity but various sorts of experiments have proved that entanglement does really exist. A physical interpretation that jeopardizes neither the principles of relativistic mechanics nor the classical causality is therefore a necessity. The model of discrete spaces yields such an interpretation because the physical time has no more an ontological status. The physical time is fully determined by the experimental set-up and is disconnected from the time experienced by the observer.

5.1. Rigid Histories

The eigenvalue Equation (6) may be seen either as a differential equation (the Klein-Gordon equation) or as a solution of this equation. The function describes the state of the quantum system for all space-time coordinates. We may consider that represents a whole history. The determination of histories is the general goal of physical theories. For example in classical mechanics the history represents the dynamics of a falling body and the history the dynamics of wave propagation. A history must be understood as a single, one piece, physical entity, called a rigid history that cannot be spontaneously broken into disconnected parts.

The parameter, called physical time, must not be confused with the experimental (or proper) time. When an experimentalist strives to verify a theory, for example the dynamics of a falling body, he looks at his watch which gives him the value of a time that we call his proper time (proper to the experimentalist). Then the experimentalist replaces the time in by 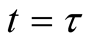and verifies whether the physical system is in state or not. When theoretician and experimentalist agree with each other, they gain some confidence in the relevance of the theory that led to. In our approach a rigid history is an eigenvector of the Lagrangian and this is the history itself that determines both time and space. The physical systems are no more considered as entities that move in a predetermined space-time, the classical background disappears, but they are entities that determine space-time itself. For example a straight line is an object defined by a constant phase: and, in our opinion, it would be more correct to say that a straight line is defined by a light beam rather than to say that a light beam follows a straight line. Likewise a pendulum is generally considered as a physical system that measures time. In our opinion it would be more convenient to consider the pendulum as a physical system whose repetitive states introduce the notion of time (in fact the proper time). These arguments are close to the ideas developed by Carlo Rovelli [6] .

5.2. Entanglement

A typical entanglement experiment [7] involves a pair of particles (1) and (2) emitted by a single source with zero total polarization, for example a pair of photons. According to the formalism of quantum theory the state of a pair of entangled bosons may be written as

.

On the path of, say, photon (1) we place a polarizer. The state of the polarizer is either or and under the control of an experimentalist. The polarizer may be seen as a projector operator. For example

then

.

Also

that is the polarizations are always anti-correlated. This anti-correlation is preserved even if the state of the polarizer is modified in times shorter than the time taken for the light to propagate from one detector to the other [8] . In other words the observation seems to violate the relativistic causality [9] .

The history of the two photons depends on experimental conditions here on the polarizer polarisation. We have therefore two types of histories that is, two sorts of eigenstates. Changing the polarizer’s polarization amounts to change one eigenstate into the other and the question is to understand the dynamics that transforms an eigenstate into the other. The central idea is that this dynamics cannot be expressed in term of physical time because the physical time is a construction inherent to eigenstates and has no meaning in the context of eigenstates (rigid histories) transformations. In particular the relativistic causality is a property of eigenstates themselves and is irrelevant in the context of the transformation of an eigenstate into another. Modifying the state of the polarizer modifies the whole history of the pair of photons instantaneously from the point of view of the observer and the anti-correlation property is conserved whatever the polarizer state.

The following metaphor (which obviously is not a proof) may help. We consider that a movie is a history (in the sense defined above) in a 3-dimensional space made of a two dimensional space and a one dimensional time space. The two dimensional space is constituted by the set of images printed on the film and the one dimensional time space is formed by the successive notches which move the film forward. The time experienced inside the movie by the protagonists has nothing to do with the notches. The speed of the film, that is the speed of the gear that moves the notches, is controlled by the projectionist. The notch number determines the proper time of the projectionist. The projectionist may be seen as an experimentalist and the script of the movie as a particular experimental set up that determines the history described in the movie. Let us assume that two movies are realized that are based upon two scripts that only differ by one detail. For example in the script of movie A the cat of the main character dies at the beginning of the story whereas he stays alive in the script of movie B. Let the projectionist starts the movie A. After a while the projectionist stops the projector at a certain notch and changes film A for film B. When the projector restarts, the main character, in the world of the movie that evolves according to, does not feel any time discontinuity but he his faced with a strange situation. He knows that the cat is dead and however he sees the cat alive exactly as the particle (2), who “knows” that the polarizer is in state, “sees” that is in state.

Let us state those arguments in a different way. The central idea is that neither time nor space has an ontological status and that they must rather be considered as constructions built along a blueprint provided by eigenstates of the Lagrangian of the system. The eigenstates, called rigid histories, depend on experimental conditions. If the conditions are modified the eigenstates are also modified and space and time have to be reconstructed anew. If the experimental conditions are modified while the experiment is in progress, the dynamics of the system proceeds as if the new conditions have existed from the start but this takes effect only after the modifications come into effect, so securing for the experimentalist the principle of classical causality.

The experimental setups determine which rigid history materializes. Two histories may be so different that no physical (natural) process can transform one into the other. For example we do not know any physical mechanism that spontaneously transforms a polarizer into a polarizer. The experimentalist, however, has the power to build bridges between histories, and to change into. The paradox is that the experimentalist himself belongs to nature. To solve the paradox one must understand that the experimentalist has a wonderful machine at his disposal, namely his brain.  The model of discrete universe that we propose is a sort of spin glass where binary entities interact through binary random interactions. We can consider that the brain is also a sort of spin glass where the neurons play the role of world points and the synapses the role of binary interactions [10] . In reality the structure of the human brain is much richer than the structure of space-time. There are of the order of synapses in a human brain. The connectivity between the neurons is similar to the connectivity in a 30 dimensional hypercube and, more than anything else, the connections between the neurons are not random but are the result of learning processes. We can consider that the possibility for human beings to make bridges between situations (rigid histories) that would remain unrelated otherwise is an act of creation. Creation is a process that, so to speak, places the experimentalist outside the usual realm of natural phenomena and the actual observation of the entanglement phenomenon needs the intervention of a human mind.

5.3. Quantum States Reduction

The phenomenon of quantum states reduction can also be understood in terms of histories. We consider an experiment where a photon, emitted by a very distant sources, possibly activates a detector.

We have two sorts of experimental setups.

a) In setup, a photon source, located at point in the three dimensional space, emits a photon in vacuum space.

We know that the history of the photon obeys a propagation equation

.

It is described therefore by a plane wave

with. The vector fully characterizes a history and we may formalize simply by a ket vector. A particular history is anisotropic but the whole set of histories with given, reconstructs the spherical electromagnetic wave generated by Maxwell equations.

b) In setup a detector is added at a point in the three dimensional space.

We assume that is a two-states system. Let be the state of the detector. Either is activated or is silent.

The plane wave created by does not couple with except if the wave vector is strictly parallel to the vector which is very unlikely. When is parallel to the state can couple with the state. The histories of the coupled system can be expressed in terms of product vectors. They are eigenvectors of the operator

with. is an operator that creates (annihilates) a photon. Explicitly

.

To the two eigenvectors there correspond two sorts of histories. The two eigenvalues are given by

and the two types of histories by

.

The probability for detector to be activated is

and for to remain silent

.

In the limit of zero coupling constant one has: remains silent. An efficient detector is characterized by the condition. Then and both types of histories end with an activated detector. .

From the point of view of the observer a particle has effectively hit the detector although no localized particle is involved in the process

6. Discussion and Conclusions

We show in this contribution that the model of discrete space-time that we put forward may constitute a convenient basis for the foundations of quantum theory. The postulates and principles that form the axiomatic framework of the theory are recovered. Most concepts that are introduced by quantum theory loose their elusive characters and gain a physical meaning. So is the case of quantum states, Hilbert spaces, etc. According to the model even particles masses become a property of space-time and are no more free parameters.

The model also introduces a cut-off in quantum theory. This, obviously, solves the problem of ultraviolet divergences but not the divergences of whole series and the renormalization procedures keep all their interest. Below the quantum theory looses its significance since the quantum states disappear. The relativity theory also looses its significance since the metrics disappears. Accordingly there are no more basic contradictions between quantum and relativistic theories and no more need to merge these theories into a single framework.

Finally, for the model to be really efficient, it remains to prove that it could account for the standard model of particles and their interactions. This is out of the scope of the present contribution but will be the object of future contributions.

Acknowledgments

I would like to thank again Pr. Roger Maynard, a friend whose comments helped me much to finalize the present article.

References

Appendix 1: The Model of Discrete Space-Time: A Summary and Reminder

We summarize in this appendix the main features of the model of discrete space-time that we have put forward previously in [1] .

a) Our universe as a whole is entirely made of a finite countable set of basic physical units called cosmic bits. The state of a cosmic bit is fully determined by a binary variable analogous to an Ising (classical) spin.

b) The state of the universe is determined by a family of cosmic bits states

.

We may write as a -dimensional vector whose norm is: In discrete spaces with finite the states of the universe are necessarily normalized.

c) The cosmic bits interact with each other through binary and quaternary random interactions and a state of the universe is obtained, at least approximately, by minimizing the Lagrangian

(1-1)

under the constraint which yields the following eigenvalue equation

(1-2)

d) Due to their interactions the cosmic bits organize in clusters of n cosmic bits all interacting with each other through ferromagnetic (negative) binary interactions. These clusters are called world points with and the world points interact with each other through random binary interactions. The state of a world point is written as a 4-dimensional vector

(1-3)

where the components obey the constraint

(1-4)

The quadratic interactions between the polarizations is written as

.

Since the states of world points do not depend on their surrounding, the matrix factorizes

.

e) Finally the Lagrangian, limited to second order terms, is expressed in terms of stateswith

and one has

(1-5)

where is a set of square, real, symmetric, 4-dimensional matrices that generates space, time, and particles and is a random, square, real, symmetric -dimensional matrix whose elements describes the interactions between world points and.

Appendix 2: Derivation of the Klein-Gordon Equation

We first remind the notion of derivatives in the context of discrete spaces. We define a square, real, -dimensional matrix by. Thanks to the LDU theorem of Baniacewicz may be expressed as a random triangular matrix and is its transpose The increment of a polarization of world point”” is given by

that is

for each component of. The first order derivative of along the axis is then defined by

where is the smallest length that has a physically measurable meaning, that is the scale where the metrics is lost and also the scale where the distinction between the particles, be they fermions or bosons, disappears. may be seen as a differential operator because it is linear and it obeys the Leibniz formula [1] .

is a scalar field but physics generally deals with vector fields that are vectors of the internal spaces of world points. The components of a vector field are given by

and the increment of the component by

The first order derivative of along the axis is then given by

.

Let us now consider second order derivatives.

The second order increment of a scalar function at world point is

that is

for each component of. The second order derivative of along the axis is then given by

and the second order derivative of the vector field component along axis by

For trivial fibre bundles where the matrix is the same whatever the world point, one entry of Equation (5), , writes

One introduces the coefficient in both members of this equation and carries out the sum over index:

.

By using the diagonal expression of, the metric matrix of vacuum, and the two parameters and, the final equation reads

(2-1)

where and (see Equation (5)). Then Equation (2-1) is recognized as a set of four KleinGordon equations.