Journal of Modern Physics
Vol.5 No.6(2014), Article ID:45400,4 pages DOI:10.4236/jmp.2014.56057
Oxygen Isotope Effects on Tc Related to Polaronic Superconductivity in Underdoped Cuprates
B. I. Kochelaev1, K. A. Müller2, A. Shengelaya3
1Institute of Physics, Kazan Federal University, Kremlevskaya 18, Kazan, Russia
2Physik-Institut der Universität Zürich, Winterthurerstr, Zürich, Switzerland
3Department of Physics, Tbilisi State University, Chavchavadze, Tbilisi, Georgia
Email: irmamf@bluewin.ch
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 February 2014; revised 24 March 2014; accepted 17 April 2014
ABSTRACT
The planar oxygen isotope effect on Tc observed in copper oxide superconductors is remarkable in that it increases from near nil at optimal doping to a value twice that derived from BCS theory in the underdoped region. This behavior is quantitatively followed by a formula proposed by Kresin and Wolf in 1994 for polarons along the c-axis. Herein it is revisited in a more transparent way, and it is pointed out that the heterogeneity of pairing is relevant and has to be taken into account to explain the unusual planar isotope effects on Tc in underdoped cuprates.
Keywords:Cuprates, High-Temperature Superconductivity, Polarons, Isotope Effect

In crystals, phase transitions from one state to another can occur. If the naturally present isotopes of certain atoms or ions are replaced by chemically identical isotopes with a different mass M the transition temperature Tc can change. This is called the isotope effect, and it is described by Tc µ M−a, where a is the isotope exponent, which for classical metal or metal alloy superconductors are mostly 1/2. It supports the value derived in BCS theory. This square-root law results from the phonon energy, which yields the coupling between the electrons forming the Cooper pair [1] .
The first experiments in copper oxides were carried out in Battlogg’s group at Bell Laboratories by substituting the naturally present 16O by the 18O isotope. At optimum doping, a vanishing effect was found [2] . This marks the starting efforts of electronic theories, such as RVB, the t − J model and others, pursued by the main community interested in the superconductivity of cuprates [3] . Thereby it was ignored that in Canada nearly simultaneously an oxygen isotope effect was reported by the group of Frank in underdoped LSCO [4] . Thus, the possibility exists that in this new type of superconductors with small carrier concentration a may actually depend on the carrier concentration n: a (n).
Several groups, especially that of Keller at the University of Zürich, have investigated this possibility and found ample evidence of it. Upon reducing n, a (n) increased to a large value of a (nSI) @ 1, i.e., twice the BCS value at the superconducting-to-insulator transition at nSI @ 0.06 [5] . From optimum doping with a @ 0 toward a reduced temperature of t = T/Tmax = 0.4, the experiments were quantitatively reproduced by a vibronic theory of Bussmann-Holder and Keller (BHK) [6] in which the electronic d-type ground-state band is coupled by a linear vibronic term to the next excited s-oxygen band. The agreement occurred for lattice distortions around the Cu2+ ions of the t2g conformation. These are the distortions that for Cu2+ are Jahn-Teller active, thus in a way confirming the original concept of Müller that JT polarons are relevant for finding high-temperature superconductivity [7] .
The deviation of the data from the above-discussed theory for smaller values of T/Tmax = 0.4 was attributed to the more heterogeneous distribution of charge carriers resulting from the lower dopings [8] , because the BHK theory is a mean-field theory that represents homogenous distributions of polarons better.
Recently Weyeneth and Müller [9] demonstrated that the planar isotope effect as a function of hole doping in various cuprate superconductors can be described very well by the formula
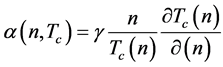 . (1)
. (1)
As can be seen from Figure 1, this formula provides an excellent description of the isotope effect from optimal doping down to the quite underdoped region with near-vanishing superconductivity.
Originally the formula in Equation (1) was obtained by Kresin and Wolf for the case of polarons, i.e., for local vibronic lattice deformations along the crystallographic c-axis [10] . However, the site-selective oxygen substitution 16O → 18O experiments showed that the observed oxygen isotope effect is predominantly due to oxygen atom vibrations in the CuO2 planes [11] . The success of this formula for describing planar isotope effects means that Equation (1) is generally valid also for polarons in the CuO2 planes, and not only for polarons along the caxis, for which it was originally obtained.
To understand the reason why Equation (1) can be valid also for planar polarons, let us first reproduce it here using the arguments of Kresin and Wolf. This is also useful as the derivation of this formula was described only
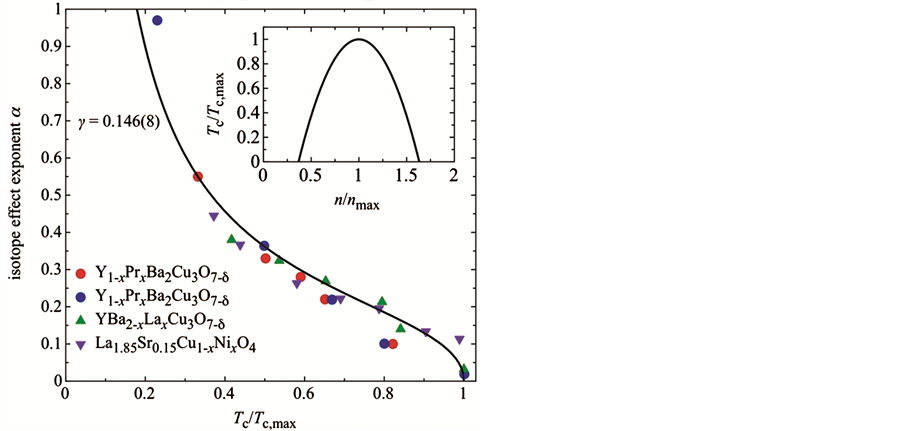
Figure 1. The oxygen isotope exponent α as a function of Tc/Tc,max for various high-Tc cuprate superconductors. The solid line represents the fit using Equation (1). From [9] .
briefly in the original publication [10] .
Kresin and Wolf proposed that the dynamic of apical oxygen along the c-axis is described by a double-well potential. As a result, the charge transfer between the charge reservoir and the CuO2 planes occurring through apical oxygen depends on the tunneling of this oxygen to another minimum of the double-well potential. The tunneling is affected by the oxygen isotope mass M. In the case of a large asymmetry between the two different potential electronic terms (double-well structure), Kresin and Wolf found that the in-plane concentration of the charge carriers is proportional to the probability of charge transfer from the charge reservoir to the CuO2 plane [10] :
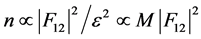 , (2)
, (2)
where ε is the splitting between the vibrational levels of the two terms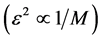 , and F12 is the FranckCondon factor (see [10] [12] ):
, and F12 is the FranckCondon factor (see [10] [12] ):
 . (3)
. (3)
Here v is a vibrational quantum number, δ is the distance between the minima, and k is the effective elastic constant. It is important to note that the strongest dependence of F12 on M yields the exponent. From Equations (2) and (3), we obtain
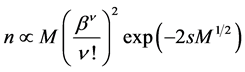 . (4)
. (4)
The isotope exponent was defined in the following way [10] :
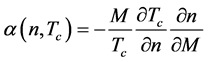 . (5)
. (5)
Using Equation (4) yields
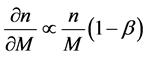 . (6)
. (6)
Finally, for the isotope exponent α(n, M) we obtain
 . (7)
. (7)
This result is consistent with Equation (1). The value of sM−1/2 actually does not depend on the doping.
According to the model of Kresin and Wolf, the isotope effect described by Equation (1) is unusual as it is not related to the change of vibrational frequency, but reflects the impact of the isotope substitution upon the charge transfer [10] . To apply this formula to the planar polarons, it is necessary to find a microscopic mechanism of how the change of the isotope mass of the in-plane oxygen ions could influence the local charge-carrier concentration in CuO2 planes. We propose that this mechanism may be related to the microscopic electronic phase separation into metallic and dielectric regions in the CuO2 plane, which is especially pronounced in underdoped cuprates. The results of an electron paramagnetic resonance (EPR) study of such a phase separation in lightly doped La2−xSrxCuO4 showed that the starting point for the creation of metallic regions is the formation of a bipolaron by two three-spin polarons (3SP) [13] . EPR experiments also demonstrated upon cooling bipolarons condense into metallic clusters or stripes. The percolation of these clusters/stripes leads to a superconducting transition [14] . Therefore we can expect that the concentration of charge carriers in the metallic regions will be related to the probability of bipolaron formation. This bears some similarity with the mechanism considered by Kresin and Wolf, but this time it concerns polarons in the CuO2 planes. Now, the interaction between polarons to form the bipolaron was considered to be a coupling via elastic interaction, which involves acoustic modes [13] . However, it is possible that the coupling via optical modes related to in-plane vibrations of oxygen atoms is more important. Then the probability of bipolaron formation due to the interaction between the 3SPs will strongly depend on M. These qualitative considerations need to be confirmed by a detailed study, which will be a subject of future work.
Acknowledgements
The authors thank Vladimir Kresin for bringing an earlier incomplete version of Equations (6) and (7) to their attention.
References
- Tinkham, M. (1975) Introduction to Superconductivity. Mc Graw Hill Inc., New York.
- Battlogg, B., Cava, R.J., Jayaraman, A., van Dover, R.B., Kourouklis, G.A., Sunshine, S., Murphy, D.W., Rupp, L.W., Chen, H.S., White, A., Short, K.T., Mujsce, A.M. and Rietman, E.A. (1987) Physical Review Letters, 58, 2333-2336.
- Schrieffer, J. R. and Brooks J.S. (2007) Handbook of High-Temperature Superconductivity. Springer Science + Business Media, LLC, New York.
- Franck, J.P., Jung, J., Mohamed, M.A.-K., Gygax, S. and Sproule, G.I. (1991) Physical Review B, 44, 5318-5321. http://dx.doi.org/10.1103/PhysRevB.44.5318
- Khasanov, R., Shengelaya, A., Morenzoni, E., Conder, K., Savić, I.M. and Keller, H. (2004) Journal of Physics: Condensing Material, 16, S4439-S4455. http://dx.doi.org/10.1088/0953-8984/16/40/003
- Bussmann-Holder, A. and Keller, H. (2005) European Physical Journal B, 44, 487-490. http://dx.doi.org/10.1140/epjb/e2005-00148-9
- Bednorz, J.G. and Müller, K.A. (1986) Zeitschrift für Physik B Condensed Matter, 64, 189-193. http://dx.doi.org/10.1007/BF01303701
- Keller, H., Bussmann-Holder, A. and Müller, K.A. (2008) Materials Today, 11, 38-46. http://dx.doi.org/10.1016/S1369-7021(08)70178-0
- Weyeneth, S. and Müller, K.A. (2011) Journal of Superconductivity and Novel Magnetism, 24, 1235-1239. http://dx.doi.org/10.1007/s10948-011-1151-3
- Kresin, V.Z. and Wolf, S.A. (1994) Physical Review B, 49, 3652-3654. http://dx.doi.org/10.1103/PhysRevB.49.3652
- Zech, D., Keller, H., Conder, K., Kaldis, E., Liarokapis, E., Poulakis, N. and Müller, K.A. (1994) Nature (London), 371, 681-683. http://dx.doi.org/10.1038/371681a0
- Kresin, V. (2010) Journal of Superconductivity and Novel Magnetism, 23, 179-182. http://dx.doi.org/10.1007/s10948-009-0591-5
- Shengelaya, A., Bruun, M., Kochelaev, B.I., Safina, A., Conder, K. and Müller, K.A. (2004) Physical Review Letters, 93, 017001. http://dx.doi.org/10.1103/PhysRevLett.93.017001
- Mihailovic, D., Kabanov, V.V. and Müller, K.A. (2002) Europhysical Letters, 57, 254-259. http://dx.doi.org/10.1209/epl/i2002-00569-0

