Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33336,25 pages DOI:10.4236/jmp.2013.46113
The Spin-Charge-Family Theory Is Explaining the Origin of Families, of the Higgs and the Yukawa Couplings
Department of Physics, FMF, University of Ljubljana, Ljubljana, Slovenia
Email: norma.mankoc@fmf.uni-lj.si
Copyright © 2013 Norma Susana Mankoč Borštnik. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 18, 2013; revised April 20, 2013; accepted May 15, 2013
Keywords: Unifying Theories; Beyond the Standard Model; Origin of Families; Origin of Mass Matrices of Leptons and Quarks; Flavour Symmetry; The Fourth Family; Origin and Properties of Scalar Fields; Origin of Dark Matter; Origin and Properties of Gauge Bosons; Kaluza-Klein-Like Theories
ABSTRACT
The (extremely efficient) standard model of the elementary particles and fields makes several assumptions, which call for explanations. Any theory offering next step beyond the standard model must explain at least the existence and properties of families and their members and correspondingly the existence of the scalar Higgs and the Yukawa couplings, which in this model take care of masses of fermions and weak bosons and influence the decaying properties of families. The spin-charge-family theory [1-11] is offering a possible explanation for the assumptions of the standard model—for the appearance of families and their members (for the charges of a family members), for the gauge fields, for the scalar fields—interpreting the standard model as its low energy effective manifestation. The spin-charge-family theory predicts at the low energy regime two decoupled groups of four families of quarks and leptons. The predicted fourth family waits to be observed, while the stable fifth family is the candidate to form the dark matter. In this paper properties of families are analysed. The appearance of several scalar fields, all in the bosonic (adjoint) representations with respect to the family groups, while they are doublets with respect to the weak charge, is presented, their properties discussed, it is explained how these scalar fields can effectively be interpreted as the standard model Higgs and the Yukawa couplings. The spin-charge-family theory predicts that there are no supersymmetric partners of the observed fermions and bosons.
1. Introduction
When the standard model of the elementary particles and fields was proposed more than 35 years ago, it offered an elegant new step in understanding the origin of fermion and boson fields and the interactions among them.
It is built on several assumptions, chosen to be in agreement with the data: 1) There exist before the electroweak break massless family members—the coloured quarks and the colourless leptons, both “left” and “right handed”, the left handed members distinguishing from the right handed ones in the weak and hyper charges; 2) There exist the gauge fields to the observed charges of the family members; 3) There exists a boson, the Higgs, with a “non zero vacuum expectation value” after the electroweak break, a scalar with the charges of a fermion. Its properties are chosen to “dress” successfully the “right handed” family members with the weak and the appropriate “hyper” charge so that they manifest the properties of the left handed partners. The Higgs takes care at the same time of the masses of fermions and of the weak gauge fields 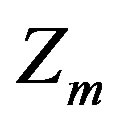 and
and ; 4) There exist the families of fermions; 5) There exist the Yukawa couplings, distinguishing among family members (
; 4) There exist the families of fermions; 5) There exist the Yukawa couplings, distinguishing among family members (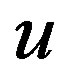 and
and 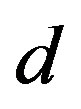 quarks,
quarks,  and
and 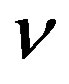 leptons) to ensure right properties of families of fermions, that is of their masses and decay properties (mixing matrices).
leptons) to ensure right properties of families of fermions, that is of their masses and decay properties (mixing matrices).
The properties of fermions and bosons as assumed by the standard model before the electroweak break are presented in Tables 1-3.
While all the so far observed fermions are spinors with the charges in the fundamental representations of the charge groups and all the so far observed bosons are vectors in the adjoint representations with respect to the charge groups, the Higgs field and its anti-Higgs are scalars with the weak charges in the fundamental representations of the (weak) charge group. Therefore, quite a strange object, which reminds us of a supersymmetric
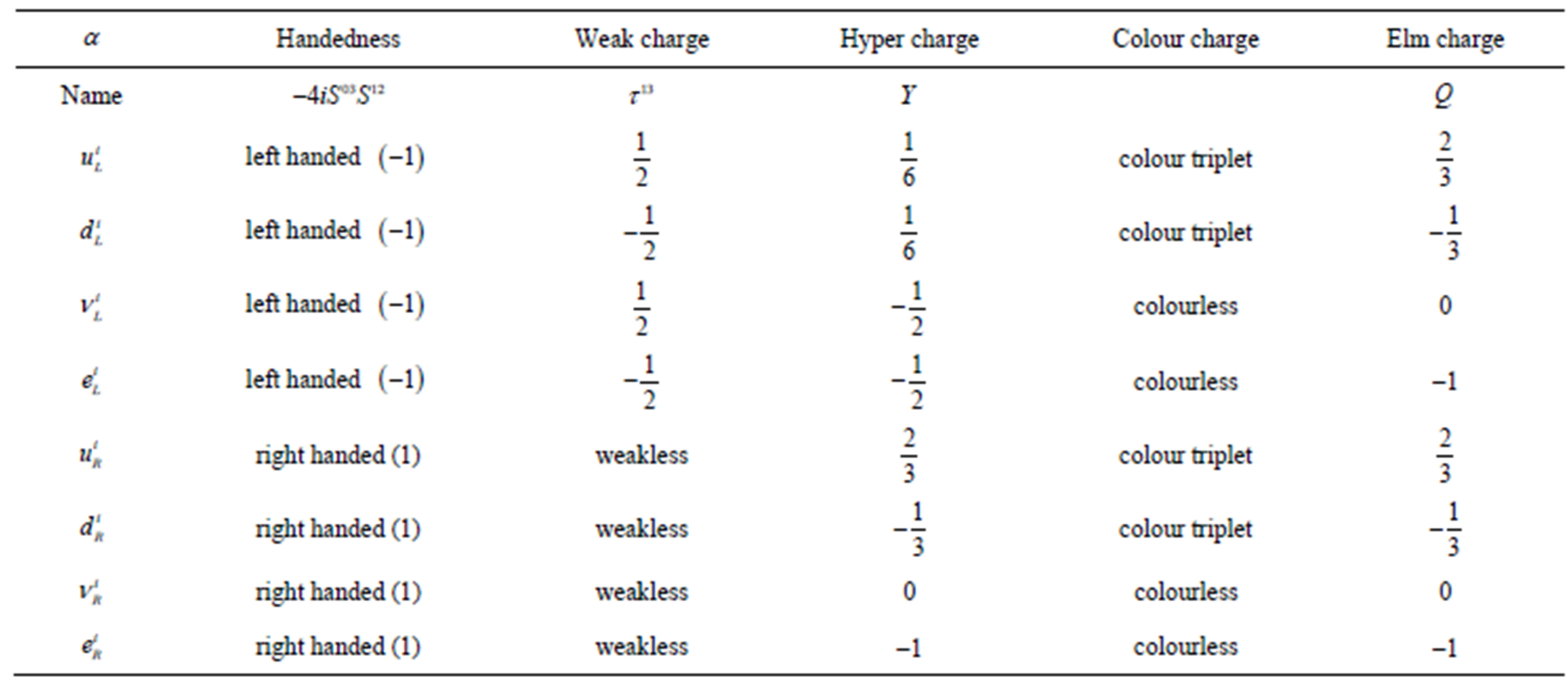
Table 1. The standard model assumes that there are before the electroweak phase transition three  so far observed massless families of quarks and leptons. Each family contains the left handed weak charged and the right handed weak chargeless quarks, belonging to the colour triplet
so far observed massless families of quarks and leptons. Each family contains the left handed weak charged and the right handed weak chargeless quarks, belonging to the colour triplet ,
,  ,
, 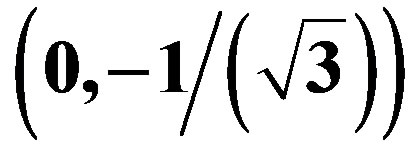 and the colourless left handed weak charged and the right handed weak chargeless leptons, if in this tiny extension of the standard model the right handed
and the colourless left handed weak charged and the right handed weak chargeless leptons, if in this tiny extension of the standard model the right handed 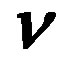 is added. Originally
is added. Originally  were excluded since no mass of
were excluded since no mass of  was measured and in the standard model assumption all the quantum numbers of
was measured and in the standard model assumption all the quantum numbers of  are zero.
are zero. 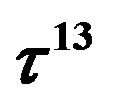 defines the third component of the weak charge,
defines the third component of the weak charge, 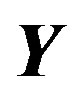 the hyper charge,
the hyper charge, 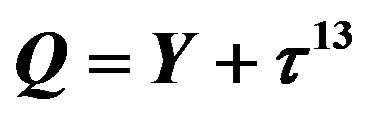 is the electromagnetic charge.
is the electromagnetic charge.

Table 2. The standard model assumes that there are before the electroweak phase transition three massless vector fields, the gauge fields of the three charges—the hyper charge , the weak charge
, the weak charge 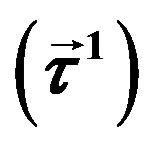 and the colour charge
and the colour charge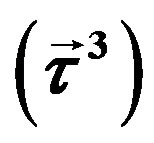 , respectively. They all are vectors in
, respectively. They all are vectors in , carrying the corresponding charges in the adjoint representations.
, carrying the corresponding charges in the adjoint representations. .
.

Table 3. The standard model assumes that there is before the electroweak phase transition the scalar field Higgs, a boson, which carries the hyper charge 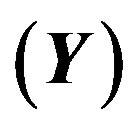 and the weak charge
and the weak charge  in the fundamental (spinor) representations of the charge groups. It contributes to the phase transition by gaining a non zero “vacuum expectation value” of that component which has the electromagnetic charge
in the fundamental (spinor) representations of the charge groups. It contributes to the phase transition by gaining a non zero “vacuum expectation value” of that component which has the electromagnetic charge 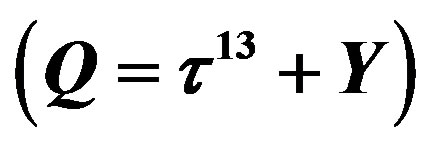 equal to zero. Correspondingly it changes properties of the vacuum. And there is the “anti-Higgs”. The Higgs “dresses” the right handed
equal to zero. Correspondingly it changes properties of the vacuum. And there is the “anti-Higgs”. The Higgs “dresses” the right handed 
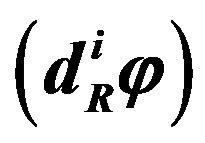 and
and 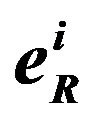
 with the weak and the appropriate hyper charge, the anti-Higgs “dresses” correspondingly
with the weak and the appropriate hyper charge, the anti-Higgs “dresses” correspondingly 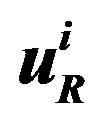
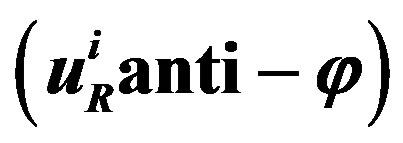 and
and 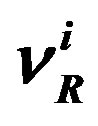
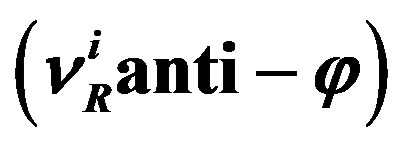 . Higgs takes care of the masses of the superposition of the weak and hyper charge gauge bosons, leaving the electromagnetic field massless. To take care of the masses and mixing matrices of fermions in agreement with the experimental data the standard model postulates the existence of Yukawa couplings, which are different for different family members.
. Higgs takes care of the masses of the superposition of the weak and hyper charge gauge bosons, leaving the electromagnetic field massless. To take care of the masses and mixing matrices of fermions in agreement with the experimental data the standard model postulates the existence of Yukawa couplings, which are different for different family members.
particle (but it is not because it does not fit the so called R parity requirement for a supersymmetric particle).
The standard model never had the ambition to explain its own assumptions, leaving the explanation of the open questions to the next step of the theory. Yet it is, without any doubt, a very efficient effective theory: There is so far no experiment which would help to show the next step beyond it, no new fermions or bosons, no supersymmetric particles, but (finally seems to be) proven Higgs.
There are many proposals in the literature [12-20] extending the standard model. Not one explains, to my knowledge, the origin of families. Many of them just extend the ideas of the standard model. 1) A tiny extension is the inclusion of the right handed neutrinos into the family (like it is already done in Table 1); 2) Supersymmetric theories assume the existence of partners to the so far observed fermions and bosons, with charges in the opposite representations, adjoint for fermions and fundamental for bosons, offering no explanation for the appearance of families; 3) The Kaluza-Klein-like [21,22] theories offer the unification of spin and charges, but do not offer the explanation for the appearance of families; 4) The  group is assumed to describe—not explain —the existence of three families [23-27]; 5) String theories [20] have possibilities to explain the origin of families but again by assuming appropriate groups in scenarios leading to an acceptable low energy regime.
group is assumed to describe—not explain —the existence of three families [23-27]; 5) String theories [20] have possibilities to explain the origin of families but again by assuming appropriate groups in scenarios leading to an acceptable low energy regime.
Any new successful proposal, model, theory, offering a step beyond the standard model, must, to my understanding, offer:
• The explanation for the appearance of families of fermions and correspondingly of their mass matrices, predicting the number of families.
• The explanation for the origin of scalar fields—of the Higgs and of the Yukawa couplings, explaining correspondingly the origin of the fermion masses and their mixing matrices.
• The explanation for the dark matter.
There are also several other questions which may not be so urgently answered, like: Where does the dark energy originate? What is the origin of charges, and correspondingly of the gauge fields? What does cause the matter-antimatter asymmetry? And (many) others.
The theory unifying spin and charges and predicting families [1-11,28,33,34,37], to be called the spin-chargefamily theory, seems promising in answering these, and several other questions, which the standard model leaves unanswered.
The spin-charge-family theory assumes in
 ,
, 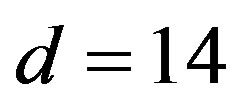 (or larger), a simple starting action for spinors and the gauge fields: Spinors carry only two kinds of the spins (no charges), namely the one postulated by Dirac 80 years ago and the second kind proposed by the author of this paper. The first kind of the spin manifests in the low energy regime as the ordinary spin and all the charges, like it is in the Kaluza-Klein-like theories. The second kind, since forming the equivalent representations with respect to the first one, is correspondingly responsible for generating families1. There is no third kind of a spin. Spinors interact with only vielbeins and the two kinds of the corresponding spin connection fields.
(or larger), a simple starting action for spinors and the gauge fields: Spinors carry only two kinds of the spins (no charges), namely the one postulated by Dirac 80 years ago and the second kind proposed by the author of this paper. The first kind of the spin manifests in the low energy regime as the ordinary spin and all the charges, like it is in the Kaluza-Klein-like theories. The second kind, since forming the equivalent representations with respect to the first one, is correspondingly responsible for generating families1. There is no third kind of a spin. Spinors interact with only vielbeins and the two kinds of the corresponding spin connection fields.
After the breaks of the starting symmetry, chosen so that they lead at the low energy regime to the observed properties of fermions and bosons2, the simple starting action (Equation (4)) manifests two decoupled groups of four families of quarks and leptons, with only the left handed (with respect to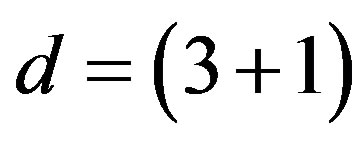 ) members of each family carrying the weak charge while the right handed ones are weak chargeless. The fourth family is predicted [8,10,11] to be possibly observed at the LHC or at somewhat higher energies, while the stable fifth family members, forming neutral (with respect to the colour and electromagnetic charge) baryons and the fifth family neutrinos are predicted to explain the origin of the dark matter [11].
) members of each family carrying the weak charge while the right handed ones are weak chargeless. The fourth family is predicted [8,10,11] to be possibly observed at the LHC or at somewhat higher energies, while the stable fifth family members, forming neutral (with respect to the colour and electromagnetic charge) baryons and the fifth family neutrinos are predicted to explain the origin of the dark matter [11].
The spin connections, associated with the two kinds of spins, together with vielbeins, all behaving as scalar fields with respect to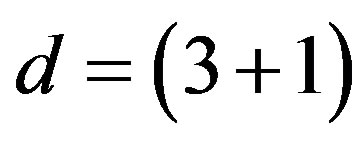 , are with their vacuum expectation values at the last two
, are with their vacuum expectation values at the last two 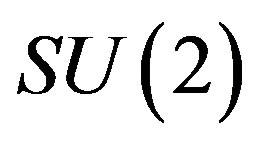 breaks (that is after the electroweak break) responsible for the nonzero mass matrices of the lower four families of fermions and also for the masses of the weak gauge fields. The spin connections together with the vielbeins, with the indices of vector fields with respect to
breaks (that is after the electroweak break) responsible for the nonzero mass matrices of the lower four families of fermions and also for the masses of the weak gauge fields. The spin connections together with the vielbeins, with the indices of vector fields with respect to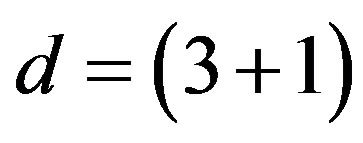 , manifest after the electroweak break of symmetry as the known gauge fields.
, manifest after the electroweak break of symmetry as the known gauge fields.
Although the properties of the scalar fields, that is their vacuum expectation values, coupling constants and masses, can not be calculated without the detailed knowledge of the mechanism of breaking the symmetries, and have been so far only roughly estimated, yet one can see, assuming breaks which lead to observable phenomena at the low energy regime, how properties of the scalar fields determine the fermion mass matrices, manifesting effectively as the standard model Higgs and its Yukawa couplings.
In this paper a short introduction into the spin-chargefamily theory is made in Section 2, the appearance of mass matrices of the two decoupled four families of fermions, as predicted by the theory, are discussed in 2.1. Their mass matrices are presented in 3, leading to the observed properties of quarks and leptons. The role of the scalar fields in breaking symmetries and in contributing to mass matrices of quarks and leptons and to masses of the gauge fields are presented in Section 4. The fact is that there are four predicted families rather than the so far observed three and the influence of this fact on properties of quarks and leptons is discussed and some estimation of the fourth family properties is made. A possible observation of more than the so far observed scalar field, the Higgs of the standard model, is discussed. In conclusion (5) the standard model is presented as a possible low energy manifestation of the spin-charge-family theory, with open problems pointed out.
2. The Spin-Charge-Family Theory from the Starting Action to the Standard Model Action
The theory assumes that the spinor carries in 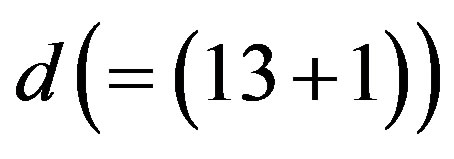 -dimensional space two kinds of the spin, no charges [1-8]: 1) The Dirac spin, described by
-dimensional space two kinds of the spin, no charges [1-8]: 1) The Dirac spin, described by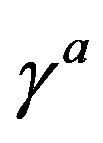 ’s, defines the spinor representations in
’s, defines the spinor representations in 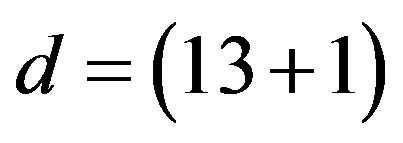
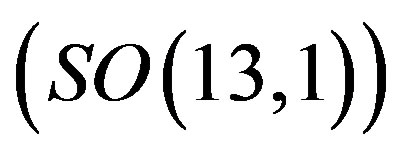 , and correspondingly in the low energy regime, after several breaks of symmetries and before the electroweak break, the spin
, and correspondingly in the low energy regime, after several breaks of symmetries and before the electroweak break, the spin 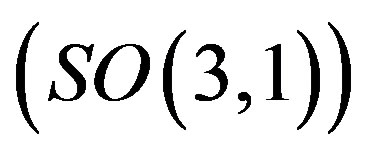 and all the charges (the colour
and all the charges (the colour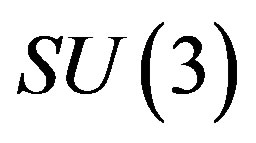 , the weak
, the weak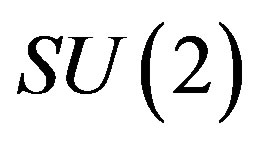 , the hyper charge
, the hyper charge 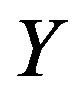 and before the electroweak break the non conserved hyper charge
and before the electroweak break the non conserved hyper charge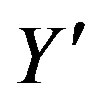 ) of quarks and leptons, the left handed weak charged and the right handed weak chargeless, the left and the right handedness determined by the spin properties in
) of quarks and leptons, the left handed weak charged and the right handed weak chargeless, the left and the right handedness determined by the spin properties in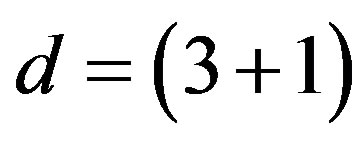 , in agreement with the standard model. 2) The second kind of the spin [32]described by
, in agreement with the standard model. 2) The second kind of the spin [32]described by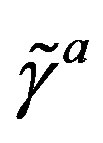 ’s
’s 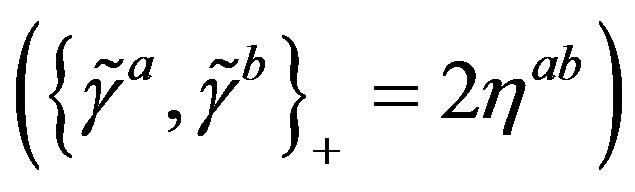 and anticommuting with the Dirac
and anticommuting with the Dirac 
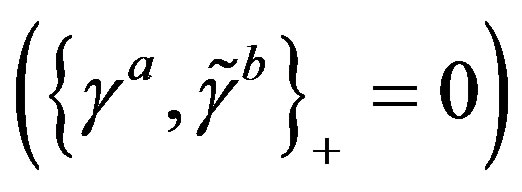 defines the families of spinors, which at the symmetries of
defines the families of spinors, which at the symmetries of 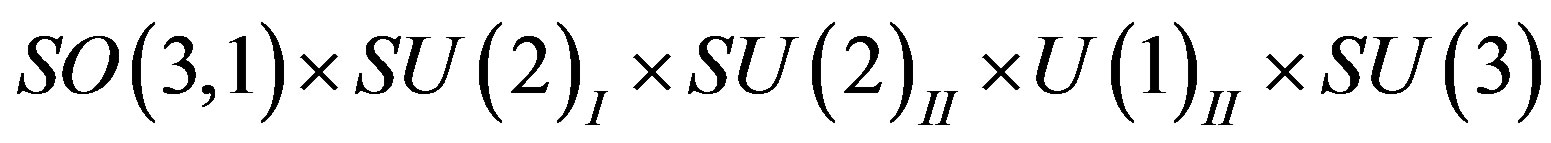
manifests two decoupled groups of four massless families, each belonging to different 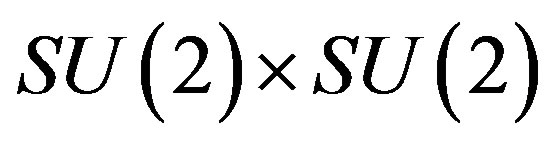 symmetry, namely:
symmetry, namely:
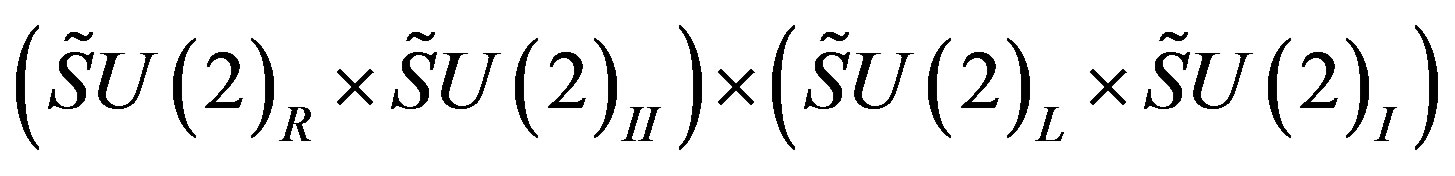 the first one determining the symmetries of the upper four families and the second one determining the symmetries of the lower four families.
the first one determining the symmetries of the upper four families and the second one determining the symmetries of the lower four families.
There is no third kind of the Clifford algebra objects. The appearance of the two kinds of the Clifford algebra objects can be understood as follows: If the Dirac one corresponds to the multiplication of any spinor object 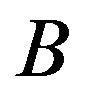 (any product of the Dirac
(any product of the Dirac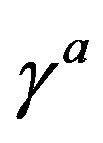 ’s, which represents a spinor state when being applied on a spinor vacuum state
’s, which represents a spinor state when being applied on a spinor vacuum state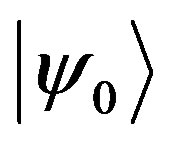 ) from the left hand side, the second kind of the Clifford objects can be understood (up to a factor, determining the Clifford evenness
) from the left hand side, the second kind of the Clifford objects can be understood (up to a factor, determining the Clifford evenness 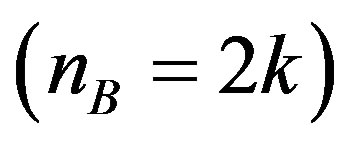 or oddness
or oddness 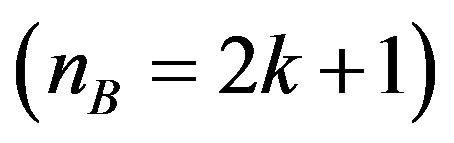 of the object
of the object 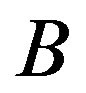 as the multiplication of the object from the right hand side
as the multiplication of the object from the right hand side
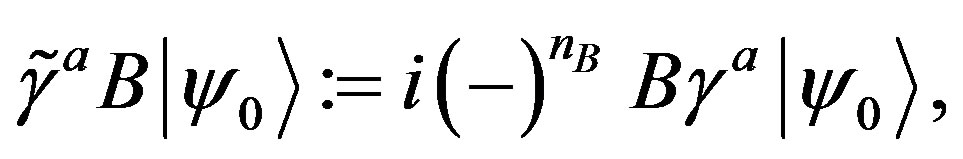 (1)
(1)
with 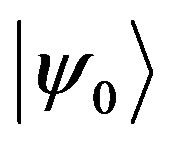 determining the spinor vacuum state. Accordingly we have
determining the spinor vacuum state. Accordingly we have
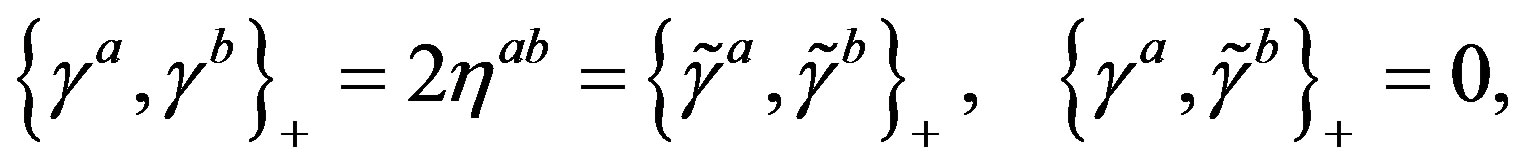
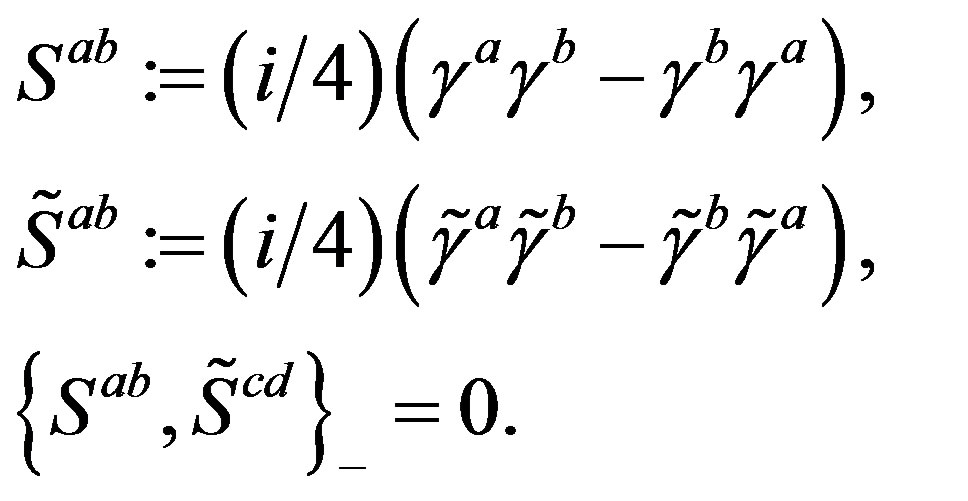 (2)
(2)
The technique is explained in more details in Appendix. The spin-charge-family theory proposes in 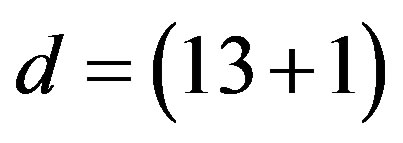 a simple action for a Weyl spinor and for the corresponding gauge fields
a simple action for a Weyl spinor and for the corresponding gauge fields
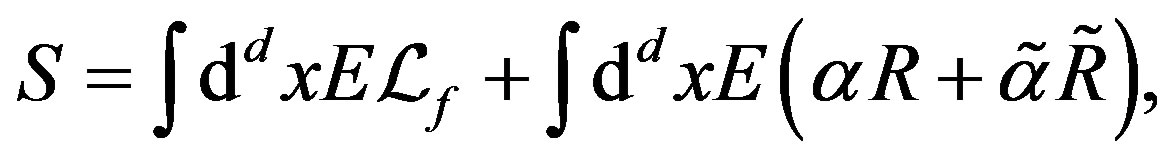 (3)
(3)
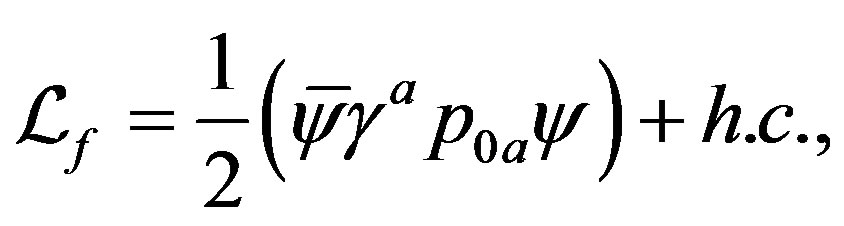

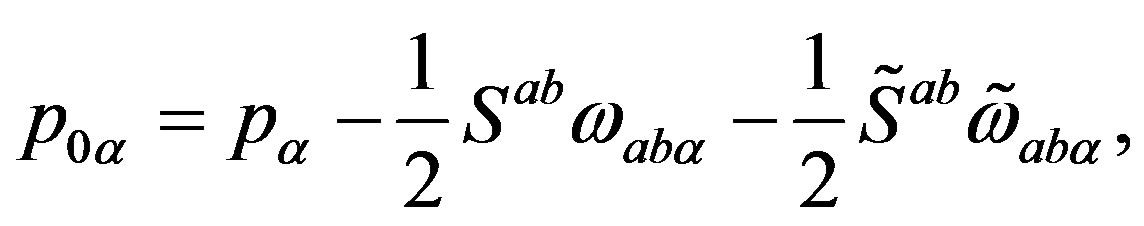

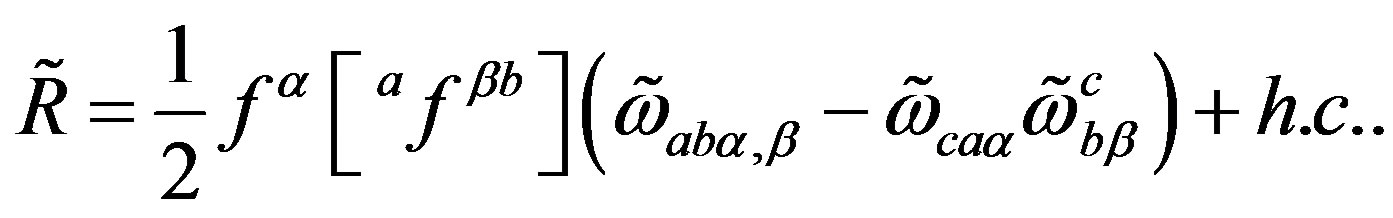 (4)
(4)
Here3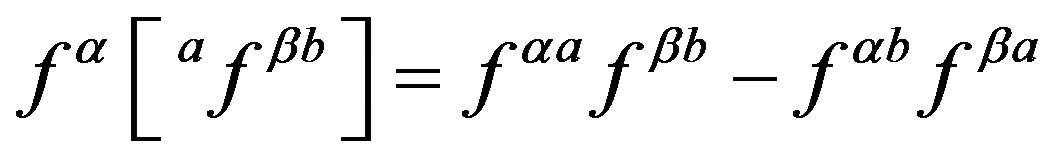 . To see that the action (Equation (4)) manifests after the break of symmetries [1-8,10,28,33,37] all the known gauge fields and the scalar fields and the mass matrices of the observed families, let us rewrite formally the action for a Weyl spinor of (Equation(4)) as follows
. To see that the action (Equation (4)) manifests after the break of symmetries [1-8,10,28,33,37] all the known gauge fields and the scalar fields and the mass matrices of the observed families, let us rewrite formally the action for a Weyl spinor of (Equation(4)) as follows
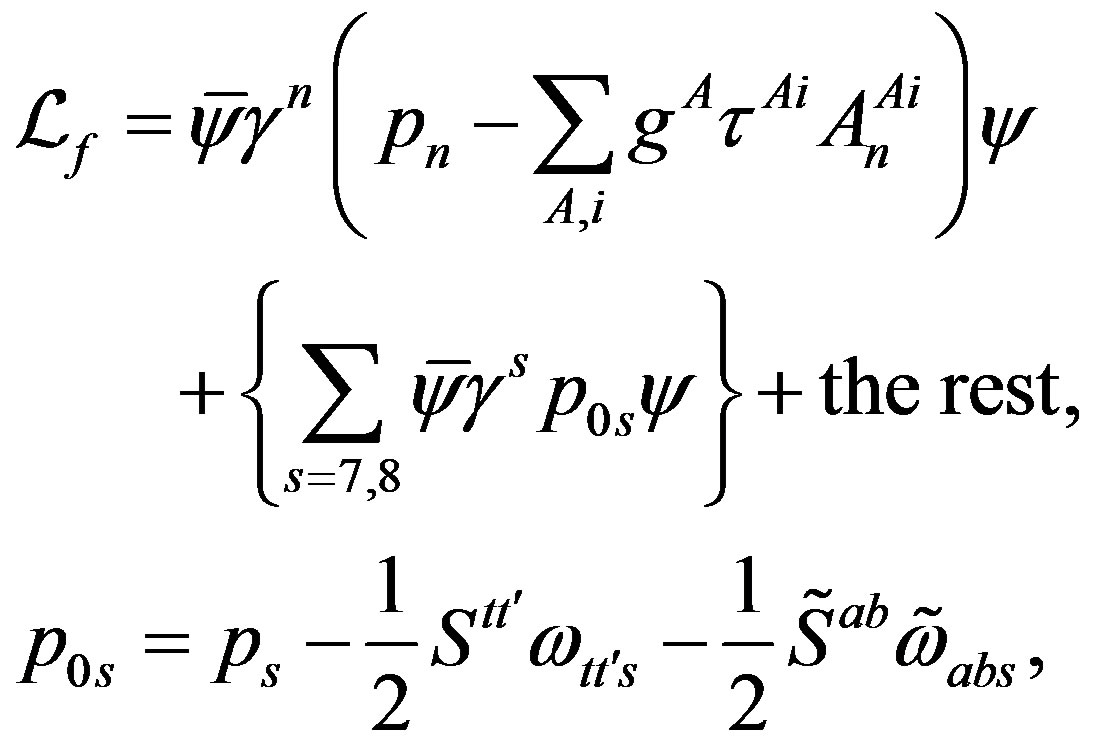 (5)
(5)
where 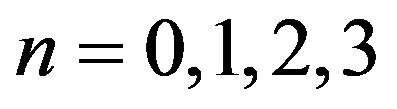 with
with
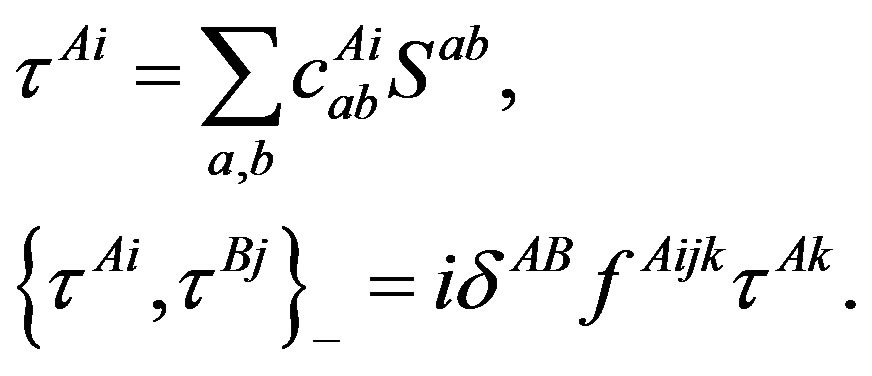 (6)
(6)
All the charges (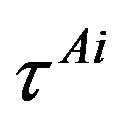 , Equations (6), (15), (16)) and the spin (Equation (14)) operators are expressible with
, Equations (6), (15), (16)) and the spin (Equation (14)) operators are expressible with , which determine all the internal degrees of freedom of one family. Families, quantum numbers of which are expressible with
, which determine all the internal degrees of freedom of one family. Families, quantum numbers of which are expressible with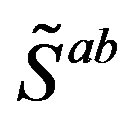 , gain masses through the interacttion with the scalar fields
, gain masses through the interacttion with the scalar fields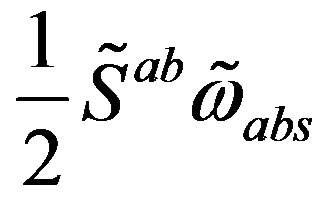 , the gauge fields of the family charges (
, the gauge fields of the family charges ( the higher four families and
the higher four families and  the lower four families), where we assume that after the breaks we end up with
the lower four families), where we assume that after the breaks we end up with 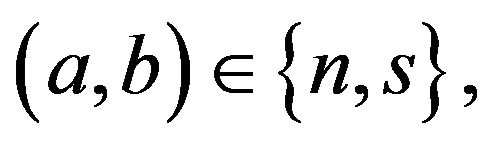
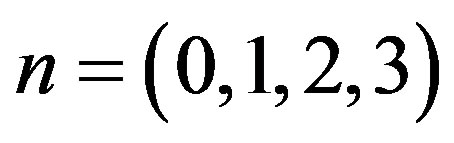 and
and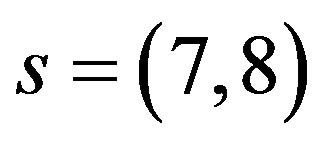 . At the electroweak break also the scalar fields which are the gauge fields of
. At the electroweak break also the scalar fields which are the gauge fields of  and
and 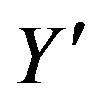 contribute.
contribute.
Index  enumerates all possible spinor charges and
enumerates all possible spinor charges and 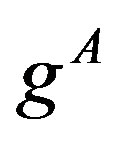 is the coupling constant to a particular gauge vector field
is the coupling constant to a particular gauge vector field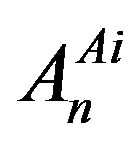 . Before the break from
. Before the break from
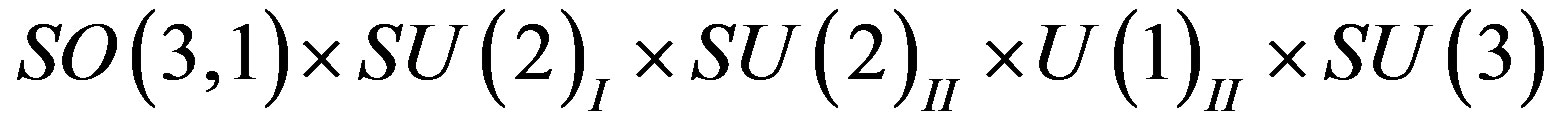
to
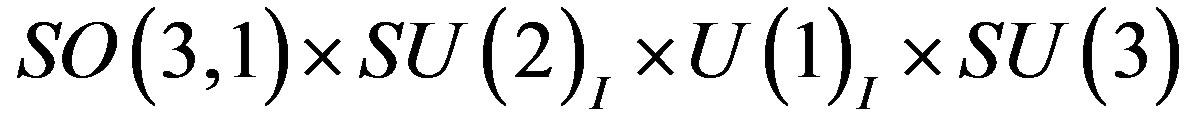 ,
,
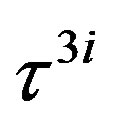 describe the colour charge
describe the colour charge ,
,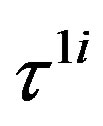 the weak charge
the weak charge ,
,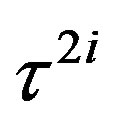 the second
the second  charge and
charge and
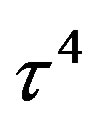 determines the
determines the 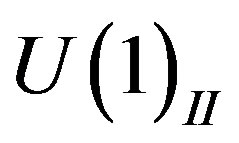 charge. After the break of
charge. After the break of
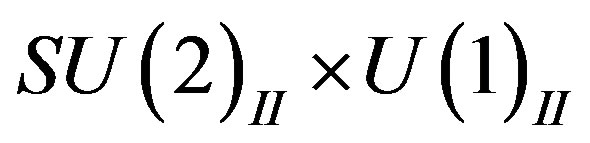 to
to  stays
stays 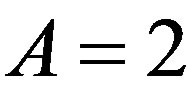 for the
for the 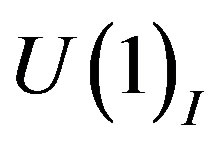
hyper charge 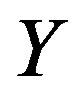 and after the second break of
and after the second break of 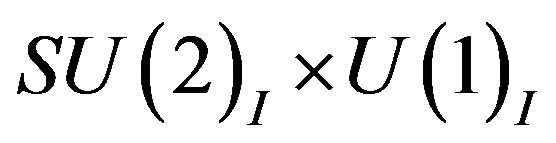 to
to 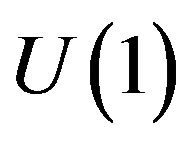 stays
stays 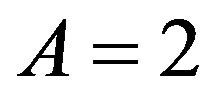 for the electromagnetic charge
for the electromagnetic charge , while instead of the weak charge
, while instead of the weak charge 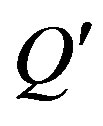 and
and 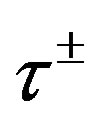 (I use the notation
(I use the notation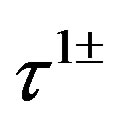 ) of the standard model manifest.
) of the standard model manifest.
The breaks of the starting symmetry from 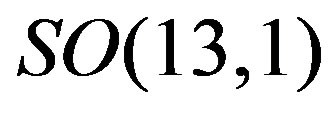 to the symmetry
to the symmetry 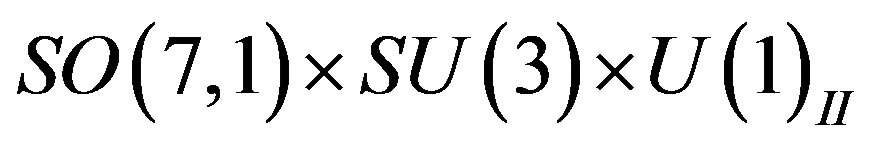 and further to
and further to 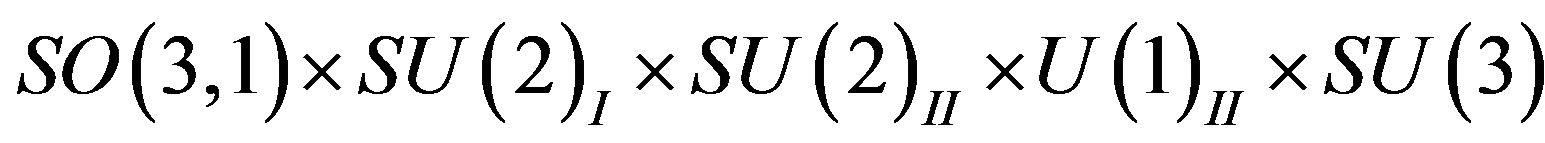 are assumed to leave the low lying eight
are assumed to leave the low lying eight 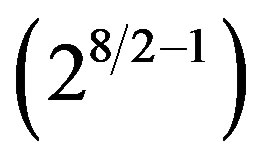 families of spinors massless4, all left handed with respect to
families of spinors massless4, all left handed with respect to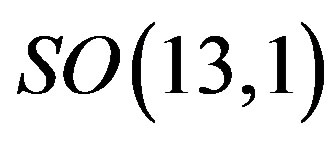 .
.
Accordingly the first line of the action in Equation (5) manifests the dynamical fermion part of the action, while the second part manifests, when (superposition of) 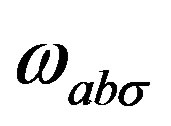 and (superposition of)
and (superposition of) 
 fields gain nonzero vacuum expectation values, the mass matrices of fermions on the tree level. Scalar fields contribute also to masses of those gauge fields, which at a particular break lose symmetries. It is assumed that the symmetries in the
fields gain nonzero vacuum expectation values, the mass matrices of fermions on the tree level. Scalar fields contribute also to masses of those gauge fields, which at a particular break lose symmetries. It is assumed that the symmetries in the 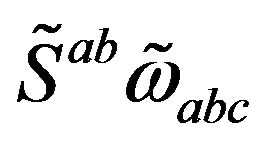 and in the
and in the 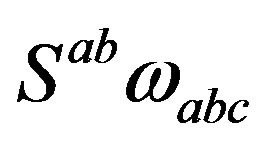 part break in a correlated way, triggered by particular superposition of scalar vielbeins and spin connections of both kinds (
part break in a correlated way, triggered by particular superposition of scalar vielbeins and spin connections of both kinds (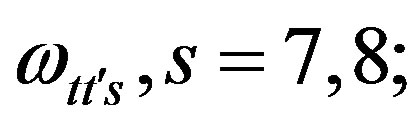 superposition of
superposition of 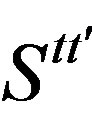 determine
determine 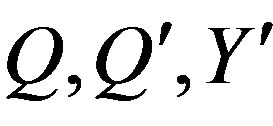 and
and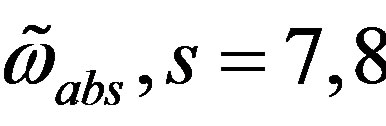 ; superposition of
; superposition of 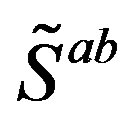 determine the family quantum numbers). I comment this part in sections 2.2, 3. The rest in the second line in Equation (5) stays for all, which is expected to be at low energies negligible or influence the mass matrices beyond the tree level.
determine the family quantum numbers). I comment this part in sections 2.2, 3. The rest in the second line in Equation (5) stays for all, which is expected to be at low energies negligible or influence the mass matrices beyond the tree level.
The generators 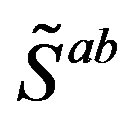 (Equations (14), (15), (16)) transform each member of one family into the same family member of another family, due to the fact that
(Equations (14), (15), (16)) transform each member of one family into the same family member of another family, due to the fact that  (Equation (2, A18)). Let me tell that although we (that is together with collaborators, in particular H.B.F. Nielsen) have started with studies which should justify the assumptions and which look so far promising, I can not yet offer the justification for the above assumed breaks. With collaborators we have published several papers [29,30], in which we present for a toy model the justification for some of these assumptions.
(Equation (2, A18)). Let me tell that although we (that is together with collaborators, in particular H.B.F. Nielsen) have started with studies which should justify the assumptions and which look so far promising, I can not yet offer the justification for the above assumed breaks. With collaborators we have published several papers [29,30], in which we present for a toy model the justification for some of these assumptions.
At the low energy regime, after the breaks of the starting symmetry, the part of the action with the vielbeins and the spin connections, the gauge fields of 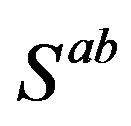 (with the Lagrange density
(with the Lagrange density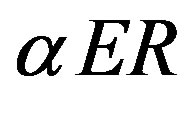 ), manifests as the known vector gauge fields -- the gauge fields of
), manifests as the known vector gauge fields -- the gauge fields of 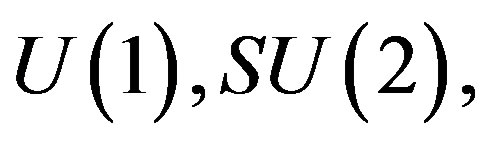
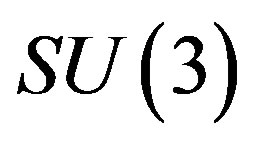 , the ordinary gravity and scalar fields, while the part
, the ordinary gravity and scalar fields, while the part 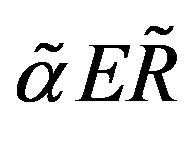 manifests the scalar fields responsible for breaking symmetries (to breaking also the gauge fields of
manifests the scalar fields responsible for breaking symmetries (to breaking also the gauge fields of  contribute) and correspondingly also for mass matrices of the fermion members and masses of the gauge fields. Beyond the tree level all the massive fields, scalars and vectors, contribute coherently to the mass matrices of fermions and to massive vector bosons [33].
contribute) and correspondingly also for mass matrices of the fermion members and masses of the gauge fields. Beyond the tree level all the massive fields, scalars and vectors, contribute coherently to the mass matrices of fermions and to massive vector bosons [33].
In the break
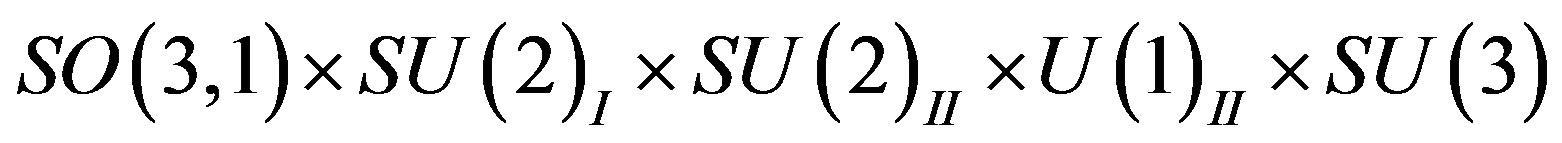
into
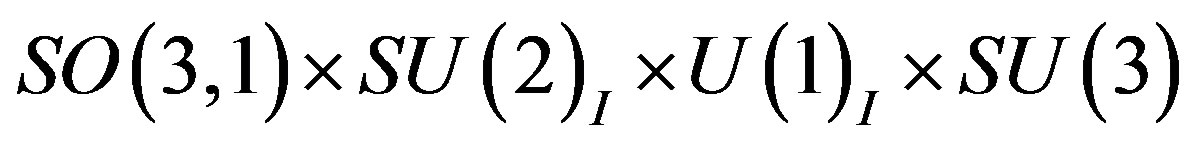 to which the scalar fields - the gauge fields of
to which the scalar fields - the gauge fields of 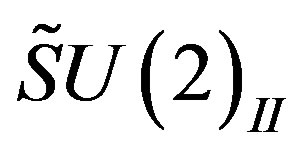 and
and 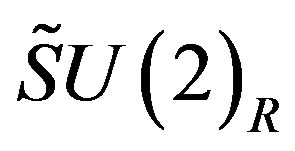 - which gain nonzero vacuum expectation values contribute, the four upper families gain masses. The weak doublets manifest at this break the same mass, keeping the (weak)
- which gain nonzero vacuum expectation values contribute, the four upper families gain masses. The weak doublets manifest at this break the same mass, keeping the (weak) 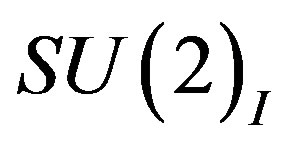 symmetry unbroken.
symmetry unbroken.
After the electroweak break (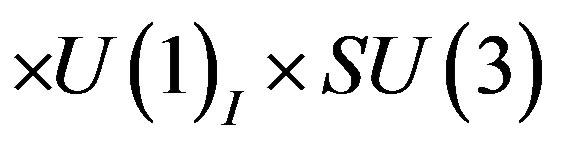
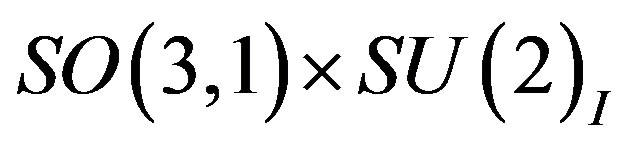 breaks into
breaks into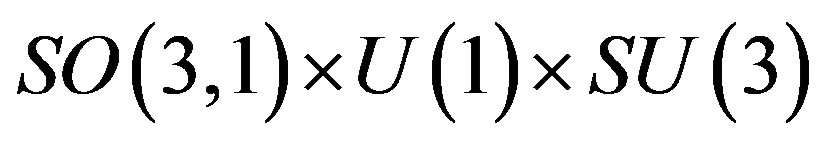 ) the effective Lagrange density for fermions (spinors) looks like
) the effective Lagrange density for fermions (spinors) looks like

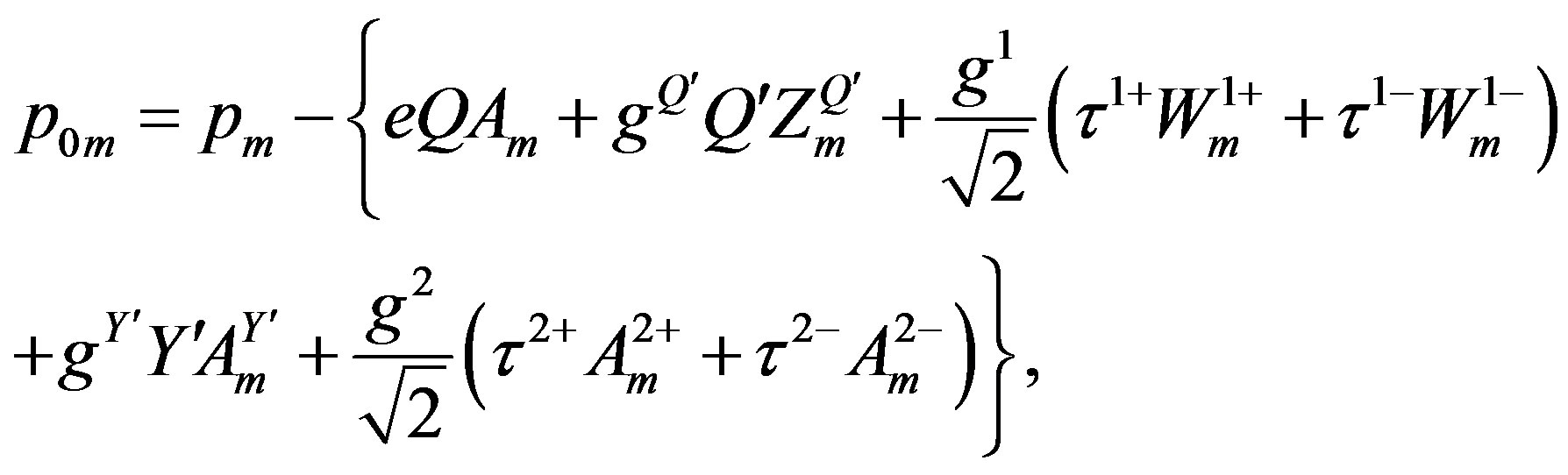
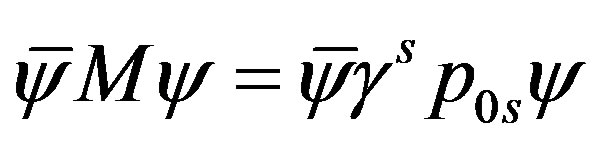
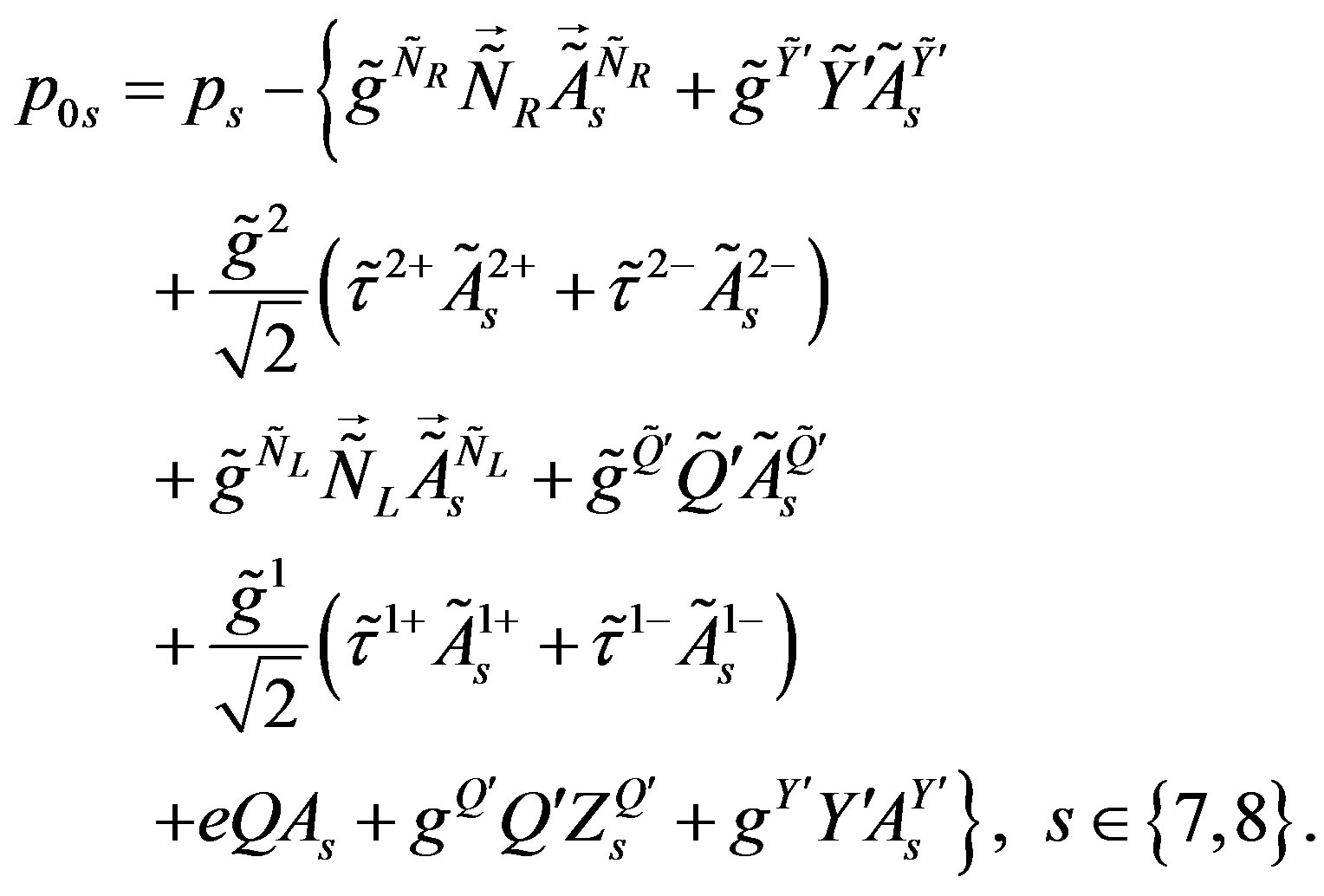 (7)
(7)
The term 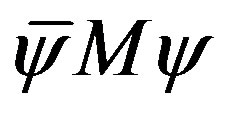 determines the tree level mass matrices of quarks and leptons. The contributions to the mass matrices appear at two very different energy scales due to two separate breaks. Before the break of
determines the tree level mass matrices of quarks and leptons. The contributions to the mass matrices appear at two very different energy scales due to two separate breaks. Before the break of  to
to 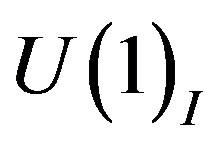 the vacuum expectation values of the scalar fields appearing in
the vacuum expectation values of the scalar fields appearing in 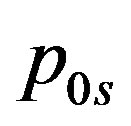 are all zero. The corresponding dynamical scalar fields are massless. All the eight families are massless and the vector gauge fields
are all zero. The corresponding dynamical scalar fields are massless. All the eight families are massless and the vector gauge fields 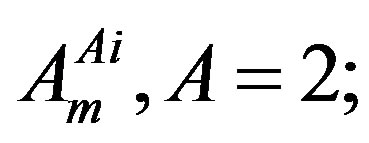 in Equation (5) are massless as well. To the break of
in Equation (5) are massless as well. To the break of 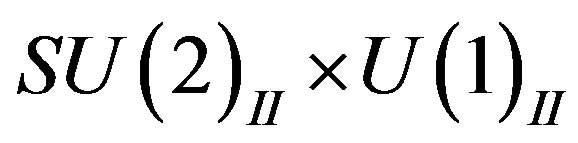 to
to  the scalar fields from the first and the second line in the covariant momentum
the scalar fields from the first and the second line in the covariant momentum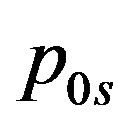 , that is the two triplets with respect to the family charges
, that is the two triplets with respect to the family charges 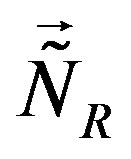 and
and ,
, 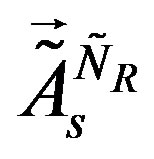 and
and 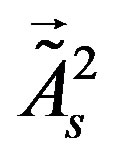 (are assumed to) contribute, gaining non zero vacuum expectation values. Both scalars are doublets
(are assumed to) contribute, gaining non zero vacuum expectation values. Both scalars are doublets 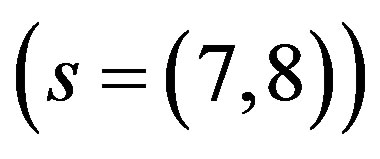 with respect to the weak charge. It is, namely,
with respect to the weak charge. It is, namely, 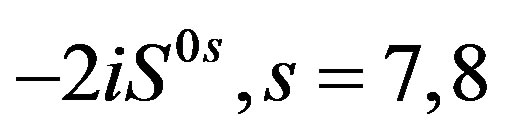 , which transforms the right handed weak chargeless quarks and leptons into the corresponding left handed weak charged partners, transforming at the same time the hyper charge
, which transforms the right handed weak chargeless quarks and leptons into the corresponding left handed weak charged partners, transforming at the same time the hyper charge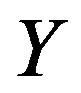 , what in the standard model the scalar Higgs with the appropriate hyper charge (for
, what in the standard model the scalar Higgs with the appropriate hyper charge (for 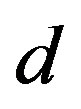 -quarks and
-quarks and  -leptons) and its “anti-Higgs” (for
-leptons) and its “anti-Higgs” (for 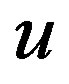 -quarks and
-quarks and  -leptons) do. The upper four families, which are doublets with respect to the infinitesimal generators of the corresponding groups, namely
-leptons) do. The upper four families, which are doublets with respect to the infinitesimal generators of the corresponding groups, namely 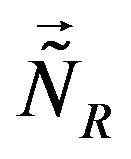 and
and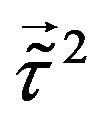 , become massive. No scalar fields of the kind
, become massive. No scalar fields of the kind 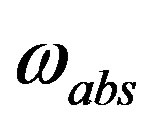 is assumed to contribute in this break. Therefore, the lower four families, which are singlets with respect to
is assumed to contribute in this break. Therefore, the lower four families, which are singlets with respect to  and
and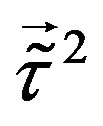 stay massless. Due to the break of
stay massless. Due to the break of 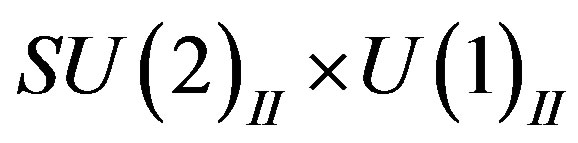
symmetries in the space of  and
and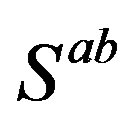 , the gauge fields
, the gauge fields 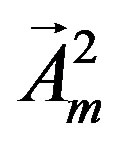 become massive. The gauge vector fields
become massive. The gauge vector fields 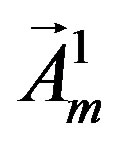 and
and 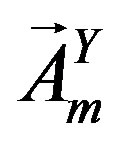 stay massless at this break.
stay massless at this break.
To the break of 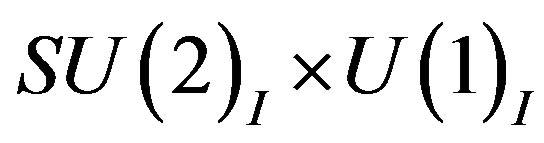 to
to 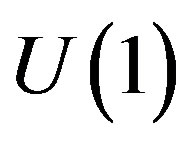 the scalar fields from last three lines in the covariant momentum
the scalar fields from last three lines in the covariant momentum , that is the triplets
, that is the triplets  and
and 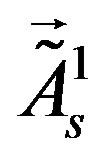 with respect to the family charges
with respect to the family charges 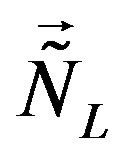 and
and 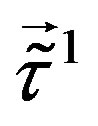 and the singlet
and the singlet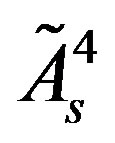 , as well as the ones from the last line originating in
, as well as the ones from the last line originating in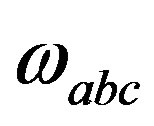 , that is (
, that is ( ,
,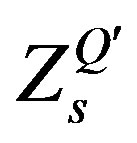 ,
,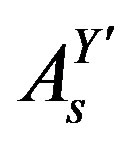 ), are assumed to contribute, by gaining non zero vacuum expectation values. All these fields are doublets with respect to the weak charge due to the fact that the operators
), are assumed to contribute, by gaining non zero vacuum expectation values. All these fields are doublets with respect to the weak charge due to the fact that the operators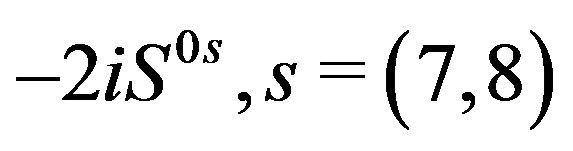 , transform the right handed weak chargeless quarks and leptons into the corresponding left handed weak charged partners.
, transform the right handed weak chargeless quarks and leptons into the corresponding left handed weak charged partners.
The electroweak break causes non zero mass matrices of the lower four families. Also the gauge fields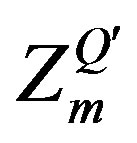 ,
, 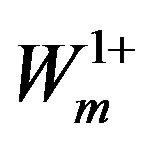 and
and ,
,  gain masses. The electroweak break influences slightly the mass matrices of the upper four families, due to the contribution of
gain masses. The electroweak break influences slightly the mass matrices of the upper four families, due to the contribution of ,
, 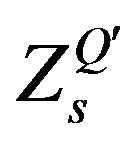 ,
, 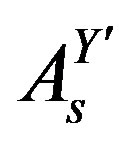 and
and .
.
To loops corrections of both groups of families the massive vector gauge fields contribute. The dynamical massive scalar fields contribute only to families of the group to which they couple.
The detailed explanation of the two phase transitions which manifest in Equation (7) is presented in what follows.
2.1. Spinor Action through Breaks
In this subsection properties of quarks, 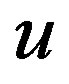 and
and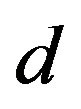 , and leptons,
, and leptons,  and
and , of two groups of four families are presented at the stage of
, of two groups of four families are presented at the stage of
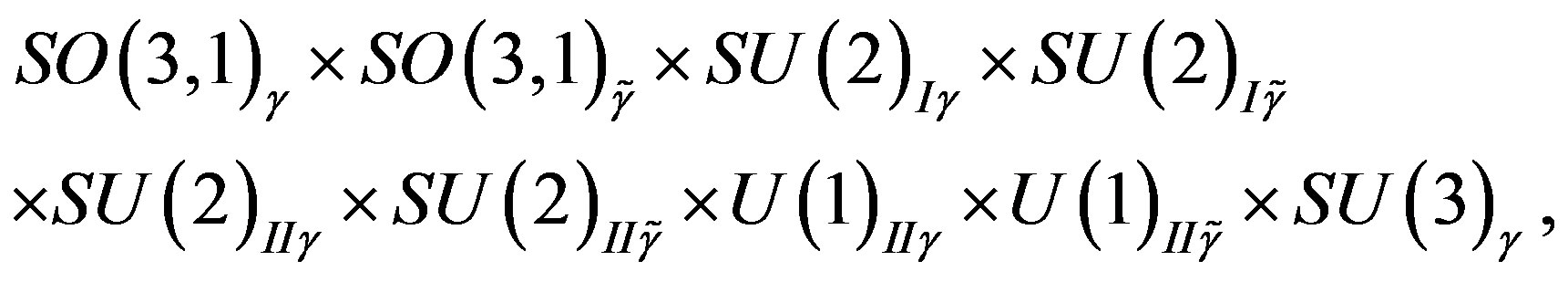 (8)
(8)
when eight families are massless, and then when in the two successive breaks, in which first four and then the last four families gain masses. The two indices 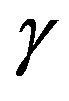 and
and 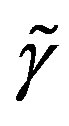 are to point out that there are two kinds of subgroups of
are to point out that there are two kinds of subgroups of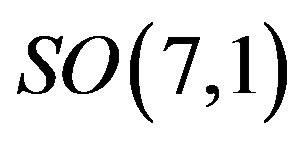 , those in the
, those in the 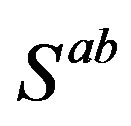 (taking care of the spin and charges) sector and those in the
(taking care of the spin and charges) sector and those in the 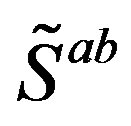 (taking care of the families) sector. We shall in what follows omit these two indices, keeping in mind that there are two kinds of groups and subgroups. Half of the eight massless families are doublets with respect to the subgroup
(taking care of the families) sector. We shall in what follows omit these two indices, keeping in mind that there are two kinds of groups and subgroups. Half of the eight massless families are doublets with respect to the subgroup 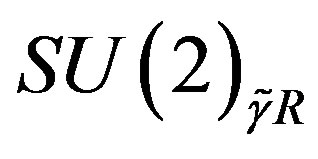 of
of 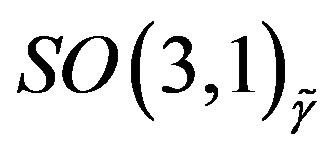 and with respect to
and with respect to 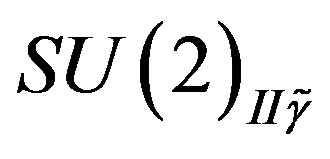 and singlets with respect to the
and singlets with respect to the 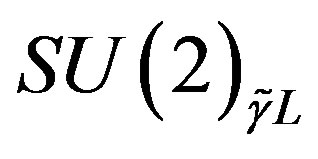 subgroup of
subgroup of 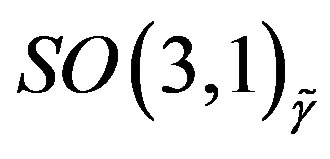 and with respect to
and with respect to , the rest four families are singlets with respect to the subgroup
, the rest four families are singlets with respect to the subgroup 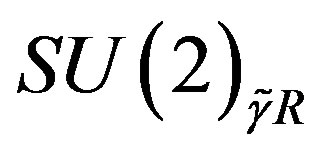 and with respect to
and with respect to 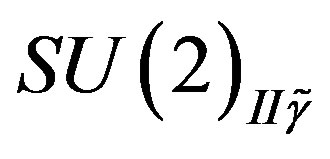 while they are doublets with respect to the
while they are doublets with respect to the 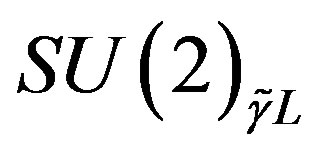 and with respect to
and with respect to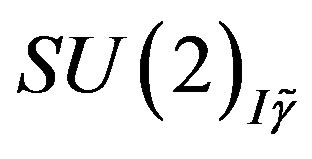 .
.
At the break of

to
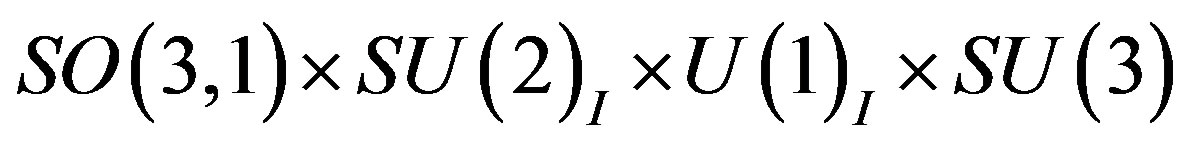
the four families coupled to the scalar fields which gain at this break nonzero vacuum expectation values become massive, while the four families which do not couple to these scalar fields stay massless, representing four massless families of left handed weak charged colour triplet quarks (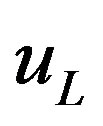 ,
,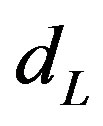 ), right handed weak chargeless colour triplet quarks (
), right handed weak chargeless colour triplet quarks (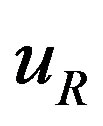 ,
,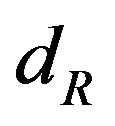 ), left handed weak charged colour singlet leptons (
), left handed weak charged colour singlet leptons (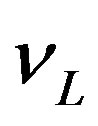 ,
, ) and right handed weak chargeless colour singlet leptons (
) and right handed weak chargeless colour singlet leptons (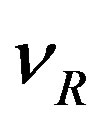 ,
, ). After the second break the members of the lowest of the upper four families, decoupled from the lower four families, are candidates to form the dark matter.
). After the second break the members of the lowest of the upper four families, decoupled from the lower four families, are candidates to form the dark matter.
After the second break from
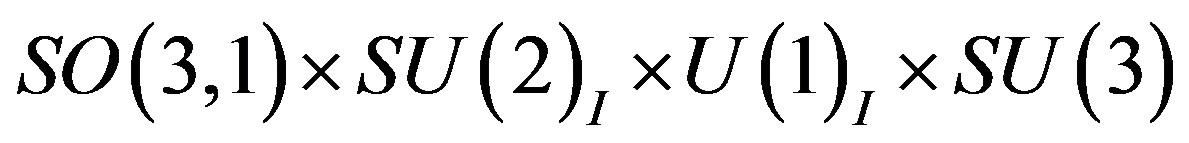
to
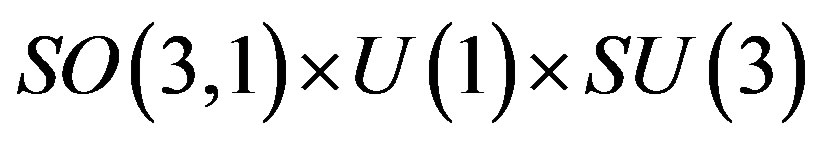
the last four families become massive due to the nonzero vacuum expectation values of the rest of scalar fields. Three of the families represent the observed families of quarks and leptons, so far included into the standard model, except the right handed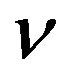 ’s (which carry the additional charge
’s (which carry the additional charge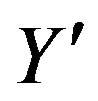 , not assumed in the standard model, as also all the other members do).
, not assumed in the standard model, as also all the other members do).
The technique [32], which offers an easy way to keep a track of the symmetry properties of spinors, is used as a tool to clearly demonstrate properties of spinors. This technique is explained in more details in Appendix. In this subsection only a short introduction, needed to follow the explanation, is presented. Mass matrices of each groups of four families, on the tree and below the tree level, originated in the scalar gauge fields, which at each of the two breaks gain a nonzero vacuum expectation values, will be discussed in Section 3.
Following the ref. [29] we define nilpotents
 and projectors
and projectors 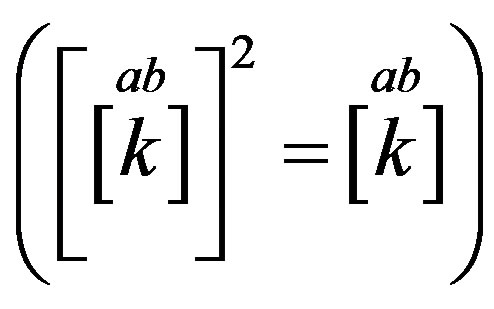 (Equations
(Equations
(A6, A10) in Appendix)
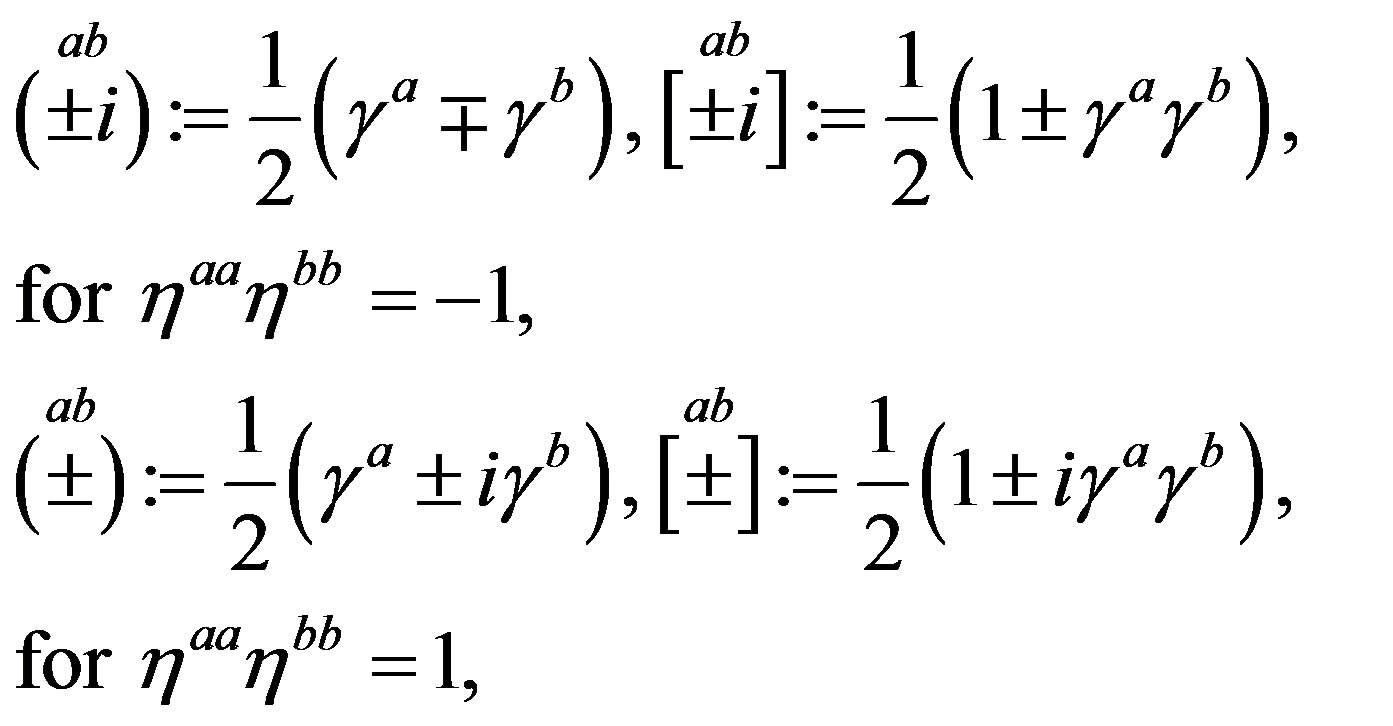 (9)
(9)
as eigenvectors of 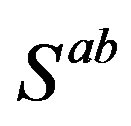 as well as of
as well as of 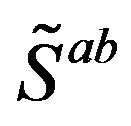 (Equation (A4)) in Appendix)
(Equation (A4)) in Appendix)
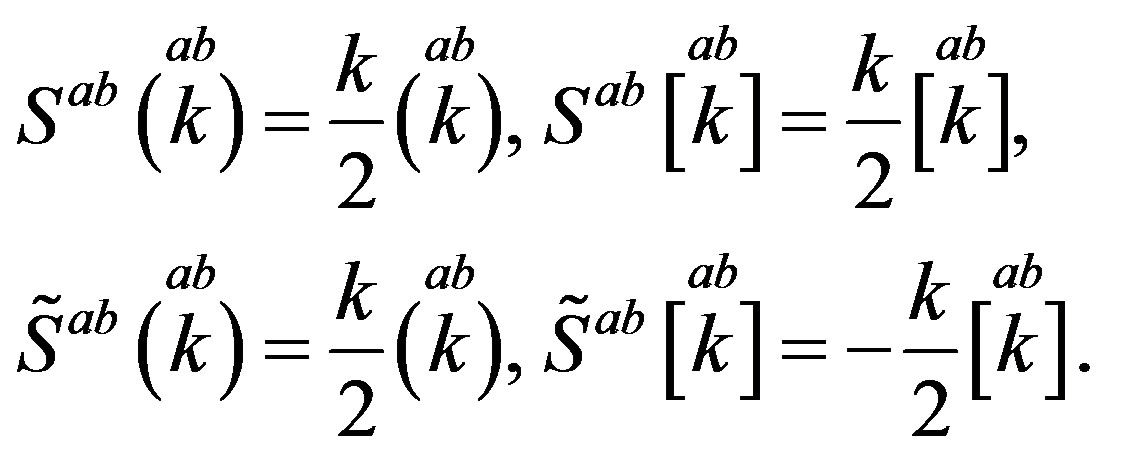 (10)
(10)
One can easily verify that 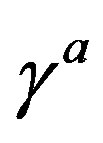 transform
transform 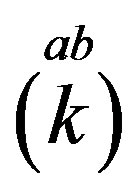 into
into
 , while
, while 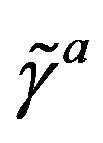 transform
transform 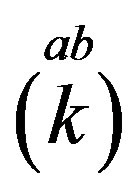 into
into 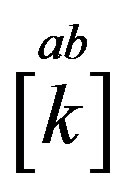 (Equation
(Equation
(A8) in Appendix )
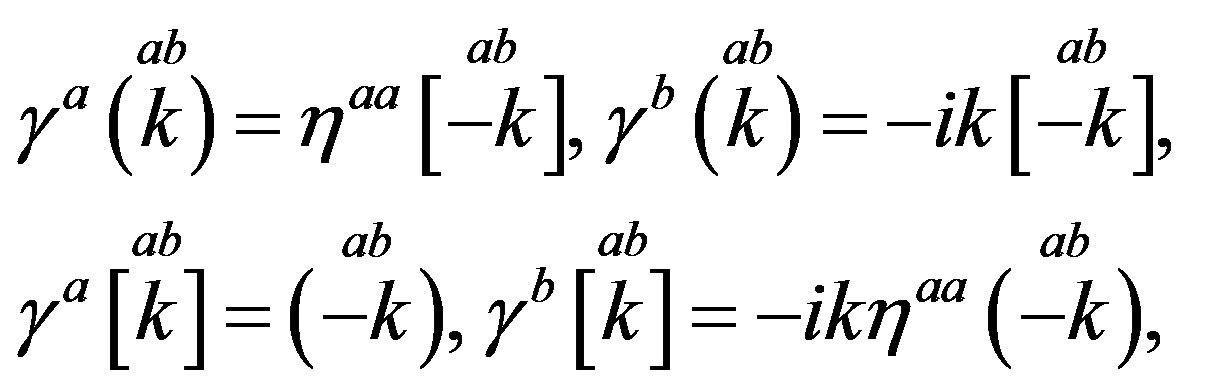 (11)
(11)
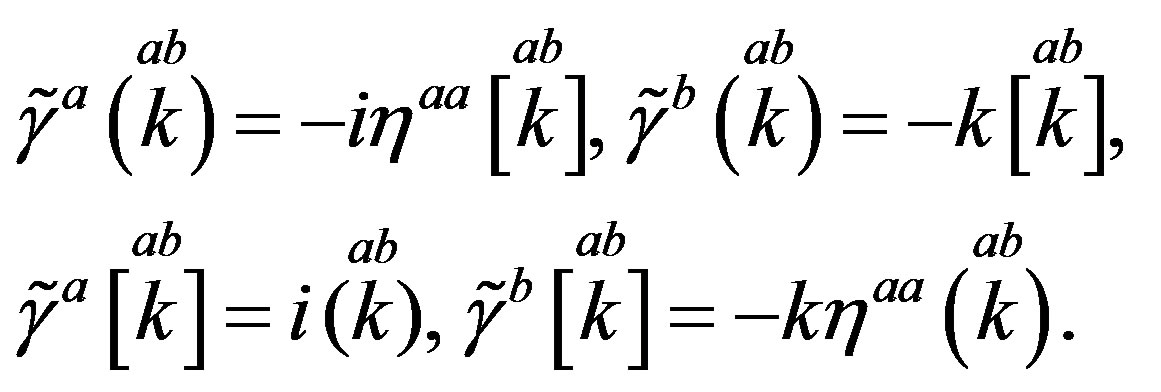 (12)
(12)
Correspondingly,  generate the equivalent representations to representations of
generate the equivalent representations to representations of , and opposite. Defining the basis vectors in the internal space of spin degrees of freedom in
, and opposite. Defining the basis vectors in the internal space of spin degrees of freedom in  as products of projectors and nilpotents from Equation (9) on the spinor vacuum state
as products of projectors and nilpotents from Equation (9) on the spinor vacuum state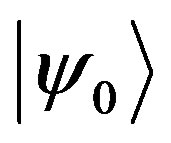 , the representation of one Weyl spinor with respect to
, the representation of one Weyl spinor with respect to 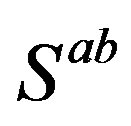 manifests after the breaks the spin and all the charges of one family members, and the gauge fields of
manifests after the breaks the spin and all the charges of one family members, and the gauge fields of  manifest as all the observed gauge fields.
manifest as all the observed gauge fields. 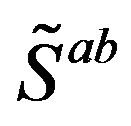 determine families and correspondingly the family quantum numbers, while scalar gauge fields of
determine families and correspondingly the family quantum numbers, while scalar gauge fields of 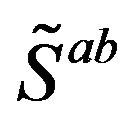 determine, together with particular scalar gauge fields of
determine, together with particular scalar gauge fields of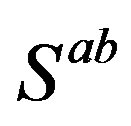 , mass matrices, manifesting effectively as Yukawa fields and Higgs.
, mass matrices, manifesting effectively as Yukawa fields and Higgs.
Expressing the operators 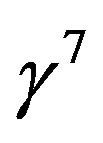 and
and  in terms of the nilpotents
in terms of the nilpotents , the mass term in Equations (5, 7) can be rewritten as follows
, the mass term in Equations (5, 7) can be rewritten as follows
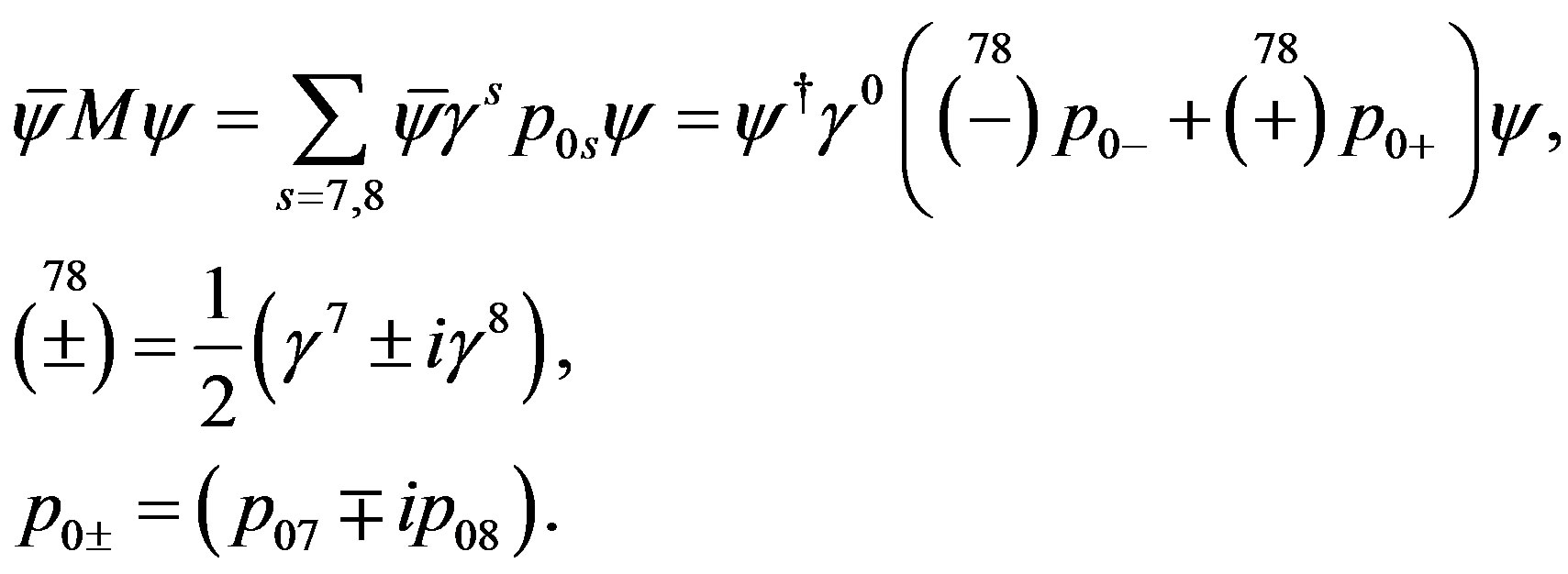 (13)
(13)
After the breaks of the starting symmetry (from 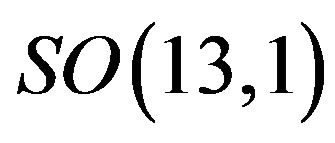 through
through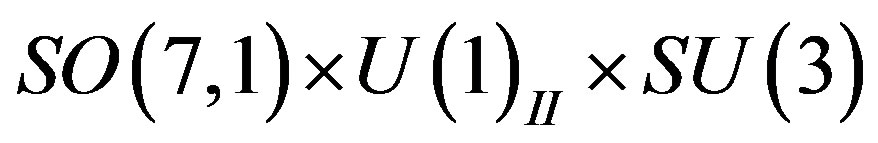 ) to
) to
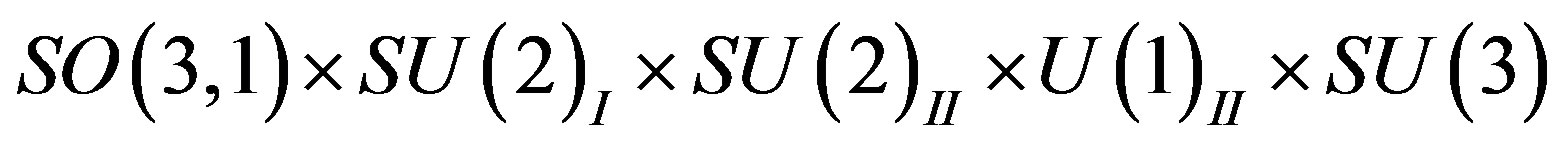 there are eight
there are eight  massless families of spinors. (Some support for this assumption is made when studying toy models [29,30].)
massless families of spinors. (Some support for this assumption is made when studying toy models [29,30].)
Family members 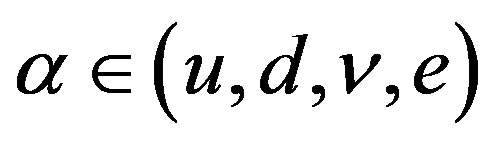 are massless and carry the
are massless and carry the  charge (the generator of the infinitesimal transformations of the group is
charge (the generator of the infinitesimal transformations of the group is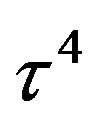 , presented in Equation (16)), the
, presented in Equation (16)), the 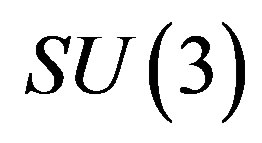 charge (the generators are
charge (the generators are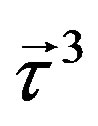 , presented in Equation (16)) and the two
, presented in Equation (16)) and the two 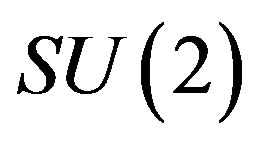
charges, 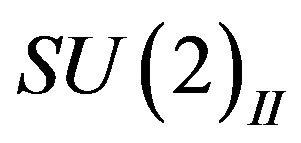 and
and 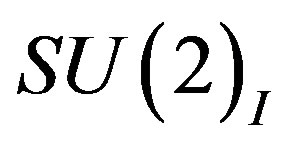 (the generators are presented in Equation (15) as
(the generators are presented in Equation (15) as 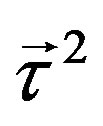 and
and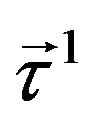 , respectively). They appear in the representations in which the left handed (with respect to
, respectively). They appear in the representations in which the left handed (with respect to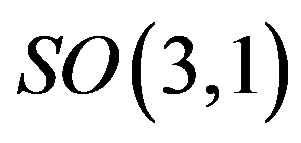 ) carry the
) carry the 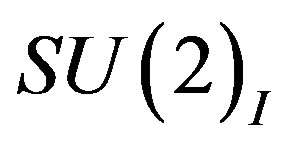 (weak) charge (with the corresponding generators
(weak) charge (with the corresponding generators ), while the right handed carry the
), while the right handed carry the 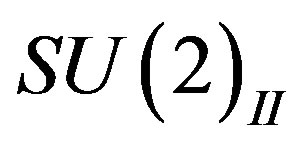 charge (with the corresponding generators
charge (with the corresponding generators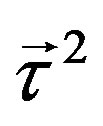 ).
).
Each family member carries also the family quantum number, which concerns 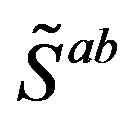 and is determined by the quantum numbers of the two
and is determined by the quantum numbers of the two  from
from 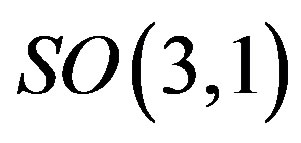 (with the generators
(with the generators , Equation (14)) and the two
, Equation (14)) and the two 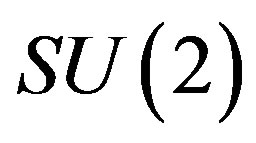 from
from 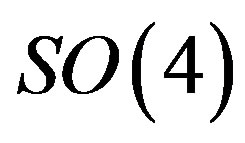 (with the generators
(with the generators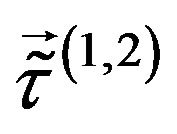 , Equation (15)).
, Equation (15)).
Properties of families of spinors can transparently be analysed if using our technique. We arrange products of nilpotents and projectors to be eigenvectors of the Cartan subalgebra 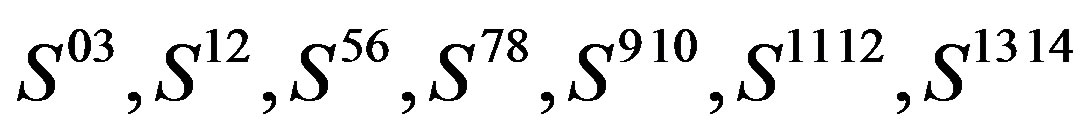 and, at the same time, they are also the eigenvectors of the corresponding
and, at the same time, they are also the eigenvectors of the corresponding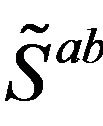 , that is of
, that is of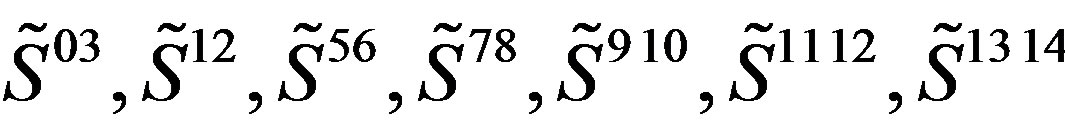 .
.
The generators of the infinitesimal transformations of the subgroups of the group  in the
in the  and
and  sectors, responsible for the properties of spinors in the low energy regime, are presented as follows:
sectors, responsible for the properties of spinors in the low energy regime, are presented as follows:
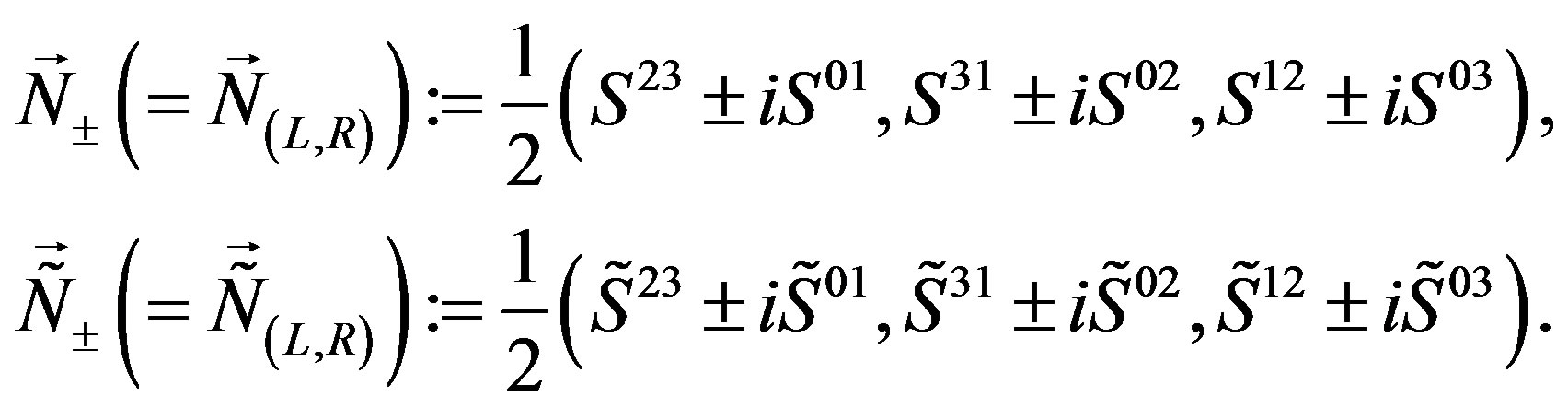 (14)
(14)
They determine representations of the two 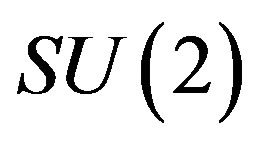 subgroups of
subgroups of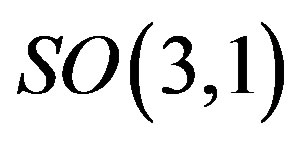 , while
, while
 (15)
(15)
determine representations of 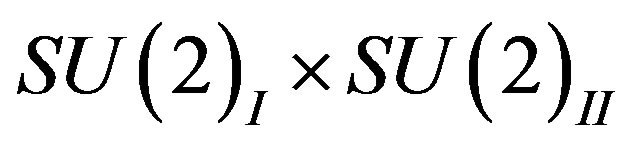 of
of 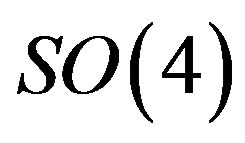 and
and
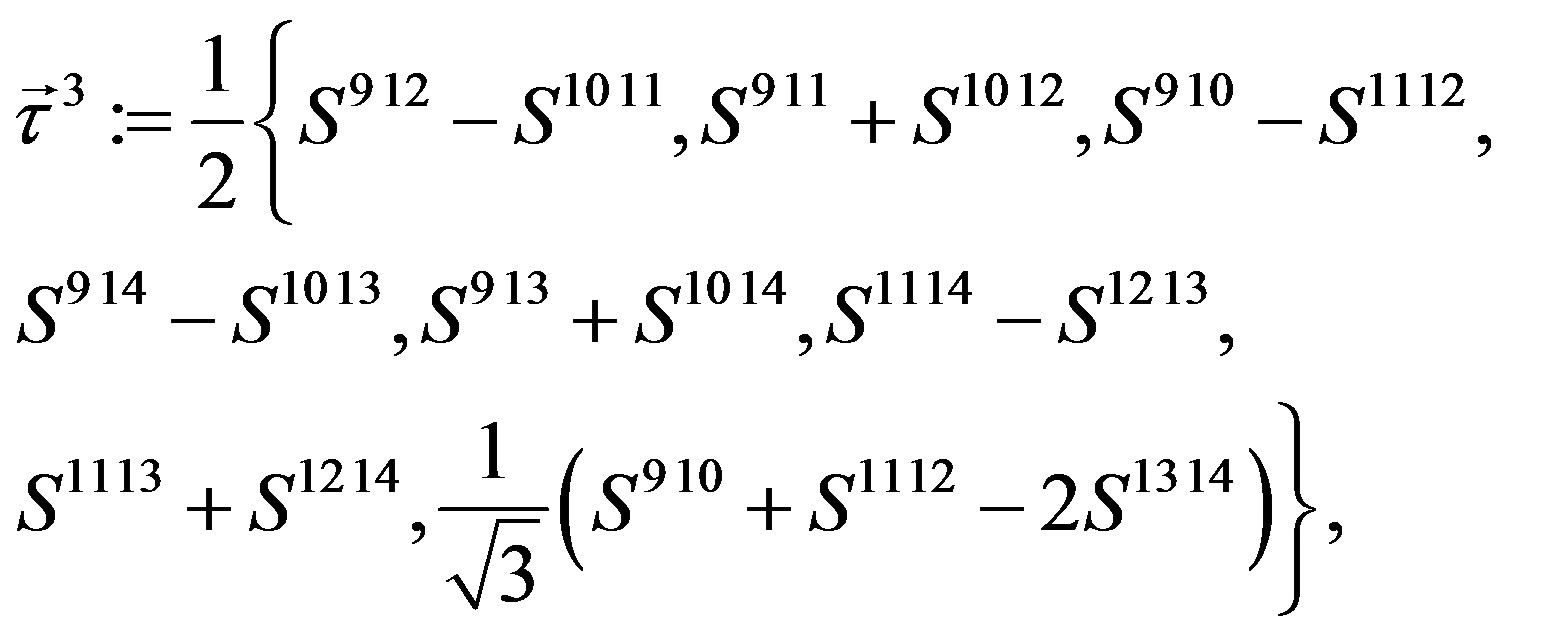
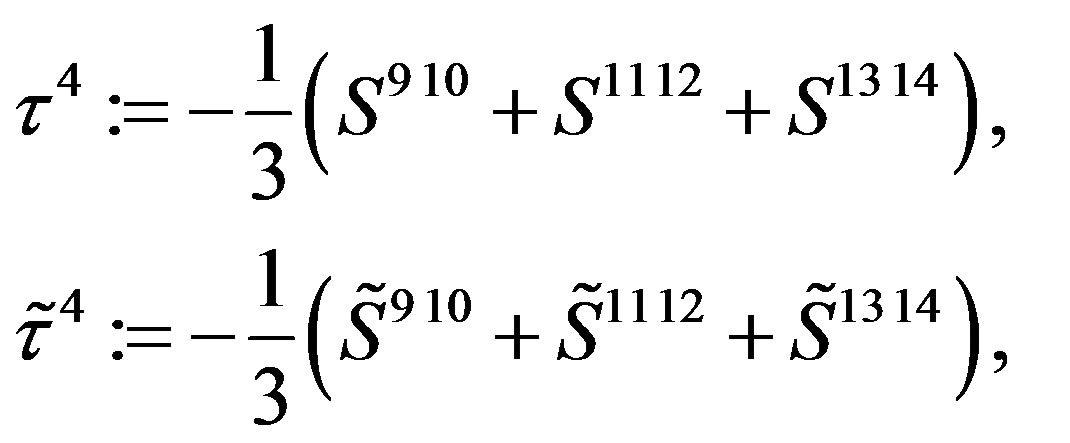 (16)
(16)
determine representations of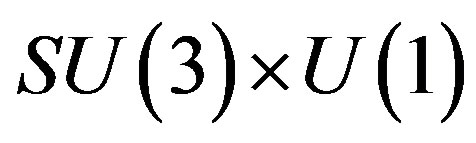 , originating in
, originating in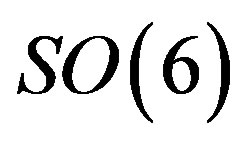 .
.
It is assumed that at the break of  to
to  all spinors but one become massive, which then manifests eight massless families generated by those generators of the infinitesimal transformations
all spinors but one become massive, which then manifests eight massless families generated by those generators of the infinitesimal transformations  which belong to the subgroup
which belong to the subgroup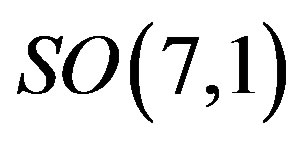 . Some justification for such an assumption can be found in the refs. [29,30].
. Some justification for such an assumption can be found in the refs. [29,30].
At the stage of the symmetry, which is
 each member of a family appears in eight massless families. Each family manifests at this symmetry, if analysed with respect to
each member of a family appears in eight massless families. Each family manifests at this symmetry, if analysed with respect to  and
and 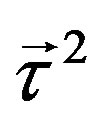 presented in Equation (15) and
presented in Equation (15) and 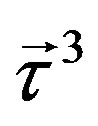 presented in Equation (16), as eightplets of
presented in Equation (16), as eightplets of 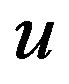 and
and  quarks, left handed weak charged and right handed weak chargeless (of spin
quarks, left handed weak charged and right handed weak chargeless (of spin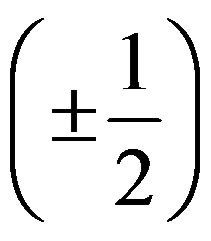 ) in three coloursand the colourless eightplet of
) in three coloursand the colourless eightplet of 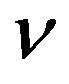 and
and  leptons, left handed weak charged and right handed weak chargeless
leptons, left handed weak charged and right handed weak chargeless
(of spin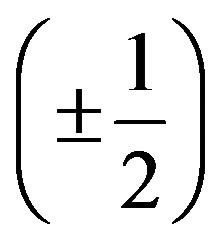 ).
).
In Table 4 the eightplet of quarks of a particular colour charge ( ,
, ) and the
) and the 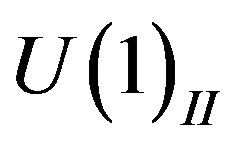 charge
charge 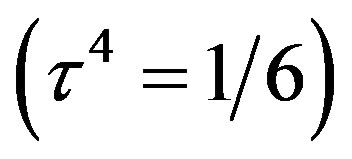 is presented in our technique [32], as products of nilpotents and projectors.
is presented in our technique [32], as products of nilpotents and projectors.
In Table 5 the eightplet of the colourless leptons of the 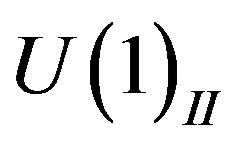 charge
charge 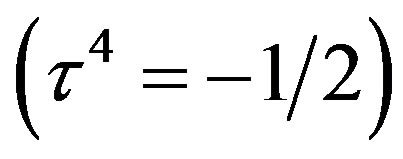 is presented in the same technique.
is presented in the same technique.
In both tables the vectors are chosen to be the eigenvectors of the operators of handedness 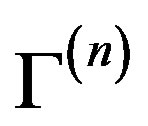 and
and , the generators
, the generators 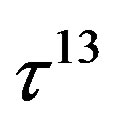 (the member of the weak
(the member of the weak 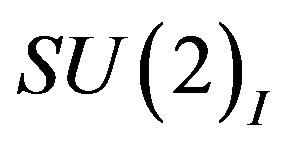 generators),
generators), 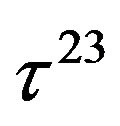 (the member of
(the member of 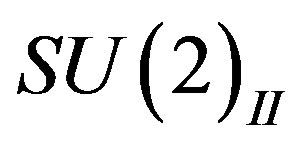 generators),
generators),
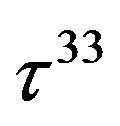 and
and 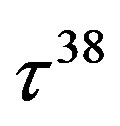 (the members of
(the members of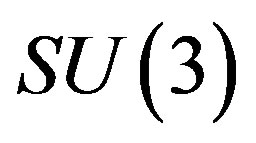 ),
), 
and . They are also eigenvectors of the corresponding
. They are also eigenvectors of the corresponding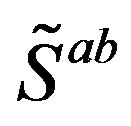 ,
,  and
and 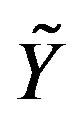 and
and . The tables for the two additional choices of the colour charge of quarks follow from Table 4 by changing the colour part of the states [28], that is by applying
. The tables for the two additional choices of the colour charge of quarks follow from Table 4 by changing the colour part of the states [28], that is by applying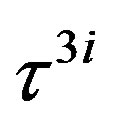 , which are not members of the Cartan subalgebra, on the states of Table 4.
, which are not members of the Cartan subalgebra, on the states of Table 4.
Looking at Tables 4 and 5 and taking into account the relation 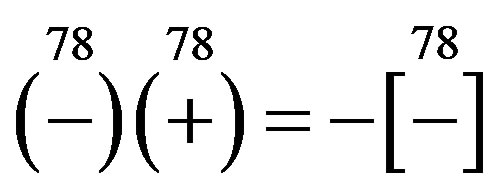 from Equation (A10) in Appendix and the relation
from Equation (A10) in Appendix and the relation 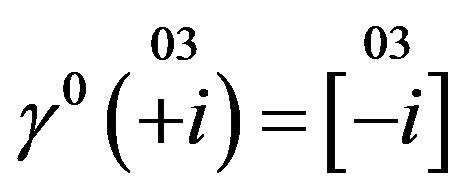 from Equation (11) one notices that the operator
from Equation (11) one notices that the operator  (Equation(13)) transforms the right handed
(Equation(13)) transforms the right handed  from the first row of Table 4 into the left handed
from the first row of Table 4 into the left handed  of the same spin and the same colour charge from the seventh row of the same table, and that it transforms the right handed
of the same spin and the same colour charge from the seventh row of the same table, and that it transforms the right handed 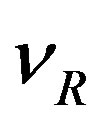 from the first
from the first
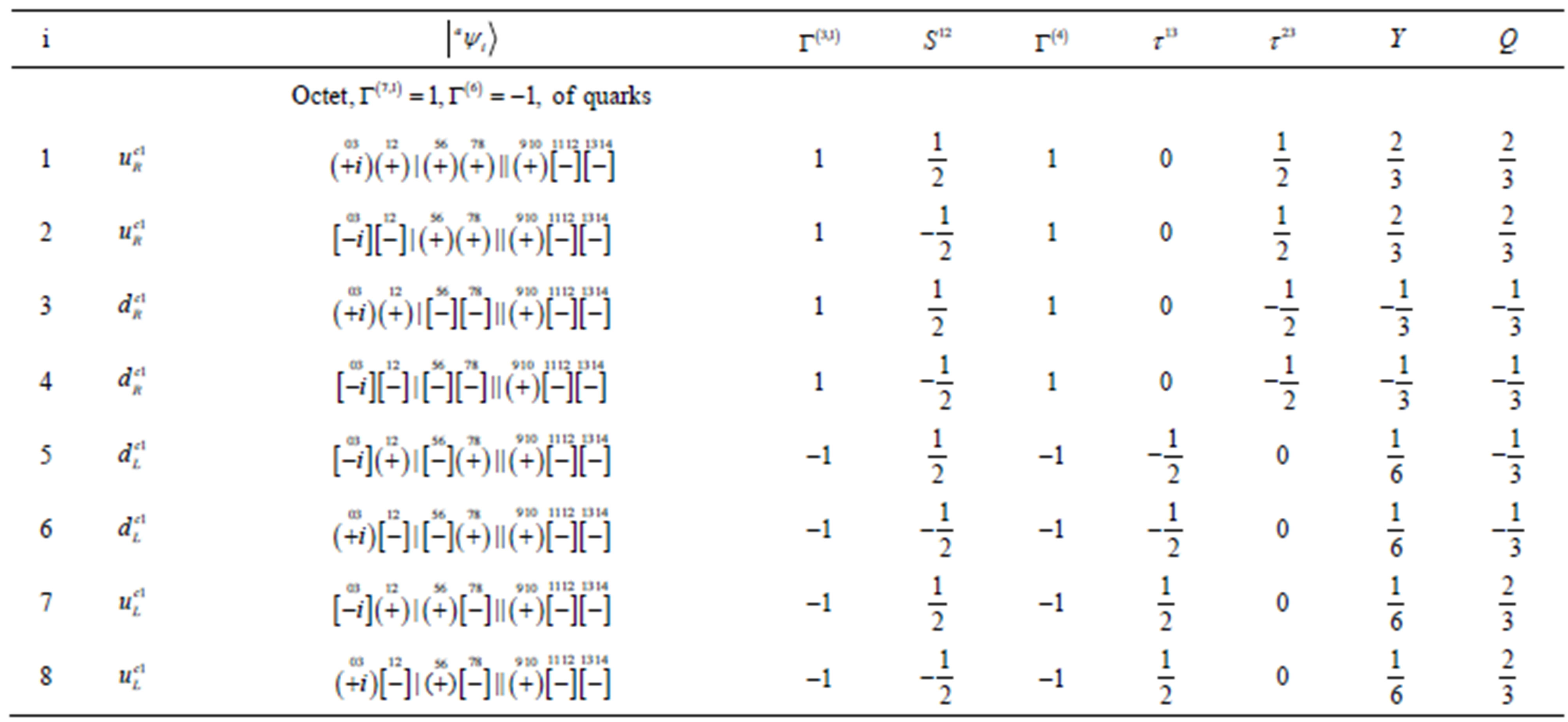
Table 4. The 8-plet of quarks—the members of 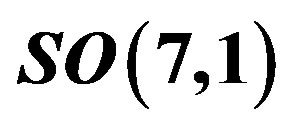 subgroup of the group
subgroup of the group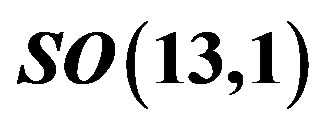 , belonging to one Weyl left handed
, belonging to one Weyl left handed  spinor representation of
spinor representation of 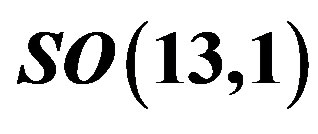 is presented in the technique [32]. It contains the left handed weak charged quarks and the right handed weak chargeless quarks of particular colour (
is presented in the technique [32]. It contains the left handed weak charged quarks and the right handed weak chargeless quarks of particular colour (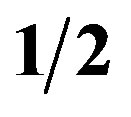 ,
, ). Here
). Here 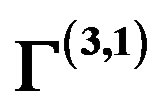 defines the handedness in (3 + 1) space, S12 defines the ordinary spin (which can also be read directly from the basic vector, both vector with both spins,
defines the handedness in (3 + 1) space, S12 defines the ordinary spin (which can also be read directly from the basic vector, both vector with both spins,  , are presented), τ13 defines the third component of the weak charge, τ23 the third component of the SU(2)II charge, τ4 (the U(1) charge) defines together with τ23 the hyper charge (Y = τ4 + τ23), Q = Y +τ13 is the electromagnetic charge. The vacuum state
, are presented), τ13 defines the third component of the weak charge, τ23 the third component of the SU(2)II charge, τ4 (the U(1) charge) defines together with τ23 the hyper charge (Y = τ4 + τ23), Q = Y +τ13 is the electromagnetic charge. The vacuum state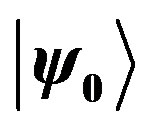 , on which the nilpotents and projectors operate, is not shown. The basis is the massless one. The reader can find the whole Weyl representation in the ref. [28].
, on which the nilpotents and projectors operate, is not shown. The basis is the massless one. The reader can find the whole Weyl representation in the ref. [28].

Table 5. The 8-plet of leptons—the members of 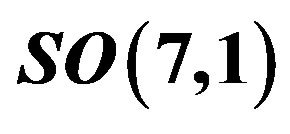 subgroup of the group
subgroup of the group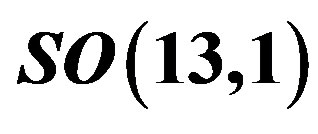 , belonging to one Weyl left handed
, belonging to one Weyl left handed  spinor representation of
spinor representation of 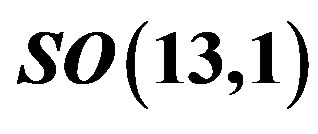 is presented in the massless basis. It contains the colour chargeless left handed weak charged leptons and the right handed weak chargeless leptons. The rest of notation is the same as in Table 4.
is presented in the massless basis. It contains the colour chargeless left handed weak charged leptons and the right handed weak chargeless leptons. The rest of notation is the same as in Table 4.
row of Table 5 into the left handed 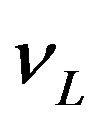 presented in the seventh row of the same table, just what the Higgs and
presented in the seventh row of the same table, just what the Higgs and  do in the standard model. Equivalently one finds that the operator
do in the standard model. Equivalently one finds that the operator 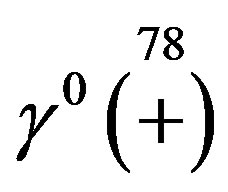 transforms the right handed
transforms the right handed
 -quark from the third row into the left handed one (of the same spin and colour) presented in the fifth row of Table 4 and that it transforms the right handed
-quark from the third row into the left handed one (of the same spin and colour) presented in the fifth row of Table 4 and that it transforms the right handed 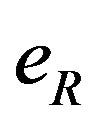 from the third row of Table 5 into the left handed one (of the same spin) presented in the fifth row of Table 5.
from the third row of Table 5 into the left handed one (of the same spin) presented in the fifth row of Table 5.
The superposition of generators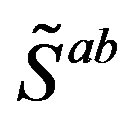 , forming generators
, forming generators 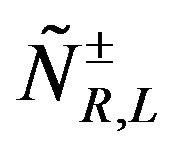 and
and , presented in Appendix, Equation (A 19), generate families, transforming each member of one family into the same member of another family, due to the fact that
, presented in Appendix, Equation (A 19), generate families, transforming each member of one family into the same member of another family, due to the fact that  (Equation (2)). The eight families of the first member of the eightplet of quarks from Table 4, for example, that is of the right handed
(Equation (2)). The eight families of the first member of the eightplet of quarks from Table 4, for example, that is of the right handed  -quark with spin
-quark with spin , are presented in the left column of Table 6. The generators
, are presented in the left column of Table 6. The generators  and
and , Equation (A 19), transform the first member of the eightplet from Table 5, that is the right handed neutrino
, Equation (A 19), transform the first member of the eightplet from Table 5, that is the right handed neutrino 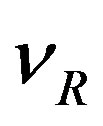 with spin
with spin , into the eight-plet of right handed neutrinos with spin up, belonging to eight different families. These families are presented in the right column of the same table. All the other members of any of the eight families of quarks or leptons follow from any member of a particular family by the application of the operators
, into the eight-plet of right handed neutrinos with spin up, belonging to eight different families. These families are presented in the right column of the same table. All the other members of any of the eight families of quarks or leptons follow from any member of a particular family by the application of the operators 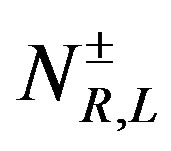 and
and  on this particular member.
on this particular member.
Let me point out that the break of 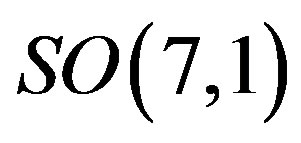 into
into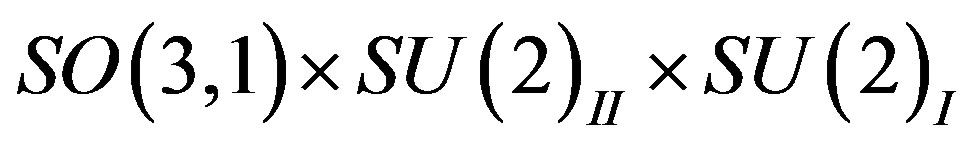 , assumed to leave all the eight families massless, allows to divide eight families into two groups of four families. One group of families contains doublets with respect to
, assumed to leave all the eight families massless, allows to divide eight families into two groups of four families. One group of families contains doublets with respect to 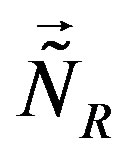 and
and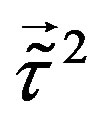 , these families are singlets with respect to
, these families are singlets with respect to 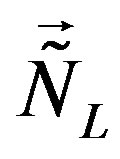 and
and . Another group of families contains doublets with respect to
. Another group of families contains doublets with respect to  and
and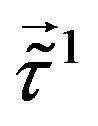 , these families are singlets with respect to
, these families are singlets with respect to 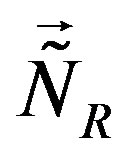 and
and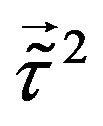 . The scalar fields which are the gauge scalars of
. The scalar fields which are the gauge scalars of 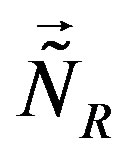 and
and 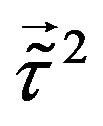 couple only to the four families which are doublets with respect to these two groups. When gaining non zero vacuum expectation values, these scalar fields cause nonzero mass matrices of the four families to which they couple. These happens at some scale (assumed to be) much higher than the electroweak scale.
couple only to the four families which are doublets with respect to these two groups. When gaining non zero vacuum expectation values, these scalar fields cause nonzero mass matrices of the four families to which they couple. These happens at some scale (assumed to be) much higher than the electroweak scale.
The group of four families, which are singlets with respect to 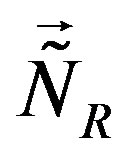 and
and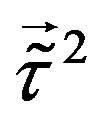 , stay massless unless the gauge scalar fields of
, stay massless unless the gauge scalar fields of 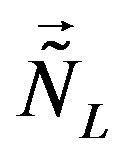 and
and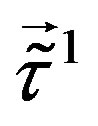 , together with the gauge scalars of
, together with the gauge scalars of  and
and , gain a nonzero vacuum expectation values at the electroweak break. Correspondingly the decoupled twice four families (the matrix elements between these two groups of four families are equal to zero) appear at two different scales determined by two different breaks.
, gain a nonzero vacuum expectation values at the electroweak break. Correspondingly the decoupled twice four families (the matrix elements between these two groups of four families are equal to zero) appear at two different scales determined by two different breaks.
To have an overview over the properties of the members of one (any one of the eight) family let us present in Table 7 quantum numbers of particular members of any

Table 6. Eight families of the right handed  quark with spin
quark with spin , the colour charge
, the colour charge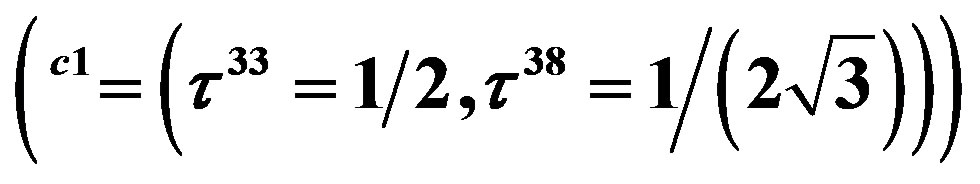 , and of the colourless right handed neutrino
, and of the colourless right handed neutrino  of spin
of spin  are presented in the left and in the right column, respectively. All the families follow from the starting one by the application of the operators (
are presented in the left and in the right column, respectively. All the families follow from the starting one by the application of the operators ( ,
, ) from Equation (A19). The generators (
) from Equation (A19). The generators ( ,
, ) (Equation (A19)) transform
) (Equation (A19)) transform  of spin
of spin  and the chosen colour
and the chosen colour 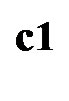 to all the members of one family of the same colour. The same generators transform equivalently the right handed neutrino
to all the members of one family of the same colour. The same generators transform equivalently the right handed neutrino 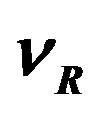 of spin
of spin 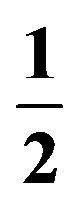 to all the colourless members of the same family.
to all the colourless members of the same family.
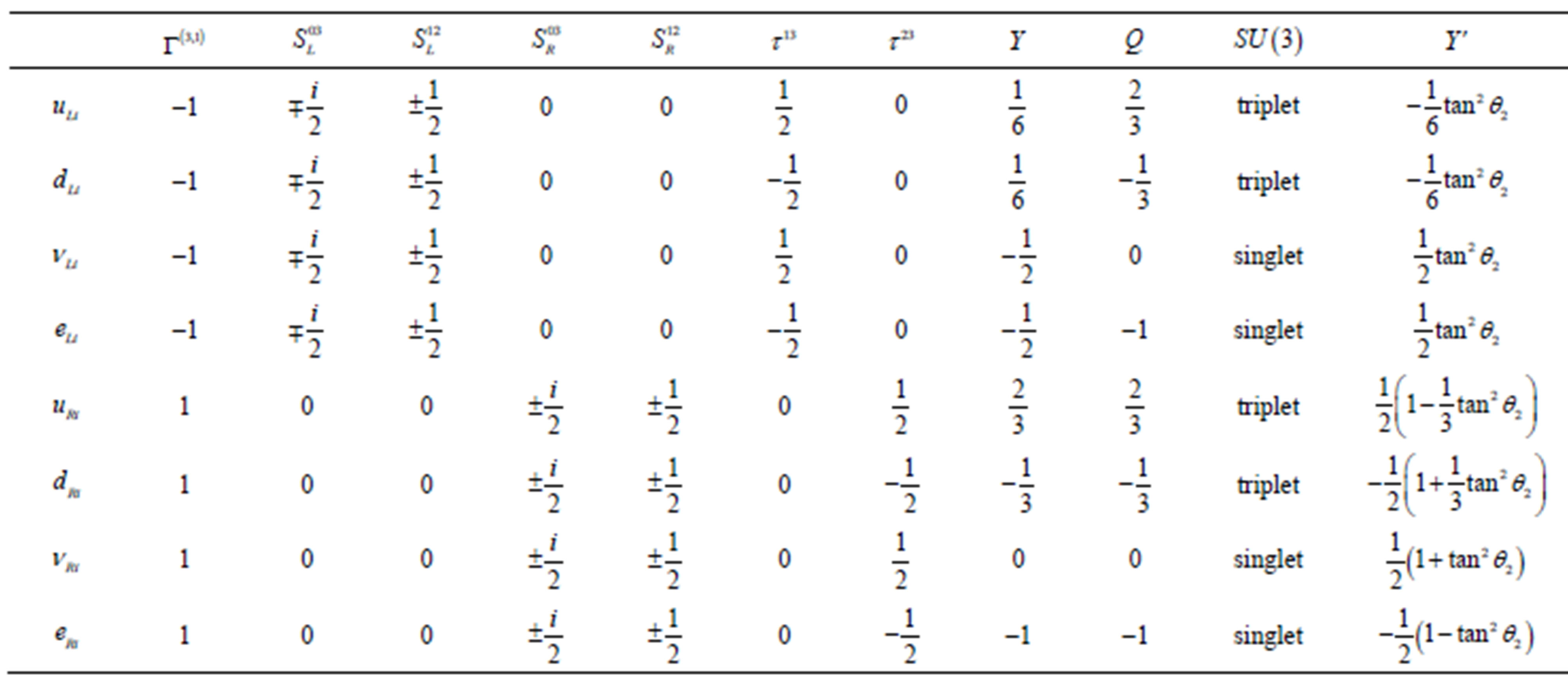
Table 7. The quantum numbers of the members—quarks and leptons, left and right handed -- of any of the eight families 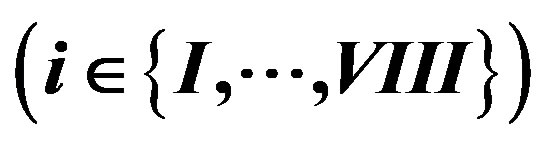 from Table 4 are presented: The handedness
from Table 4 are presented: The handedness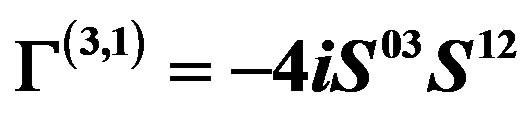 ,
,  ,
,  ,
, 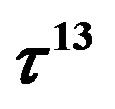 of the weak
of the weak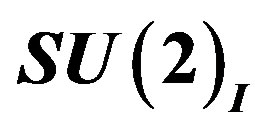 ,
,  of the second
of the second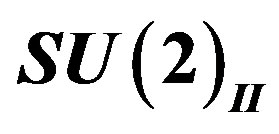 , the hyper charge
, the hyper charge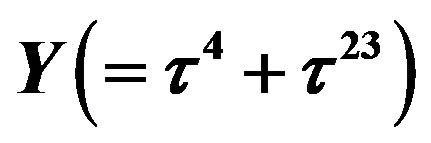 , the electromagnetic charge
, the electromagnetic charge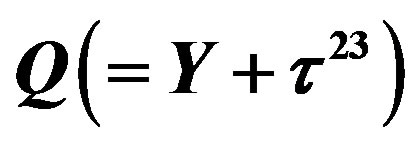 , the
, the 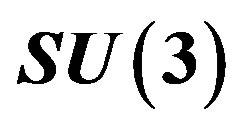 status, that is, whether the member is a triplet—the quark with the one of the charges determined by
status, that is, whether the member is a triplet—the quark with the one of the charges determined by 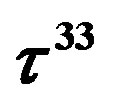 and
and , that is one of
, that is one of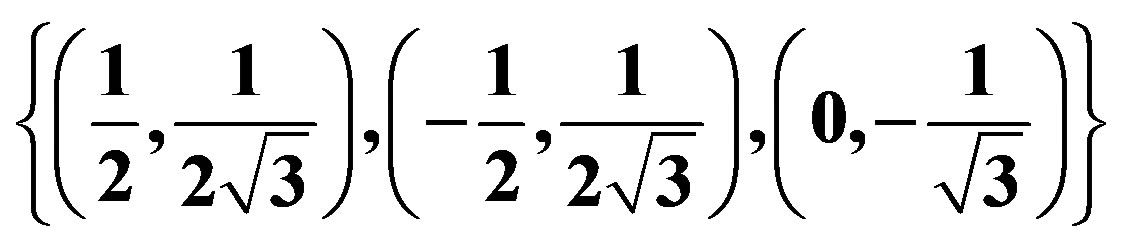 —or a singlet, and the charge
—or a singlet, and the charge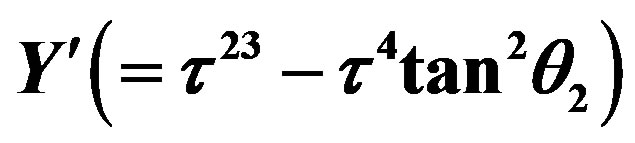 ).
).
of the eight families: The handedness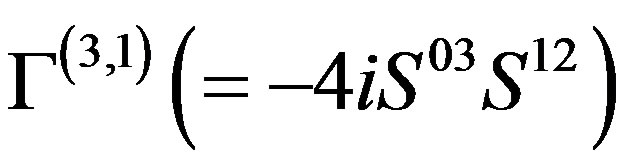 ,
,
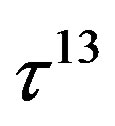 (of the weak
(of the weak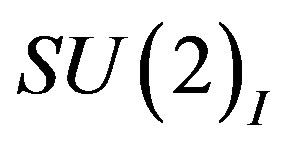 ),
), 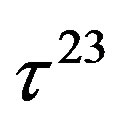 (of
(of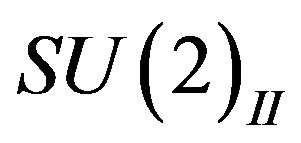 ), the hyper charge
), the hyper charge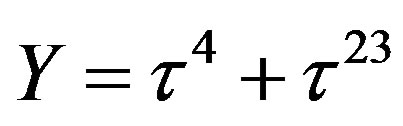 , the electromagnetic charge
, the electromagnetic charge , the
, the  status, that is, whether the member is a member of a triplet (the quark with the one of the charges
status, that is, whether the member is a member of a triplet (the quark with the one of the charges
 ) or the colourless lepton, we present also
) or the colourless lepton, we present also ,
,  , and, after the break of
, and, after the break of 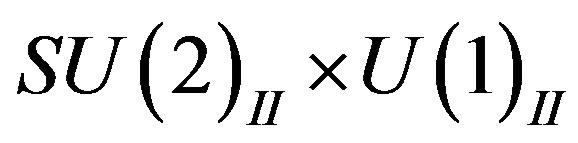 into
into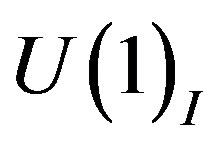 , also
, also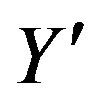 .
.
Before the break of 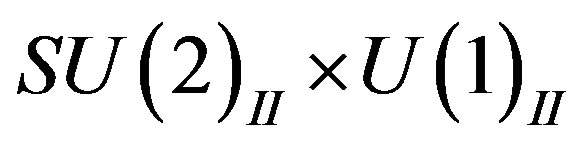 into
into 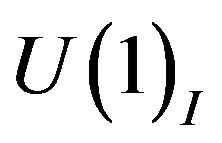 the members of one family from Tables 4 and 5 share the family quantum numbers presented in Table 8: The
the members of one family from Tables 4 and 5 share the family quantum numbers presented in Table 8: The
“tilde handedness” of the families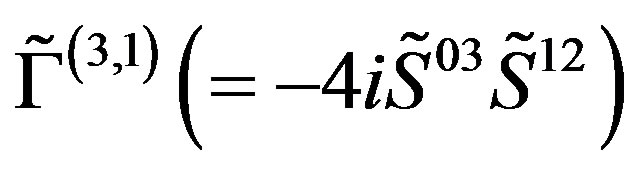 ,
,  ,
,  (the diagonal matrices of
(the diagonal matrices of  ),
),
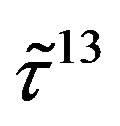 (of one of the two
(of one of the two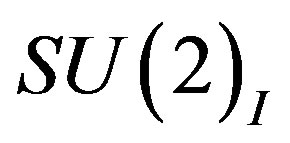 ),
), 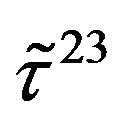 (of the second
(of the second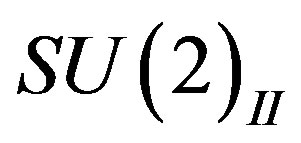 ).
).
We see in Table 8 that the first four of the eight families are singlets with respect to subgroups determined by 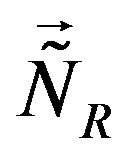 and
and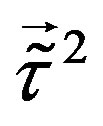 , and doublets with respect to
, and doublets with respect to 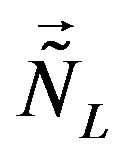 and
and , while the rest four families are doublets with respect to
, while the rest four families are doublets with respect to 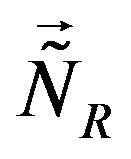 and
and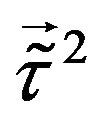 , and singlets with respect to
, and singlets with respect to  and
and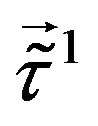 .
.
When the break from 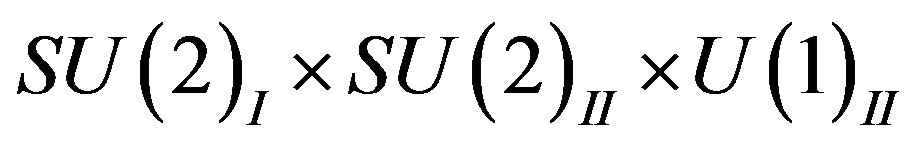 to
to 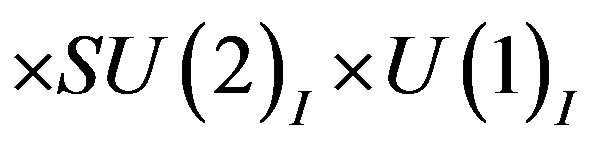 appears, the scalar fields, the superposition of
appears, the scalar fields, the superposition of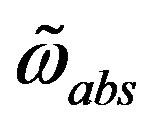 , which are triplets with respect to
, which are triplets with respect to  and
and 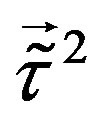 (are assumed to) gain a nonzero vacuum expectation values. As one can read from Equation (5) these scalar fields cause nonzero mass matrices of the families which are doublets with respect to
(are assumed to) gain a nonzero vacuum expectation values. As one can read from Equation (5) these scalar fields cause nonzero mass matrices of the families which are doublets with respect to 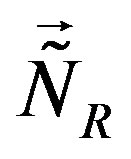 and
and 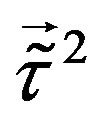 and correspondingly couple to these scalar fields with nonzero vacuum expectation values. The four families which do not couple to these scalar fields stay massless. The vacuum expectation value of
and correspondingly couple to these scalar fields with nonzero vacuum expectation values. The four families which do not couple to these scalar fields stay massless. The vacuum expectation value of 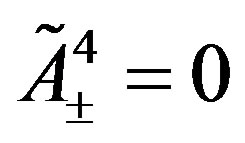 (is assumed to) stays zero at the first break. In this break also the vector (with respect to (3 + 1)) gauge fields of
(is assumed to) stays zero at the first break. In this break also the vector (with respect to (3 + 1)) gauge fields of 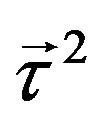 (the generators of
(the generators of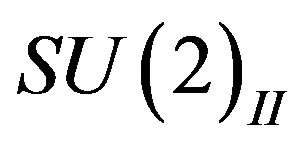 ) become massive.
) become massive.
In the successive (electroweak) break the scalar gauge fields of 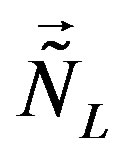 and
and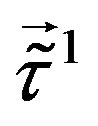 , coupled to the rest of eight families, gain nonzero vacuum expectation values. Together with them also the scalar gauge fields
, coupled to the rest of eight families, gain nonzero vacuum expectation values. Together with them also the scalar gauge fields ,
, 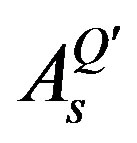 and
and 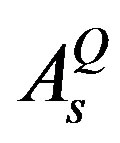 (the superposition of
(the superposition of 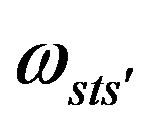 spin connection fields) gain nonzero vacuum expectation values. The scalar fields
spin connection fields) gain nonzero vacuum expectation values. The scalar fields ,
, 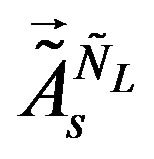 ,
, 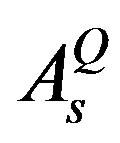 ,
, 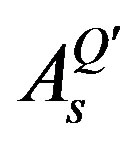 and
and 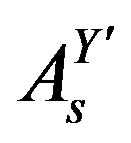 determine mass matrices of the last four massless families. At this break also the vector gauge fields of
determine mass matrices of the last four massless families. At this break also the vector gauge fields of 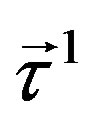 become massive.
become massive.
The second break, which (is assumed to) occurs at much lower energy scale, influences slightly also properties of the upper four families.
Let us end this subsection by admitting that it is assumed (not yet showed or proved) that there is no contributions to the mass matrices from 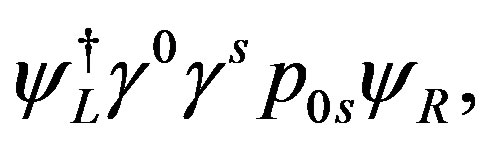 with
with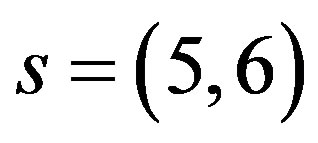 . Such a contribution to the mass term would namely mix states with different electromagnetic charges (
. Such a contribution to the mass term would namely mix states with different electromagnetic charges (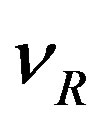 and
and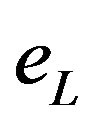 ,
, 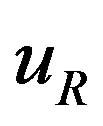 and
and ), in disagreement with what
), in disagreement with what
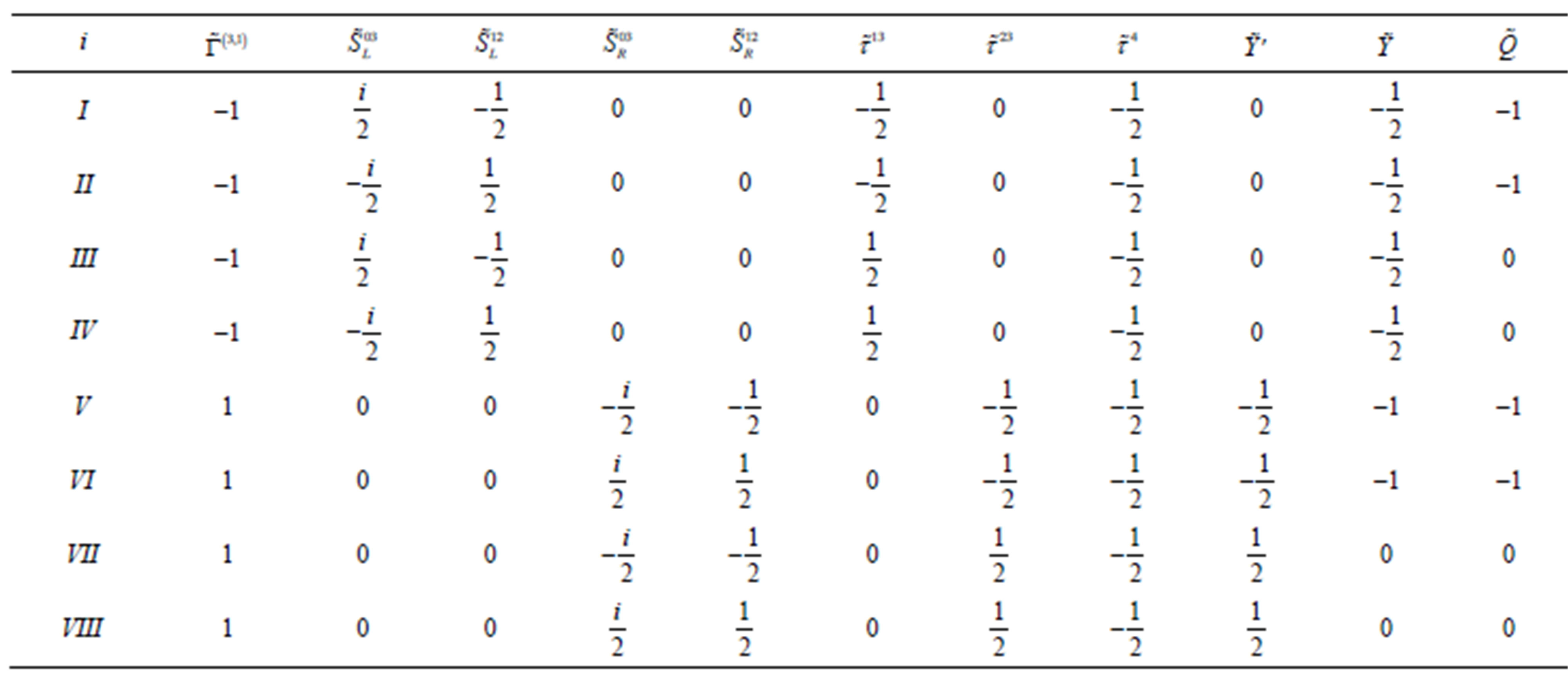
Table 8. The quantum numbers of a member of the eight families from Table 6, the same for all the members of one family, are presented: The “tilde handedness” of the families , the left and right handed
, the left and right handed  quantum numbers (Equation (14),
quantum numbers (Equation (14),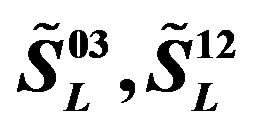 ,
, of
of  group in the
group in the 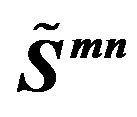 sector),
sector), 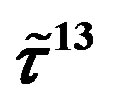 of
of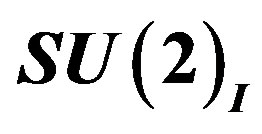 ,
,  of the second
of the second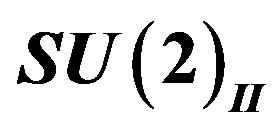 ,
, 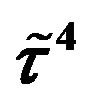 (Equation (16)),
(Equation (16)),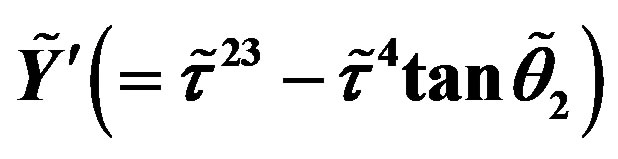 , taking
, taking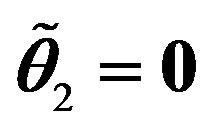 ,
, 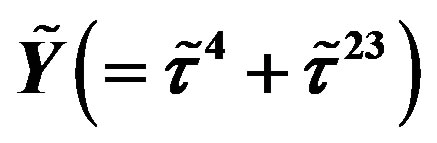 ,
, .
.
is observed. The choice that scalars  and
and  with only
with only 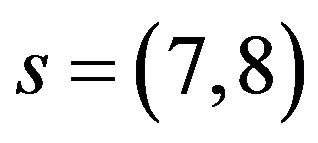 manifest makes all the scalar fields behaving as weak doublets.
manifest makes all the scalar fields behaving as weak doublets.
2.2. Scalar and Gauge Fields in  through Breaks
through Breaks
In the spin-charge-family theory there are the vielbeins 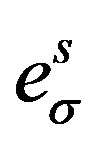
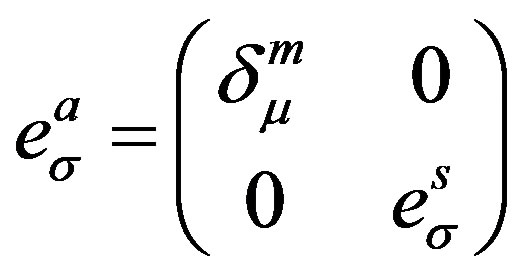
in a strong correlation with the spin connection fields of both kinds, 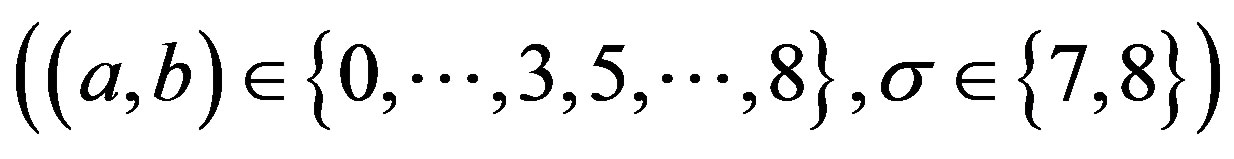
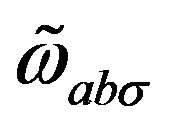
and with 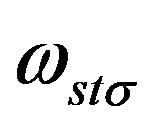
 , which manifest in
, which manifest in 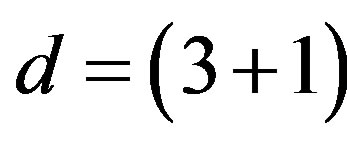 -dimensional space as scalar fields after particular breaks of a starting symmetry. Phase transitions are (assumed to be) triggered by the nonzero vacuum expectation values of the fields
-dimensional space as scalar fields after particular breaks of a starting symmetry. Phase transitions are (assumed to be) triggered by the nonzero vacuum expectation values of the fields 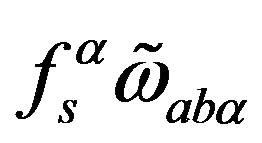 and
and .
.
The gauge fields then correspondingly appear as
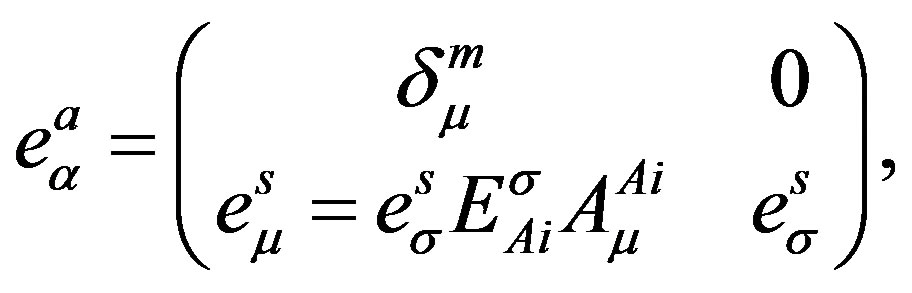
with 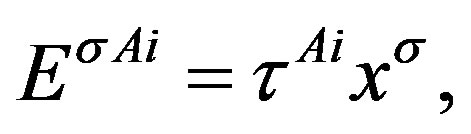 where
where 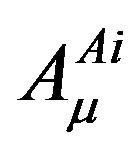 are the gauge fields, corresponding to (all possible) Kaluza-Klein charges
are the gauge fields, corresponding to (all possible) Kaluza-Klein charges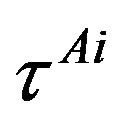 , manifesting in
, manifesting in . Since the space symmetries include only
. Since the space symmetries include only 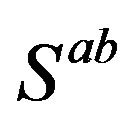
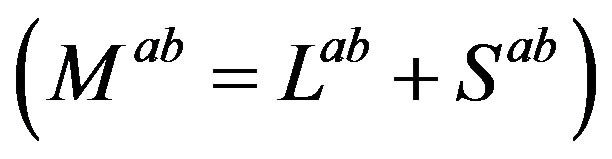 and not
and not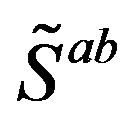 there are no vector gauge fields of the type
there are no vector gauge fields of the type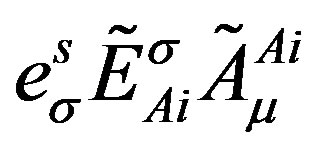 , with
, with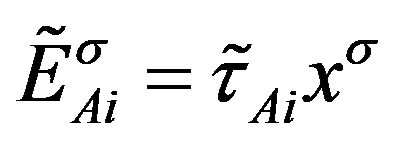 . The gauge fields of
. The gauge fields of  manifest in
manifest in 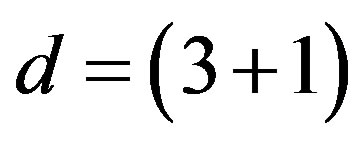 only as scalar fields.
only as scalar fields.
The vielbeins and spin connection fields from Equation (4) 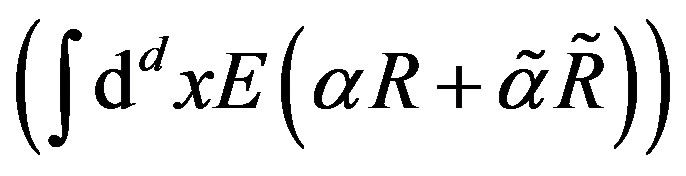 are manifesting in
are manifesting in
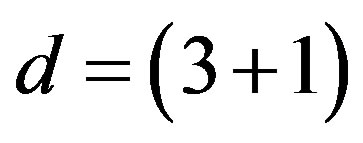 in the effective action, if no gravity is assumed in
in the effective action, if no gravity is assumed in 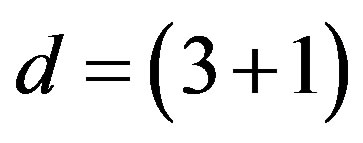
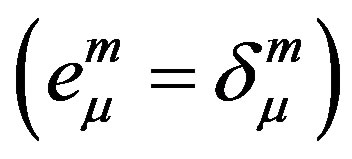
 (17)
(17)
Masses of gauge fields of the charges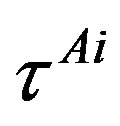 , which symmetries are unbroken, are zero, nonzero masses correspond to the broken symmetries.
, which symmetries are unbroken, are zero, nonzero masses correspond to the broken symmetries.
In the breaking procedures, when
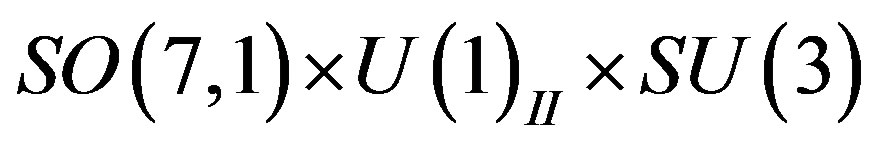
breaks into
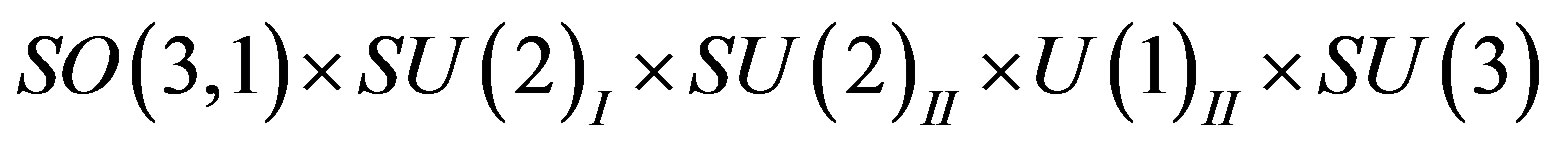 there are massless gauge fields
there are massless gauge fields

and 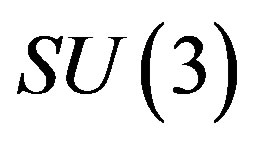 (and eight massless families of quarks and leptons, as discussed above).
(and eight massless families of quarks and leptons, as discussed above).
In the break from
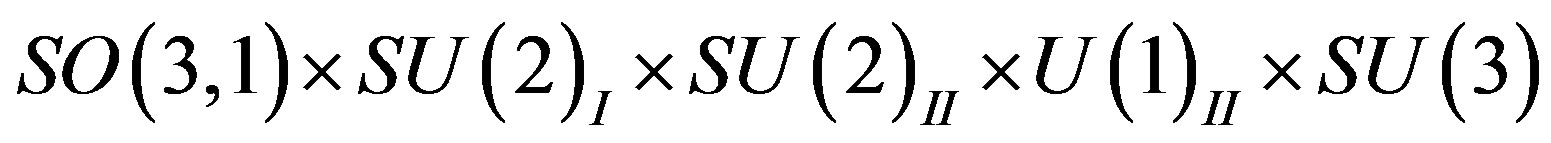
to
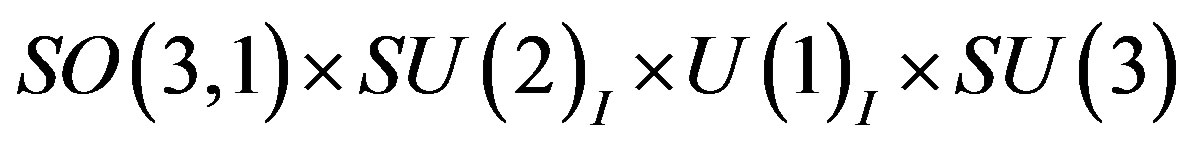
the scalar fields originating in 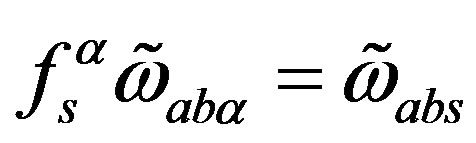 gain nonzero vacuum expectation values causing the break of symmetries, which manifests on the tree level in masses of the superposition of gauge fields
gain nonzero vacuum expectation values causing the break of symmetries, which manifests on the tree level in masses of the superposition of gauge fields 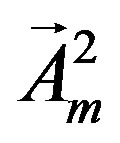 and
and , as well as in mass matrices of the upper four families.
, as well as in mass matrices of the upper four families.
To the break from  to
to  both kinds of scalar fields, superposition of
both kinds of scalar fields, superposition of  and of
and of 
with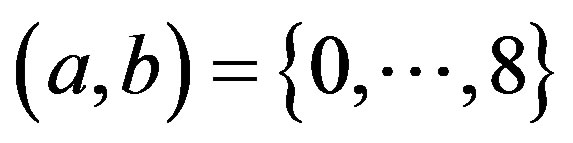 ,
, 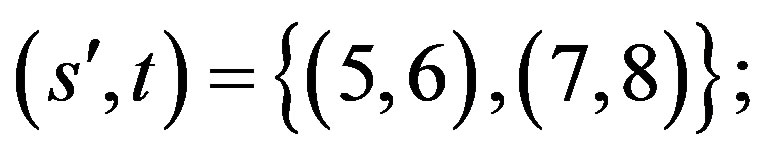 and
and
 , as well as
, as well as 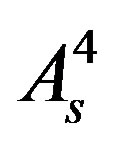 contribute, which manifests in the masses of
contribute, which manifests in the masses of 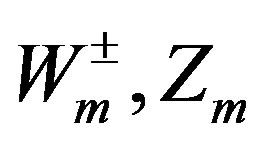 and in mass matrices of the lower four families.
and in mass matrices of the lower four families.
Detailed studies of the appearance of breaks of symmetries as they follow from the starting action, the corresponding manifestation of masses of the gauge fields involved in these breaks, as well as the appearance of nonzero vacuum expectation values of the scalar fields which manifest in mass matrices of the families involved in particular breaks are under consideration. We have studied successfully so far [29,30] a toy model where the break appears from 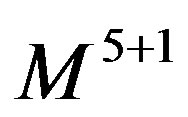 to
to 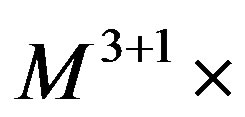 an infinite disc, curled by the vielbein into an almost
an infinite disc, curled by the vielbein into an almost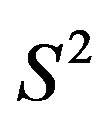 , and with a spin connection on this infinite disc, which enables massless fermions after the break.
, and with a spin connection on this infinite disc, which enables massless fermions after the break.
Although the symmetries of the vacuum expectation values of the scalar fields are known when once the way of breaking symmetries is assumed, yet their values (numbers) are not known. Masses and interactions determining the dynamics of these scalar fields are also not known.
But knowing the number of with mixing matrices related families, which is four in the spin-charge-family theory, the symmetry of the 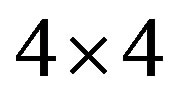 mass matrices, which is in the spin-charge-family theory the same for all the family members and the experimental values for the so far measured masses and mixing matrices, we are able to comment about properties of the fourth family members [34] and about the vector and scalar fields.
mass matrices, which is in the spin-charge-family theory the same for all the family members and the experimental values for the so far measured masses and mixing matrices, we are able to comment about properties of the fourth family members [34] and about the vector and scalar fields.
Let us repeat that the gauge fields originating in 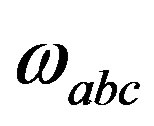 are after the breaks in the adjoint representations with respect to all the charges, while the scalar fields are as well in the adjoint representations with respect to the family charges, while they form doublets as the “gauge fields” of
are after the breaks in the adjoint representations with respect to all the charges, while the scalar fields are as well in the adjoint representations with respect to the family charges, while they form doublets as the “gauge fields” of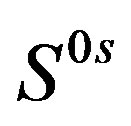 ,
,  with respect to the weak charge.
with respect to the weak charge.
2.2.1. Scalar and Gauge Fields after the Break from 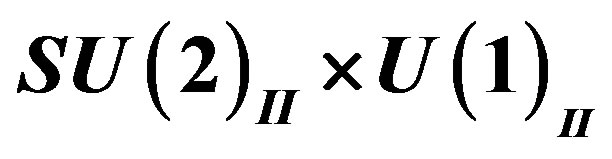 to
to 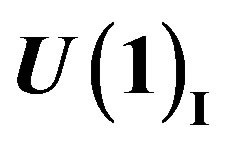
Before the break of
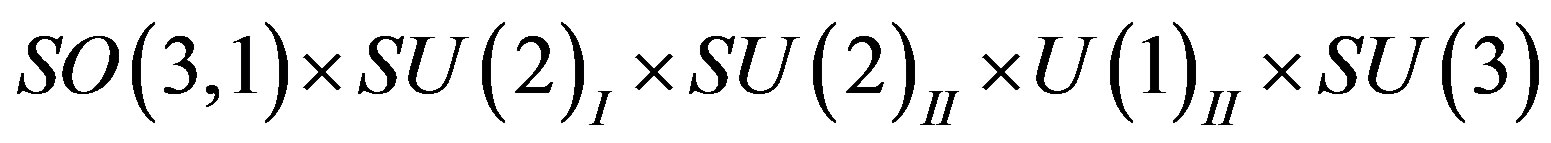
to
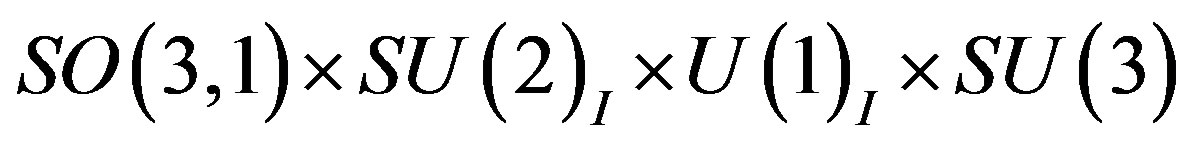
the gauge fields  (
( ,
,
 ,
,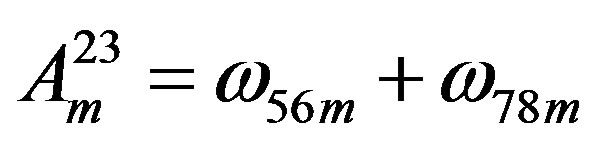 ),
), 
(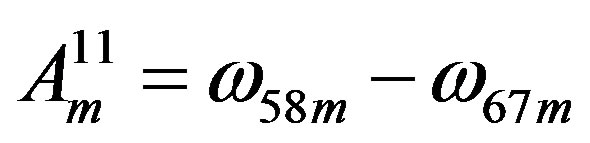 ,
, 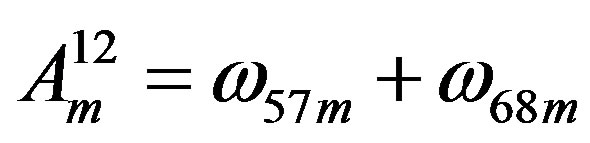 ,
,
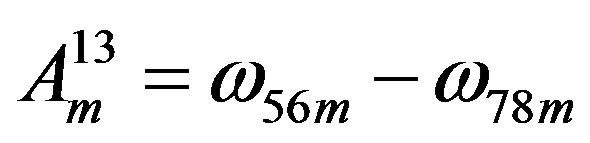 ) and
) and  are all massless.
are all massless.
After this break the gauge fields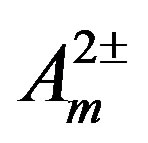 , as well as one superposition of
, as well as one superposition of 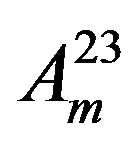 and
and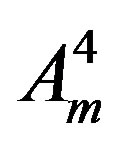 , become massive, while another superposition
, become massive, while another superposition  and the gauge fields
and the gauge fields 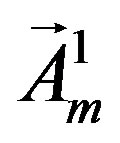 stay massless.
stay massless.
The fields 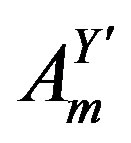 and
and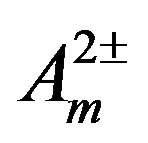 , manifesting as massive fields, and
, manifesting as massive fields, and 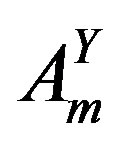 which stay massless, are defined as the superposition of the old ones as follows
which stay massless, are defined as the superposition of the old ones as follows
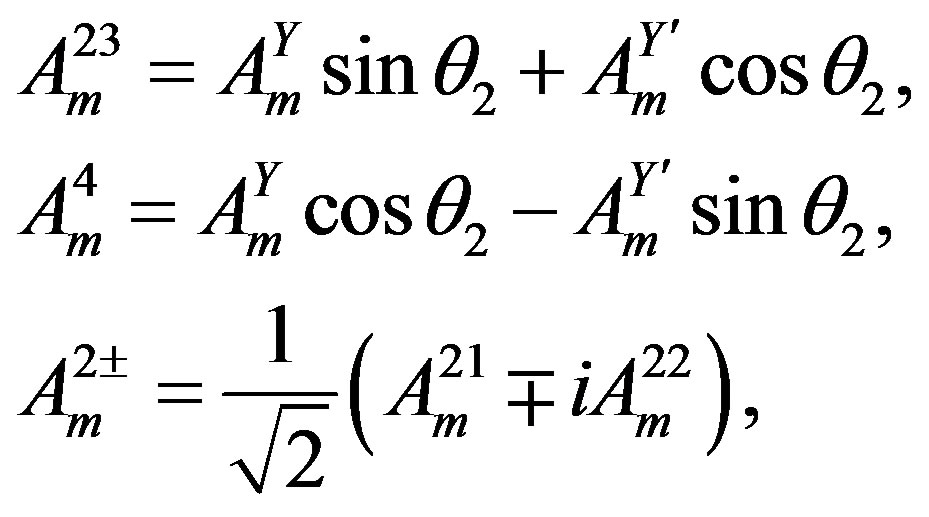 (18)
(18)
for  and a particular value of
and a particular value of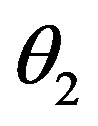 . The scalar fields
. The scalar fields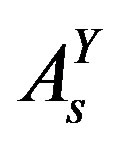 ,
, 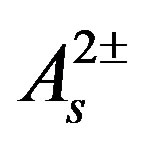 ,
, 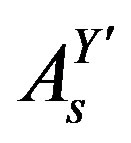 , which do not gain in this break any vacuum expectation values, stay massless. This assumption guarantees that they do not contribute to masses of the lower four families on the tree level.
, which do not gain in this break any vacuum expectation values, stay massless. This assumption guarantees that they do not contribute to masses of the lower four families on the tree level.
The corresponding operators for the new charges which couple these new gauge fields to fermions are
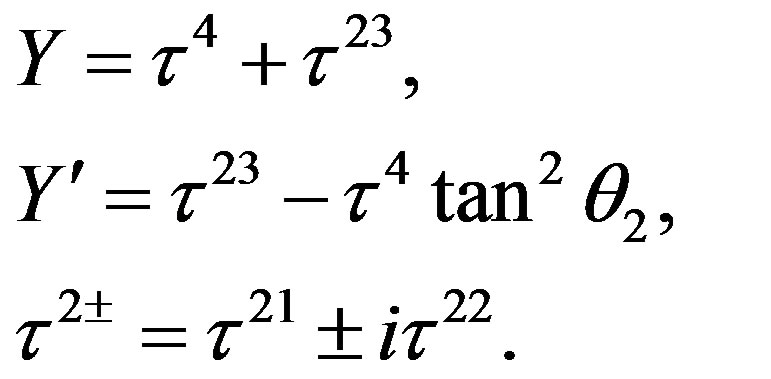 (19)
(19)
The new coupling constants become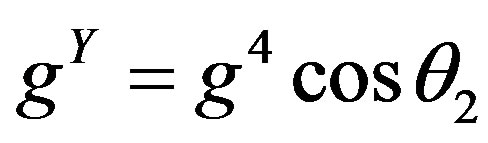 ,
, 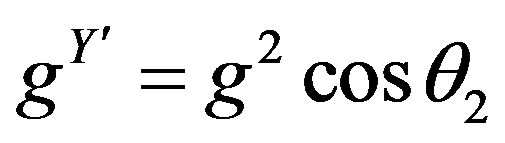 , while
, while 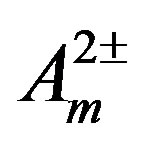 have a coupling constant
have a coupling constant
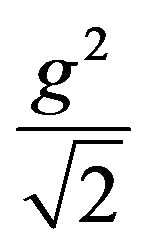 .
.
To this break the scalar fields originating in 
contribute so that the symmetries in both sectors, 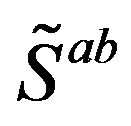
and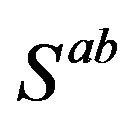 , are broken simultaneously. The scalar fields
, are broken simultaneously. The scalar fields  (which are the superposition of
(which are the superposition of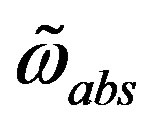 ,
, 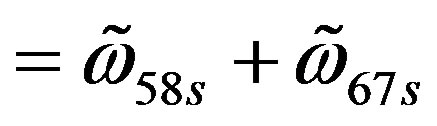
 ,
, 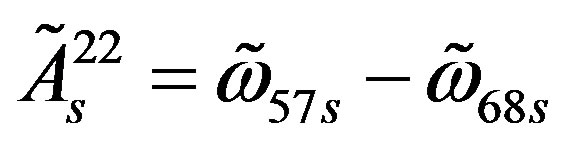 ,
,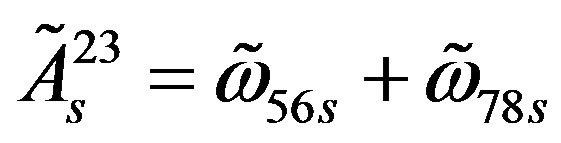 ) gain a nonzero vacuum expectation values.
) gain a nonzero vacuum expectation values.
We have for the scalar fields correspondingly
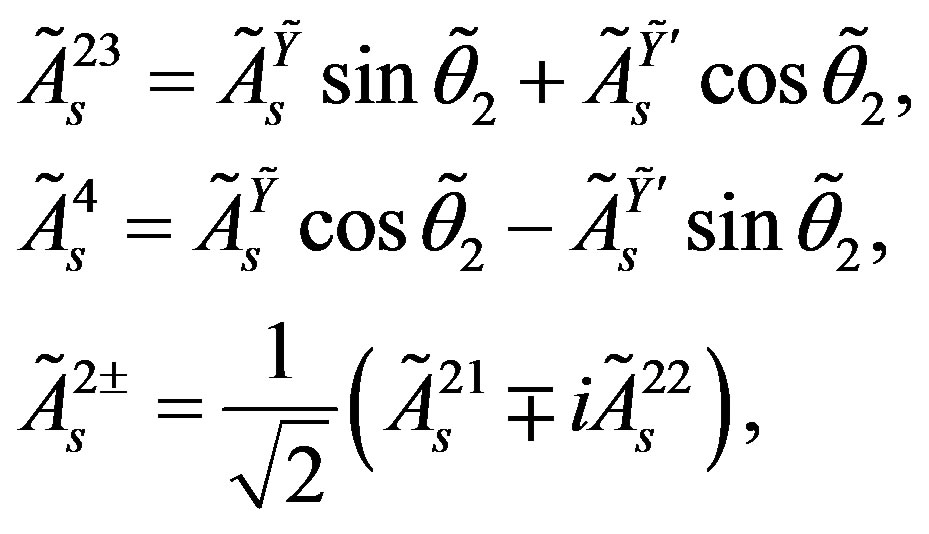 (20)
(20)
for  and a particular value of
and a particular value of . These scalar fields, having a nonzero vacuum expectation values, define according to Equation (7) mass matrices of the upper four families, which are doublets with respect to
. These scalar fields, having a nonzero vacuum expectation values, define according to Equation (7) mass matrices of the upper four families, which are doublets with respect to  and
and .
.
To this break and correspondingly to the mass matrices of the upper four families the scalar fields which couple to the upper four families
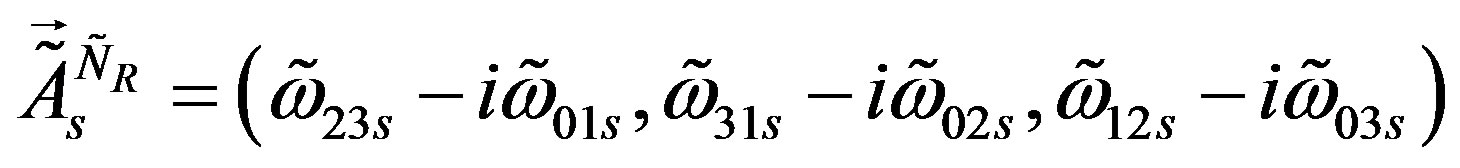 (21)
(21)
contribute. The lower four families, which are singlets with respect to both groups, stay correspondingly massless.
The corresponding new operators are then
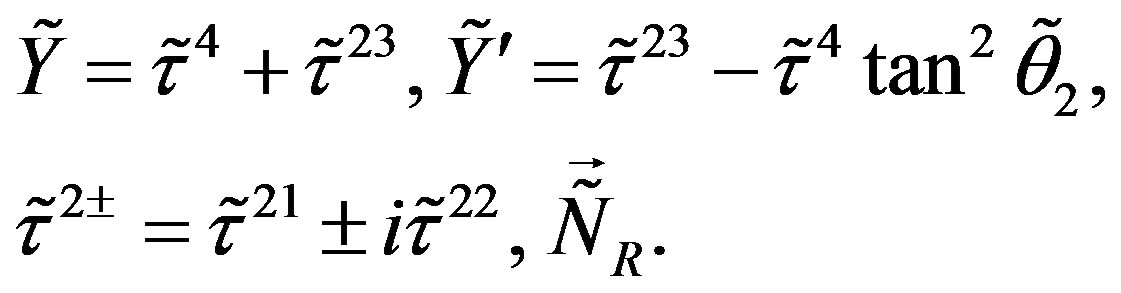 (22)
(22)
New coupling constants are correspondingly
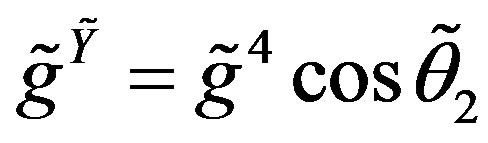 ,
,  ,
, 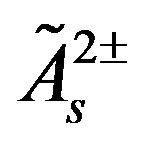 have a coupling constant
have a coupling constant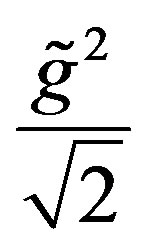 , and
, and  the coupling constant
the coupling constant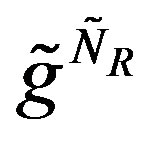 .
.
To assure masslessness of the lower four families 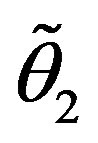 must be equal to zero.
must be equal to zero.
2.2.2. Scalar and Gauge Fields after the Break from 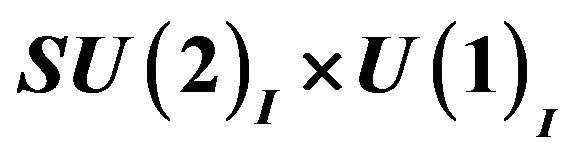 to
to 
To the electroweak break, when
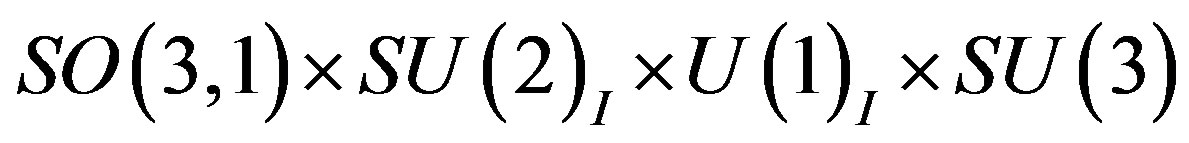
breaks into
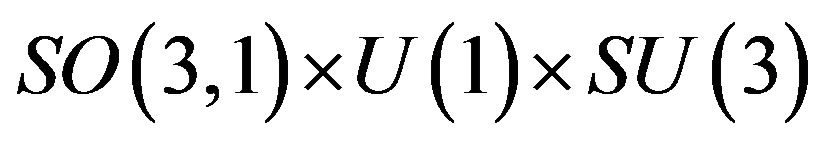 both kinds of the scalar spin connection fields contribute. That means that a superposition of
both kinds of the scalar spin connection fields contribute. That means that a superposition of  (which is orthogonal to the one trigging the first break)
(which is orthogonal to the one trigging the first break)
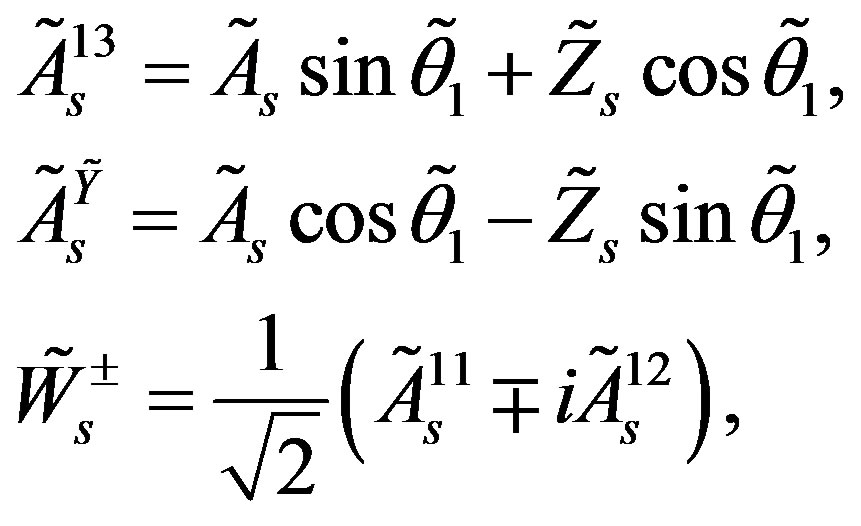 (23)
(23)
and
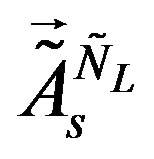 (24)
(24)
and a superposition of 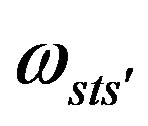
 (25)
(25)
 contribute. While the superposition of Equations (23, 24) couple to the lower four families only, since the lower four families are doublets with respect to
contribute. While the superposition of Equations (23, 24) couple to the lower four families only, since the lower four families are doublets with respect to 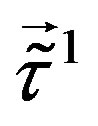 and
and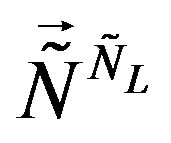 , and the upper four families are singlets with respect to
, and the upper four families are singlets with respect to 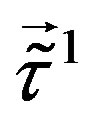 and
and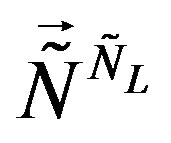 , the scalar fields
, the scalar fields ,
,  and
and
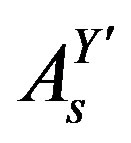 (they are a superposition of
(they are a superposition of 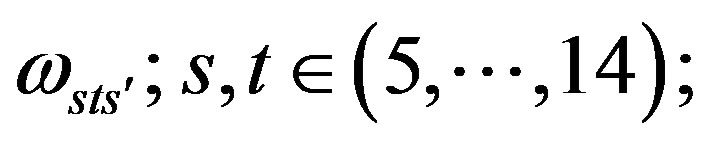
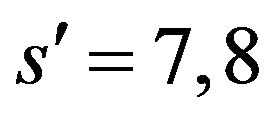 ) couple to all the eight families, distinguishing among the family members.
) couple to all the eight families, distinguishing among the family members.
Correspondingly a superposition of the vector fields 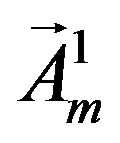 and
and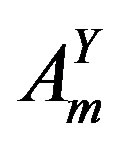 ,
,
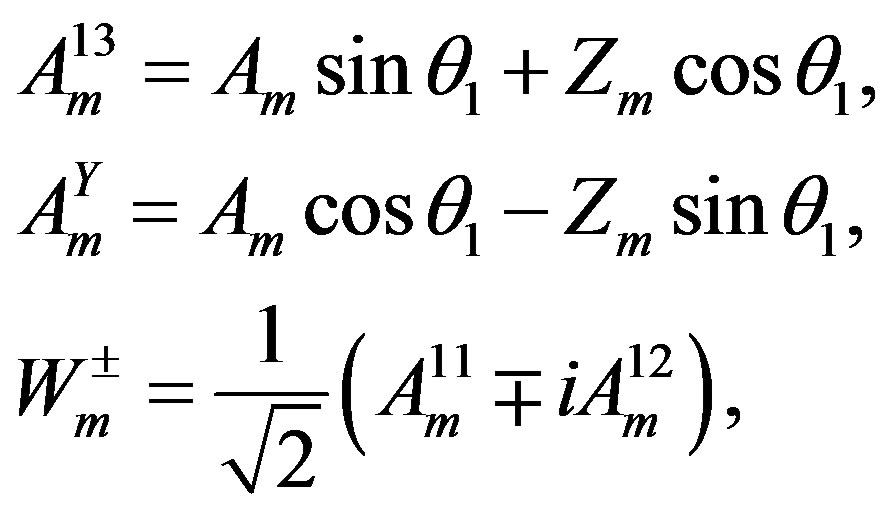 (26)
(26)
that is 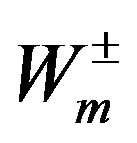 and
and , become massive, while
, become massive, while 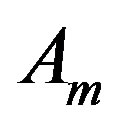 stays with
stays with 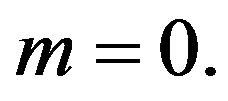 The new operators for charges are
The new operators for charges are
 (27)
(27)
and the new coupling constants are correspondingly
 ,
,  and
and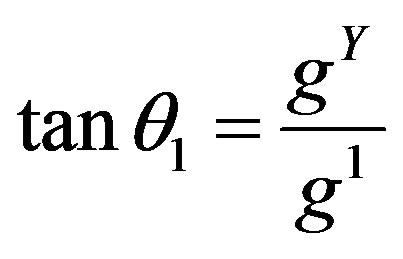 , in agreement with the standard model. It will be assumed, for simplicity, that in the scalar sector of superposition of
, in agreement with the standard model. It will be assumed, for simplicity, that in the scalar sector of superposition of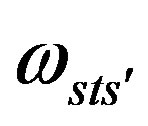 , Equation (25), the same
, Equation (25), the same 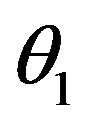 determines properties of the coupling constants as it does in the vector sector of
determines properties of the coupling constants as it does in the vector sector of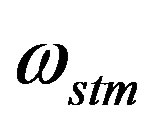 , Equation (26).
, Equation (26).
In the sector of the superposition of 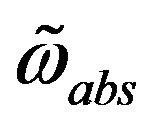 scalars the corresponding new operators are
scalars the corresponding new operators are
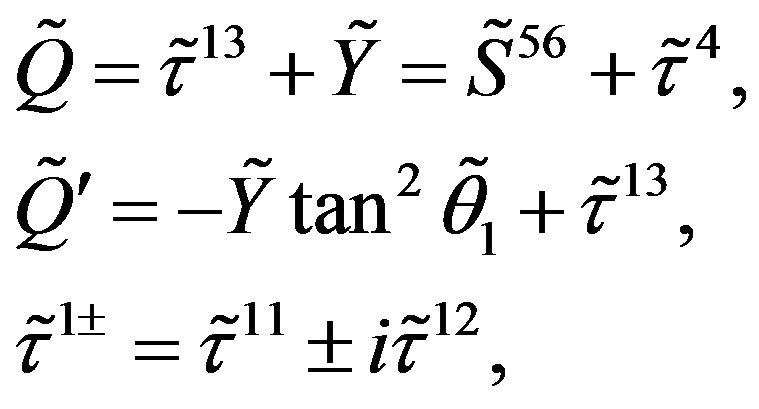 (28)
(28)
with the new coupling constants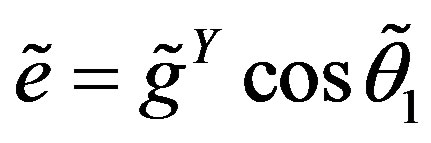 ,
,
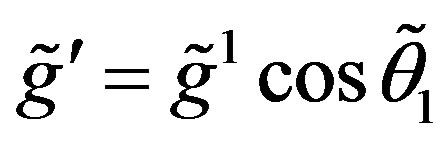 and
and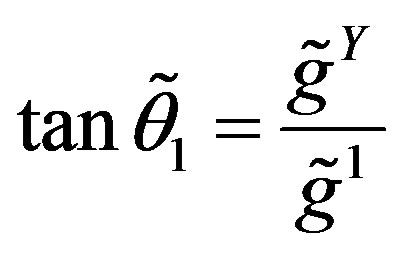 .
.
To this break and correspondingly to the mass matrices of the lower four families besides fields of Equation (23), orthogonal to 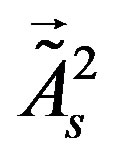 also the scalar fields
also the scalar fields 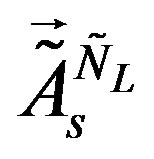 (they are orthogonal to
(they are orthogonal to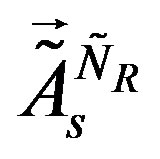 ) contribute.
) contribute.
All the scalar fields presented in this and the previous subsection are after the particular break massive dynamical fields, coupled to fermions and governed by the corresponding scalar potentials, for which we assume that they behave as normalizable ones (at least up to some reasonable accuracy).
3. Mass Matrices on the Tree Level and Beyond in the Spin-Charge-Family Theory
The starting fermion action (Equation (5)) manifests after the two successive breaks of symmetries the effective low energy action presented in Equation (7). The mass term (Equation (13)) manifests correspondingly the fermion mass matrices.
The first break leaves the lower four families, which are singlets with respect to the groups (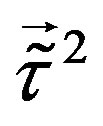 and
and  ) involved in the break, massless. At the electroweak break all the families become massive. While the scalar fields which are the gauge fields of
) involved in the break, massless. At the electroweak break all the families become massive. While the scalar fields which are the gauge fields of 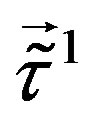 and
and 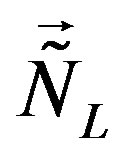 couple only to fermions of the lower four families, the scalars which are the gauge fields of
couple only to fermions of the lower four families, the scalars which are the gauge fields of ,
, 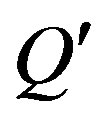 and
and 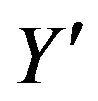 influence the mass matrices of all the eight families.
influence the mass matrices of all the eight families.
The scalar fields, originating in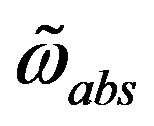 , determine on the tree level with their vacuum expectation values diagonal and off diagonal matrix elements of mass matrices. These fields do not distinguish among the family members. The scalar fields
, determine on the tree level with their vacuum expectation values diagonal and off diagonal matrix elements of mass matrices. These fields do not distinguish among the family members. The scalar fields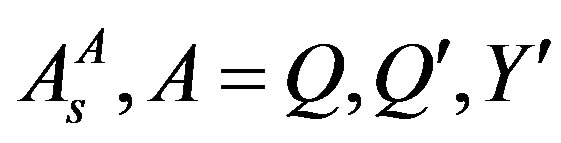 , contribute only to diagonal matrix element - the same value for all the families - distinguishing among the family members. The two
, contribute only to diagonal matrix element - the same value for all the families - distinguishing among the family members. The two 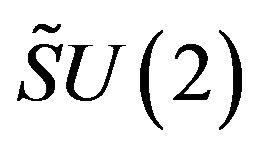 groups (for the upper four families are the generators
groups (for the upper four families are the generators 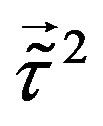 and
and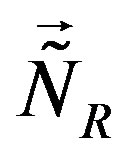 , for the lower four families are the generators
, for the lower four families are the generators 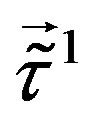 and
and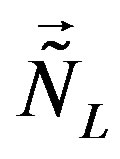 ) determine symmetries of mass matrices, valid also in all loop corrections.
) determine symmetries of mass matrices, valid also in all loop corrections.
Table 9 represents the mass matrix elements on the tree level for the upper four families after the first break. Loop corrections change the values, also the four zeros, keeping the symmetries of mass matrices unchanged. The notation  is used. The sign
is used. The sign  distinguishes between the values of the two pairs (
distinguishes between the values of the two pairs (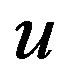 -quarks,
-quarks, 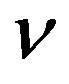 -lepton) and (
-lepton) and (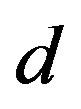 -quark,
-quark,  -lepton), respectively. The lower four families, which are singlets with respect to the two groups (
-lepton), respectively. The lower four families, which are singlets with respect to the two groups ( and
and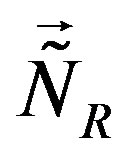 ), as can be seen in Tables 4 and 5, stay massless after the first break.
), as can be seen in Tables 4 and 5, stay massless after the first break.
In loop corrections the symmetry of mass matrices stays unchanged, zeros are replaced by values.
Masses of the lowest of the higher four families were evaluated in the ref. [11] from the cosmological and direct measurements, when assuming that baryons of this stable family (with no mixing matrix to the lower four families) constitute the dark matter.
The lower four families obtain masses when the electroweak break (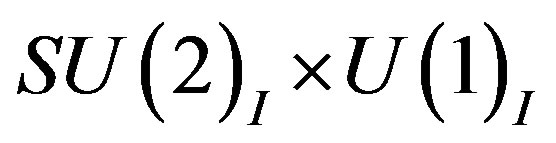 into
into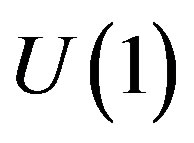 ) occurs, manifesting in nonzero vacuum expectation values of the two triplet scalar fields
) occurs, manifesting in nonzero vacuum expectation values of the two triplet scalar fields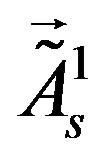 ,
, 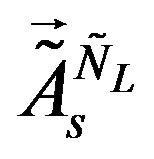 , and of the
, and of the  scalar fields
scalar fields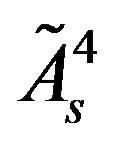 , as well as of
, as well as of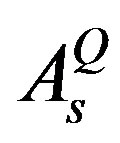 ,
, 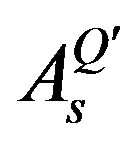 and
and . The scalar fields bring masses also to the gauge fields
. The scalar fields bring masses also to the gauge fields 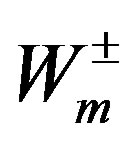 and
and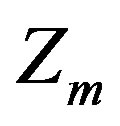 . All the scalar fields are doublets with respect to the weak charge:
. All the scalar fields are doublets with respect to the weak charge: 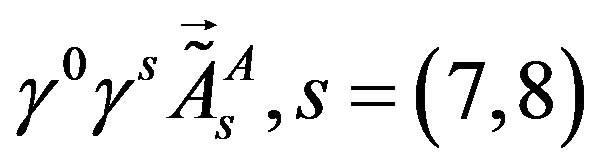 transform the right handed weak chargeless quarks and leptons (of the appropriate hyper charges) to the left handed partners.
transform the right handed weak chargeless quarks and leptons (of the appropriate hyper charges) to the left handed partners.
On the tree level the mass matrices gain contribution from nonzero vacuum expectation values of scalar fields, the same for 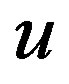 -quarks and
-quarks and  -leptons and the same for
-leptons and the same for  -quarks and
-quarks and  -leptons.
-leptons.  distinguishes between values of the
distinguishes between values of the 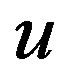 -quarks and
-quarks and 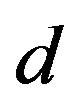 -quarks and correspondingly between the leptons
-quarks and correspondingly between the leptons 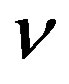 and
and  . The contributions from
. The contributions from ,
, 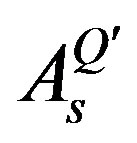 and
and 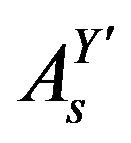 to mass matrices are different for different family members and the same for all the families of a particular family member.
to mass matrices are different for different family members and the same for all the families of a particular family member.
Beyond the tree level all mass matrix elements of a family member become dependent on the family member quantum number, through coherent contributions of the vector and all the scalar dynamical fields, keeping symmetry, which is determined by the two 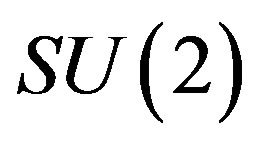 groups (
groups (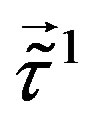 and
and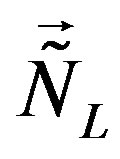 ).
).
Table 10 represents the contribution of  and
and
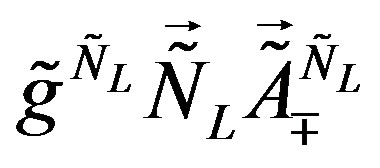 to the mass matrix elements on the tree level for the lower four families after the electroweak break. The contribution from
to the mass matrix elements on the tree level for the lower four families after the electroweak break. The contribution from 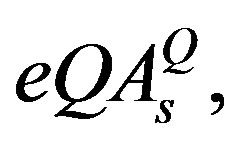
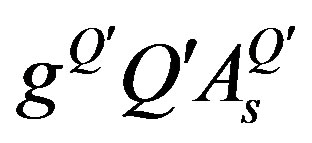 and
and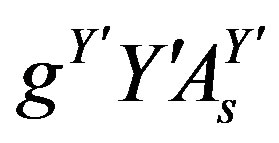 , which are diagonal and equal for all the families, but distinguish among the members of one family, are not presented. The notation
, which are diagonal and equal for all the families, but distinguish among the members of one family, are not presented. The notation  is used,
is used, 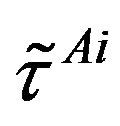 stays for
stays for  and
and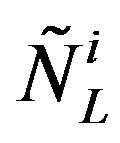 , the corresponding notation for the
, the corresponding notation for the
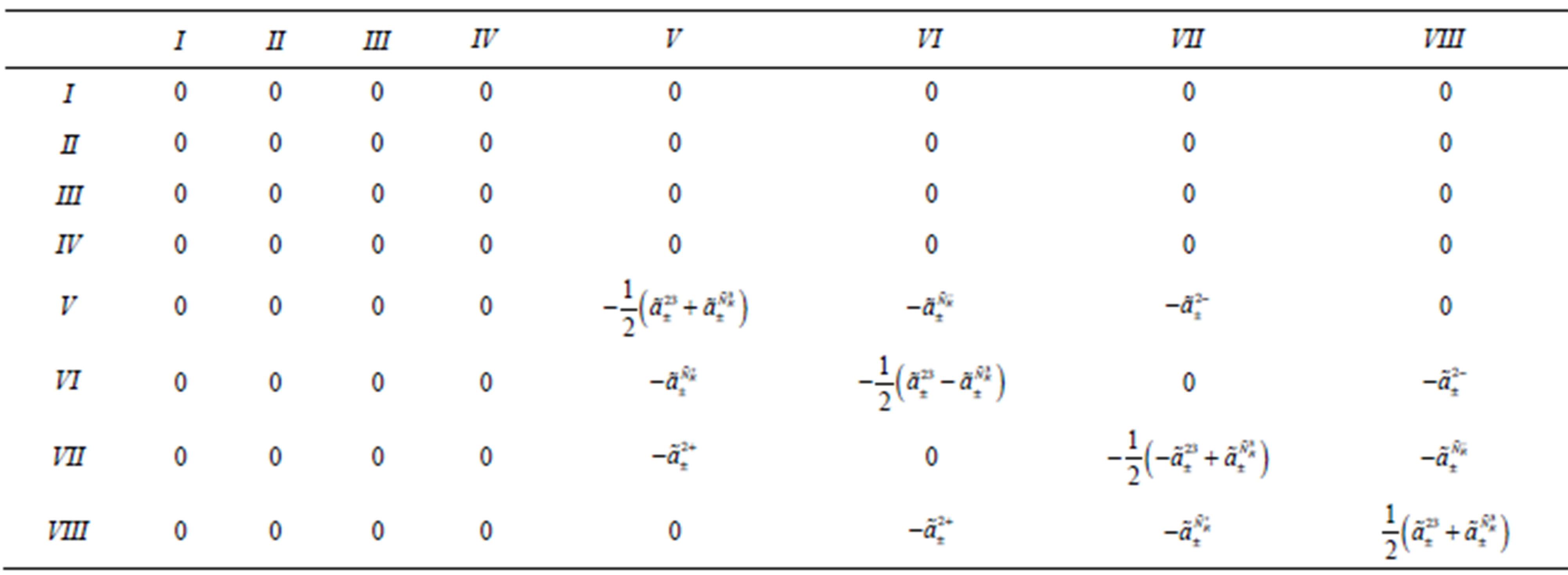
Table 9. The mass matrix on the tree level for the eight families of quarks and leptons after the break of 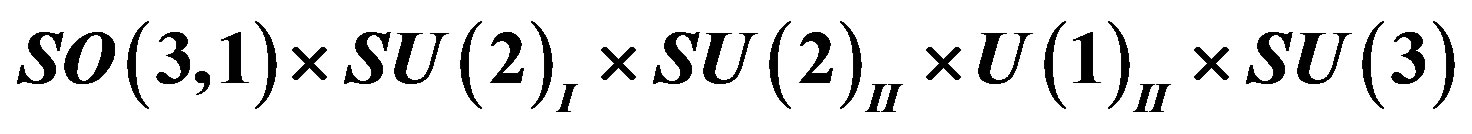 to
to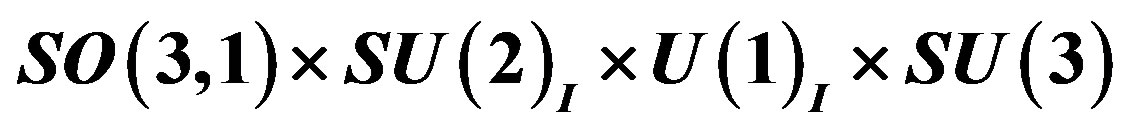 . The notation
. The notation  stays for
stays for ,
,  distinguishes
distinguishes 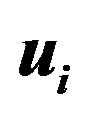 from
from 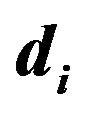 and
and 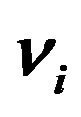 from
from , index
, index  determines families.
determines families.
coupling constants and the triplet scalar fields is used.
The absolute values of the vacuum expectation values of the scalar fields contributing to the first break are expected to be much larger than those contributing to the second break .
.
The mass matrices of the lower four families were studied and evaluated in the ref. [10] under the assumption that if going beyond the tree level the differences in the mass matrices of different family members start to manifest. In that ref. the symmetry properties of the mass matrices from Table 10 were assumed and the explicit values for matrix elements fitted to the experimental data within the experimental accuracy. Taking the fourth family masses as parameters within the experimental data we were able to calculate matrix elements of mass matrices, predicting mixing matrices for all the members of the four lowest families.
In Table 11 we present quantum numbers of all members of a family, any one, after the electroweak break.
Table 12 presents the quantum numbers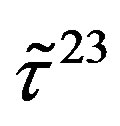 ,
,  ,
, 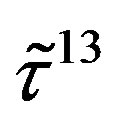 and
and  for all eight families. The first four families are singlets with respect to
for all eight families. The first four families are singlets with respect to 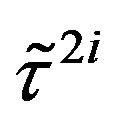 and
and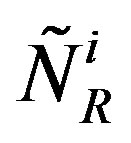 , while they are doublets with respect to
, while they are doublets with respect to 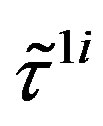 and
and 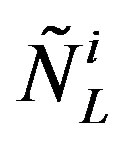 (all before the break of symmetries). The upper four families are correspondingly doublets with respect to
(all before the break of symmetries). The upper four families are correspondingly doublets with respect to 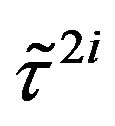 and
and 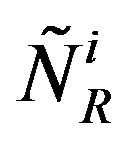 and are singlets with respect to
and are singlets with respect to 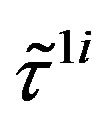 and
and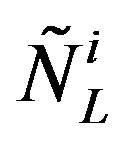 .
.
3.1. Mass Matrices beyond the Tree Level
To the vacuum expectation values of the scalars presented in Tables 9, the diagonal matrices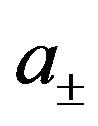 , the contributions of
, the contributions of 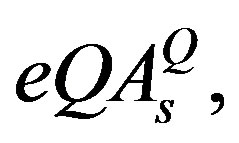
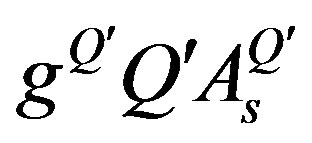 and
and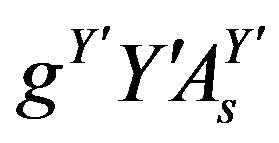 , have to be added on the tree level. They are the same, after the electroweak break, for all eight families and different for each of the family member
, have to be added on the tree level. They are the same, after the electroweak break, for all eight families and different for each of the family member ,
, 
 (29)
(29)
While the mass matrices of ( and
and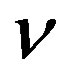 ) and (
) and (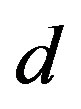 and
and ) have on the tree level the same off diagonal elements
) have on the tree level the same off diagonal elements

Table 10. The mass matrix on the tree level for the lower four families of quarks and leptons after the electroweak break. Only the contributions coming from the terms 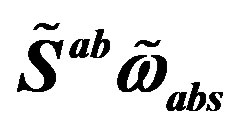 in
in  in Equation (7) are presented. The notation
in Equation (7) are presented. The notation  stays for
stays for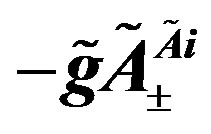 , where
, where  distinguishes between the values of the (
distinguishes between the values of the (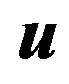 -quarks and
-quarks and 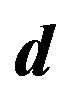 -quarks) and between the values of (
-quarks) and between the values of (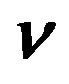 and
and ).
).
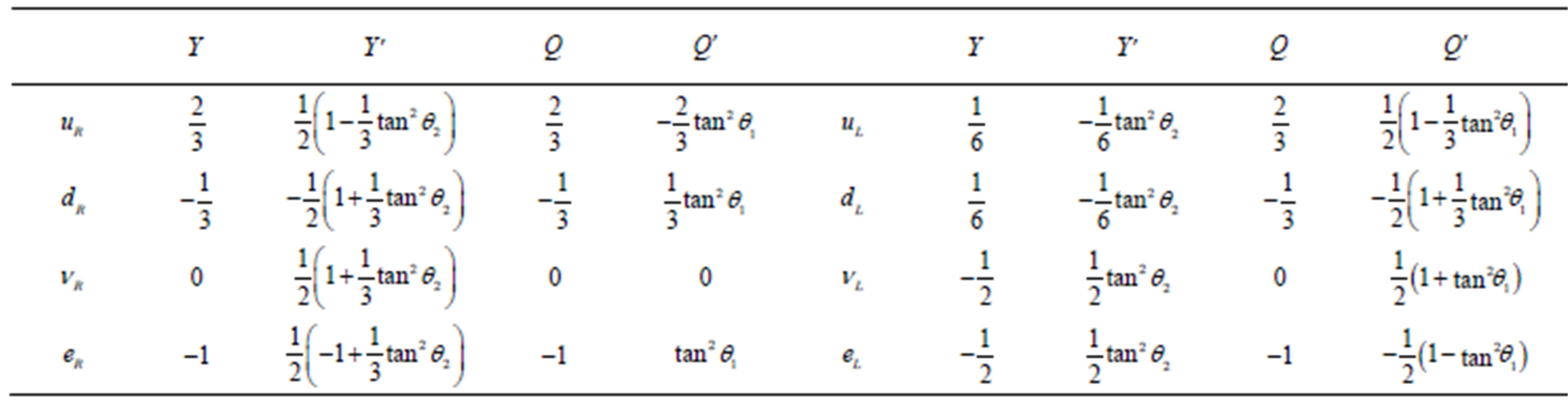
Table 11. The quantum numbers  of the members of one family.
of the members of one family.
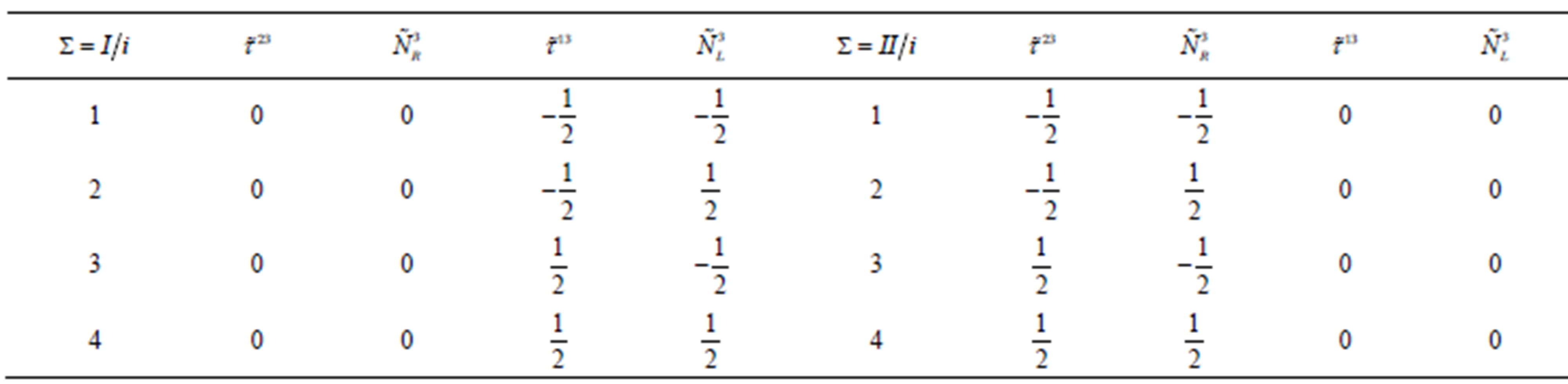
Table 12. The quantum numbers ,
, 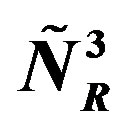 ,
, 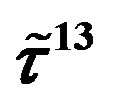 and
and 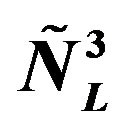 for the two groups of four families are presented.
for the two groups of four families are presented.
and differ only in diagonal elements, loop corrections, to which massive gauge fields and dynamical scalar fields of both origins ( and
and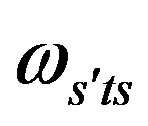 ) contribute coherently, change mass matrices of the lower four families drastically, but not the symmetry. For the upper four families, for which the diagonal terms from
) contribute coherently, change mass matrices of the lower four families drastically, but not the symmetry. For the upper four families, for which the diagonal terms from 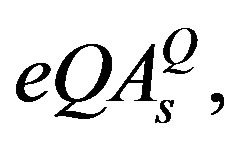
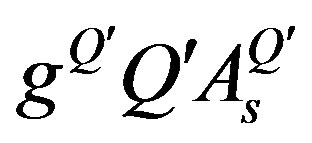 and
and  are small, since they are the same for all eight families, loop corrections are not expected to bring drastic changes in mass matrices between different family members. The mass matrices with loop corrections in all orders demonstrate twice four by diagonal matrices
are small, since they are the same for all eight families, loop corrections are not expected to bring drastic changes in mass matrices between different family members. The mass matrices with loop corrections in all orders demonstrate twice four by diagonal matrices
 (30)
(30)
where 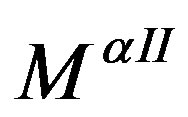 and
and 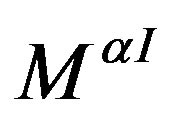 have the structure
have the structure
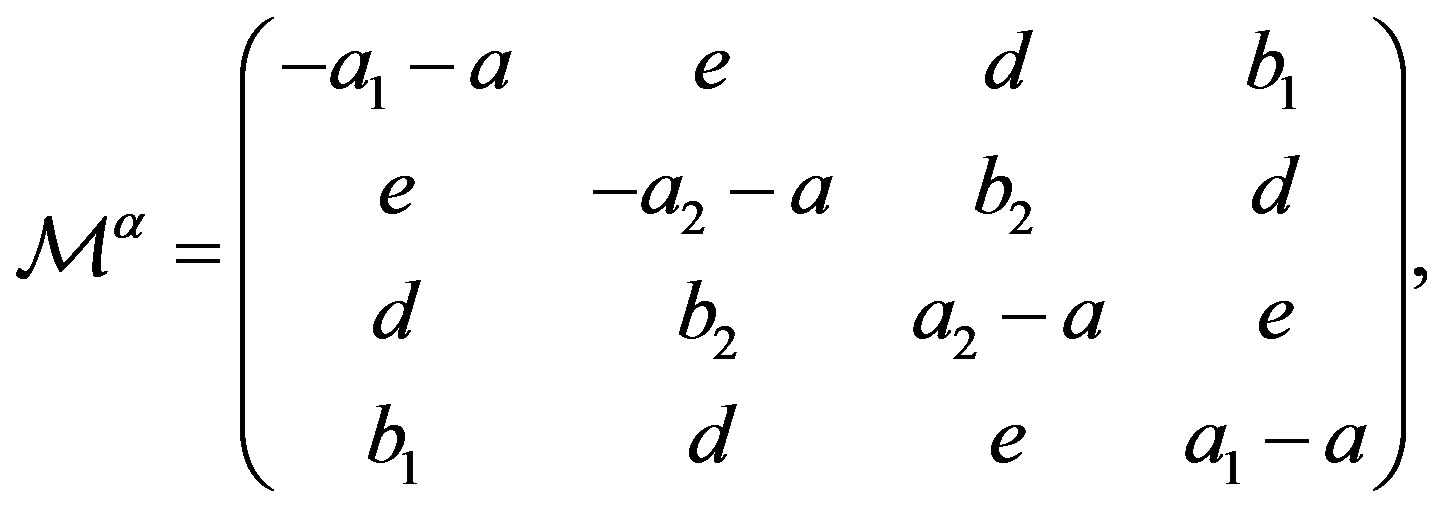 (31)
(31)
the same for all the family members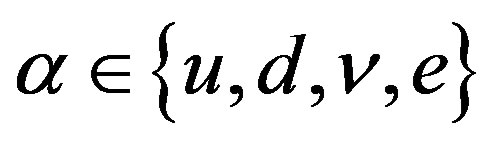 . The values
. The values 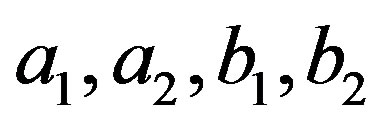 and
and  are different for the upper
are different for the upper  and the lower
and the lower 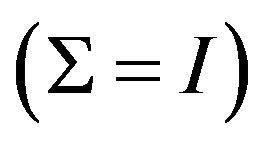 four families, due to two different scales of two different breaks. Correspondingly the two tree level mass matrices
four families, due to two different scales of two different breaks. Correspondingly the two tree level mass matrices 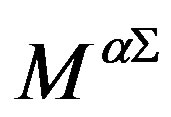 have very little in common, besides the symmetries and the contributions from Equation (29).
have very little in common, besides the symmetries and the contributions from Equation (29).
Let us introduce the notation, which would help to make clear the loop corrections contributions [33]. We have before the two breaks two times (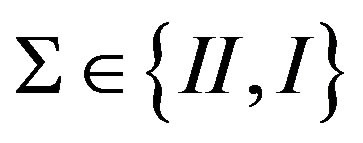 ,
,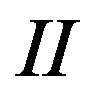 denoting the upper four and
denoting the upper four and 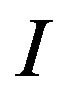 the lower four families) four massless vectors
the lower four families) four massless vectors 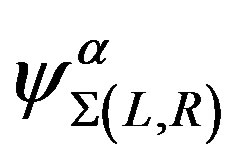 for each member of a family
for each member of a family . Let
. Let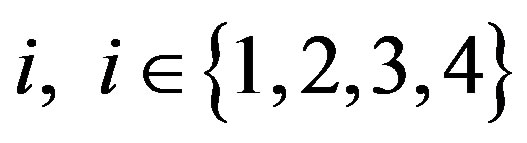 , denotes one of the four family members of each of the two groups of massless families
, denotes one of the four family members of each of the two groups of massless families
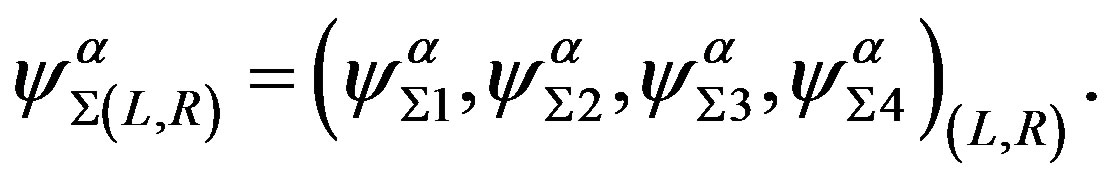 (32)
(32)
Let 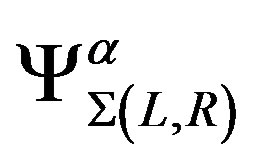 be the final massive four vectors for each of the two groups of families, with all loop corrections included
be the final massive four vectors for each of the two groups of families, with all loop corrections included
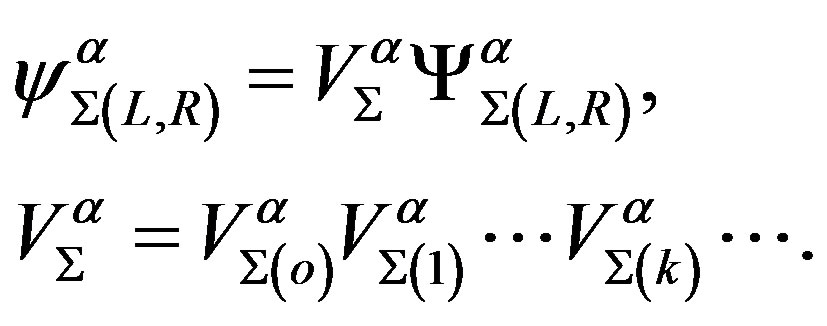 (33)
(33)
Then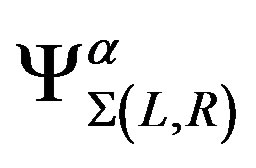 , which include loops corrections in all orders, read
, which include loops corrections in all orders, read
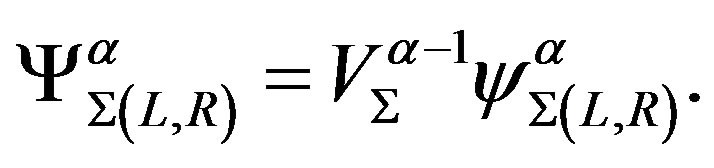 (34)
(34)
Correspondingly we have
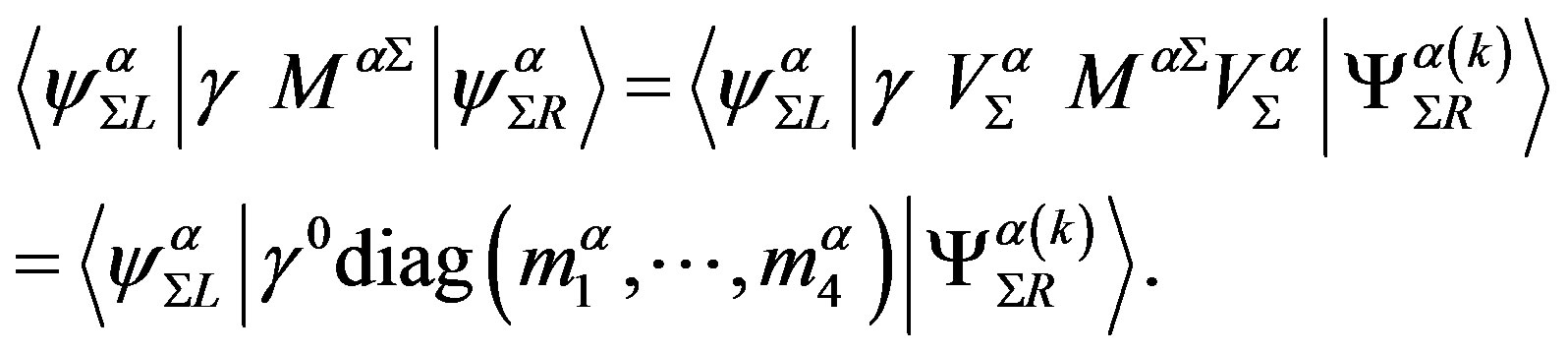 (35)
(35)
It follows then that  determines the superposition of the scalar dynamical fields which couple with the coupling constants
determines the superposition of the scalar dynamical fields which couple with the coupling constants 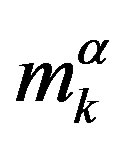 (in some units) to the family member belonging to the
(in some units) to the family member belonging to the  family
family
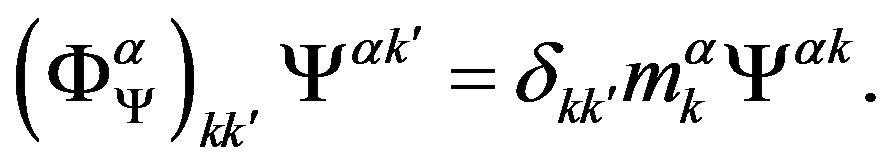 (36)
(36)
Let us repeat that to the loop corrections two kinds of the scalar dynamical fields contribute, those originating in 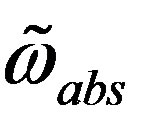 (
(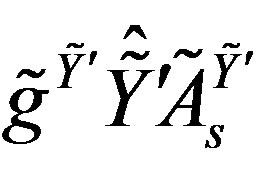 ,
, 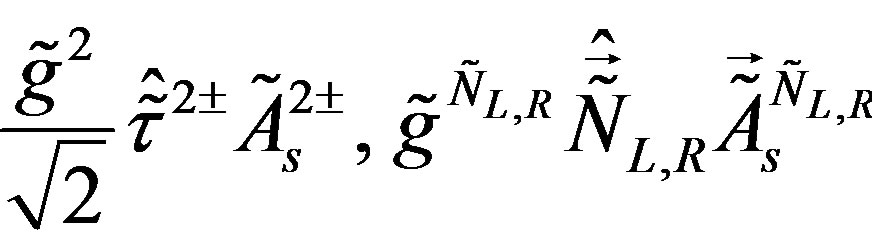 ,
, 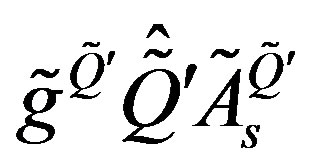 ,
,
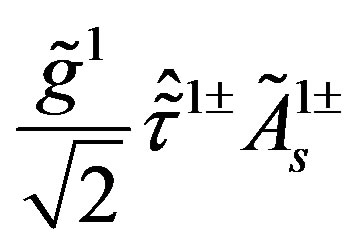 ) and those originating in
) and those originating in 
(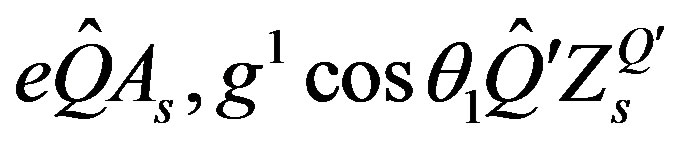 ,
,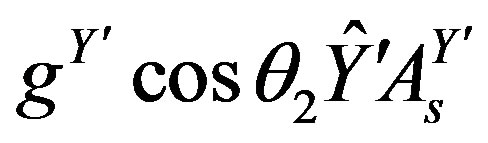 ) and the gauge fields (
) and the gauge fields ( ,
,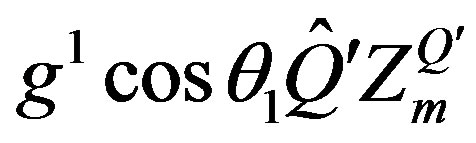 ) as it follow from Equation (7).
) as it follow from Equation (7).
In the ref. [33] loop diagrams for these contributions to loop corrections in first order are presented and numerical results discussed for both groups of four families. The masses and coupling constants of dynamical scalar fields and of the massive vector fields are taken as an input and the influence of loop corrections on properties of fermions is studied.
Let us arrange mass matrices, after the electroweak break and when all the loop corrections are taken into account, as a sum of matrices as follows
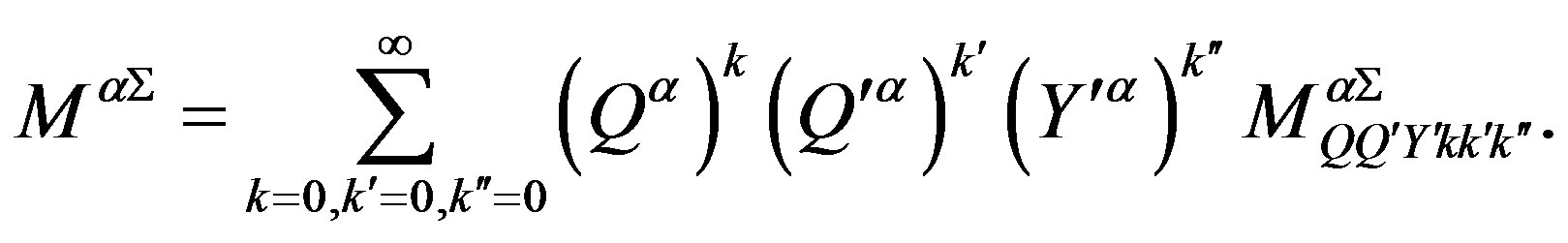 (37)
(37)
To each family member there corresponds its own matrix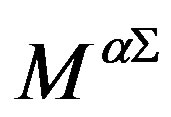 . It is a hope, that the matrices
. It is a hope, that the matrices 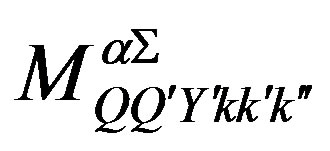 might not depend on the family member index
might not depend on the family member index 
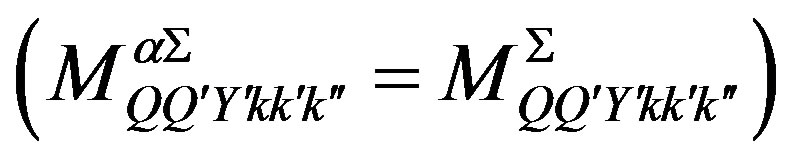 and that the eigenvalues of the operators
and that the eigenvalues of the operators 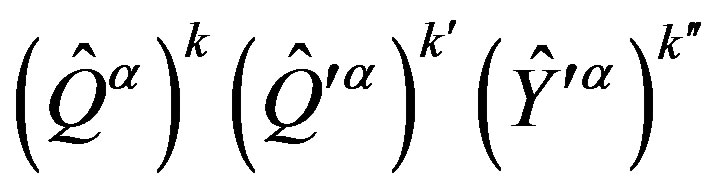 on the massless states
on the massless states
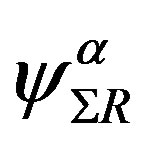 make the mass matrices
make the mass matrices 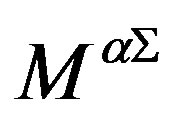 dependent on
dependent on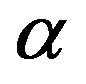 . To masses of neutrinos only the terms
. To masses of neutrinos only the terms
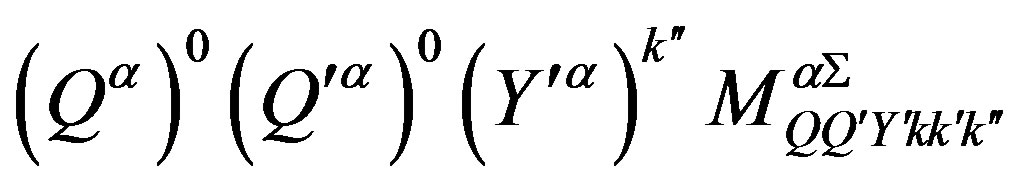 contribute.
contribute.
More about the mass matrices below the tree level can be found in the ref. [33].
Numerical Results for the Lowest Four Families of Quarks and Leptons
I present here a part of our study with G. Bregar [34], which is still in progress.
In this study we take the mass matrix as presented in Equation (31) and fit the parameters of this matrix for the lower four families so that masses and mixing matrices of quarks and leptons agree within the experimental accuracy with the measured values.
We proceed as follows:
1) After assuming that the mass matrices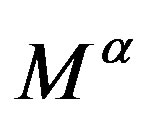 ,
, 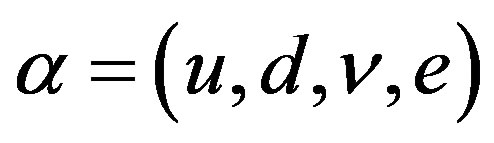 , are Hermitian, the unitary matrices
, are Hermitian, the unitary matrices 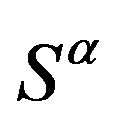 and
and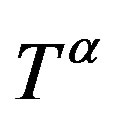 , which we look for to diagonalize
, which we look for to diagonalize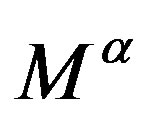 , differ only in phase factors depending on phases of the right and left handed basic vectors of each family member
, differ only in phase factors depending on phases of the right and left handed basic vectors of each family member , and manifesting in two diagonal matrices,
, and manifesting in two diagonal matrices, 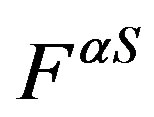 and
and , respectively. For Hermitian mass matrices we therefore have:
, respectively. For Hermitian mass matrices we therefore have: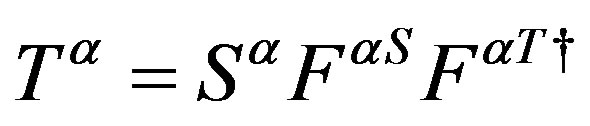 .
.
2) 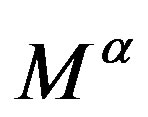 are treated for all the family members
are treated for all the family members  in an equivalent way.
in an equivalent way.
3) We take the diagonal matrices 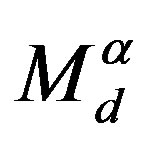 and the mixing matrices
and the mixing matrices 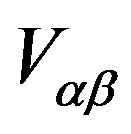 from the available experimental data [35, 36], taking into account experimental accuracy. The fourth family members properties are free parameters, limited by the experimental data.
from the available experimental data [35, 36], taking into account experimental accuracy. The fourth family members properties are free parameters, limited by the experimental data.
4) The mass matrices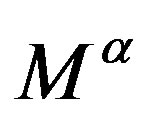 , with the symmetry presented in Equation (31), follow from the procedure:
, with the symmetry presented in Equation (31), follow from the procedure:
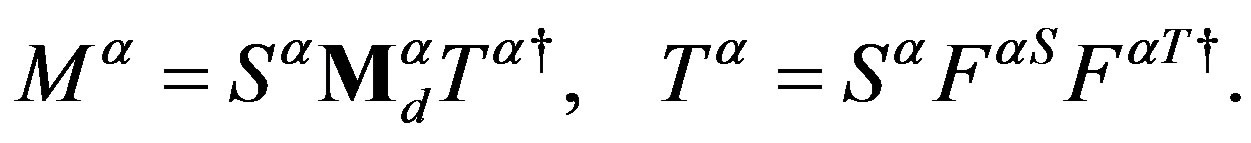 (38)
(38)
5) We proceed so that we iterate the procedure  and
and :
:
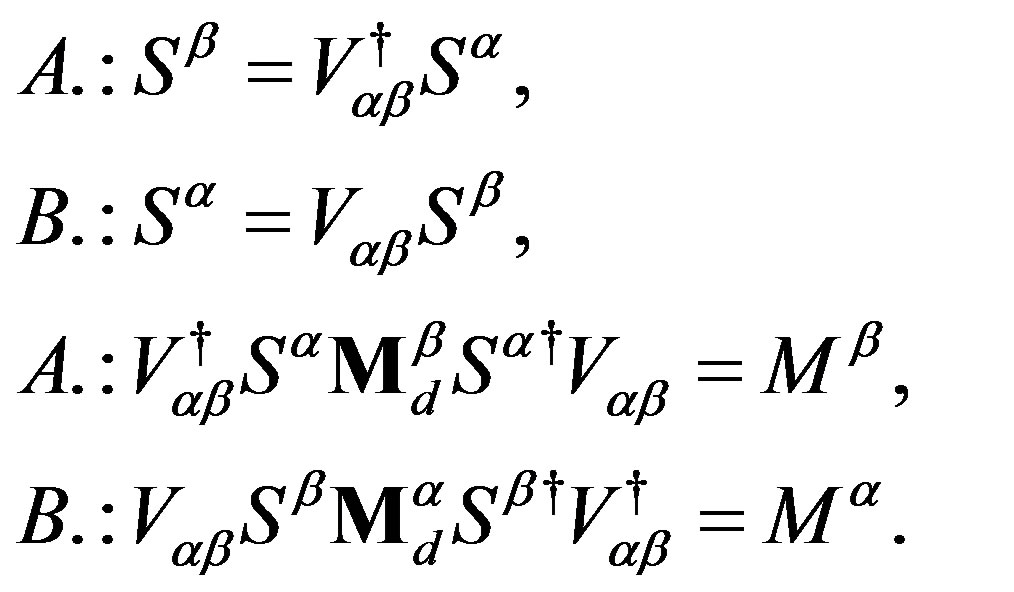 (39)
(39)
6) We further simplify the procedure by assuming that 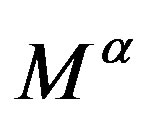 are real and can therefore be diagonalized with orthogonal matrices
are real and can therefore be diagonalized with orthogonal matrices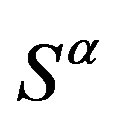 .
.
7) We keep the symmetry of mass matrix accurate, while fulfilling the experimental requirements as accurate as they are.
The differences among family members originate in the eigenvalues of the operators 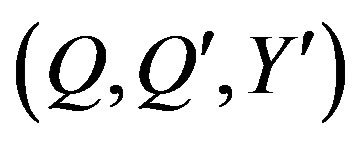 which in loop corrections in all orders contribute to all mass matrix elements and distinguish among family members. There are possible differences also in
which in loop corrections in all orders contribute to all mass matrix elements and distinguish among family members. There are possible differences also in 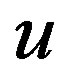 and
and 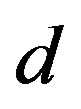 quarks and in
quarks and in 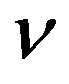 and
and  leptons due to differences in the vacuum expectation values of
leptons due to differences in the vacuum expectation values of  of scalars
of scalars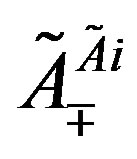 ,
, 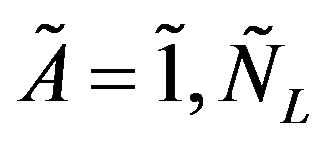 and
and
 ,
,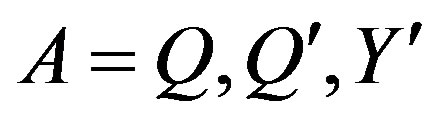 .
.
We obtain the mass matrices for either quarks or leptons, the matrix elements of which differ among themselves for a factor (from 1.2 to 10) while they respect the symmetry of Equation (31).
There are more than one solution. Solutions are namely connected by discrete rotations of basic states. We present one solution for each of the family member, all fulfilling the experimental data within experimental accuracy. Masses of the fourth family are chosen as free parameters, although one can not fit to experimental data either too low or too high values for the fourth family members. For quark we found as one of the acceptable results
 (40)
(40)

which lead to quark masses
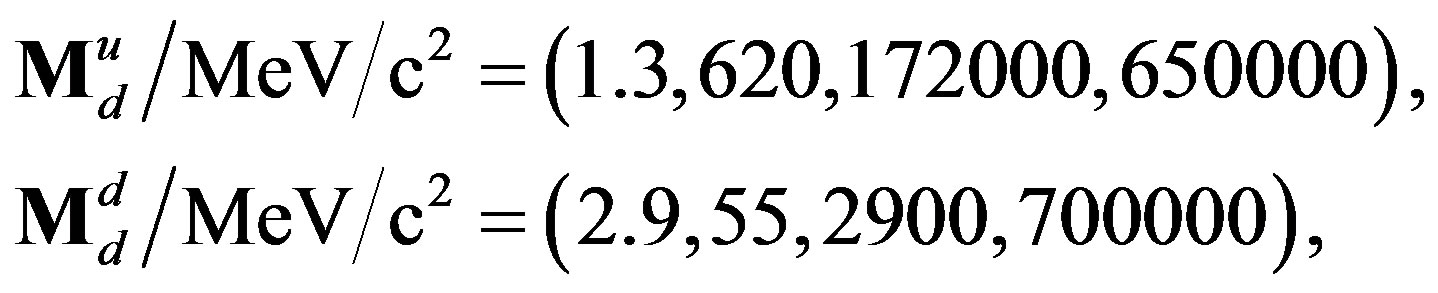 (41)
(41)
and the mixing matrix
 (42)
(42)
The mass matrices for leptons again depend on the choice of the fourth family lepton masses. The fourth family leptons are almost decoupled from the lowest four families.
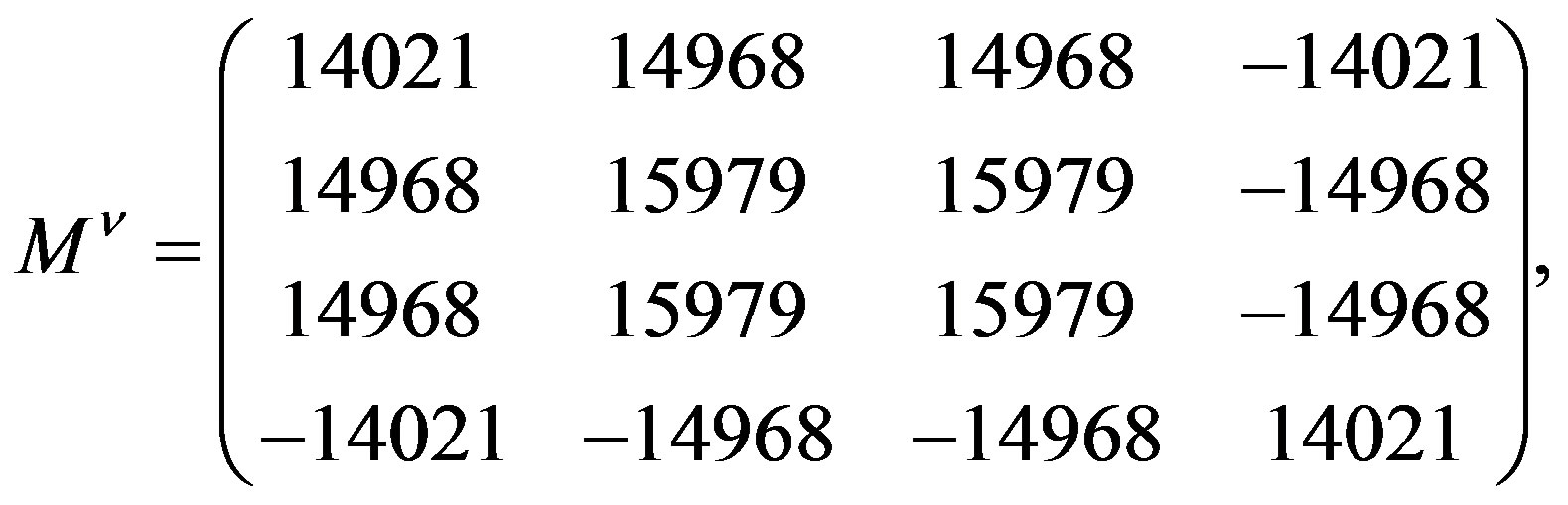 (43)
(43)
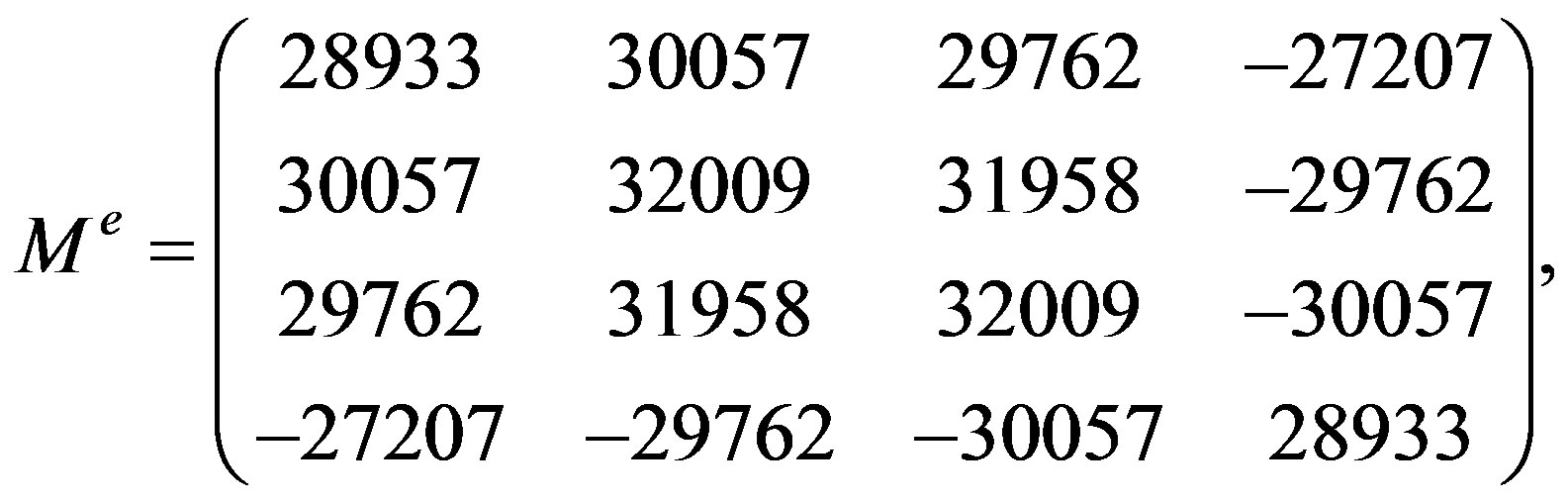
leading to masses
 (44)
(44)
and the mixing matrix
 (45)
(45)
These very preliminary results manifest that quarks and leptons behave similarly with respect to the scalar and gauge fields, which determine their properties. Mass matrices, which all obey the same symmetry, are within a factor from 1.1 close to 7 or 8 manifesting a democratic matrix. The masses and mixing matrices, reproduced for the lower three families within experimental accuracy, do not allow to push the fourth family masses either to low or too high. The lepton mixing matrix with nonzero couplings to the lower three families do not contradict the experimental data if they are small enough. The very democratic like mass matrix for neutrinos seems convenient to assure extremely small masses of the first three families of neutrinos in comparison with the masses of the charged leptons and quarks.
4. Scalar Fields of the Spin-Charge-Family Theory Manifesting Effectively as the Standard Model Higgs and Yukawa Couplings
I refer here to the paper [37] (sent for publication). Let us introduce a common notation for all the scalar fields, which influence properties of the lower four families and correspondingly of the weak boson fields
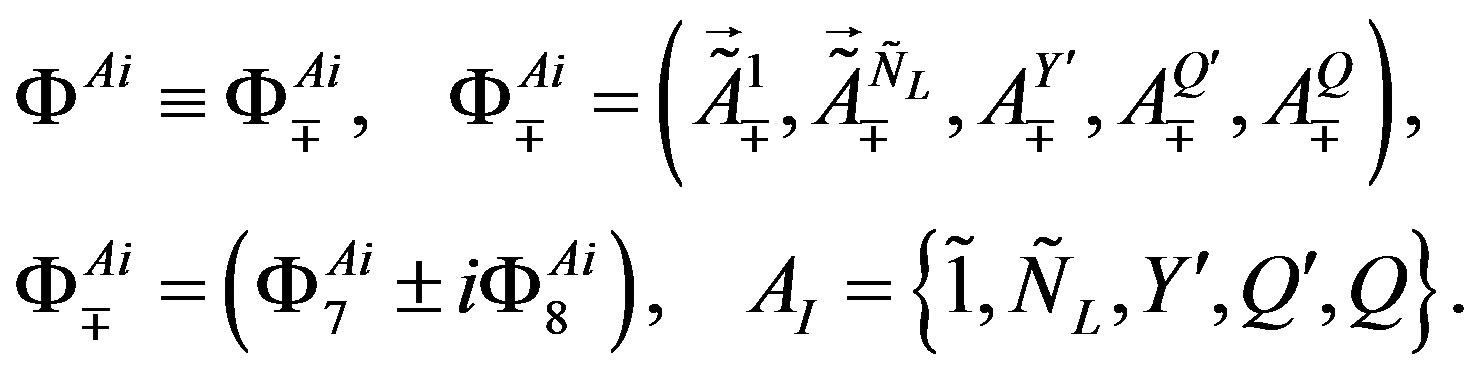 (46)
(46)
 and
and  are the gauge scalar fields of the charges
are the gauge scalar fields of the charges  and
and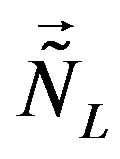 , respectively, while
, respectively, while 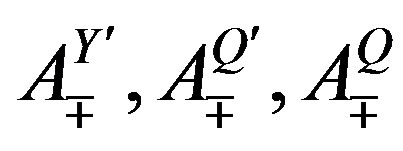 are the gauge scalar fields of
are the gauge scalar fields of 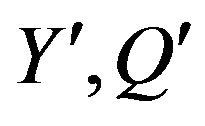 and
and , respectively.
, respectively.
We assume a renormalizable effective potential  for the real scalar fields
for the real scalar fields 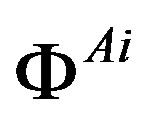 (Equation (46)), which couple among themselves
(Equation (46)), which couple among themselves
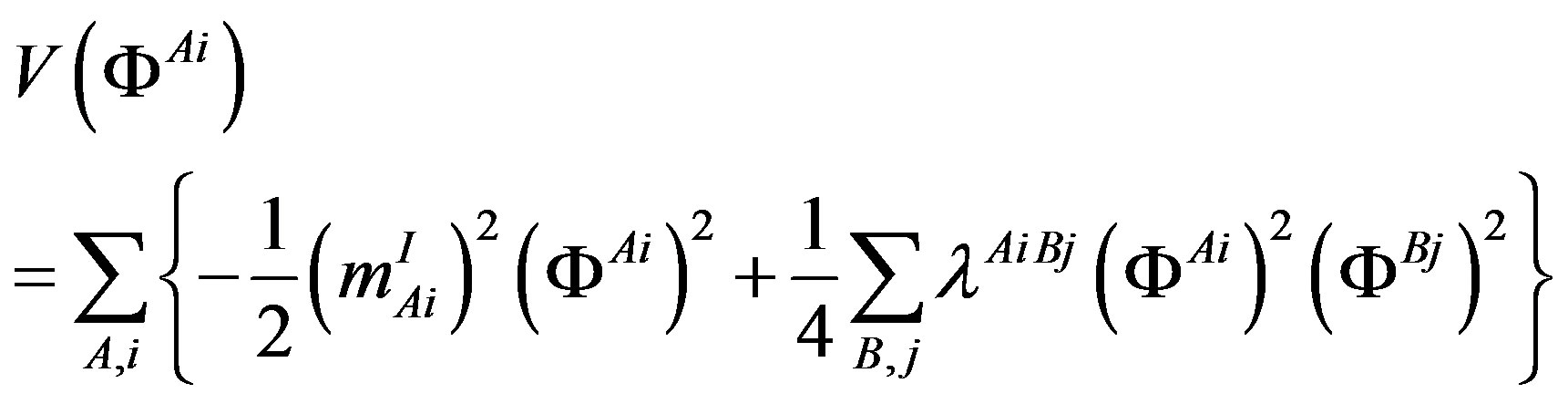 (47)
(47)
and have the symmetry: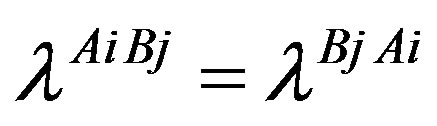 .
.
Scalar fields couple to the gauge bosons at the electroweak break as follows
 (48)
(48)
All the scalar fields are either 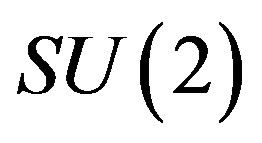 triplets with respect to the family charges
triplets with respect to the family charges 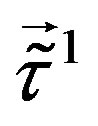 and
and 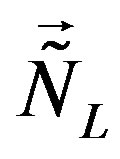 and singlets with respect to
and singlets with respect to 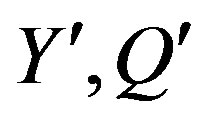 and
and , while they all are doublets with respect to the weak charge, due to the fact that they carry the space index
, while they all are doublets with respect to the weak charge, due to the fact that they carry the space index  and couple to fermions through
and couple to fermions through 
 , where
, where 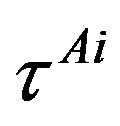 denotes the operators
denotes the operators ,
, 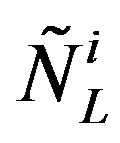 ,
,  and
and  and
and  the corresponding coupling constants. We also can write
the corresponding coupling constants. We also can write
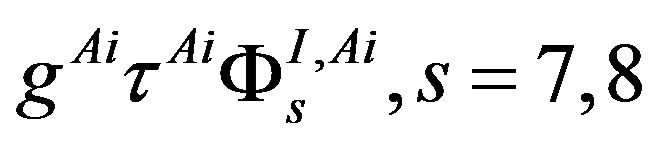
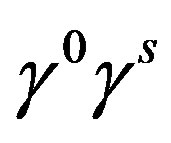 as
as 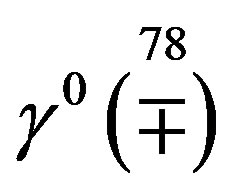
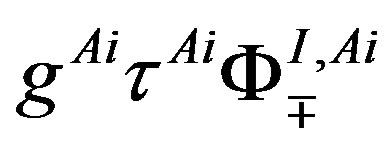 where
where 
 contributes to mass matrices of
contributes to mass matrices of  -quarks and
-quarks and  leptons, while
leptons, while 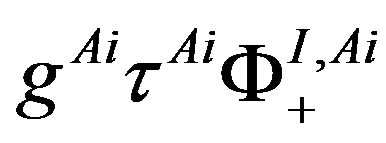
 contributes to mass matrices of
contributes to mass matrices of 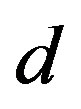 -quarks and
-quarks and  -leptons.
-leptons.
When looking for the mass eigenstates 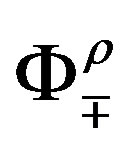
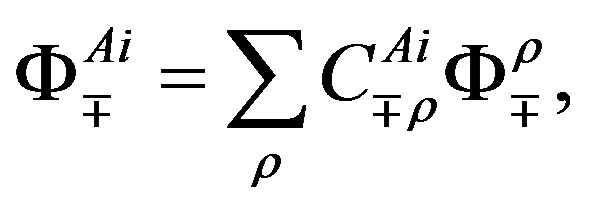 (49)
(49)
in which on the tree level the potential is diagonal
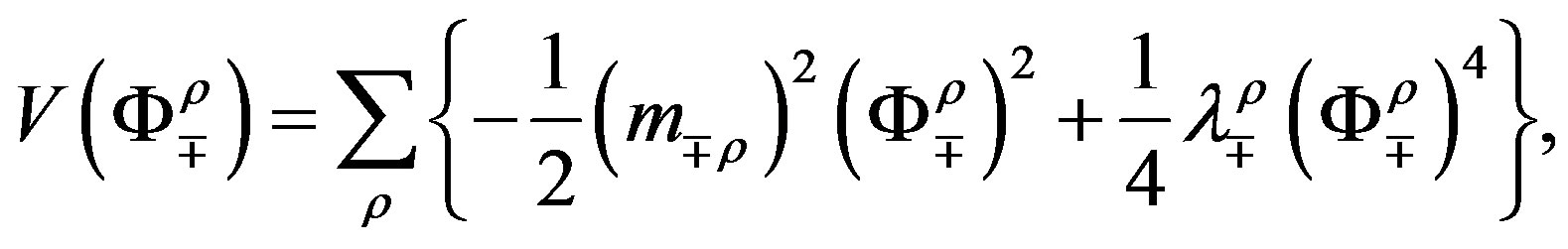 (50)
(50)
we diagonalize the matrix of the second derivatives of the potential 
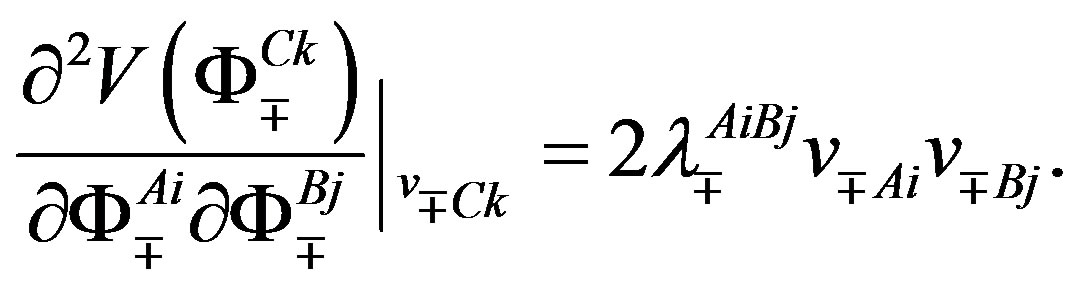 (51)
(51)
From the first derivative
 (52)
(52)
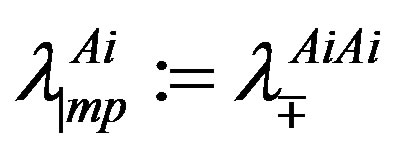 we obtain the minimal values of the scalar fields,
we obtain the minimal values of the scalar fields, 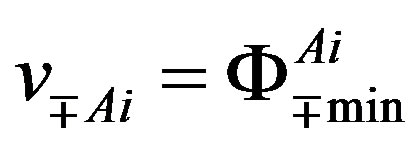 , as functions of the parameters,
, as functions of the parameters,
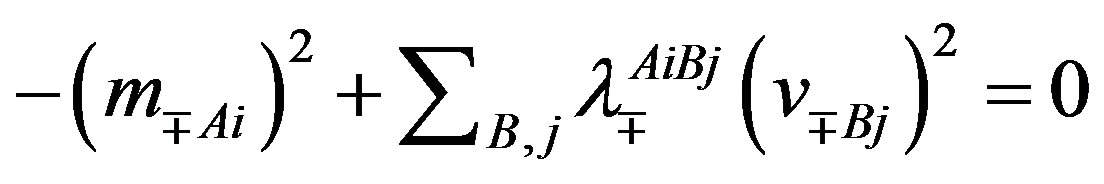 .
.
Comparing the scalar mass eigenstates 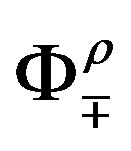 from Equation (49) with the superposition of scalars to which couple each member of each family (Equation (36)) one notices that the second ones are superposition of the first ones.
from Equation (49) with the superposition of scalars to which couple each member of each family (Equation (36)) one notices that the second ones are superposition of the first ones.
All the scalar doublets, which couple to the lower four families, contribute to masses of the weak bosons, reproducing on the tree level the expression for the masses of the standard model. [37]
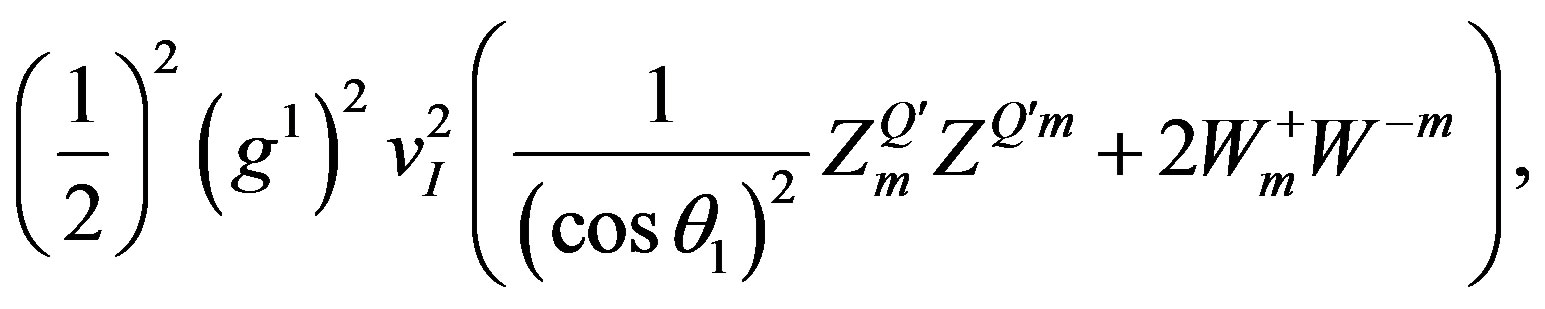 (53)
(53)
where  are the contribution to the vacuum expectation value of all the scalar fields
are the contribution to the vacuum expectation value of all the scalar fields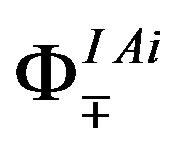 .
.
5. Conclusions
I discuss in this paper the possibility that the spincharge-family theory [1-11,28,37], proposing the mechanism for generating families of quarks and leptons and consequently predicting the number of families at low (sooner or later observable) energies and the mass matrices for each of the family member (and correspondingly the masses and the mixing matrices of families of quarks and leptons), is offering the right way beyond the standard model. This paper is partly a short overview of several other papers.
The spin-charge-family theory predicts the fourth family to be possibly measured at the LHC and the fifth family which is, since it is decoupled in the mixing matrices from the lower four families and it is correspondingly stable, the candidate to form the dark matter [11].
The proposed theory also predicts that there are several scalar fields, taking care of mass matrices of the two times four families and of the masses of the weak gauge bosons. At low energies these scalar dynamical fields manifest effectively pretty much as the standard model Higgs field together with the Yukawa couplings, predicting at the same time that observation of these scalar fields is expected to deviate from what for the Higgs the standard model predicts.
To the mass matrices of fermions two kinds of scalar fields contribute, the one interacting with fermions through the Dirac spin and the one interacting with fermions through the second kind of the Clifford operators (anticommuting with the Dirac ones, there is no third kind of the Clifford algebra object). The first one distinguishes among the family members, taking care of the spin and the charges of all the family members, the second one distinguishes among the families. Beyond the tree level these two kinds of scalar fields and the vector massive fields start to contribute coherently, leading hopefully to the measured properties of the so far observed three families of fermions and to the measured properties of the observed weak gauge fields.
In the ref. [8,10] we made a rough estimation of properties of quarks of the lower four families as predicted by the spin-charge-family theory. The mass matrices of quarks and leptons turn out to be strongly related on the tree level. Taking into account that loop corrections change elements of mass matrices considerably, but keep the symmetry of mass matrices, we took mass matrix element of the lower four families as free parameters. We fitted the matrix elements to the existing experimental data for the observed three families within the experimental accuracy and for a chosen mass of each of the fourth family member. We predicted then elements of the mixing matrices for the fourth family members as well as the weakly measured matrix elements of the three observed families.
In the ref. [11] we evaluated the masses of the stable fifth family (belonging to the upper four families) under the assumption that neutrons and neutrinos of this stable fifth family form the dark matter. We study the properties of the fifth family neutrons, their freezing out of the cosmic plasma during the evolution of the universe, as well as their interaction among themselves and with the ordinary matter in the direct experiments.
In this paper we present studies of the properties of the gauge vector and scalar fields and their influence on the properties of the eight families of quarks and leptons as they follow from the spin-charge-family theory on the tree and below the tree level after the two successive breaks, the first one from
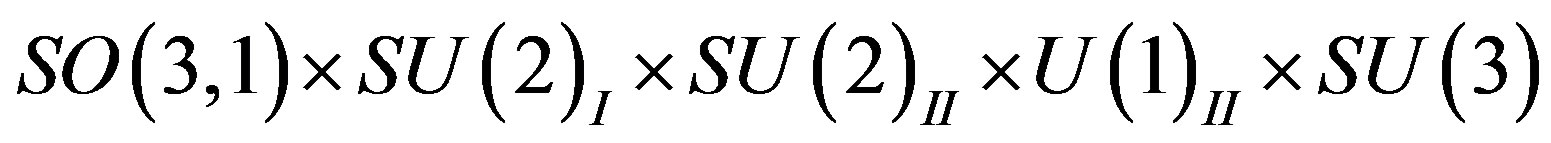
to
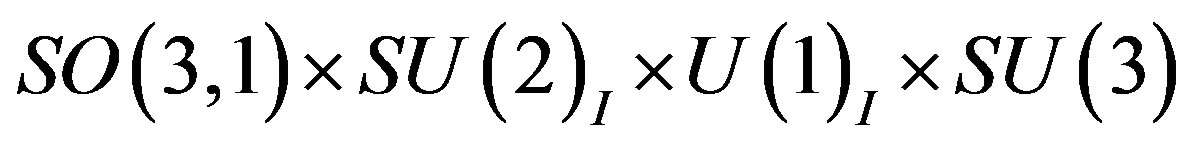
and the second one further to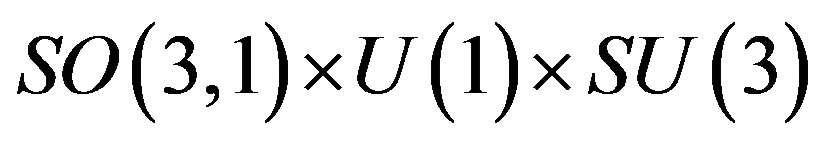 , trying to understand better what happens during these two breaks and after them.
, trying to understand better what happens during these two breaks and after them.
In the break from
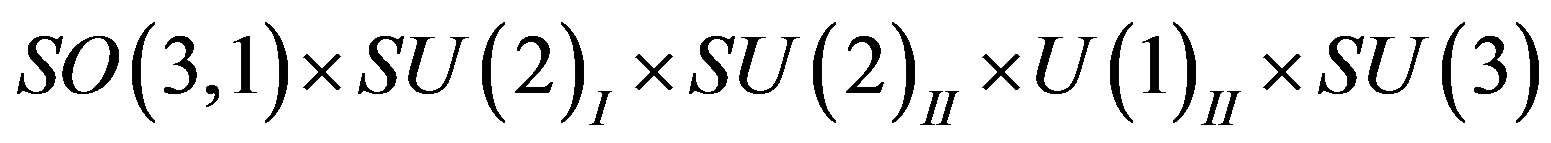
to

several scalar fields (the superposition of
 ) contribute to the break as gauge triplet fields of
) contribute to the break as gauge triplet fields of 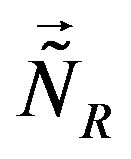 and of
and of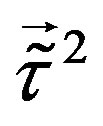 , gaining nonzero vacuum expectation values. Correspondingly they cause nonzero mass matrices of the upper four families to which they couple, giving the same mass to weak doublets, and nonzero masses of vector fields, the superposition of the gauge triplet fields of
, gaining nonzero vacuum expectation values. Correspondingly they cause nonzero mass matrices of the upper four families to which they couple, giving the same mass to weak doublets, and nonzero masses of vector fields, the superposition of the gauge triplet fields of  and of the gauge singlet field of
and of the gauge singlet field of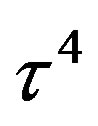 . Since these scalar fields do not couple to the lower four families (they are singlets with respect to
. Since these scalar fields do not couple to the lower four families (they are singlets with respect to  and
and ) the lower four families stay massless at this break.
) the lower four families stay massless at this break.
At the electroweak break several other superposition of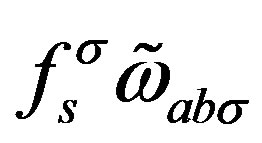 , the gauge triplets of
, the gauge triplets of  and of
and of  (which are orthogonal to the previous triplets), together with some superposition of the scalar fields
(which are orthogonal to the previous triplets), together with some superposition of the scalar fields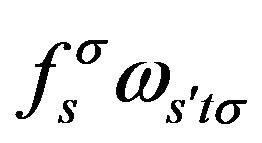 , the gauge fields of
, the gauge fields of 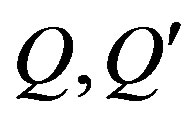 and
and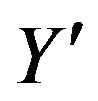 , gain nonzero vacuum expectation values, and contribute correspondingly to mass matrices of the lower four families and to masses of the gauge fields
, gain nonzero vacuum expectation values, and contribute correspondingly to mass matrices of the lower four families and to masses of the gauge fields 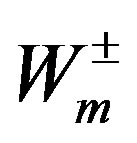 and
and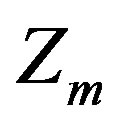 . The gauge scalars of
. The gauge scalars of  and
and 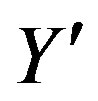 influence slightly, together with the vector fields, also mass matrices of the upper four families. The weak
influence slightly, together with the vector fields, also mass matrices of the upper four families. The weak 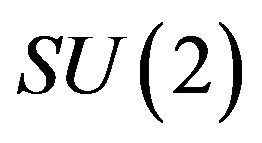 symmetry is definitively broken.
symmetry is definitively broken.
Although mass matrices of the family members are, in each of the two groups of four families separately, very much related on the tree level (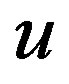 -quarks are related to
-quarks are related to 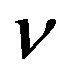 -leptons and
-leptons and 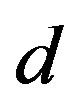 -quarks to
-quarks to  -leptons), loop corrections, in which the scalar fields of both kinds contribute, those distinguishing among the families and those distinguishing among the family members
-leptons), loop corrections, in which the scalar fields of both kinds contribute, those distinguishing among the families and those distinguishing among the family members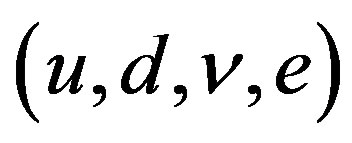 , together with the massive vector gauge fields which distinguish only among the family members, start to hopefully (as so far done calculations [33] manifest) explain why are properties of the so far observed quarks and leptons so different. Numerical evaluations of the loop corrections to the tree level are in preparation (the ref. [33, 34]).
, together with the massive vector gauge fields which distinguish only among the family members, start to hopefully (as so far done calculations [33] manifest) explain why are properties of the so far observed quarks and leptons so different. Numerical evaluations of the loop corrections to the tree level are in preparation (the ref. [33, 34]).
Some results [34], which were obtained by keeping the symmetry of mass matrices, the same for all the family members, and fitting free parameters to the experimental data within experimental accuracy, are presented (Equations (40, 43)). The results for the lower four families manifest that in the spin-charge-family theory quarks and leptons behave equivalently. The fourth family masses are limited to certain region, which can not be too low or too high.
The theory predicts several scalar fields (Equation (46)), which couple to each family member of each family with a different superposition (Equation (36)). These superposition differ from the scalar mass eigenstates (Equation (49)), while to the masses of the weak boson fields all the scalar fields contribute equivalently (Equation (53)). All the scalar fields are triplets with respect to the family charge groups, while they manifest as doublets with respect to the weak charge. The theory consequently predicts that the scalar fields measurements at the LHC will probably observe several scalar fields, not only one Higgs.
The standard model seems to be the low energy effective manifestation of the spin-charge-family theory, which—by having a real chance to explain many of the open questions of this (very efficient and elegant) model —has offering a new step beyond the standard model.
Let me end by pointing out that the spin-charge-family theory, very promising in offering explanation for the appearance of spin, charges and families of fermions, and for the appearance of gauge vector and scalar boson fields at the low energy regime, still needs careful studies, numerical ones and also proofs, that it is, under some conditions, a consistent theory to demonstrate that/whether this is the right next step beyond the standard model.
REFERENCES
- N. S. Manko
 Borštnik, Physics Letters B, Vol. 292, 1992, pp. 25-29.
Borštnik, Physics Letters B, Vol. 292, 1992, pp. 25-29. - N. S. Manko
 Borštnik, Journal of Mathematical Physics, Vol. 34, 1993, pp. 3731-3745.
Borštnik, Journal of Mathematical Physics, Vol. 34, 1993, pp. 3731-3745. - N. S. Manko
 Borštnik, International Journal of Theoretical Physics, Vol. 40, 2001, pp. 315-338.
Borštnik, International Journal of Theoretical Physics, Vol. 40, 2001, pp. 315-338. - N. S. Manko
 Borštnik, Modern Physics Letters A, Vol. 10, 1995, pp. 587-595.
Borštnik, Modern Physics Letters A, Vol. 10, 1995, pp. 587-595. - N. S. Manko
 Borštnik, World Scientific, Proceedings of the 13th Lomonosov Conference on Elementary Physics Particle Physics in the EVE of LHC, Moscow State University, Moscow, 3 - 29 August, 2007, pp. 371-378.
Borštnik, World Scientific, Proceedings of the 13th Lomonosov Conference on Elementary Physics Particle Physics in the EVE of LHC, Moscow State University, Moscow, 3 - 29 August, 2007, pp. 371-378. - N. S. Manko
 Borštnik, Proceedings to the 10th International Workshop “What Comes Beyond the Standard Models”, Bled, 17-27 July, 2007, pp. 94-113. arXiv:0711.4681.
Borštnik, Proceedings to the 10th International Workshop “What Comes Beyond the Standard Models”, Bled, 17-27 July, 2007, pp. 94-113. arXiv:0711.4681. - N. S. Manko
 Borštnik, Proceedings to the 5th International Conference on Beyond the Standard Models of Particle Physics, Cosmology and Astrophysics, Cape Town, 1-6 February, 2010, pp. 543-553. arXiv:1005.2288.
Borštnik, Proceedings to the 5th International Conference on Beyond the Standard Models of Particle Physics, Cosmology and Astrophysics, Cape Town, 1-6 February, 2010, pp. 543-553. arXiv:1005.2288. - A. Borštnik and N. S. Manko
 Borštnik, Physical Review D, Vol. 74, 2006, Article ID: 0703013. doi:10.1103/PhysRevD.74.073013
Borštnik, Physical Review D, Vol. 74, 2006, Article ID: 0703013. doi:10.1103/PhysRevD.74.073013 - N. S. Manko
 Borštnik, “The Spin-Charge-Family Theory Is Explaining the Origin of Families, of the Higgs and the Yukawa Couplings,” Proceedings to the 14th International Workshop “What comes beyond the standard models”, Bled, 11-21 July, 2011, pp. 112-148. http://viavca.in2p3.fr/what_comes_beyond_the_standard_models_xiv.html
Borštnik, “The Spin-Charge-Family Theory Is Explaining the Origin of Families, of the Higgs and the Yukawa Couplings,” Proceedings to the 14th International Workshop “What comes beyond the standard models”, Bled, 11-21 July, 2011, pp. 112-148. http://viavca.in2p3.fr/what_comes_beyond_the_standard_models_xiv.html - G. Bregar, M. Breskvar, D. Lukman and N. S. Manko
 Borštnik, New Journal of Physics, Vol. 10, 2008, pp. 53-70.
Borštnik, New Journal of Physics, Vol. 10, 2008, pp. 53-70. - G. Bregar and N. S. Manko
 Borštnik, Physical Review D, Vol. 80, 2009, pp. 1-16.
Borštnik, Physical Review D, Vol. 80, 2009, pp. 1-16. - R. Jackiw and K. Johnson, Physical Review D, Vol. 8, 1973, pp. 2386-2398. doi:10.1103/PhysRevD.8.2386
- S. Weinberg, Physical Review D, Vol. 19, 1979, pp. 1277-1280. S. Dimopoulos and L. Susskind, Nuclear Physics B, Vol. 155, 1979, pp. 237-252.
- T. Appelquist and J. Terning, Physics Review D, Vol. 50, 1994, pp. 2116-2126. doi:10.1103/PhysRevD.50.2116
- P. Q. Hung, Physical Review Letters, Vol. 80, 1998, pp. 3000-3003. P. H. Frampton, P. Q. Hung and M. Sher, Physics Report, Vol. 330, 2000, pp. 263-348.
- S. J. Huber, C. A. Lee and Q. Shafi, Physics Letters B, Vol. 531, 2002, pp. 112-118. doi:10.1016/S0370-2693(02)01368-0
- A. J. Buras, B. Duling and T. Feldmann, Journal of High Energy Physics, Vol. 9, 2010, pp. 106-176.
- Y. A. Simonov, Physics of Atomic Nuclei, Vol. 74, 2011, pp. 643-649.
- T. A. Ryttov and R. Shrock, Physical Review D, Vol. 81, 2010, pp. 1-21.
- Z. Kakushadze and S. H. H. Tye, Physical Review Letters, Vol. 77, 1996, pp. 2612-2615.
- H. C. Lee, “An Introduction to Kaluza-Klein Theories,” World Scientific, Singapore, 1983.
- “Modern Kaluza-Klein Theories,” In: T. Appelquist, A. Chodos and P. G. O. Freund, Eds., Reading, Addison Wesley, Boston, 1987.
- R. S. Chivukula and H. Georgi, Physics Letters B, Vol. 188, 1987, pp. 99-104. doi:10.1016/0370-2693(87)90713-1
- G. D. Ambrosio, G. Giudice, G. Isidori and A. Strumia, Nuclear Physics B, Vol. 645, 2002, pp. 155-187. doi:10.1016/S0550-3213(02)00836-2
- R. D. Peccei and H. R. Quinn, Physical Review D, Vol. 16, 1977, pp. 1791-1797. doi:10.1103/PhysRevD.16.1791
- R. Alonso, M. B. Gavela, L. Merlo and S. Rigolin, Journal of High Energy Physics, Vol. 7, 2011, pp. 1-32.
- C. D. Froggatt and H. B. Nielsen, Nuclear Physics B, Vol. 147, 1979, pp. 277-298. doi:10.1016/0550-3213(79)90316-X
- A. Borštnik Bra
 i
i and N. S. Manko
and N. S. Manko Borštnik, “The approach Unifying Spins and Charges and Its Predictions,” Proceedings to the Euroconference on Symmetries Beyond the Standard Model, Portorož, 12-17 July, 2003, pp. 31-57.
Borštnik, “The approach Unifying Spins and Charges and Its Predictions,” Proceedings to the Euroconference on Symmetries Beyond the Standard Model, Portorož, 12-17 July, 2003, pp. 31-57. - N. S. Manko
 Borštnik and H. B. Nielsen, Physics Letters B, Vol. 633, 2006, pp. 771-775. Physics Letters B, Vol. 644, 2007, pp. 198-202. Physics Letters B, Vol. 663, 2008, pp. 265-269. Physics Letters B, Vol. 486, 2000, pp. 314-321.
Borštnik and H. B. Nielsen, Physics Letters B, Vol. 633, 2006, pp. 771-775. Physics Letters B, Vol. 644, 2007, pp. 198-202. Physics Letters B, Vol. 663, 2008, pp. 265-269. Physics Letters B, Vol. 486, 2000, pp. 314-321. - D. Lukman, N. S. Manko
 Borštnik and H. B. Nielsen, New Journal of Physics, Vol. 13, 2011, pp. 1-25, http://arxiv.org/abs/1001.4679.
Borštnik and H. B. Nielsen, New Journal of Physics, Vol. 13, 2011, pp. 1-25, http://arxiv.org/abs/1001.4679. - E. Witten, Nuclear Physics B, Vol. 186, 1981, pp. 412- 428. “Fermion Quantum Numbers in Kaluza-Klein Theories,” Princeton Technical Report, Institute for Advanced Studies, Princeton, 1983.
- N. S. Manko
 Borštnik, Journal of Mathematical Physics, Vol. 34, 1993, pp. 3731-3745. N. S. Manko
Borštnik, Journal of Mathematical Physics, Vol. 34, 1993, pp. 3731-3745. N. S. Manko Borštnik and H. B. Nielsen, Journal of Mathematical Physics, Vol. 43, 2002, pp. 5782-5803. Journal of Mathematical Physics, Vol. 44, 2003, pp. 4817-4827.
Borštnik and H. B. Nielsen, Journal of Mathematical Physics, Vol. 43, 2002, pp. 5782-5803. Journal of Mathematical Physics, Vol. 44, 2003, pp. 4817-4827. - A. Hernández-Galeana and N. S. Manko
 Borštnik, “Masses and Mixing Matrices of Families of Quarks and Leptons Within the Spin-Charge-Family-Theory Beyond the Tree Level,” Proceedings to the 13th workshop What Comes Beyond the Standard Models, Bled, 13-23 July, 2010, pp. 166-176.
Borštnik, “Masses and Mixing Matrices of Families of Quarks and Leptons Within the Spin-Charge-Family-Theory Beyond the Tree Level,” Proceedings to the 13th workshop What Comes Beyond the Standard Models, Bled, 13-23 July, 2010, pp. 166-176. - G. Bregar and N. S. Manko
 Borštnik, “How Similar Are Properties of Mass Matrices of Quarks to Those of Leptons?” Paper in Preparation.
Borštnik, “How Similar Are Properties of Mass Matrices of Quarks to Those of Leptons?” Paper in Preparation. - J. Beringer, et al. (Particle Data Group), Physical Review D, Vol. 86, 2012, Article ID: 010001.
- V. A. Novikov, L. B. Okun, A. N. Rozanov and M. I. Vysotsky, Physics Letter B, Vol. 529, 2002, pp. 111-116. M. Maltoni, V. A. Novikov, L. B. Okun, A. N. Rozanov and M. I. Vysotsky, Physics Letter B, Vol. 476, 2000, pp. 107-115.
- N. S. Manko
 Borštnik, “Do we Have the Explanation for the Higgs and Yukawa Couplings of the Standard Model,” http://arxiv.org/abs/1212.3184v2
Borštnik, “Do we Have the Explanation for the Higgs and Yukawa Couplings of the Standard Model,” http://arxiv.org/abs/1212.3184v2
Appendix: Short Presentation of Technique [1,2,32]
I make in this appendix a short review of the technique [32], initiated and developed by me when proposing the spin-charge-family theory [1-11,28,37] assuming that all the internal degrees of freedom of spinors, with family quantum number included, are describable in the space of  -anticommuting (Grassmann) coordinates [32], if the dimension of ordinary space is also
-anticommuting (Grassmann) coordinates [32], if the dimension of ordinary space is also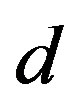 . There are two kinds of operators in the Grassmann space, fulfilling the Clifford algebra which anticommute with one another. The technique was further developed in the present shape together with H.B. Nielsen [32] by identifying one kind of the Clifford objects with
. There are two kinds of operators in the Grassmann space, fulfilling the Clifford algebra which anticommute with one another. The technique was further developed in the present shape together with H.B. Nielsen [32] by identifying one kind of the Clifford objects with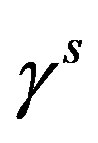 ’s and another kind with
’s and another kind with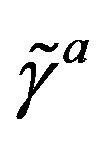 ’s. In this last stage we constructed a spinor basis as products of nilpotents and projections formed as odd and even objects of
’s. In this last stage we constructed a spinor basis as products of nilpotents and projections formed as odd and even objects of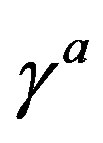 ’s, respectively, and chosen to be eigenstates of a Cartan subalgebra of the Lorentz groups defined by
’s, respectively, and chosen to be eigenstates of a Cartan subalgebra of the Lorentz groups defined by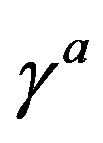 ’s and
’s and ’s. The technique can be used to construct a spinor basis for any dimension
’s. The technique can be used to construct a spinor basis for any dimension 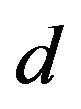 and any signature in an easy and transparent way. Equipped with the graphic presentation of basic states, the technique offers an elegant way to see all the quantum numbers of states with respect to the two Lorentz groups, as well as transformation properties of the states under any Clifford algebra object.
and any signature in an easy and transparent way. Equipped with the graphic presentation of basic states, the technique offers an elegant way to see all the quantum numbers of states with respect to the two Lorentz groups, as well as transformation properties of the states under any Clifford algebra object.
The objects 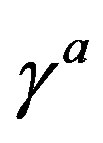 and
and 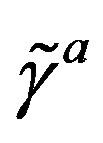 have properties (2),
have properties (2),
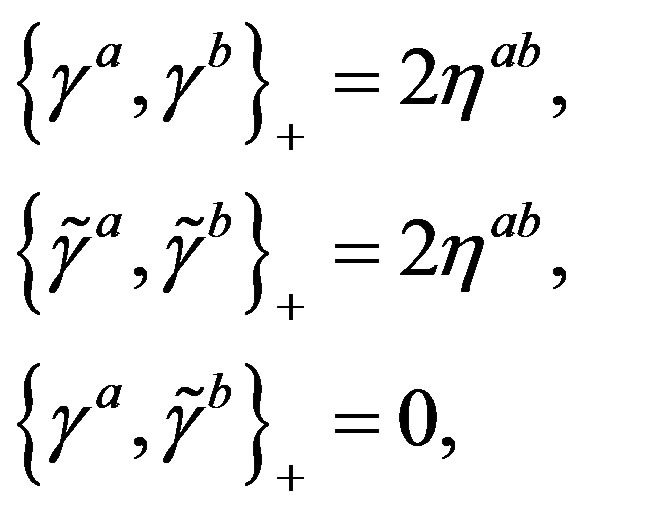 (A1)
(A1)
for any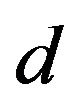 , even or odd.
, even or odd.  is the unit element in the Clifford algebra.
is the unit element in the Clifford algebra.
The Clifford algebra objects 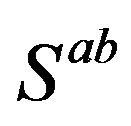 and
and  close the algebra of the Lorentz group
close the algebra of the Lorentz group
 (A1)
(A1)
We assume the “Hermiticity’’ property for 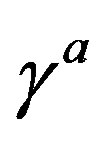 ‘s and
‘s and  ‘s
‘s
 (A3)
(A3)
in order that 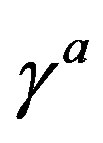 and
and 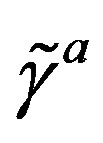 are compatible with (A1) and formally unitary, i.e.
are compatible with (A1) and formally unitary, i.e. 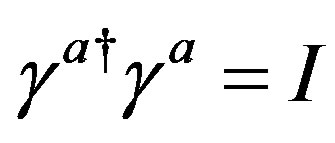 and
and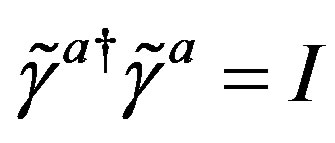 .
.
One finds from Equation(A3) that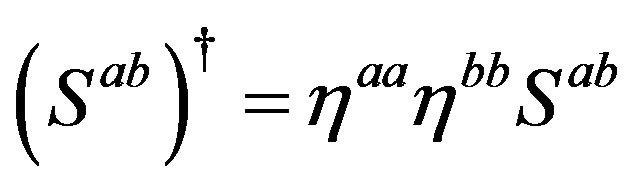 .
.
Recognizing from Equation (A2) that two Clifford algebra objects 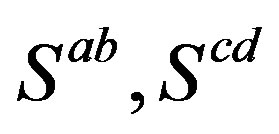 with all indices different commute, and equivalently for
with all indices different commute, and equivalently for , we select the Cartan subalgebra of the algebra of the two groups, which form equivalent representations with respect to one another
, we select the Cartan subalgebra of the algebra of the two groups, which form equivalent representations with respect to one another
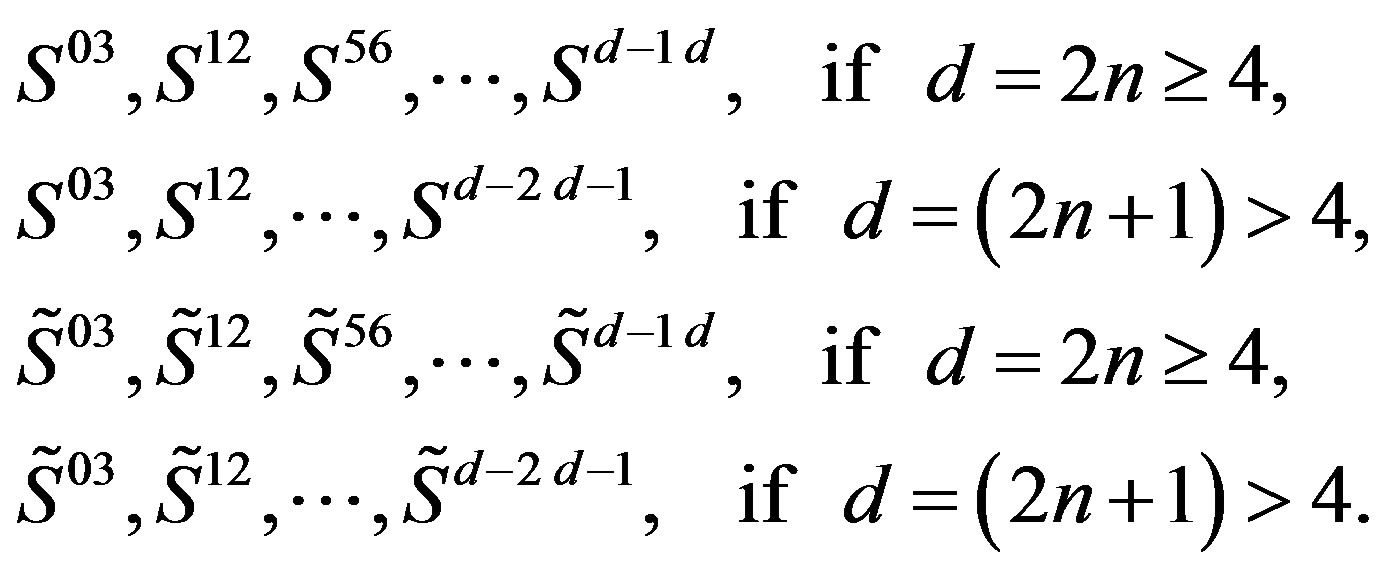 (A4)
(A4)
The choice for the Cartan subalgebra in d < 4 is straight forward. It is useful to define one of the Casimirs of the Lorentz group - the handedness 
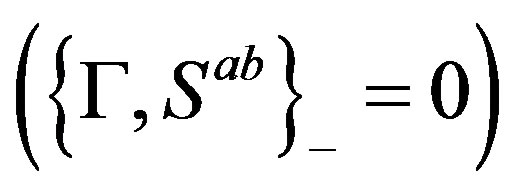 in any
in any 
 (A5)
(A5)
One can proceed equivalently for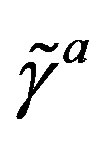 ’s. We understand the product of
’s. We understand the product of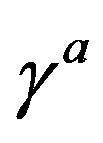 ’s in the ascending order with respect to the index
’s in the ascending order with respect to the index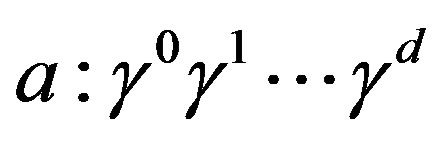 . It follows from Equation (A3) for any choice of the signature
. It follows from Equation (A3) for any choice of the signature  that
that
 We also find that for
We also find that for  even the handedness anticommutes with the Clifford algebra objects
even the handedness anticommutes with the Clifford algebra objects 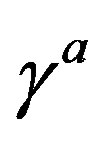
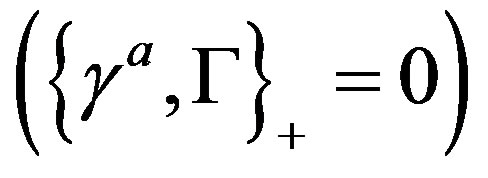 , while for
, while for 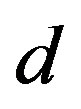 odd it commutes with
odd it commutes with 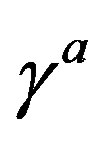
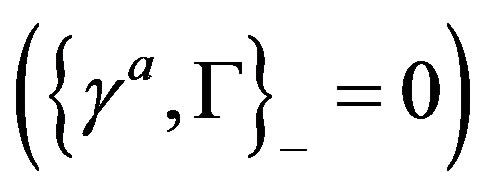 .
.
To make the technique simple we introduce the graphic presentation as follows (Equation (9))
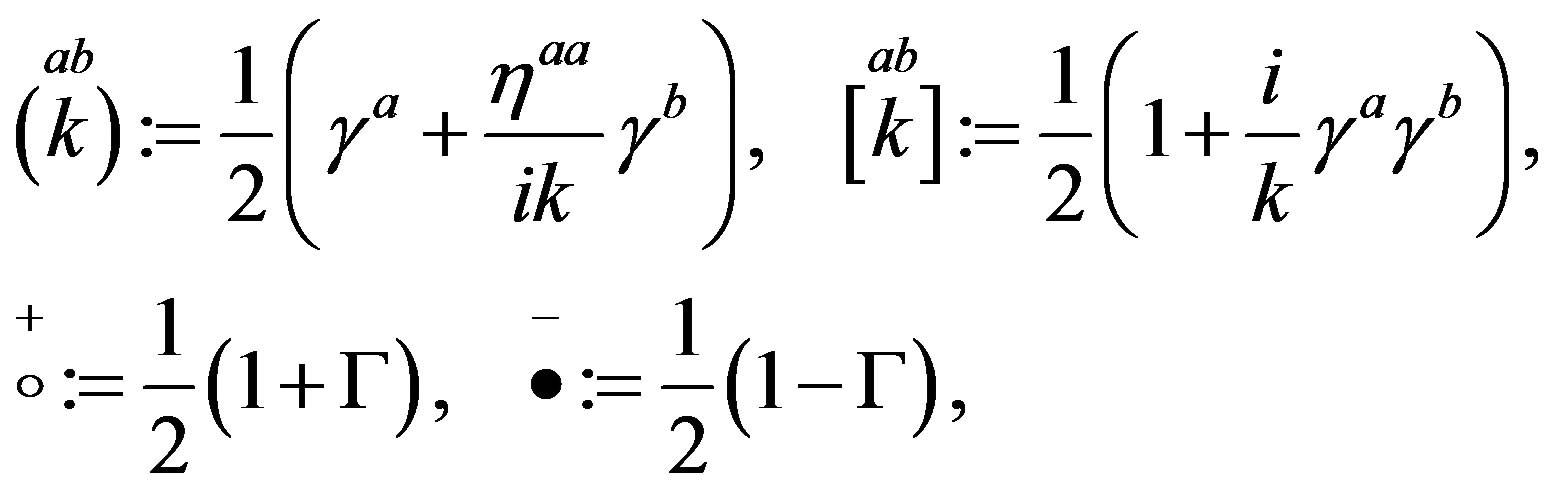 (A6)
(A6)
where . One can easily check by taking into account the Clifford algebra relation (Equation (A1)) and the definition of
. One can easily check by taking into account the Clifford algebra relation (Equation (A1)) and the definition of  and
and 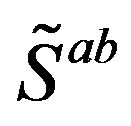 (Equation (A2)) that if one multiplies from the left hand side by
(Equation (A2)) that if one multiplies from the left hand side by 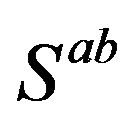 or
or 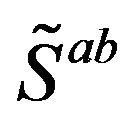 the Clifford algebra objects
the Clifford algebra objects 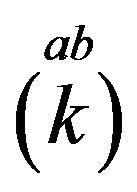 and
and , it follows that
, it follows that
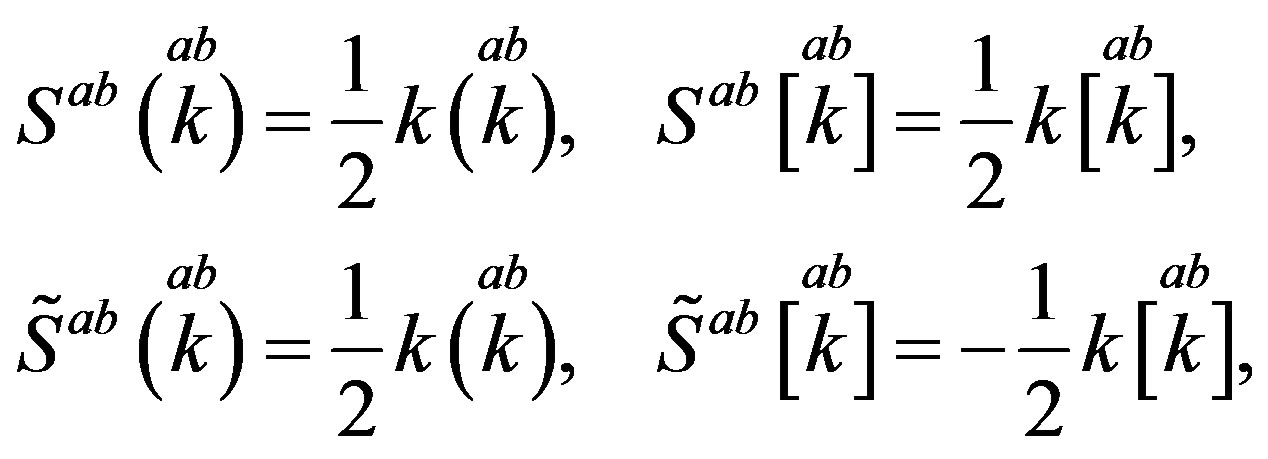 (A7)
(A7)
which means that we get the same objects back multiplied by the constant 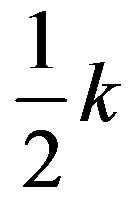 in the case of
in the case of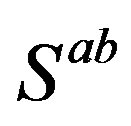 , while
, while 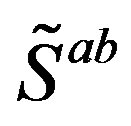 multiply
multiply  by
by  and
and  by
by  rather than
rather than . This also means that when
. This also means that when 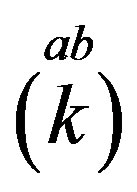 and
and 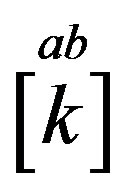 act from the left hand side on a vacuum state
act from the left hand side on a vacuum state 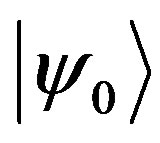 the obtained states are the eigenvectors of
the obtained states are the eigenvectors of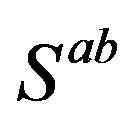 . We further recognize
. We further recognize
(Equation 11,12) that 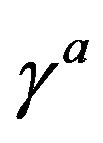 transform
transform 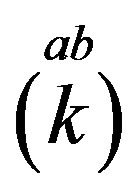 into
into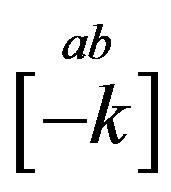 , never to
, never to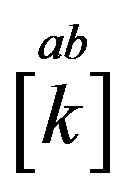 , while
, while 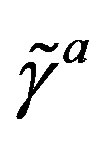 transform
transform 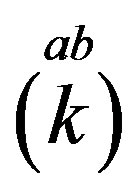 into
into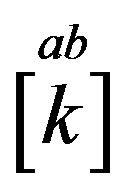 , never to
, never to 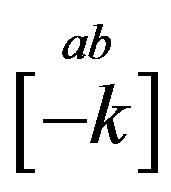
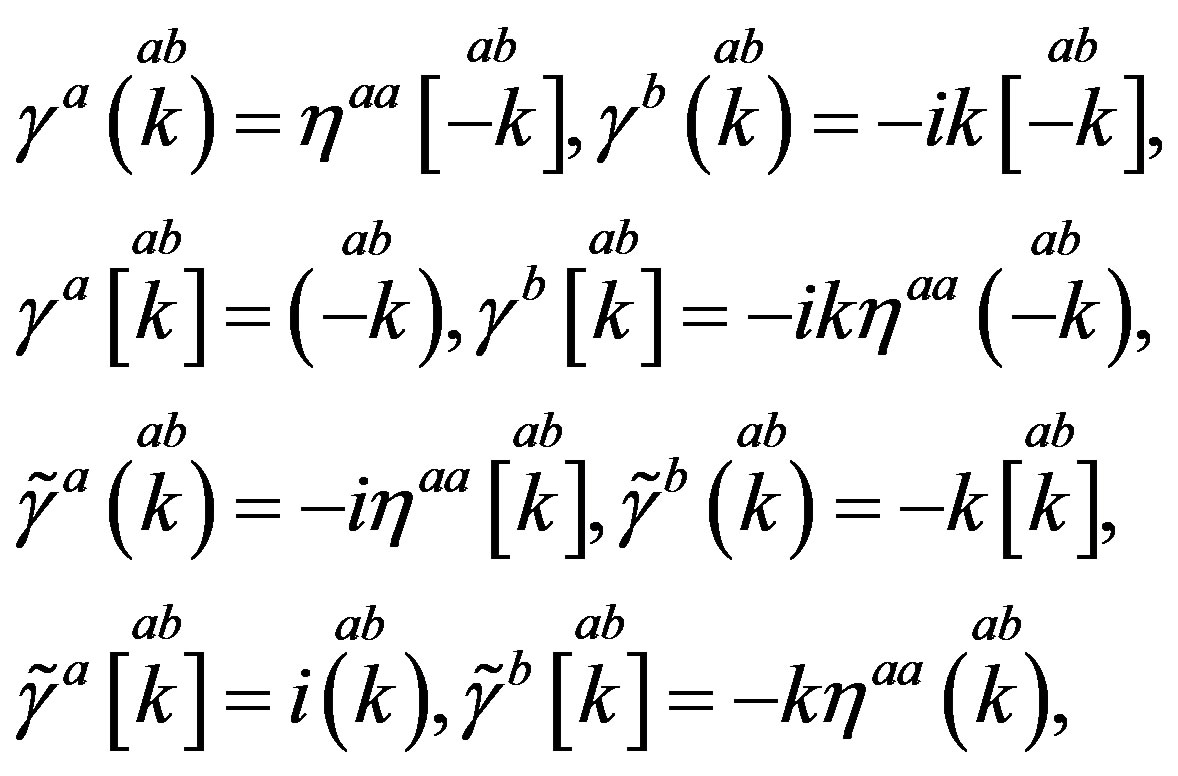 (A8)
(A8)
From Equation (A8) it follows
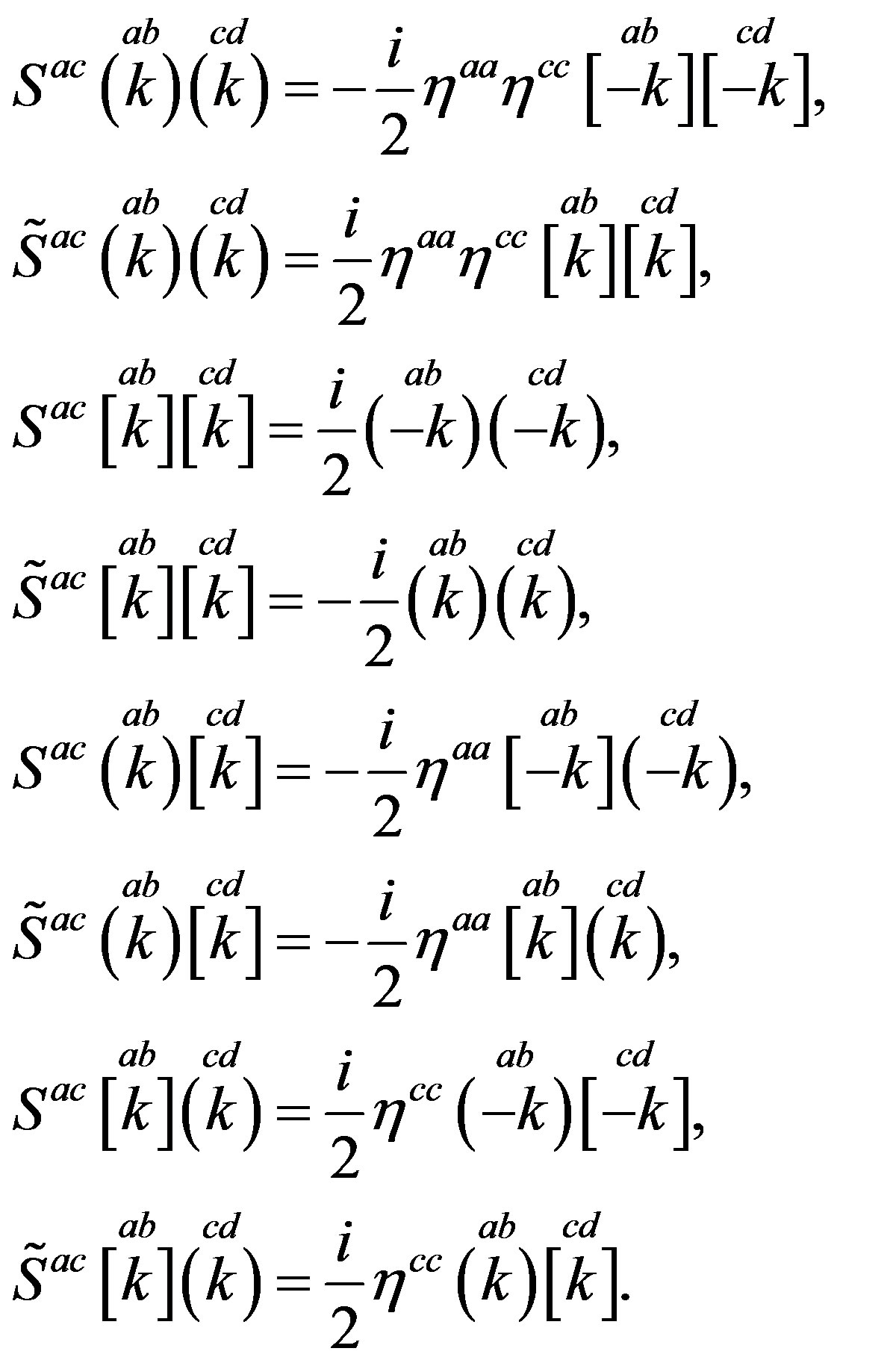 (A9)
(A9)
From Equations (A9) we conclude that  generate the equivalent representations with respect to
generate the equivalent representations with respect to 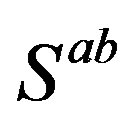 and opposite.
and opposite.
Let us deduce some useful relations
 (A10)
(A10)
We recognize in the first equation of the first line and the first equation of the second line the demonstration of the nilpotent and the projector character of the Clifford algebra objects 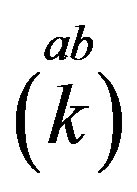 and
and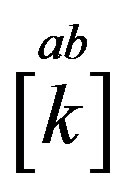 , respectively. Defining
, respectively. Defining
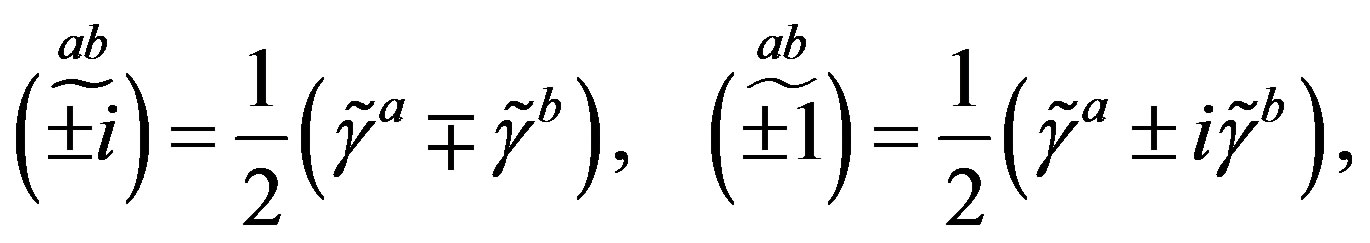 (A11)
(A11)
one recognizes that
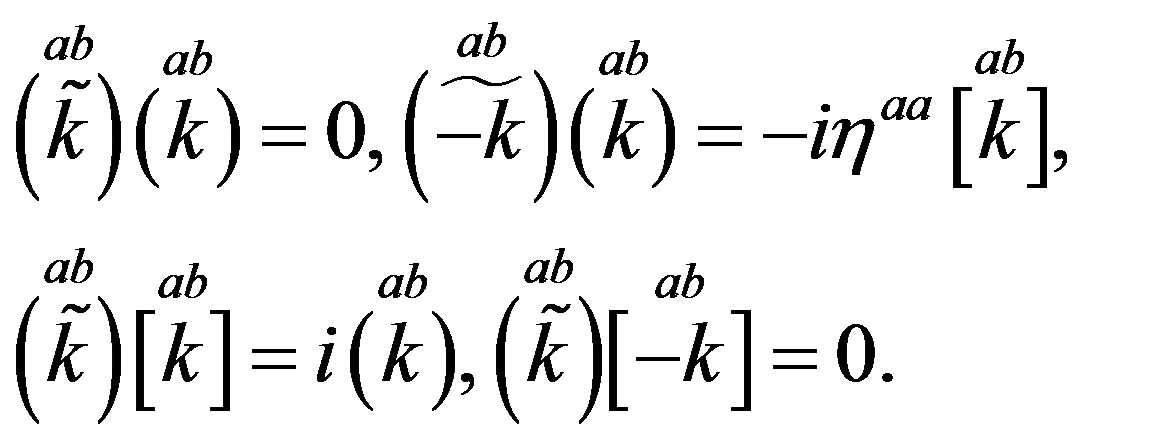 (A12)
(A12)
Recognizing that
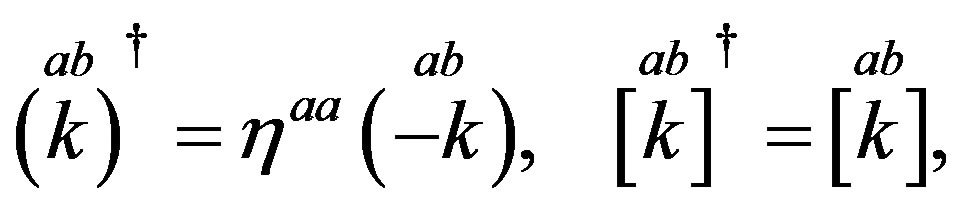 (A13)
(A13)
we define a vacuum state  so that one finds
so that one finds
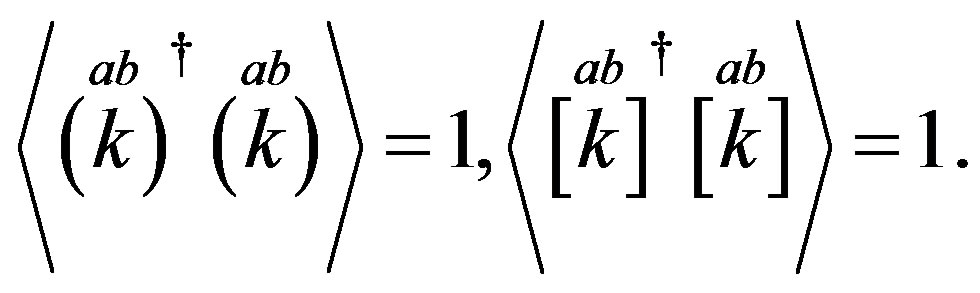 (A14)
(A14)
Taking into account the above equations it is easy to find a Weyl spinor irreducible representation for  - dimensional space, with
- dimensional space, with  even or odd.
even or odd.
For 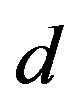 even we simply make a starting state as a product of
even we simply make a starting state as a product of , let us say, only nilpotents
, let us say, only nilpotents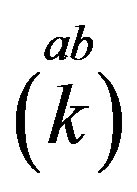 , one for each
, one for each 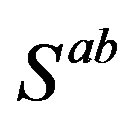 of the Cartan subalgebra elements (Equation (A4)), applying it on an (unimportant) vacuum state. For
of the Cartan subalgebra elements (Equation (A4)), applying it on an (unimportant) vacuum state. For 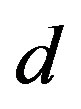 odd the basic states are products of
odd the basic states are products of  nilpotents and a factor
nilpotents and a factor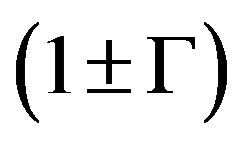 . Then the generators
. Then the generators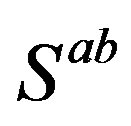 , which do not belong to the Cartan subalgebra, being applied on the starting state from the left, generate all the members of one Weyl spinor.
, which do not belong to the Cartan subalgebra, being applied on the starting state from the left, generate all the members of one Weyl spinor.
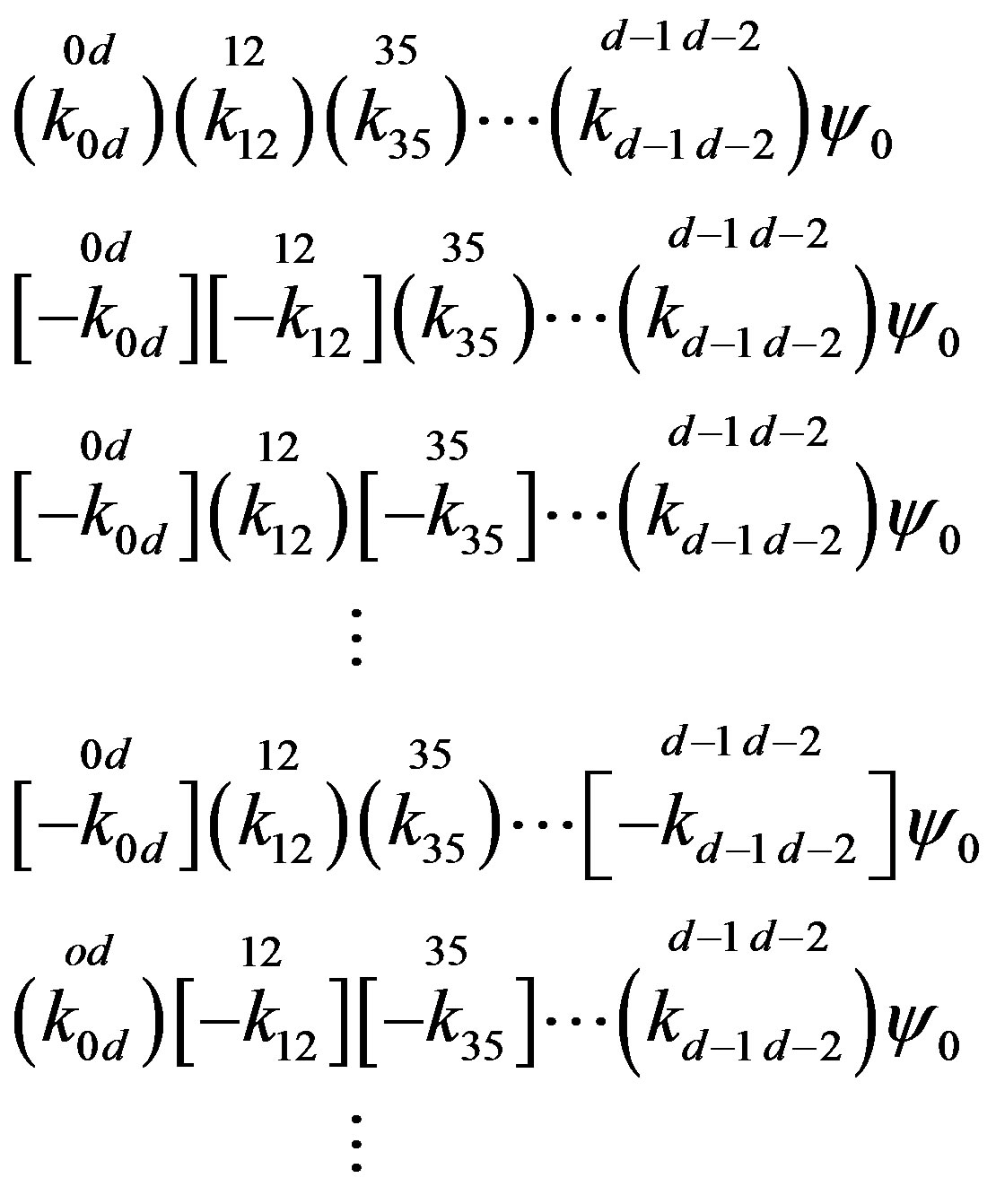 (A15)
(A15)
All the states have the handedness , since
, since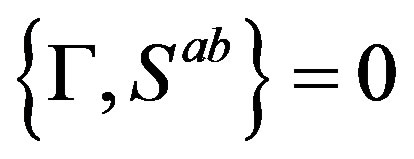 . States, belonging to one multiplet with respect to the group
. States, belonging to one multiplet with respect to the group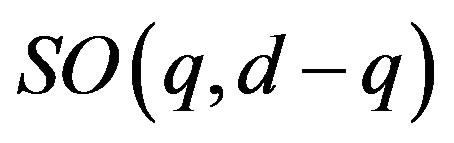 , that is to one irreducible representation of spinors (one Weyl spinor), can have any phase. We made a choice of the simplest one, taking all phases equal to one.
, that is to one irreducible representation of spinors (one Weyl spinor), can have any phase. We made a choice of the simplest one, taking all phases equal to one.
The above graphic representation demonstrates that for 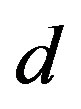 even all the states of one irreducible Weyl representation of a definite handedness follow from a starting state, which is, for example, a product of nilpotents
even all the states of one irreducible Weyl representation of a definite handedness follow from a starting state, which is, for example, a product of nilpotents
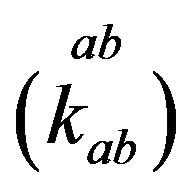 , by transforming all possible pairs of
, by transforming all possible pairs of 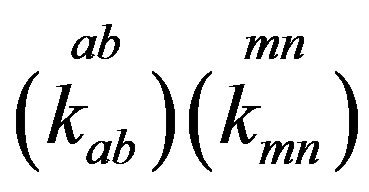 into
into . There are
. There are , which do this. The procedure gives
, which do this. The procedure gives  states. A Clifford algebra object
states. A Clifford algebra object 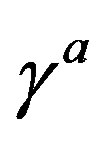 being applied from the left hand side, transforms a Weyl spinor of one handedness into a Weyl spinor of the opposite handedness. Both Weyl spinors form a Dirac spinor.
being applied from the left hand side, transforms a Weyl spinor of one handedness into a Weyl spinor of the opposite handedness. Both Weyl spinors form a Dirac spinor.
For 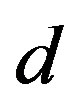 odd a Weyl spinor has besides a product of
odd a Weyl spinor has besides a product of 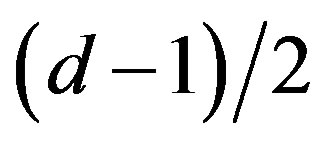 nilpotents or projectors also either the factor
nilpotents or projectors also either the factor
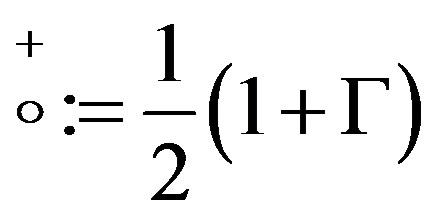 or the factor
or the factor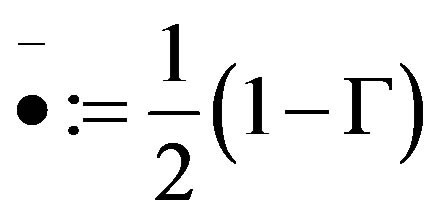 . As in the case of
. As in the case of  even, all the states of one irreducible Weyl representation of a definite handedness follow from a starting state, which is, for example, a product of
even, all the states of one irreducible Weyl representation of a definite handedness follow from a starting state, which is, for example, a product of 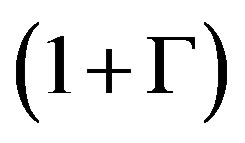 and
and
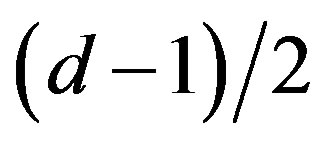 nilpotents
nilpotents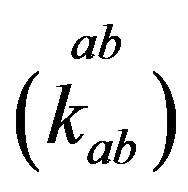 , by transforming all possible pairs of
, by transforming all possible pairs of  into
into . But
. But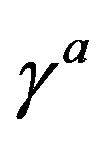 ’s, being applied from the left hand side, do not change the handedness of the Weyl spinor, since
’s, being applied from the left hand side, do not change the handedness of the Weyl spinor, since 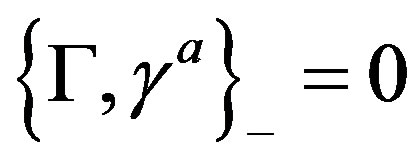 for
for  odd. A Dirac and a Weyl spinor are for
odd. A Dirac and a Weyl spinor are for 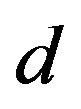 odd identical and a ‘‘family’’ has accordingly
odd identical and a ‘‘family’’ has accordingly 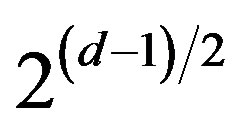 members of basic states of a definite handedness.
members of basic states of a definite handedness.
We shall speak about left handedness when 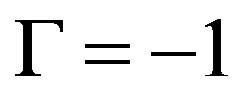 and about right handedness when
and about right handedness when 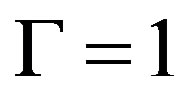 for either
for either 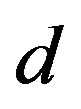 even or odd.
even or odd.
While 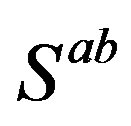 which do not belong to the Cartan subalgebra (Equation (A4)) generate all the states of one representation, generate
which do not belong to the Cartan subalgebra (Equation (A4)) generate all the states of one representation, generate 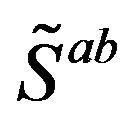 which do not belong to the Cartan subalgebra(Equation (A4)) the states of
which do not belong to the Cartan subalgebra(Equation (A4)) the states of 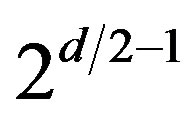 equivalent representations.
equivalent representations.
Making a choice of the Cartan subalgebra set of the algebra  and
and 
 (A16)
(A16)
a left handed  eigen state of all the members of the Cartan subalgebra, representing a weak chargeless
eigen state of all the members of the Cartan subalgebra, representing a weak chargeless 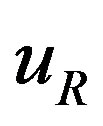 -quark with spin up, hyper charge
-quark with spin up, hyper charge  and colour
and colour , for example, can be written as
, for example, can be written as
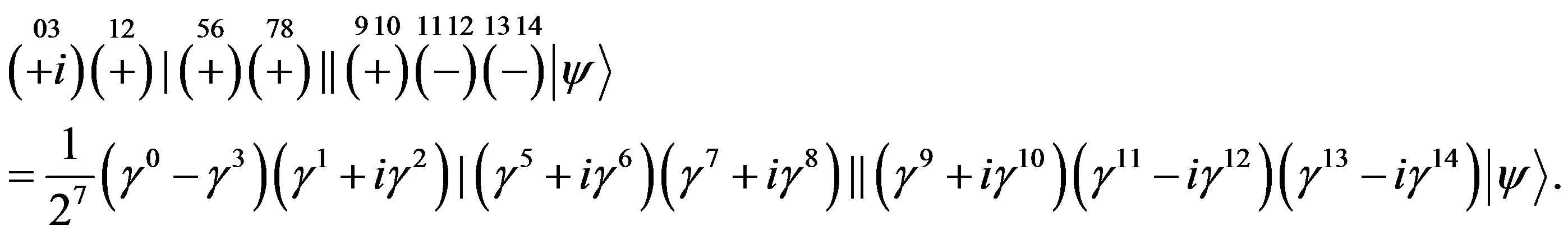 (A17)
(A17)
This state is an eigen state of all  and
and 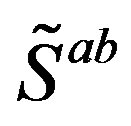 which are members of the Cartan subalgebra (Equation (A16)).
which are members of the Cartan subalgebra (Equation (A16)).
The operators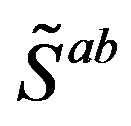 , which do not belong to the Cartan subalgebra (Equation (A16)), generate families from the starting
, which do not belong to the Cartan subalgebra (Equation (A16)), generate families from the starting 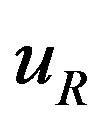 quark, transforming
quark, transforming 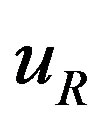 quark from Equation (A17) to the
quark from Equation (A17) to the 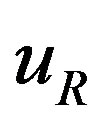 of another family, keeping all the properties with respect to
of another family, keeping all the properties with respect to 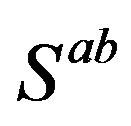 unchanged. In particular
unchanged. In particular 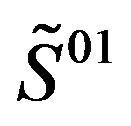 applied on a right handed
applied on a right handed 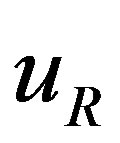 -quark, weak chargeless, with spin up, hyper charge
-quark, weak chargeless, with spin up, hyper charge  and the colour charge
and the colour charge 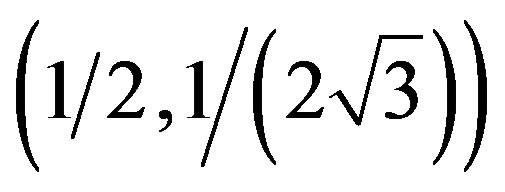 from Equation (A17) generates a state which is again a right handed
from Equation (A17) generates a state which is again a right handed  -quark, weak chargeless, with spin up, hyper charge
-quark, weak chargeless, with spin up, hyper charge  and the colour charge
and the colour charge 
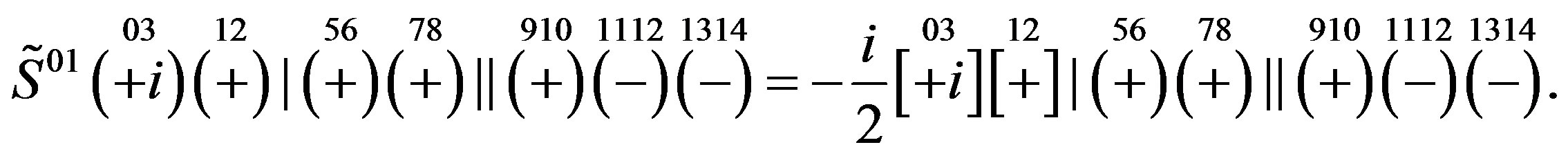 (A18)
(A18)
Below some useful relations [2] are presented
NOTES
1Since there are two kinds of the spin, the second kind must either manifest, and it does, since we do have families, or we should prove that it does not manifest at the low energy regime.
2Although there are not a lot of possibilities how to break the starting symmetry, it is still a lot of open problems to be solved to come to the low energy regime. I made, together with the collaborators, a lot of efforts, to prove that in noncompact spaces there are after the break of symmetries massless fermions [29,30], which is not the case for compact spaces [31]. Each break of symmetry is a complicated many body problem, simulated, for example, in the standard model for the electroweak one, with the assumed vacuum expectation value of the Higgs field.
3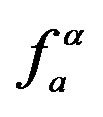 are inverted vielbeins to
are inverted vielbeins to 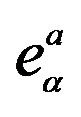 with the properties
with the properties 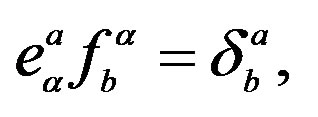
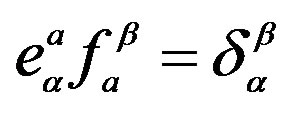 . Latin indices
. Latin indices  denote a tangent space (a flat index), while Greek indices
denote a tangent space (a flat index), while Greek indices  denote an Einstein index (a curved index). Letters from the beginning of both the alphabets indicate a general index (
denote an Einstein index (a curved index). Letters from the beginning of both the alphabets indicate a general index ( and
and  ), from the middle of both the alphabets the observed dimensions
), from the middle of both the alphabets the observed dimensions  (
(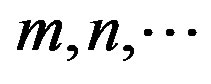 and
and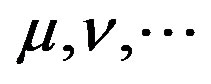 ), indices from the bottom of the alphabets indicate the compactified dimensions (
), indices from the bottom of the alphabets indicate the compactified dimensions ( and
and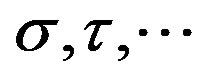 ). We assume the signature
). We assume the signature .
.
4We proved that it is possible to have massless fermions after a (particular) break if we start with massless fermions and assume particular boundary conditions after the break or the "effective two dimensionality" cases [29,30].

