Journal of Modern Physics
Vol.4 No.2(2013), Article ID:28335,8 pages DOI:10.4236/jmp.2013.42037
Defect Core Structures in Twisted Nematic and Twisted Chiral Liquid Crystals
1Department of Physics, Hebei University of Technology, Tianjin, China
2State Key Lab of Applied Optics, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun, China
3Graduate School of the Chinese Academy of Sciences, Beijing, China
Email: zhidong_zhang@yahoo.cn
Received November 30, 2012; revised December 31, 2012; accepted January 9, 2013
Keywords: Disclinations; Eigenvalue Exchange; Defect Core; Landau-de Gennes Theory
ABSTRACT
The defect structures of s = ±1/2 twist disclinations in twisted nematic and twisted chiral liquid crystals have been investigated within the Landau-de Gennes theory numerically. Our results show that there exists eigenvalue exchange across the defect core of both the two models. The defect core is essentially biaxial and never isotropic. The defect centre is uniaxial and is surrounded by a strong biaxial region.
1. Introduction
Topological defects arise as a result of broken continuous symmetry and are ubiquitous in nature, from microscopic condensed matter systems governed by quantum mechanics to a universe in which gravity plays a decisive role [1-3]. Defects in liquid crystals (LCs) have been the subject of much interest, still offering unsolved problems. Commonly observed defects in the uniaxial nematic phase are typically point defects with topological charge s = 1 and line defects with topological charge s = ±1/2 [4]. There are two types of s = ±1/2 disclination lines [5]. The first type is wedge disclination with the rotation vector parallel to the disclination line, while the second is twist disclination with the rotation vector perpendicular to the disclination line. The region where the presence of a defect causes apparent deviations from bulk ordering is referred to as the defect core [6]. Eigenvalue exchange (also called order reconstruction) was first shown by Schopohl and Sluckin within the core of s = ±1/2 wedge disclinations [7], and has aroused numerous subsequent studies on the detailed core structure in nematic LCs for various boundary conditions [8-12]. This mechanism has confirmed that biaxial, rather than isotropic, core structures of both line and point defects are more likely to occur.
The structures of s = ±1/2 twist disclination have been observed in a twisted nematic (TN) cell with planar orientations on both plates with the easy axes perpendicular to each other (called 90˚ twisted structure). These defects essentially involve two symmetric twist distortions, respectively left-handed and right-handed with degenerate energy, corresponding to ±π/2 twists over the cell thickness [13]. These twist disclinations can be stable under particular anchoring conditions on to the plates [14].
The helical structure of twisted chiral nematic (TCN) cells with planar anchoring have been studied [15]. It is shown that a mismatch between the equilibrium pitch p0 and the twist imposed by the boundary conditions may produce two stable helical configurations that are degenerate in energy and can be switched to each other. In Appendix A, we give that a TCN cell of thickness d = p0/2 with 90˚ twisted structure has bistable states, being respectively π/2 and 3π/2 twists over the cell thickness.
Dislocations also appear in chiral LCs as a result of temperature quenching from the isotropic phase, applied fields, and surface boundary conditions [4]. The structures of defects in chiral LCs have been studied in the so-called Grandjean-Cano wedges both analytically [16, 17] and experimentally [18-21]. De Gennes [16] and Scheffer [17] have given the analytical solution of the director orientation for the Grandjean-Cano disclination, based on the Frank elastic theory, using the method of images and conformal mapping, respectively. These defects correspond to the disclinations of Burgers vector b = p0/2 introduced in References [18,19], which can be splits into a pair of τ−1/2 and τ+1/2 disclinations.
In this study, we will investigate the defect structure of a TN cell and a TCN cell of thickness p0/2, both of which have 90˚ twisted structure. Our study is based on the Landau-de Gennes theory describing the orientational order of a LC in terms of a second-rank tensor Q, which encompasses both uniaxial and biaxial state.
2. Theoretical Basis
2.1. Landau-de Gennes Theory
Our theoretical argument is based on the Landau-de Gennes theory [14], in which the orientational order of a LC is described by a second-rank symmetric and traceless tensor [22]
 (1)
(1)
Here λi and ei are the ith eigenvalue and the ith eigenvector of Q, respectively. In isotropic phase, Q vanishes. In the uniaxial ordering, Q has two degenerate eigenvalues and can be represented by
 (2)
(2)
where S is the uniaxial scalar parameter, and the unit vector n is the nematic director pointing along the local uniaxial ordering direction. In Equation (2), S can have either sign: when it is positive the ensemble of molecules represented by Q tends to be aligned along n, whereas when S is negative it tends to lie in the plane orthogonal to n.
Finally, when all eigenvalues of Q are distinct, the LC is in a biaxial state. The degree of biaxiality is measured by the biaxiality parameter β2, defined as [23]
 (3)
(3)
which ranges in the interval [0, 1]. In all uniaxial states with two degenerate eigenvalues, β2 = 0, while states with maximal biaxiality correspond to β2 = 1. Since  , the states with maximal biaxiality are precisely those where detQ = 0, which further implies that at least one eigenvalue of Q vanishes in the biaxial states.
, the states with maximal biaxiality are precisely those where detQ = 0, which further implies that at least one eigenvalue of Q vanishes in the biaxial states.
Following the notation in Reference [24], the free energy density of a chiral LC is given by
 in which
in which
 (4)
(4)
is the local free energy in the Landau-de Gennes expansion,
 (5)
(5)
is the free energy due to the inhomogeneity of LC order. In fbulk, a and b are positive constants and c is assumed to vary with temperature. In Equation (5), summations over repeated indices are implied,  , and
, and  with εαγβ being the Levi-Civita symbol. The variables K1 and K0 are the elastic constants, and
with εαγβ being the Levi-Civita symbol. The variables K1 and K0 are the elastic constants, and  characterizes the strength and sign of the chirality (hereafter, we consider the case with q0 > 0). We also note that following the spirit of the Landau expansion, we assume that the temperature dependence appears only in the parameter c and neglect the temperature dependence of the other material parameters. Moreover, the bulk equilibrium value of the uniaxial scalar order parameter in Equation (2):
characterizes the strength and sign of the chirality (hereafter, we consider the case with q0 > 0). We also note that following the spirit of the Landau expansion, we assume that the temperature dependence appears only in the parameter c and neglect the temperature dependence of the other material parameters. Moreover, the bulk equilibrium value of the uniaxial scalar order parameter in Equation (2):
 , also depends on the temperature.
, also depends on the temperature.
When q0 = 0, the condition reduces to the ordinary nematic limit with infinite pitch, and Equation (5) reduces to
 (6)
(6)
After an appropriate rescaling of the variables, we can reduce the number of relevant parameters. Here we follow the rescaling of Wright and Mermin [24] and the rescaled free-energy density  is written, in terms of a rescaled tensor order parameter
is written, in terms of a rescaled tensor order parameter 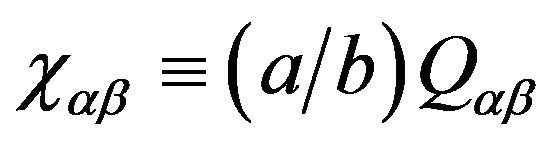 , the rescaled form of Equations (4)-(6) can be written as
, the rescaled form of Equations (4)-(6) can be written as
 (7)
(7)
 (8)
(8)
 (9)
(9)
where the rescaled parameters

denote temperature, strength of chirality, and the anisotropy of elasticity, respectively, where  is the coherence length, the rescaled spatial derivative is
is the coherence length, the rescaled spatial derivative is  in Equation (8) and
in Equation (8) and  in Equation (9). We notice that the isotropic-nematic transition takes place at
in Equation (9). We notice that the isotropic-nematic transition takes place at , while the isotropic-cholesteric transition takes place at
, while the isotropic-cholesteric transition takes place at
 which depends on the chirality [24].
which depends on the chirality [24].
In the scaling employed above, the rescaled uniaxial ordering has the form
 (10)
(10)
where  is the rescaled uniaxial scalar parameter at equilibrium.
is the rescaled uniaxial scalar parameter at equilibrium.
2.2. Geometry of the Problem
We choose a TN cell of thickness d = 15ξ and a TCN cell of thickness d = p0/2 with 90˚ twisted structure. Both of the two models have two stable degenerate configurations with a twist difference of π. The plates are placed at z = ±d/2 of a Cartesian coordinate system. The lengths dx and dy of the cell along the x and the y axes are much larger than .
.
We study the structure of s = ±1/2 twist disclinations. The disclination line is parallel to the y axis of the simulation cells, and we seek solutions independent of y. At the two plates z = ±d/2, we enforce the fixed uniaxial anchoring represented by  and
and
 (11)
(11)
 (12)
(12)
On the lateral walls at x = dx/2, we also prescribe fixed boundary conditions with uniaxial ordering. For the TN cell, the total twist at x = dx/2 are ±π/2 respectively, while for the TCN cell, the total twist at x = dx/2 are π/2 and 3π/2 respectively. These boundary conditions are compatible with the generation of line defects with topological charge s = 1/2, with which we shall deal also apply to line defects with topological charge s = −1/2, with the conditions at the lateral walls exchanged.
2.3. Numerical Methods
In the rescaled space, the length is rescaled so that the cell thickness d = 15ξ is rescaled to d = 15 for the TN cell and d = p0/2 is rescaled to d = 2π for the TCN cell, respectively. The numerical calculations are to be intended with respect to the scaled variables.
We let the system relax from an initial condition under the fixed boundary conditions given above. In our simulation, we have identified that the value of dx = 3d is enough to exhibit the behavior of the equilibrium configuration in the limit as dx ® ∞; there is no visual difference as the value of dx continues to increase.
We employ
 (13)
(13)
as the relaxation equation to iterate the order parameter χαβ, where f is the total rescaled free energy of the system,
 (14)
(14)
and λ0 is the Lagrange multiplier ensuring Trχ ≡ 0 which can be eliminated in the numerical procedure [7]. To discretize Equation (13), we replace the derivatives with the two-dimensional finite-difference method employed in our previous studies in [25]. In our numerical calculations, we have found that a discretization with time step given by 10−5 is sufficient to guarantee the stability of the numerical procedure. In addition, our equilibration runs take 105, which have been confirmed sufficient for the system to reach equilibrium state.
We have calculated the tensor Q after the system to reach equilibrium state, and then the current tensor is diagonalized. Accordingly, the director is identified by the eigenvector possessing the largest eigenvalue, and the eigenvalues are scaled to the largest eigenvalue at the boundary. Then the degree of biaxiality is measured by the biaxiality parameter β2 given by Equation (3).
3. Results
In this section, we present our numerical results. In our simulations, we set η = 1 (one-constant approximation) just for simplicity, and the scaled temperature is set equal to τ = −1, corresponding to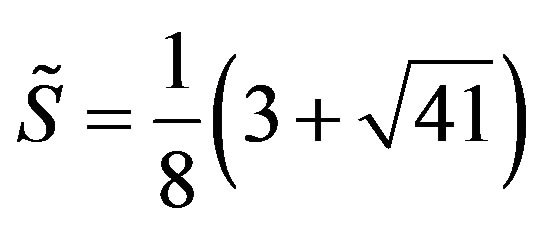 .
.
3.1. s = 1/2 Disclination in TN Cell
Figure 1 shows the director orientation diagram of s = 1/2 disclinations in the cross section through the defect line, i.e., x-z plane. The lines are “equiorientational” contours. Note that the position of the defect center (xdef,

Figure 1. Director orientation contours of s = 1/2 disclination in the x-z plane of a TN cell.
zdef) is located at the center of x-z plane, i.e., (0, 0), and the major disturbances of the defect structure in x-z space take place within a nearly-circular region around the defect center.
In Figure 2 we plot the three eigenvalues of the matrix Q along the two lines across the defect center in both x and z directions, that is z = 0 (Figure 2(a)) and x = 0 (Figure 2(b)), respectively. Outside about 0.2d from the defect line, the tensor order parameter essentially takes the form of Equation (2). Inside this region, the order parameter becomes increasingly biaxial, in that the degeneracy between two of the eigenvalues is broken. On a ring around the defect center, of radius ρ ≈ 0.02d, the LC is maximally biaxial; one of the eigenvalues is now zero. At the defect center, the order parameter once again approximately takes the form of Equation (2). However, now the symmetry axis is the defect axis itself, and as compared with the bulk, the order parameter has changed its sign.
A more detailed analysis of the defect core, directly showing the degree of biaxiality, is given in Figure 3. There, we plot β2 across the defect center along z = 0 (Figures 3(a) and (b)) and x = 0 (Figures 3(c) and (d)). Figures 3(b) and (d) are the partial enlarged detail. At the defect center, β2 = 0. On increasing the distance ρ from the defect, the degree of biaxiality β2 at first gradually increases; it reaches its maximum value β2 = 1 at ρ ≈ 0.02d. Upon further increasing ρ, the uniaxial ordering with β2 = 0 is asymptotically approached, and the nematic can be described by the director field.
All of the above analysis indicates that there exists eigenvalue exchange across the defect core, where two uniaxial states with orthogonal directors are changed into each other through a transformation that does not involve any director rotation, but instead implies a wealth of biaxial configurations bridging the uniaxial limits.
 (a)
(a) (b)
(b)
Figure 2. Eigenvalues of Q along z = 0 (a) and x = 0 (b) across the s = 1/2 disclination in TN cell. The eigenvalues are scaled to the largest eigenvalue at the boundary.
3.2. s = 1/2 Disclination in TCN Cell
In the simulation of the s = 1/2 disclination in TCN, we choose κ = 0.4 that amount to the cholesteric pitch p0 ≌ 280 nm, corresponding to relatively strong chirality. According to [26,27], and the isotropic-cholesteric transition temperature given above, the most stable phases at τ = −1 is a nematic helical phase.
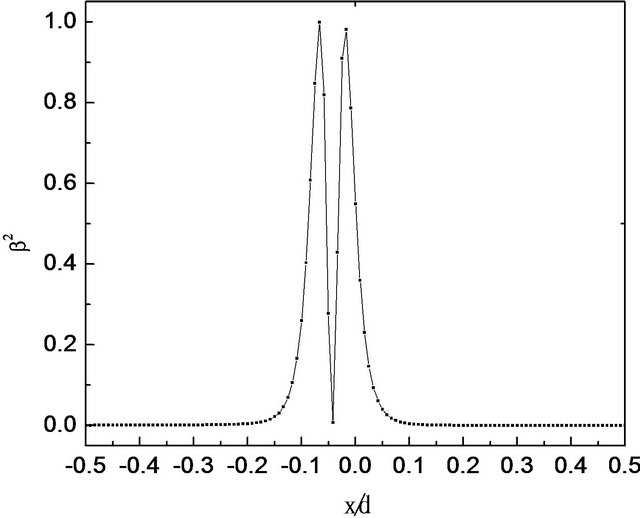
Figures 4-6 give the corresponding diagrams of director orientation “equiorientational” contours, eigenvalues of Q and biaxiality β2, respectively, which show the similar features as in TN cell. However, there are also subtle differences. Figure 4 shows that the position of the defect centre (xdef, zdef) is located at (−0.04167d, 0), rather than (0, 0), which results from the asymmetry distribution of the director at the system.
We should notice that Figure 4 gives the similar director orientation contours as that given by Scheffer based on the Frank theory [17], which confirms the correctness and rationality of our method.
4. Conclusions and Discussions
We carried out a numerical study on the structure of s =
 (a)
(a) (b)
(b)
Figure 3. Plot of β2 along z = 0 (a) and (b) and x = 0 (c) and (d) revealing the core structure of s = 1/2 disclinations in TN cell. (b) and (d) are the partial enlarged detail of (a) and (b) respectively.

Figure 4. Director orientation contours of s = 1/2 disclination in the x-z plane of TCN cell.
±1/2 twist disclinations in TN and TCN cells with 90˚ twisted structure, based on the Landau-de Gennes approach, in which the orientational order of the LC is taken into account by introducing a second-rank tensor order parameter. In numerical calculations, we chose a relatively low temterature τ = −1, where the nematic LCs are in deep nematic phase and respond to distortions by entering biaxial states, rather than melting [9]; while the most stable phase for chiral LC at τ = −1 is a helical phase, avoiding the emergence of blue phase [26,27].
We have confirmed that two symmetric twist distortions with equal elastic energy in the TN cell may give rise to steady twist disclinations with topological charge s = ±1/2; in the chiral LC model we proposed, the frustrations between the helical structure and the confining surfaces induce s = ±1/2 disclinations, which also appears in the Grandjean-Cano wedges [18-21].
The detailed analysis of the defect structures indicates that the defect core is essentially biaxial and never isotropic. In the very central core region, the nematic is uniaxial and constrained to lie in the direction of the disclination line; however, away from it, the texture is almost uniaxial and can approximately be described by the director field. Moreover, we can conclude that there exists eigenvalue exchange across the defect core of both TN and TCN cells, which confirms that eigenvalue
 (a)
(a)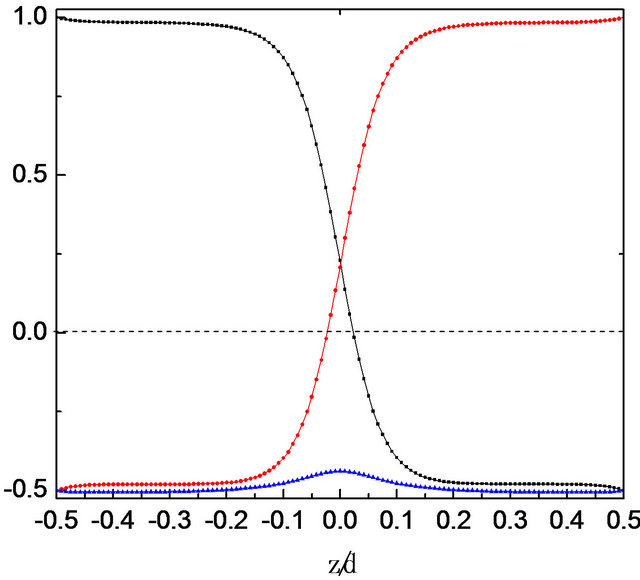 (b)
(b)
Figure 5. Eigenvalues of Q along z = 0 (a) and x = −0.04167d (b) across the s = 1/2 disclination in TCN cell. The eigenvalues are scaled to the largest eigenvalue at the boundary.
exchange is a generally existent phenomenon in defects.
A natural question is whether our simulation describes a realistic scenario within a nematic cell. When the LC is cooled down from the isotropic to the nematic phase within the cell, by symmetry breaking, line defects is formed and dominates the Scene [9,28]. Individual defects that are not too close to one another tend to straighten up to equalize the elastic distortions in their vicinity. By topological and energetic reasons, the most probable scenario is that a sequence of line defects in a given direction with alternating charges s = ±1/2 form disclination loops or terminate on the surface of the sample because of the prohibitive energy cost of the free line end [29,30]. However, the details of loop are well beyond the scope of our study. Our simulation describes reasonably well such an isolated and stabilized defect, where the y axis is set along the average local line defect (on a scale comparable to the cell thickness).
The defects we studied can be used to the operation of bistable LC devices (so-called bistable twisted nematics) that have attracted considerable attention over past few decades [31-34], and can be used for a better understanding of the defect structure in Grandjean-Cano wedges
 (a)
(a) (b)
(b)
Figure 6. Plot of β2 along z = 0 (a) and x = −0.04167d (b) revealing the core structure of s = 1/2 disclinations in TCN cell.
[18-21]. We should note that most of previous study on defects in Grandjean-Cano wedges have focused on the case in which the confining surfaces imposes parallel anchoring of the same direction, while our study provided the similar defect structures in the particular 90˚ twist cell.
It can be predicted that for the two models we proposed, the core size should be affected by the cell thickness of the TN cell, the chirality of chiral LC, as well as the temperature, the detailed results is the task for the future.
5. Acknowledgements
This research was supported by Natural Science Foundation of Hebei Province under Grant No. A2010000004 and Key Subject Construction Project of Hebei Province University.
REFERENCES
- N. D. Mermin, “Topological Theory of Defects,” Review Modern Physics, Vol. 51, No. 3, 1979, pp. 591-648. doi:10.1103/RevModPhys.51.591
- H.-R. Trebin, “The Topology of Non-Uniform Media in Condensed Matter Physics,” Advances in Physics, Vol. 31, No. 3, 1982, pp. 195-254.
- P. Chaikin and T. Lubensky, “Principles of Condensed Matter Physics,” Cambridge University Press, Cambridge, 1995.
- M. Kléman, “Points, Lines and Walls in: Liquid Crystals, Magnetic Systems and Various Disordered Media,” Wiley, New York, 1983.
- M. V. Kurik and O. D. Lavrentovich, “Defects in Liquid Crystals: Homotopy Theory and Experimental Studies,” Soviet Physics Uspekhi, Vol. 31, No. 3, 1988, pp. 196- 224.
- S. Kralj and E. G. Virga, “Universal Fine Structure of Nematic Hedgehogs,” Journal of Physics A, Vol. 34, No. 4, 2001, pp. 829-838.
- N. Schopohl and T. J. Sluckin, “Defect Core Structure in Nematic Liquid Crystals,” Physical Review Letters, Vol. 59, No. 22, 1987, pp. 2582-2584.
- R. Rosso and E. G. Virga, “Metastable Nematic Hedgehogs,” Journal of Physics A, Vol. 29, No. 14, 1996, pp. 4247-4264.
- S. Kralj, E. G. Virga and S. Žumer, “Biaxial Torus around Nematic Point Defects,” Physical Review E, Vol. 60, No. 2, 1999, pp. 1858-1866.
- M. Ambrožič, S. Kralj and E. G. Virga, “Defect-Enhanced Nematic Surface Order Reconstruction,” Physical Review E, Vol. 75, No. 3, 2007, pp. 1-9.
- R. Barberi, F. Ciuchi, G. E. Durand, M. Iovane, D. Sikharulidze, A. M. Sonnet and E. G. Virga, “Electric Field Induced Order Reconstruction in a Nematic Cell,” European Physical Journal E, Vol. 13, No. 1, 2004, pp. 61-71.
- S. Kralj, R. Rosso and E. G. Virga, “Finite-Size Effects on Order Reconstruction around Nematic Defects,” Physical Review E, Vol. 81, No. 2, 2010, pp. 1-15.
- D. Pires and Y. Galerne, “Recording of Virtual Disclination Lines by Means of Surface Polymerization in a Nematic Liquid Crystal,” Molecular Crystal and Liquid Crystals, Vol. 438, No. 1, 2005, pp. 1681-1686.
- P. G. De Gennes and J. Prost, “The Physics of Liquid Crystals,” Oxford University Press, Oxford, London, 1993.
- A. D. Kiselev and T. J. Sluckin, “Twist of Cholesteric Liquid Crystal Cells: Stability of Helical Structures and Anchoring Energy Effects,” Physical Review E, Vol. 71, No. 3, 2005, pp. 1-11.
- P. G. De Gennes, “Long Range Order and Thermal Fluctuations in Liquid Crystals,” Molecular Crystal and Liquid Crystals, Vol. 7, No. 1, 1969, pp. 325-345.
- T. J. Scheffer, “Structures and Energies of GrandjeanCano Liquid-Crystal Disclinations,” Physical Review A, Vol. 5, No. 3, 1972, pp. 1327-1336.
- I. I. Smalyukh and O. D. Lavrentovich, “Three-Dimensional Director Structures of Defects in Grandjean-Cano Wedges of Cholesteric Liquid Crystals Studied by Fluorescence Confocal Polarizing Microscopy,” Physical Review E, Vol. 66, No. 5, 2002, pp. 1-16.
- D. Engström, R. P. Trivedi, M. Persson, M. Goksör, K. A. Bertness and I. I. Smalyukh, “Three-Dimensional Imaging of Liquid Crystal Structures and Defects by Means of Holographic Manipulation of Colloidal Nanowires with Faceted Sidewalls,” Soft Matter, Vol. 7, No. 13, 2011, pp. 6304-6312.
- I. I. Smalyukh, S. V. Shiyanovskii and O. D. Lavrentovich, “Three-Dimensional Imaging of Orientational Order by Fluorescence Confocal Polarizing Microscopy,” Chemical Physics Letters, Vol. 336, No. 1-2, 2001, pp. 88-96.
- I. I. Smalyukh and O. D. Lavrentovich, “Anchoring-Mediated Interaction of Edge Dislocations with Bounding Surfaces in Confined Cholesteric Liquid Crystals,” Physical Review Letters, Vol. 90, No. 8, 2003, pp. 1-4.
- E. G. Virga, “Variational Theories for Liquid Crystals,” Chapman Hall, London, 1994.
- P. Kaiser, W. Wiese and S. Hess, “Stability and Instability of a Uniaxial Alignment against Biaxial Distortions in the Isotropic and Nematic Phases of Liquid Crystals,” Journal of Non-Equilibrium Thermodynamics, Vol. 17, No. 2, 1992, pp. 153-169.
- D. C. Wright and N. D. Mermin, “Mermin, Crystalline Liquids: The Blue Phases,” Reviews of Modern Physics, Vol. 61, No. 2, 1989, pp. 385-432.
- X. Zhou, Z. D. Zhang and L. Xuan, “Surface-Groove-Induced Boundary-Roughness Effects in Nematics: A Comparison between Models Allowing or Not,” Molecular Crystal and Liquid Crystals, Vol. 562, No. 1, 2012, pp. 66-75.
- J. Fukuda, “Stabilization of a Blue Phase by a Guest Component: An Approach Based on a Landau-de Gennes Theory,” Physical Review E, Vol. 82, No. 6, 2010, pp. 1-5.
- J. Fukuda and S. Žumer, “Ring Defects in a Strongly Confined Chiral Liquid Crystal,” Physical Review Letters, Vol. 106, No. 9, 2011, pp. 1-4.
- Z. Bradač, S. Kralj and S. Žumer, “Molecular Dynamics Study of the Isotropic-Nematic Quench,” Physical Review E, Vol. 65, No. 2, 2002, pp. 1-10.
- H. Mori and H. Nakanishi, “On the Stability of Topologically Non-Trivial Point Defects,” Journal of the Physical Society of Japan, Vol. 57, No. 4, 1988, pp. 1281- 1286.
- N. V. Priezjev and R. A. Pelcovits, “Disclination Loop Behavior near the Nematic-Isotropic Transition,” Physical Review E, Vol. 64, No. 3, 2001, pp. 1-7.
- Z. L. Xie and H. S. Kwok, “New Bistable Twisted Nematic Liquid Crystal Displays,” Journal of Applied Physics, Vol. 84, No. 1, 1998, pp. 77-82.
- Z. Zhuang, Y. J. Kim and J. S. Patel, “Bistable Twisted Nematic Liquid-Crystal Optical Switch,” Applied Physics Letters, Vol. 75, No. 19, 1999, pp. 3008-3010.
- Z. L. Xie, Y. M. Dong, S. Y. Xu, H. J. Gao and H. S. Kwok, “π/2 and 5π/2 Twisted Bistable Nematic Liquid Crystal Display,” Journal of Applied Physics, Vol. 87, No. 6, 2000, pp. 2673-2676.
- F. S. Y. Yeung and H. S. Kwok, “Truly Bistable Twisted Nematic Liquid Crystal Display Using Photoalignment Technology,” Applied Physics Letters, Vol. 83, No. 21, 2003, pp. 4291-4293.
Appendix A: The Helical Structures of Chiral LCs with 90˚ Twist Structure
The Frank elastic energy density of Chiral LCs can be described in terms of n as
 (A.1)
(A.1)
where Ks is the surface-like elastic constant. The director  of chiral LCs is written as
of chiral LCs is written as
 (A.2)
(A.2)
with by . Equation (A.2) gives
. Equation (A.2) gives
 (A.3)
(A.3)
 (A.4)
(A.4)
 (A.5)
(A.5)
 (A.6)
(A.6)
Substituting Equations (A.3-A.6) into (A.1) leads to
 (A.7)
(A.7)
The Euler-Lagrange equation is
 (A.8)
(A.8)
The general solution of Equation (A.8) is
 (A.9)
(A.9)
with boundary conditions
 (A.10)
(A.10)
Through simple calculation we can get
 (A.11)
(A.11)
When , the Frank elastic energy density is
, the Frank elastic energy density is
 (A.12)
(A.12)
Apparently, m = 1 and m = 0 have the same and the lowest energy,  , i.e., for the condition we considered, the two helical structures
, i.e., for the condition we considered, the two helical structures  and
and  have the same and lowest energy.
have the same and lowest energy.

