Journal of Modern Physics
Vol.3 No.11(2012), Article ID:24867,11 pages DOI:10.4236/jmp.2012.311225
Born Rule and Noncontextual Probability
1INO-CNR BEC Center and Physics Department, Trento University, Povo, Italy
2QSTAR, INO-CNR and LENS, Largo Enrico Fermi, Firenze, Italy
Email: *log@science.unitn.it
Received September 2, 2012; revised October 2, 2012; accepted October 10, 2012
Keywords: Born Rule; Non Contextual Probability
ABSTRACT
We present a new derivation of the Born rule from the assumption of noncontextual probability (NCP). Within the theorem we also demonstrate the continuity of probability with respect to the amplitudes, which has been suggested to be a gap in Zurek’s and Deutsch’s approaches, and we show that NCP is implicitly postulated also in their derivations. Finally, physical motivations of NCP are given based on an invariance principle with respect to a resolution change of measurements and with respect to the principle of no-faster-than-light signalling.
1. Introduction
The fundamental probabilistic postulate which allows QM its successful predictions was first introduced by Born (from a suggestion by Einstein) in 1926 within the scattering theory [1]. The question if such postulate could be derived as a theorem from other postulates of QM was quickly posed. A first answer was provided by Von Neumann and included in his famous book of 1932 on the mathematical foundations of QM [2]. His theorem nowadays does not enjoy much attention since it is believed to contain more assumptions than Gleason’s [3,4]. Different attempts have been discussed in the context of the relative-state [5] and the many-worlds interpretations [6] of QM by Finkelstein [7] and Hartle [8], which have analyzed an endless sequence of measurements to show that the relative frequency follows the Born rule. However, the meaning in the real world of an infinite sequence of measurements is controversial and it is doubtful whether these proofs contain circularities [9-14].
The 1957 Gleason work [4] is regarded as the most important derivation of the Born rule [15], but this theorem is usually considered quite formal and difficult to grasp. Moreover, it is based on the concept of noncontextual probability (NCP), whose connection with physics is not clear. In the structure of the Gleason theorem, every Hilbert subspace 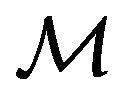 corresponds to an observable quantity. Each one of such subspaces is representable by a projection operator
corresponds to an observable quantity. Each one of such subspaces is representable by a projection operator . A projector
. A projector  can represent the question with answer yes or not concerning an experiment testing whether the system has the respective state
can represent the question with answer yes or not concerning an experiment testing whether the system has the respective state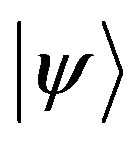 . A complete set of mutually commuting projectors
. A complete set of mutually commuting projectors  corresponds to a set of questions which can simultaneously be asked in a measurement. In the logical-algebraic approach [16], probability is a measure defined over a projection lattice (set of closed subspaces) of Hilbert space
corresponds to a set of questions which can simultaneously be asked in a measurement. In the logical-algebraic approach [16], probability is a measure defined over a projection lattice (set of closed subspaces) of Hilbert space , a mapping
, a mapping . The postulates on which the theorem rests are:
. The postulates on which the theorem rests are:
1) The probability assigned to a complete set of 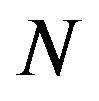 projectors
projectors  is normalized:
is normalized:
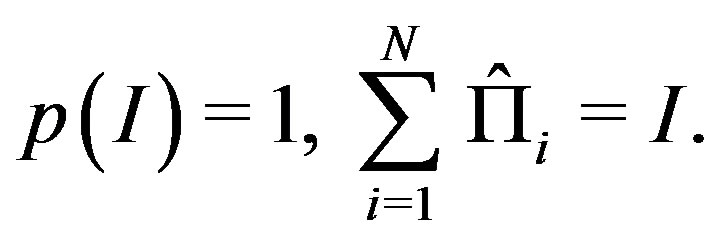 (1)
(1)
2) For any sequence of  mutually orthogonal projectors:
mutually orthogonal projectors:
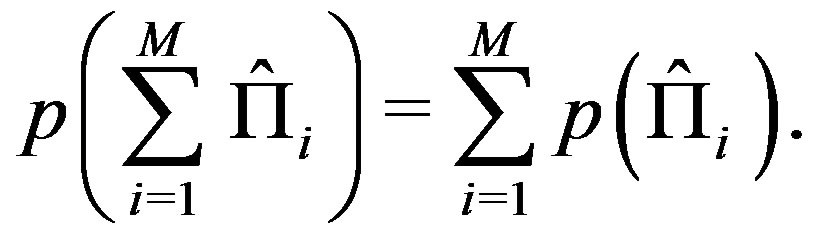 (2)
(2)
Assuming Postulate 2) is equivalent to postulating NCP for projective measurements (or, i.e., according to the definition by Spekkens, measurement noncontextuality [17]): the probability of a certain occurrence, for example the answer yes for a projector, does not depend on other questions simultaneously tested, that is, on other projectors. In terms of basis vectors, the probability of obtaining a given state is independent of the basis it belongs to. To illustrate this important point, let us consider, for instance, two complete set of mutually orthogonal projectors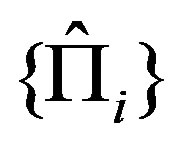 ,
,  with
with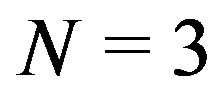 , where
, where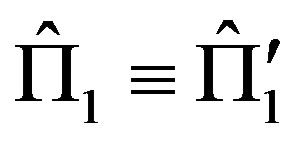 . From the normalization postulate of probability:
. From the normalization postulate of probability:
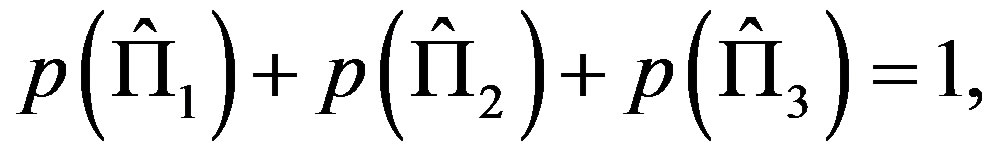 (3)
(3)
 (4)
(4)
where in principle 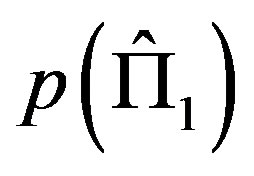 and
and 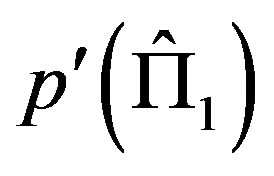 may be different. In the subspace orthogonal to
may be different. In the subspace orthogonal to  we have
we have
 , then
, then 
and from Postulate 2:
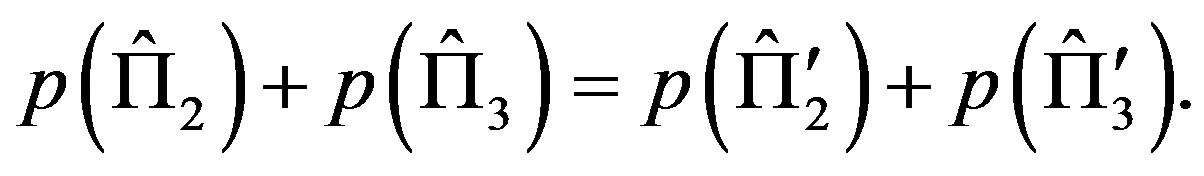 (5)
(5)
Then, by comparing Equation (3) and Equation (4), we get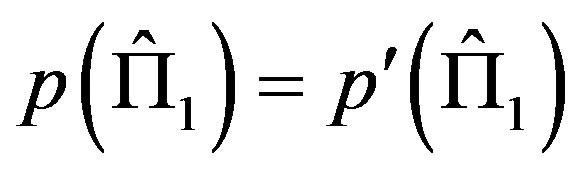 . It is also possible to show the vice versa, i.e, if NCP holds then Postulate 2 is true.
. It is also possible to show the vice versa, i.e, if NCP holds then Postulate 2 is true.
From Postulates 1 and 2 it follows Gleason’s Theorem: For a Hilbert space with dimension  there exists a density operator
there exists a density operator  which acts on
which acts on 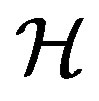 such that the probability measure for every projector
such that the probability measure for every projector  is the trace rule:
is the trace rule:
 (6)
(6)
namely, the Born rule.
More recently, new proofs appeared in the literature with the intention of being “more physically motivated than the theorem of Gleason” [18]. Their aim, as the ours in the present work, is to shed new light on the physical principles of QM, particularly on the origin of the Born rule. Indeed, Gleason’s theorem gives “rather little insight into the emergence of quantum probabilities and the Born rule” [19].
Particularly interesting are Deutsch’s and Zurek’s derivations [18,20-25]. Their approaches to the Born rule have similar structures. As a first step, they use an invariance principle in order to show that equal amplitudes correspond to equal probabilities. Deutsch finds such principle in the theory of decisions (for critical discussions and further elaborations see [26-28]). Zurek introduces an environment-assisted invariance principle [29,30], envariance, in the framework of a relative-state approach where the system  under measurement jointly evolves with the environment
under measurement jointly evolves with the environment  and, possibly, with one or more auxiliary measurement devices. After demonstrating the correspondence between equal amplitudes and equal probabilities, both Zurek and Deutsch consider a finegraining technique to deal with the general case of different amplitudes of the initial state. For this purpose they have to introduce auxiliary systems which become entangled with
and, possibly, with one or more auxiliary measurement devices. After demonstrating the correspondence between equal amplitudes and equal probabilities, both Zurek and Deutsch consider a finegraining technique to deal with the general case of different amplitudes of the initial state. For this purpose they have to introduce auxiliary systems which become entangled with .
.
However, fine-graining has been questioned: Caves [23] considers disturbing the necessity of introducing additional systems of adequate dimensions, possibly in an infinite Hilbert space, in order to reach the wanted approximation to irrational probabilities. Barnum [25] points out an even more stringent weakness: the step from rational to irrational amplitudes requires the continuity of the probability with respect to such amplitudes and such a property is not demonstrated by Zurek and Deutsch. We note that a fundamental and extensive part of Gleason’s theorem is actually devoted to prove that the probability is continuous. For several other controversial points of Zurek’s demonstration, the most of them shares with Deutsch’s, we refer to [19,23-25].
So, although Gleason-type theorems are usually considered well established, a simple, physically justified and shared derivation of the Born rule is not yet present in the literature. With our work we intend to fill this gap.
In the next section we propose a new derivation of the Born rule from the NCP assumption for projective measurements and pure states, the generalization to mixed states being immediate. Whereas Gleason assumes that a density operator acting on  describes a general quantum state of the system only at the final step of his work, we introduce vectors of the Hilbert space describing quantum states from the very beginning of our derivation. On the one hand it allows a much more elementary deduction of the Born rule, and on the other hand it makes the postulates and the physical principles of our theorem easier to analyze in comparison with the previous demonstrations. Moreover, involving Zurek’s and Deutsch’s demonstrations pure states, also the connections between those works, the Gleason Theorem and the ours are clearer.
describes a general quantum state of the system only at the final step of his work, we introduce vectors of the Hilbert space describing quantum states from the very beginning of our derivation. On the one hand it allows a much more elementary deduction of the Born rule, and on the other hand it makes the postulates and the physical principles of our theorem easier to analyze in comparison with the previous demonstrations. Moreover, involving Zurek’s and Deutsch’s demonstrations pure states, also the connections between those works, the Gleason Theorem and the ours are clearer.
We do not enter into the controversy about the origin and the meaning of probability, and following Gleason and others (see also Mohrhoff in [24]), we assume the existence of probability defined on a quantum state. In addition, differently by Zurek, we do not suppose unitary evolution and consider a single system. As Gleason’s Theorem, our result holds for a Hilbert space with , whereas in general, because of fine-graining, Zurek’s and Deutsch’s hold for
, whereas in general, because of fine-graining, Zurek’s and Deutsch’s hold for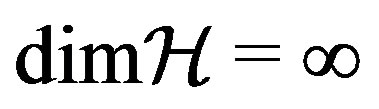 . We also give a rather simple derivation that the probability is continuous from NCP. Without this proof, Deutch’s and Zurek’s results only hold for rational values of amplitudes.
. We also give a rather simple derivation that the probability is continuous from NCP. Without this proof, Deutch’s and Zurek’s results only hold for rational values of amplitudes.
In Section III we generalize our theorem to include entangled states and multi-particles systems. Since the Hilbert space  of such systems has dimension which is the product of the dimensions of its components, the coupling of a subsystem with
of such systems has dimension which is the product of the dimensions of its components, the coupling of a subsystem with 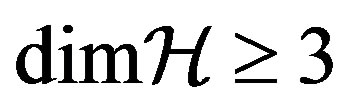 with another subsystem with
with another subsystem with 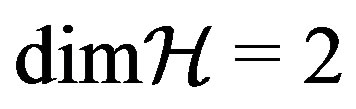 enables us to extend the Born rule also to such space.
enables us to extend the Born rule also to such space.
In Section IV we show that the Gleason postulate of NCP occurs in the use of fine-graining and that such a postulate is a hidden assumption of Zurek’s and Deutsch’s proofs. Indeed, fine-graining is a resolution change of our measurements and NCP is equivalent to a condition of invariance with respect to such a change: finegraining on a subspace of the state must not alter the probability of finding the system in a different subspace. This resolution invariance is an intuitive and physically natural interpretation of measurement noncontextuality.
Finally, in Section V, we show that the condition of noncontextual probability, or resolution invariance, can also be deduced by the hypothesis of no-faster-than-light signalling of the Special Relativity.
2. Born Rule as a Theorem from Noncontextual Probability
Contrarily to the principles of classical mechanics, the axioms of QM do not have an equally shared and clear formulation. We do not want to enter into such a thorny issue, related to the interpretative problems of QM. For our purpose, from the quantum postulates generally considered in standard presentations of QM (see, e.g., [31-34]), we can extract the following common assumptions:
Postulate I:
At the time  the state of every physical system
the state of every physical system  is described by a normalized vector
is described by a normalized vector 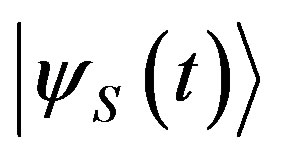 belonging to a Hilbert space
belonging to a Hilbert space .
.
Postulate II:
Every measurable physical quantity  is described by a Hermitian operator
is described by a Hermitian operator  acting in
acting in .
.
Postulate III:
The only possible result of a measurement of an observable  is one of the eigenvalues
is one of the eigenvalues 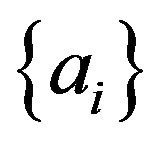 of
of , (as the customary habit, from now on we will identify the observable with its operator).
, (as the customary habit, from now on we will identify the observable with its operator).
Postulate IV:
If the measurement of the observable  on the system in the state
on the system in the state 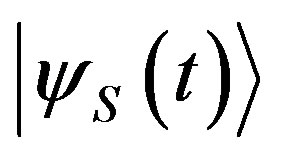 gives the result
gives the result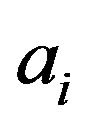 , the state of the system immediately after the measurement is the associate normalized eigenstate
, the state of the system immediately after the measurement is the associate normalized eigenstate  (non-degenerate case).
(non-degenerate case).
Postulate I is known as the Completeness Postulate of QM. Postulate II links an observable quantity with an operator in a Hilbert space (observable-operator link). Postulate III connects a particular value of that observable with an eigenvalue of the corresponding operator (value-eigenvalue link). Postulate IV relates a detected eigenvalue with the state of the system (eigenvalueeigenstate link).
Now consider a Hermitian observable  with discrete eigenvalues
with discrete eigenvalues 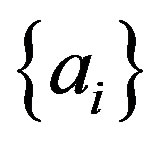 and eigenstates
and eigenstates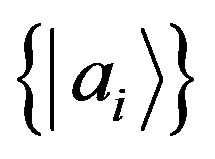 ,
, 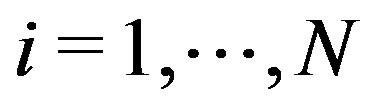 , and a single system
, and a single system 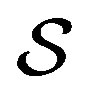 described by the state
described by the state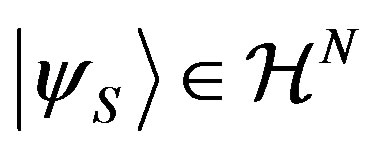 .
. 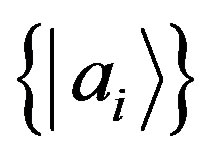 is a complete orthonormal set and
is a complete orthonormal set and 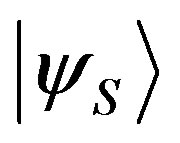 can be decomposed into components:
can be decomposed into components:
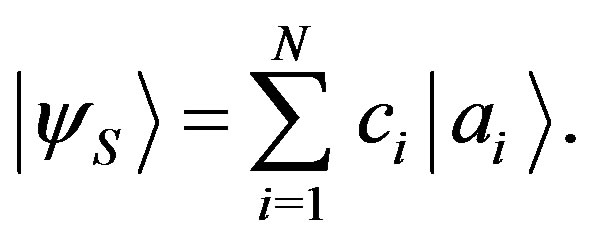 (7)
(7)
We intend to prove the following
Theorem 1:
If NCP and Postulates I-IV hold, then for 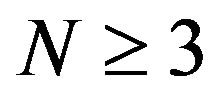 the probability of obtaining the non-degenerate eigenvalue
the probability of obtaining the non-degenerate eigenvalue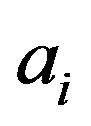 , measuring
, measuring  on the state
on the state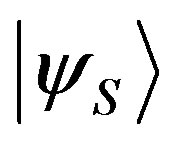 , is necessarily given by the square modulus of the inner product:
, is necessarily given by the square modulus of the inner product:
 (8)
(8)
where  is the eigenstate associated with the eigenvalue
is the eigenstate associated with the eigenvalue .
.
We assume the probability as a primitive concept and we begin the derivation of Theorem 1 by proving some simple lemmas. We underline that any theorem having the aim to prove the Born rule has to face the fact that the connection between probability and quantum state must be postulated or deduced by other means. Gleason, for instance, postulates the probability to be a measure defined on states of the basis. As Gleason, we suppose QM to be a probabilistic theory, which makes predictions about probabilities of occurrences of observable quantities, and that probabilities are functions of quantum states. Then, from QM postulates we want to show that
Lemma 1:
The probability of obtaining an eigenvalue  is equal to the probability of obtaining the respective eigenstate
is equal to the probability of obtaining the respective eigenstate 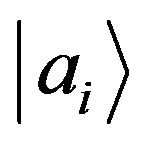 (statistical case):
(statistical case):
 (9)
(9)
wang#title3_4:spProof:
Suppose that the system is prepared with the eigenvalue , in this case
, in this case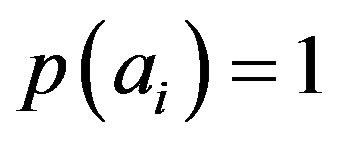 . According to Postulate IV if
. According to Postulate IV if 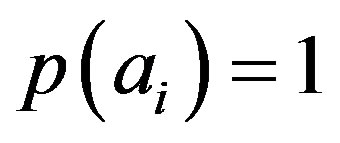 then
then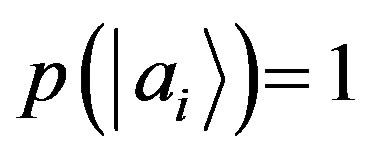 , and vice versa. But
, and vice versa. But  correspond to mutually exclusive events, thus has to be
correspond to mutually exclusive events, thus has to be  for
for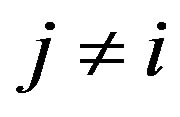 . Then must necessarily be
. Then must necessarily be 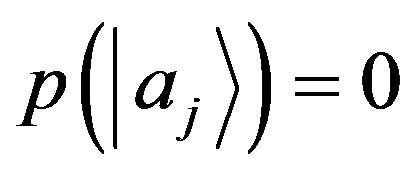 too, since, otherwise, having obtained with a measurement the state
too, since, otherwise, having obtained with a measurement the state 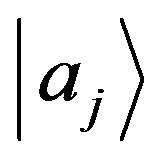 we should assign to the system the eigenvalue
we should assign to the system the eigenvalue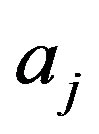 , in contradiction with the exclusivity property of
, in contradiction with the exclusivity property of 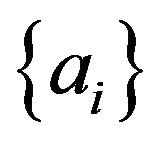 events. Therefore we have the equations for the conditional probabilities for a non-statistical case:
events. Therefore we have the equations for the conditional probabilities for a non-statistical case:
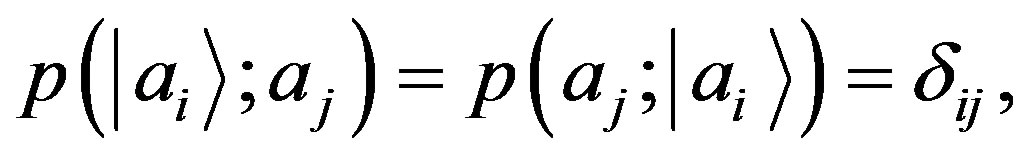 (10)
(10)
which represent the probability of finding the state 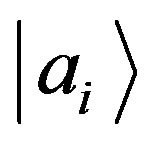 for systems prepared with certainty with eigenvalue
for systems prepared with certainty with eigenvalue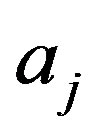 , and vice versa. Because of Postulate III, the only possible result of a measurement is one of the eigenvalues of
, and vice versa. Because of Postulate III, the only possible result of a measurement is one of the eigenvalues of . Consider then a generic preparation
. Consider then a generic preparation 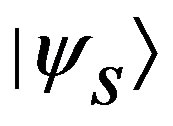 of the initial state with
of the initial state with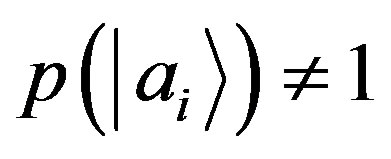 . Introducing the joint probability
. Introducing the joint probability 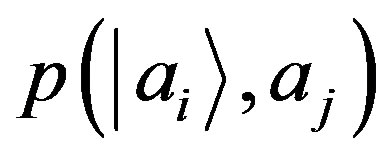 and considering the general validity of the Bayesian formula for the joint probabilities
and considering the general validity of the Bayesian formula for the joint probabilities , we have
, we have
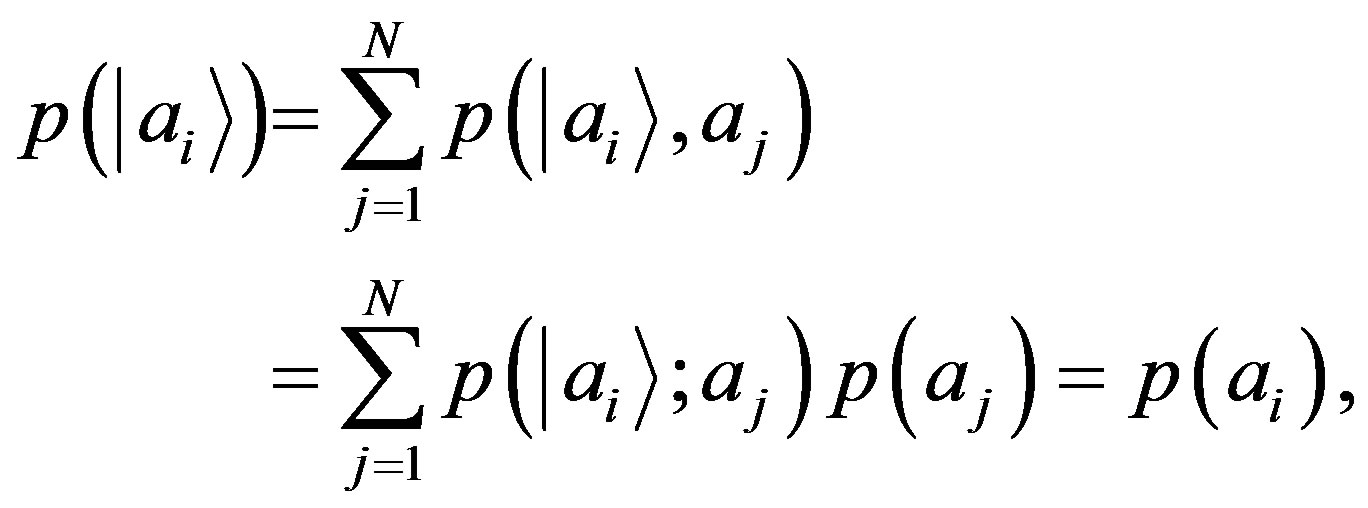 (11)
(11)
where we have used Equation (10) in the conditional probabilities of Equation (11).
We note from Equations (10) and (11) that
 and that
and that  represent a set of complete and mutually exclusive events:
represent a set of complete and mutually exclusive events:
 (12)
(12)
Lemma 1 can be easily generalized for entangled states as well. For instance, consider the state:
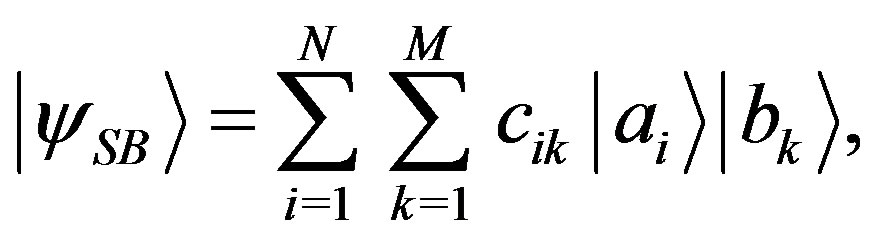 (13)
(13)
where  is a new observable commuting with
is a new observable commuting with , with eigenvalues
, with eigenvalues 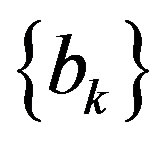 and eigenstates
and eigenstates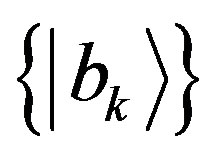 ,
, 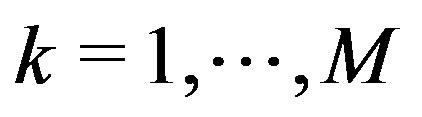 , and
, and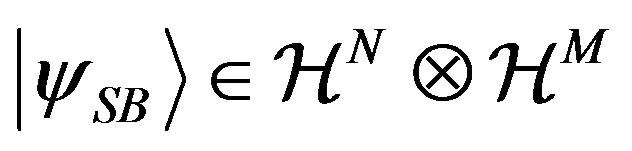 , (we point out that
, (we point out that  does not necessarily have to belong to another system: for example,
does not necessarily have to belong to another system: for example,  could be the spin observable and
could be the spin observable and 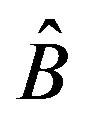 the position observable of one particle). Consider the pairs of eigenvalues
the position observable of one particle). Consider the pairs of eigenvalues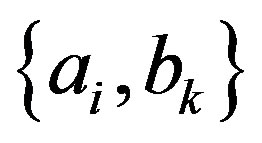 , and eigenstates
, and eigenstates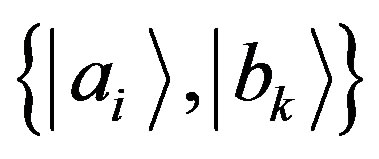 . By using conditional probabilities, it follows that on the generic state
. By using conditional probabilities, it follows that on the generic state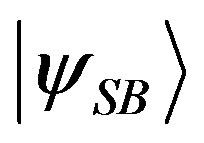 :
:
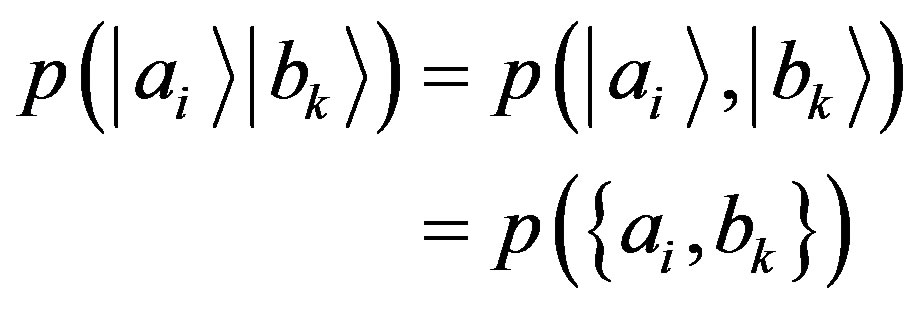 (14)
(14)
(see Appendix A for a proof of this). Then the probability 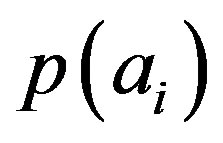 is again given by:
is again given by:
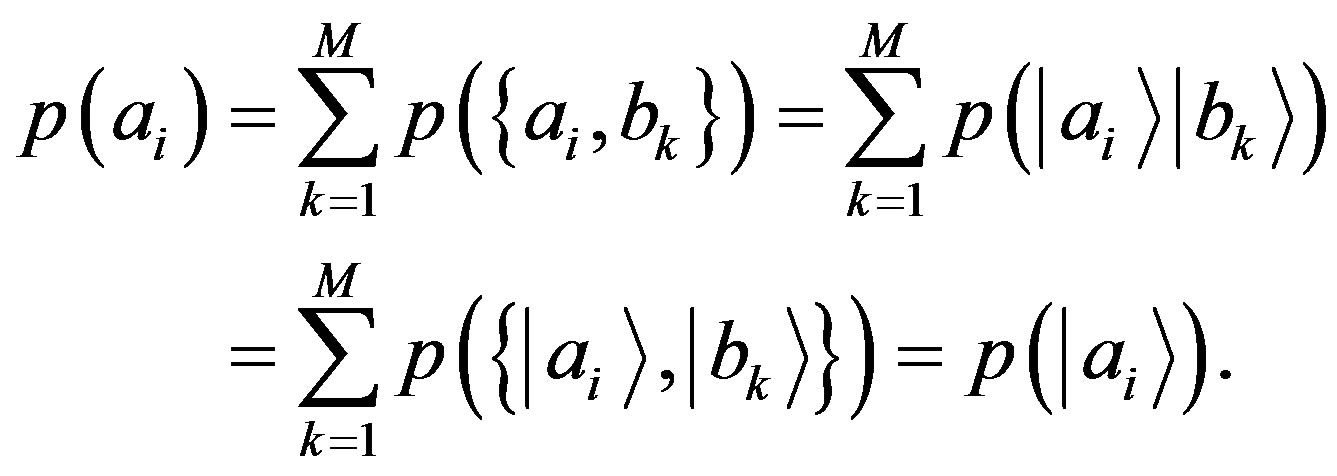 (15)
(15)
With a similar reasoning we can also show that . We notice from Equations (14) and (15) that the outcomes of
. We notice from Equations (14) and (15) that the outcomes of 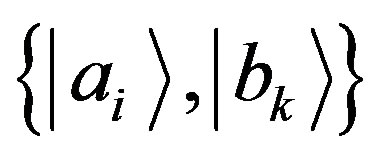 are mutually exclusive events as well, with the condition of normalization following from the normalization of
are mutually exclusive events as well, with the condition of normalization following from the normalization of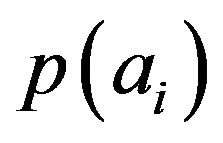 .
.
Lemma 2: If a coefficient of an eigenstate in Equation (7) is zero, the probability of obtaining the corresponding eigenvalue and eigenstate is zero as well.
Proof: If, for instance,  , the corresponding state
, the corresponding state  will be orthogonal to
will be orthogonal to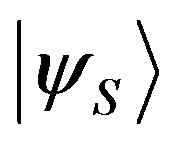 . We can think
. We can think 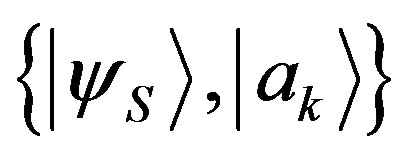 as eigenstates of the projector
as eigenstates of the projector
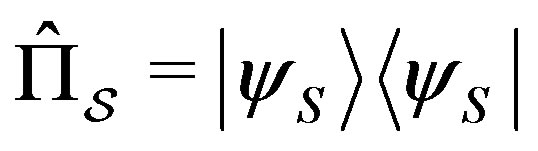 with eigenvalues
with eigenvalues . The Hermitian operator
. The Hermitian operator 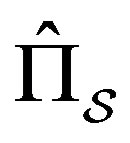 represents the observable testing whether the system
represents the observable testing whether the system  is prepared with the state
is prepared with the state  or not.
or not.
The pair 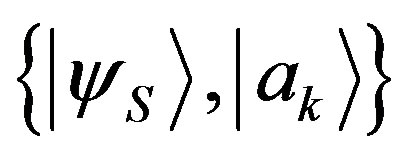 is a complete orthonormal basis of a subspace
is a complete orthonormal basis of a subspace  of
of .
.
With the system prepared in the state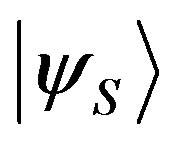 :
:
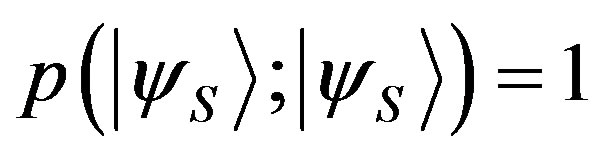 . From Lemma 1, it follows that
. From Lemma 1, it follows that
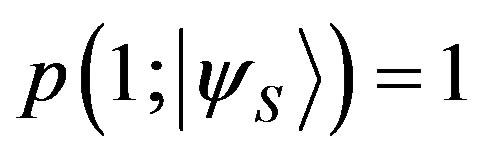 and because eigenvalues are exclusive events
and because eigenvalues are exclusive events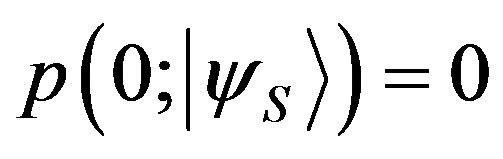 . So, if we apply Lemma 1 again to the previous equation, considering that
. So, if we apply Lemma 1 again to the previous equation, considering that  is eigenstate of both
is eigenstate of both 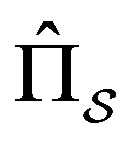 and
and , we have
, we have 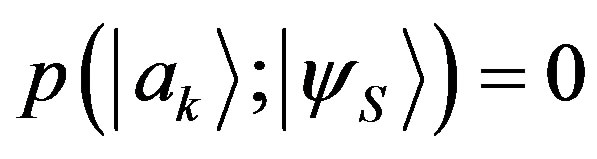
and .
.
Also Lemma 2 can be directly generalized to entangled states. For instance, if in the state  the coefficient
the coefficient 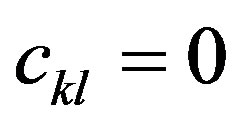 then
then . In particular, if the state of the system is in a Schmidt decomposition:
. In particular, if the state of the system is in a Schmidt decomposition:
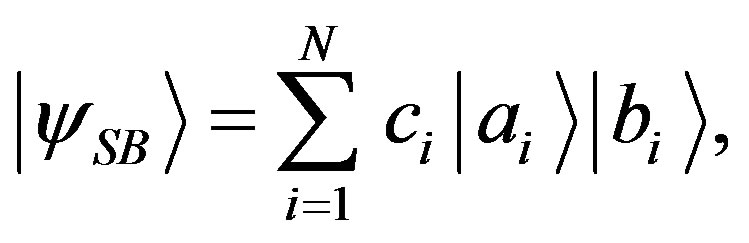 (16)
(16)
from Lemma 1 and Lemma 2, since  for
for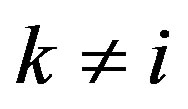 , it follows the perfect correlation property
, it follows the perfect correlation property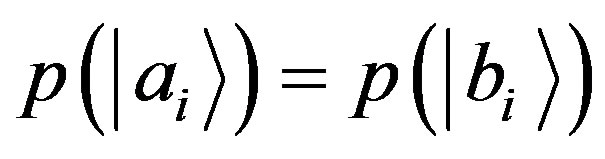 :
:
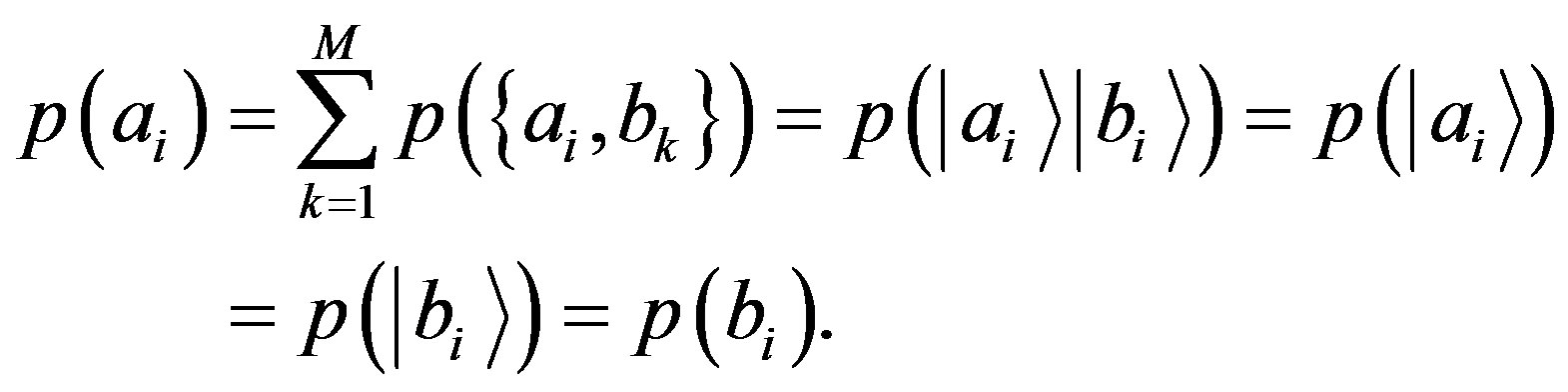 (17)
(17)
Lemma 3:
If the measurement is noncontextual then the probability of obtaining the eigenvalue 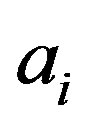 can only depend on the modulus of the coefficient
can only depend on the modulus of the coefficient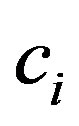 :
:
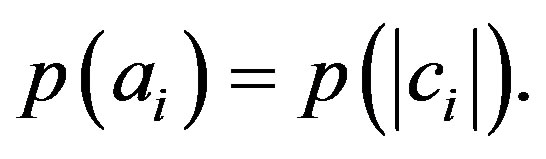 (18)
(18)
wang#title3_4:spProof:
Let us recall the meaning of NCP with an example (we refer to the work by Spekkens for an extensive analysis of the contextuality concept in arbitrary operational theories and in QM [17]). Consider two operators  and
and 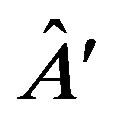 which do not commute, [
which do not commute, [ ]
] 0, in a Hilbert space with
0, in a Hilbert space with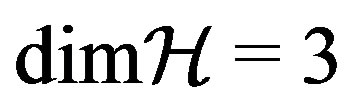 . Eigenvalues and eigenstates of
. Eigenvalues and eigenstates of  and
and  are, respectively:
are, respectively:
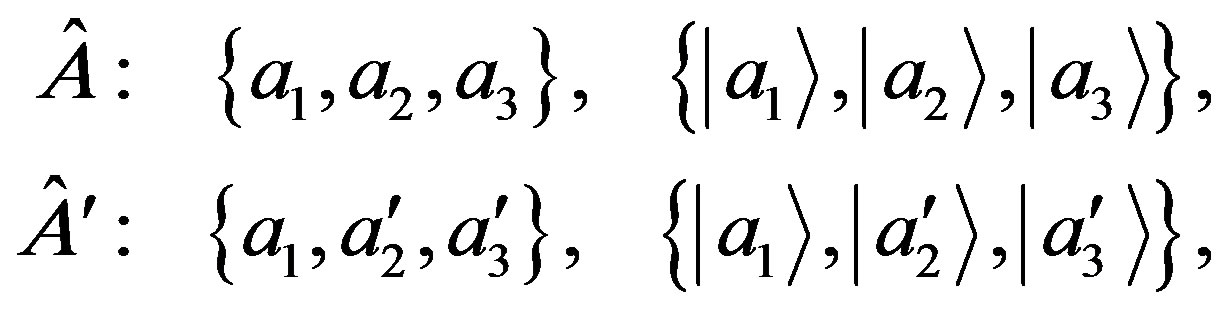 (19)
(19)
where they have in common the eigenvalue 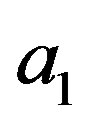 and the associate eigenstate (we see that this is possible, if
and the associate eigenstate (we see that this is possible, if  and
and  must not commute, just for
must not commute, just for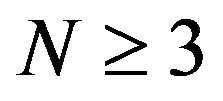 ). We can write the state
). We can write the state 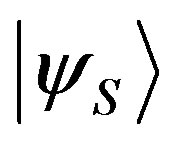 in the two different bases of Equation (19):
in the two different bases of Equation (19):
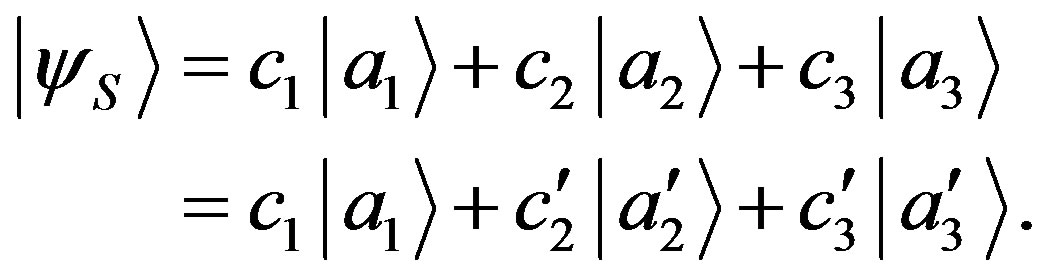 (20)
(20)
In general, the probability of obtaining the eigenvalue  could depend on whether we measure the observable
could depend on whether we measure the observable  or
or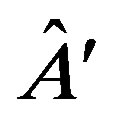 . In other words, the probability
. In other words, the probability 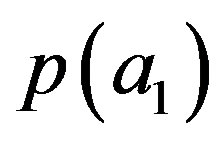 could be different if we were in the experimental context which is prepared for measuring which value
could be different if we were in the experimental context which is prepared for measuring which value  assumes of the triplet
assumes of the triplet  or which value
or which value 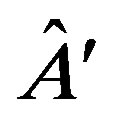 assumes of the triple
assumes of the triple .
.
With the result of Lemma 1 and the completeness postulate of QM, we can write the more general probability in different experimental contexts as:
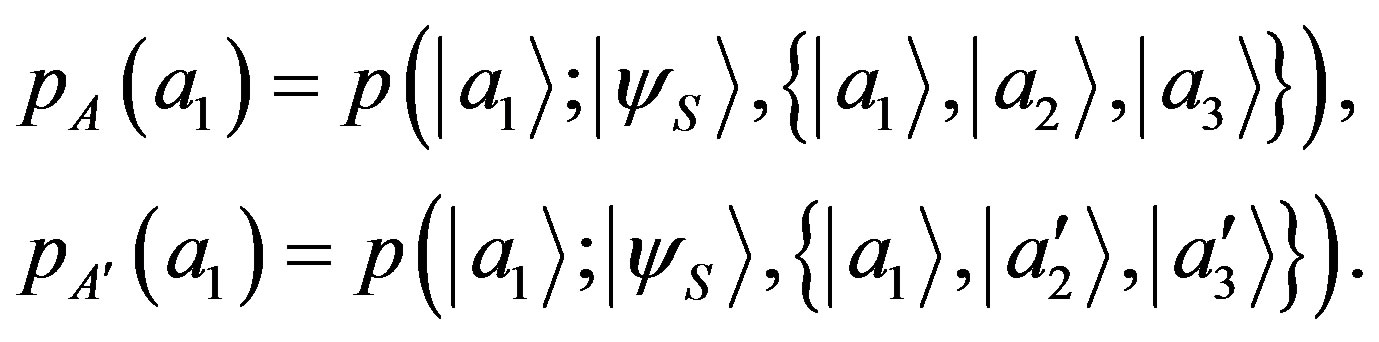 (21)
(21)
The probability is noncontextual, and we have measurement noncontextuality, if 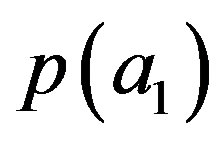 does not depend on the measurement with other eigenvalues:
does not depend on the measurement with other eigenvalues:
 (22)
(22)
or, according to Lemma 1, the probability 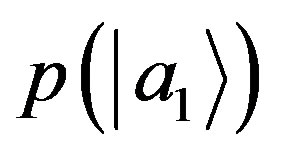 does not depend on the measurement with other eigenstates:
does not depend on the measurement with other eigenstates:
 (23)
(23)
Then, by assuming NCP, Equations (21) can be reduced to the equation:
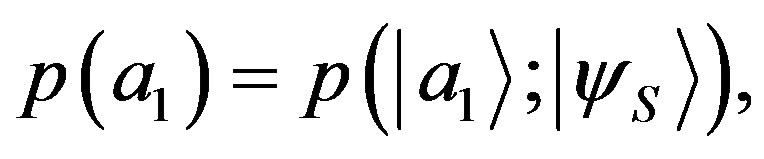 (24)
(24)
stating that the probability only depends on the eigenstate  and, from the completeness postulate of QM and NCP, on the state of the system
and, from the completeness postulate of QM and NCP, on the state of the system .
.
Thus, let us choose a new basis  such that the state in Equation (7) is written with only two components:
such that the state in Equation (7) is written with only two components:
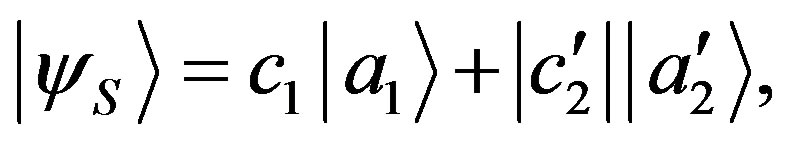 (25)
(25)
where 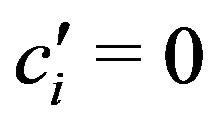 for
for ,
, 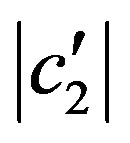 is the modulus of the amplitude
is the modulus of the amplitude 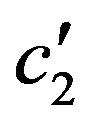 and
and
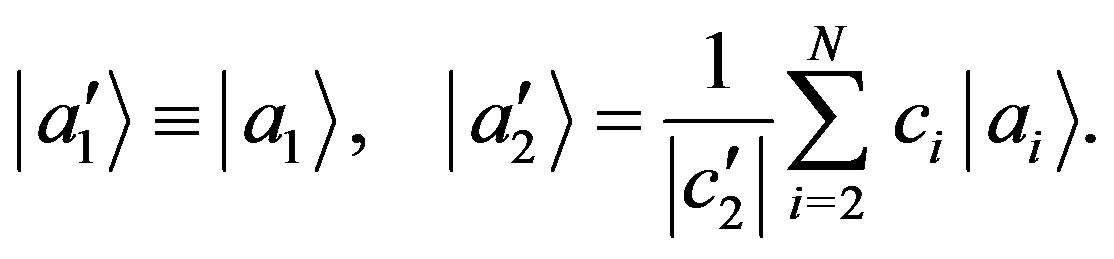 (26)
(26)
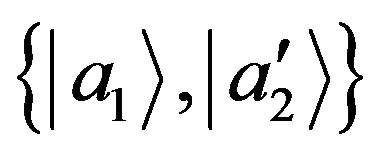 could be regarded as eigenstates of an observable
could be regarded as eigenstates of an observable 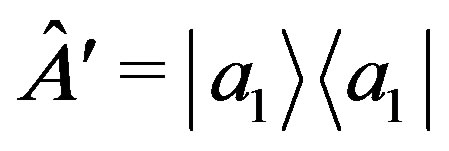 with eigenvalues
with eigenvalues 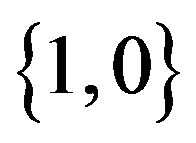 checking whether our system is in the state
checking whether our system is in the state 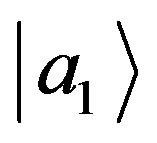 or not.
or not.
According to NCP the transformation of basis 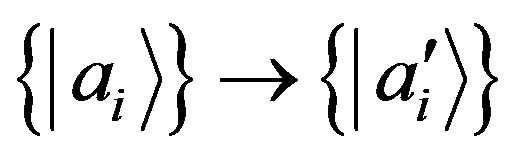 of the state cannot change the probability:
of the state cannot change the probability:
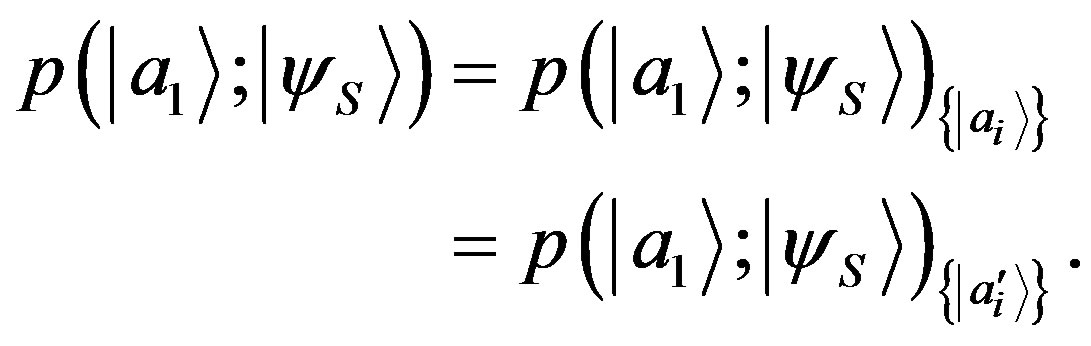 (27)
(27)
Now we expressly write the phase of the coefficient  in the state of Equation (25):
in the state of Equation (25):
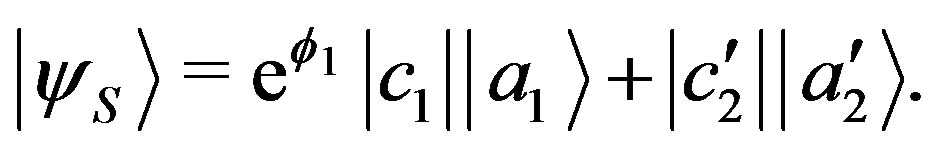 (28)
(28)
We get for the state 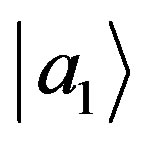 the probability:
the probability:
 (29)
(29)
Therefore, considering the normalization 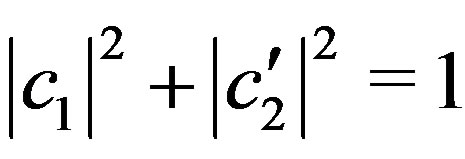 and that the components of the orthonormal basis are the constants
and that the components of the orthonormal basis are the constants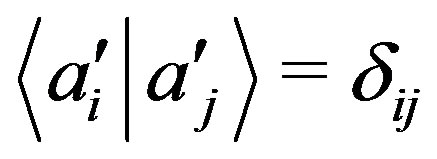 , the most general function of the probability in Equation (29) can be written as:
, the most general function of the probability in Equation (29) can be written as:
 (30)
(30)
A similar argument when applied to every state 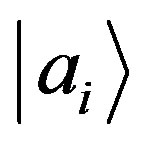 gives
gives
 (31)
(31)
However, by using the conservation of probability we can show the independence from the phase of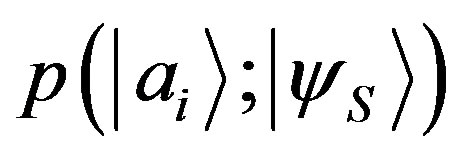 . Indeed, let us suppose to have two different states
. Indeed, let us suppose to have two different states  and
and 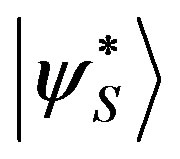 which are distinct just with respect to the phase of the component
which are distinct just with respect to the phase of the component 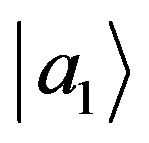 (to simplify the notation, we select a basis such that the components of the states are different from zero only in a subspace with
(to simplify the notation, we select a basis such that the components of the states are different from zero only in a subspace with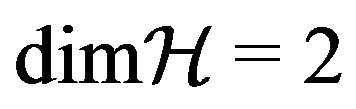 ):
):
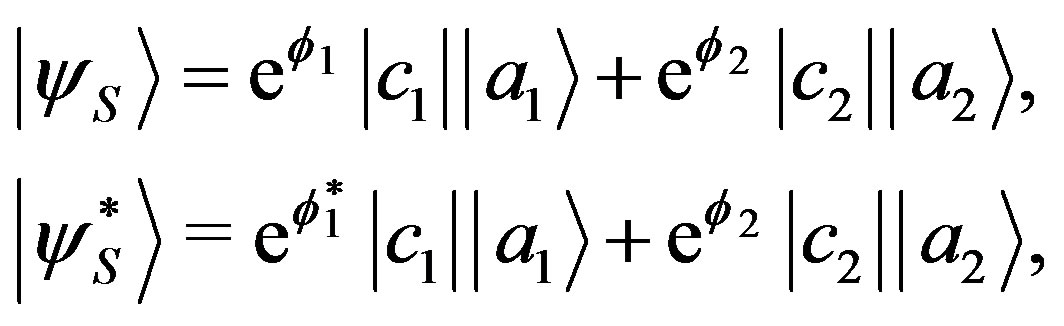 (32)
(32)
where with  we have denoted the new phase. The conservation of the probability requires:
we have denoted the new phase. The conservation of the probability requires:
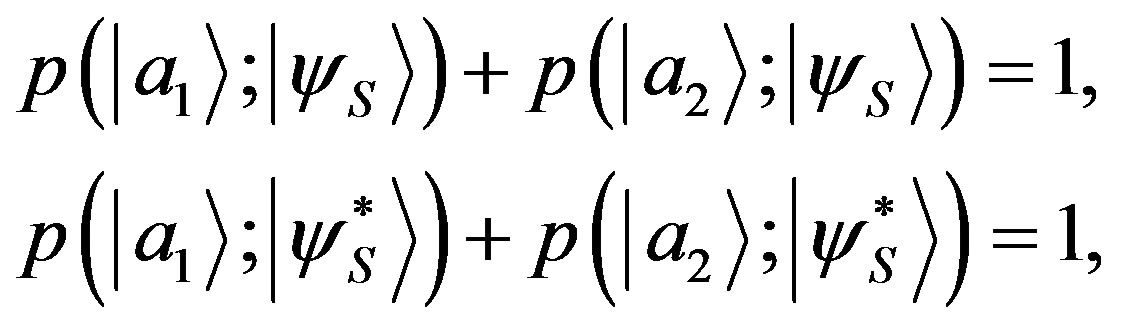 (33)
(33)
where from Lemma 2 we have used the fact that  if
if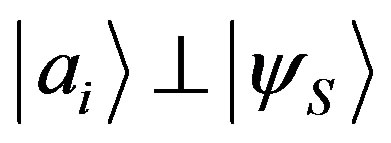 . Thanks to Equation (31), we have that
. Thanks to Equation (31), we have that
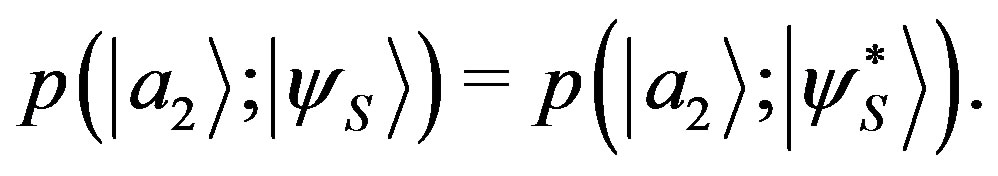 (34)
(34)
From this and Equation (33), we also get:
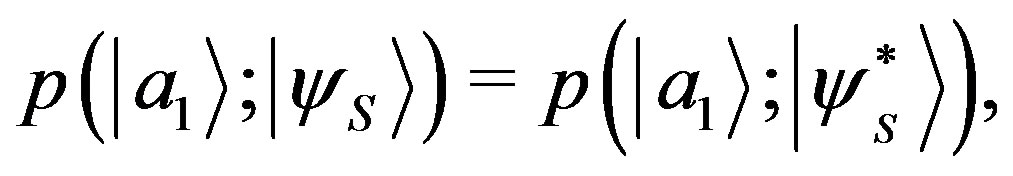 (35)
(35)
which is equivalent to write:
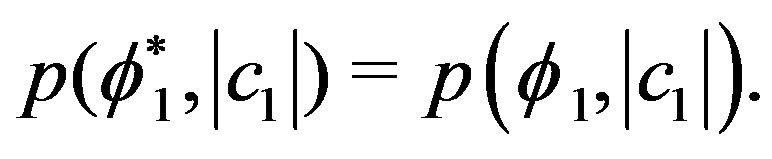 (36)
(36)
Therefore, since 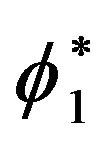 is an arbitrary phase, the probability
is an arbitrary phase, the probability  does not depend on it but can only depend on the modulus
does not depend on it but can only depend on the modulus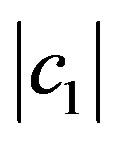 . So, we can set
. So, we can set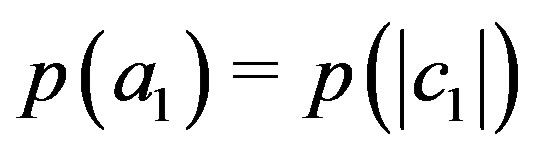 , and this proves our lemma (the generalization to probabilities of other eigenvalues
, and this proves our lemma (the generalization to probabilities of other eigenvalues  is immediate).
is immediate).
Now we have all the ingredients to prove our
Theorem 1:
the probability  is given by the square modulus of coefficient
is given by the square modulus of coefficient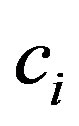 .
.
Proof:
Let us consider the state 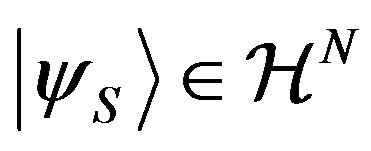 with
with  in Equations (7). For the sake of simplicity we focus our attention again on
in Equations (7). For the sake of simplicity we focus our attention again on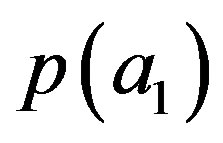 . We choose two bases
. We choose two bases 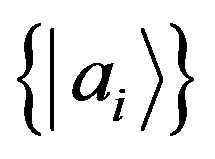 and
and 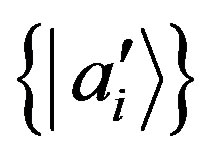 such that
such that
 (37)
(37)
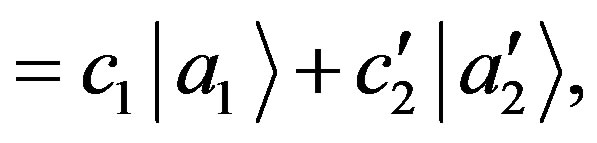 (38)
(38)
where  for
for ,
,  for
for 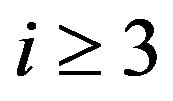 and
and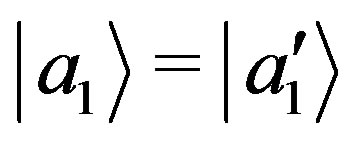 . From the conservation of the total probability for the states of the two different bases we get respectively:
. From the conservation of the total probability for the states of the two different bases we get respectively:
 (39)
(39)
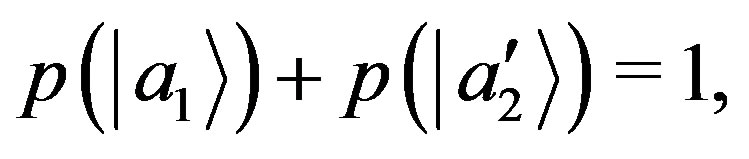 (40)
(40)
where from NCP we have the same probability 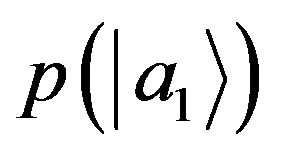 in both Equations (39) and (40). With a change of variable we can write Equation (18) as
in both Equations (39) and (40). With a change of variable we can write Equation (18) as . From Equations (39) and (40) it follows that
. From Equations (39) and (40) it follows that
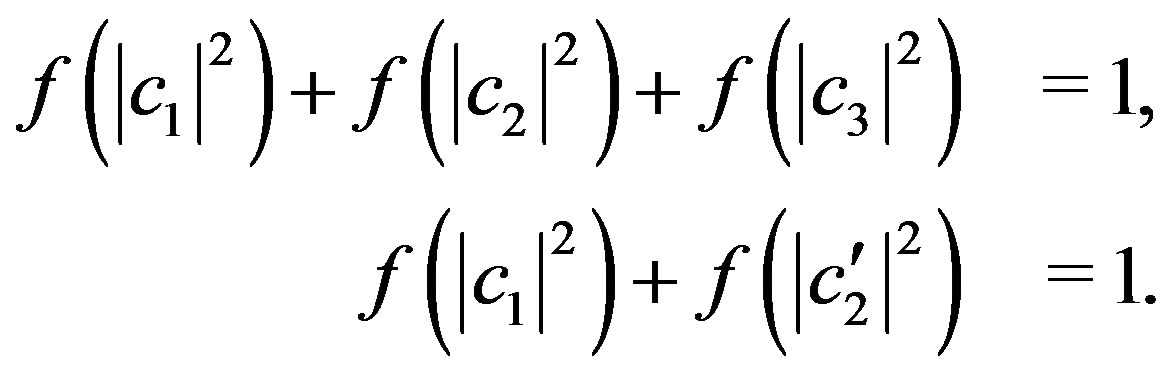 (41)
(41)
By comparing the two Equations (41) we get:
 (42)
(42)
Since the state 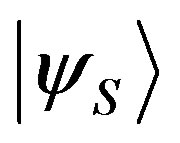 is normalized, we also have
is normalized, we also have
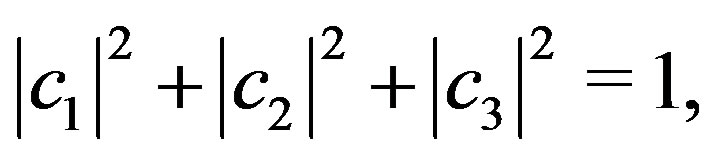 (43)
(43)
 (44)
(44)
and
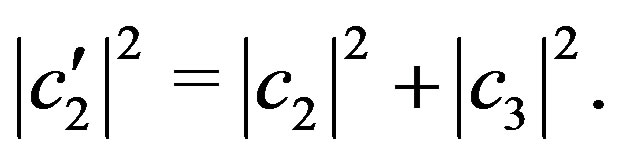 (45)
(45)
Putting this in Equation (42):
 (46)
(46)
Now we recall that a function 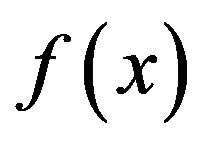 is linear with respect to the variable
is linear with respect to the variable  if and only if the two following properties are jointly satisfied:
if and only if the two following properties are jointly satisfied:
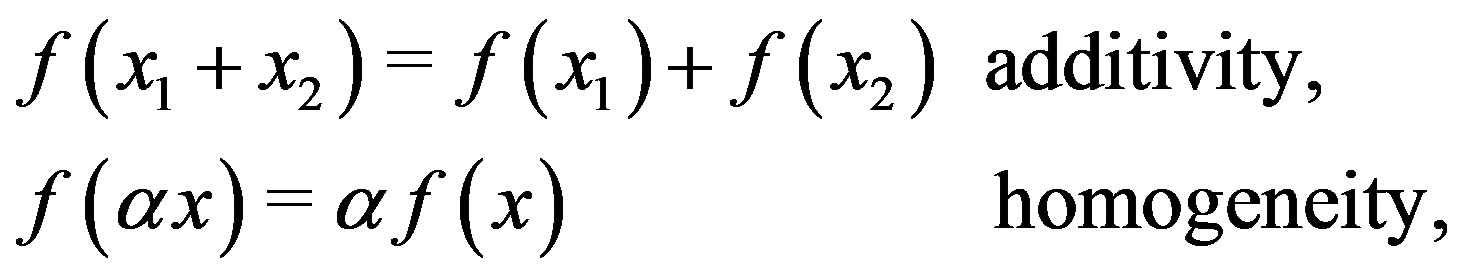 (47)
(47)
where 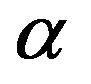 is any real number. We remark that if
is any real number. We remark that if  is a rational number, it can be shown that the homogeneity follows from the additivity. Furthermore, since rational numbers form a subset dense in the set of real numbers, such derivation can be extended to the case of irrational
is a rational number, it can be shown that the homogeneity follows from the additivity. Furthermore, since rational numbers form a subset dense in the set of real numbers, such derivation can be extended to the case of irrational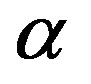 , if
, if 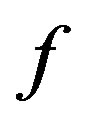 is a continuous function [35].
is a continuous function [35].
Therefore, the condition of additivity is sufficient to establish the linearity if  is a continuous function. On the contrary, if
is a continuous function. On the contrary, if 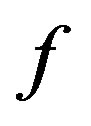 is not assumed to be continuous, the condition of additivity implies linearity only for rational values of the variable
is not assumed to be continuous, the condition of additivity implies linearity only for rational values of the variable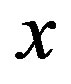 .
.
Hence, if we assume that the probability is continuous with respect to the coefficients , Equation (46) is a constraint of linearity for the probability. In this case we can write:
, Equation (46) is a constraint of linearity for the probability. In this case we can write:
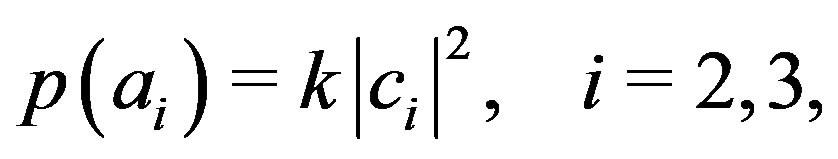 (48)
(48)
where 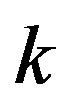 denotes a constant. From Lemma 1 we have that
denotes a constant. From Lemma 1 we have that  and therefore
and therefore  and
and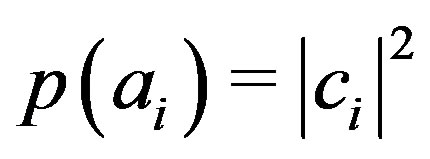 . Hence, the Born rule is deduced for continuous probabilities.
. Hence, the Born rule is deduced for continuous probabilities.
We point out that we have postulated the continuity of probability. However, a derivation of such a property from noncontextuality is present in Gleason’s work and it occupies a prominent part of that paper. Therefore in comparison to Gleason we have only accomplished half the job: as Bertrand Russell once said, postulating is equivalent to theft on the honest fatigue. On the other hand, if the continuity of probability is neither postulated nor demonstrated, we can only say that the Born rule applies only for rational values of the coefficients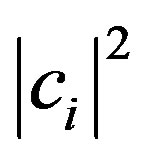 .
.
Thus we now intend to complete our derivation by showing from NCP that the probability is continuous and that the Born rule also holds for irrational coefficients.
Consider, once again,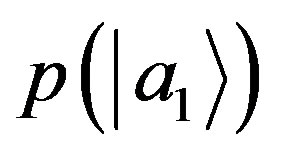 . We select a basis
. We select a basis
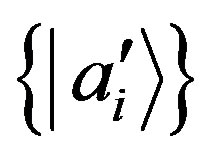 such that the state
such that the state 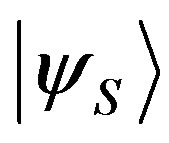 is written with two components as in Equation (38), with
is written with two components as in Equation (38), with , and the conservation of probability is given by Equation (40).
, and the conservation of probability is given by Equation (40).
Then we choose a new basis 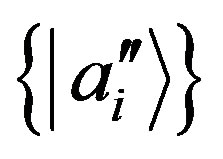 in general with
in general with ,
,  for
for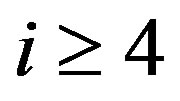 , but with
, but with 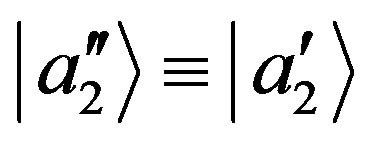 so that we can write
so that we can write
 (49)
(49)
The conservation of probability for the new states of the basis requires that
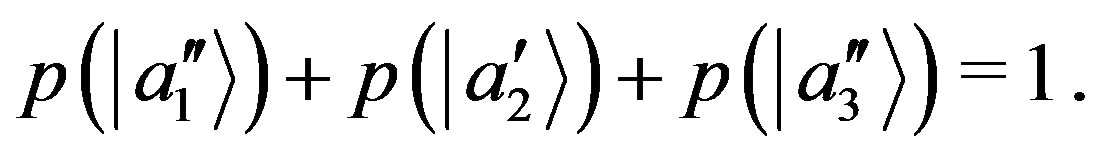 (50)
(50)
From the previous condition we have the inequality:
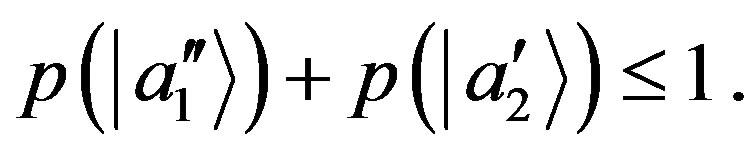 (51)
(51)
By comparing Equation (40) with Equation (51) and since, thanks to NCP, the probability 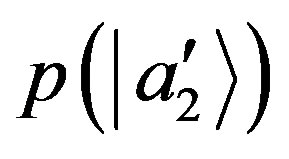 is the same in these equations, we get
is the same in these equations, we get
 (52)
(52)
Finally, we choose a third basis 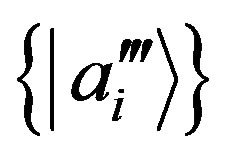 such that
such that 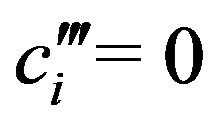 for
for , this time with
, this time with :
:
 (53)
(53)
The conservation of probability gives us:
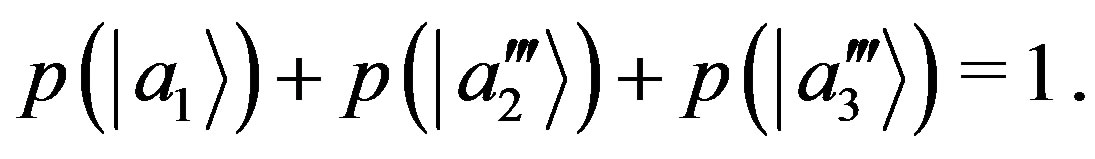 (54)
(54)
From Equation (54) we get the inequality:
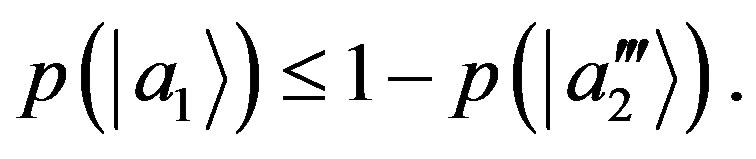 (55)
(55)
Therefore the probability  is in the range:
is in the range:
 (56)
(56)
Suppose 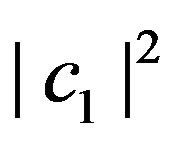 to be an irrational number, we choose rational values for
to be an irrational number, we choose rational values for 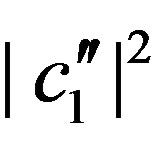 and
and  so that
so that 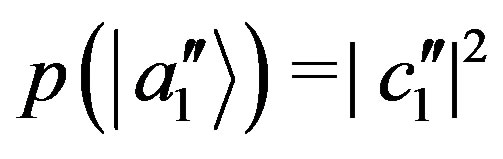 and
and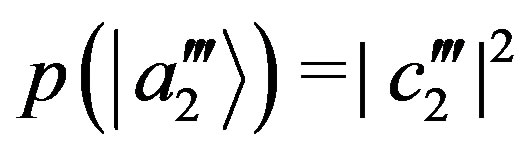 . By putting
. By putting , Equation (56) becomes
, Equation (56) becomes
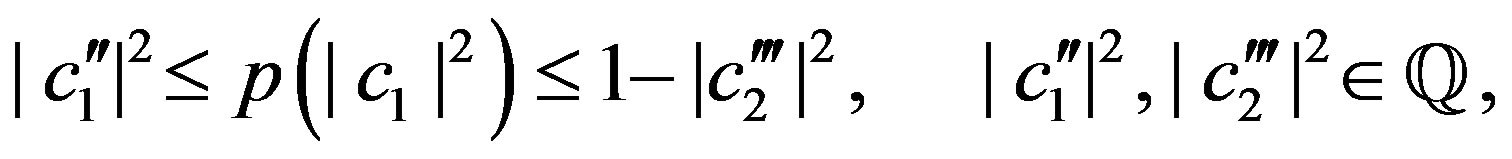 (57)
(57)
with . Let us denote with
. Let us denote with  the orthonormal state to
the orthonormal state to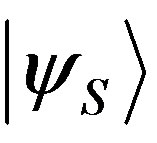 . Consider the limits
. Consider the limits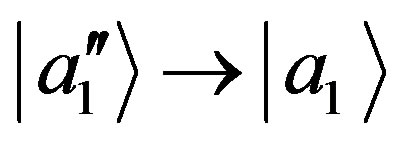 ,
,
 and
and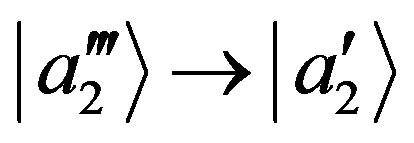 ,
, . From Equation (38) we have
. From Equation (38) we have ,
, 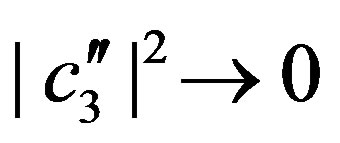 and
and ,
, . Summarizing, with the normalization condition in Equation (44) we get:
. Summarizing, with the normalization condition in Equation (44) we get:
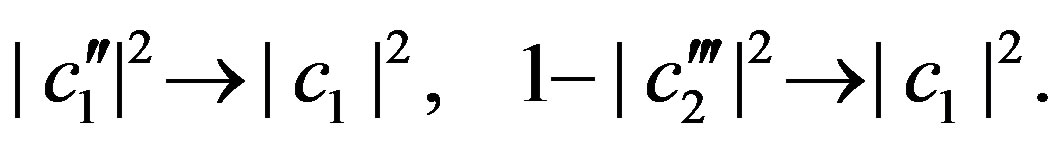 (58)
(58)
Because rational numbers form a dense set in the set of real numbers, we can always find a couple of numbers  which are as near as we want to the irrational number
which are as near as we want to the irrational number . Therefore, from Equation (57) it follows that the oscillation of the function
. Therefore, from Equation (57) it follows that the oscillation of the function  is zero at
is zero at . Consequently, the probability must be continuous at
. Consequently, the probability must be continuous at 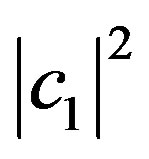 and
and  even if
even if .
.
3. Noncontextual Probability for Entangled States
Theorem 1 with NCP can be generalized to include also entangled states, bipartite or multipartite systems and quantum measurement devices.
Let us indicate with 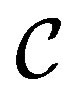 the context, including our experimental devices and the environment, and with
the context, including our experimental devices and the environment, and with  its possible states. Consider again the measurement of the two observables
its possible states. Consider again the measurement of the two observables  and
and  introduced in the proof of Lemma 3 in the previous section. The choice of measuring either the eigenvalues
introduced in the proof of Lemma 3 in the previous section. The choice of measuring either the eigenvalues  or
or 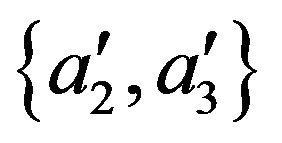 together with
together with 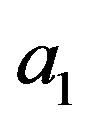 corresponds to two different experimental arrangements
corresponds to two different experimental arrangements  and
and .
.
Suppose that at time  the system is in the initial state
the system is in the initial state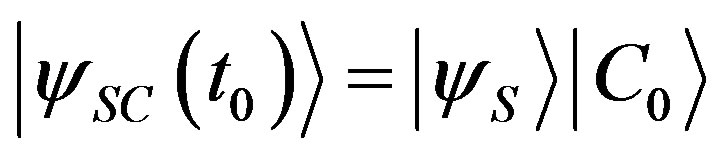 . At time
. At time , after the interaction with the measurement device, the entanglement between the system
, after the interaction with the measurement device, the entanglement between the system 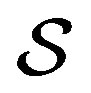 with the experimental setup
with the experimental setup 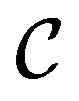 correlates the observable
correlates the observable  (or
(or ) of the system with the pointers of the experimental device. If we measure
) of the system with the pointers of the experimental device. If we measure  we have the state:
we have the state:
 (59)
(59)
while if we measure 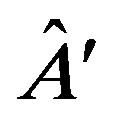 we get:
we get:
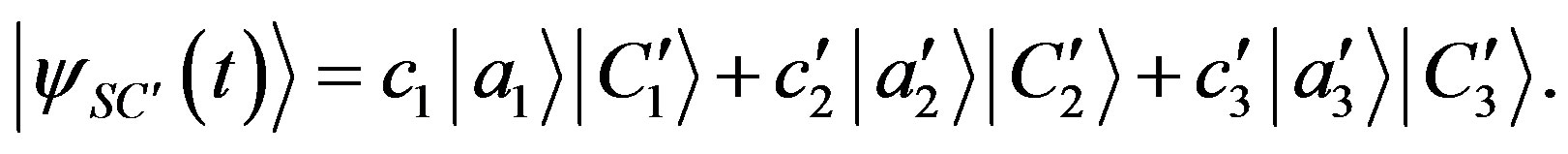 (60)
(60)
The global wave functions Equations (59) and (60) are different in the different contexts  and
and . So the two probabilities
. So the two probabilities
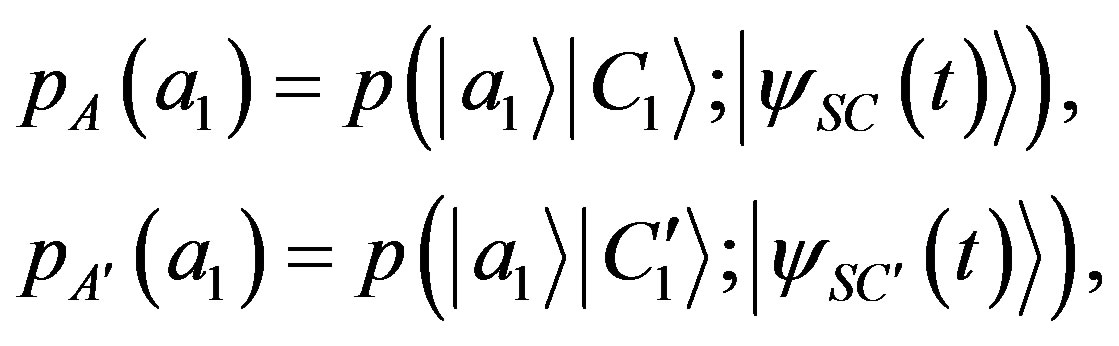 (61)
(61)
may be different. The possible contextuality of probability is now included inside the description of the global system  of the quantum state. We notice that it is no longer possible to write
of the quantum state. We notice that it is no longer possible to write
 (62)
(62)
if we accept the completeness of QM. Otherwise, indeed, some parameters would be outside the description of the state , which now englobes not only the system but also the context of the measurement. This should imply the existence of hidden variables.
, which now englobes not only the system but also the context of the measurement. This should imply the existence of hidden variables.
Assuming NCP requires the equality between the probabilities in Equation (61):
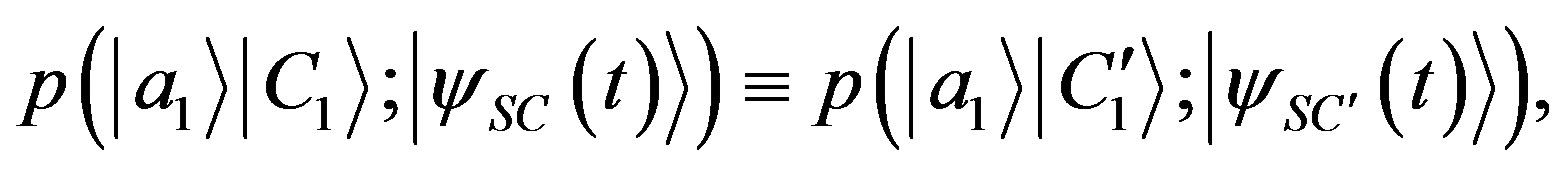 (63)
(63)
which generalizes the condition in Equation (23). In fact, Equation (63), by the perfect correlation property of Equation (17), becomes equivalent to Equation (23).
In a similar way as in the previous derivation, by using the state of Equation (59) and a state 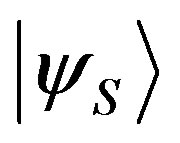 with a new basis
with a new basis 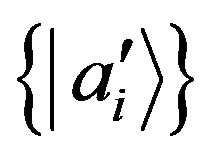 such that
such that 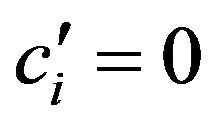 for
for ,
,  we can write:
we can write:
 (64)
(64)
From the condition of NCP it is not difficult to deduce that 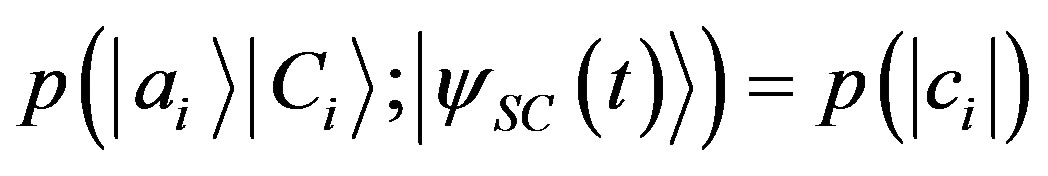 must hold. Then, employing states like in Equation (59) and Equation (64) and from NCP, normalization condition and conservation of probability, it is possible to prove again the linearity of the probabilities with respect to the square moduli of the amplitudes (continuity can also be generalized to the present case). Putting all pieces together, we get
must hold. Then, employing states like in Equation (59) and Equation (64) and from NCP, normalization condition and conservation of probability, it is possible to prove again the linearity of the probabilities with respect to the square moduli of the amplitudes (continuity can also be generalized to the present case). Putting all pieces together, we get
 (65)
(65)
We note that the state of the global system 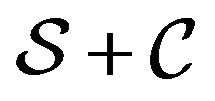 is in the Hilbert space
is in the Hilbert space  with dimension
with dimension . If
. If 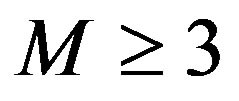 this allows us to include in the derivation of the Born rule also states with
this allows us to include in the derivation of the Born rule also states with . In fact, consider a system
. In fact, consider a system  described by a state
described by a state  in a Hilbert space with
in a Hilbert space with 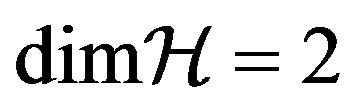 and basis
and basis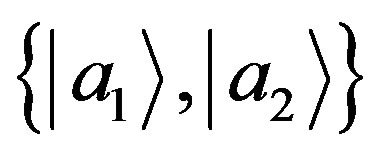 . With a measurement we could use the context
. With a measurement we could use the context  as an ancilla system to build the following entangled states:
as an ancilla system to build the following entangled states:
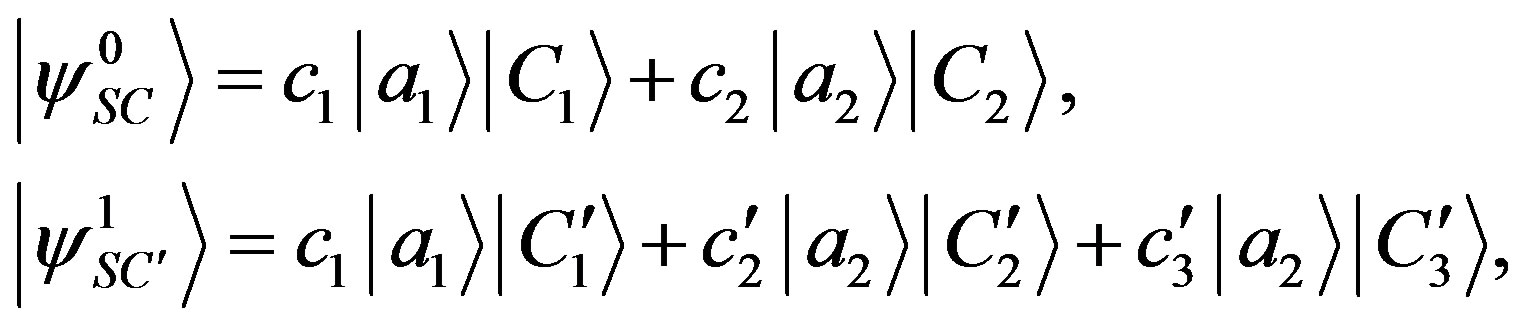 (66)
(66)
where  is obtained by dividing the part of the state
is obtained by dividing the part of the state  associated with the eigenvalue
associated with the eigenvalue 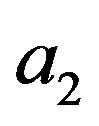 into two regions. So it is possible to demonstrate that
into two regions. So it is possible to demonstrate that
 as in the previous cases. We note that the condition
as in the previous cases. We note that the condition  for the state of the ancilla system
for the state of the ancilla system 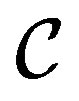 coupled with
coupled with  is necessary to obtain, from Equations (66) by the NCP property of Equation (63), a constraint of additivity and linearity similar to that which is at Equations (39)-(46).
is necessary to obtain, from Equations (66) by the NCP property of Equation (63), a constraint of additivity and linearity similar to that which is at Equations (39)-(46).
4. Noncontextual Probability and Resolution of the Measurement
A simple application of Lemma 3 shows that equal amplitudes are related to equal probabilities, i.e: if  with
with  then
then . Whereas Lemma 3 is derived from the NCP principle, the same result was obtained by Zurek and Deutsch on the base of two different invariance principles. Then both authors study the more general case with states having different rational amplitudes using the fine-graining technique. We shortly summarize their results. We consider the fine-graining in Zurek’s approach with the environment in a simple situation (our remarks also hold for Deutsch’s similar derivation). We assume that the state of the system
. Whereas Lemma 3 is derived from the NCP principle, the same result was obtained by Zurek and Deutsch on the base of two different invariance principles. Then both authors study the more general case with states having different rational amplitudes using the fine-graining technique. We shortly summarize their results. We consider the fine-graining in Zurek’s approach with the environment in a simple situation (our remarks also hold for Deutsch’s similar derivation). We assume that the state of the system  is in a Hilbert space with
is in a Hilbert space with , entangled with the state of the environment
, entangled with the state of the environment 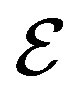 such that their joint state is
such that their joint state is
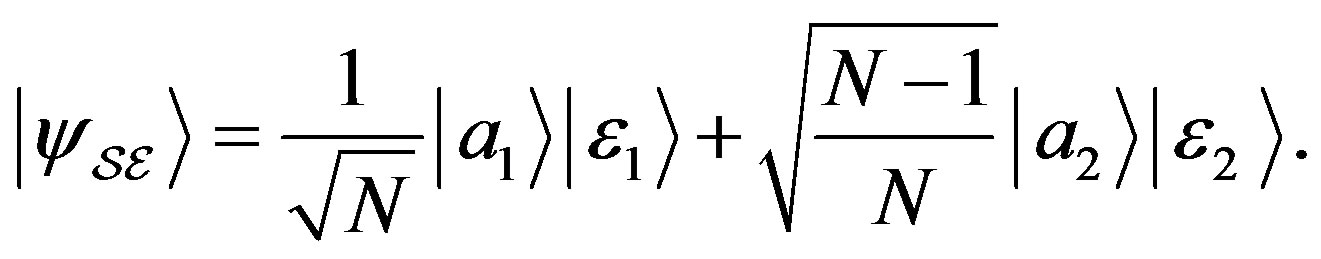 (67)
(67)
The idea is to transform this state with unequal coefficients into a state with equal coefficients by fine-graining. This goal is reached by extracting from the environment an ancilla system 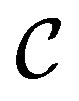 having states
having states
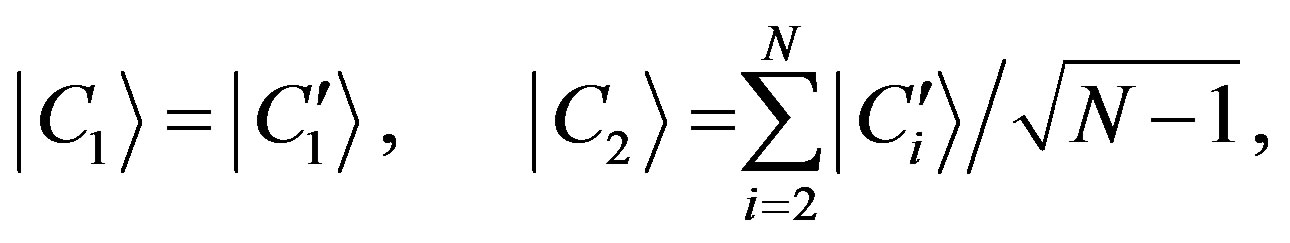 (68)
(68)
which become correlated with the states 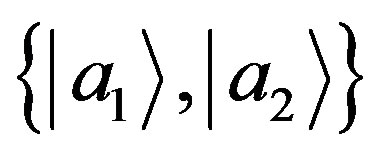 of
of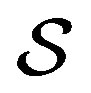 . Within a quantum measurement,
. Within a quantum measurement, 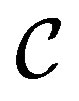 can be regarded as a counter and
can be regarded as a counter and  as a new orthonormal basis of pointer states. Denoting with
as a new orthonormal basis of pointer states. Denoting with 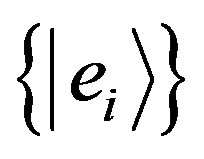 the new states of the environment without
the new states of the environment without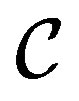 , after the interaction between
, after the interaction between 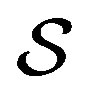 and
and 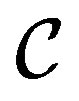 we have the joint system
we have the joint system
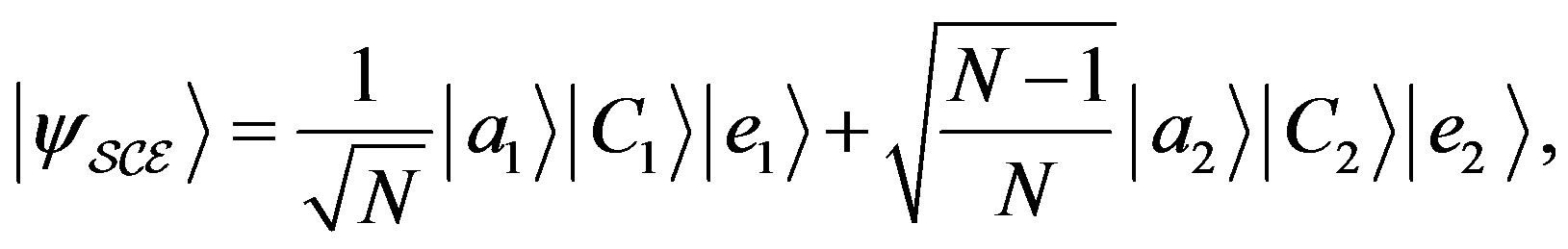 (69)
(69)
which can be expressed with the new basis of pointer states of Equation (68):
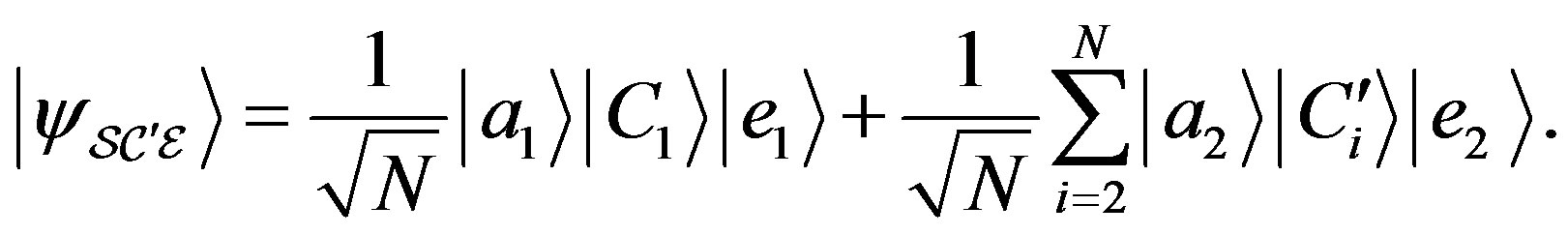 (70)
(70)
Now we have a new state with equal amplitudes. But how can we be sure that after fine-graining the probability 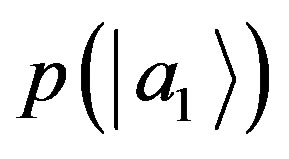 with the state
with the state 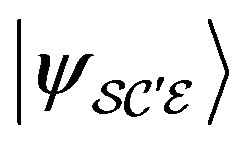 is the same with the state
is the same with the state 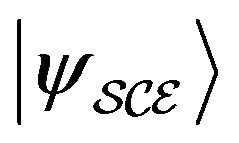 or
or ? In principle they could be different, so to legitimately use the fine-graining reasoning we have to assume the equality:
? In principle they could be different, so to legitimately use the fine-graining reasoning we have to assume the equality:
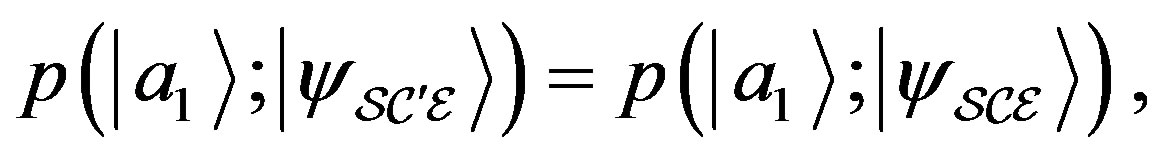 (71)
(71)
equivalent to the condition of NCP encountered in Equation (63) of Section 3. Then, in their derivations Zurek and Deutsch implicitly assume NCP. We notice that fine-graining is equivalent to a change of measurement resolution, and this has been used in our derivation as well. A change of resolution, for instance, is considered going from Equation (39) to Equation (40). There we assumed from NCP that 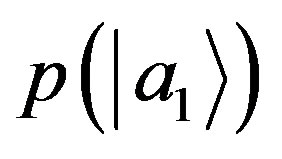 is the same in the two equations and therefore:
is the same in the two equations and therefore:
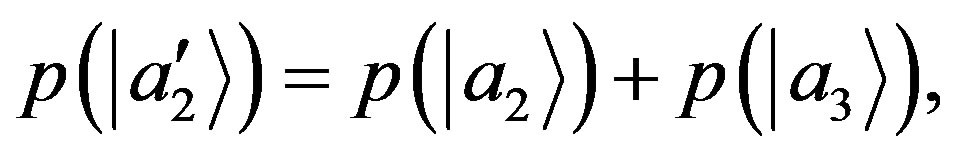 (72)
(72)
where 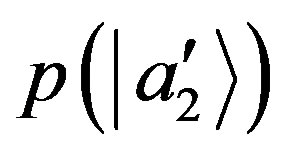 is the probability of finding the state of the system in the subspace orthonormal to
is the probability of finding the state of the system in the subspace orthonormal to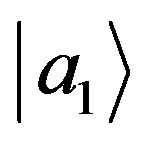 , whereas
, whereas  and
and  are the probabilities of finding it, respectively, in the subspaces
are the probabilities of finding it, respectively, in the subspaces 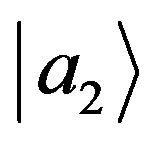 and
and 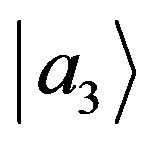 of the subspace orthonormal to
of the subspace orthonormal to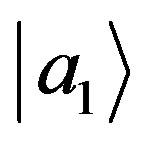 . In fact, in terms of projectors, Equation (72) can be written as Gleason’s Postulate 2:
. In fact, in terms of projectors, Equation (72) can be written as Gleason’s Postulate 2:
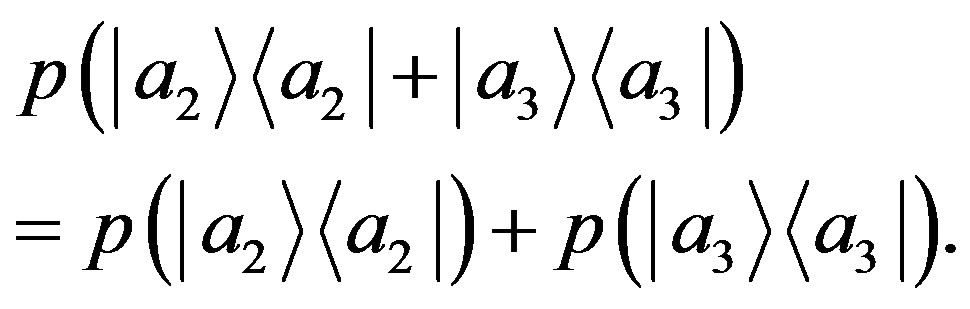 (73)
(73)
Thus NCP could be physically interpreted as a probability invariance when we change the resolution of the measurement connected with other properties of the system. This interpretation gives physical insight to the NCP principle as an invariance under changing resolution. The probability of one measurement outcome should not change if we make coarse or fine-graining over other measurement outcomes. We point out that coarse/fine graining could be done through a post-processing after the first measurement. Therefore, NCP is a natural assumption if we do not want signalling from the future to the past.
5. Noncontextual Probability and No-Faster-than-Light Signalling
In general, every measurement in the real world happens in the spacetime. Every measurement of any observable is necessarily reduced to a measurement of position at a certain time. For instance, the Stern-Gerlach apparatus correlates a spin observable with a position observable so that different values of the spin univocally correspond to different position values of the system. A measurement of position detects the spin value of the system.
Let us introduce in our representation of  the observable position
the observable position . We assume that at time
. We assume that at time , the system is in the initial state
, the system is in the initial state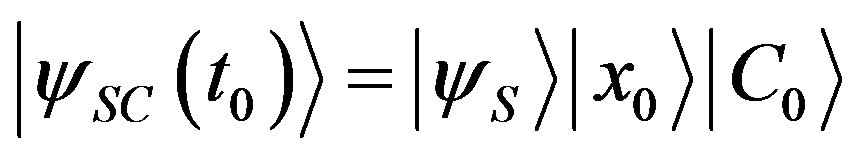 . For simplicity of notation, from now on we denote with
. For simplicity of notation, from now on we denote with 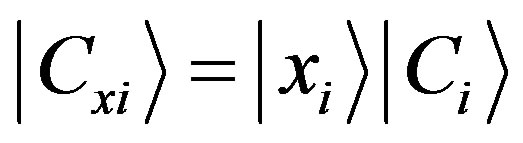 the position state of the system with its context, where the letter
the position state of the system with its context, where the letter 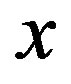 will remind us the dependence on the position of the system and the experimental apparatus. Suppose that we can measure either the values of the observable
will remind us the dependence on the position of the system and the experimental apparatus. Suppose that we can measure either the values of the observable  or the values of the observable
or the values of the observable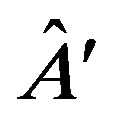 . In the context
. In the context  of measurement we get:
of measurement we get:
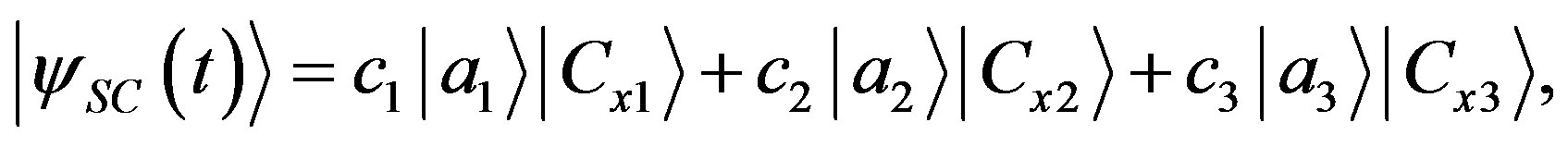 (74)
(74)
while for the experimental context  we have the different state:
we have the different state:
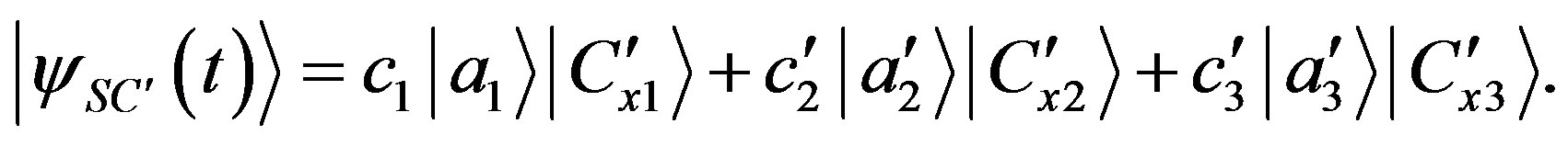 (75)
(75)
We want to prove the following
Theorem 2:
If we assume the no-faster-than-light signalling condition for measurement events which are spacelike separate, then the probability 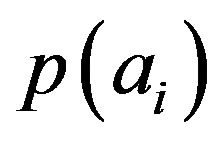 must be noncontextual.
must be noncontextual.
Proof:
Consider a set of identically prepared systems  in the initial state
in the initial state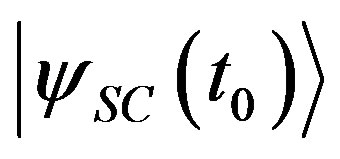 . In order to estimate the probabilities
. In order to estimate the probabilities  and
and
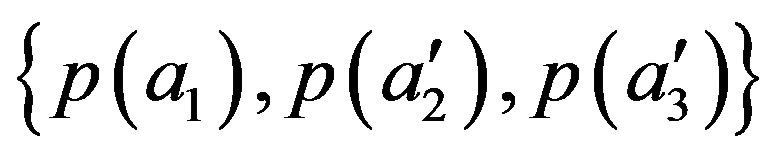 , let us assume that our experimental device is arranged to measure how many systems have the eigenvalue
, let us assume that our experimental device is arranged to measure how many systems have the eigenvalue 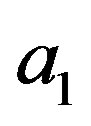 at the point
at the point 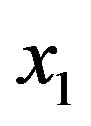 and the eigenvalues
and the eigenvalues 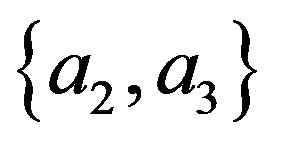 (Equation (74)) or the eigenvalues
(Equation (74)) or the eigenvalues  (Equation (75)) at the points
(Equation (75)) at the points  and
and . This could be done by first dividing the systems
. This could be done by first dividing the systems  in two parts, one associated with the state
in two parts, one associated with the state  at the point
at the point 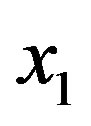 and an other one associated with the orthogonal state
and an other one associated with the orthogonal state 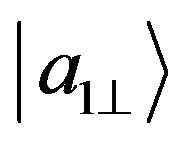 at a different point
at a different point 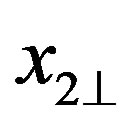 (see the superposition state in Equation (78)), then by dividing such a state in two sub-parts, associated either with the basis
(see the superposition state in Equation (78)), then by dividing such a state in two sub-parts, associated either with the basis , or with the basis
, or with the basis 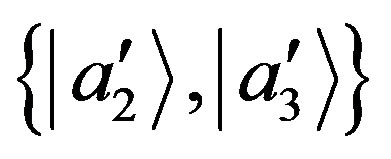 at the points
at the points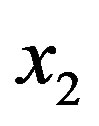 ,
,  , respectively connected with the states in Equations (74)-(75).
, respectively connected with the states in Equations (74)-(75).
If the measurements of  or
or 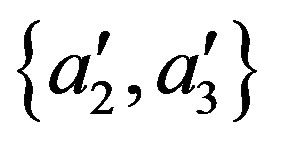 at the points
at the points  and
and  are events spacelike separate with respect to the measurement of
are events spacelike separate with respect to the measurement of 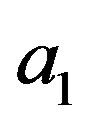 at
at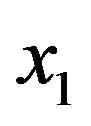 , according to the relativistic hypothesis of no-signalling, the probability
, according to the relativistic hypothesis of no-signalling, the probability  of getting the eigenvalue
of getting the eigenvalue 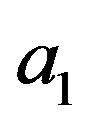 has to be the same in both different experimental contexts
has to be the same in both different experimental contexts  and
and . Otherwise an observer situated in the place of measurement of
. Otherwise an observer situated in the place of measurement of 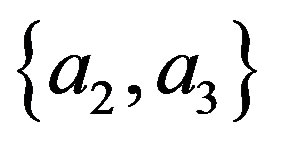 or
or  would be able to send a superluminal signal to another observer situated in the place where
would be able to send a superluminal signal to another observer situated in the place where 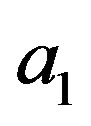 is measured. Then, according to the no-faster-than-light signalling hypothesis:
is measured. Then, according to the no-faster-than-light signalling hypothesis:
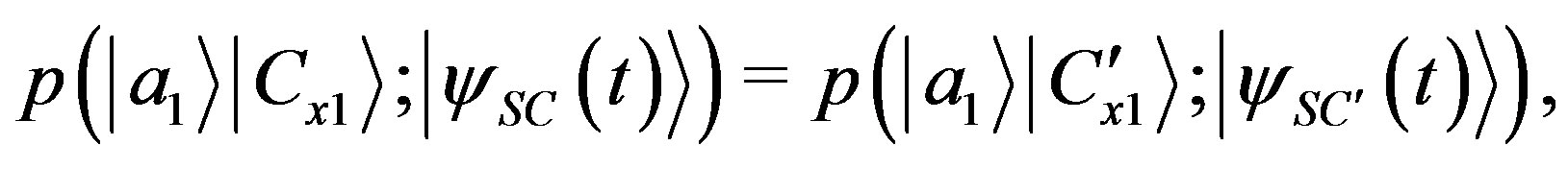 (76)
(76)
which is to say, with the result of Equation (17):
 (77)
(77)
Therefore 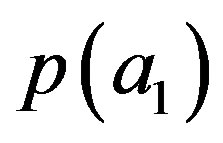 must be noncontextual.
must be noncontextual.
Consider, beside the measurement of the eigenvalues  of the observable
of the observable , also the simple possibility of measuring whether our systems assume the eigenvalue
, also the simple possibility of measuring whether our systems assume the eigenvalue 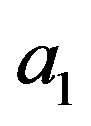 or not, which is equivalent to check whether the systems
or not, which is equivalent to check whether the systems  are in the state
are in the state 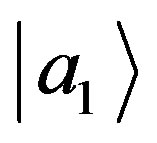 or in the subspace
or in the subspace 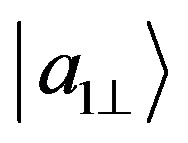 orthogonal to it. In such a case, during the process of measurement, the systems
orthogonal to it. In such a case, during the process of measurement, the systems 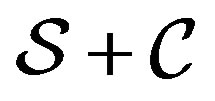 will be in the state:
will be in the state:
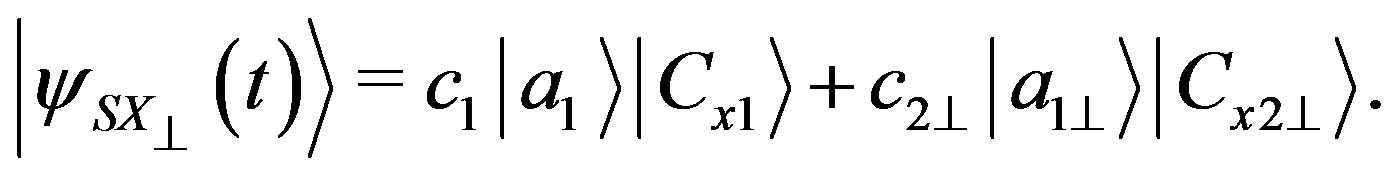 (78)
(78)
If the two choices of measuring either 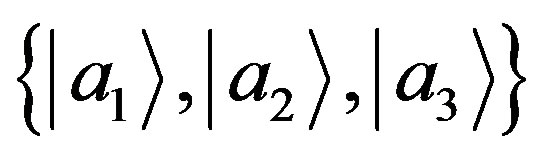 or
or 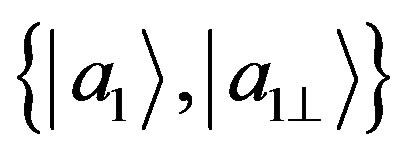 correspond to events spacelike separate, as mentioned above, from the condition of no-signalling we must have the NCP condition:
correspond to events spacelike separate, as mentioned above, from the condition of no-signalling we must have the NCP condition:
 (79)
(79)
From Equation (79) the conservation of probability imposes also the equation:
 (80)
(80)
As we showed at the end of Section IV, Equation (80) is equivalent to the initial hypothesis adopted by Gleason. Moreover, by examining Equation (79) we understand that it is analogous to assuming an invariance condition of the probability under a resolution change of our measurement, or fine/coarse graining. So, at least for spacelike separate measurements, NCP could be deduced by a relativistic principle. However, the Born rule holds for general events, not only for spacelike separate ones. Hence NCP or, equivalently, the invariance of probability when we change resolution, seem to be more general principles.
6. Concluding Remarks
We have given a new derivation of the Born rule based on the noncontextuality for projective measurements and on some non-statistical postulates of QM. The introduction of a pure quantum state of the system has allowed a more elementary proof than Gleason’s theorem. This may seem, at first sight, a loss of generality with respect to Gleason’s proof, however Gleason also introduces vectors of basis which can be regarded as states of the system. Moreover, the step from pure states to density operators and to the trace rule for mixed ensembles is quite natural when we already have the Born rule [36].
As in Gleason’s, our derivation holds for , where
, where  could be finite or infinite. The origin of this dimensional limitation lies in the fact that for
could be finite or infinite. The origin of this dimensional limitation lies in the fact that for  the same state vector may belong to several distinct orthonormal bases. This, with NCP, the normalization of the probability and the quantum state, brings us to a constraint of functional linearity between the probability and the amplitude square modulus. Our theorem can be simply generalized in order to include multipartite states. In such a case, if a part of the global system has
the same state vector may belong to several distinct orthonormal bases. This, with NCP, the normalization of the probability and the quantum state, brings us to a constraint of functional linearity between the probability and the amplitude square modulus. Our theorem can be simply generalized in order to include multipartite states. In such a case, if a part of the global system has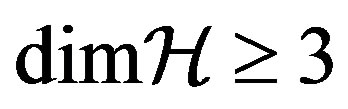 , the Born rule can also be proved to hold in subspaces with
, the Born rule can also be proved to hold in subspaces with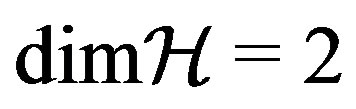 .
.
We have also given a derivation that the probability is continuous with respect to the amplitudes using measurement noncontextuality. This fills a gap of Zurek’s and Deutsch’s demonstrations.
Physical motivation for NCP could come from a relativistic principle of no-faster-than-light signalling. However, the Born rule also holds for measurements which are non-spacelike separate, hence NCP seems to be a more fundamental principle. Finally, we have given an interpretation of measurement noncontextuality as an invariance of the probability under a resolution change of our measurement.
7. Acknowledgements
This work has been supported by the EU-STREP Project QIBEC within the activities of the BEC center. QSTAR is the MPQ, IIT, LENS, UniFi joint center for Quantum Science and Technology in Arcetri.
REFERENCES
- J. A. Wheeler and W. H. Zurek, Eds., “Quantum Theory and Measurement,” Princeton University Press, Princeton, 1963.
- J. von Neumann, “Mathematical Foundations of Quantum Mechanics,” Princeton University Press, Princeton, 1955. doi:10.1063/1.3061789
- T. F. Jordan, “Linear Operators for Quantum Mechanics,” John Wiley Sons, New York, 1969. doi:10.1119/1.1975255
- A. M. Gleason, “Measures on the Closed Subspaces of a Hilbert Space,” Journal of Mathematics and Mechanics, Vol. 6, No. 6, 1957, pp. 885-893.
- H. Everett, “Relative State Formulation of Quantum Mechanics,” Reviews of Modern Physics, Vol. 29, No. 3, 1957, pp. 454-462. doi:10.1103/RevModPhys.29.454
- B. S. DeWitt, “The Many-Universes Interpretation of Quantum Mechanics,” In: B. d’Espagnat, Ed., Foundations of Quantum Mechanics, Academic Press, New York, 1971.
- D. Finkelstein, “The Logic of Quantum Mechanics,” Transactions of the New York Academy of Sciences, Vol. 25, No. 6, 1965, pp. 621-637. doi:10.1111/j.2164-0947.1963.tb01483.x
- J. B. Hartle, “Quantum Mechanics of Individual Systems,” American Journal of Physics, Vol. 36, No. 8, 1968, pp. 704-712. doi:10.1119/1.1975096
- N. Graham, “The Measurement of Relative Frequency,” In: B. S. DeWitt and N. Graham, Eds., The Many-Worlds Interpretation of Quantum Mechanics, Princeton University Press, Princeton, 1973.
- R. Geroch, “The Everett Interpretation,” Noûs, Vol. 18, No. 4, 1984, pp. 617-633. doi:10.2307/2214880
- E. Farhi, J. Goldstone and S. Gutmann, “How Probability Arises in Quantum Mechanics,” Annals of Physics, Vol. 192, No. 2, 1989, pp. 368-382. doi:10.1016/0003-4916(89)90141-3
- H. Stein, “The Everett Interpretation of Quantum Mechanics: Many Worlds or None?” Noûs, Vol. 18, No. 4, 1984, pp. 635-652. doi:10.2307/2214881
- A. Kent, “Against Many-Worlds Interpretations,” International Journal of Modern Physics A, Vol. 5, No. 9, 1990, pp. 1745-1762. doi:10.1142/S0217751X90000805
- T. Endo, “Verification of Born’s Rule by a Quantum Mechanical Meter,” Physics Letters A, Vol. 308, No. 4, 2003, pp. 256-258. doi:10.1016/S0375-9601(03)00083-5
- C M. Caves, C. A. Fuchs and R. Schack, “Quantum Probabilities as Bayesian Probabilities,” Physical Review A, Vol. 65, No. 2, 2002, pp. 1-6. doi:10.1103/PhysRevA.65.022305
- M. Redhead, “Incompleteness, Nonlocality and Realism,” Claredon Press, Oxford, 1989. doi:10.1119/1.16032
- R. W. Spekkens, “Contextuality for Preparations, Transformations, and Unsharp Measurements,” Physical Review A, Vol. 71, No. 5, 2005, pp. 1-17. doi:10.1103/PhysRevA.71.052108
- W. H. Zurek, “Environment-Assisted Invariance, Entanglement, and Probabilities in Quantum Physics,” Physical Review Letters, Vol. 90, No. 12, 2003, pp. 1-4. doi:10.1103/PhysRevLett.90.120404
- M. Schlosshauer and A. Fine, “On Zurek’s Derivation of the Born Rule,” Foundations of Physics, Vol. 35, No. 197, 2005, pp. 197-213. doi:10.1007/s10701-004-1941-6
- D. Deutsch, “Quantum Theory of Probability and Decisions,” Proceedings of the Royal Society of London A, Vol. 455, No. 1988, 1999, pp. 3129-3137. doi:10.1098/rspa.1999.0443
- W. H. Zurek, “Probabilities from Entanglement, Born’s Rule from Envariance,” Physical Review A, Vol. 71, 2005, pp. 1-29. doi:10.1103/PhysRevA.71.052105
- W. H. Zurek, “Entanglement Symmetry, Amplitudes, and Probabilities: Inverting Born’s Rule,” Physical Review Letters, Vol. 106, No. 25, 2011, pp 1-4. doi:10.1103/PhysRevLett.106.250402
- C. M. Caves, “Notes on Zurek’s Derivation of the Quantum Probability Rule,” 2005. http://info.phys.unm.edu/caves/reports/ZurekBornderivation.pdf
- U. Mohrhoff, “Probabilities from Envariance?” International Journal of Quantum Information, Vol. 2, No. 2, 2004, pp. 221-230. doi:10.1142/S0219749904000195
- H. Barnum, “No-Signalling-Based Version of Zurek’s Derivation of Quantum Probabilities: A Note on Environment-Assisted Invariance, Entanglement, and Probabilities in Quantum Physics,” 2003. arXiv: quant-ph/0312150
- H. Barnum, C. M. Caves, J. Finkelstein, C. A. Fuchs and R. Schack, “Quantum Probability from Decision Theory?” Proceedings of the Royal Society of London A, Vol. 456, No. 1997, 2000, pp. 1175-1182. doi:10.1098/rspa.2000.0557
- S. Saunders, “Derivation of the Born Rule from Operational Assumptions,” Proceedings of the Royal Society of London A, Vol. 460, No. 2046, 2004, pp. 1-18. doi:10.1098/rspa.2003.1230
- D. Wallace, “Everettian Rationality: Defending Deutsch’s approach to probability in the Everett interpretation,” Studies in History and Philosophy of Modern Physics, Vol. 34, No. 3, 2003, pp. 415-438. doi:10.1016/S1355-2198(03)00036-4
- W. H. Zurek, “Decoherence, Einselection, and the Quantum Origins of the Classical,” Reviews of Moder Physics, Vol. 75, No. 3, 2003, pp. 715-775. doi:10.1103/RevModPhys.75.715
- W. H. Zurek, “Quantum Darwinism and Envariance,” 2003. arXiv: quant-ph/0308163
- C. Cohen-Tannoudji, B. Diu and F. Laloë, “Quantum Mechanics,” Hermann and Wiley, Paris, 1977.
- N. Zettili, “Quantum Mechanics, Concepts and Applications,” Wiley, Chichester, 2001.
- W. Greiner, “Quantum Mechanics, An Introduction,” Springer-Verlag, Berlin, 2000.
- A. Galindo and P. Pascual, “Quantum Mechanics I,” Springer-Verlag, Berlin, 1990. doi:10.1007/978-3-642-83854-5_2
- M. Kuczma, “An Introduction to the Theory of Functional Equations and Inequalities,” Birkhäuser, Basel, 2009. doi:10.1007/978-3-7643-8749-5
- J. J. Sakurai, “Modern Quantum Mechanics,” Addison-Wesley, San Francisco, 1994.
Appendix A
We want to generalize the result of Lemma 1 for entangled states. Suppose that the system is prepared with eigenvalues  and therefore with eigenstates
and therefore with eigenstates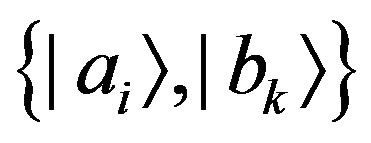 . Similarly to the unentangled case, we can deduce that
. Similarly to the unentangled case, we can deduce that 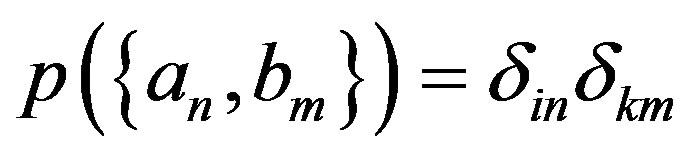 if and only if
if and only if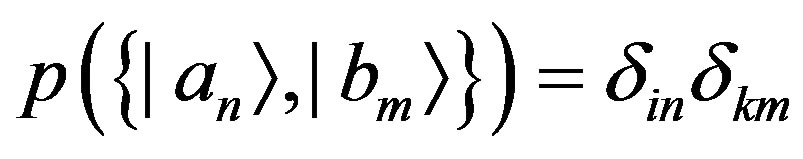 . This relation, translated into conditional probabilities, is equivalent to writing:
. This relation, translated into conditional probabilities, is equivalent to writing:
 (81)
(81)
Then, from Equation (81) we have that for a generic state as in Equation (13):
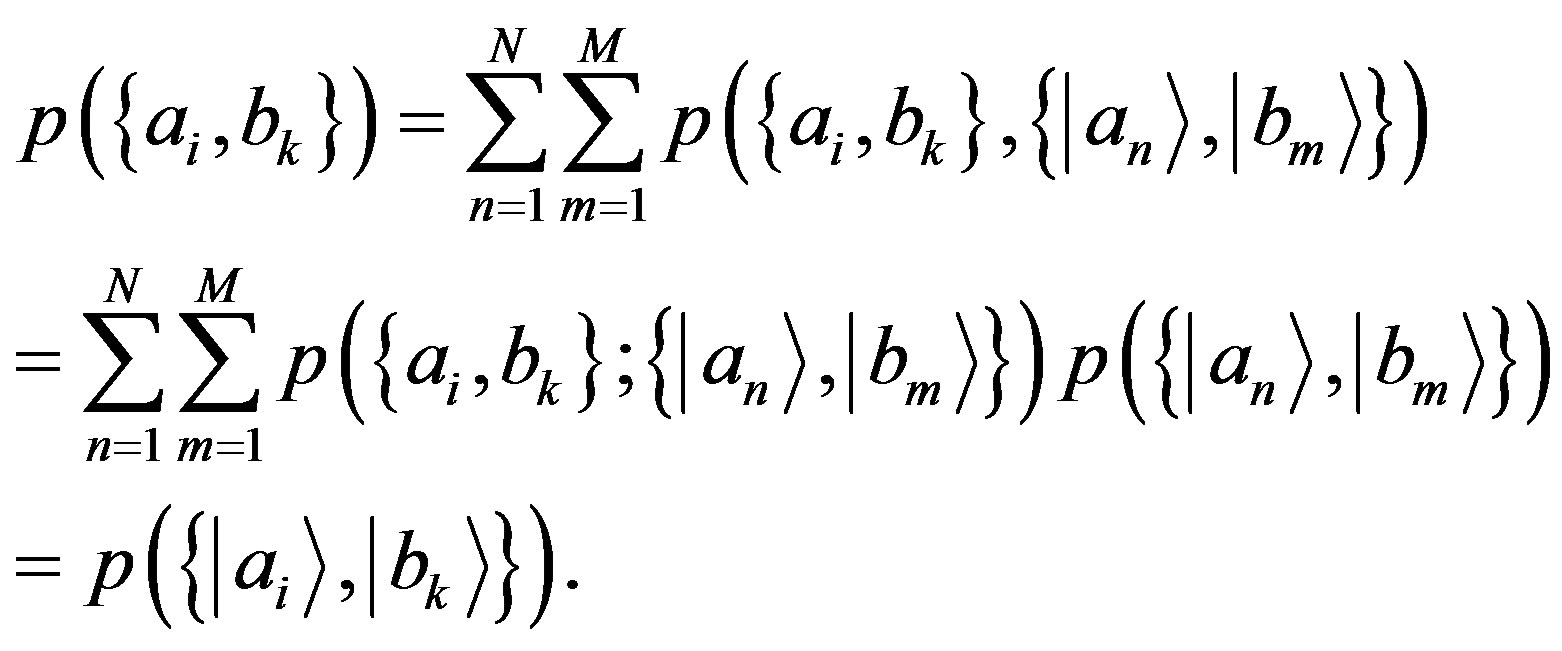 (82)
(82)
If the observable  has an eigenstate
has an eigenstate  and the observable
and the observable 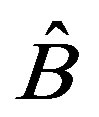 has an eigenstate
has an eigenstate  then the tensorial product
then the tensorial product 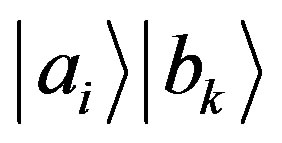 is an eigenstate of the observable
is an eigenstate of the observable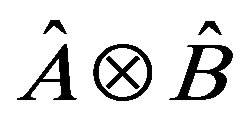 , and vice versa. The eigenstates
, and vice versa. The eigenstates
 of
of 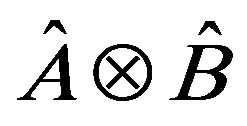 form a basis of Hilbert space
form a basis of Hilbert space
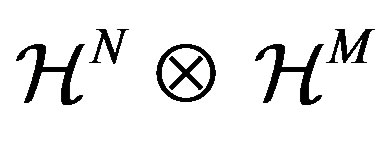 .
.
If we indicate with  the probability of obtaining the eigenstate
the probability of obtaining the eigenstate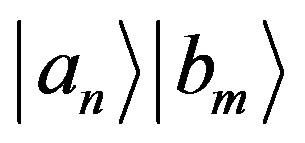 , with a measurement of
, with a measurement of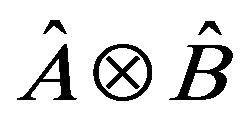 , we have
, we have 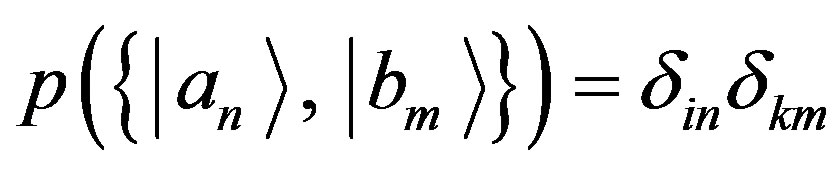 if and only if
if and only if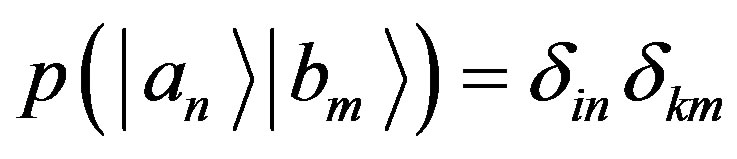 , or, in equivalence:
, or, in equivalence:
 (83)
(83)
From Equations (82)-(83), through the use of the conditional probabilities, it immediately follows that on the state 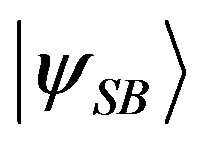 we have
we have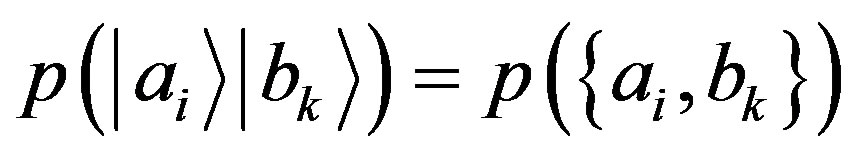 .
.
NOTES
*Corresponding author.

