Journal of Modern Physics
 Vol.3 No.1(2012), Article ID:17109,5 pages DOI:10.4236/jmp.2012.31017

An Analytical and Numerical Approach to the Self-Consistent Method for Computing the Proportion of 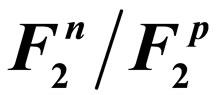Using the 3He and 3H Nucleuses’ Structure Function and EMC Ratio

Alireza Heidari, Mohammadali Ghorbani*

Institute for Advanced Studies, Tehran, Iran

Email: *mohammadalighorbani1983@yahoo.com

Received October 20, 2011; revised December 6, 2011; accepted December 21, 2011

Keywords: Structure function; Fermi motion; EMC effect; Convolution model; Iteration self-consistent equation; Bjorken scale

ABSTRACT

First, the structure function of 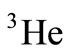and 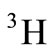nucleuses is calculated through the nuclear convolution model including the Fermi motion and nuclear binding energy. In these calculations, the results of the free nucleons structure function obtained by the GRV research group (Glück et al.) are employed. 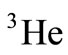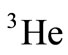Moreover, the European muon collaboration (EMC) ratio of and nucleuses is achieved; and in this paper, it is tried to review the proportion of the neutron structure function to proton structure function that can be written as a self-consistent equation according to the and 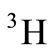nucleuses’ structure function and EMC ratio which this leads to improving the results at large Bjorken x scale.

1. Introduction

Within the framework of nucleons’ standard model, the quark sea and gluons are composed of delicate quarks that at small Bjorken variables (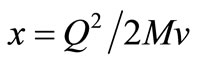), the quarks sea and gluons play a basic role in justification of nucleons structure function whereas the data on nucleons structure function is obtained from the distribution of up and down delicate quarks (d, u) at the large x.

Nowadays, the proton structure function is completely known in empirical and theoretical terms whereas the data on deuteron’s deep inelastic scattering is generally utilized to compute neutron structure function [1-12]. However, the results are not precisely accurate yet which this inaccuracy is due to the effects of nuclear ambience on the bound nucleon structure function, and causes bound and free nucleon structure functions to be different from each other (this phenomenon is known as the EMC effect [13,14]). In order to more investigate the neutron structure function, calculating the proportion of neutron structure function to proton structure function is useful. In this paper, it is tried to compute this proportion at the large x. Not only does the investigation of this proportion at give information about the neutron structure function at this level, but also it can give some information about the color-spin symmetry breaking in nucleons [15] (through computing the ratio of down quarks to up quarks (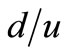)), and also provide some information on the uncertainty in the contribution of gluons. Calculating through fitting the standard data relating to the deep scattering of deuteron and hydrogen in which the nuclear impacts are still considerable leads to an approximate 50% error in or 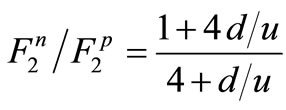[16]. The value of this proportion at 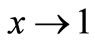becomes a quarter in this way whereas Nachtmann achieved 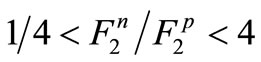for all regions of x. A more complete analysis conducted by means of the perturbative quantum chromo dynamic (PQCD) results 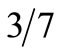for this proportion at 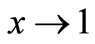[17-20], and even is expected in the calculations with considering the SU(6) symmetries [17-20]. Recently, at the Jefferson laboratory, they are planning on scattering electron from 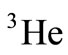and 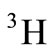targets in high energy (about 11 GeV) [16]. Their aim is to measure 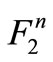by virtue of the proportion of the structure functions of 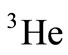and. This case has caused scientists to propose various theoretical methods for investigating 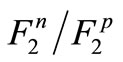according to the 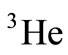and 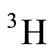nucleuses’ structure function and EMC ratio [16-25] that it brings about an iteration self-consistent equation for computing 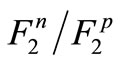so that they can moderate the errors in the results obtained for this proportion from fitting the data on deuteron and hydrogen. All these cases have persuaded us to investigate this proportion in this paper.

2. The Calculation of Tralphium and Tritium Nucleuses’ Structure Function and EMC Ratio

In this section, the and nucleuses’ structure function is computed in the momentum approximation. The nuclear convolution model is used to perform this purpose. According to the model that is as follows [26, 27]:

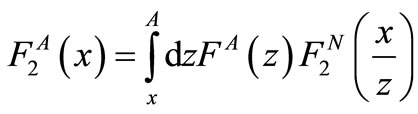(1)

where 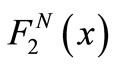is the nucleon structure function, is the distribution function of the quarks inside the A nucleus, and x is the carried-by-quark momentum fraction of the total nucleus’s momentum. represents the possibility of discovering nucleons inside the nucleus that the distribution function introduced by Akulinichev et al. is applied in this paper [26,27]. They utilized the nuclear harmonic oscillator wave functions to achieve the momentum distribution of the nucleons inside the nucleus [27].

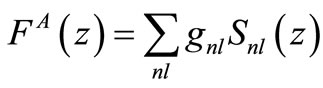(2)

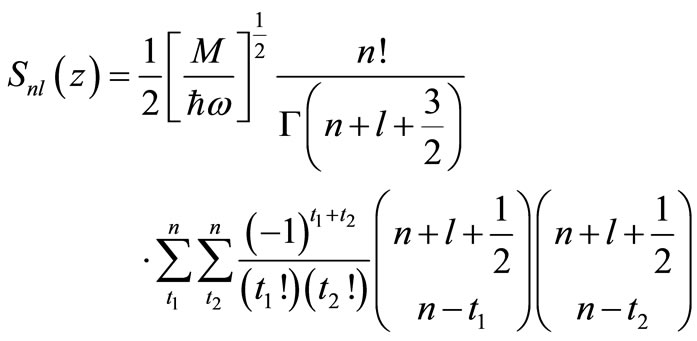
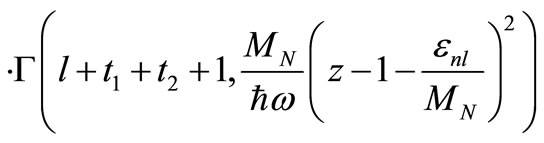(3)

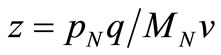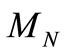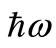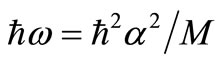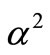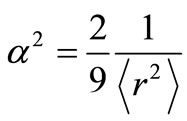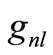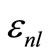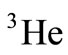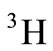where denotes the carried-by-nucleon momentum fraction of the total nucleus’s momentum, is the nucleon’s mass, and is the oscillator model’s parameter ().relates to the root mean square radii of the nucleuses participating in the scattering as [24-27]. and respectively represent the number of nucleons at the nl level and the energy of this level. Through using equations (1) to (3) for and nucleuses [26,27]:

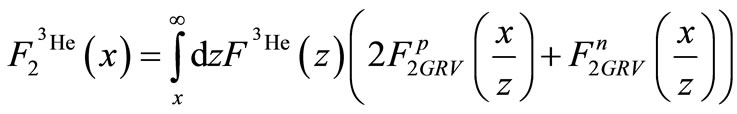(4)

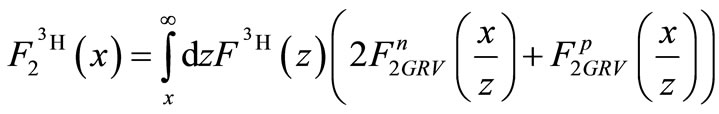(5)

where 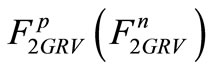represents the structure function of free proton (neutron). It should be noted that the results of the GRV group is utilized herein for fitting the empirical data resulted from the deep scattering of deuteron and hydrogen [1-12]. Furthermore, and are considered, and the values of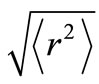for and 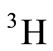nucleuses are 1.95 and 1.70 Fermi, respectively [23-25]. More, the EMC ratio for these nucleuses is computed as the proportion of the nuclear structure function per nucleon unit (the bound nucleon structure function) to the free nucleon structure function (equations (6) and (7)). 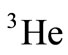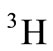In Figure 1, the proportion of the EMC of and nucleuses, the following equations, are illustrated:

(6)

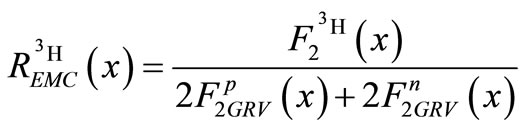(7)

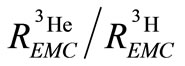is demonstrated in Figure 2. As can be seen in the figures, to, the nuclear ambience’s effects for and nucleuses are similar. However, for the larger x, the nuclear size’s impacts differ because the 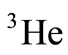radius is larger than the 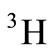radius (at the large x, the Fermi motion’s effect takes the main role in the computation of nucleus’s structure function and EMC ratio). Therefore, starts to decline for the x larger than 0.6.

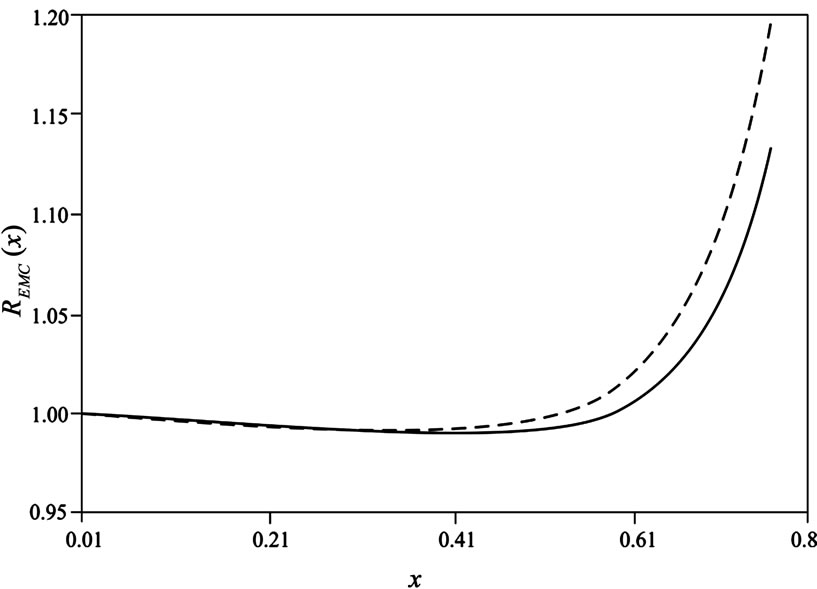
Figure 1. The proportion of the EMC of 3He (line) and 3H (dashed line) nucleuses.

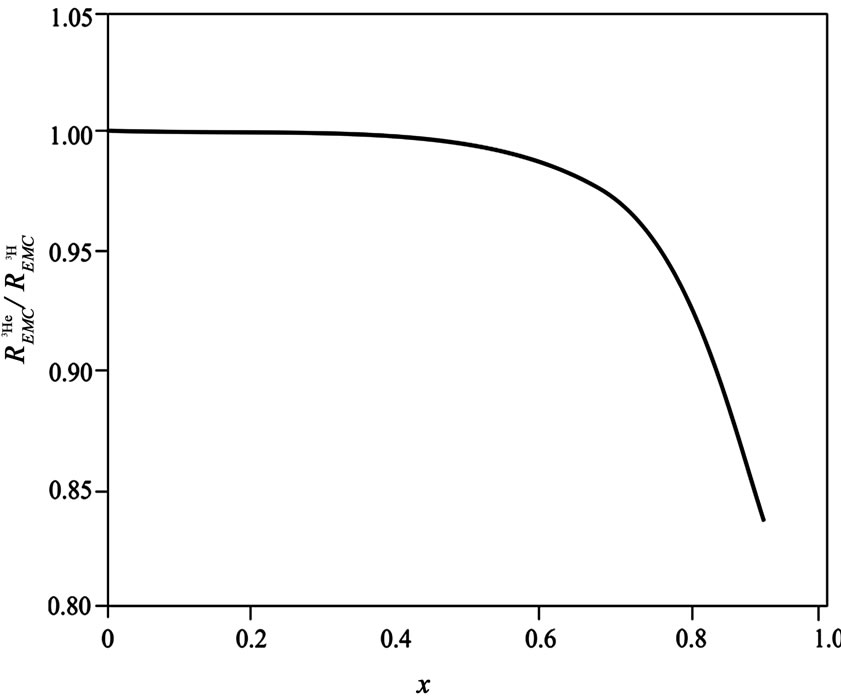
Figure 2. The proportion of the EMC of 3He nucleus to EMC of 3H nucleus.

3. The Calculation of According to the 3He and 3H Nucleuses’ Structure Functions and EMC Ratio

First, 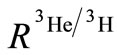is computed to obtain an equation for 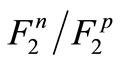according to the 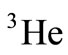and 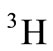nucleuses’ structure functions and EMC ratio [21,22,24,25]:

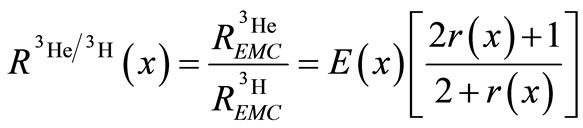(8)

where 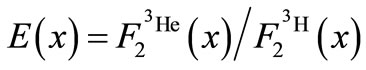and 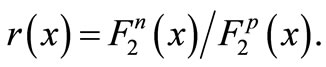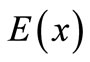is independent of As equation (8) indicates, 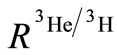is dependent upon 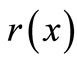in the momentum approximation. Consequently, can be achieved according to 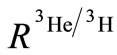and 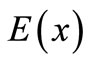as the below form [21, 23,27]:

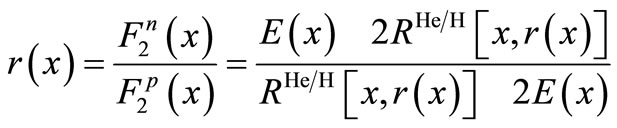(9)

In the momentum approximation, equation (9) is a self-consistent equation that affords a freedom to determine; and this equation can be written as the below iteration equation [16,21,22]:

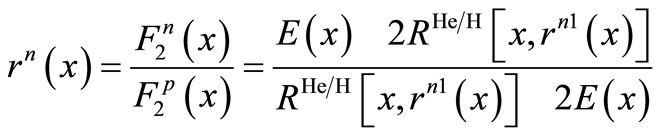(10)

First, a logical zero-order approximation, , is employed. On the one hand, 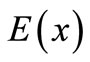must be substituted from empirical data so that its dependence on can be neglected; however, due to lack of empirical data on the tritium structure function, this quantity is simulated through the theoretical approximations that equations (1) to (3) are utilized herein to compute this proportion. The last issue is to determine. As proposed by Salme et al., can be considered as the following form [21,22]:

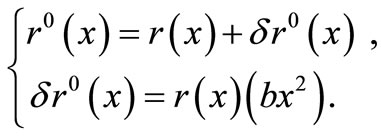(11)

with regards to the fact that the structure function of GRV research group is used for the structure function of free neutron and proton; therefore, is transformed into the following equation [21,22]:

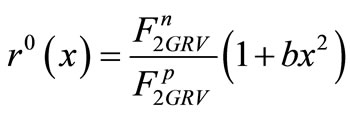(12)

In the above equation, b must be determined so that is not illogical. Salme et al. considered b = 0.5; consequently, at equals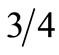. Considering the fact that 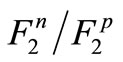can be within the range of to 4, it can be concluded that equation (12) is a logical approximation. The computation of 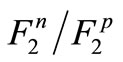with considering as equation (12) for n = 2 and n = 5 is illustrated in Figure 3. Moreover, Figure 3 demonstrates the empirical results of the proportion of the neutron structure function to proton structure function

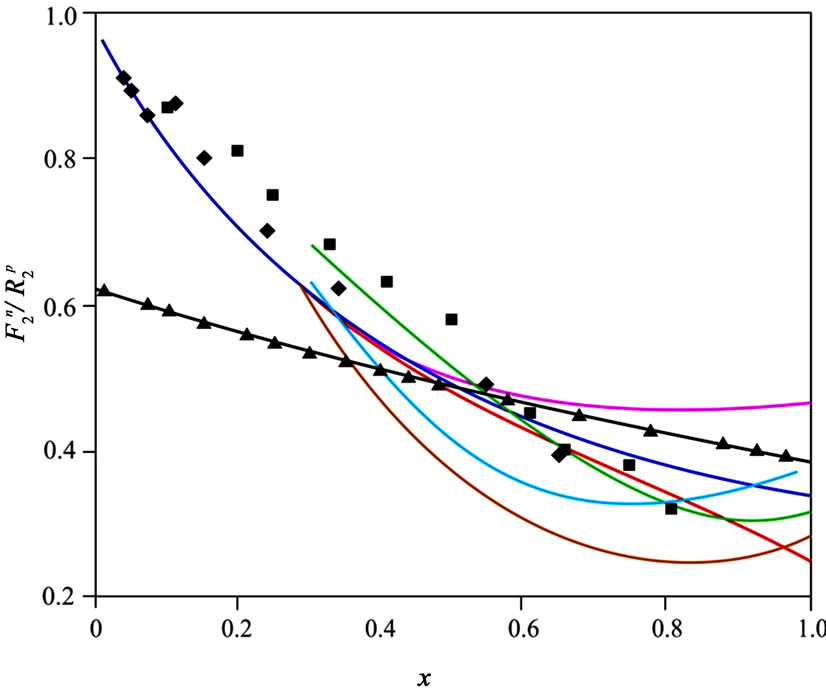
Figure 3. The computation results of the proportion of the neutron structure function to proton structure function through using the iteration self-consistent equation given in equation (10) (the purple line n = 2, and the dark blue line n = 5) are compared with the results obtained by Salme et al. [21,22] (the green line in which the nucleonic structure function achieved in the references [13,14] is used; the light blue line in which the nucleonic structure function achieved in the references [19,20] is used; the brown line is the results of the iteration self-consistent equation for n = 20 in which the nucleonic structure function achieved in the references [19,20] is used), the results of the reference [23] (line-triangle), the GRV group’s results (the red line), and also the empirical results of EMC (square) and SLAC (diamond).

that is computed through analyzing the structure function of deuteron and hydrogen. As is evident in this figure, by means of equation (10), 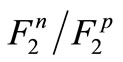for the large x (near to 1) approaches from (the empirical results) to 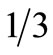that is satisfactory with regards to the descriptions given in the first section.

4. Conclusion

As a brief of this paper, first, the structure function of 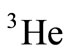and nucleuses is computed using the nuclear convolution model including the Fermi motion and nuclear binding energy. In these calculations, the results of the free nucleons structure function obtained by the GRV research group (Glück et al.) are utilized. 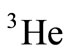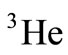More, the proportion of EMC for and nucleuses is achieved; the proportion of the neutron structure function to proton structure function as a self-consistent equation according to the structure function and EMC ratio of and 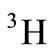nucleuses that can be written are reviewed. The obtained results are compared with other articles’ results (demonstrated in Figure 3). As can be observed in this figure, the computation results are satisfactory, and lead to improving the values of 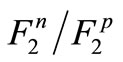at the large x.

5. Acknowledgements

The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.

REFERENCES

  1. M. Glück, E. Reya and A. Vogt, “Photonic Parton Distributions,” Physical Review D, Vol. 46, No. 5, 1992, pp. 1973-1979. doi:10.1103/PhysRevD.46.1973
  2. M. Glück, E. Reya and A. Vogt, “Dynamical Parton Distributions Revisited,” The European Physical Journal C, Vol. 5, No. 3, 1998, pp. 461-470. doi:10.1007/s100529800978
  3. M. Glück, E. Reya and A. Vogt, “Dynamical Parton Distributions of the Proton and Small-x Physics,” Zeitschrift für Physik C, Vol. 67, No. 3, 1995, pp. 433-447. doi:10.1007/BF01624586
  4. M. Glück, E. Reya and A. Vogt, “Parton Distributions for High Energy Collisions,” Zeitschrift für Physik C, Vol. 53, No. 1, 1992, pp. 127-134. doi:10.1007/BF01483880
  5. M. Glück, E. Reya and A. Vogt, “Parton Structure of the Photon beyond the Leading Order,” Physical Review D, Vol. 45, No. 11, 1992, pp. 3986-3994. doi:10.1103/PhysRevD.45.3986
  6. M. Glück, E. Reya and A. Vogt, “Pionic Parton Distributions,” Zeitschrift für Physik C, Vol. 53, No. 4, 1992, pp. 651-655. p://dx.doi.org/10.1007/BF01559743
  7. M. Glück, E. Reya and A. Vogt, “Radiatively Generated Parton Distributions for High Energy Collisions,” Zeitschrift für Physik C, Vol. 48, No. 3, 1990, pp. 471- 482. doi:10.1007/BF01572029
  8. M. Glück, E. Reya and A. Vogt, “Comparing Radiatively Generated Parton Distributions with Recent Measurements of F2(x, Q2) in the Small-x Region,” Physics Letters B, Vol. 306, No. 3-4, 1993, pp. 391-394. doi:10.1016/0370-2693(93)90096-Z
  9. M. Glück, E. Reya and A. Vogt, “Next-to-Leading-Order Radiative Parton Model Analysis of Polarized Deep Inelastic Lepton-Nucleon Scattering,” Physical Reviwe D, Vol. 53, No. 9, 1996, pp. 4775-4786. doi:10.1103/PhysRevD.53.4775
  10. M. Glück, E. Reya and A. Vogt, “Parton Fragmentation into Photons beyond the Leading Order,” Physical Reviwe D, Vol. 48, No. 1, 1993, pp. 116-128. doi:10.1103/PhysRevD.48.116
  11. M. Glück, E. Reya and A. Vogt, “Photonic Parton Distributions beyond the Leading Order. Heavy Quark and Dilepton Production at ep Colliders,” Physics Letters B, Vol. 285, No. 3, 1992, pp. 285-290. doi:10.1016/0370-2693(92)91466-M
  12. M. Glück, E. Reya and A. Vogt, “Radiatively Generated Hadronic Photon Structure at Low Q2,” Physics Letters B, Vol. 222, No. 1, 1989, pp. 149-151. doi:10.1016/0370-2693(89)90738-7
  13. J. J. Aubert, G. Bassompierre, K. H. Becks, C. Best, E. Böhm, X. de Bouard, F. W. Brasse, C. Broll, S. Brown, J. Carrj, R. W. Clifft, J. H. Cobb, G. Coignet, F. Combley, G. R. Court, G. D’Agostini, W. D. Dau, J. K. Davies, Y. Déclais, R. W. Dobinson, U. Dosselli, J. Drees, A. W. Edwards, M. Edwardsi, J. Favier, M. I. Ferrero, W. Flauger, E. Gabathuler, R. Gamet, J. Gayler, V. Gerhardt, C. Gössling, J. Haas, K. Hamacher, P. Hayman, M. Henckes, V. Korbel, U. Landgraf, M. Leenen, M. Maire, H. Minssieux, W. Mohr, H. E. Montgomery, K. Moser, R. P. Mount, P. R. Norton, J. McNicholas, A. M. Osborne, P. Payre, C. Peroni, H. Pessard, U. Pietrzyk, K. Rith, M. Schneegans, T. loan, H. E. Stier, W. Stockhausen, J. M. Thénard, J. C. Thompson, L. Urban, M. Villers, H. Wahlen, M. Whalley, D. Williams, W. S. C. Williams, J. Williamson and S. J. Wimpenny, “The Ratio of the Nucleon Structure Functions F2N for Iron and Deuterium,” Phyicss Letters B, Vol. 123, No. 3-4, 1983, pp. 275-278. doi:10.1016/0370-2693(83)90437-9
  14. J. J. Aubert, G. Bassompierre, K. H. Becks, C. Best, E. Böhm, X. de Bouard, F. W. Brasse, C. Broll, S. C. Brown, J. Carr, R. W. Clifft, J. H. Cobb, G. Coignet, F. Combley, G. D’Agostini, W. D. Dau, J. K. Davies, Y. Déclais, R. W. Dobinson, U. Dosselli, J. Drees, A. Edwards, M. Edwards, J. Favier, M. I. Ferrero, W. Flauger, E. Gabathuler, R. Gamet, J. Gayler, V. Gerhardt, V. Gibson, C. Gössling, J. Haas, K. Hamacher, P. Hayman, M. Henckes, V. Korbel, U. Landgraf, M. Leenen, M. Maire, W. Mohr, H. E. Montgomery, K. Moser, R. P. Mount, P. R. Norton, J. McNicholas, A. M. Osborne, P. Payre, C. Peroni, H. Pessard, U. Pietrzyk, P. B. Renton, K. Rith, M. Schneegans, T. Sloan, H. E. Stier, W. S. Stockhausen, J. M. Thénard, J. C. Thompson, L. Urbàn, H. Wahlen, M. Whalley, W. S. C. Williams, J. Williamson and S. J. Wimpenny, “Measurements of the Nucleon Structure Functions F2N in Deep Inelastic Muon Scattering from Deuterium and Comparison with Those from Hydrogen and Iron,” Nuclear Physics B, Vol. 293, 1987, pp. 740-786. doi:10.1016/0550-3213(87)90090-3
  15. J. G. H. de Groot, T. Hansl, M. Holder, J. Knobloch, J. May, H. P. Paar, P. Palazzi, A. Para, F. Ranjard, D. Schlatter, J. Steinberger, H. Suter, W. von Rüden, H. Wahl, S. Whitaker, E. G. H. Williams, F. Eisele, K. Kleinknecht, H. Lierl, G. Spahn, H. J. Willutzki, W. Dorth, F. Dydak, C. Geweniger, V. Hepp, K. Tittel, J. Wotschack, P. Bloch, B. Devaux, S. Loucatos, J. Maillard, J. P. Merlo, B. Peyaud, J. Rander, A. Savoy-Navarro, R. Turlay and F. L. Navarria, “Comparison of Moments from the Valence Structure Function with QCD Predictions,” Physics Letters B, Vol. 82, No. 2, 1979, pp. 292-296. doi:10.1016/0370-2693(79)90759-7
  16. I. R. Afnan, F. Bissey, J. Gomez, A. T. Katramatou, W. Melnitchouk, G. G. Petratos and A. W. Thomas, “Neutron Structure Function and A = 3 Mirror Nuclei,” Physics Letters B, Vol. 493, No. 1-2, 2000, pp. 36-42. doi:10.1016/S0370-2693(00)01012-1
  17. G. B. West, “Total Neutron Cross Sections May Not Be What They Seem to Be,” Physics Letters B, Vol. 37, No. 5, 1971, pp. 509-512. doi:10.1016/0370-2693(71)90358-3
  18. J. Kuti and V. F. Weisskopf, “Inelastic Lepton-Nucleon Scattering and Lepton Pair Production in the Relativistic Quark-Parton Model,” Physical Review D, Vol. 4, No. 11, 1971, pp. 3418-3439. doi:10.1103/PhysRevD.4.3418
  19. S. J. Brodsky, M Burkardt and I Schmidt, “QCD Constraints on the Shape of Polarized Quark and Gluon Distributions,” Nuclear Physics B, Vol. 441, No. 1-2, 1995, pp. 197-214. doi:10.1016/0550-3213(95)00009-H
  20. G. R. Farrar and D. R. Jackson, “Pion and Nucleon Structure Functions near x = 1,” Physical Review Letters, Vol. 35, No. 21, 1975, pp. 1416-1419. doi:10.1103/PhysRevLett.35.1416
  21. E. Pace, G. Salmè, S. Scopetta and A. Kievsky, “Neutron Structure Function F2n(x) from Deep Inelastic Electron Scattering off Few-Nucleon Systems,” Physical Review C, Vol. 64, No. 5, 2001, pp. 055203-055209. doi:10.1103/PhysRevC.64.055203
  22. E. Pace, C. Salmè and S. Scopetta, “Neutron Unpolarized Structure Function F2n(x) from Deep Inelastic Scattering off 3He and 3H,” Nuclear Physics A, Vol. 689, No. 1-2, 2001, pp. 453-456. doi:10.1016/S0375-9474(01)00877-6
  23. N. Isgur, “Quark Exchange Forces,” Nuclear Physics A, Vol. 497, 1989, pp. 91-107. doi:10.1016/0375-9474(89)90457-0
  24. J. C. Owen, R. F. Bishop and J. M. Irvine, “Model Nuclear Matter Calculations with a New Fermion Lowest Order Constrained Variational Method,” Nuclear Physics A, Vol. 274, No. 1-2, 1976, pp. 108-124. doi:10.1016/0375-9474(76)90230-X
  25. E. Krotscheck, “Variational Method for Liquid 3He. I. The Fermi Hypernetted-Chain Approach,” Journal of Low Temperature Physics, Vol. 27, No. 1-2, 1977, pp. 199-215. doi:10.1007/BF00654646
  26. S. V. Akulinichev, S. A. Kulagin and G. M. Vagradov, “The Role of Nuclear Binding in Deep Inelastic Lepton-Nucleon Scattering,” Physics Letters B, Vol. 158, No. 6, 1985, pp. 485-488. doi:10.1016/0370-2693(85)90799-3
  27. S. V. Akulinichev, S. Shlomo, S. A. Kulagin and G. M. Vagradov, “Lepton-Nucleus Deep-Inelastic Scattering,” Physical Review Letters, Vol. 55, No. 21, 1985, pp. 2239- 2241. doi:10.1103/PhysRevLett.55.2239

NOTES

*Corresponding author.

Journal Menu >>