Journal of Modern Physics
Vol.2 No.12(2011), Article ID:9038,5 pages DOI:10.4236/jmp.2011.212192
Frequency-Concentration Dependence of Optical Activity of a Non-Ideal 1D-Superlattice
Physics Technology Department, A.A. Galkin Donetsk Institute for Physics and Engineering of National Academy of Sciences, Donetsk, Ukraine
E-mail: rumyants@teor.fti.ac.donetsk.ua
Received August 11, 2011; revised October 16, 2011; accepted November 10, 2011
Keywords: Light propagation, Non-ideal 1D-superlattice, Optical activity, Exciton region of the spectrum
ABSTRACT
In the present work the widths of layers constituting the non-ideal superlattice are much bigger then the characteristic scales of space dispersion. In such a case the contribution of individual layers to gyrotropy can be regarded as independed. Thus the corresponding optical quantities can be expressed through the layers’ gyrotropic characteristics. This approach is applied to calculate the specific rotation angle of plane of polarization of light propagating through a nonideal 1D-superlattice, which varies in composition as well as in layers’ width. We carry out numerical calculation of the frequency dispersion of optical activity of a non-ideal superlattice, which includes impurity layers with point defects.
1. Introduction
The procedures used to calculate the transmission coefficients and refractive indices for light developed in [1] allow the frequency-concentration dependence is exposed and turn out to be useful in simulation of composite materials with preset parameters with no spatial dispersion taken into account. At the same time, the investigation of the gyrotropy of crystals is often the only way to determine stereoand crystallochemical characteristics as well as the fine details in construction of respective space-dispersing structures. Such investigations are even more urgent as now there exists a large quantity of organic complexes and polymers, which are optically active due to structure peculiarities or to the optical activity of molecules they are composed of [2,3].
The problem of finding polariton modes (necessary for calculating gyrotropic characteristics) in spatially dispersed superlattices remains as yet unsolved. At the same time it allows for an approximate treatment at an assumption that the widths of the layers comprising a multilayer much exceed the characteristic scales of space dispersion. In such a case the contribution of individual layers to gyrotropy can be regarded as independent. With regard to the natural optical activity (NOA) this means that a sole knowledge of the layerwise specific angles of rotation  (
(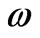 —is the frequency of light,
—is the frequency of light,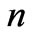 —is the number of the elementary cell in a one-dimensional superlattice,
—is the number of the elementary cell in a one-dimensional superlattice,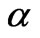 —is the number of the layer in the given cell) and the concentration of impurity layers (if any) is sufficient for finding the total specific angle of rotation
—is the number of the layer in the given cell) and the concentration of impurity layers (if any) is sufficient for finding the total specific angle of rotation . In paper [4] the described approximation is adopted for calculation of
. In paper [4] the described approximation is adopted for calculation of 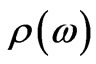 in a 1D superlattice comprising randomly distributed impurity layers, whose composition and/or the widths differ from those of the corresponding layers of an ideal system. The obtained expression for
in a 1D superlattice comprising randomly distributed impurity layers, whose composition and/or the widths differ from those of the corresponding layers of an ideal system. The obtained expression for 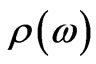 permits to carry out numerical modeling of the concentration dependence of optical activity; this is done in [5] for a SiO2-liquid-crystal multilayer. For a specified microscopic expression for
permits to carry out numerical modeling of the concentration dependence of optical activity; this is done in [5] for a SiO2-liquid-crystal multilayer. For a specified microscopic expression for 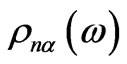 the proposed approach enables to identify the dominating experimentally relevant mechanisms of gyrotropy as well as to determine the connection of the given function to the micro-characteristics of the medium (such as dipole, quadrupole, magneto-dipole moments of the structural units etc.) and to find the corresponding frequency characteristics. Of special interest are the superlattices comprised by macroscopically homogeneous systems, which include point defects. In such a case
the proposed approach enables to identify the dominating experimentally relevant mechanisms of gyrotropy as well as to determine the connection of the given function to the micro-characteristics of the medium (such as dipole, quadrupole, magneto-dipole moments of the structural units etc.) and to find the corresponding frequency characteristics. Of special interest are the superlattices comprised by macroscopically homogeneous systems, which include point defects. In such a case 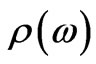 is a function not only of the concentration of impurity layers, but of the concentration of point defects as well. In the present work we carry out numerical calculation of the frequency dispersion of optical activity of a non-ideal superlattice, which includes impurity molecular layers. This extends the capabilities of modeling of composite materials so that their gyrotropic properties and parameters of disordering can be continuously varied.
is a function not only of the concentration of impurity layers, but of the concentration of point defects as well. In the present work we carry out numerical calculation of the frequency dispersion of optical activity of a non-ideal superlattice, which includes impurity molecular layers. This extends the capabilities of modeling of composite materials so that their gyrotropic properties and parameters of disordering can be continuously varied.
2. Modeling
The above-mentioned approach [4,5] gives the following expression for the angle of optical rotation 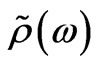 in an imperfect topologically ordered one-dimensional superlattice composed of N unit cells:
in an imperfect topologically ordered one-dimensional superlattice composed of N unit cells:
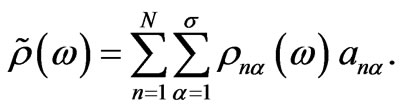 (1)
(1)
We assume N to be big enough to be able to do configuration averaging. In (1)  and
and 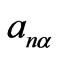 are the configuration-dependent specific angle of the light propagation plane rotation and thickness of the α-th layer of the n-th unit cell; σ is the number of unit-cell layers.
are the configuration-dependent specific angle of the light propagation plane rotation and thickness of the α-th layer of the n-th unit cell; σ is the number of unit-cell layers.
According to the general principles of the physics of disordered systems, the rotation angle measured experimentally should be equal to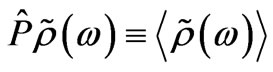 , where
, where 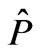 is the configuration averaging operator [6] influencing the configuration-dependent function
is the configuration averaging operator [6] influencing the configuration-dependent function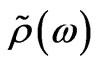 . In the imperfect 1D-superlattice under consideration, the disordering is of two types, consequently, there are two types of configuration dependence. The first disorder is due to heterogeneous (defective) layers present in the superlattice, which differ from the perfect-system layers in composition (the configuration-dependent quantity is
. In the imperfect 1D-superlattice under consideration, the disordering is of two types, consequently, there are two types of configuration dependence. The first disorder is due to heterogeneous (defective) layers present in the superlattice, which differ from the perfect-system layers in composition (the configuration-dependent quantity is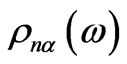 ). The second disordering is caused by the presence of layer defects that differ from an ideal superlattice in thickness (the corresponding configuration-dependent quantity is
). The second disordering is caused by the presence of layer defects that differ from an ideal superlattice in thickness (the corresponding configuration-dependent quantity is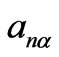 ).
).
Below we consider propagation of linearly polarized light through an imperfect molecular superlattice with two elements-layers per cell, one layer being a mixed molecular crystal and the second being an orientationally disordered crystal. In such a case the expression for the specific angle of optical rotation 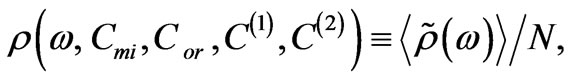 as it follows from
as it follows from
[5], has the form:
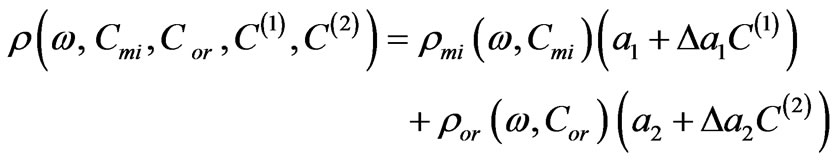 (2)
(2)
where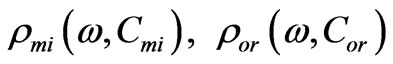 —specific rotation angles for mixed and orientationally disordered molecular crystals;
—specific rotation angles for mixed and orientationally disordered molecular crystals;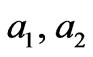 —thicknesses of first and second layers of corresponding perfect superlattice;
—thicknesses of first and second layers of corresponding perfect superlattice;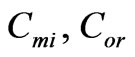 —concentrations of isotopic impurities and orientationally disordered molecules,
—concentrations of isotopic impurities and orientationally disordered molecules,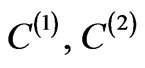 —concentrations of foreign layers in relevant sublattices with thickness differing
—concentrations of foreign layers in relevant sublattices with thickness differing 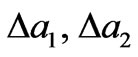 from those of the perfect system. Here each of the summands has the sense of the rotation angle (by a corresponding sublattice) per one unit cell.
from those of the perfect system. Here each of the summands has the sense of the rotation angle (by a corresponding sublattice) per one unit cell.
In the most general case, the specific rotation angle 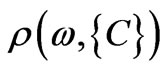 for a multicomponent topologically ordered impurity (including both mixed and orientationally disordered) molecular crystal with a primitive lattice in the exciton region of the spectrum is, within the framework of single-level model, of the form:
for a multicomponent topologically ordered impurity (including both mixed and orientationally disordered) molecular crystal with a primitive lattice in the exciton region of the spectrum is, within the framework of single-level model, of the form:
 . (3)
. (3)
Here —volume of the unit cell of molecular crystal, r—number of molecular groups, each relating to a definite
—volume of the unit cell of molecular crystal, r—number of molecular groups, each relating to a definite 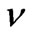 -th or
-th or 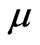 -th type of molecules;
-th type of molecules; 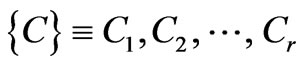 . Quantities
. Quantities 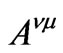 and
and 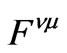 are:
are:
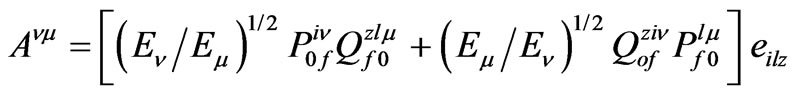 ,(4)
,(4)
 (5)
(5)
In formulae (4), (5) —Levy-Civita tensor,
—Levy-Civita tensor,  ,
,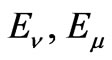 —molecular excitation energies,
—molecular excitation energies,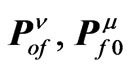 —matrix elements of the dipole-moment operators,
—matrix elements of the dipole-moment operators, 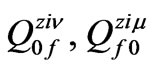 —matrix elements of operators derived from operators of molecular currents of the
—matrix elements of operators derived from operators of molecular currents of the 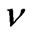 -th and
-th and 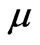 -th molecular types, respectively. Matrix
-th molecular types, respectively. Matrix  is locator function and matrix
is locator function and matrix 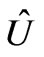 is proportional to matrix
is proportional to matrix 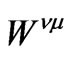 of the resonance intermolecular interaction (figuring in exciton Hamiltonian [7]).
of the resonance intermolecular interaction (figuring in exciton Hamiltonian [7]).
3. Results and Discussion
Let us consider the propagation of electromagnetic radiation in an imperfect SiO2/liquid crystal layered system. The results of modeling the concentration dependence of the specific angle of rotation for this non-ideal superstructure presented in Figure 1. Corresponding gyrotropic characteristics of such 1D superlattice are 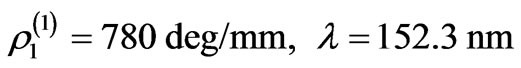 , (for SiO2) and
, (for SiO2) and 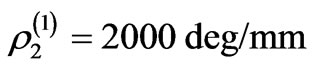 (for model liquid crystal sublattice). The thickness of base-substance layer are denoted by
(for model liquid crystal sublattice). The thickness of base-substance layer are denoted by 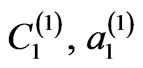 and
and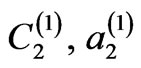 , respectively,
, respectively, 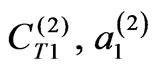 and
and  are those of the impurity (index Т stands for variation of impurity layers in thickness).
are those of the impurity (index Т stands for variation of impurity layers in thickness).
For non-ideal superlattice, which includes impurity
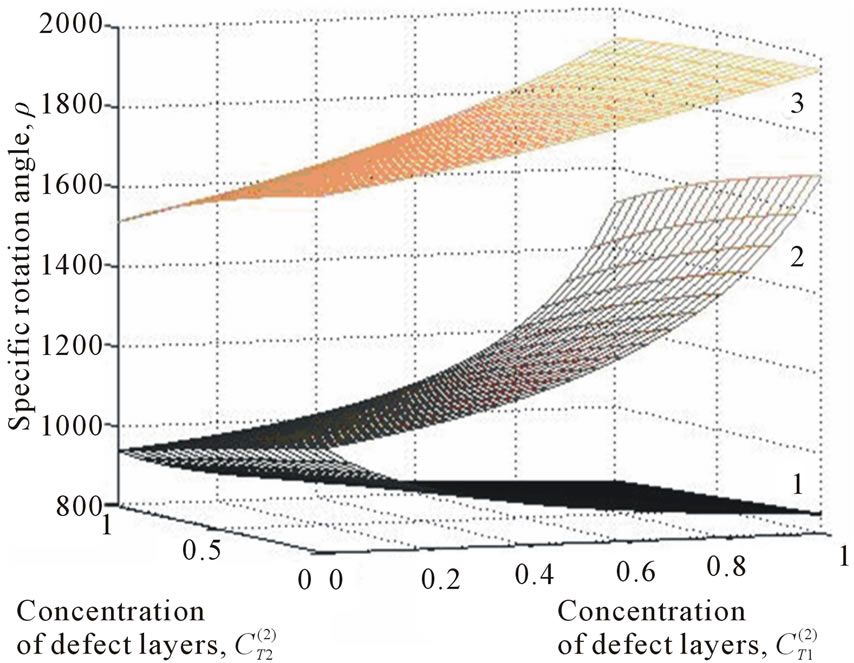
Figure 1. Concentration dependence of the specific angle 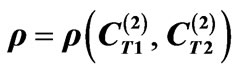 for SiO2-liquid crystal imperfect superlattice;
for SiO2-liquid crystal imperfect superlattice;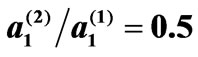 ,
, 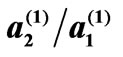 and
and 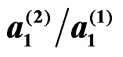 being equal 0.3 and 0.5, 0.3 and 0.1, 3 and 0.1 for cases 1, 2, 3 respectively.
being equal 0.3 and 0.5, 0.3 and 0.1, 3 and 0.1 for cases 1, 2, 3 respectively.
molecular crystal layers with point defects sublattice, we use values 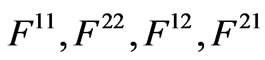 in mononodal approximation [8]. For numerical calculations we limit ourselves with the case out of variety of types of the optical-activity concentration dependence for certain frequencies of electromagnetic wave (see Figure 2):
in mononodal approximation [8]. For numerical calculations we limit ourselves with the case out of variety of types of the optical-activity concentration dependence for certain frequencies of electromagnetic wave (see Figure 2):  Corresponding dependence of exciton energy levels of binary system on concentration of isotopic impurities and orientationally disordered molecules shown in Figures 3.
Corresponding dependence of exciton energy levels of binary system on concentration of isotopic impurities and orientationally disordered molecules shown in Figures 3.
The character of the frequency-concentration dependence of rotator power is specified by the relative position of exciton energies and by values of parameters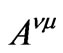 ,
,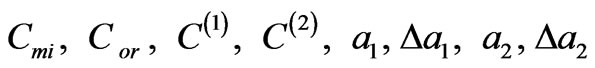 .
.
In particular calculations it is considered that for a mixed molecular crystal it can be, within a good accuracy, assumed [9]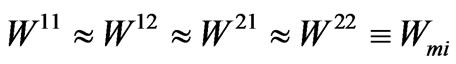 ,
,
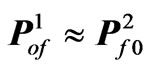 ,
, 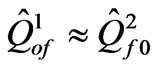 (as a consequence, all
(as a consequence, all
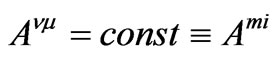 ). For an orientationally disordered molecular crystal [10]
). For an orientationally disordered molecular crystal [10]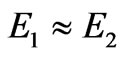 . It is assumed that for a mixed molecular crystal
. It is assumed that for a mixed molecular crystal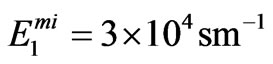 ,
,
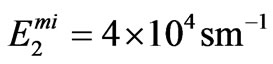 ,
, 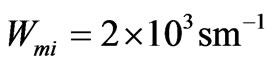 , whereas for the orientationally disordered one—
, whereas for the orientationally disordered one—
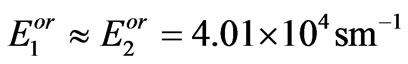 ,
, 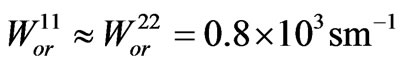 ,
, 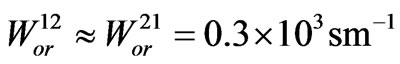 and
and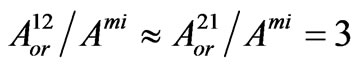 ,
, 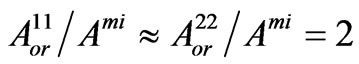 . Here, the numerical simulation was done for the following values of concentration of heterogeneous superlattice layers:
. Here, the numerical simulation was done for the following values of concentration of heterogeneous superlattice layers: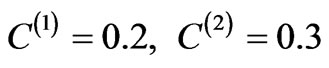 , and for relative thicknesses
, and for relative thicknesses 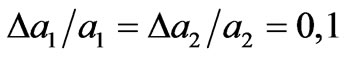 (
(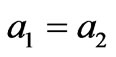 ). The concentration dependences of the specific rotation angle of light are graphically shown in Figures
). The concentration dependences of the specific rotation angle of light are graphically shown in Figures
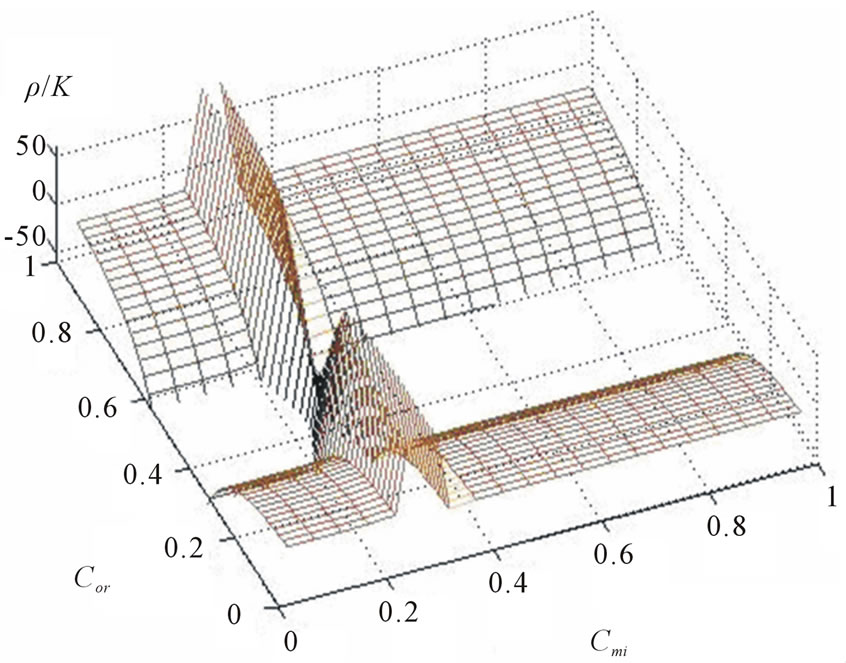
Figure 2. Concentration dependence of the specific rotation angle 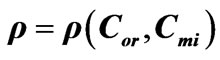 for
for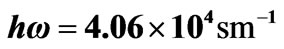 .
.
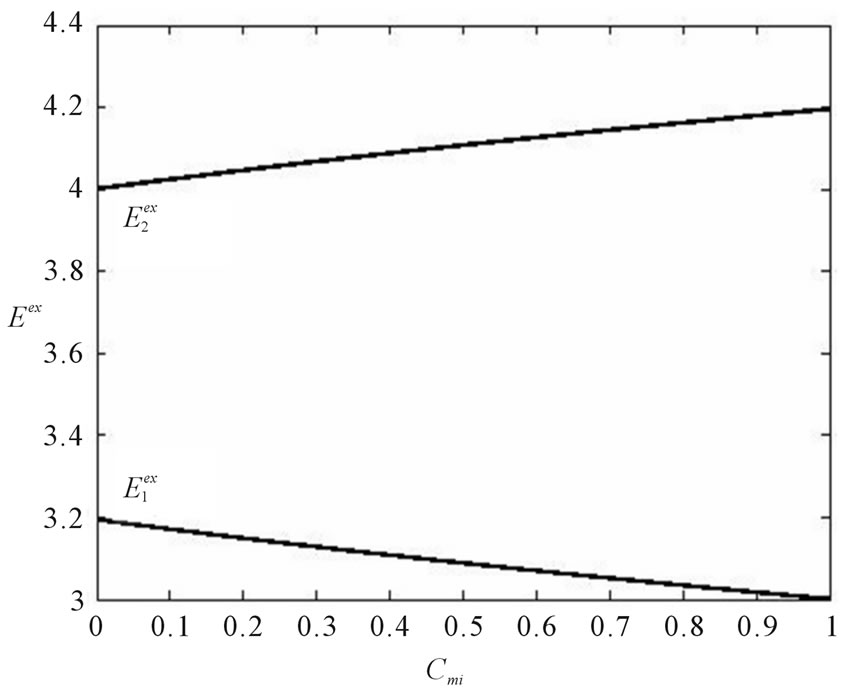
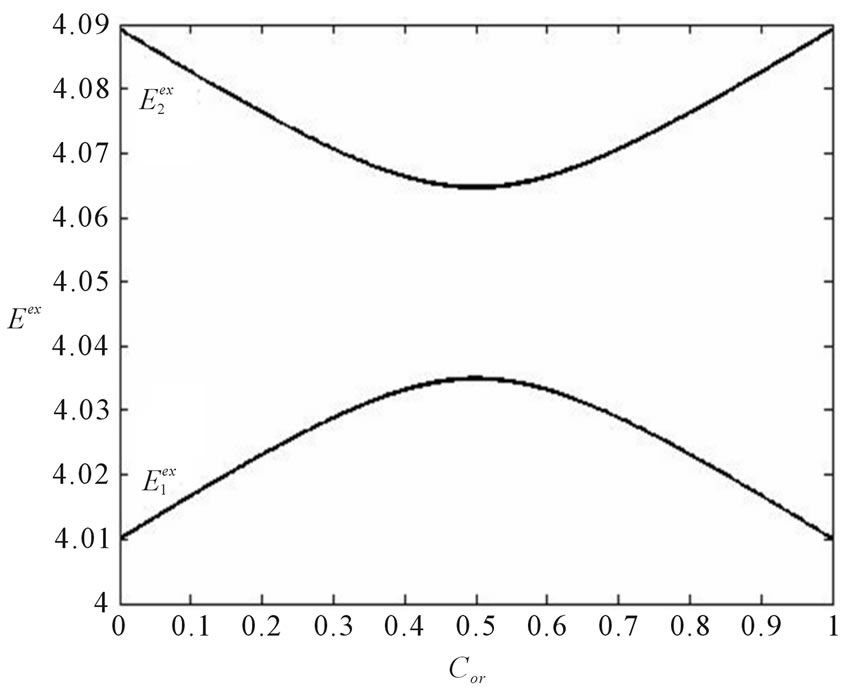
Figure 3. Concentration dependence of exciton energy levels of a binary molecular crystal with point defects: upper ; lower
; lower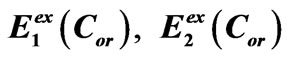 .
.
2-4 in relative units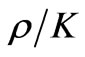 , where
, where 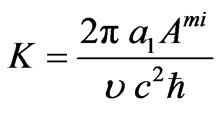 (see
(see
(3)).
The frequency dependences of the specific rotation angle 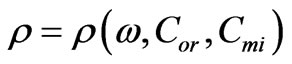 for specific values of concentration
for specific values of concentration 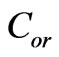 and
and 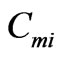 is illustrated in Figures 4 and 5. It is seen that changes in concentration
is illustrated in Figures 4 and 5. It is seen that changes in concentration 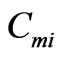 with
with 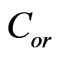 constant result in mutual removal of resonance frequencies (Figure 4), whereas changes in
constant result in mutual removal of resonance frequencies (Figure 4), whereas changes in  with
with 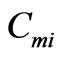 constant – in their approaching (Figure 5).
constant – in their approaching (Figure 5).
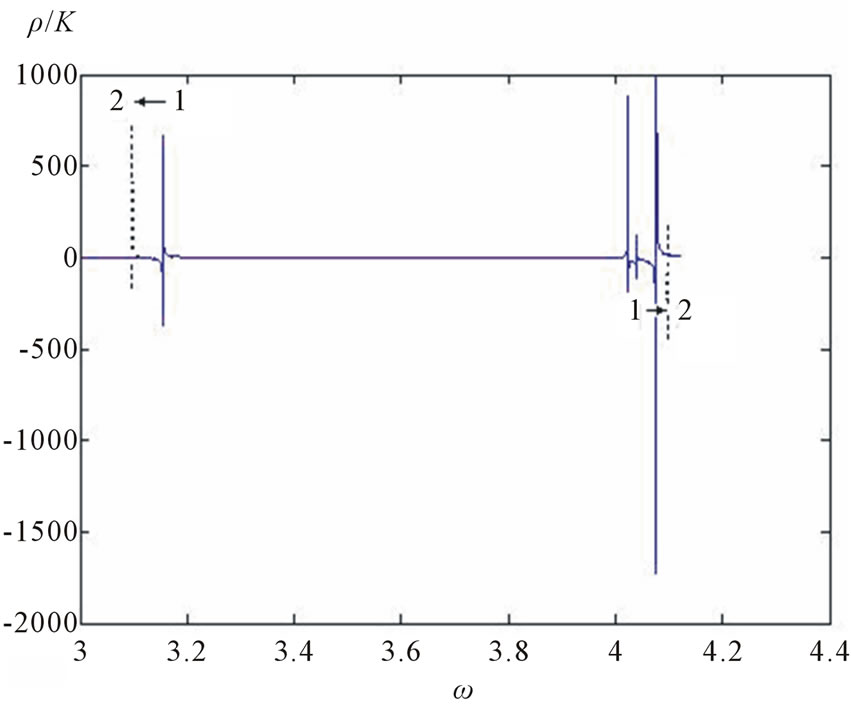
Figure 4. Frequency dependences of the specific rotation angle 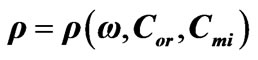 for values of concentration
for values of concentration 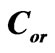 and
and 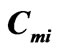 equal, respectively, to case 1—0.2 and 0.17; 2— 0.2 and 0.45.
equal, respectively, to case 1—0.2 and 0.17; 2— 0.2 and 0.45.
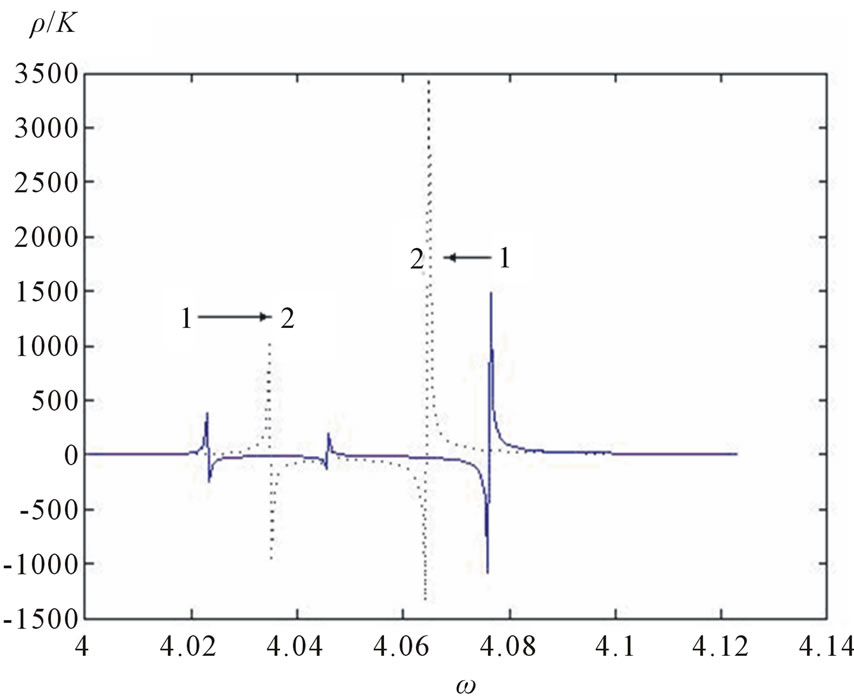
Figure 5. Frequency dependences of the specific rotation angle 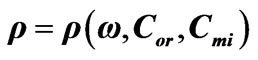 for values of concentration
for values of concentration 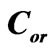 and
and 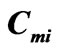 equal, respectively, to case 1—0.2 and 0.2; 2—0.5 and 0.2.
equal, respectively, to case 1—0.2 and 0.2; 2—0.5 and 0.2.
4. Conclusions
The present microscopic consideration of dispersion of the optical activity of imperfect 1D-multilayer material is helpful for a numerical simulation of the frequencyconcentration dependence of the specific rotation angle for molecular superlattices in the exciton region of the spectrum.
The model was a two-sublattice system with parameters typical of orientationally disordered and mixed molecular crystals. Gyrotropy features due to disorder types have been studied. An 1D-superlattice with layers containing point defects has been investigated. This creates additional possibilities for simulation of optically active multilayer composite materials.
5. Acknowledgements
The authors are grateful to Dr. Esfir Shtaerman for his help in numerical simulation. This work is supported by Project “Dynamical and static properties of complex low-dimensional systems in external fields” of National Academy of Sciences of Ukraine.
REFERENCES
- A. Yariv and P. Yeh, “Optical Waves in Crystals,” John Willey & Sons, New York, 1987.
- A. J. Ryan and R. A. L. Jones, “Polymers: The Quest for Motility,” Materials Today, Vol. 11, No. 7-8, 2008, pp. 21-23. doi:10.1016/S1369-7021(08)70145-7
- M. L. Sierra, R.Kumar, V. S. J. De Mel and J. P. Oliver, “Synthesis and Spectroscopic Investigations of Alkylaluminum Alkoxides Derived from Optically Active Alcohols. The First Structural Identification of an Optically Active Organoaluminum Alkoxide,” Organometallics, Vol. 11, No. 1, 1992, pp. 206-214. doi:10.1021/om00037a039
- V. V. Rumyantsev and S. A. Fedorov, “Optical Rotation of Linearly Polarized Light Propagating through a Nonideal 1D-Superlattice,” Materials Sciences and Applications, Vol. 1, No. 1, 2010, pp. 32-35. doi:10.4236/msa.2010.11006
- V. V. Rumyantsev, S. A. Fedorov and K. V. Gumennyk, “Optical Rotation of a Nonideal Liquid Crystal Superlattice,” Liquid Crystals and Their Application, Vol. 3, 2009, pp. 55-60.
- J. M. Ziman, “Models of Disorder,” John Willey & Sons, New York, 1979.
- Yu. G. Pashkevich and S. A. Fedorov, “Gyrotropy of Molecular Crystals with Vacancies,” Optics and Spectroscopy, Vol. 88, No. 3, 2000, pp. 448-452. doi:10.1134/1.626816
- V. V. Rumyantsev and S. A. Fedorov, “Optical Activity of Dielectric Superlattices with Defects,” Optics and Spectroscopy, Vol. 110, No. 5, 2011, pp. 799-805. doi:10.1134/S0030400X11050122
- O. A. Dubovskii, “The Theory of Shape of Light Absorption Exciton Bands in Crystals,” Fizika Tverdogo Tela, Vol. 15, 1973, pp. 205-211.
- O. A. Dubovskii, “Line Shape of Exciton Absorption of Light in Orientation-Disordered Crystals,” Fizika Tverdogo Tela, Vol. 13, 1971, pp. 3032-3034.

