Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8060 , 7 pages DOI:10.4236/jmp.2011.210151
Bianchi Type-II, VIII & IX Perfect Fluid Cosmological Models in Brans Dicke Theory of Gravitation
Department of Applied Mathematics, Andhra University, Visakhapatnam, India
E-mail: umrao57@hotmail.com
Received March 26, 2011; revised May 23, 2011; accepted June 6, 2011
Keywords: Bianchi Type-II, VIII & IX, Brans Dicke Scalar Tensor Theory, Perfect Fluid Distribution
ABSTRACT
Field equations in the presence of perfect fluid distribution are obtained in a scalar tensor theory of gravitation proposed by Brans and Dicke [1] with the aid of Bianchi type-II, VIII & IX metrics. Exact prefect fluid Bianchi type-IX cosmological model is presented since other models doesn’t exist in Brans-Dicke scalar tensor theory of gravitation. Some physical and geometrical properties of the models are also discussed.
1. Introduction
Brans and Dicke [1] theory of gravitation is well known modified version of Einstein’s theory. It is a scalar tensor theory in which the gravitational interaction is mediated by a scalar field 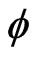 as well as the tensor field
as well as the tensor field 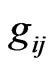 of Einstein’s theory. In this theory the scalar field
of Einstein’s theory. In this theory the scalar field 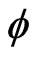 has the dimension of the inverse of the gravitational constant.In recent years, there has been a renewed interest of the gravitational constant. The latest inflationary models (Mathiazhagan and Johri [2]), possible “graceful exit” problem (Pimental [3]) and extended chaotic inflations (Linde [4]) are based on Brans and Dicke theory of gravitation.
has the dimension of the inverse of the gravitational constant.In recent years, there has been a renewed interest of the gravitational constant. The latest inflationary models (Mathiazhagan and Johri [2]), possible “graceful exit” problem (Pimental [3]) and extended chaotic inflations (Linde [4]) are based on Brans and Dicke theory of gravitation.
Brans-Dicke field equations for combined scalar and tensor field are
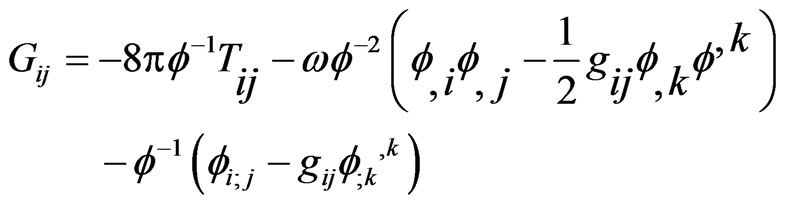 (1.1)
(1.1)
and
 (1.2)
(1.2)
where  is an Einstein tensor,
is an Einstein tensor,
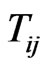 is the stress energy tensor of the matter,
is the stress energy tensor of the matter, ![]() is the dimensionless coupling constant and comma and semicolon denote partial and covariant differentiation respecttively.
is the dimensionless coupling constant and comma and semicolon denote partial and covariant differentiation respecttively.
The equation of motion
 (1.3)
(1.3)
is a consequence of the field Equations (1.1) and (1.2).
Several aspects of Brans-Dicke cosmology have been extensively investigated by many authors. The work of Singh and Rai [5] gives a detailed discussion of BransDicke cosmological models. In particular, spatially homogeneous Bianchi models in Brans-Dicke theory in the presence of perfect fluid with or with out radiation are quite important to discuss the early stages of evolution of the universe.
Nariai [6], Belinskii and Khalatnikov [7], Reddy and Rao [8], Banerjee and Santos [9], Singh et al. [10], Shriram [11], Shriram and Singh [12], Berman et al. [13], Reddy [14], Reddy et al. [15], Adhav et al. [16] and Rao et al. [17,18] are some of the authors who have investigated several aspects of this theory.
Chakraborty [19], Raj Bali and Dave [20], Raj Bali and Yadav [21] studied Bianchi type IX string as well as viscous fluid models in general relativity. Reddy, Patrudu and Venkateswarlu [22] studied Bianchi typeII, VIII & IX models in scale covariant theory of gravitation. Shanthi and Rao [23] studied Bianchi type-VIII & IX models in Lyttleton-Bondi Universe. Also Rao and Sanyasi Raju [24] and Sanyasi Raju and Rao [25] have studied Bianchi type-VIII & IX models in Zero mass scalar fields and self creation cosmology. Rahaman et al. [26] have investigated Bianchi type-IX string cosmological model in a scalar-tensor theory formulated by Sen [27] based on Lyra [28] manifold. Rao et al. [29-31] have studied Bianchi type-II, VIII & IX string cosmological models, perfect fluid cosmological models in SaezBallester scalar-tensor theory of gravitation and string cosmological models in general relativity as well as self creation theory of gravitation respectively.
In this paper we discuss Bianchi type-II, VIII & IX perfect fluid cosmological models in a scalar-tensor theory proposed by Brans and Dicke [1].
2. Metric and Energy Momentum Tensor
We consider a spatially homogeneous Bianchi type-II, VIII and IX metrics of the form
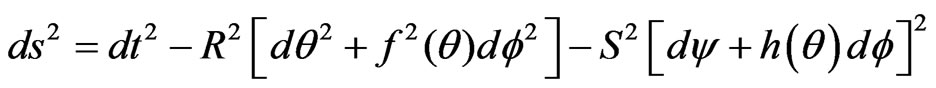 (2.1)
(2.1)
where 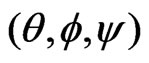 are the Eulerian angles,
are the Eulerian angles,  and
and ![]() are functions of t only. It represents Bianchi type-II if
are functions of t only. It represents Bianchi type-II if 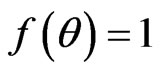 and
and 
Bianchi type-VIII if  and
and 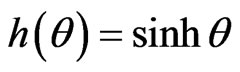
Bianchi type-IX if 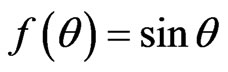 and
and 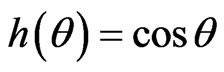
The energy momentum tensor for perfect fluid distribution is given by
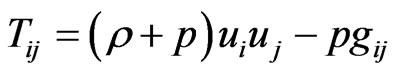 (2.2)
(2.2)
where r is the density and ![]() is the pressure.
is the pressure.
Also
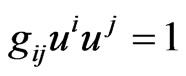 (2.3)
(2.3)
In the co moving coordinate system, we have from Equations (2.2) and (2.3)
 ,
, and
and 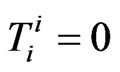 for
for 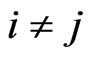 (2.4)
(2.4)
The quantities 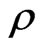 and
and ![]() are functions of “t” only.
are functions of “t” only.
3. Bianchi Type-II, VIII & IX Perfect Fluidcosmological Models in Brans-Dicke Theory of Gravitation
The field Equations (1.1), (1.2) & (1.3) for the metric (2.1) with the help of Equations (2.2), (2.3) and (2.4) can be written as
 (3.1)
(3.1)
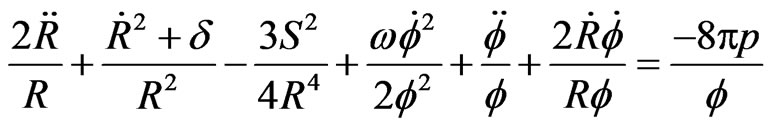 (3.2)
(3.2)
 (3.3)
(3.3)
 (3.4)
(3.4)
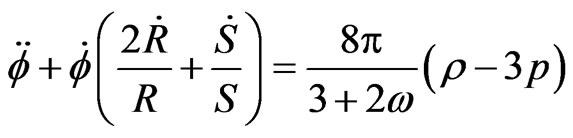 (3.5)
(3.5)
and
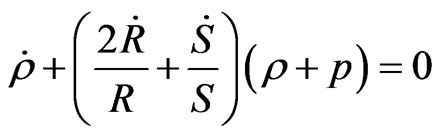 (3.6)
(3.6)
where “ ” denotes differentiation with respect to “t”.
” denotes differentiation with respect to “t”.
When ![]() = 0, –1 & +1, the field Equations (3.1)-(3.6) correspond to the Bianchi type-II, VIII & IX universes respectively.
= 0, –1 & +1, the field Equations (3.1)-(3.6) correspond to the Bianchi type-II, VIII & IX universes respectively.
Using the transformation ,
, ,
,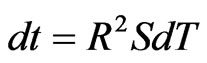 , where
, where ![]() and
and 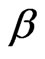 are functions of “T” only.
are functions of “T” only.
The field Equations (3.1) to (3.6) reduce to
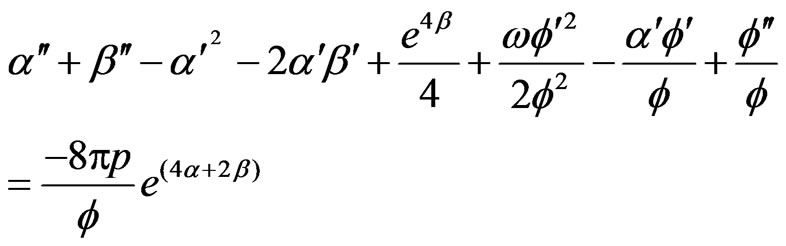 (3.7)
(3.7)
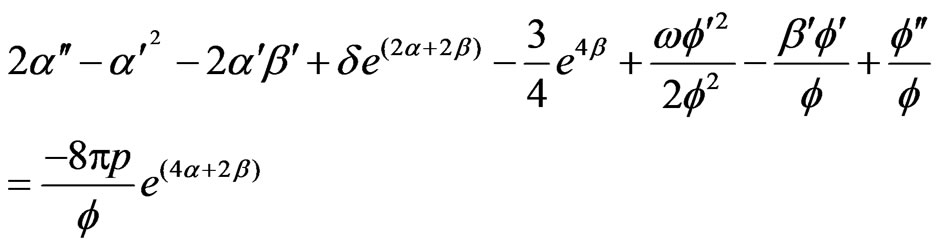 (3.8)
(3.8)
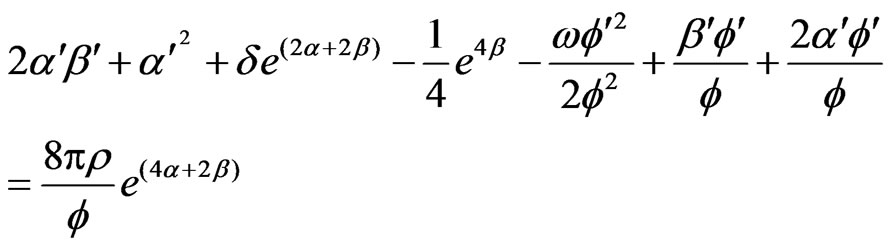 (3.9)
(3.9)
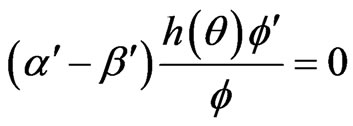 (3.10)
(3.10)
 (3.11)
(3.11)
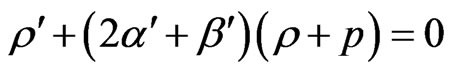 (3.12)
(3.12)
where “ ′ ” denotes differentiation with respect to “T”.
Since we are considering the Bianchi type-II, VIII and IX metrics, we have ,
, 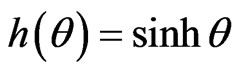 &
& 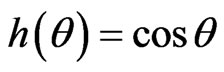 for Bianchi type-II, VIII and IX metrics respectively. Therefore, from the Equation (3.10), we will consider the following possible cases with
for Bianchi type-II, VIII and IX metrics respectively. Therefore, from the Equation (3.10), we will consider the following possible cases with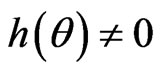 .
.
1)  and
and 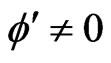
2) 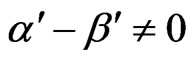 and
and 
3)  and
and 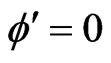
CASE (1): 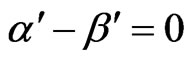 and
and :
:
Here, we get 
Without loss of generality by taking the constant of integration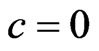 , we get
, we get
 (3.13)
(3.13)
By using (3.13), the field Equations (3.7) to (3.12) will reduce to
 (3.14)
(3.14)
 (3.15)
(3.15)
 (3.16)
(3.16)
 (3.17)
(3.17)
 (3.18)
(3.18)
where “ ′ ” denotes differentiation with respect to “T”.
From (3.14) and (3.15), we have
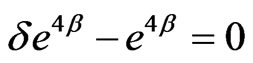 (3.19)
(3.19)
From (3.19), we observe that, we can’t find Bianchi type-II (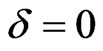 ) and VIII (
) and VIII (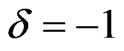 ) perfect fluid cosmological models in Brans-Dicke theory of gravitation. But we can get Bianchi type-IX
) perfect fluid cosmological models in Brans-Dicke theory of gravitation. But we can get Bianchi type-IX 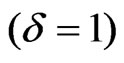 perfect fluid cosmological model in Brans-Dicke theory of gravitation.
perfect fluid cosmological model in Brans-Dicke theory of gravitation.
For , the field Equations (3.14)-(3.18) reduce to
, the field Equations (3.14)-(3.18) reduce to
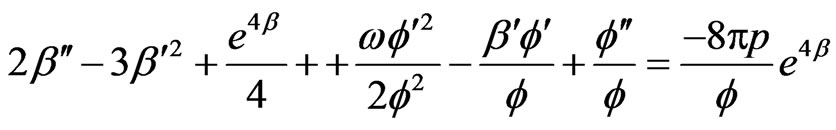 (3.20)
(3.20)
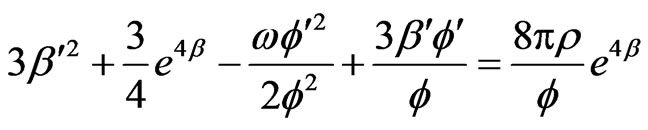 (3.21)
(3.21)
 (3.22)
(3.22)
 (3.23)
(3.23)
From (3.20), (3.21) & (3.23), we get
 (3.24)
(3.24)
Then from (3.24), we get
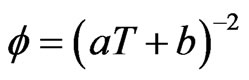 (3.25)
(3.25)
 (3.26)
(3.26)
with the relation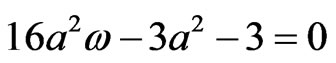 , where
, where  are arbitrary constants.
are arbitrary constants.
Using (3.25) & (3.26) in (3.20) & (3.21), we get
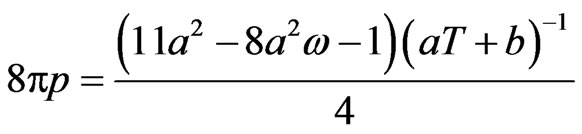 (3.27)
(3.27)
 (3.28)
(3.28)
The corresponding metric can be written in the form
 (3.29)
(3.29)
Thus (3.29) together with (3.27) and (3.28) constitutes an exact Bianchi type-IX perfect fluid cosmological model in Brans-Dicke scalar-tensor theory of gravitation.
PHYSICAL AND GEOMETRICAL PROPERTIES:
The volume element of the Bianchi type-IX perfect fluid cosmological model is given by
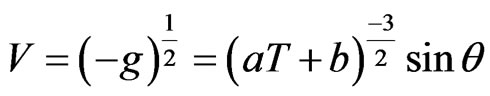
We can observe that the spatial volume 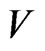 decreases as time “
decreases as time “![]() ” increases, i.e., the model is contracting. Also the model has initial singularity at
” increases, i.e., the model is contracting. Also the model has initial singularity at ,
, 
The scalar expansion 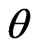 and shear
and shear ![]() are given by
are given by

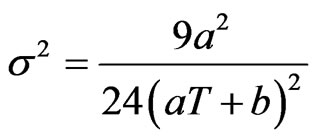
for Bianchi type-IX perfect fluid cosmological model in Brans-Dicke theory of gravitation. The scalar expansion 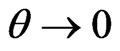 as
as  and
and 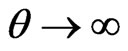 as
as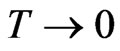 . So, the rate of expansion is rapid as time decreases and it becomes slow as time increases. The shear scalar
. So, the rate of expansion is rapid as time decreases and it becomes slow as time increases. The shear scalar 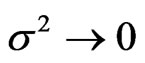 as
as 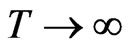 and
and 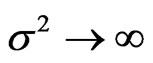 as
as . Thus the shape of universe changes uniformly. The deceleration parameter q is obtained as
. Thus the shape of universe changes uniformly. The deceleration parameter q is obtained as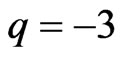 . The negative value of q indicates that the model is inflationary. Since
. The negative value of q indicates that the model is inflationary. Since 
which confirms that the universe remains anisotropic throughout the evolution.
CASE (2): 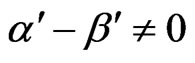 and
and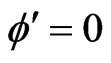 :
:
In this case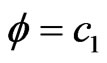 , where
, where ![]() is a constant of integration, without loss of generality we can take
is a constant of integration, without loss of generality we can take .
.
Hence the field Equations (3.7) to (3.12) reduce to general relativity field equations with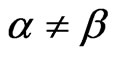 .
.
 (3.30)
(3.30)
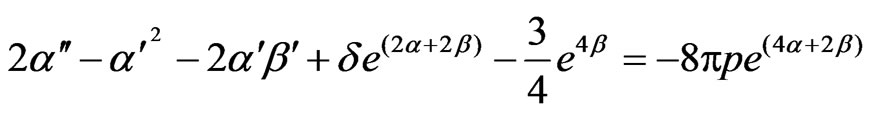 (3.31)
(3.31)
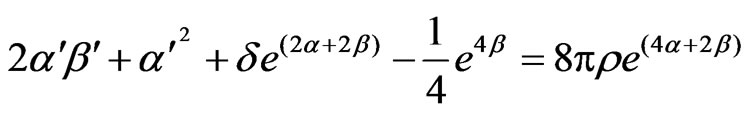 (3.32)
(3.32)
 (3.33)
(3.33)
 (3.34)
(3.34)
From (3.33), we get
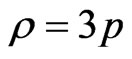 (3.35)
(3.35)
Since , we will get only radiating universe in this case.
, we will get only radiating universe in this case.
The field Equations (3.30) to (3.34) reduce to
 (3.36)
(3.36)
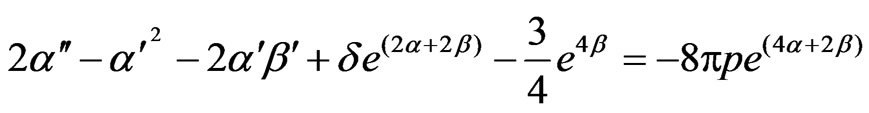 (3.37)
(3.37)
 (3.38)
(3.38)
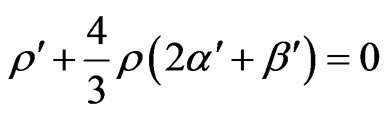 (3.39)
(3.39)
From (3.36) to (3.38), we have
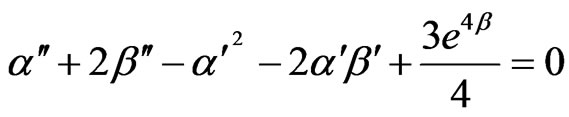 (3.40)
(3.40)
Then from (3.40), we get
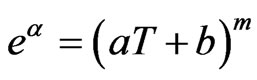 (3.41)
(3.41)
 (3.42)
(3.42)
where![]() ,
, ![]() and
and  are arbitrary constants satisfying
are arbitrary constants satisfying
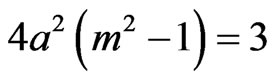 ,
, .
.
FOR BIANCHI TYPEII METRIC :
:
From (3.36)-(3.38), we get
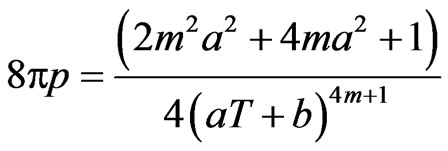 (3.43)
(3.43)
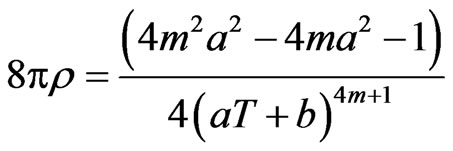 (3.44)
(3.44)
The corresponding metric can be written in the form
 (3.45)
(3.45)
Thus (3.45) together with (3.43) & (3.44) constitutes Bianchi type-II Perfect fluid radiating cosmological models in general theory of relativity.
FOR BIANCHI TYPE-VIII METRIC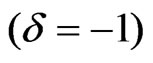 :
:
From (3.36)-(3.38), we get
 (3.46)
(3.46)
 (3.47)
(3.47)
The corresponding metric can be written in the form
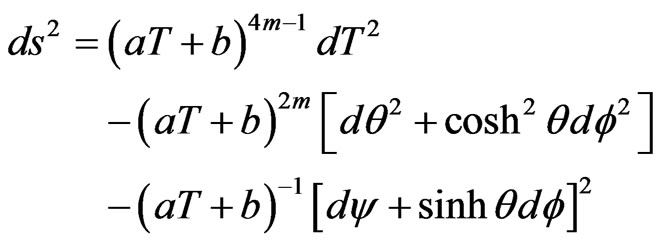 (3.48)
(3.48)
Thus (3.48) together with (3.46) & (3.47) constitutes Bianchi type-VIII Perfect fluid radiating cosmological models in general theory of relativity.
FOR BIANCHI TYPE-IX METRIC :
:
From (3.36)-(3.38), we get
 (3.49)
(3.49)
 (3.50)
(3.50)
The corresponding metric can be written in the form
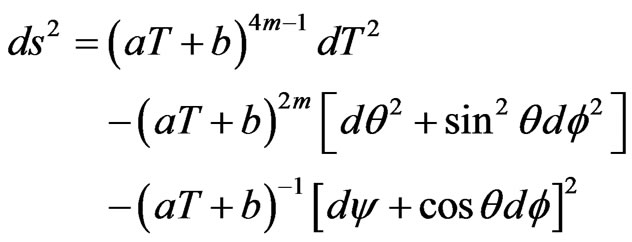 (3.51)
(3.51)
Thus (3.51) together with (3.49) & (3.50) constitutes Bianchi type-IX Perfect fluid radiating cosmological models in general theory of relativity.
PHYSICAL AND GEOMETRICAL PROPERTIES:
The volume element of the above three models [(3.45), (3.48) & (3.51)] are given by

where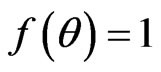 , sinhθ and sinθ respectively.
, sinhθ and sinθ respectively.
In the above expressions, the volume decreases as time increases if  i.e., the models are contracting, the volume increases as time increases if
i.e., the models are contracting, the volume increases as time increases if 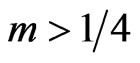 i.e., the models are expanding and the volume is independent of time T if
i.e., the models are expanding and the volume is independent of time T if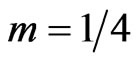 . Also the models have initial singularity at
. Also the models have initial singularity at ,
,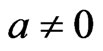 .
.
The expansion  and shear
and shear ![]() are equal for all Bianchi type-II, VIII & IX perfect fluid radiating cosmological models in general relativity. Which are given by
are equal for all Bianchi type-II, VIII & IX perfect fluid radiating cosmological models in general relativity. Which are given by
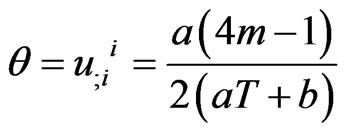

The deceleration parameter
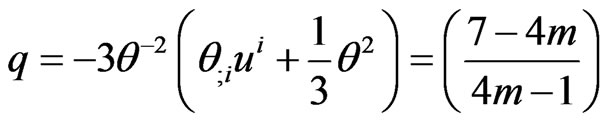
It can be seen that for large “![]() ” the quantities
” the quantities  and
and ![]() will become zero if
will become zero if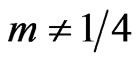 . Also the quantities
. Also the quantities  and
and ![]() tends to +∞ as
tends to +∞ as  if
if  and tends to –∞ if
and tends to –∞ if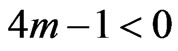 .Thus the rate of expansion is rapid as time decreases, it becomes slow as time increases and the shape of universe changes uniformly. In the case of
.Thus the rate of expansion is rapid as time decreases, it becomes slow as time increases and the shape of universe changes uniformly. In the case of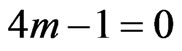 , we can see that the Spatial Volume “V” is independent of time “T” and
, we can see that the Spatial Volume “V” is independent of time “T” and ,
, ![]() will become zero.
will become zero.
Also, since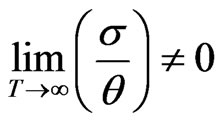 , the models are not isotropic for large T. The negative value of the deceleration parameter q shows that the models inflate except for m = 1.
, the models are not isotropic for large T. The negative value of the deceleration parameter q shows that the models inflate except for m = 1.
CASE (3): 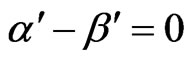 and
and 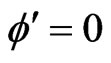
Here, we get 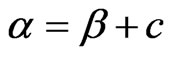
Without loss of generality by taking the constant of integration , we get
, we get
 (3.52)
(3.52)
Since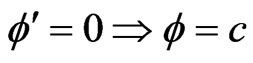 where
where ![]() is a constant of integration, without loss of generality we can take
is a constant of integration, without loss of generality we can take .
.
Hence the field equations (3.7) to (3.12) reduce to general relativity field equations with .
.
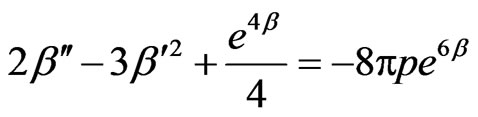 (3.53)
(3.53)
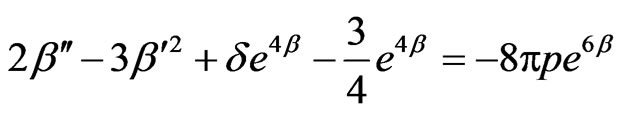 (3.54)
(3.54)
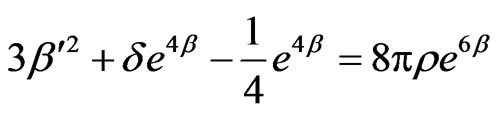 (3.55)
(3.55)
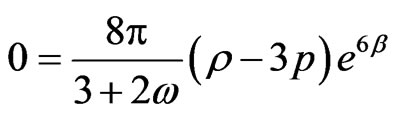 (3.56)
(3.56)
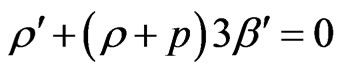 (3.57)
(3.57)
where “ ′ ” denotes differentiation with respect to “T”.
From (3.53) and (3.54), we have
 (3.58)
(3.58)
From (3.58), we observe that, we can’t find Bianchi type II ( ) and VIII (
) and VIII ( ) perfect fluid cosmological models of general relativity. But we can get only Bianchi type IX
) perfect fluid cosmological models of general relativity. But we can get only Bianchi type IX 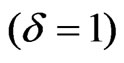 perfect fluid cosmological model of general relativity.
perfect fluid cosmological model of general relativity.
For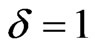 , the field equations (3.53)-(3.57) reduce to
, the field equations (3.53)-(3.57) reduce to
 (3.59)
(3.59)
 (3.60)
(3.60)
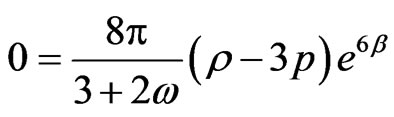 (3.61)
(3.61)
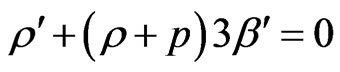 (3.62)
(3.62)
From (3.61), we get
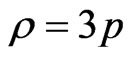 (3.63)
(3.63)
Since from , we will get only radiating universe in this case.
, we will get only radiating universe in this case.
Now from (3.59), (3.60) and (3.61), we have
 (3.64)
(3.64)
From (3.64), we get
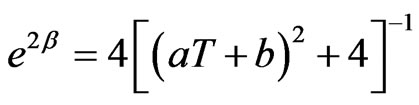 (3.65)
(3.65)
Using (3.65) in (3.59) & (3.60), we get
 (3.66)
(3.66)
The corresponding metric can be written in the form
 (3.67)
(3.67)
Thus (3.67) together with (3.66) constitutes Bianchi type-IX radiating perfect fluid cosmological model in general theory of relativity.
PHYSICAL AND GEOMETRICAL PROPERTIES:
The volume element of the model (3.67) is given by

Now the expression for expansion  and shear
and shear ![]() are given by
are given by

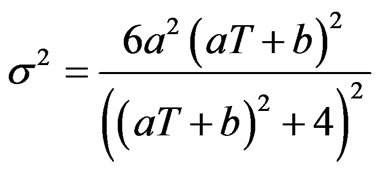
for Bianchi type-IX perfect fluid radiating cosmological model in Brans-Dicke theory of gravitation. The spatial volume tends to zero as T→∞. Thus the model is contracting with the increase of time and also the model has no real singularity. The deceleration parameter q is obtained as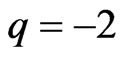 . The negative value of q indicates that the model is inflationary. Also, since
. The negative value of q indicates that the model is inflationary. Also, since 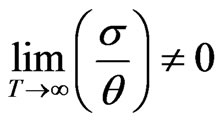
which confirms that the universe remains anisotropic throughout the evolution.
4. Conclusions
Bianchi type space-times play a vital role in understanding and description of the early stages of evolution of the universe. In particular, the study of Bianchi type-II, VIII & IX universes are important because familiar solutions like FRW universe with positive curvature, the desitter universe, the Taub-Nut solutions etc correspond of Bianchi type-II, VIII & IX space-times. In view of the importance of Bianchi type-II, VIII & IX spacetimes and also since exact solutions offer an alternative and complementary approach to study various cosmological models, in this paper we have presented Bianchi type-II, VIII & IX perfect fluid cosmological models in BransDicke theory of gravitation.
In case of 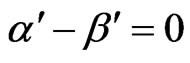 and
and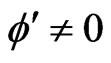 , we can observe that the only Bianchi type-IX perfect fluid cosmological model exists in Brans-Dicke theory of gravitation. The model is anisotropic, inflationary and has initial singularity at
, we can observe that the only Bianchi type-IX perfect fluid cosmological model exists in Brans-Dicke theory of gravitation. The model is anisotropic, inflationary and has initial singularity at ,
, . Also established the non-existence of Bianchi type-II & VIII perfect fluid cosmological models in this theory. Since “a” is an arbitrary constant and “ω” is a coupling constant, it is always possible to assign specific values to “a” and “ω” to keep the pressure “p” (3.27) and density “ρ” (3.28) be always positive.
. Also established the non-existence of Bianchi type-II & VIII perfect fluid cosmological models in this theory. Since “a” is an arbitrary constant and “ω” is a coupling constant, it is always possible to assign specific values to “a” and “ω” to keep the pressure “p” (3.27) and density “ρ” (3.28) be always positive.
In case of 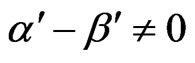 and
and , we can observe that Bianchi type-II, VIII & IX perfect fluid radiating cosmological models of general relativity exist in this theory. The models have initial singularity at
, we can observe that Bianchi type-II, VIII & IX perfect fluid radiating cosmological models of general relativity exist in this theory. The models have initial singularity at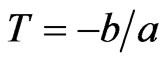 ,
, 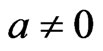 and remain anisotropic throughout the evolution.
and remain anisotropic throughout the evolution.
In case of 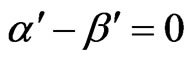 and
and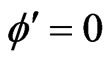 , we have obtained only Bianchi type-IX anisotropic radiating perfect fluid cosmological model of general relativity with
, we have obtained only Bianchi type-IX anisotropic radiating perfect fluid cosmological model of general relativity with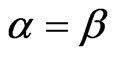 . In this case also we have observed that Bianchi type-II & VIII cosmological models doesn’t exist in this theory.
. In this case also we have observed that Bianchi type-II & VIII cosmological models doesn’t exist in this theory.
REFERENCES
- H. Brans and R. H. Dicke, “Mach’s Principle and a Relativistic Theory of Gravitation,” Physical Review A, Vol. 124, No. 3, 1961, pp.925-935. doi:10.1103/PhysRev.124.925
- C. Mathiazhagan and V. B. Johri, “An Inflationary Universe in Brans-Dicke Theory: A Hopeful Sign of Theoretical Estimation of the Gravitational Constant,” Classical and Quantum Gravity, Vol. 1, No.2, 1984, pp. L29- L32. doi:10.1088/0264-9381/1/2/005
- L. O. Pimentel, “New Exact Vacuum Solutions in BransDicke Theory,” Modern Physics Letters A, Vol. 12, No. 25, 1997, pp. 1865-1870. doi:10.1142/S0217732397001904
- A. D. Linde, “Extended Chaotic Inflation and Spatial Variations of the Gravitational Constant,” Physics Letters B, Vol. 238, No. 2-4, 1990, pp. 160-165. doi:10.1016/0370-2693(90)91713-L
- T. Singh and L. N. Rai, “Scalar-Tensor Theories of Gravitation: Foundations and Prospects,” General Relativity and Gravitation, Vol. 15, No. 9, 1983, pp. 875-902. doi:10.1007/BF00778798
- H. Nariai, “Hamiltonian Approach to the Dynamics of Expanding Homogeneous Universes in the Brans-Dicke Cosmology,” Progress of Theoretical Physics, Vol. 47, No. 6, 1972, pp. 1824-1843. doi:10.1143/PTP.47.1824
- V. A. Belinskii and I. M. Khalatnikov, “Effect of Scalar and Vector Fields on the Nature of the Cosmological Singularity,” Soviet Physics—JETP, Vol. 36, No. 4, 1973, pp. 591-597.
- D. R. K. Reddy and V. U. M. Rao, “Field of a Charged Particle in Brans-Dicke Theory of Gravitation,” Journal of Physics A: Mathematical and General, Vol. 14, No. 8, 1981, pp. 1973-1976. doi:10.1088/0305-4470/14/8/021
- A. Banerjee and N. O. Santos, “Bianchi Type-II Cosmological Models in Brans-Dicke Theory,” Il Nuovo Cimento B, Vol. 67, No. 1, 1982, pp. 31-40. doi:10.1007/BF02721068
- T. Singh, L. N. Rai and T. Singh, “An Anisotropic Cosmological Model in Brans-Dicke Theory,” Astrophysics and Space Science, Vol. 96, No. 1, 1983, pp. 95-105.
- S. Ram, “Spatially Homogeneous and Anisotropic Cosmological Solution in Brans-Dicke Theory,” General Relativity and Gravitation, Vol. 15, No. 7, 1983, pp. 635- 640. doi:10.1007/BF00759040
- S. Ram and D. K. Singh, “LRS Bianchi Type-V Vacuum Cosmological Solution in Brans-Dicke Theory,” Astrophysics and Space Science, Vol. 98, No. 1, 1984, pp. 193- 196. doi:10.1007/BF00651959
- M. S. Berman, M. M. Som and F. M. Gomide, “BransDicke Static Universes,” General Relativity and Gravitation, Vol. 21, No. 3, 1989, pp. 287-292. doi:10.1007/BF00764101
- D. R. K. Reddy, “A String Cosmological Model in a Scalar-Tensor Theory of Gravitation,” Astrophysics and Space Science, Vol. 286, No. 3-4, 2003, pp. 359-363. doi:10.1023/A:1026370732619
- D. R. K. Reddy and R. L. Naidu, “Five Dimensional String Cosmological Models in a Scalar-Tensor Theory of Gravitation,” Astrophysics and Space Science, Vol. 307, No. 4, 2007, pp. 395-398. doi:10.1007/s10509-007-9387-x
- K. S. Adhav, A. S. Nimkar and M. V. Dawande, “NDimensional String Cosmological Model in Brans-Dicke Theory of Gravitation,” Astrophysics and Space Science, Vol. 310, No. 3-4, 2007, pp. 231-235. doi:10.1007/s10509-007-9506-8
- V. U. M. Rao, T. Vinutha, M. V. Shanthi and K. V. S. Sireesha, “Exact Bianchi Type-V Perfect Fluid Cosmological Models in Brans-Dicke Theory of Gravitation,” Astrophysics and Space Science, Vol. 315, No. 1-4, 2008, pp. 211-214. doi:10.1007/s10509-008-9820-9
- V. U. M. Rao, T. Vinutha and M. V. Santhi, “Bianchi Type-V Cosmological Model with Perfect Fluid Using Negative Constant Deceleration Parameter in a Scalar Tensor Theory Based on Lyra Manifold,” Astrophysics and Space Science, Vol. 314, No. 1-3, 2008, pp. 213-216. doi:10.1007/s10509-008-9757-z
- S. Chakraborty, “A Study on Bianchi-IX Cosmological Model,” Astrophysics and Space Science, Vol. 180, No. 2, 1991, pp. 293-303. doi:10.1007/BF00648184
- R. Bali and S. Dave, “Bianchi Type IX String Cosmological Model in General Relativity,” Pramana Journal of Physics, Vol. 56, No. 4, 2001, pp. 513-518. doi:10.1007/s12043-001-0100-2
- R. Bali and M. K. Yadav, “Bianchi Type-IX Viscous Fluid Cosmological Model in General Relativity,” Pramana Journal of Physics, Vol. 64, No. 2, 2005, pp. 187- 196. doi:10.1007/BF02704873
- D. R. K. Reddy, B. M. Patrudu and R. Venkateswarlu, “Exact Bianchi Type-II, VIII and IX Cosmological Models in Scale-Covariant Theory of Gravitation,” Astrophysics and Space Science, Vol. 204, No. 1, 1993, pp. 155-160. doi:10.1007/BF00658101
- K. Shanthi and V. U. M. Rao, “Bianchi Type-II and III Models in Self-Creation Cosmology,” Astrophysics and Space Science, Vol. 179, No.1, 1991, pp. 147-153. doi:10.1007/BF00642359
- V. U. M. Rao and Y. V. S. S. Sanyasiraju, “Exact Bianchi-Type VIII and IX Models in the Presence of ZeroMass Scalar Fields,” Astrophysics and Space Science, Vol. 187, No. 1, 1992, pp.113-117. doi:10.1007/BF00642691
- Y. V. S. S. Sanyasiraju and V. U. M. Rao, “Exact Bianchi-Type VIII and IX Models in the Presence of the Self-Creation Theory of Cosmology,” Astrophysics and Space Science, Vol. 189, No. 1, 1992, pp. 39-43. doi:10.1007/BF00642950
- F. Rahaman, S. Chakraborty, N. Begum, M. Hossain and M. Kalam, “Bianchi-IX String Cosmological Model in Lyra Geometry,” Pramana Journal of Physics, Vol. 60, No. 6, 2003, pp. 1153-1159. doi:10.1007/BF02704282
- D. K. Sen, “A Static Cosmological Model,” Zeitschrift for Physics A, Vol. 149, No. 3, 1957, pp. 311-323.
- G. Lyra, “Über eine Modifikation der Riemannschen Geometrie,” Mathematische Zeitschrift, Vol. 54, No. 1, 1951, pp. 52-64. doi:10.1007/BF01175135
- V. U. M. Rao, M. V. Santhi and T. Vinutha, “Exact Bianchi Type-II, VIII and IX String Cosmological Models in Saez-Ballester Theory of Gravitation,” Astrophysics and Space Science, Vol. 314, No. 1-3, 2008, pp. 73-77. doi:10.1007/s10509-008-9739-1
- V. U. M. Rao, M. V. Santhi and T. Vinutha, “Exact Bianchi Type-II, VIII and IX Perfect Fluid Cosmological Models in Saez-Ballester Theory of Gravitation,” Astrophysics and Space Science, Vol. 317, No. 1-2, 2008, pp. 27-30. doi:10.1007/s10509-008-9849-9
- V. U. M. Rao, M. V. Santhi and T. Vinutha, “Exact Bianchi Type-II, VIII and IX String Cosmological Models in General Relativity and Self-Creation Theory of Gravitation,” Astrophysics and Space Science, Vol. 317, No. 1-2, 2008, pp. 83-88. doi:10.1007/s10509-008-9859-7

