Received 2 May 2016; accepted 27 June 2016; published 30 June 2016

ABSTRACT

The main theorem of the present paper is the bistability theorem for a four dimensional cancer model, in the variables 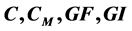representing primary cancer C, metastatic cancer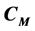, growth factor GF and growth inhibitor GI, respectively. It says that for some values of the para- meters this system is bistable, in the sense that there are exactly two positive singular points of this vector field. And one is stable and the other unstable. We also find an expression for 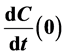for the discrete model T of the introduction, with variables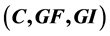, where C is cancer, 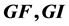are growth factors and growth inhibitors respectively. We find an affine vector field Y whose time one map is T² and then compute, where 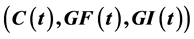is an integral curve of Y through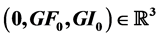. We also find a formula for the first escape time for the vector field associated to T, see section four.

Keywords:

Bistability, Cancer, Mass Action Kinetic System, Discrete Dynamical System

1. Introduction

1.1. Summary of the Paper

We continue the study of the cancer model from Larsen (2016) [1] . The model is

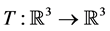
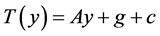
where

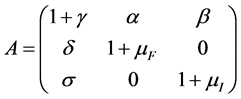
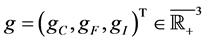are birth rates and T denotes transpose. Here is chemotherapy

and 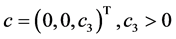is immune therapy. The parameters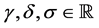, , ,. We have shown previously Larsen (2016) [1] , that there are affine vector fields on, such that their time one map is T, when the eigenvalues of A have positive real part. This enables you to find a formula for the rate of change of cancer growth in. The characteristic polynomial of A is

when The discriminant of this polynomial is

The eigenvalues are

In section two we prove the Bistability Theorem for a mass action kinetic system of metastatic cancer and primary cancer C. The model also has growth factors and growth inhibitors. We show that for some values of the parameters there are exactly two positive singular points where We prove that is unstable and is stable, when one of the rate constants is small.

For we have: if the eigenvalue of A has then one can find an affine vector field, whose time one map is. Similarly, when and the eigenvalues of the cha- racteristic polynomial of A are nonzero, then one can find an affine vector field on, whose time one map is. This enables us to find a formula for the rate of change of cancer growth in This is the subject of Section 3.

The phase space of our model T is. In section four we show, that when, , , orbits of the vector field associated to T will escape phase space for both and. We obtain a formula for the first escape time. There is a similar treatment for

1.2. The Litterature

uPAR (urokinase plasminogen activator receptor) is a cell surface protein, that is associated with invasion and metastasis of cancer cells. In Liu et al. (2014) [2] a cytoplasmic protein Sprouty1 (SPRY1) an inhibitor of the (Ras-mitogen activated protein kinase) MAPK pathway is shown to interact with uPAR and cause it to be degraded. Overexpression of SPRY1 in HCT116 or A549 xenograft in athymic nude mice, led to great suppression of tumor growth. SPRY1 is an inhibitor of the MAPK pathway. Several cancer cells have a low basal expression of SPRY1, e.g. breast, prostate and liver cancer. SPRY1 promotes the lysosomal mediated degradation of uPAR. SPRY1 overexpression results in a decreased expression of uPAR protein. This paper suggests that SPRY1 regulates cell adhesion through an uPAR dependant mechanism. SPRY1 inhibits proliferation via two distinct pathways: 1) SPRY1 is an intrinsic inhibitor of the Raf/MEK/ERK pathway; 2) SPRY1 promotes degradation of uPAR, which leads to inhibition of FAK and ERK activation.

According to Luo and Fu (2014), [3] EGFR (endoplasmic growth factor receptor) tyrosine kinase inhibitors (TKIs) are very efficient against tumors with EGFR activating mutations in the EGFR intracytoplasmic tyrosin kinase domain and cell apoptosis was the result. However some patients developed resistance and this reference aimed to elucidate molecular events involved in the resistance to EGFR-TKIs. The first EGFR-TKI s to be approved by the FDA (Food and Drug Administration, USA) for treatment of NSCLC (non small cell lung cancer) were gefitinib and erlotinib. The mode of action is known. These drugs bind to the ATP binding site of EGFR preventing autophosphorylation and then blocking downstream signalling cascades of pathways RAS/ RAF/MEK/ERK and PI3K/AKT with the results, proliferation inhibition, cell cycle progression delay and cell apoptosis.

There are several important monographs relevant to the present paper, see Adam & Bellomo (1997), [4] , Geha & Notarangelo (2012), [5] , Murphy (2012), [6] , Marks (2009), [7] , Molina (2011), [8] .

2. A mass Action Kinetic Model of Metastatic Cancer

The main result of this section is Theorem 1 below that proves the bistability of the mass action kinetic system (1) to (8). Consider then the mass action kinetic system from Larsen (2016), [9] , in the species primary cancer cells, metastatic cancer cells, growth factor, growth inhibitor respectively.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

The complexes are And this defines the rate constants. With mass action kinetics the ODE s become

all We shall now find the singular points of this vector field denoted

But first we state a theorem, we shall next prove. A positive (nonnegative) singular point

of f is a singular point of f, such that Define

Theorem 1 Assume When there are exactly two positive singular points

where is unstable. Given such that

and, then there exists such that

is stable when

Consider a singular point of f and linearize

Setting the last coordinate of f equal to zero gives

when Now insert this into the first and second coordinates of f to get

(9)

and

(10)

When we get from (9)

and from (10) we get

This means that B simplifies to

Let denote the matrix you obtain by deleting row three and column three in B. Then

Also

The characteristic polynomial of is denoted

Finally

In Larsen (2016) [9] , we found two cubic polynomials such that

whenever is a nonnegative singular point of f. We shall need the following lemma.

Lemma 1 Assume Then

where

Proof. The coefficient to is according to Larsen (2016), [9]

and The coefficient to is according to Larsen (2016), [9]

Everything cancels out and leaves a zero. The coefficient to is according to Larsen (2016), [9]

Square and multiply to get

Everything cancels out except

The coefficient to is according to Larsen (2016), [9]

Multiply

Everything cancels out except

Finally the constant term is

The lemma follows.

Theorem 2 Assume When there are exactly two positive singular points of f

where

Proof. We have

where

and

due to symmetry of When P and have two positive roots

in P and

in, see (15) and (16) below. We are going to verify that

(11)

are singular points of f and that

(12)

are not singular points of f. Here

and

Also

(13)

(14)

We have

(15)

and logically equivalent

(16)

where To see (15) compute

So

and from this the formula follows. And (16) is a similar computation.

We shall insert (15), (16) in the first coordinate of f, multiplied with

Now abbreviate and find

Multiply with to get

But this amounts to

and this vanishes due to the formula for roots of quadratic polynomials. That the second coordinate vanishes is logically equivalent. So (11) are singular points of f.

We shall now argue, that

is not a singular point of f. To this end define

Insert the formulas (15), (16) for in the first coordinate of f multiplied with to get

Multiply with to find

(17)

(18)

But (17) is zero by the above and (18) is nonzero. So is not a singular point. That is not a singular of f is logically equivalent. The theorem follows.

In the remainder of the proof of Theorem 1, we assume, that

We shall now verify that is unstable. We shall show that

But we have

Simply insert (15) and (16) in the numerator

Now we use that

so

is equivalent to

The right hand side here is negative and the left hand side is positive. Thus has a positive eigenvalue. So is unstable.

We shall now show that is stable, when is small. We shall use the Routh Hurwitz criterion. So we start by showing, that But similarly to the above

But this amounts to

which is equivalent to

and this again is equivalent to

and from this it follows that We have the following formula for

And a formula for

Define

so that

Now introduce these two formulas in the formulas for

Notice that for small Also

is negative for small The Routh Hurwitz criterion says in our framework, that

is equivalent to stability of But is equivalent to

because our assumptions imply So is equivalent to

This equation holds for small. So is stable for small. This follows by writing

where and h is smooth. This is the standard trick from singularity theory. Then

And from this it follows that is stable for small. To be precise, given such that and, then there exists such that is stable when Theorem 2 follows.

Consider the mass action kinetic system in the species cancer cells, growth factor, growth inhibitor and a protein, respectively.

(19)

(20)

(21)

(22)

(23)

(24)

(25)

The complexes are And this defines the rate constants. With mass action kinetics the ODE s become

see Horn and Jackson (1972), [10] . Notice that (24), (25) are the Brusselator, which is known to have oscillating solutions for some values of the parameters, see Sarmah et al. (2015), [11] . Subtracting on both sides of (25) gives the reaction Let With these parameter values and initial conditions the system oscillates, see Figure 1.

3. Eigenvalues with Negative Real Part

In this section in the discrete model T of the introduction. The purpose of this section is to find a formula for the rate of change of cancer growth

on the hyperplane Here is an integral curve of the vector field Y, defined below. There are four cases to consider. First assume, that Let We shall assume that Define

and compute, when

If has negative real part we might be able to find an affine vector field whose time one map is. Notice that

By Larsen (2016), [1] ,

Then

Define the vector field

(26)

and let

where The flow of X is

(27)

(28)

where Also

If

then

Assume that Then we can let

But this means that

because we have

So we get

i.e. Consider first the immune therapy model

So assuming

We want to have

and

such that

Here denotes the time one map of X and Define

Then

Thus

Now

Define

Let denote the first row in U. Compute letting

where is an integral curve of Y through And, because this is equal to

Now suppose and distinct and define

Then

when because the columns of D are eigenvectors of A corresponding to eigenvalues respectively. Compute, when the inverse

Then

Define the vector field

(29)

X has flow

(30)

and the time one map is

and we want this to be

Then define the vector field

This vector field has time one map

Then arguing as before

and

We can now find

Next consider the chemo therapy model

and initially, that Define the vector field X by (26). It has flow (27), (28). Define the vector field

We want this vector field to have time one map

Then we find

Now compute arguing as above

Finally we can find

and this becomes

Now consider the chemo therapy model, when and distinct. Define the vector field X by (29). It has flow (30). Here

The second coordinate here should be equal to

while the third coordinate should be equal to

in order that the time one map of is. Now we can find

and this is simplified to

Remark 1 When then that is So

by the above you can find an affine vector field whose time one map is. Similarly when

then and So by the above, you have a formula for on

4. Escaping Phase Space

In this section The phase space of our model T of the introduction is. When integral curves of B from theorem 1 in Larsen (2016), [1] , starting in will always escape phase space for both and Here

and where

U as in section 3. This vector field, B, has time one map T, see Larsen (2016), [1] , or argue as in Section 3.

The purpose of this section is to prove, that there exists a first escape time, i.e. the existence of a smallest, such that

When we prove, that either

or there exists a smallest such that

Proposition 3 Suppose Given then there exists such that

Proof. We have the following formula for the flow of B

Here

and

Define

Since we can define by

It follows that we have the following formula

Since the proposition follows.

Remark 2 By the proof we have

implies Here. Let denote the smallest positive solution to

When we have the following proposition using the definitions

These formulas are explained in the proof of Proposition 4.

Let where

D as in section 3. B has time one map T, see Larsen (2016), [1] , or argue as in section three.

Proposition 4 Suppose Let be given. (i) If then there exists a unique such that

If then

for all.

(ii) If then there exists a unique such that

If then

for all.

Proof. First of all the flow of F is

We have the following formula

where is the first row of D. From this equation, (i) follows. For (ii) write

From this formula, (ii) follows.

Remark 3 In case (i) of the proposition, if we have

implies

In case (ii) of the proposition, if we have

implies

We shall now derive a formula for the first escape time To start with, assume that Notice that

and

where

i.e.

Compute

where

If let If define by

Then we have the following formulas

(31)

(32)

Assume that Then there exists such that

for If there exists such that

we claim that there are atmost finitely many such solutions and hence that there exists a smallest such that

Assume for contradiction, that there are infinitely many solutions to

By (31) there are exactly solutions to

Since there are infinitely many solutions to there exist

in such that

By the mean value theorem, there exists such that

Hence

A contradiction and there are only finitely many solutions to If there exists a such that let denote the smallest such number, and otherwise let

If then

Since then Define by

(33)

so

By denote the smallest positive solution to Suppose and if let otherwise write (33). If

let otherwise let

so that

By denote the smallest positive. Here

Suppose If let otherwise write (33). Then there exists such that By denote the smallest positive solution to arguing as above.

If for all let otherwise denote by the smallest positive solution to Now define the first escape time by

We shall now find the first escape time when Then we have

and

where

i.e.

Assume in the notation of Proposition 4, that and let

If let Now compute

and

There are atmost two solutions to If there exists such that let denote the smallest such solution, otherwise let If there exists such that let denote the smallest such solution, otherwise let Now define the first escape time, when

5. Summary and Discussion

In this paper we proved that the model of primary and metastatic cancer in Section 2 is bistable, in the sense, that there are exactly two positive singular points. One of them is unstable, and when one of the rate constants is small the other is stable. Then we found formulas for the rate of change of cancer growth for the model T of the introduction, when for the eigenvalues are nonzero and for when In section four we proved that there is a first escape time for the flow of the affine vector field associated to T when A similar result when was also treated.

It would be interesting to figure out what happens if the polynomials of section 2 are cubic polynomials and not quadratic as in Theorem 1.

About the References

How do cancer cells coordinate glycolysis and biosynthesis. They do that with the aid of an enzyme called Phosphoglycerate Mutase 1. In the reference [12] , the authors suggest a dynamical system for their findings in a figure at the end of the paper. In the reference [13] , A. K. Laird showed that solid tumors do not grow exponentially, but rather like a Gompertz function. The publications of the author are concerned with semi Riemannian dynamical systems, e.g. Lorentzian Geodesic Flows, see [14] and electrical network theory of countable graphs, see [15] , [16] .

Cite this paper

Jens Christian Larsen, (2016) The Bistability Theorem in a Model of Metastatic Cancer. Applied Mathematics,07,1183-1206. doi: 10.4236/am.2016.710105

References