Received 27 September 2014; revised 20 October 2014; accepted 2 November 2014

ABSTRACT

Consider the linear dynamic equation on time scales

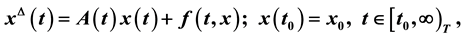(1)

where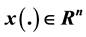, , 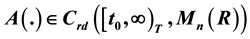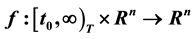is a rd-continuous function, T is a time scales. In this paper, we shall investigate some results for the exponential stability of the dynamic Equation (1) by combinating the first approximate method and the second method of Lyapunov.

Keywords:

Time Scales, Exponential Stability, Linear Dynamic Equation

1. Introduction

Let 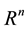be a n-dimension Euclidean space, T be a time scales (a nonempty closed subset of R). We denote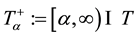. For convenience, we shall use the notions which appear in the book by Bohner and Peterson (see [1] [2] ). The notions related to the Lyapunov function that we use follow the results of B. Kaymakcalan (see [3] ). For necessary, we recall them in this process.

We consider a dynamic equation

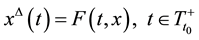, (2)

where with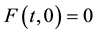. We suppose that F satisfies all conditions such that (2) has a unique solution 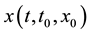with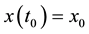. In this paper, we define the stable notions of the trivial solution 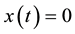of (2) as the followings:

Definition 1. The trivial solution 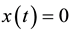of (2) is stable on 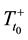forall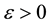, there exists 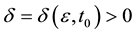that satisfies then,.

Definition 2. The trivial solution of (2) is asymptotically stable if it is stable and there exists satisfies then

In these definitions, if the numbers and do not depend on, we say that the trivial solution of (2) is uniformly stable (uniformly asymptotically stable).

Definition 3. The trivial solution of (2) is exponential stable on if there exists and with −q is positively regressive which satisfies

In the simple case (see [2] ), consider the dynamic equation

(3)

The solution of (3) is exponential function. We recall some properties of the exponential function which are used later.

Assume, we denote

.

We have the following equalities

1);

2);

3);

4);

5);

6);

7).

In the special case, we have

.

Using the notations

,

where

,

,

is set of exponential stability of (see [4] ).

Theory of stability of dynamic equation on time scales is an area of mathematics that has recently received a lot of attention (see [1] [2] [4] -[7] ). And almost of the results which involve the methods of Lyapunov to investigate the stability, have been developed and obtained the interesting results to expand for dynamic equation on time scales. Besides that the criterions and sufficient conditions were given, there were short of some particular examples. We know that the calculus for functions on general time scales is complex and difficult to implement. In order to overcome obstacles, in some cases we can combine the different methods of Lyapunov to investigate the stability of the solution. The content of this paper contains two parts: the first part presents the sufficient conditions following the first approximate method for the exponential stability of the solution of the linear dynamic Equation (1) on time scales. The second one gives some specific examples for applications. Besides the part two we add a theorem about the stability of the solution following the second method of Lyapunov. This theorem can be seen as a corollary of the stable criterion which was presented in [3] .

2. Main Results

2.1. The Stability of Linear Dynamic Equation under Perturbation on Time Scales

Consider the dynamic equation

, (4)

where, , with on.

In proportion to the system (4), we consider

, (5)

where,.

We assume that is regressive. We denote is exponential matrix of (5) with.

We easily verify that and.

Theorem 4. We assume that the trivial solution of (5) is exponentially stable, there exists, to satisfy

,

then the trivial solution of (4) is exponentially stable if one of these conditions is satisfied

i)

.

ii) There exists a function to satisfy

,

where

.

Proof. We assume that is the solution of (4) with,

.

By taking the norms of two sides, combinating the condition of the theorem, we obtain

,

,

,

.

Following the assumption i), for all, there exists satisfies where,. We obtain

.

Let is a positive satisfies, put, then

.

By using the Gronwall inequality (see [7] ), we obtain

.

Equivalent

,

.

By the assumption, put.

We obtain

.

Therefore

.

With, we can choose, which is sufficiently small and. So that the trivial solution of (4) is exponentially stable on.

For ii), by argument similarly as in i), the proof is completed.

2.2. The Stability of Scalar Dynamic Equation on Time Scales

For convenience, the first we consider the scalar dynamic equation

, (6)

where,.

Theorem 5. We assume that satisfies the condition

.

Then the trivial solution of (6) is exponentially stable if one of these conditions is satisfied

i)

.

ii) There exists a function to satisfy

,

where

.

Proof. Let is the solution of (6) with, we have

.

By taking two sides

.

By argument similarly as the proof in theorem 4, we obtain results.

In the next part, for convenience to investigate the stability in specific examples, we represent a theorem about the sufficient condition for the exponential stability of the trivial solution of system (2). This result can be seen as a corollary of the stable criterion B. Kaymakcalan (see [3] ).

We assume is Delta differential of t, continuous differential of x and is the solution of (2) with. Then derivative of following the trajectory of is defined by and

Function with above properties is a Lyapunov function.

Theorem 6. We assume that there exists function is a Lyapunov function which satisfies the following conditions

,

,

where and are positive real numbers,.

If the trivial solution of

, (7)

is exponentially stable then the trivial solution of (2) is also exponentially stable.

Proof. By the assumption the trivial solution of (7) is exponentially stable, then the maximal solution of (7) with satisfies

,

where and. By theorem 2.1 (see [3] ) we obtain

.

Using the assumption, we have

.

Therefore

.

By the assumption implies the trivial solution of (2) is exponentially stable.

3. Applications

In this part, we represent some examples of applications.

Example 1. Assume that are positive constants. These functions; satis- fy one of the conditions i) or ii) of theorem 4. Consider system

. (8)

We assume that in order that system (8) has the trivial solution. We consider

. (9)

In order to investigate the stability of (9), we choose Lyapunov function.

Taking Delta derivative, we obtain

.

Therefore the derivative of right-hand side of (9) is

,

which implies if then the trivial solution of scalar dynamic equation

.

is exponentially stable.

By using the results of theorem 6, the trivial solution of (9) is exponentially stable.

Therefore following theorem 4, the trivial solution of (8) is exponentially stable.

Example 2. Consider system

. (10)

In proportion to system (10), we investigate the stability of the trivial solution of system

. (11)

We choose Lyapunov function, we obtain

Therefore

,

which implies if then the trivial solution of scalar dynamic equation

,

is exponentially stable.

By using the results of theorem 6, the trivial solution of (11) is exponentially stable.

Consider function

,

.

By taking the right-hand side, we obtain

.

By argument similarly as the above inequality

,

,

which implies

,

,

.

Therefore

,

by using theorem 4, which implies the trivial solution of system (10) is exponentially stable.

References