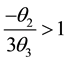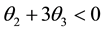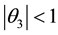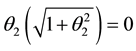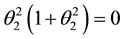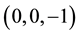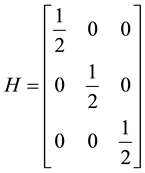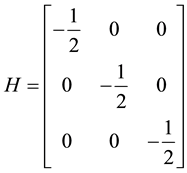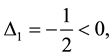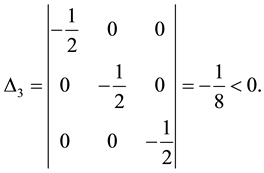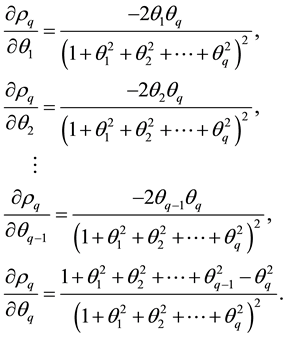Applied Mathematics
Vol.06 No.01(2015), Article ID:53342,8 pages
10.4236/am.2015.61017
Necessary Conditions for the Application of Moving Average Process of Order Three
O. E. Okereke1, I. S. Iwueze2, J. Ohakwe3
1Department of Statistics, Michael Okpara University of Agriculture, Umudike, Nigeria
2Department of Statistics, Federal University of Technology, Owerri, Nigeria
3Department of Mathematical, Computer and Physical Sciences, Federal University, Otueke, Nigeria
Email: emmastat5000@yahoo.co.uk
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 November 2014; accepted 12 December 2014; published 19 January 2015
ABSTRACT
Invertibility is one of the desirable properties of moving average processes. This study derives consequences of the invertibility condition on the parameters of a moving average process of order three. The study also establishes the intervals for the first three autocorrelation coefficients of the moving average process of order three for the purpose of distinguishing between the process and any other process (linear or nonlinear) with similar autocorrelation structure. For an invertible moving average process of order three, the intervals obtained are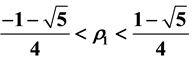 ,
,
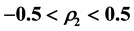 and
and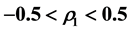 .
.
Keywords:
Moving Average Process of Order Three, Characteristic Equation, Invertibility Condition, Autocorrelation Coefficient, Second Derivative Test

1. Introduction
Moving average processes (models) constitute a special class of linear time series models. A moving average process of order
 (
(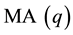 process) is of the form:
process) is of the form:
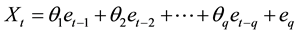 (1.1)
(1.1)
where
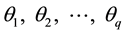 are real constants and
are real constants and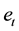 ,
,
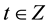 is a sequence of independent and identically distributed random variables with zero mean and constant variance. These processes have been widely used to model time series data from many fields [1] -[3] . The model in (1.1) is always stationary. Hence, a required condition for the use of the moving average process is that it is invertible. Let
is a sequence of independent and identically distributed random variables with zero mean and constant variance. These processes have been widely used to model time series data from many fields [1] -[3] . The model in (1.1) is always stationary. Hence, a required condition for the use of the moving average process is that it is invertible. Let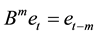 , then the model in (1.1) is invertible if the roots of the characteristic equation
, then the model in (1.1) is invertible if the roots of the characteristic equation
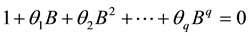 (1.2)
(1.2)
lie outside the unit circle. The invertibility conditions of the first order and second order moving average models have been derived [4] [5] .
Ref. [6] used a moving average process of order three (MA (3) process) in his simulation study. Though, higher order moving average processes have been used to model time series data, not much has been said about the properties of their autocorrelation functions. This study focuses on the invertibility condition of an MA (3) process. Consideration is also given to the properties of its autocorrelation coefficients of an invertible moving average process of order three.
2. Consequence of Invertibility Condition on the Parameters of an MA (3) Process
For , the following moving average process of order 3 is obtained from (1.1):
, the following moving average process of order 3 is obtained from (1.1):
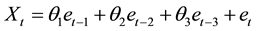 (2.1)
(2.1)
The characteristic equation corresponding to (2.1) is given by
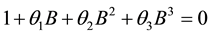 (2.2)
(2.2)
Dividing (2.2) by
 yields
yields
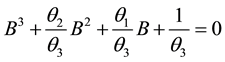 (2.3)
(2.3)
It is important to know that (2.2) is a cubic equation. Detailed information on how to solve cubic equations can be found in [7] [8] among others. It has been a common tradition to consider the nature of the roots of a characteristic equation while determining the invertibility condition of a time series model [9] . As a cubic equation, (2.2) may have three distinct real roots, one real root and two complex roots, two real equal roots or three real equal roots. The nature of the roots of (2.2) is determined with the help of the discriminant [8]
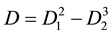
where
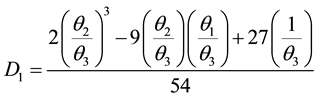
and
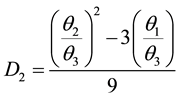
If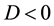
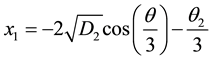
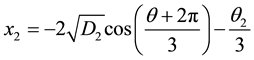
and
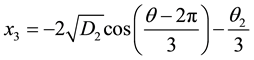
where
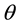
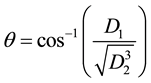
When
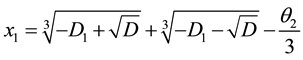
The other roots are [8]
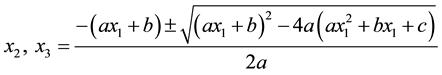
If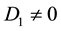
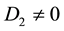
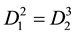
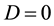
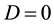
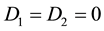
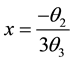
For (2.1) to be invertible, the roots of (2.2) are all expected to lie outside the unit circle and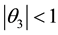
Theorem 1. If the characteristic equation
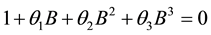
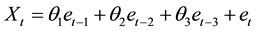

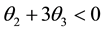
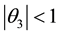
Proof
For invertibility, we expect each of the three real equal roots to lie outside the unit circle. Thus,
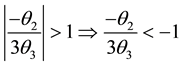
Solving the inequality
For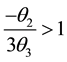
Since each of the roots lie outside the unit circle, the absolute value of their product must therefore be greater than one. Hence,
This completes the proof.
The invertibility region of a moving average of order three with equal roots of the characteristic Equation (2.2) is enclosed by triangle OAB in Figure 1.
Figure 1. Invertibility region of an MA (3) process when the characteristic equation has three real equal roots.
3. Identification of Moving Average Process
Model identification is a crucial aspect of time series analysis. A common practice is to examine the structures of the autocorrelation function (ACF) and partial autocorrelation function (PACF) of a given time series. In this regard, a time series is said to follow a moving average process of order

4. Intervals for Autocorrelation Coefficients of a Moving Average Process of Order Three
As stated in Section 3, knowledge of the extreme values of the autocorrelation coefficient of a moving average process of a particular order can enable us ensure proper identification of the process. It has been observed that for a moving average process of order one,
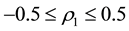
two
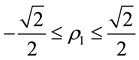
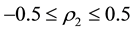
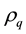
moving average process of order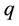
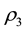
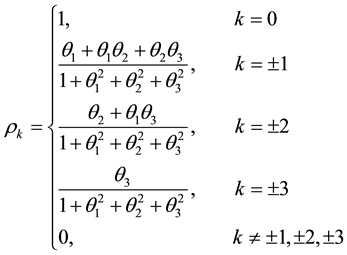
We can deduce from (4.1) that the autocorrelation function at lag one of the MA (3) process is
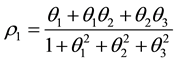
Using the Scientific Note Book, the minimum and maximum values of
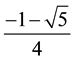
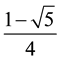
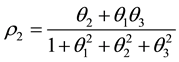
The extreme values of
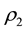
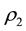
From (4.1), we obtain
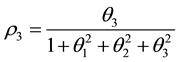
Based on the result obtained from the Scientific Notebook,
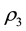
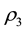

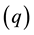
The partial derivatives of
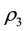
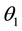
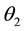
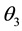
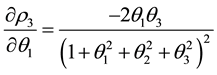
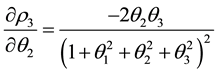
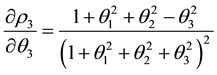
The critical points of
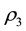
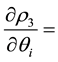
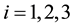
(4.6) and (4.7) to zero, we obtain
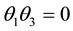
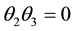
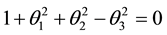
From (4.10), we have

Using (4.8), we obtain
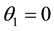
or
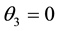
Substituting
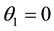
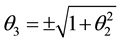
For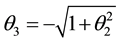
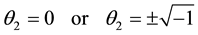
If we also substitute
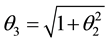

When we substitute
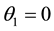
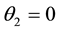
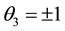
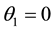

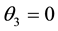

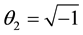
Hence, the critical points of
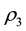
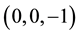
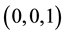


The minimum and maximum values of a function occur at it critical points. To determine which of the critical points is a local minimum, local maximum or a saddle point, we shall apply the second derivative test. The second derivative test for critical points of a function of three variables

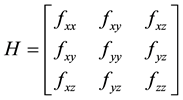
where
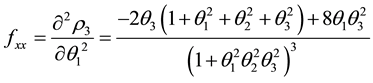

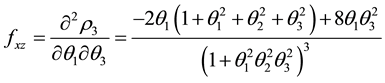
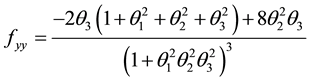
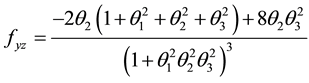
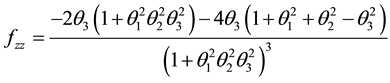
Let
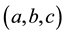
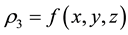
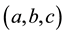
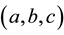
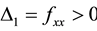
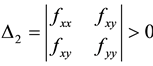
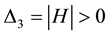
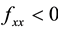
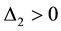
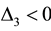
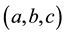
then
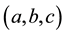
A critical point that is neither a local minimum nor a local maximum is called a saddle point.
Though
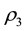
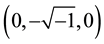

At
Hence,

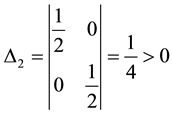
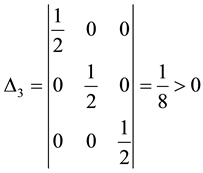
Therefore,
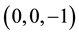
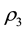
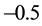
For the critical points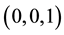
Consequently,
and
We therefore conclude that
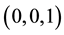
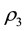
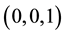
We can deduce from the result in this section and other previous works that for MA (1) process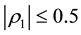
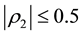

In what follows, we establish the bounds for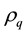
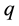
Theorem 2.
Let
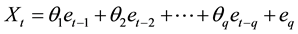
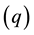
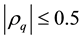
Proof
It is easily seen that for the MA
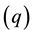
Partial derivatives of
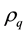

Equating each of the partial derivatives to zero yields

From (4.24), we obtain
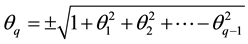
Since
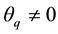
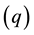
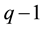
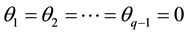
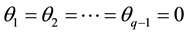
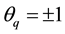
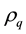

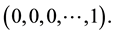
At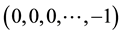
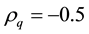
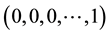
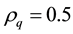
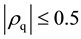
Remark: For an invertible MA (3) process,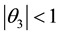
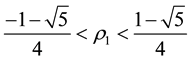
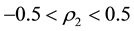
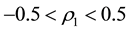
5. Conclusion
We have established necessary conditions for the parameters of an invertible MA (3) process. When the characteristic equation has three real equal roots, the conditions are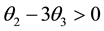
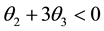
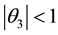
lished. These are

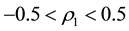
condition on
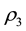

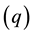
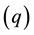

References
- Moses, R.L. and Liu, D. (1991) Optimal Nonnegative Definite Approximation of Estimated Moving Average Covariance Sequences. IEEE Transactions on Signal Processing, 39, 2007-2015. http://dx.doi.org/10.1109/78.134433
- Qian, G. and Zhao, X. (2007) On Time Series Model Selection Involving Many Candidate ARMA Models. Computational Statistics and Data Analysis, 51, 6180-6196. http://dx.doi.org/10.1016/j.csda.2006.12.044
- Li, Z.Y. and Li, D.G. (2008) Strong Approximation for Moving Average Processes under Dependence Assumptions. Acta Mathematica Scientia, 28, 217-224. http://dx.doi.org/10.1016/S0252-9602(08)60023-5
- Box, G.E.P., Jenkins, G.M. and Reinsel, G.C. (1994) Time Series Analysis: Forecasting and Control. 3rd Edition, Prentice-Hall, Englewood Cliffs.
- Okereke, O.E., Iwueze, I.S. and Johnson, O. (2013) Extrema of Autocorrelation Coefficients for Moving Average Processes of Order Two. Far East Journal of Theoretical Statistics, 42, 137-150.
- Al-Marshadi, A.H. (2012) Improving the Order Selection of Moving Average Time Series Model. African Journal of Mathematics and Computer Science Research, 5, 102-106.
- Adewumi, M. (2014) Solution Techniques for Cubic Expressions and Root Finding. Courseware Module, Pennsylvania State University, Pennsylvania.
- Okereke, O.E., Iwueze, I.S. and Johnson, O. (2014) Some Contributions to the Solution of Cubic Equations. British Journal of Mathematics and Computer Science, 4, 2929-2941. http://dx.doi.org/10.9734/BJMCS/2014/10934
- Wei, W.W.S. (2006) Time Series Analysis, Univariate and Multivariate Methods. 2nd Edition, Pearson Addision Wesley, New York.
- Chatfield, C. (1995) The Analysis of Time Series. 5th Edition, Chapman and Hall, London.
- Palma, W. and Zevallos, M. (2004) Analysis of the Correlation Structure of Square of Time Series. Journal of Time Series Analysis, 25, 529-550. http://dx.doi.org/10.1111/j.1467-9892.2004.01797.x
- Iwueze, I.S. and Ohakwe, J. (2011) Covariance Analysis of the Squares of the Purely Diagonal Bilinear Time Series Models. Brazilian Journal of Probability and Statistics, 25, 90-98. http://dx.doi.org/10.1214/09-BJPS111
- Iwueze, I.S. and Ohakwe, J. (2009) Penalties for Misclassification of First Order Bilinear and Linear Moving Average Time Series Processes. http://interstatjournals.net/Year/2009/articles/0906003.pdf
- Okereke, O.E. and Iwueze, I.S. (2013) Region of Comparison for Second Order Moving Average and Pure Diagonal Bilinear Processes. International Journal of Applied Mathematics and Statistical Sciences, 2, 17-26.
- Montgomery, D.C., Jennings, C.L. and Kaluchi, M. (2008) Introduction to Time Series Analysis and Forecasting. John Wiley and Sons, New Jersey.
- Sittinger, B.D. (2010) The Second Derivative Test. www.faculty.csuci.edu/brian.sittinger/2nd_Derivtest.pdf