ABSTRACT

In this paper, the heat, resolvent and wave kernels associated to the Schrödinger operator with multi-inverse square potential on the Euclidian space are given in explicit forms.

Keywords:Heat Kernel, Wave Kernel, Resolvent Kernel, Multiple-Inverse Square Potential, Bessel Function, Lauricella Hypergeometric Function

1. Introduction

This article is devoted to the explicit formulas for the Schwartz integral kernels of the heat, resolvent and wave operators, and 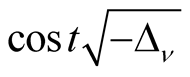attached to the Schrödinger operator with Multiple-inverse square potential on the Euclidian space: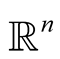

(1.1)

where.

Note that the Schrödinger operator with bi-inverse square potential in the Euclidian plane is considered in Boyer [1] and Ould Moustapha [2] .

For future use we recall the following formulas for the modified Bessel function of the first kind 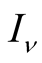and the Hankel function of the first kind.

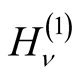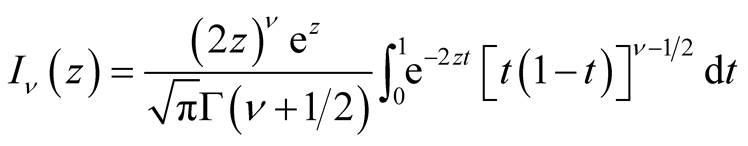(1.2)

(see Temme [3] , p. 237).

(1.3)

(see Temme [3] , p. 234).

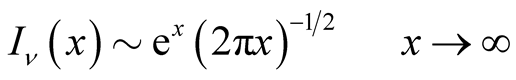(1.4)

(see Temme [3] , p. 240).

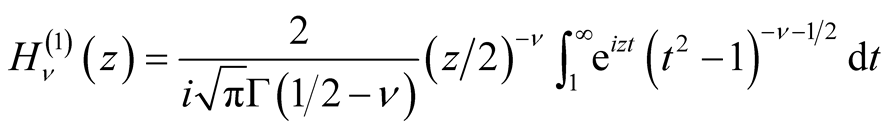(1.5)

(see Erdély et al. [4] , p. 83).

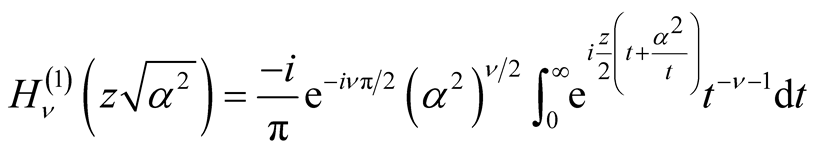(1.6)

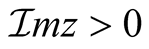and (see Magnus et al. [5] , p. 84). Recall also that the variables Lauricella hypergeometric function is given by (see Appell et al. [6] , p. 114)

(1.7)

where, ,;,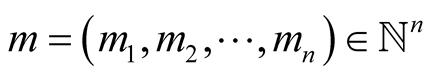

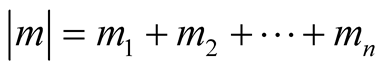and 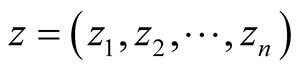are in. In the sekel we use the integral representation (see Appell et al. [6] , p. 115)

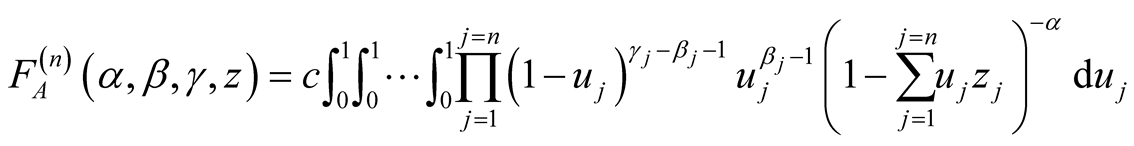(1.8)

where

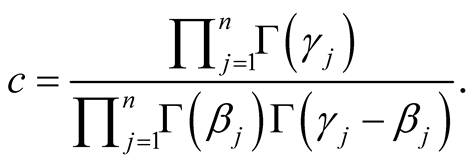(1.9)

For 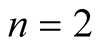we have

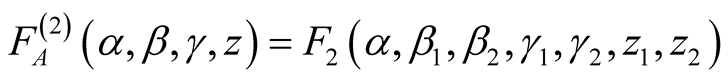(1.10)

where is the Apple hyprgeometric function of two variables.

Recall also the following formulas for the heat kernel associated to the Schrödinger operator with inverse square potential.

(see Calin et al. [7] , p. 68).

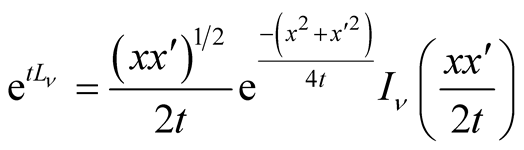(1.11)

where is the modified Bessel function of the first kind.

Proposition 1.1. The Schwartz integral kernel of the heat operator with multiple-inverse square potential

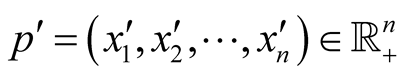can be written for, and as

(1.12)

where is the modified Bessel function of the first kind and of order.

Proof. The Formula (1.12) is a direct consequence of the Formula (1.11) and the properties of the operator (1.1).

2. Resolvent Kernel with Multiple-Inverse Square Potential on the Euclidian Space

Theorem 2.1. The Schwartz integral kernel for the resolvent operator is given by the formula.

(2.1)

where is the Hankel function of the first kind and.

Proof. We use the well known formula connecting the resolvent and the heat kernels:

(2.2)

We combine the Formulas (2.2), (1.12) and (1.2) then use the Formulas (1.3) and (1.4) to appley the Fubini theorem and in view of the Formula (1.6) we get the Formula (2.1) and the proof of the Theorem 2.1 is finished.

Theorem 2.2. The Schwartz integral kernel of the resolvent operator 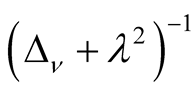can be written as

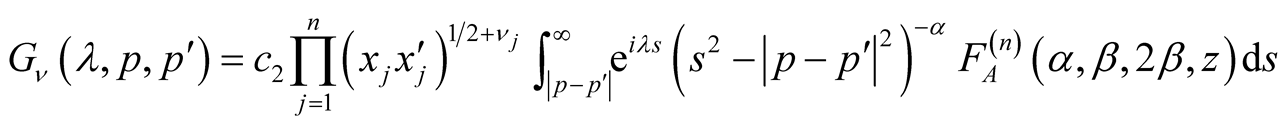(2.3)

with , and

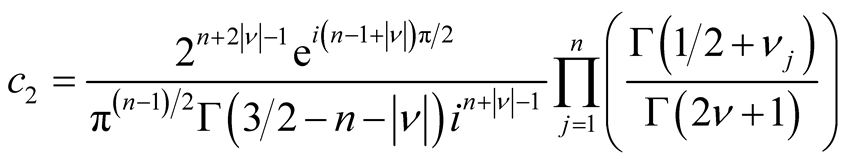(2.4)

where 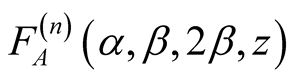is the n-variables Lauricella hypergeometric function given in (1.7).

Proof. We use the Formulas (2.1) and (1.5) as well as the Fubini theorem to arrive at the announced Formula (2.3).

3. Wave Kernel with Multiple-Inverse Square Potential on the Euclidian Space

It is known that the energy and information can only be transmitted with finite speed, smaller or equal to the speed of light. The mathematical framework, which allows an analysis and proof of this phenomenon, is the theory the wave equation. The result, which may be obtained, runs under the name finite propagation speed (see Cheeger et al. [8] ). The following theorem illustrates the principle of the finite propagation speed in the case of the Schrödinger operator with multiple-inverse square potential.

Theorem 3.1. (Finite propagation speed) Let be the Schwartz integral kernel of the wave operator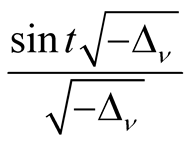, then we have

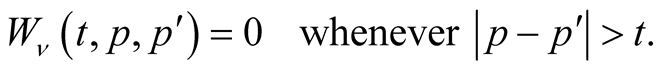(3.1)

Proof. The proof of this result use an argument of analytic continuation from the identity

(3.2)

We recall the formula [9] , p. 50

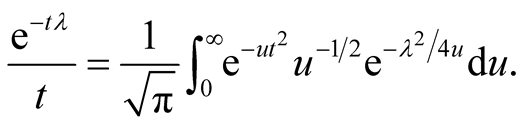
(3.3)

By setting and 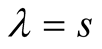in (3.3) we can write

(3.4)

and let be the integral kernel of then we can write

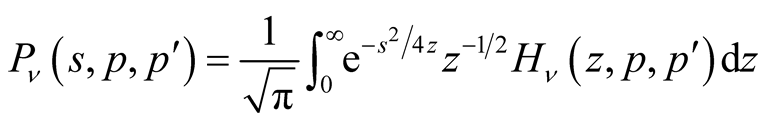(3.5)

where is the heat kernel with the multiple-inverse square potential given by (1.12).

Consider the integral

(3.6)

using (1.12) we have

(3.7)

From (3.2) we have

(3.8)

Now set

(3.9)

where

(3.10)

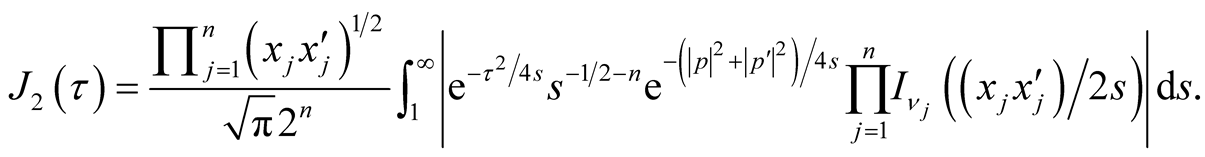(3.11)

Using the Formula (1.3) we see that the last integral 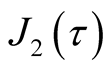converge absolutely and is analytic in for

.

For the first integral we obtain

(3.12)

and from the Formula (1.4) we see that

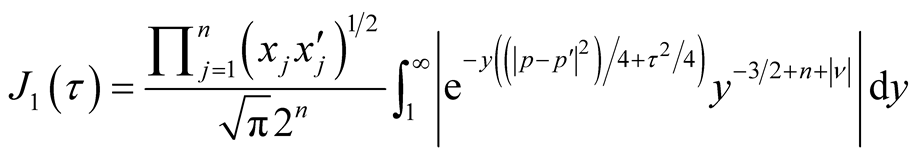(3.13)

is analytic in and converge if, hence the integral is absolutely convergent if (i.e.) 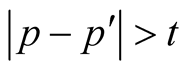and in view of (3.8) we have for 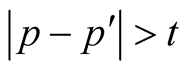and the proof of the Theorem 3.1 is finished.

Theorem 3.2. The Schwartz integral kernel for the wave operator with multiple-inverse square potential on the Euclidian space can be written on the two following forms

(3.14)

and

(3.15)

where is the first kind modified Bessel functions of order.

Proof. We start by recalling the formula (see Magnus et al. [5] , p. 73).

(3.16)

where 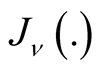is the Bessel function of first kind and of order defined by (see Magnus et al. [5] , p. 83).

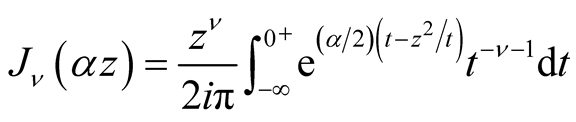(3.17)

provided that 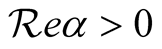and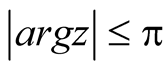. Here we should note that the integral in (3.17) can be extended over a contour starting at, going clockwise around 0, and returning back to without cutting the real negative semi-axis.

For 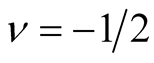the equation (3.17) can be combined with Equation (3.16) to derive the following formula.

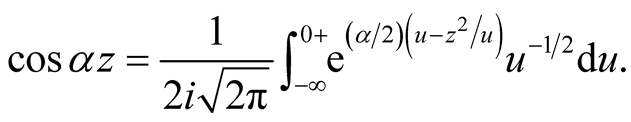(3.18)

Putting and replacing the variable 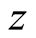by the symbol 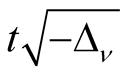in (3.18) we obtain

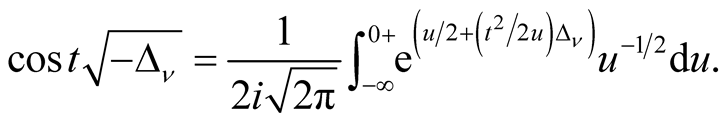(3.19)

Finally making use of (1.12) in (3.19), we get the Formula (3.14).

To see the Formula (3.15) set

(3.20)

and

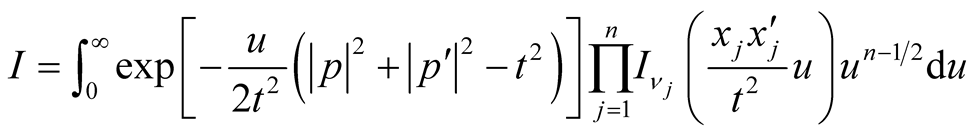(3.21)

we have

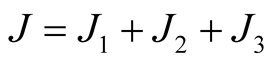(3.22)

(3.23)

(3.24)

and

(3.25)

where the paths, and are given by

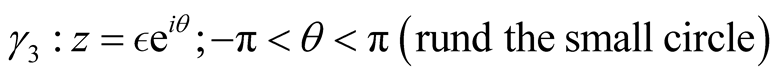
as, we have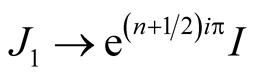, and.

Adding the integrals establishes the required results.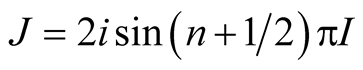

Theorem 3.3. The integral kernel for the wave operator 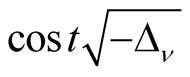with multiple-inverse square potential on the Euclidian plane can be written as

(3.26)

where 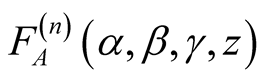is the n-variables Lauricella hypergeometric function 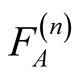given in (1.7),

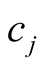, , and and the constant is given by

(3.27)

Proof. We use essetially the Formula (3.15) of Theorem 3.2, the Formulas (1.2), the Fubini theorem and the Formula (1.8).

4. Applications and Further Studies

We give an application of the Theorem 3.3.

Corollary 4.1. The integral kernel of the heat operator 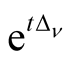can be written in the form

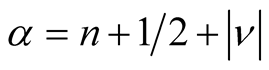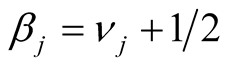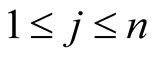with, and, and

Proof. We use the transmutation formula (see Greiner et al. [10] , p. 362)

We suggest here a certain number of open related problems connected to this paper. For example the semilinear wave and heat equations associated to the multiple-inverse square potential and its global solution and a possible blow up of the solution in finite times.

We can also to look for the dispersive and Strichartz estimates for the Schrödinger and the wave equations with multiple-inverse square potential, for the case of inverse square potential (Burg et al. [11] and Planchon et al. [12] ).

References