Applied Mathematics
Vol.5 No.4(2014), Article ID:43841,9 pages DOI:10.4236/am.2014.54071
Common Fixed Point Results for Occasionally Weakly Compatible Maps in G-Symmetric Spaces
Kanayo Stella Eke1, Johnson Olaleru2
1Department of Computer and Information Science/Mathematics, Covenant University, Ota, Nigeria
2Department of Mathematics, University of Lagos, Lagos, Nigeria
Email: ugbohstella@yahoo.com, olaleru1@yahoo.co.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 4 October 2013; revised 4 November 2013; accepted 14 November 2013
ABSTRACT
The notion of a G-symmetric space is introduced and the common fixed points for some pairs of occasionally weakly compatible maps satisfying some contractive conditions in a G-symmetric space are proved. The results extend and improve some results in literature.
Keywords: Common Fixed Points; Generalized Contractive Mappings; Occasionally Weakly Compatible Maps; Compatible Maps; (E-A) Property; G-Symmetric Spaces

1. Introduction
The notion of metric spaces is widely used in fixed point theory and applications. Different authors had generalized the notions of metric spaces. Recently, Eke and Olaleru [1] introduced the concept of G-partial metric spaces by introducing the non-zero self-distance to the notion of G-metric spaces. The G-partial metrics are useful in modeling partially defined information which often appears in Computer Science. The concept of symmetric spaces in which the triangle inequality of a metric space is not included was introduced by Cartan [2] and defined as:
A symmetric on a set X is a real valued function d on X × X such that
(i) 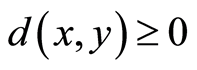 and
and 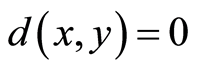 if and only if
if and only if ;
;
(ii) 
Wilson [3] also gave two more axioms of a symmetric d on X as:
(W1) Given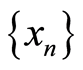 ,
, 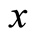 and
and 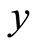 in
in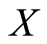 ,
,  and
and 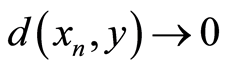 imply that
imply that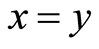 ;
;
(W2) Given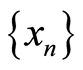 ,
,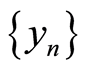 and
and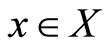 ;
; 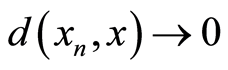 and
and 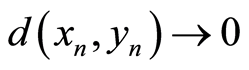 imply that
imply that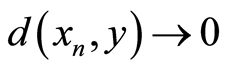 .
.
Hicks and Rhoades [4] observed that the use of the triangle inequality is not necessary in certain proof of metric theorems. Based on this idea, they proved some common fixed point results in symmetric spaces.
Different generalizations of the metric space have been introduced by many authors in literature. In particular, Mustafa and Sims [5] generalized the concept of a metric space by assigning a real number to every triplet of an arbitrary set. Thus, it is defined as:
Definition 1.1 [5] : Let  be a nonempty set, and let
be a nonempty set, and let 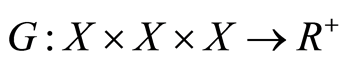 be a function satisfying:
be a function satisfying:
(G1) 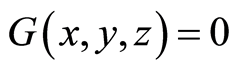 if
if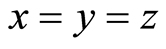 (G2)
(G2) 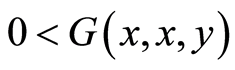 for all
for all 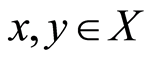 with
with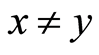 (G3)
(G3) 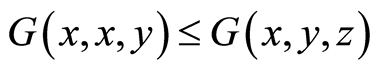 for all
for all 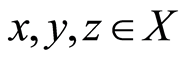 with
with (G4)
(G4) 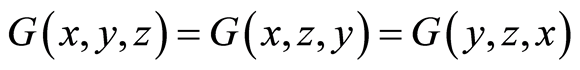 (symmetry in all three variables)(G5)
(symmetry in all three variables)(G5) 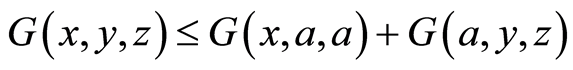 for all
for all 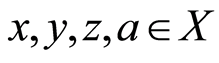 (rectangle inequality).
(rectangle inequality).
Then, the function 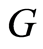 is called a generalized metric, or more specifically a G-metric on
is called a generalized metric, or more specifically a G-metric on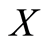 , and the pair
, and the pair  is a G-metric space.
is a G-metric space.
Example 1.2 [5] : Let 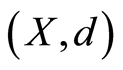 be a metric space. The function
be a metric space. The function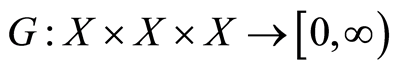 , defined by
, defined by
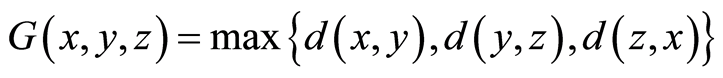
or

for all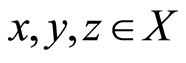 , is a G-metric on
, is a G-metric on .
.
In this work, we generalize the symmetric spaces by omitting the rectangle inequality axiom of G-metric space. This leads to our introduction of the notion of a G-symmetric space defined as follows:
Definition 1.3: A G-symmetric on a set 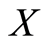 is a function
is a function  such that for all
such that for all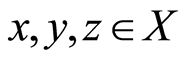 , the following conditions are satisfied:
, the following conditions are satisfied:
 and
and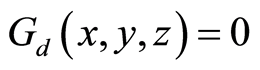 , if
, if ;
;
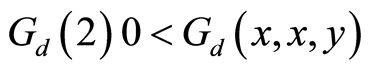 for all
for all 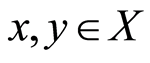 with
with 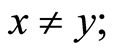
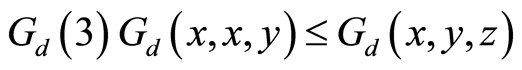 , for all
, for all 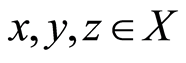 with
with 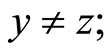
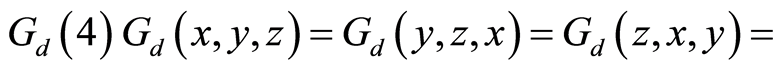 ,×××, (symmetry in all three variables).
,×××, (symmetry in all three variables).
It should be observed that our notion of a G-symmetric space is the same as that of G-metric space (Definition 1.1) without the rectangular property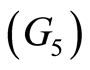 .
.
Example 1.4: Let  equipped with a G-symmetric defined by:
equipped with a G-symmetric defined by:
 for all
for all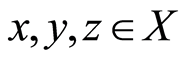 . Then, the pair
. Then, the pair 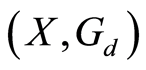 is a G-symmetric space. This does not satisfy the rectangle inequality property of a G-metric space, hence it is not a G-metric space.
is a G-symmetric space. This does not satisfy the rectangle inequality property of a G-metric space, hence it is not a G-metric space.
The analogue of axioms of Wilson [3] in G-symmetric space is as follows:
(W3) Given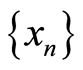 ,
, 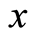 and
and 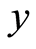 in
in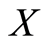 ;
; 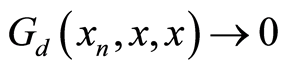 and
and  imply that
imply that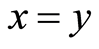 .
.
(W4) Given 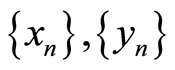 and an
and an 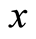 in
in ;
;  and
and 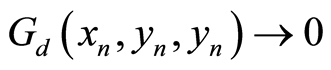 imply that
imply that .
.
Definition 1.5: Let 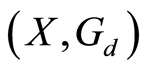 be a G-symmetric space.
be a G-symmetric space.
(i) 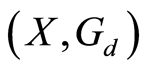 is
is 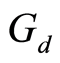 -complete if for every
-complete if for every 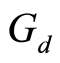 -Cauchy sequence
-Cauchy sequence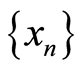 , there exists
, there exists 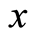 in
in 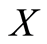 with
with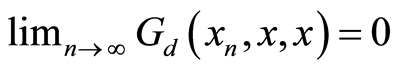 .
.
(ii) 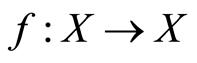 is
is 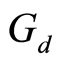 -continuous if
-continuous if

Definition 1.6: Let 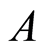 be a nonempty subset of
be a nonempty subset of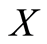 .
. 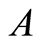 is said to be
is said to be 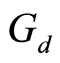 -bounded if and only if
-bounded if and only if
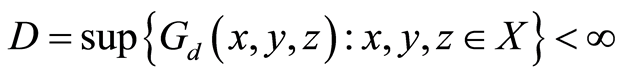 .
.
The principle of studying the fixed point of contractive maps without continuity at each point of the set was initiated by Kannan [6] in 1968. The establishment of a common fixed point for a contractive pair of commuting maps was proved by Jungck [7] . Thereafter, Sessa [8] introduced the notion of weakly commuting maps. Jungck [9] introduced the concept of compatible maps which is more general than the weakly commuting maps. Jungck further weakened the notion of compatibility by introducing weakly compatibility. Al-Thagafi and Shahzad [10] defined the notion of occasionally weakly compatible maps which is more general than that of weakly compatible maps. Pant [11] further introduced the concept of non-compatible maps. The importance of non-compatibility is that it permits the existence of the common fixed points for the class of Lipschitz type mapping pairs without assuming continuity of the mappings involved or completeness of the space. In 2002, Aamri and El Moutawakil [12] introduced the (E-A) property and thus generalized the concept of non-compatible maps.
This work proves the existence of a unique common fixed point for pairs of occasionally weakly compatible maps defined on a G-symmetric space satisfying some strict contractive conditions. The work generalized many known results in literature.
The following definitions are important for our study.
Definition 1.9: Two selfmaps 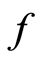 and
and 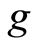 in a G-symmetric space
in a G-symmetric space 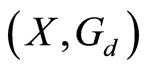 are said to be weakly compatible if they commute at their points of coincidence, that is, if
are said to be weakly compatible if they commute at their points of coincidence, that is, if 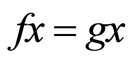 for some
for some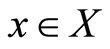 , then
, then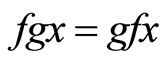 .
.
Definition 1.11 [10] : Two self maps  and
and  of a set X are occasionally weakly compatible if and only if there is a point
of a set X are occasionally weakly compatible if and only if there is a point 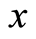 in
in 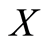 which is a coincidence point of
which is a coincidence point of 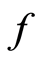 and
and 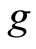 at which f and g commute.
at which f and g commute.
Lemma 1.12 [13] : Let  be a set,
be a set,  ,
, 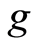 occasionally weakly compatible self maps of
occasionally weakly compatible self maps of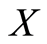 . If
. If 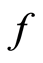 and
and 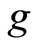 have a unique point of coincidence,
have a unique point of coincidence, 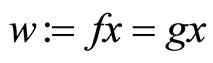 , then
, then 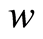 is the unique common fixed point of
is the unique common fixed point of 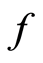 and g.
and g.
The existence of some common fixed point results for two generalized contractive maps in a symmetric (semimetric) space satisfying certain contractive conditions were proved by Hicks and Rhoades [4] and Imdad et al. [14] . Jungck and Rhoades [13] proved the existence of common fixed points for two pairs of occasionally weakly compatible mappings defined on symmetric spaces by using a short process of obtaining the unique common fixed point of the maps. Bhatt et al. [15] proved the existence and uniqueness of a common fixed point for pairs of maps defined on symmetric spaces without using the (E-A) property and completeness, under a relaxed condition by assuming symmetry only on the set of points of coincidence. Abbas and Rhoades [16] proved the existence of a unique common fixed point for a class of operators called occasionally weakly compatible maps defined on a symmetric space satisfying a generalized contractive condition.
In this work, the existence of common fixed points for two occasionally weakly compatible maps satisfying certain contractive conditions in a G-symmetric space is proved. Our results are analogue of the result of Abbas and Rhoades [16] and an improvement of the results of Imdad et al. [14] and others in literature.
2. Main Results
Theorem 2.1: Let 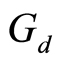 be a bounded G-symmetric for
be a bounded G-symmetric for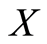 . Suppose
. Suppose  is
is 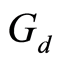 -complete and
-complete and 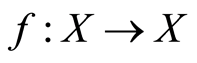 is
is 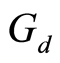 -continuous. Then
-continuous. Then  has a fixed point if and only if there exists
has a fixed point if and only if there exists 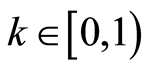 and a
and a 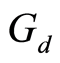 -continuous function
-continuous function 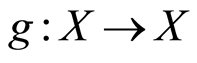 which is compatible with
which is compatible with 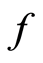 and satisfies
and satisfies 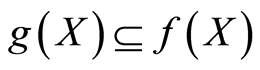 and
and
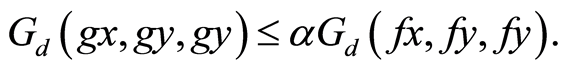 (1)
(1)
For all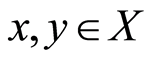 . Moreover, suppose
. Moreover, suppose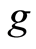 ,
, 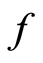 are occasionally weakly compatible, then
are occasionally weakly compatible, then 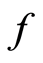 and
and 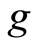 have a unique common fixed point.
have a unique common fixed point.
Proof: Suppose 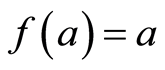 for some
for some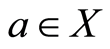 , put
, put 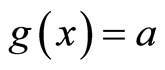 for all
for all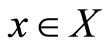 . Then the conditions of the theorem are satisfied.
. Then the conditions of the theorem are satisfied.
Conversely, suppose there exists 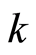 and
and 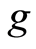 so that Equation (1) holds. Let
so that Equation (1) holds. Let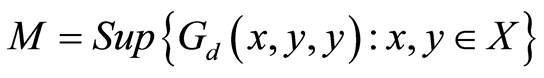 .
.
Suppose 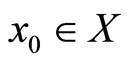 is arbitrarily chosen.
is arbitrarily chosen. 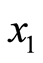 can be chosen such that
can be chosen such that . Continuing in this process,
. Continuing in this process, 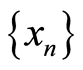
can be chosen such that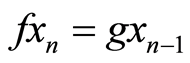 . Using Equation (1) and the sequence
. Using Equation (1) and the sequence ,
,
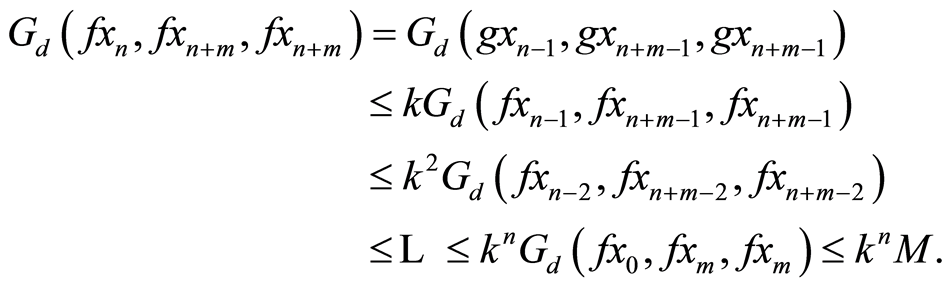
Thus  is a
is a  -Cauchy sequence and since
-Cauchy sequence and since 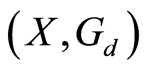 is
is 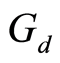 -complete, there exists
-complete, there exists 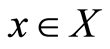 with
with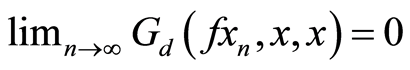 . Since g is
. Since g is  -continuous, it implies that
-continuous, it implies that 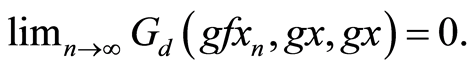 Also
Also 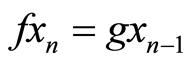 yields
yields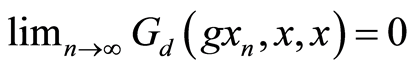 .
. 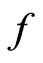 is
is 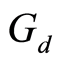 -continuous implying that
-continuous implying that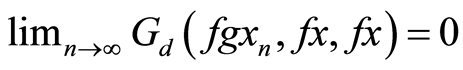 . The compatibility of
. The compatibility of 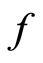 and
and 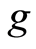 gives
gives , that is
, that is 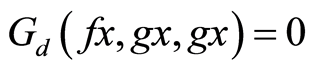 which implies that
which implies that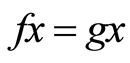 . Suppose there exists another point in
. Suppose there exists another point in  saying
saying 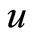 such that
such that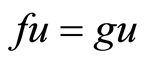 . Now we claim that
. Now we claim that . Suppose
. Suppose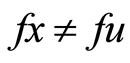 , then using Equation (1) gives
, then using Equation (1) gives
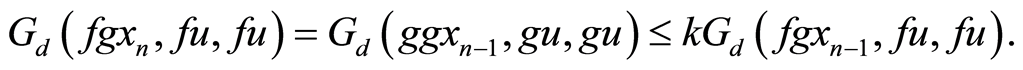
Letting 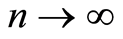 yields
yields

This is a contradiction since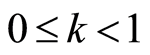 , hence
, hence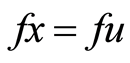 . Therefore
. Therefore 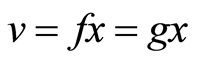 is the unique point of coincidence
is the unique point of coincidence  and
and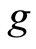 . By Lemma (1.12),
. By Lemma (1.12), 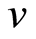 is the unique common fixed point of
is the unique common fixed point of 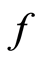 and
and 
Corollary 2.2 [15] : Let  be a bounded
be a bounded 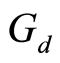 -symmetric for X that satisfies
-symmetric for X that satisfies 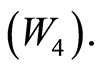 Suppose that
Suppose that 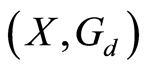 is
is 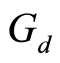 -complete and
-complete and 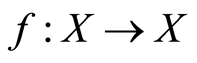 is
is 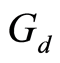 -continuous. Then
-continuous. Then 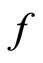 has a fixed point if and only if there exists
has a fixed point if and only if there exists 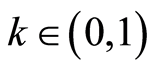 and a
and a 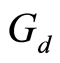 -continuous function
-continuous function  which commutes with
which commutes with 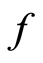 and satisfies
and satisfies 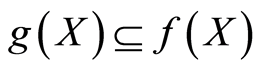 and
and
 , (2)
, (2)
for all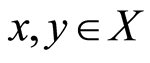 . Indeed,
. Indeed,  and
and  have a unique common fixed point if Equation (2) holds.
have a unique common fixed point if Equation (2) holds.
Remark 2.3: Corollary 2.2 is an analogue of ([15] , Theorem 2.1) in the setting of G-symmetric space. Theorem 2.1 is an improvement of Bhatt et al. ([15] , Theorem 2.1) since occasionally weakly compatible maps are more general than commuting maps and the concept of a  -symmetric space extends that of a symmetric space.
-symmetric space extends that of a symmetric space.
Theorem 2.4: Let 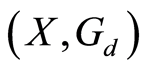 be a
be a 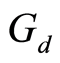 -symmetric space that satisfies
-symmetric space that satisfies 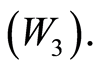 Let
Let 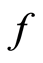 and
and 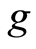 be two selfmappings of
be two selfmappings of 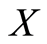 such that
such that
(i)  and
and 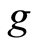 satisfy property (E-A)(ii) for all
satisfy property (E-A)(ii) for all 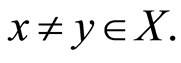
Suppose
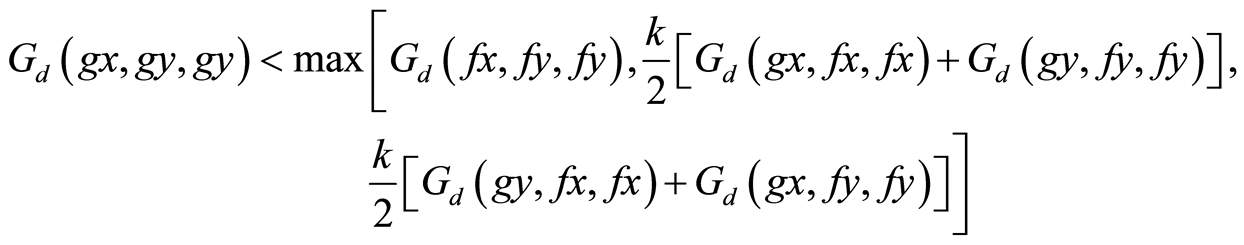 (3)
(3)
And
 (4)
(4)
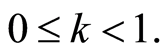 Suppose
Suppose  is a
is a 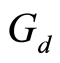 -closed subset of X with
-closed subset of X with 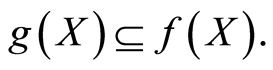 If
If 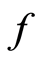 and
and 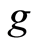 are occasionally weakly compatible, then
are occasionally weakly compatible, then  and
and 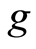 have a unique common fixed point.
have a unique common fixed point.
Proof: Since 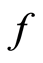 and
and 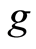 satisfy property (E-A), there exists a sequence
satisfy property (E-A), there exists a sequence 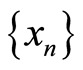 in X such that
in X such that 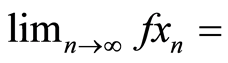
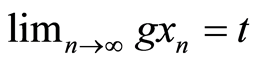 for some
for some 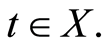 Also
Also 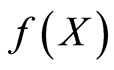 is closed implying that there exist some
is closed implying that there exist some 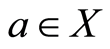 such that
such that . This yields that
. This yields that  by
by 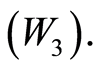 We claim that
We claim that 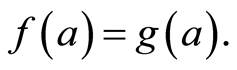 Suppose
Suppose then using Equation (3) we get,
then using Equation (3) we get,
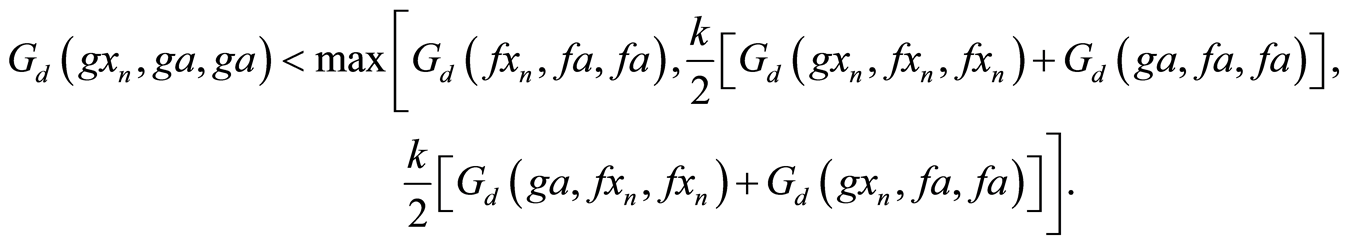
Letting 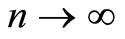 we have,
we have,
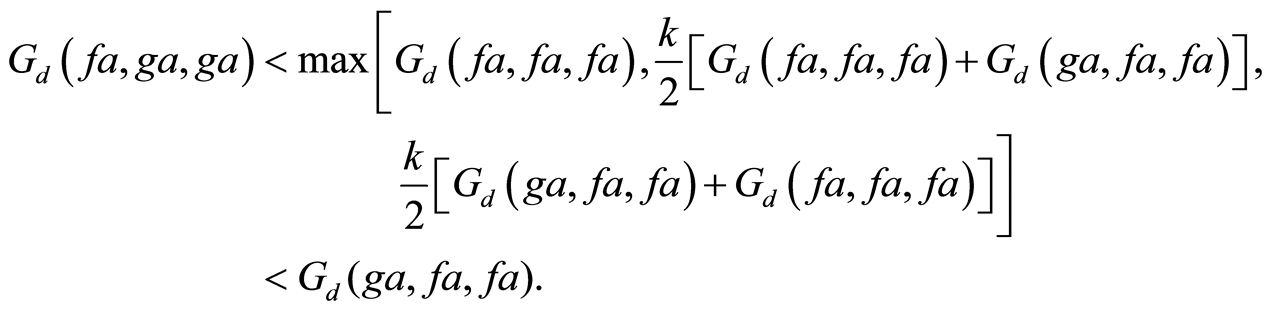 (5)
(5)
Using Equation (4) we have
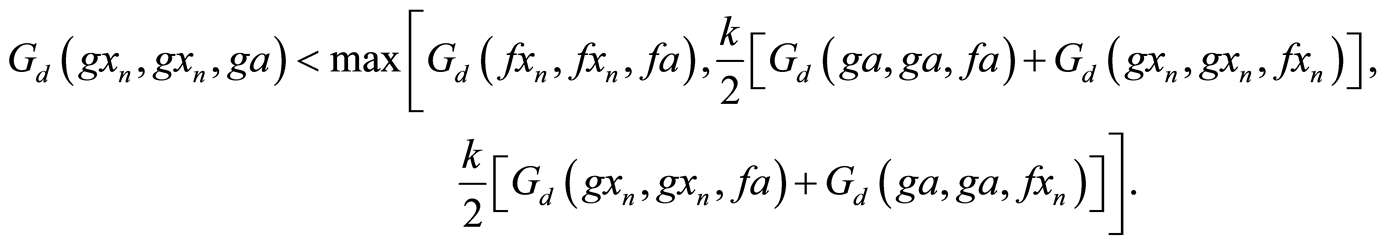
Letting  gives,
gives,
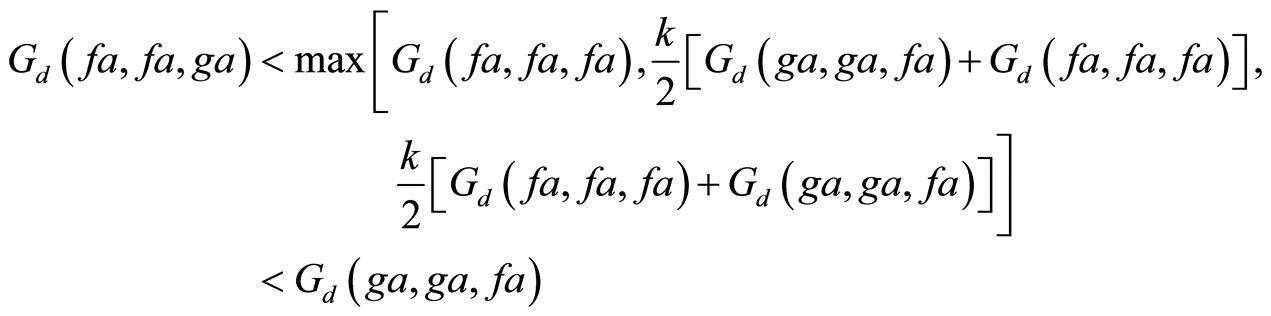 (6)
(6)
Combining Equations (5) and (6) yields,
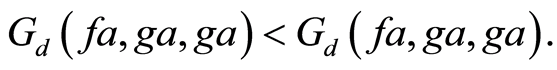
Suppose there exists 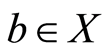 such that
such that  Suppose
Suppose 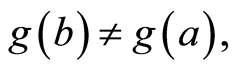 then using Equation (3) we have,
then using Equation (3) we have,
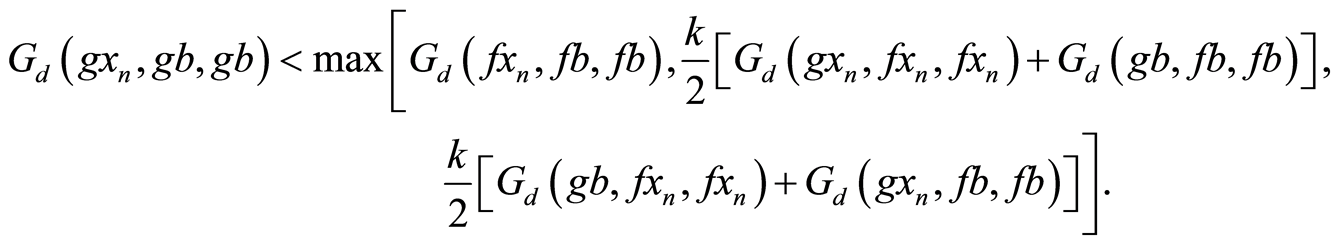
Letting  yields,
yields,
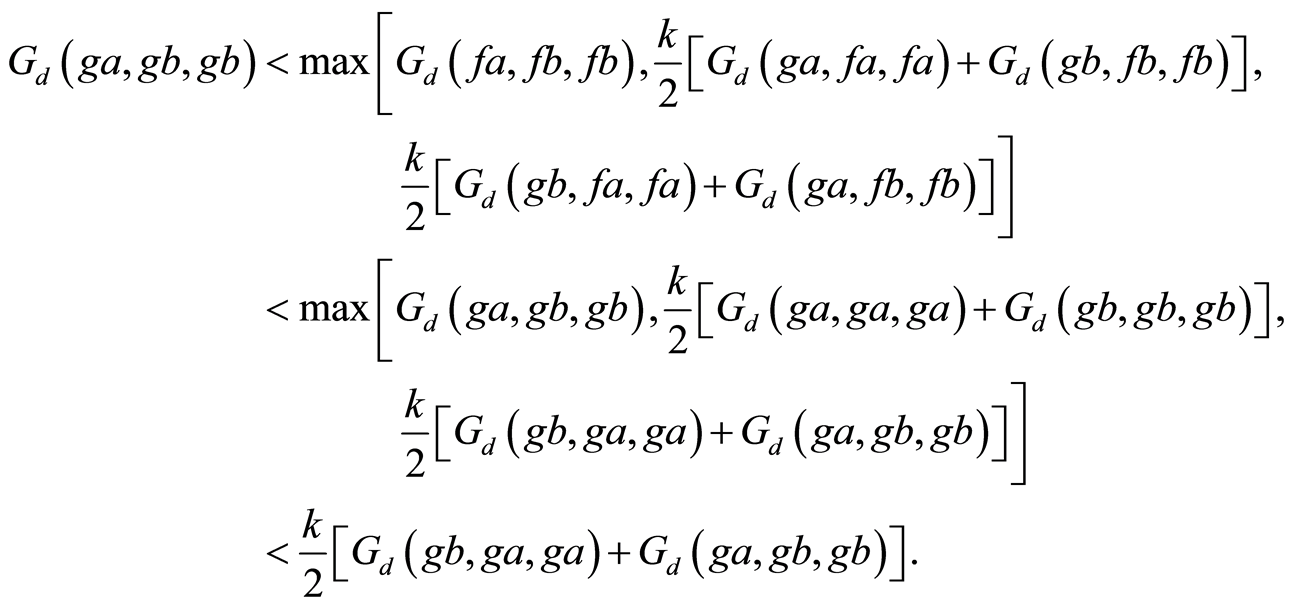
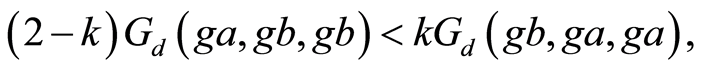
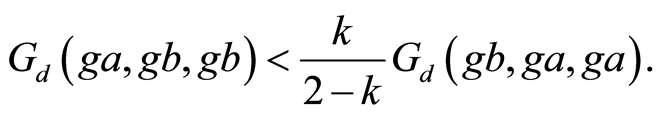 (7)
(7)
Using Equation (4), we obtain
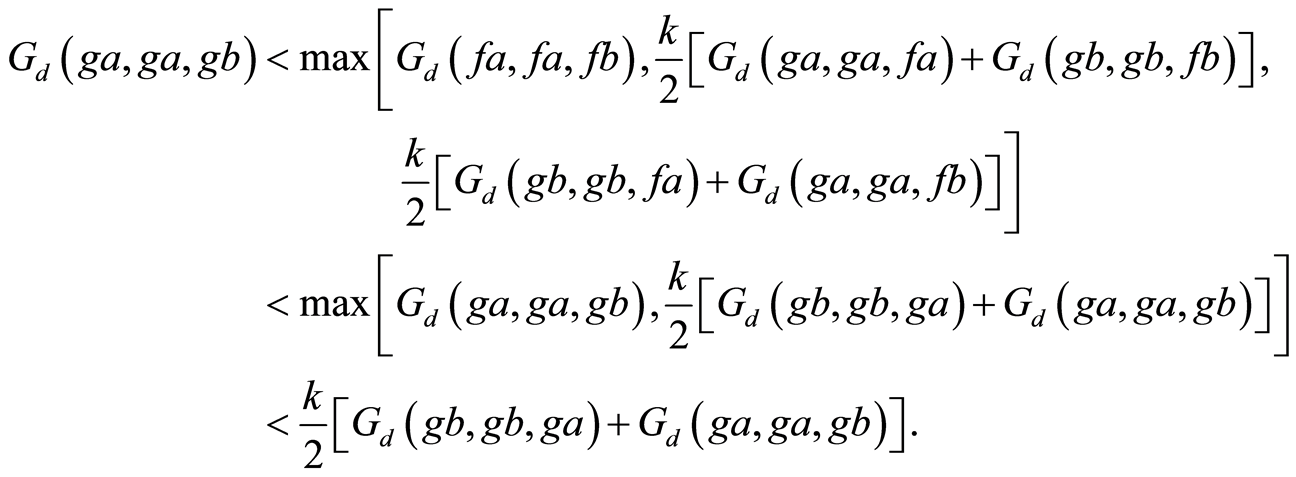
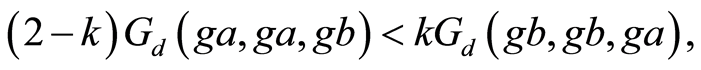
 (8)
(8)
Combining Equations (7) and (8) gives,

Since , we obtain
, we obtain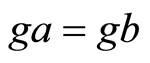 . Therefore
. Therefore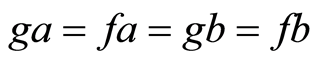 . Hence w is the unique point of coincidence of
. Hence w is the unique point of coincidence of  and
and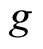 . By Lemma 1.12, w is the unique common fixed point of
. By Lemma 1.12, w is the unique common fixed point of 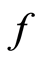 and g.
and g.
Corollary 2.5: Let 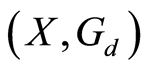 be a
be a 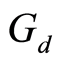 -symmetric space that satisfies
-symmetric space that satisfies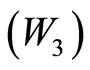 . Let f and g be two self-mappings of
. Let f and g be two self-mappings of 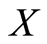 such that
such that
(i)  and
and 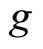 satisfy property (E.A)
satisfy property (E.A)
(ii) for all 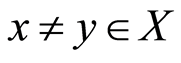
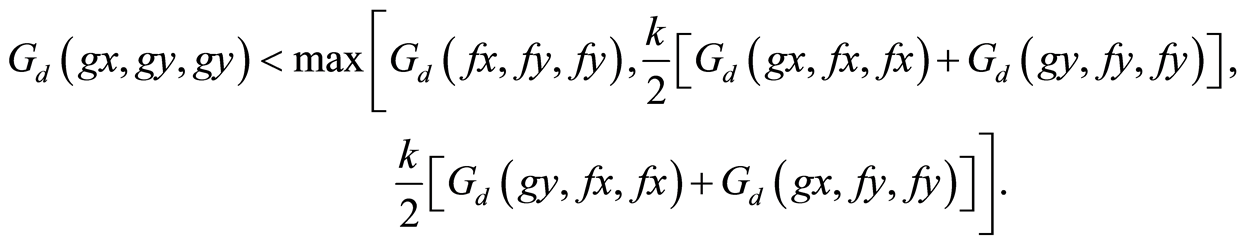 (9)
(9)
and
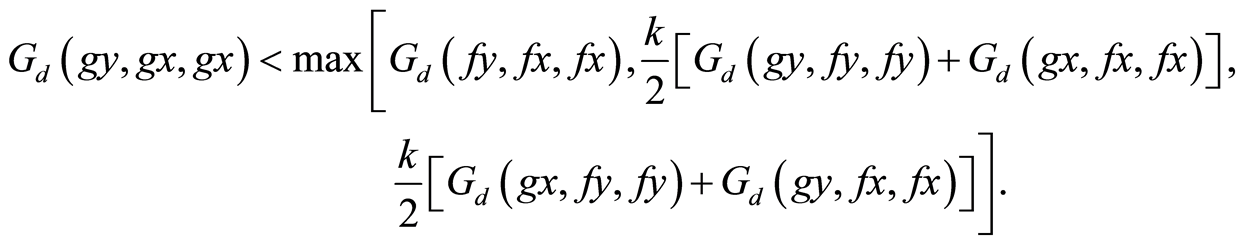 (10)
(10)
 Assume
Assume 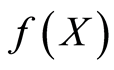 is
is 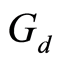 -closed subsets of
-closed subsets of 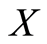 with
with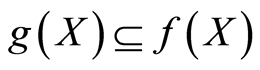 . Suppose that
. Suppose that 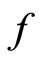 and
and 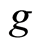 are weakly compatible, then
are weakly compatible, then 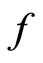 and
and 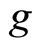 have a unique common fixed point.
have a unique common fixed point.
Remarks 2.6: Theorem 2.4 is an extension of ([14] , Theorems 2.1, 2.2, 2.3) to G-symmetric spaces from symmetric spaces.
The following results are analogue of ([16] Theorem 1).
First we state the following definitions given by Abbas and Rhoades [16] .
Let 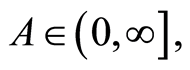
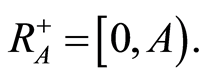 Let
Let 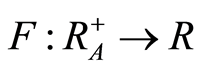 satisfy
satisfy
(i) 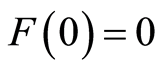 and
and 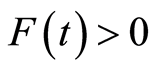 for each
for each 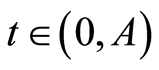 and
and
(ii) F is nondecreasing on 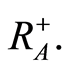
Define 
Let 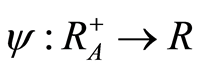 satisfy
satisfy
(i) 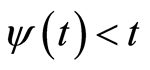 for each
for each 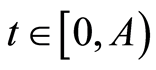 and
and
(ii) 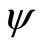 is nondecreasing.
is nondecreasing.
Define
Theorem 2.6: Let 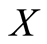 be a set with
be a set with 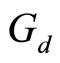 -symmetric
-symmetric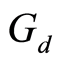 . Let
. Let 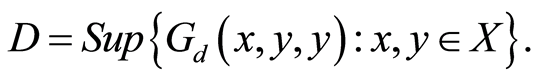 Suppose that
Suppose that 

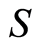 and
and 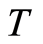 are self-maps of
are self-maps of  and that the pairs
and that the pairs 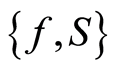 and
and 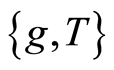 are each occasionally weakly compatible. If for each
are each occasionally weakly compatible. If for each 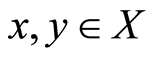 for which
for which 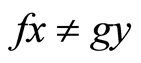 we have
we have
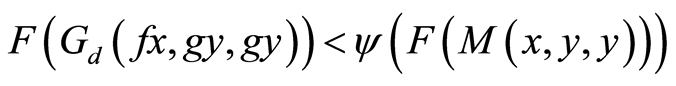 (11)
(11)
and
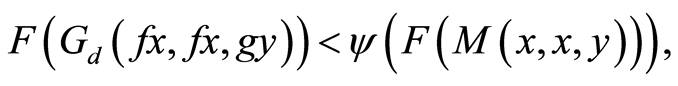 (12)
(12)
for each 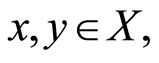
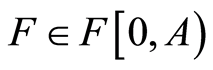 and
and 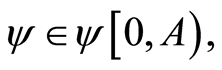 where
where  if
if 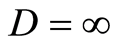 and
and 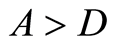 if
if  and
and
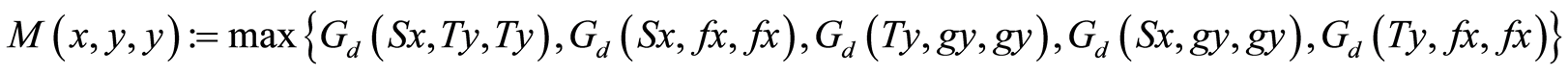
and
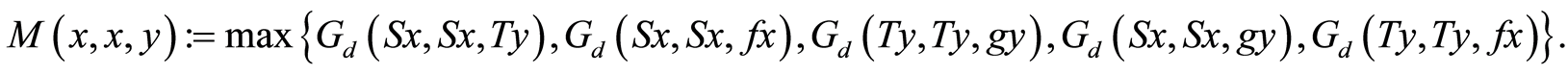
then there is a unique point  such that
such that 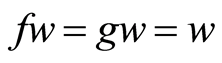 and a unique point
and a unique point 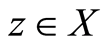 such that
such that 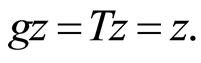 Moreover,
Moreover, 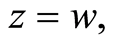 so that there is a unique common fixed point of
so that there is a unique common fixed point of 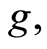
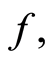
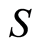 and
and 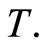
Proof: Since the pairs  and
and 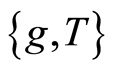 are each occasionally weakly compatible, then there exist
are each occasionally weakly compatible, then there exist 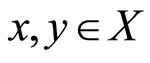 such that
such that  and
and 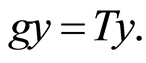 We claim that
We claim that 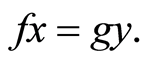 On the contrary, suppose
On the contrary, suppose 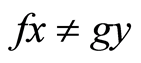 then
then
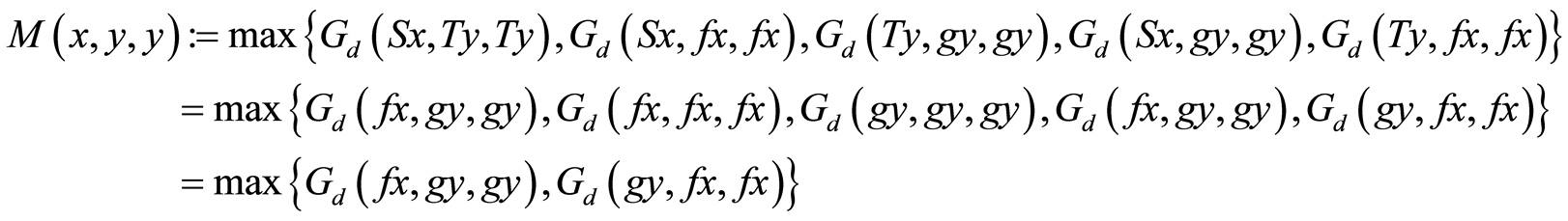
Case (i)
If max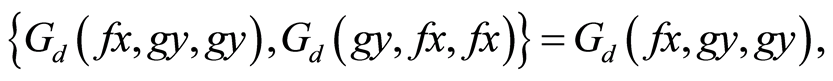 then Equation (11) becomes
then Equation (11) becomes
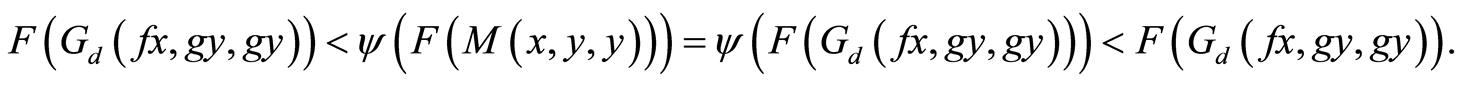
Case (ii)
If  then Equation (11) becomes
then Equation (11) becomes
 (13)
(13)

Case (iii)
If 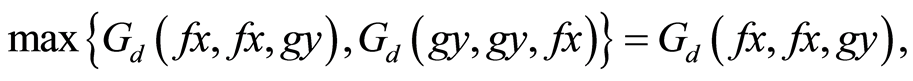 then Equation (12) becomes,
then Equation (12) becomes,
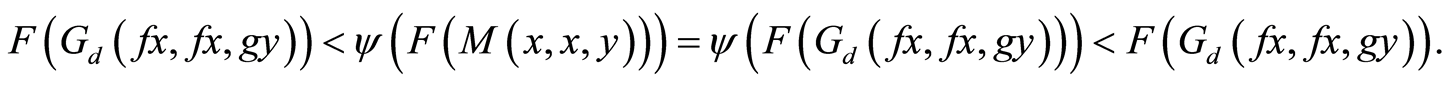
Case (iv)
If  then Equation (13) becomes,
then Equation (13) becomes,
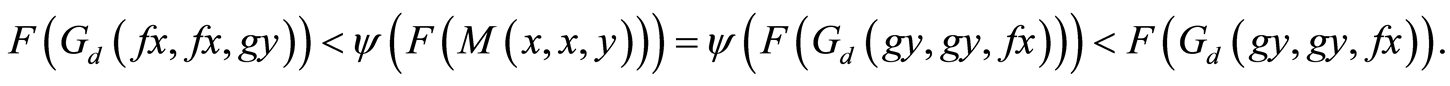 (14)
(14)
Combining Equations (13) and (14) gives,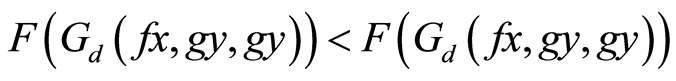 —a contradiction. Therefore
—a contradiction. Therefore  That is,
That is, 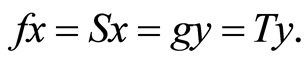
Moreover, if there is another point u such that 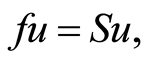 then, using Equations (12) and (13) it follows that
then, using Equations (12) and (13) it follows that 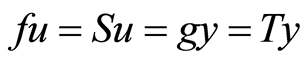 or
or 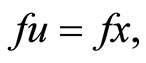 and
and 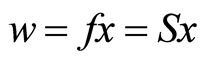 is a unique point of coincidence of
is a unique point of coincidence of 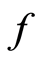 and
and . By Lemma 1.12,
. By Lemma 1.12, 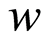 is the only common fixed point of f and S. That is
is the only common fixed point of f and S. That is 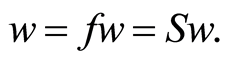 Similarly there is a unique point
Similarly there is a unique point 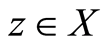 such that
such that  Suppose that
Suppose that 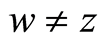 then using Equation (12) we have,
then using Equation (12) we have,
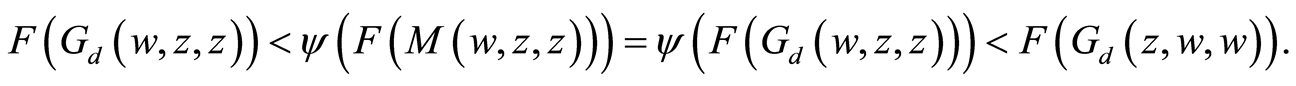 (15)
(15)
Using Equation (12) we get,
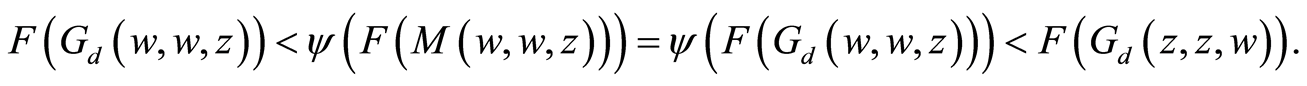 (16)
(16)
Combining Equations (15) and (16) gives,
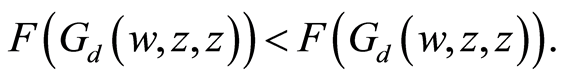
a contradiction. Therefore 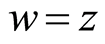 and w is a common fixed point of
and w is a common fixed point of ,
, 
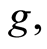 and
and 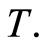 Following the preceding argument, it is clear that
Following the preceding argument, it is clear that 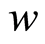 is unique.
is unique.
Remarks 2.7: Theorem 2.2 is an analogue of ([16] Theorem 1) in the setting of G-symmetric spaces.
Corollary 2.7: Let 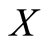 be a set with
be a set with 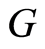 -symmetric
-symmetric . Let
. Let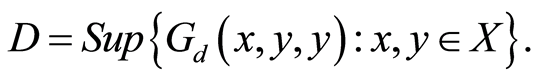 Suppose that
Suppose that 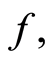
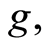
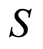 and
and  are self-maps of
are self-maps of  and that the pairs
and that the pairs 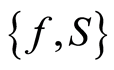 and
and 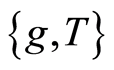 are each occasionally weakly compatible (owc). If for each
are each occasionally weakly compatible (owc). If for each 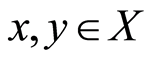 for which
for which 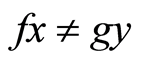 we have
we have
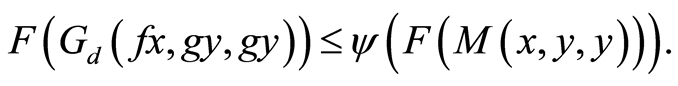 (17)
(17)
and
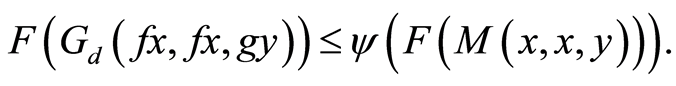 (18)
(18)
for each 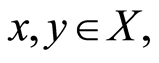
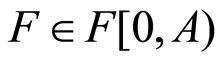 and
and 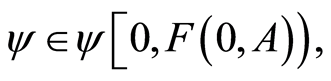 where
where  if
if 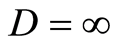 and
and 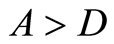 if
if  and
and

and

and 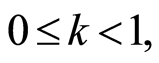 then
then 
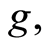
 and
and 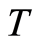 have a unique common fixed point.
have a unique common fixed point.
Proof: Since Equations (17) and (18) are special cases of Equations (11) and (12), then the proof of the corollary follows immediately from Theorem 2.6.
Acknowledgements
The authors would like to appreciate the Deanship of Scientific Research for supporting this work through their careful editing of this manuscript.
References
- Eke, K.S. and Olaleru, J.O. (2013) Some Fixed Point Results on Ordered G-Partial Metric Spaces. ICASTOR Journal of Mathematical Sciences, 7, 65-78.
- Cartan, E. (1929) Sur la Determination d’un Systeme Orthogonal Complet dans un Espace de Riemman Symetrique Clos. Rendiconti del Circolo Matematico di Palermo, 53, 217-252. http://dx.doi.org/10.1007/BF03024106
- Wilson, W.A. (1931) On Semi-Metric Spaces. American Journal of Mathematics, 53, 361-373. http://dx.doi.org/10.2307/2370790
- Hicks, T.I. and Rhoades, B.E. (1999) Fixed Point Theory in Symmetric Spaces with Applications to Probabilistic Spaces. Nonlinear Analysis, 36, 331-344. http://dx.doi.org/10.1016/S0362-546X(98)00002-9
- Mustafa, Z. and Sims, B. (2006) A New Approach to Generalized Metric Spaces. Journal of Nonlinear and Convex Analysis, 7, 289-297.
- Kannan, R. (1968) Some Results on Fixed Points. Bulletin Calcutta Mathematical Society, 10, 71-76.
- Jungck, G. (1976) Commuting Mappings and Fixed Points. American Mathematics Monthly, 73, 261-263. http://dx.doi.org/10.2307/2318216
- Sessa, S. (1982) On a Weak Commutativity Condition of Mappings in Fixed Point Considerations. Publications of Institutional Mathematics, 32, 149-153.
- Jungck, G. (1986) Compatible Mappings and Common Fixed Points. International Journal of Mathematics and Mathematical Science, 9, 771-779. http://dx.doi.org/10.1155/S0161171286000935
- Al-Thagafi, M.A. and Shahzad, N. (2008) Generalised I-Nonexpansive Selfmaps and Invariant Approximations. Acta Mathematica Sinica, 24, 867-876. http://dx.doi.org/10.1007/s10114-007-5598-x
- Pant, R.P. (1998) Common Fixed Points of Four Maps. Bulletin Calcutta Mathematical Society, 90, 281-286.
- Aamri, M. and El Moutawakil, D. (2002) Some New Common Fixed Point Theorems under Strict Contractive Conditions. Journal Mathematical Analysis and Applications, 270, 181-188. http://dx.doi.org/10.1016/S0022-247X(02)00059-8
- Jungck, G. and Rhoades, B.E. (2006) Fixed Point Theorems for Occasionally Weakly Compatible Mappings. Fixed Point Theory, 7, 287-296.
- Imdad, M., Ali, J. and Khan, L. (2006) Coincidence and Fixed Points in Symmetric Spaces under Strict Contractions. Journal of Mathematical Analysis and Applications, 320, 352-360. http://dx.doi.org/10.1016/j.jmaa.2005.07.004
- Bhatt, A., Chandra, H. and Sahu, D.R. (2010) Common Fixed Point Theorems for Occasionally Weakly Compatible Mappings under Relaxed Conditions. Nonlinear Analysis, 73, 176-182. http://dx.doi.org/10.1016/j.na.2010.03.011
- Abbas, M. and Rhoades, B.E. (2008) Common Fixed Point Theorems for Occasionally Weakly Compatible Mappings Satisfying a Generalized Contractive Condition. Mathematical Communication, 13, 295-301.

