Applied Mathematics
Vol.4 No.8(2013), Article ID:35588,6 pages DOI:10.4236/am.2013.48164
On the Behavior of the Positive Solutions of the System of Two Higher-Order Rational Difference Equations
1College of Science, Guangxi University of Science and Technology, Liuzhou, China
2College of Mathematics and Information Science, Guangxi University, Nanning, China
Email: *zgrzaw@gxu.edu.cn
Copyright © 2013 Qi Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 21, 2013; revised March 21, 2013; accepted April 1, 2013
Keywords: System of Difference Equations; Convergence; Positive Solution; Behavior
ABSTRACT
We study the convergence of the positive solutions of the system of the following two difference equations:

where 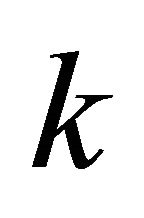 is a positive integer, the parameters
is a positive integer, the parameters  QUOTE
QUOTE 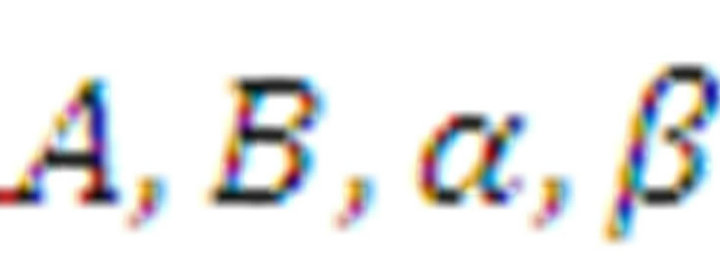
![]() and the initial conditions are positive real numbers. Our results generalize well known results in [1,2].
and the initial conditions are positive real numbers. Our results generalize well known results in [1,2].
1. Introduction
Difference equations and the system of difference equations play an important role in the analysis of mathematical models of biology, physics and engineering. The study of dynamical properties of nonlinear difference equations and the system of difference equations have been an area of intense interest in recent years (for example, see [1-11]).
In [1], Kurbanlı, Ģinar and Yalçinkaya studied the behavior of the positive solutions of the following system of difference equations

In [2], Stevo Stević investigated the system of the following difference equations
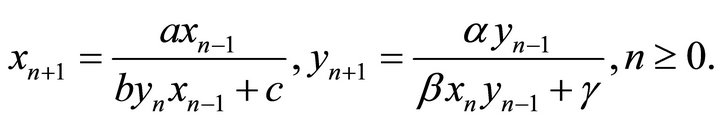
Motivated by the above studies, in this note, we consider the system of the following difference equations
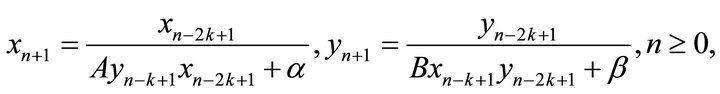 (1)
(1)
where  is a positive integer, the parameters A,
is a positive integer, the parameters A,  and the initial conditions are positive real numbers.
and the initial conditions are positive real numbers.
System (1) is a particular case of the system of the following difference equations
 (2)
(2)
If  , then system (2) is trivial. If
, then system (2) is trivial. If  , system is reduced to system (1) with
, system is reduced to system (1) with
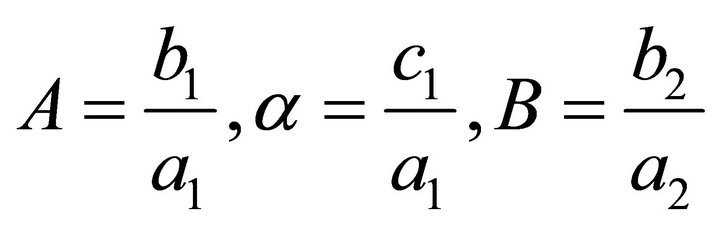 and
and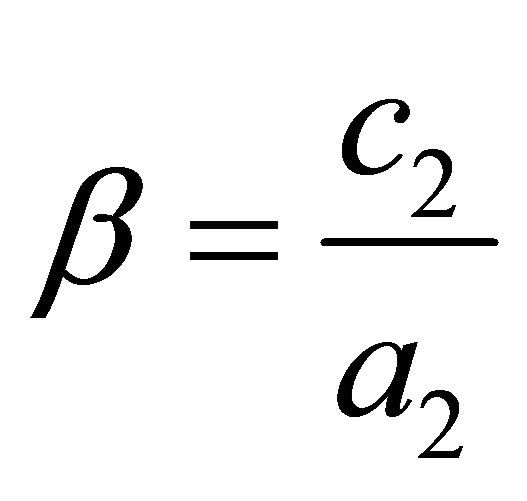 . Hence from now on, we will consider system (1).
. Hence from now on, we will consider system (1).
On the other hand, system (1) is a natural generalizetion of the equation
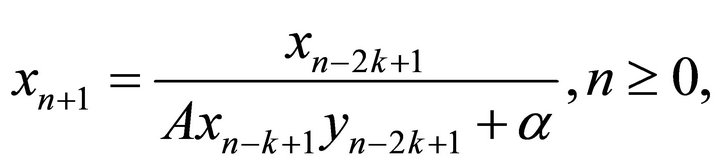 (3)
(3)
where  is a positive integer, the parameters
is a positive integer, the parameters 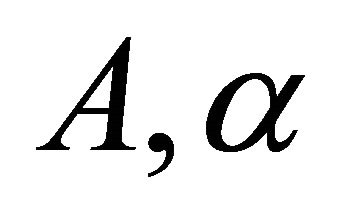 are positive real numbers. Hence the results which we obtained can also apply to (3).
are positive real numbers. Hence the results which we obtained can also apply to (3).
The essential problem we consider in this paper is the behavior of the positive solutions of system (1). We establish the convergence of the positive solutions of system (1). To some extent, this generalizes the results obtained in [1,2]. It is interesting that a modification of our method enables us to investigate the form of the positive solutions of system (1).
2. Main Results
For convenience, set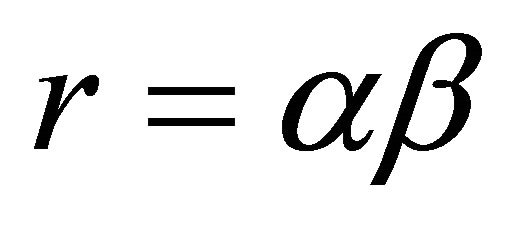 ,
,
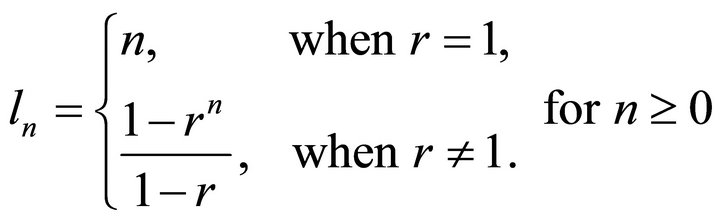
Let  be a positive solution of (1). Set
be a positive solution of (1). Set
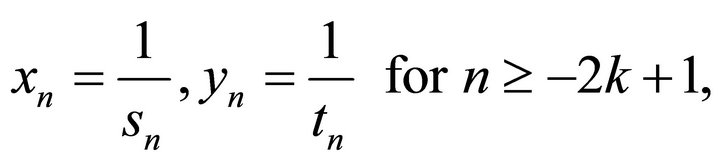 (4)
(4)
then (1) translates into
 (5)
(5)
Set

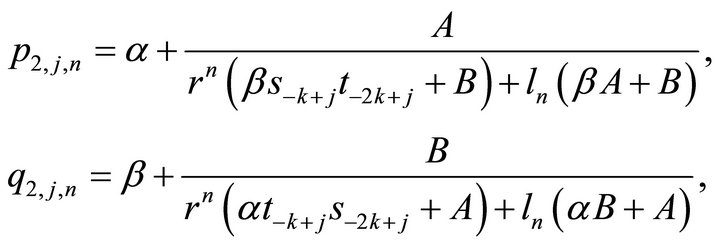
for 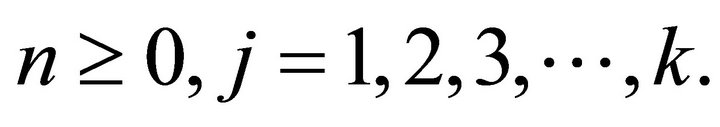
Lemma 2.1 For (5), we have
 (6)
(6)
Proof. Since

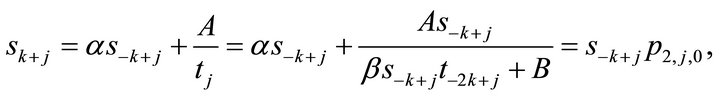

Hence (6) holds for 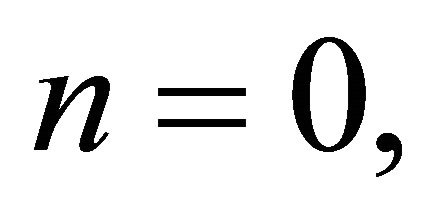
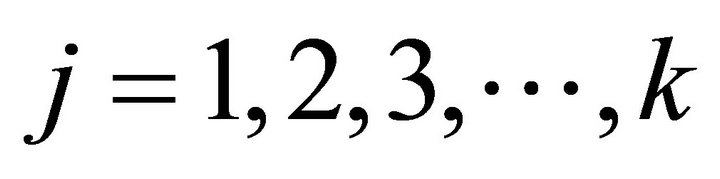 .
.
For  assume that (6) is true.
assume that (6) is true.
Note that, for 


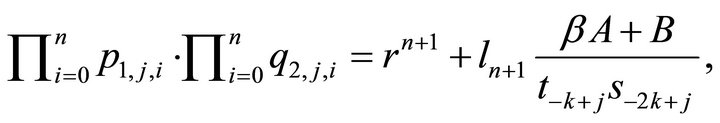
Then for  we have
we have
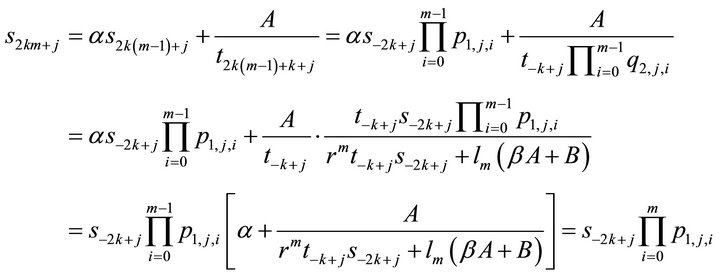
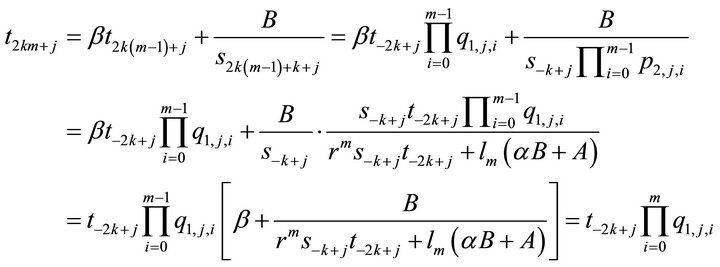

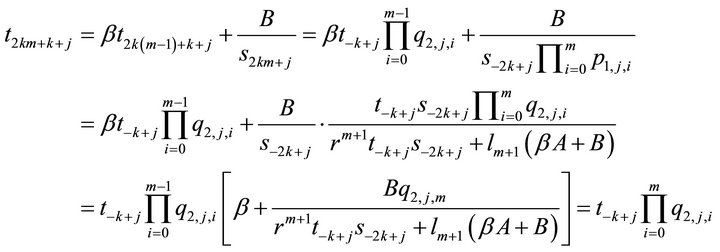
Hence (6) is true.
Theorem 2.2 Let 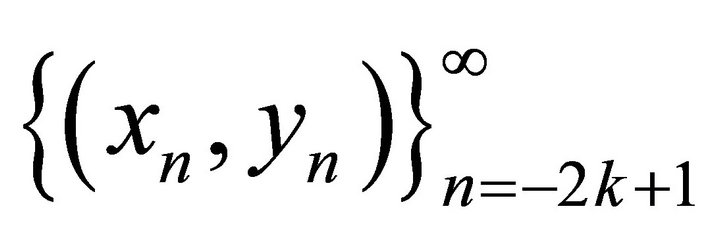 be a positive solution of (1). For
be a positive solution of (1). For 
1) When , we have
, we have
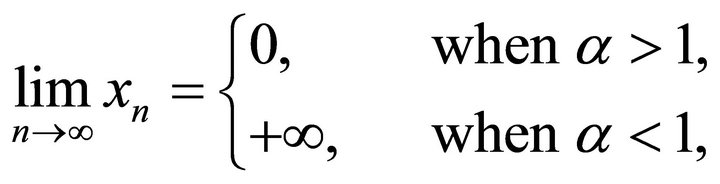 ,
,
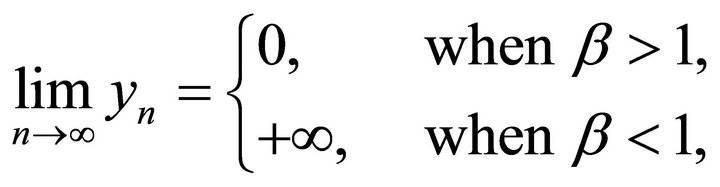
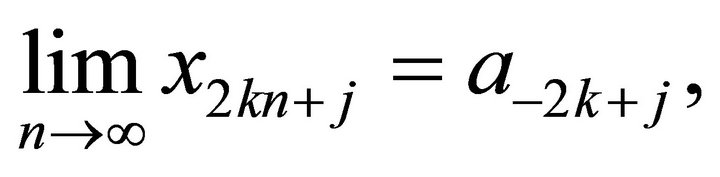

where
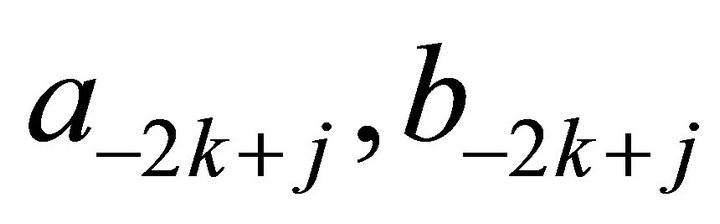
satisfy:
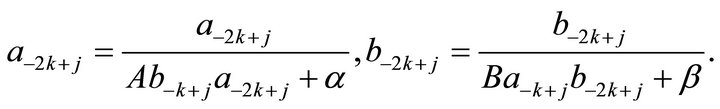
2) When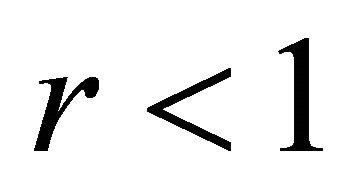 .
.
a) Suppose , then
, then 
b) Suppose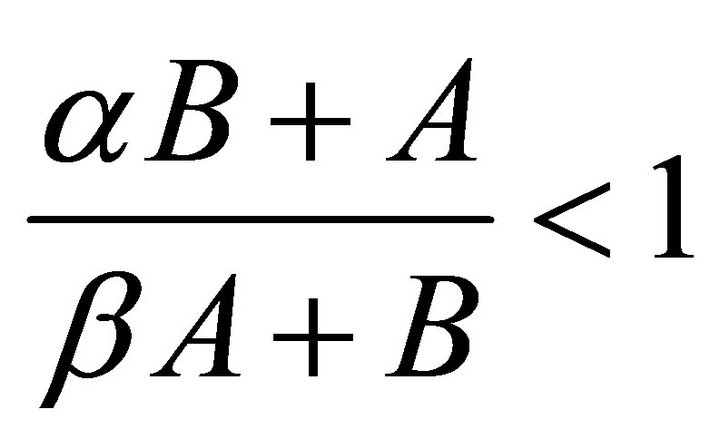 , then
, then 
c) Suppose 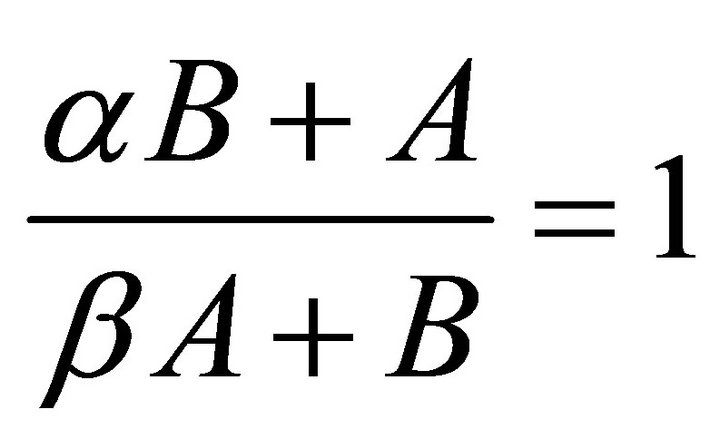
i) If 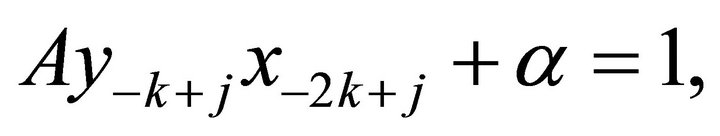 then
then  for
for 
ii) If 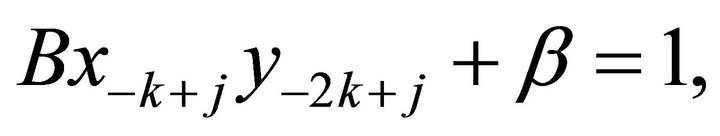 then
then 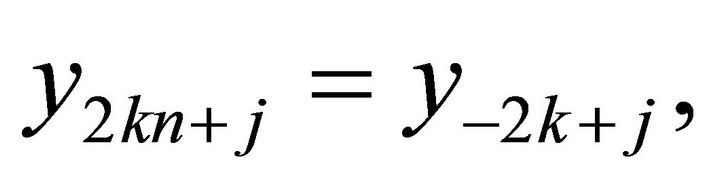 for
for 
iii) If 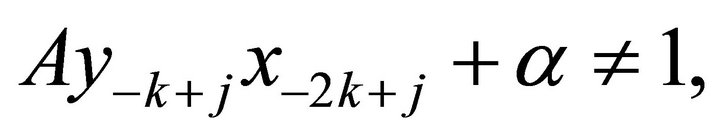 then
then 
iv) If  then
then 
where
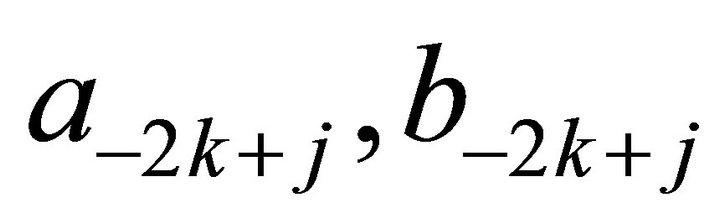
satisfy
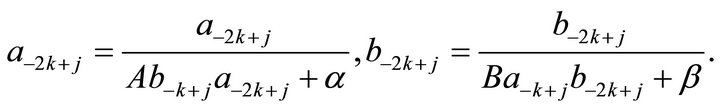
Proof. Note that for 


Hence
 (7)
(7)
 (8)
(8)
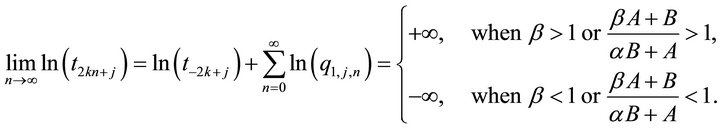 (9)
(9)
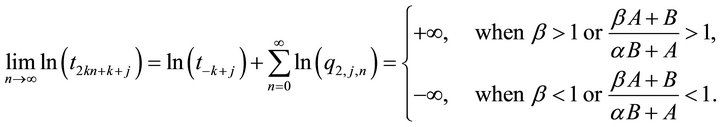 (10)
(10)
1) When . In view of (4), (6), (7) and (8), we drive
. In view of (4), (6), (7) and (8), we drive
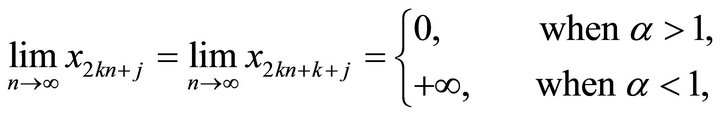
Thus

Similarly, in view of (4), (6), (9) and (10), we get
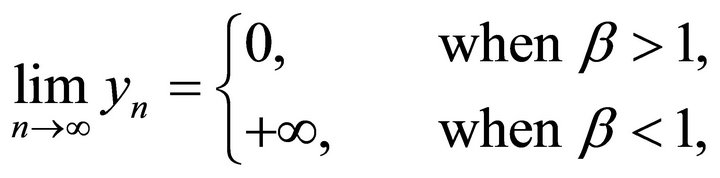
When  note that the positive series
note that the positive series
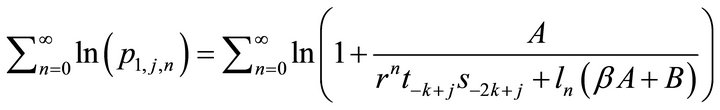
is convergent, in view of (4) and (6), we drive 
Similarly, we get

2) When 
a) b) The proof is similar to the proof of 1, we get
 ,
,
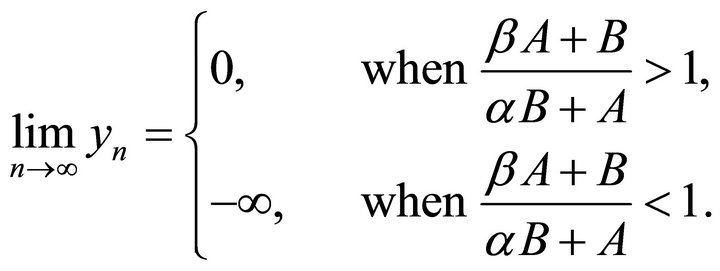
c) Suppose .
.
i) If  In view of (1), by induction, we drive
In view of (1), by induction, we drive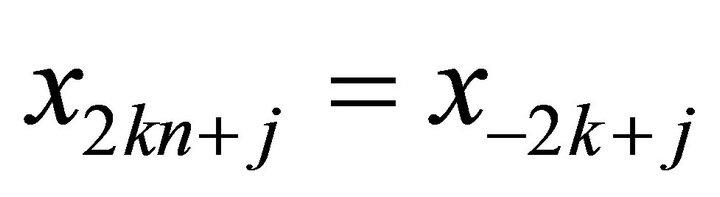 , for
, for 
ii) If , Similarly, we drive
, Similarly, we drive 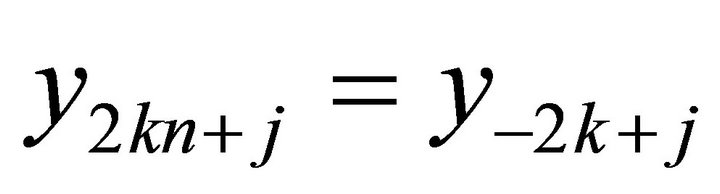 for
for 
iii) Note that
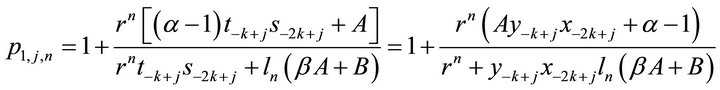

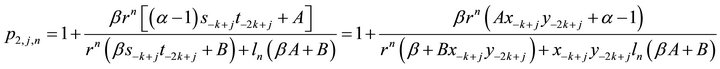

Hence, if  the positive series
the positive series
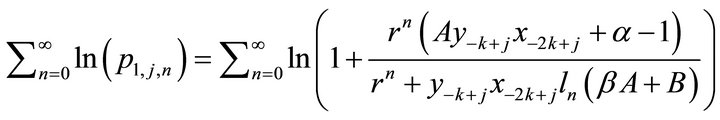 is convergent. If
is convergent. If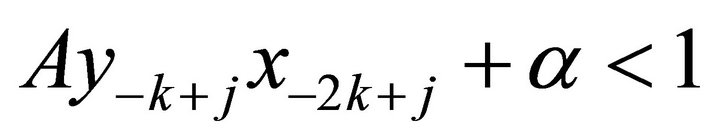 , the negative series
, the negative series  is convergent.
is convergent.
In view of (4) and (6), thus if 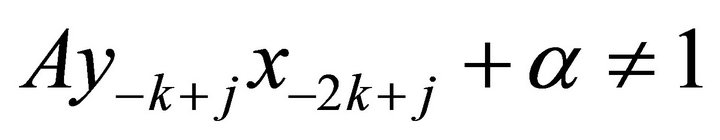 then
then 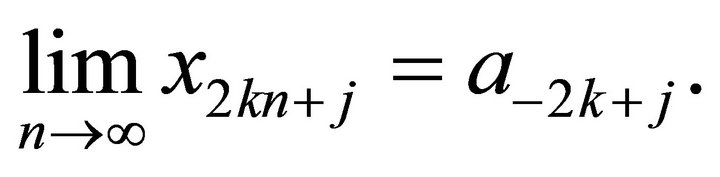 Similarly, we get
Similarly, we get 
iv) If  Similarly, we get
Similarly, we get 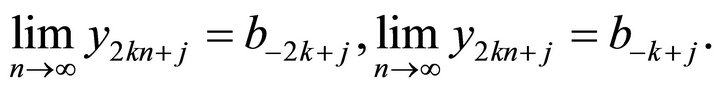
3. Acknowledgements
This work was supported by the NSF of China (No. 11161029), and supported by NSF of Guangxi (No. 2012GXNSFDA276040, 2013GXNSFBA019020), NSF of the Department of Education of Guangxi Province (No. 200103YB157). NSF of Guangxi University of Science and Technology (No. 1166218).
REFERENCES
- A. S. Kurbanlı, C. Ģinar and Ì. Yalçinkaya, “On the Behavior of Positive Solutions of the System of Rational Difference Equation
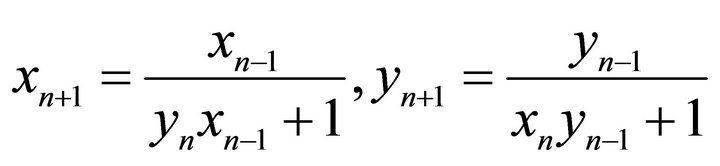 ,” Mathematical and Computer Modelling, Vol. 53, No. 5-6, 2011, pp. 1261- 1267. doi:10.1016/j.mcm.2010.12.009
,” Mathematical and Computer Modelling, Vol. 53, No. 5-6, 2011, pp. 1261- 1267. doi:10.1016/j.mcm.2010.12.009 - S. Stević, “On a System of Difference Equations,” Applied Mathematics and Computation, Vol. 218, No. 7, 2011, pp. 3372-3378. doi:10.1016/j.amc.2011.08.079
- E. Camouzis and G. Papaschinopoulos, “Global Asymptotic Behavior of Positive Solutions on the System of Rational Difference Equations
 ,” Applied Mathematics Letters. Vol. 17, No. 6, 2004, pp. 733-737. doi:10.1016/S0893-9659(04)90113-9
,” Applied Mathematics Letters. Vol. 17, No. 6, 2004, pp. 733-737. doi:10.1016/S0893-9659(04)90113-9 - X. Yang, “On the System of Rational Difference Equations
 ,” Journal of Mathematical Analysis and Applications, Vol. 307, No. 1, 2005, pp. 305-311. doi:10.1016/j.jmaa.2004.10.045
,” Journal of Mathematical Analysis and Applications, Vol. 307, No. 1, 2005, pp. 305-311. doi:10.1016/j.jmaa.2004.10.045 - Q. Wang, F. P. Zeng, G. R. Zhang and X. H. Liu, “Dynamics of the Difference Equation
 ,” Journal of Difference Equations and Applications, Vol. 12, No. 5, 2006, pp. 399-417. doi:10.1080/10236190500453695
,” Journal of Difference Equations and Applications, Vol. 12, No. 5, 2006, pp. 399-417. doi:10.1080/10236190500453695 - Y. Zhang, X. Yang, D. J. Evans and C. Zhu, “On the Nonlinear Difference Equation System
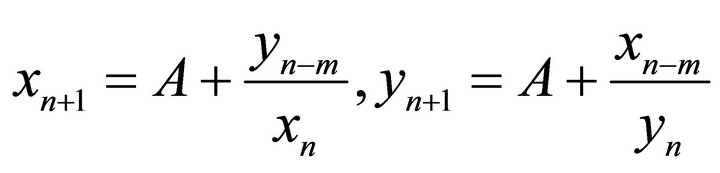 ,” Computers & Mathematics with Applications, Vol. 53, No. 10, 2007, pp. 1561- 1566. doi:10.1016/j.camwa.2006.04.030
,” Computers & Mathematics with Applications, Vol. 53, No. 10, 2007, pp. 1561- 1566. doi:10.1016/j.camwa.2006.04.030 - K. S. Berenhaut, J. D. Foley and S. Stević, “The Global Attractivity of the Rational Difference Equation
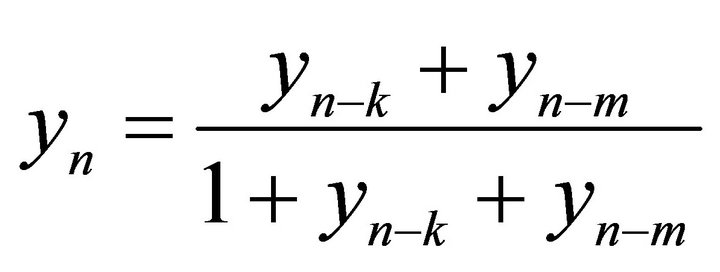 ,” Applied Mathematics Letters, Vol. 20, No. 1, 2007, pp. 54-58. doi:10.1016/j.aml.2006.02.022
,” Applied Mathematics Letters, Vol. 20, No. 1, 2007, pp. 54-58. doi:10.1016/j.aml.2006.02.022 - K. S. Berenhaut, J. D. Foley and S. Stević, “The Global Attractivity of the Rational Difference Equation
 ,” Proceedings of the American Mathematical Society, Vol. 135, No. 1, 2007, pp. 1133-1140. doi:10.1090/S0002-9939-06-08580-7
,” Proceedings of the American Mathematical Society, Vol. 135, No. 1, 2007, pp. 1133-1140. doi:10.1090/S0002-9939-06-08580-7 - K. S. Berenhaut, J. D. Foley and S. Stević, “The Global Attractivity of the Rational Difference Equation
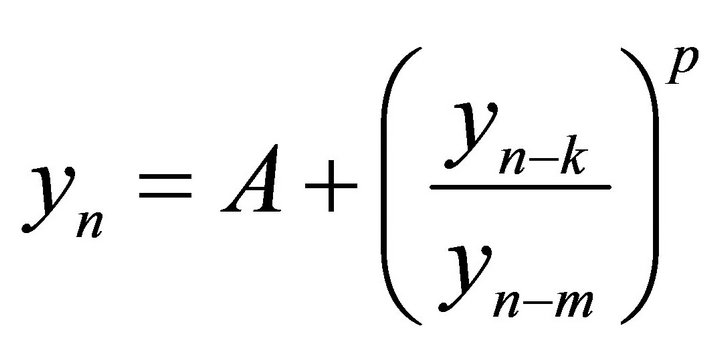 ,” Proceedings of the American Mathematical Society, Vol. 136, No. 1, 2008, pp. 103-110. doi:10.1090/S0002-9939-07-08860-0
,” Proceedings of the American Mathematical Society, Vol. 136, No. 1, 2008, pp. 103-110. doi:10.1090/S0002-9939-07-08860-0 - B. Iričanin and S. Stević, “Eventually Constant Solutions of a Rational Difference Equation,” Applied Mathematics and Computation, Vol. 215, No. 2, 2009, pp. 854-856. doi:10.1016/j.amc.2009.05.044
- I. Yalcinkaya and C. Ģinar, “Global Asymptotic Stability of Two Nonlinear Difference Equations
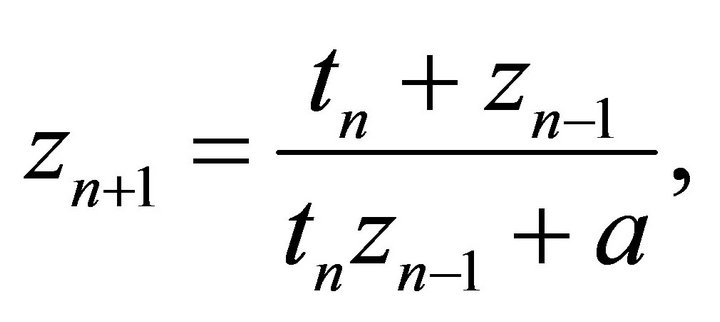
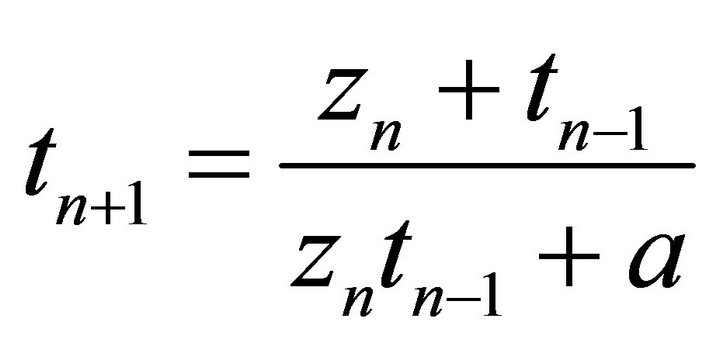 ,” Fasciculi Mathematici, Vol. 43, 2010, pp. 171-180.
,” Fasciculi Mathematici, Vol. 43, 2010, pp. 171-180.
NOTES
*Corresponding author.

