Applied Mathematics
Vol.3 No.12A(2012), Article ID:26062,10 pages DOI:10.4236/am.2012.312A293
Stochastic Approximation Method for Fixed Point Problems
1Department of Mathematics, The Technion-Israel Institute of Technology, Haifa, Israel
2The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy
3Department of Mathematical Sciences, Shawnee State University, Portsmouth, USA
Email: alberya@yahoo.com, alberya@gmail.com
Received August 28, 2012; revised November 28, 2012; accepted December 5, 2012
Keywords: Hilbert Spaces; Stochastic Approximation Algorithm; Weakly Contractive Operators; Nonexpansive Operators; Fixed Points; Convergence in Mean Square; Convergence Almost Sure (a.s.); Nonasymptotic Estimates of Convergence Rate
ABSTRACT
We study iterative processes of stochastic approximation for finding fixed points of weakly contractive and nonexpansive operators in Hilbert spaces under the condition that operators are given with random errors. We prove mean square convergence and convergence almost sure (a.s.) of iterative approximations and establish both asymptotic and nonasymptotic estimates of the convergence rate in degenerate and non-degenerate cases. Previously the stochastic approximation algorithms were studied mainly for optimization problems.
1. Introduction
In this paper the following problem is solved: To find a fixed point  of the operator
of the operator  in other words, to find a solution
in other words, to find a solution 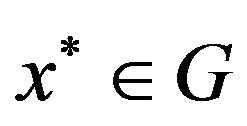 of the equation
of the equation
 (1.1)
(1.1)
where ![]() is a Lipschitz continuous mapping,
is a Lipschitz continuous mapping,  is a Hilbert space,
is a Hilbert space,  is a closed convex subset. We suppose that
is a closed convex subset. We suppose that  exists, i.e., the fixed point set
exists, i.e., the fixed point set  of
of ![]() is nonempty. Note in different particular cases of the Equation (1.1), for example, when
is nonempty. Note in different particular cases of the Equation (1.1), for example, when 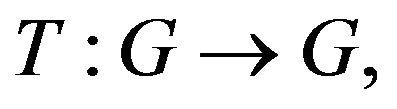 the solution existence and solution uniqueness can be proved under some additional assumptions.
the solution existence and solution uniqueness can be proved under some additional assumptions.
We separately consider two classes of mappings T: the class of weakly contractive maps and more general class of nonexpansive ones. Let us recall their definitions.
Definition 1.1. A mapping 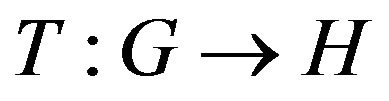 is said to be weakly contractive of class
is said to be weakly contractive of class ![]() on a closed convex subset
on a closed convex subset  if there exists a continuous and increasing function
if there exists a continuous and increasing function 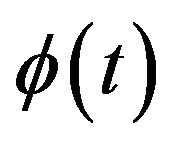 defined on
defined on 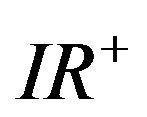 such that
such that  is positive on
is positive on  and for all
and for all
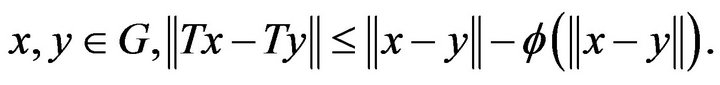 (1.2)
(1.2)
Remark 1.2. It follows from (1.2) that  and in real problems an argument
and in real problems an argument  of the function
of the function  doesn’t necessary approaches to
doesn’t necessary approaches to  obeying the condition
obeying the condition 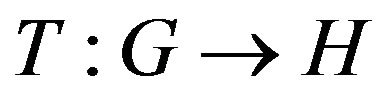 (see the example in Remark 3.4).
(see the example in Remark 3.4).
Definition 1.3. A mapping  is said to be nonexpansive on the closed convex subset
is said to be nonexpansive on the closed convex subset  if for all
if for all 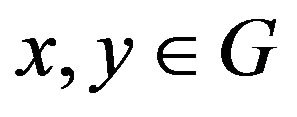

It is obvious that the class of weakly contractive maps is contained in the class of nonexpansive maps because the right-hand side of (1.2) is estimated as
 (1.3)
(1.3)
and it contains the class of strongly contractive maps because  with
with 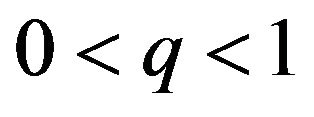 gives us
gives us
 (1.4)
(1.4)
We study the following algorithm of stochastic approximation:
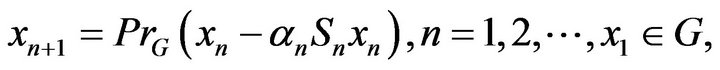 (1.5)
(1.5)
where 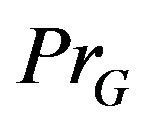 is the metric projection operator from
is the metric projection operator from  onto G and deterministic step-parameters
onto G and deterministic step-parameters  satisfy the standard conditions:
satisfy the standard conditions:
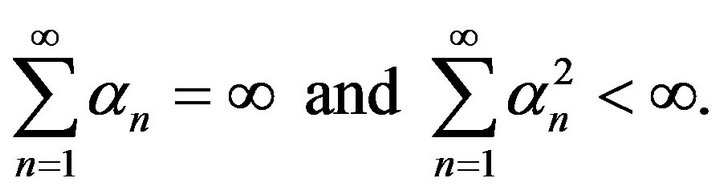 (1.6)
(1.6)
The factor 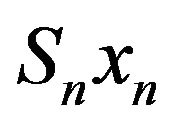 in (1.5) is an infinite-dimensional vector of random observations of the clearance operator
in (1.5) is an infinite-dimensional vector of random observations of the clearance operator 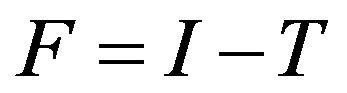 at random points
at random points  given for all
given for all  on the same probability space
on the same probability space 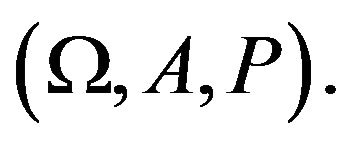 We set
We set
 (1.7)
(1.7)
where  and
and 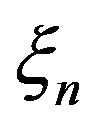 is a sequence of independent random vectors with the conditions
is a sequence of independent random vectors with the conditions
 (1.8)
(1.8)
Here 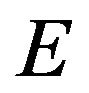 is a symbol of the mathematical expectation. In order to calculate conditional mathematical expectations of different random variables we define the
is a symbol of the mathematical expectation. In order to calculate conditional mathematical expectations of different random variables we define the ![]() - subalgebra
- subalgebra 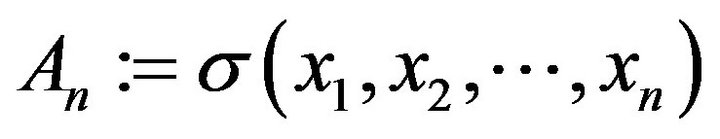 on
on 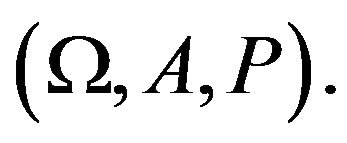 And then
And then 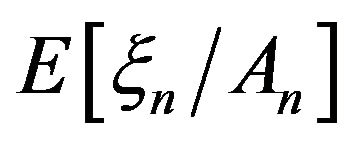 means
means  function with the following property: for any
function with the following property: for any 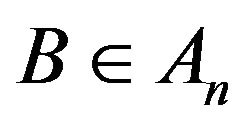

We also assume in the sequel that 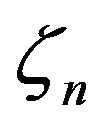 is An-measurable for all
is An-measurable for all 
Let us recall the mean square convergence and almost sure (a.s.) convergence.
We say that the sequence 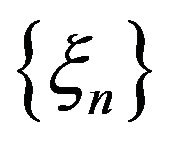 of random variables
of random variables  converges in mean square to
converges in mean square to  if
if  exists and
exists and

The sequence  converges to
converges to  almost surely or with probability 1 if
almost surely or with probability 1 if

Almost sure convergence and convergence in mean square imply convergence in the sense of probability: The sequence  of random variables
of random variables 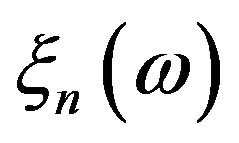 converges in the sense of probability to
converges in the sense of probability to  if for all
if for all 

So, we consider iterative processes of stochastic approximation in the form (1.5) for finding fixed points of weakly contractive (Definition 1.1) and nonexpansive (Definition 1.3) mappings in Hilbert spaces under the conditions (1.8). We prove mean square convergence and convergence almost sure of iterative approximations and establish both asymptotic and nonasymptotic estimates of the convergence rate. Perhaps, we present here the first results of this sort for fixed point problems. Formerly the stochastic approximation methods were studied mainly to find minimal and maximal points in optimization problems (see, for example, [1-6] and references within).
2. Auxiliary Recurrent Inequalities
Lemma 2.1. [3,4] Let  be sequences of nonnegative real numbers satisfying the recurrent inequality.
be sequences of nonnegative real numbers satisfying the recurrent inequality.
 (2.1)
(2.1)
Assume that  and
and  Then
Then 
is bounded and converges to some limit.
Lemma 2.2. [3,4] Let 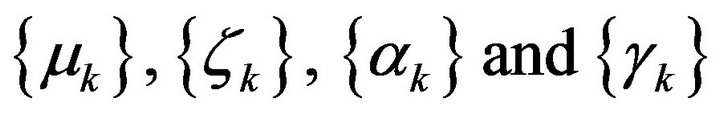 be sequences of nonnegative real numbers satisfying the recurrent inequality.
be sequences of nonnegative real numbers satisfying the recurrent inequality.
 (2.2)
(2.2)
where 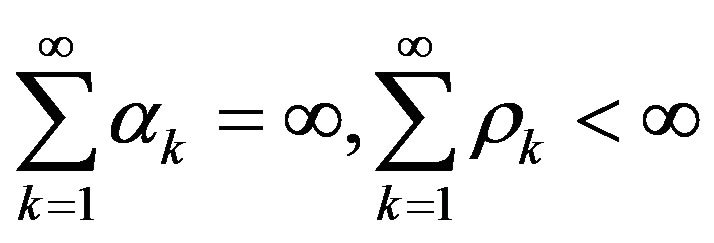 and either
and either  or
or
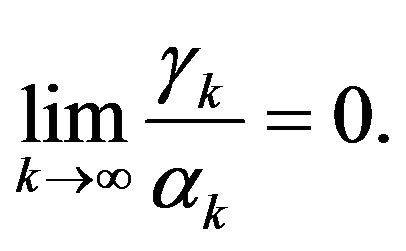 (2.3)
(2.3)
Assume that 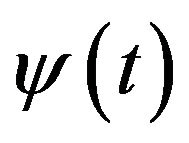 is continuous and increasing function defined on
is continuous and increasing function defined on 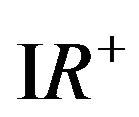 such that
such that  is positive on
is positive on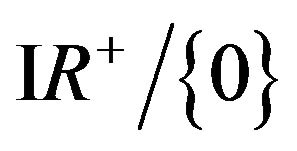 ,
, 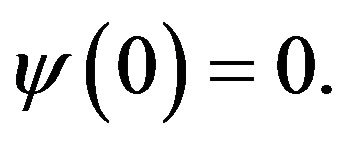 Then
Then 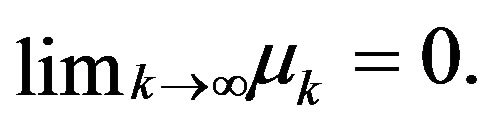 There exists an infinite subsequence
There exists an infinite subsequence  such that
such that
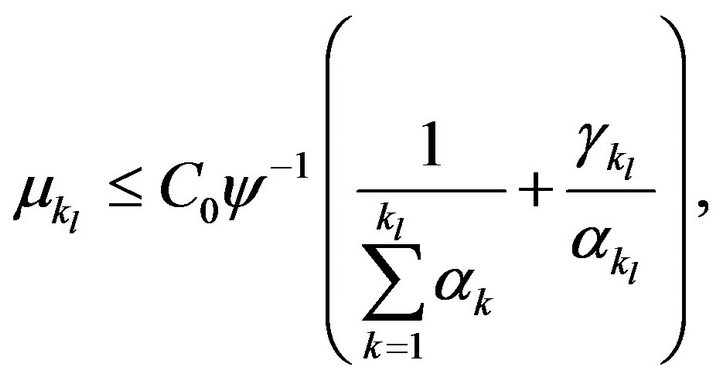
where 
In the following two lemmas we want to present nonasymptotic estimates for the whole sequence 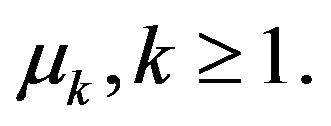 For this the stronger requirements are made of parameters
For this the stronger requirements are made of parameters  and function
and function 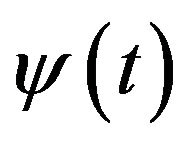 in the recurrent inequality.
in the recurrent inequality.
Suppose that 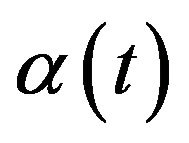 such that
such that 
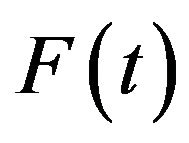 and
and
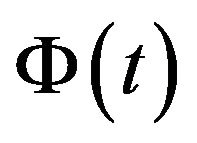 are antiderivatives from
are antiderivatives from  and
and  respectively, with arbitrary constants
respectively, with arbitrary constants  (without loss of generality, one can put
(without loss of generality, one can put ), i.e.
), i.e.

Observe that 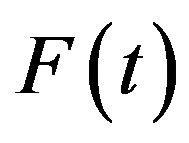 has the following properties:
has the following properties:
i) 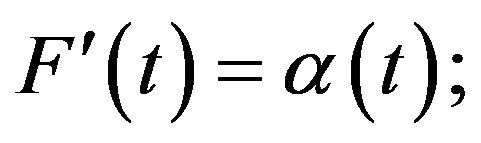
ii) 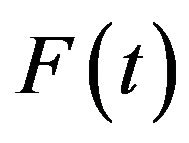 is strictly increasing on
is strictly increasing on 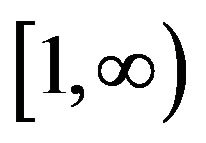 and
and 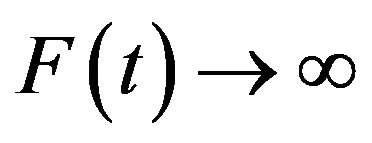 as
as 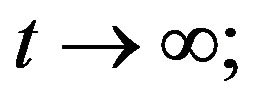
iii) The function  is decreasing;
is decreasing;
iv) 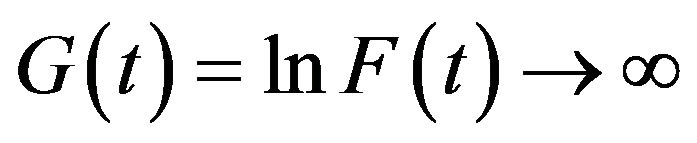 as
as 
Introduce the following denotations:
1)  and
and  are the inverse functions to
are the inverse functions to 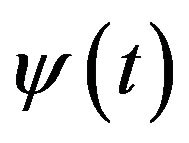 and
and 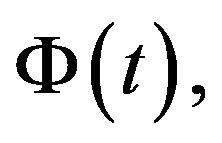 respectively;
respectively;
2)  is a fixed control parameter;
is a fixed control parameter;
3) 

4) 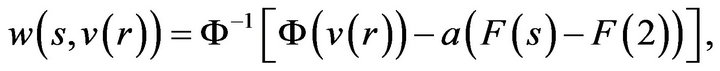

5)  where
where
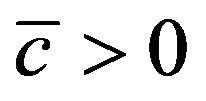 is an arbitrary fixed number;
is an arbitrary fixed number;
We present now the based condition (P): The graphs of the scalar functions 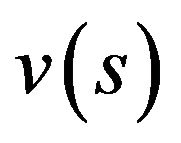 and
and  with any fixed
with any fixed 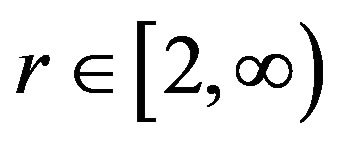 are intersected on the interval
are intersected on the interval 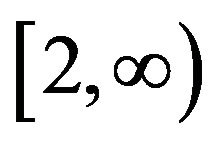 not more than at two points
not more than at two points ![]() and
and  (we do not consider contact points as intersection ones excepting
(we do not consider contact points as intersection ones excepting 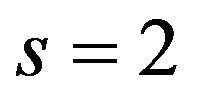 if any).
if any).
For example, the graphs of the functions  and
and
 calculated for
calculated for 
and 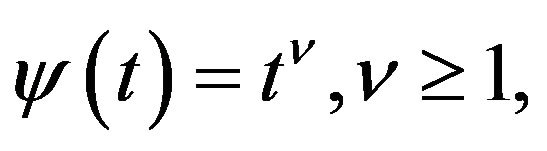 satisfy the condition (P).
satisfy the condition (P).
Lemma 2.3. [3,4] Assume that 1) the property (P) is carried out for the function  and
and
 2)
2) 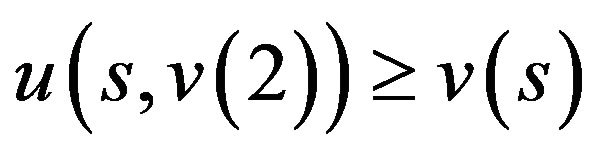 as
as 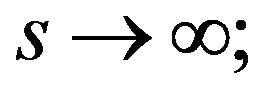 3) the control parameter
3) the control parameter 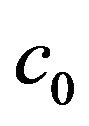 is chosen such that
is chosen such that
 (2.4)
(2.4)
Then for the sequence  generated by the inequality
generated by the inequality
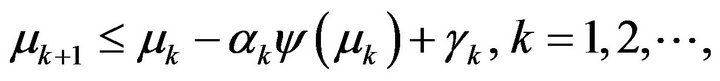 (2.5)
(2.5)
it follows:  and for all
and for all 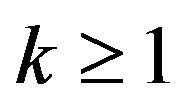
 (2.6)
(2.6)
Lemma 2.4. [3,4] Assume that 1) the property (P) is carried out for all the function 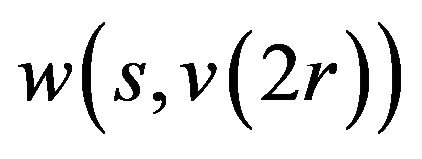 and
and 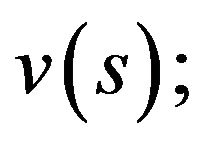 2)
2)  as
as ![]() Then for the sequence
Then for the sequence  generated by the inequality (2.5)
generated by the inequality (2.5) 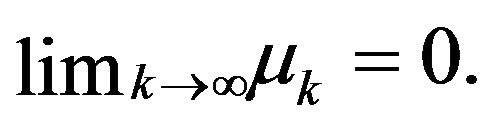 In additiona) if
In additiona) if 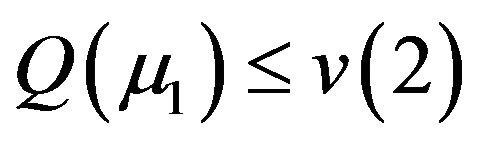 and the control parameter
and the control parameter 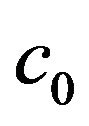 is chosen such that
is chosen such that  as
as 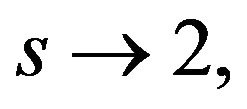 then for all
then for all 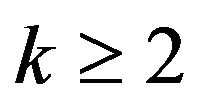
 (2.7)
(2.7)
b) in all remaining cases
 (2.8)
(2.8)
 (2.9)
(2.9)
where  is a unique root of the equation
is a unique root of the equation
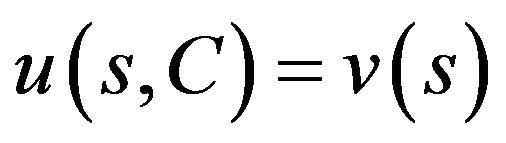 (2.10)
(2.10)
on the interval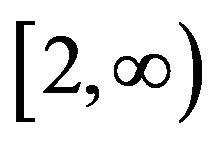 .
.
The following lemmas deal with another sort of recurrent inequalities:
Lemma 2.5. [7,8] Let  be sequences of non-negative real numbers satisfying the recurrence inequality.
be sequences of non-negative real numbers satisfying the recurrence inequality.
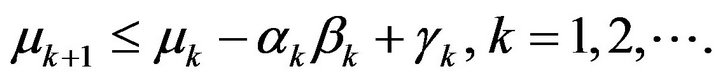 (2.11)
(2.11)
Assume that
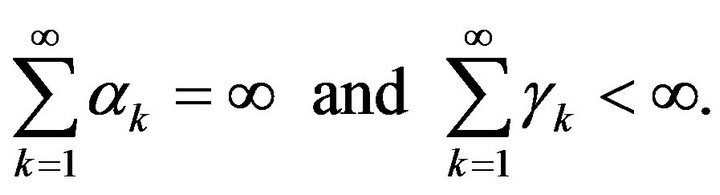
Then:
i) There exists an infinite subsequence 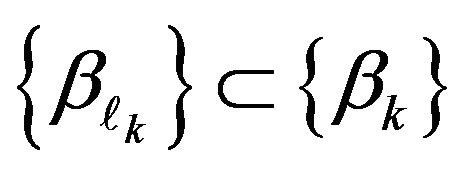 such that
such that
 (2.12)
(2.12)
and, consequently, 
ii) if  and there exists
and there exists  such that
such that
 (2.13)
(2.13)
for all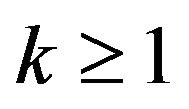 , then
, then 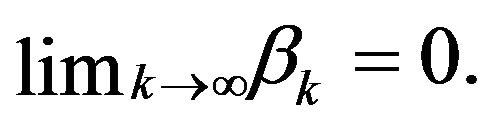
Lemma 2.6. [7,8] Let 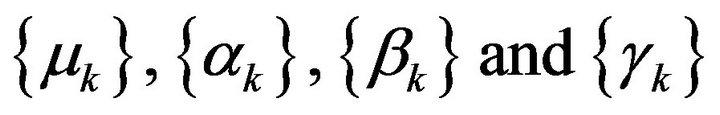 be sequences of non-negative real numbers satisfying the recurrence inequality (2.11). Assume that
be sequences of non-negative real numbers satisfying the recurrence inequality (2.11). Assume that 
and (2.3) is satisfied. Then there exists an infinite subsequence  such that
such that 
3. Mean Square Convergence of Stochastic Approximations
Theorem 3.1. Assume that  is a weakly contractive mapping of the class
is a weakly contractive mapping of the class 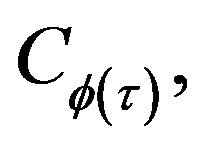
 is a convex function with respect to
is a convex function with respect to 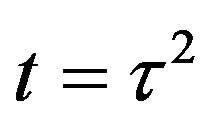 and
and
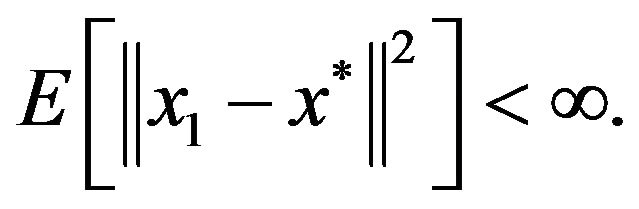 Then the sequence
Then the sequence 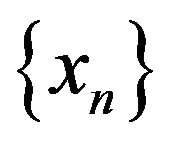 generated by (1.5)-(1.7) converges in mean square to a unique fixed point
generated by (1.5)-(1.7) converges in mean square to a unique fixed point 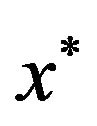 of
of 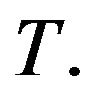 There exists an infinite subsequence
There exists an infinite subsequence  such that
such that
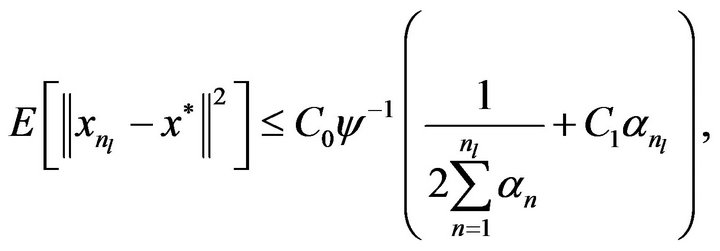 (3.1)
(3.1)
where 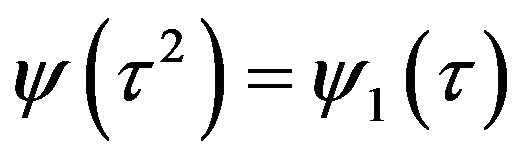 and some positive constant
and some positive constant 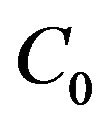 satisfies the inequality
satisfies the inequality
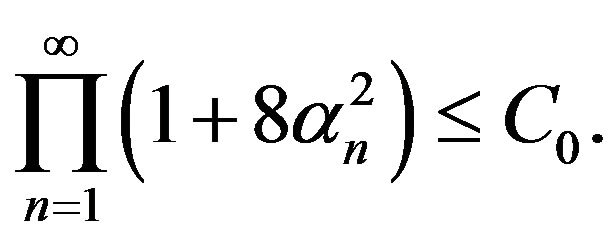 (3.2)
(3.2)
Remark 3.2.  exists in view of the second condition in (1.6).
exists in view of the second condition in (1.6).
Proof. First of all, we note that the method (1.5)-(1.7) guarantees inclusion  for all
for all 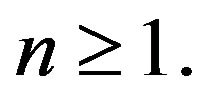 Since the metric projection operator
Since the metric projection operator  is nonexpansive in a Hilbert space and
is nonexpansive in a Hilbert space and  exists, we can write
exists, we can write
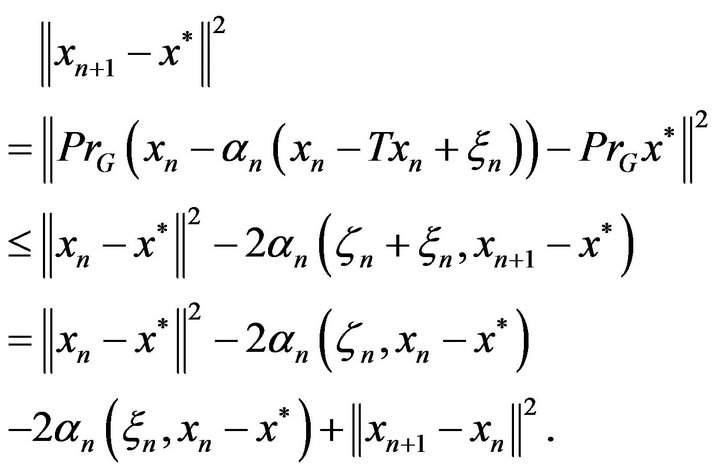 (3.3)
(3.3)
Let us evaluate the first scalar product in (3.3). We have
 (3.4)
(3.4)
We remember that 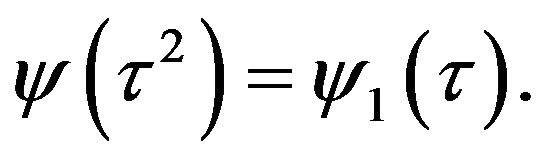 Then the inequalities (3.3) and (3.4) yield
Then the inequalities (3.3) and (3.4) yield
 (3.5)
(3.5)
Applying the conditional expectation with respect to  to the both sides of (3.5) we obtain
to the both sides of (3.5) we obtain
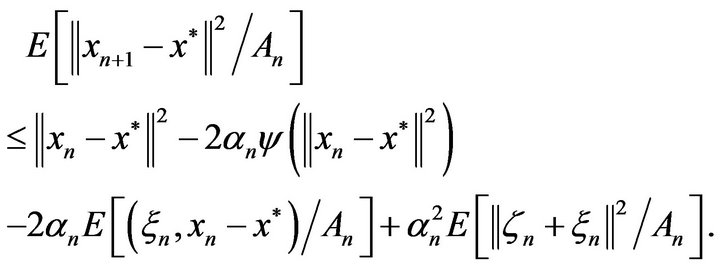 (3.6)
(3.6)
It is easy to see that
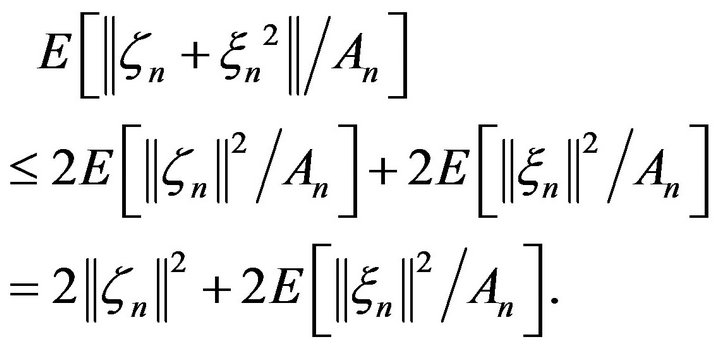 (3.7)
(3.7)
Since ![]() is weakly contractive and therefore nonexpansive, one gets
is weakly contractive and therefore nonexpansive, one gets
Taking into account (3.7), the inequality (3.9) is estimated as follows:
 (3.8)
(3.8)
Now the unconditional expectation implies
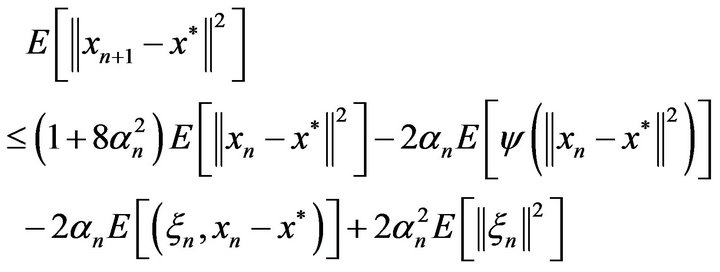 (3.9)
(3.9)
Next we need the Jensen inequality for a convex function 
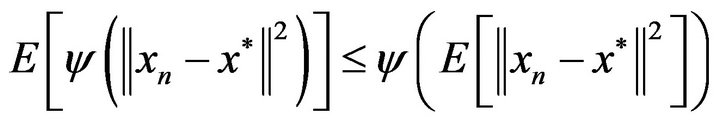
(see [9,10]). This allows us to rewrite (3.9) in the form
 (3.10)
(3.10)
because of
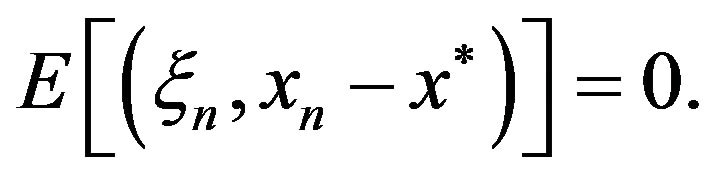
Denoting  we have
we have
 (3.11)
(3.11)
where in view of Definition 1.1, 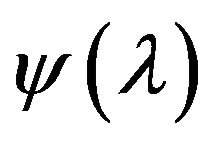 is a continuous and increasing function with
is a continuous and increasing function with 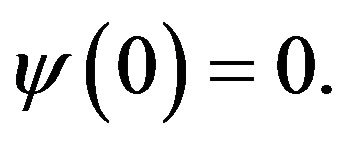 Due to (6), from Lemma 2.2 it follows
Due to (6), from Lemma 2.2 it follows

and the estimate (3.1) holds too. The theorem is proved. □
Remark 3.3. If a fixed point of weakly contractive mapping 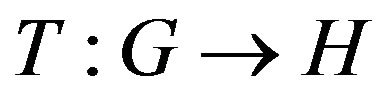 exists, then it is unique [11].
exists, then it is unique [11].
Remark 3.4. The following example was presented in [11]: Let 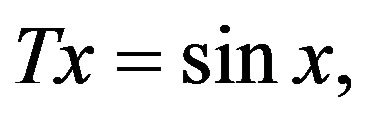
 and
and 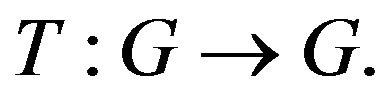 It has been shown in [11] that
It has been shown in [11] that

for all 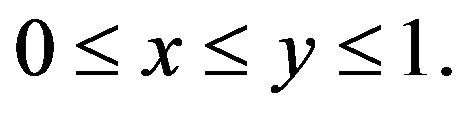 Then
Then
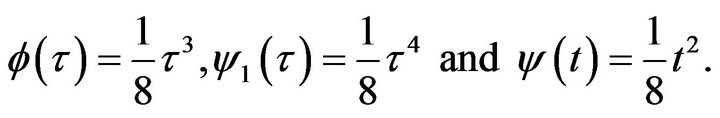
Definition 3.5. Let a nonexpansive mapping
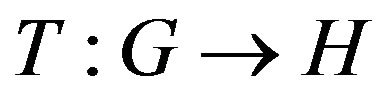 have a unique fixed point
have a unique fixed point . T is said to be weakly sub-contractive on the closed convex subset
. T is said to be weakly sub-contractive on the closed convex subset  if there exists continuous and increasing function
if there exists continuous and increasing function  defined on
defined on  such that
such that 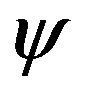 is positive on
is positive on
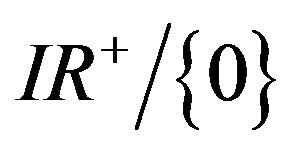 ,
, 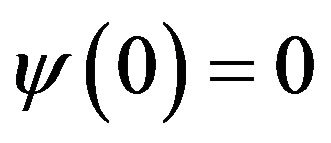 ,
, ![]() such that for all
such that for all
 .
.
 (3.12)
(3.12)
Theorem 3.6. Assume that a mapping  is weakly sub-contractive and the function
is weakly sub-contractive and the function  in (3.12) is convex on
in (3.12) is convex on  Then the results of Theorem 3.1 holds for the sequence
Then the results of Theorem 3.1 holds for the sequence  generated by (1.5)-(1.7).
generated by (1.5)-(1.7).
The second inequality in (1.6) can be omitted if we assume not less than linear growth of 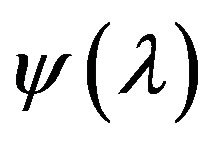 “on infinity” and put
“on infinity” and put 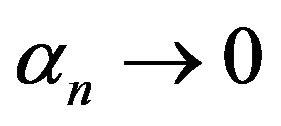 as
as ![]()
Theorem 3.7. Assume that a mapping  is weakly sub-contractive and the function
is weakly sub-contractive and the function  in (3.12) is convex on
in (3.12) is convex on  Suppose that instead of (1.6) the conditions
Suppose that instead of (1.6) the conditions
 (3.13)
(3.13)
hold. In addition, let 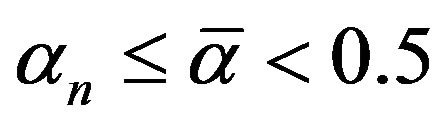 and
and
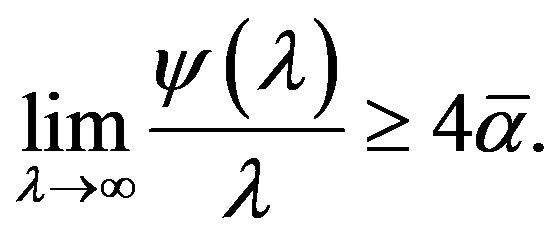 (3.14)
(3.14)
Then the sequence  generated by (1.5), (1.7) and (3.13) converges in mean square to
generated by (1.5), (1.7) and (3.13) converges in mean square to 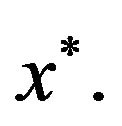 There exists an infinite subsequence
There exists an infinite subsequence 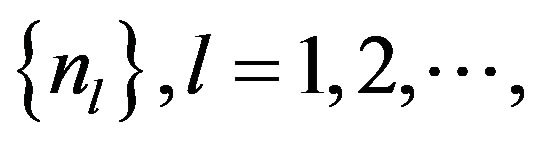 such that
such that

where
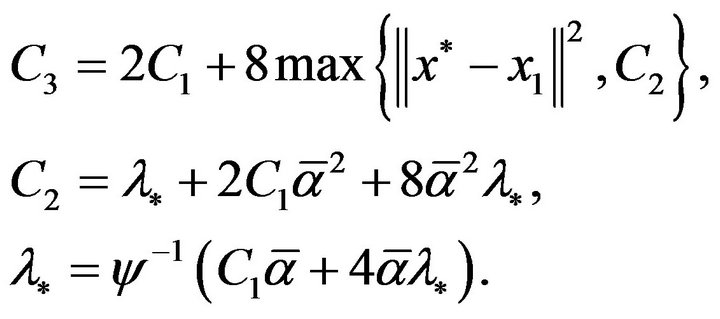 (3.15)
(3.15)
Proof. Consider the inequality ( 11) in the form
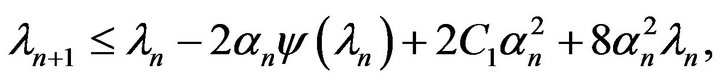 (3.16)
(3.16)
where 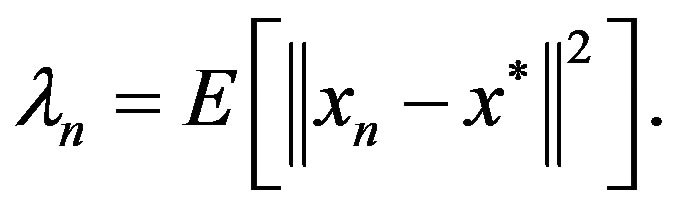 Observe that it is derived by making use of (3.4) and the nonexpansivity property of
Observe that it is derived by making use of (3.4) and the nonexpansivity property of  We shall show that
We shall show that 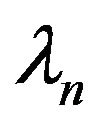 are bounded for all
are bounded for all  Indeed, since
Indeed, since  is a convex increasing continuous function, we conclude that
is a convex increasing continuous function, we conclude that
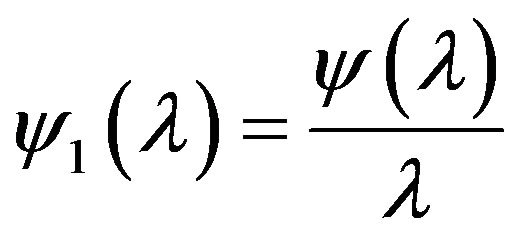 is nondecreasing and since (3.14) holdsthe inequality
is nondecreasing and since (3.14) holdsthe inequality 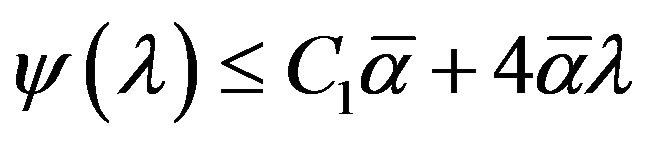 has a solution
has a solution 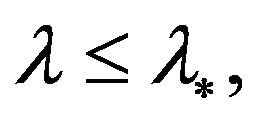 where
where  is the unique root of the scalar equ0 ation
is the unique root of the scalar equ0 ation  Together with this, (3.4) and (3.14) are co-ordinated by the parameter
Together with this, (3.4) and (3.14) are co-ordinated by the parameter 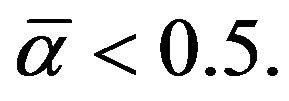
Only one alternative can happen for each 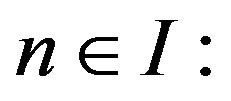 either
either
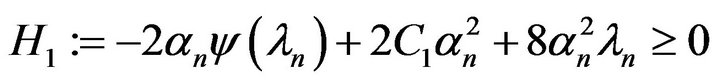
or
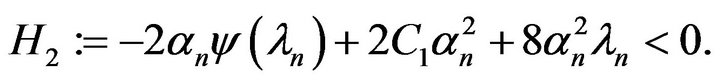
Denote 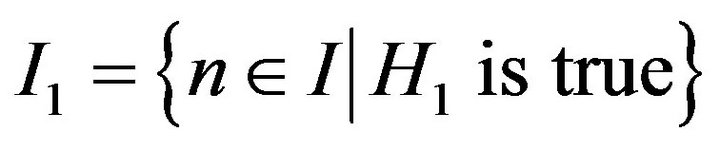 and
and
 . It is clear that
. It is clear that  From the hypothesis
From the hypothesis 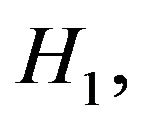 it arises
it arises

and then  for all
for all 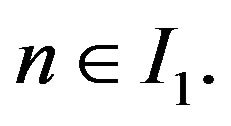 From the hypothesis
From the hypothesis 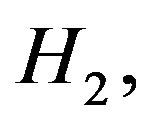 we have:
we have: 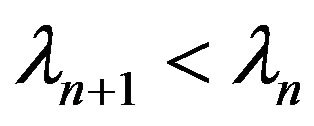 for all
for all  Consider all the possible cases:
Consider all the possible cases:
1) 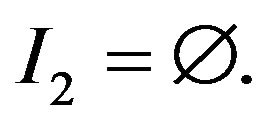 Then
Then  for all
for all 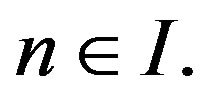
2) 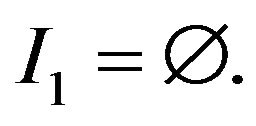 Then
Then  for all
for all 
3) Let  and
and 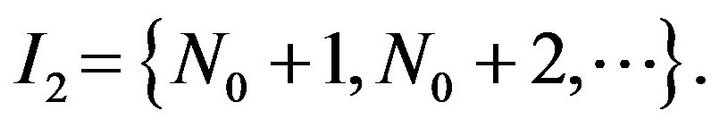 Then
Then 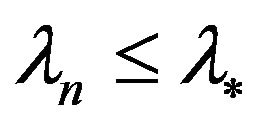 for
for 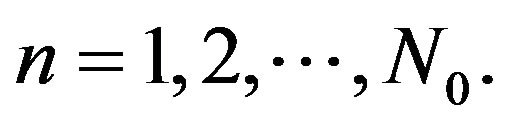 By (3.16),
By (3.16), 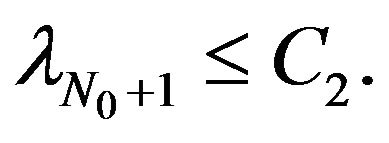 It is obvious that
It is obvious that  for
for 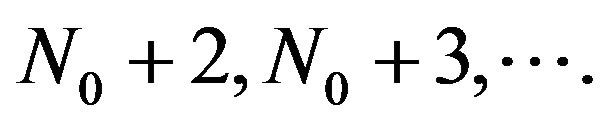 Therefore,
Therefore, 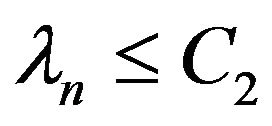 for all
for all 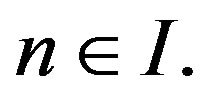
4) Let  and
and  Then
Then 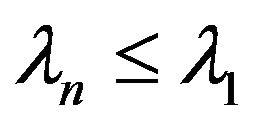 for
for 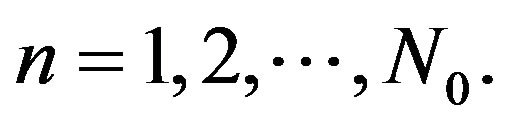 and
and  for
for  Thus,
Thus, 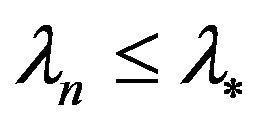 for all
for all 
5) Let ![]() and
and 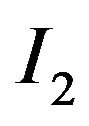 be unbounded sets. Consider an arbitrary interval
be unbounded sets. Consider an arbitrary interval
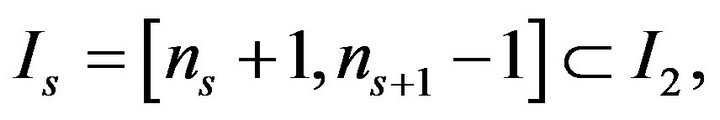
where  It is easy to be sure that
It is easy to be sure that 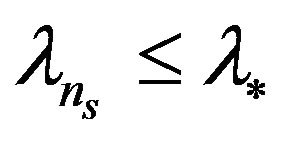 and
and 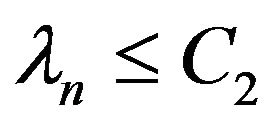 for all
for all 
6) The other situations of bounded and unbounded sets ![]() and
and  are covered by the items 1)-5). Consequently, we have the final result:
are covered by the items 1)-5). Consequently, we have the final result:  for all
for all 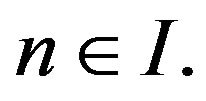
Thus, we obtain the inequality
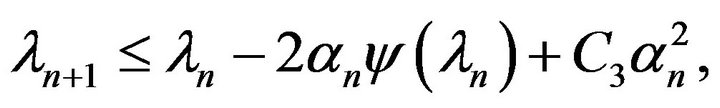 (3.17)
(3.17)
where 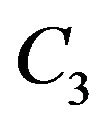 is defined by (3.15). Now Lemma 2.2 with the condition (2.3) implies the result. □
is defined by (3.15). Now Lemma 2.2 with the condition (2.3) implies the result. □
Remark 3.8. For a linear function 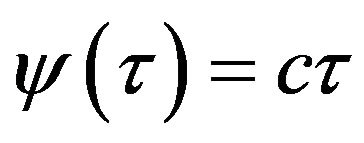 which is convex and concave at the same time we suppose
which is convex and concave at the same time we suppose 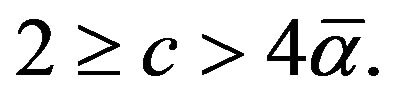
Remark 3.9. If  is bounded or more generally
is bounded or more generally 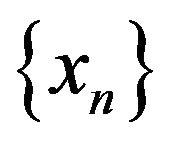 is bounded, then the inequality (3.17) (with some different constant
is bounded, then the inequality (3.17) (with some different constant ) immediately follows from (3.16).
) immediately follows from (3.16).
4. Estimates of the Mean Square Convergence Rate
Using Lemmas 2.3 and 2.4 we are able to give two general theorems on the nonasymptotic estimates of the mean square convergence rate for sequence 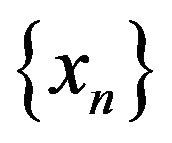 generated by the stochastic approximation algorithm (1.5)- (1.7).
generated by the stochastic approximation algorithm (1.5)- (1.7).
Again we introduce denotations 1)-5) from Section 2 induced now by the recurrent inequality (3.11):
1)  and
and 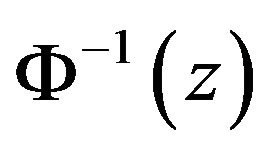 are the inverse functions to
are the inverse functions to 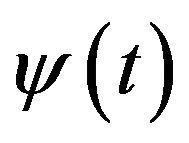 and
and 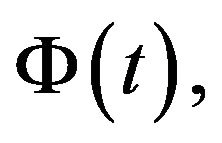 respectively;
respectively;
2)  is a fixed control parameter;
is a fixed control parameter;
3) 

4) 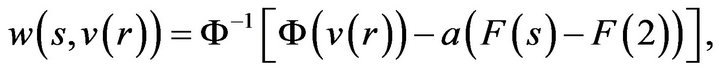
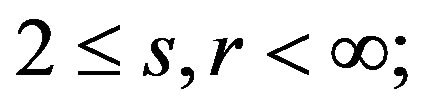
5) 
Introduce also the basic condition (P).
Theorem 4.1. Assume that all the conditions of Theorem 3.1 are fulfiled and i) the condition (P) holds for the functions
 and
and 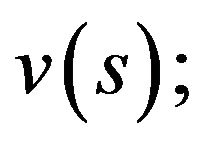
ii) 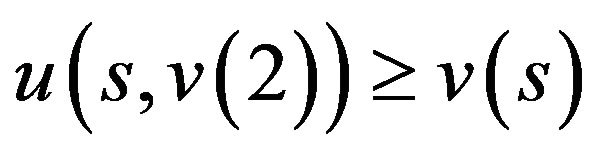 as
as 
iii) 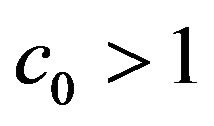 is chosen such that
is chosen such that  as
as 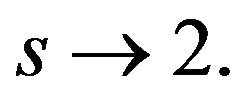
Then the sequence  generated by (1.5)-(1.7) converges in average to a unique fixed point
generated by (1.5)-(1.7) converges in average to a unique fixed point 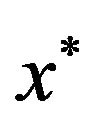 of
of ![]() and for all
and for all 
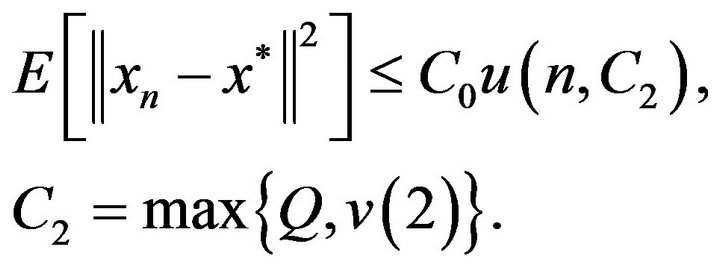 (4.1)
(4.1)
Theorem 4.2. Assume that all the conditions of Theorem 3.1 are fulfiled and i) the condition (P) holds for the functions 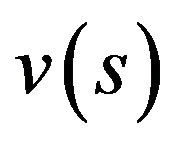
and  with any fixed
with any fixed 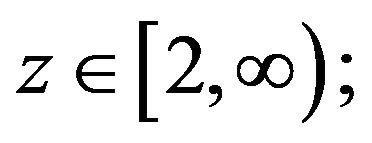
ii) 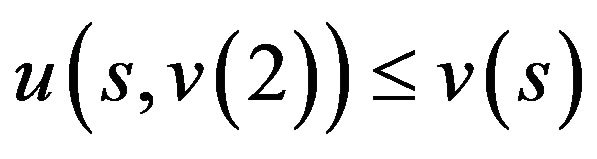 as
as 
iii) If  and
and 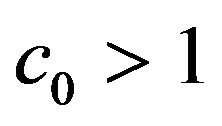 is chosen such that
is chosen such that  as
as  then the sequence
then the sequence 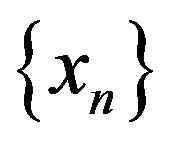
generated by (1.5)-(1.7) converges in average to a unique fixed point  of
of ![]() and for all
and for all 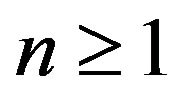
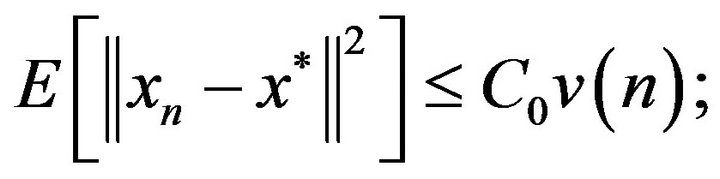 (4.2)
(4.2)
iv) In all the remaining cases, (4.1) holds for  and (4.2) for
and (4.2) for 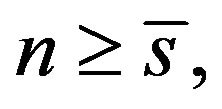 where
where 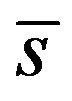 is a unique root of the equation
is a unique root of the equation 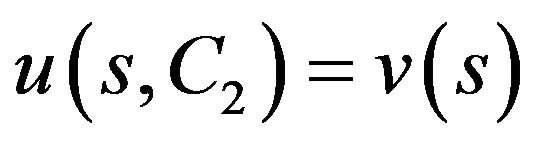 on the interval
on the interval .
.
Let us provide the examples of functions  and
and 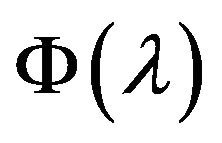 suitable for Theorems 4.1 and 4.2 (see [12,13]).
suitable for Theorems 4.1 and 4.2 (see [12,13]).
1) Below in Corollaries 4.3-4.6 we use the functions 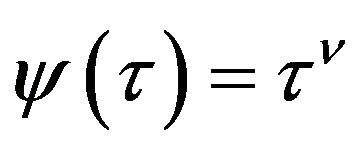 with
with 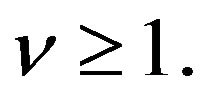 For them
For them
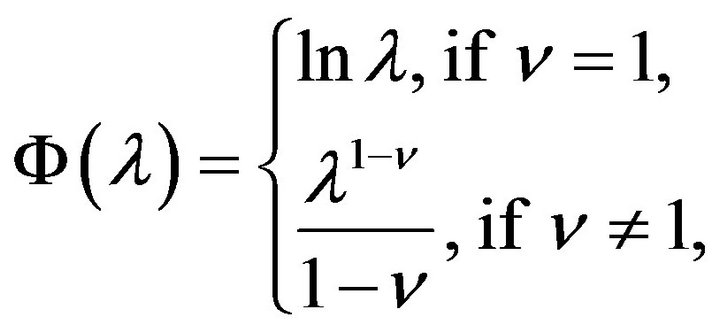 (4.3)
(4.3)
and
 (4.4)
(4.4)
2) If  then
then
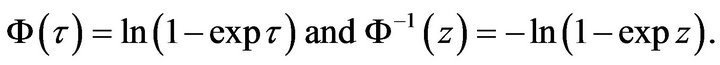
3) If  then
then
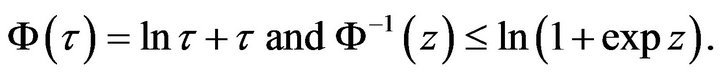
4) If 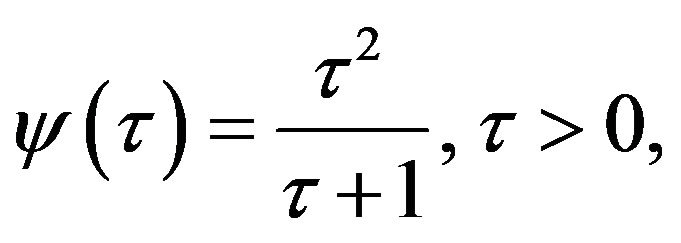 then
then

In this example we are unable to define  in analitical form, therefore suggest to calculate it numerically by computer.
in analitical form, therefore suggest to calculate it numerically by computer.
We next present very important corollaries from Theorems 4.1 and 4.2, where their assumptions automatically guarantee accomplishment of the condition (P) (see [4]). The functions 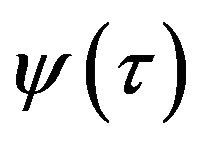 coincide with the point 1) above.
coincide with the point 1) above.
Corollary 4.3. Assume that 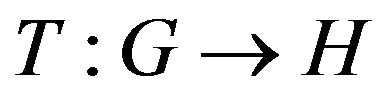 is a strongly contractive mapping, that is, (1.4) is satisfied with
is a strongly contractive mapping, that is, (1.4) is satisfied with
 Let in (1.5)
Let in (1.5) 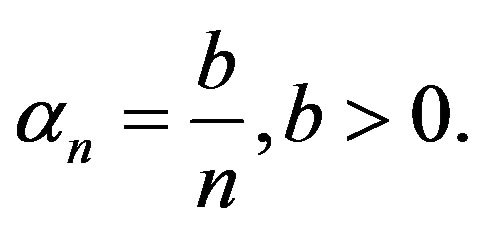 Then
Then
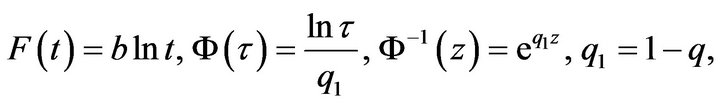

I. Suppose that  and
and  Then
Then
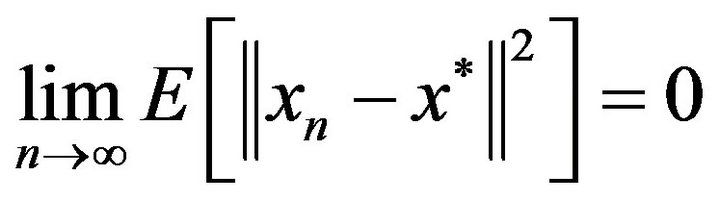 and 1) If
and 1) If 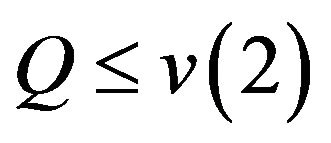 and
and  we have for all
we have for all 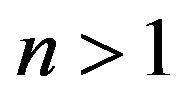
 (4.5)
(4.5)
2) In all the remain cases
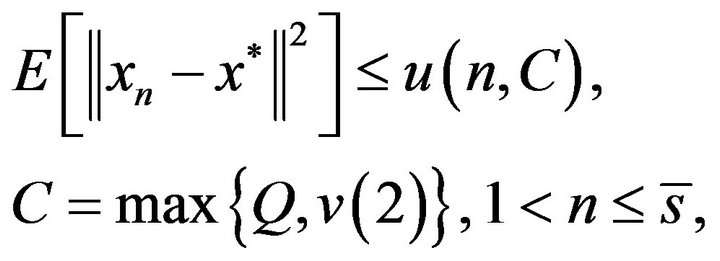 (4.6)
(4.6)
and
 (4.7)
(4.7)
where  is a unique root of the equation
is a unique root of the equation
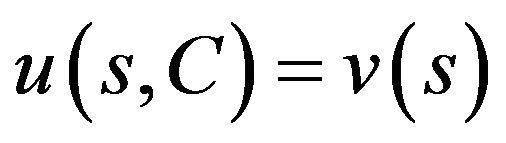 on the interval
on the interval .
.
II. Suppose that 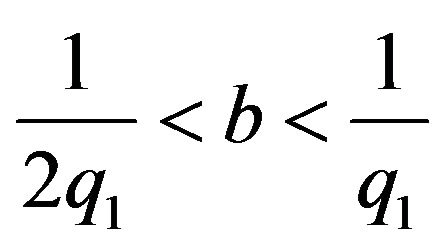 and
and 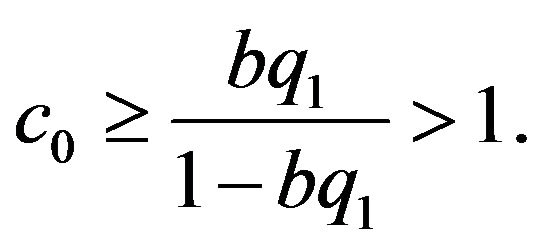
Then  and the estimate (4.6) holds for all
and the estimate (4.6) holds for all 
Corollary 4.4. Assume that  is a strongly contractive mapping, that is, in (1.4) is satisfied with
is a strongly contractive mapping, that is, in (1.4) is satisfied with
 Let in (1.5)
Let in (1.5) 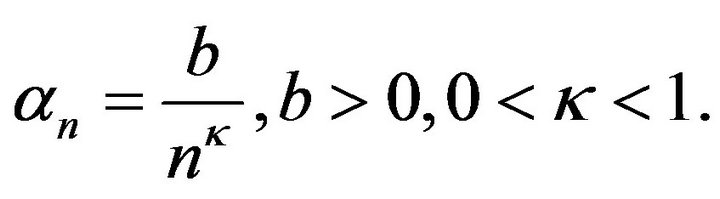 Then
Then
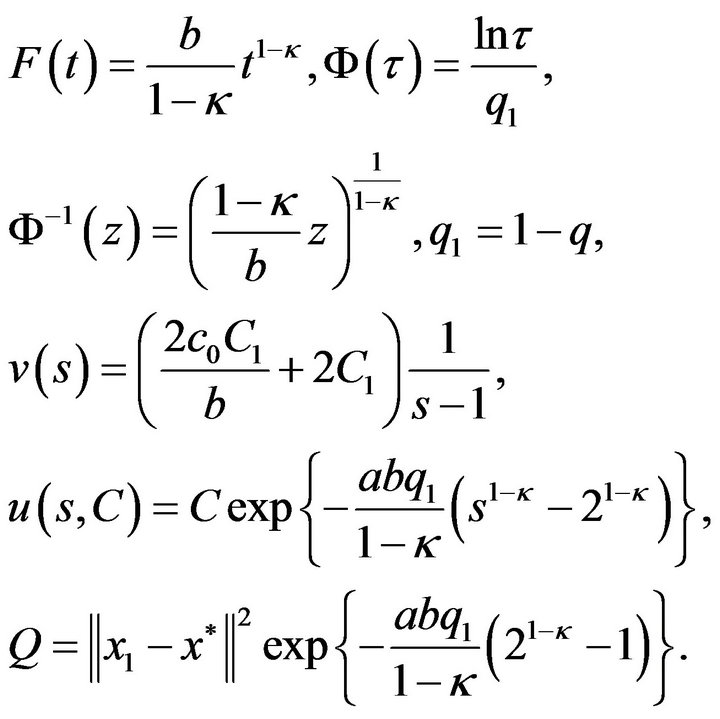
Suppose that  Then
Then 
and 1) If 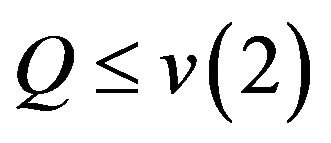 and
and  we have for all
we have for all
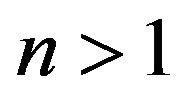
 (4.8)
(4.8)
2) In all the remain cases the estimates (4.6) and (4.7) hold.
Corollary 4.5. Assume that 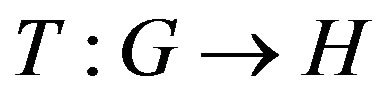 is a weakly contractive mapping of the class
is a weakly contractive mapping of the class ![]() that is, in Theorem 3.1
that is, in Theorem 3.1 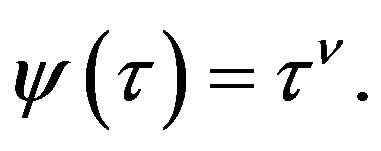 Let in (1.5)
Let in (1.5)
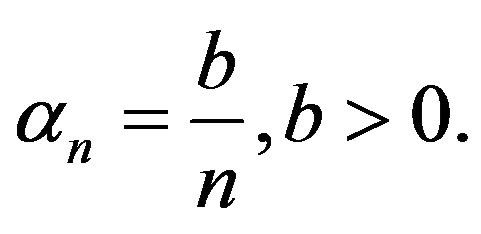 Then
Then
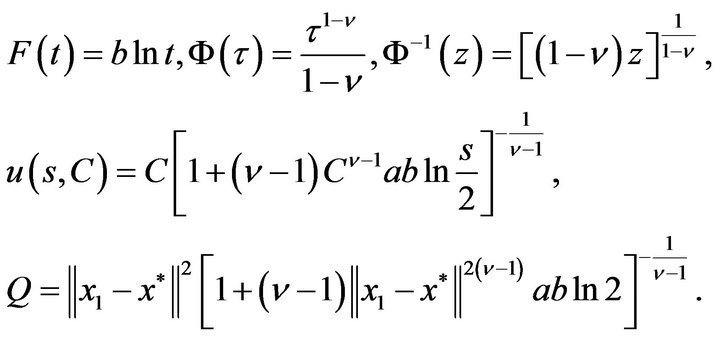
If 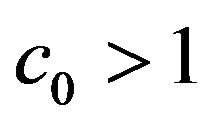 is chosen from the condition
is chosen from the condition

then  and for all
and for all 
 (4.9)
(4.9)
Corollary 4.6. Assume that 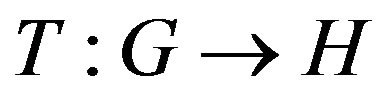 is a weakly contractive mapping of the class
is a weakly contractive mapping of the class ![]() that is, in Theorem 3.1
that is, in Theorem 3.1  Let in (1.5)
Let in (1.5)
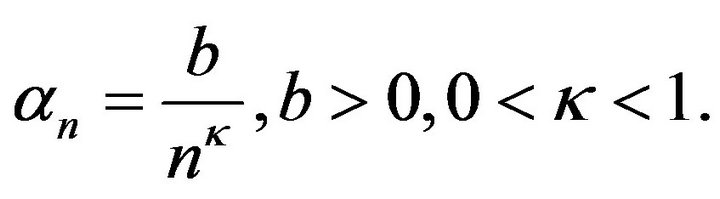 Then
Then

I. Suppose that

1) If  and
and 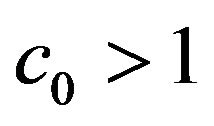 is chosen from the condition
is chosen from the condition

then 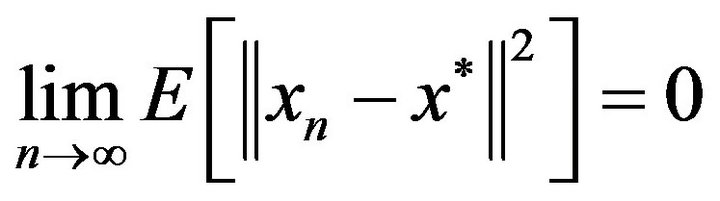 and for all
and for all 
 (4.10)
(4.10)
2) In all the remain cases the estimates (4.6) and (4.7) hold.
II. Suppose that
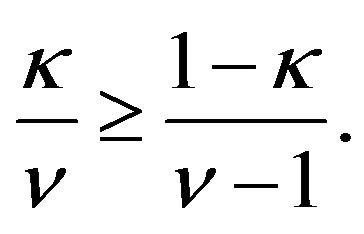
If 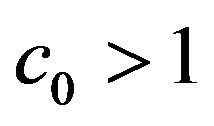 is chosen from the condition
is chosen from the condition

then  and for all
and for all 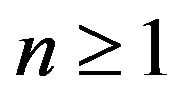
 (4.11)
(4.11)
In addition to the examples presented in this section, we produce the functions 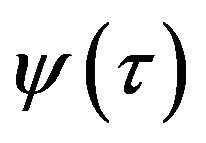 and
and  which have
which have 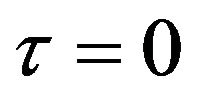 as a tangency point of the infinite degree multiplicity and given logarithmic estimates of the convergence rate.
as a tangency point of the infinite degree multiplicity and given logarithmic estimates of the convergence rate.
We define the function  by the following way:
by the following way:

where 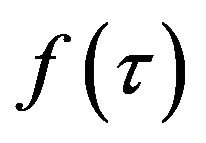 is differentiable and decreasing function,
is differentiable and decreasing function,
![]() and
and
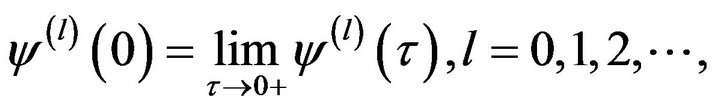
where 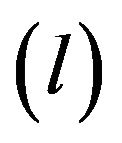 denote the derivative degrees of the function
denote the derivative degrees of the function
 It is easy to see that
It is easy to see that
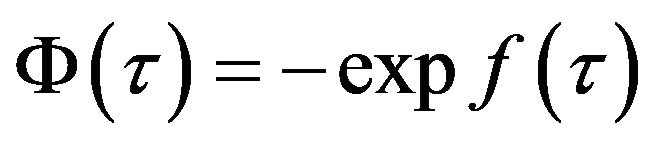
and

In particulari) 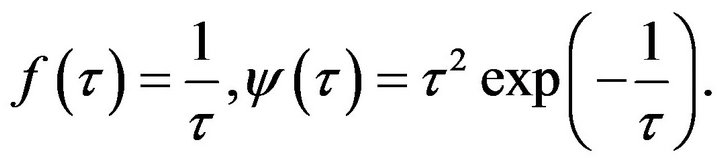 We have
We have
 and
and 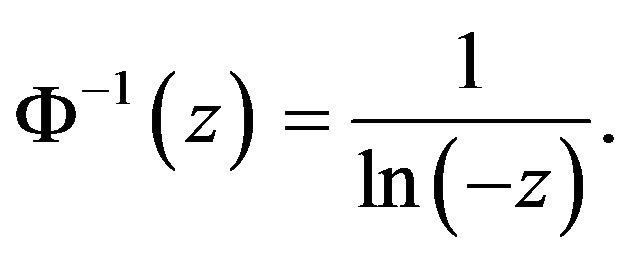 We have to verify that
We have to verify that 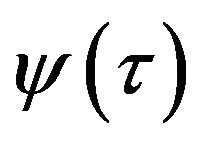 is convex. In fact, it is true because
is convex. In fact, it is true because
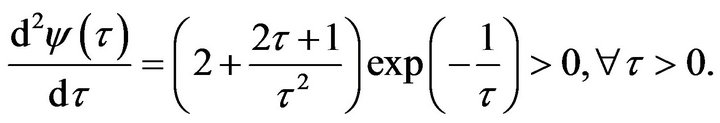
Beside this, it is easy to see that 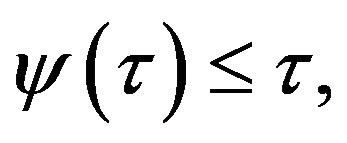 at least, on the interval
at least, on the interval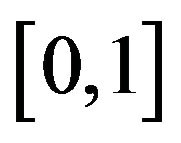 . In the next examples we leave to readers to check these properties.
. In the next examples we leave to readers to check these properties.
ii) 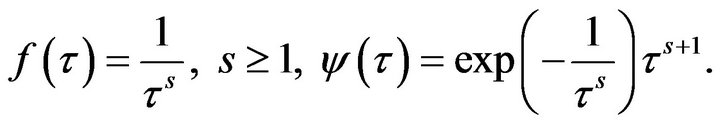
We have  and
and 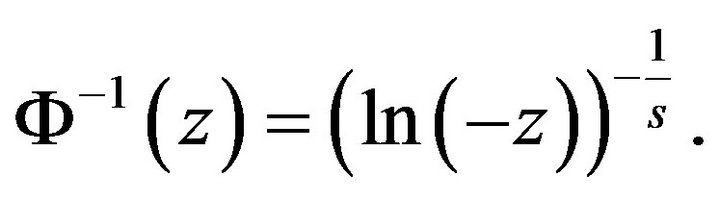
iii) 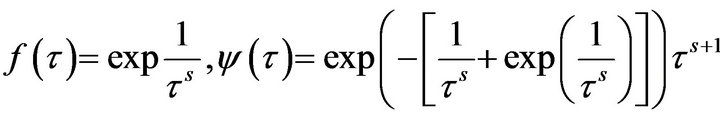
We have
 and
and 
5. Almost Sure Convergence of Stochastic Approximations for Nonexpansive Mappings
Consider next the almost surely convergence of stochastic approximations. First of all, we need the stochastic analogy of Lemma 2.5:
Lemma 5.1. Let 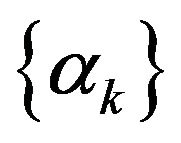 be sequences of non-negative real numbers and
be sequences of non-negative real numbers and  be sequence of random
be sequence of random 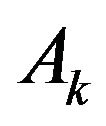 measurable variables, a.s. nonnegative for all
measurable variables, a.s. nonnegative for all  Assume that
Assume that
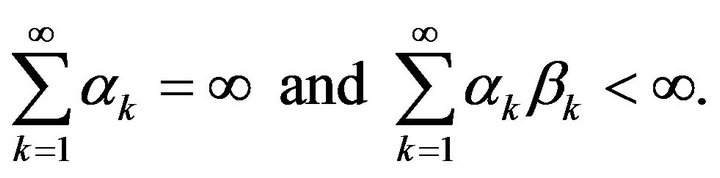
If 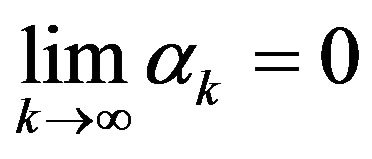 and there exists
and there exists 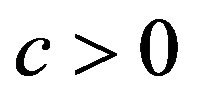 such that for all
such that for all

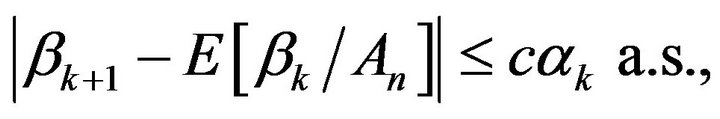 (5.1)
(5.1)
then 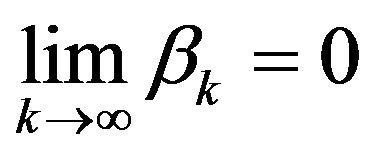 a.s.
a.s.
The proof can be provided by the scheme of nonstochastic case (see Proposition 2 in [8]) or as it was done in [5].
We need also the following lemma from [14] as applied to our case of Hilbert spaces (the concepts of modulus of convexity 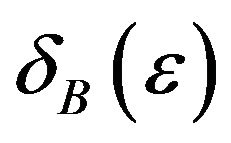 of Banach spaces B or Hilbert spaces
of Banach spaces B or Hilbert spaces  can be found in [15] and [16]).
can be found in [15] and [16]).
Lemma 5.2. If  with a nonexpansive mapping
with a nonexpansive mapping  then for all
then for all 
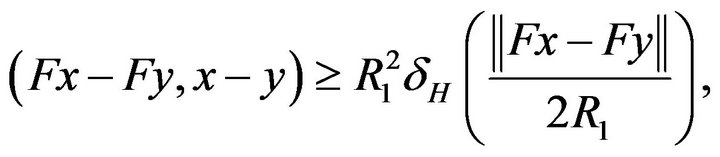
where

If  and
and  with
with 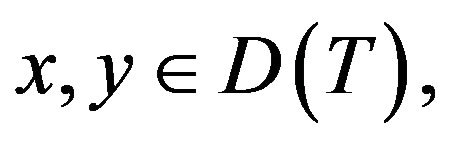 then
then 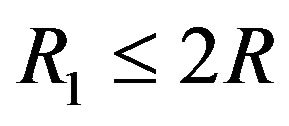 and
and

Theorem 5.3. Assume that a mapping  is nonexpansive and its fixed point set
is nonexpansive and its fixed point set  is nonempty. If
is nonempty. If
(1.8) holds and 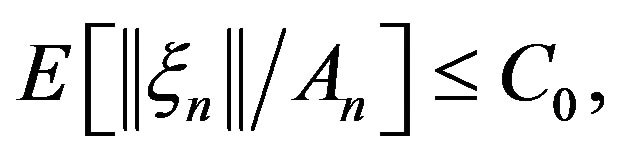 then the sequence
then the sequence
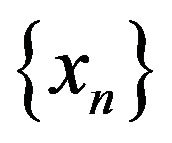 generated by (1.5)-(1.7) weakly almost surely converges to some
generated by (1.5)-(1.7) weakly almost surely converges to some 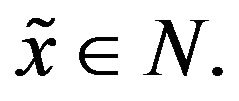
Proof. Let 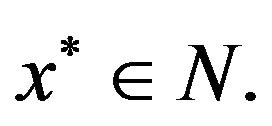 We next use Lemma 5.2 and the estimate (see [17], p. 49)
We next use Lemma 5.2 and the estimate (see [17], p. 49)

to get
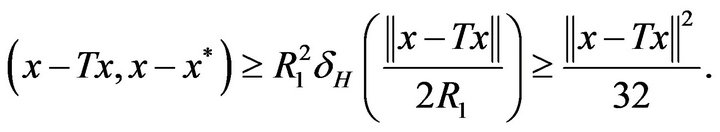
In this case the inequality (3.3) implies
 (5.2)
(5.2)
Similarly to (3.10), we have
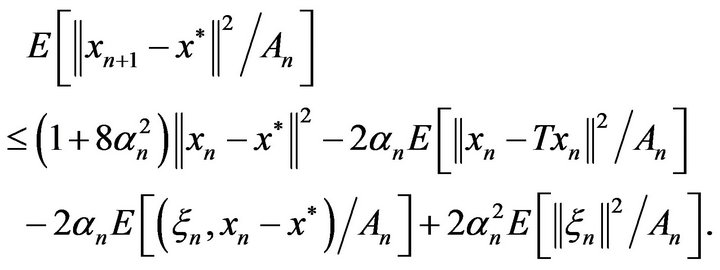 (5.3)
(5.3)
Denote 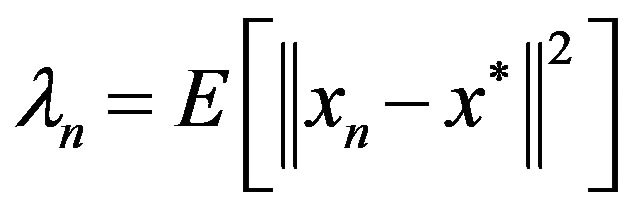 and
and 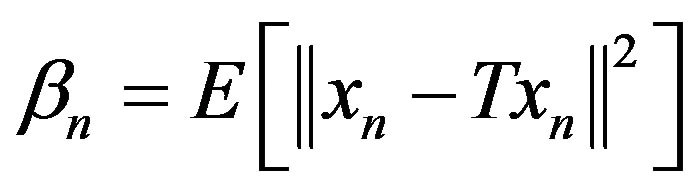
and apply the unconditional expectation to both sides of (5.3). Then
 (5.4)
(5.4)
It follows from this that
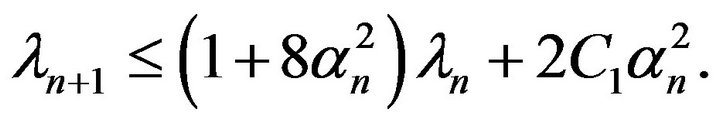
Since  and due to Lemma 2.1, we conclude that
and due to Lemma 2.1, we conclude that  is bounded. Consequently,
is bounded. Consequently,  is bounded a.s. that follows from the theory of convergent quasimartingales (see [5,18]).
is bounded a.s. that follows from the theory of convergent quasimartingales (see [5,18]).
We now need Lemma 5.1. It is not difficult to see that
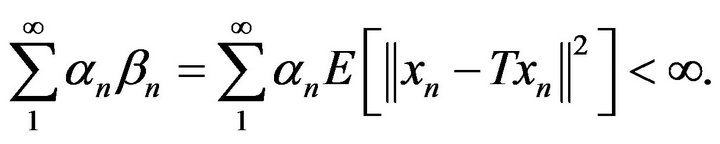 (5.5)
(5.5)
The last gives us

Next we evaluate the following difference:

It is easy to see that 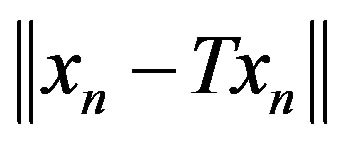 is bounded a.s. Indeed, since
is bounded a.s. Indeed, since  a.s., there exists a constant
a.s., there exists a constant 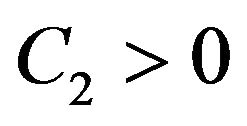 such that
such that

Therefore
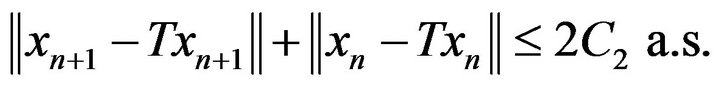
It is obviously that

Thus,

By Lemma 5.1,  a.s. as
a.s. as ![]()
Since 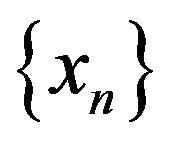 is bounded a.s., there is a subsequence
is bounded a.s., there is a subsequence 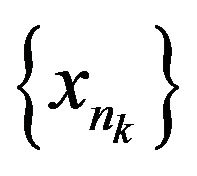 weakly convergent to some point
weakly convergent to some point 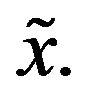 Since
Since 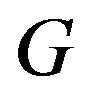 is convex and closed, consequently, weakly closed, we assert that
is convex and closed, consequently, weakly closed, we assert that  It is known that a nonexpansive mapping
It is known that a nonexpansive mapping ![]() is weakly demiclosed, therefore,
is weakly demiclosed, therefore, 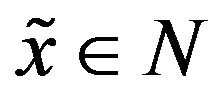 a.s. Weak almost surely convergence of whole sequence
a.s. Weak almost surely convergence of whole sequence  is shown by the standard way [8]. □
is shown by the standard way [8]. □
Corollary 5.4. Assume that  is a weakly contractive mapping of the class
is a weakly contractive mapping of the class 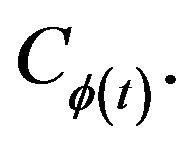 If
If 
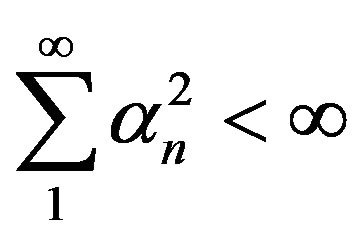 and
and  then the sequence
then the sequence
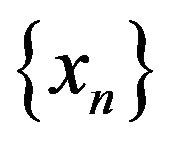 generated by (1.5)-(1.7) strongly almost surely converges to unique fixed point
generated by (1.5)-(1.7) strongly almost surely converges to unique fixed point 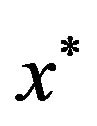 of
of 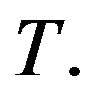
Proof. We have from (3.4)
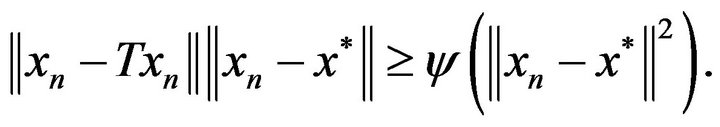 (5.6)
(5.6)
Since 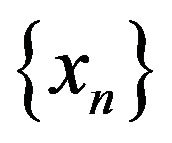 is bounded a.s. and
is bounded a.s. and 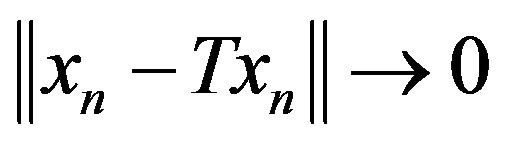 a.s.
a.s.
as 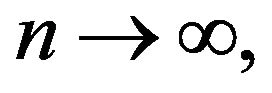 we conclude that
we conclude that 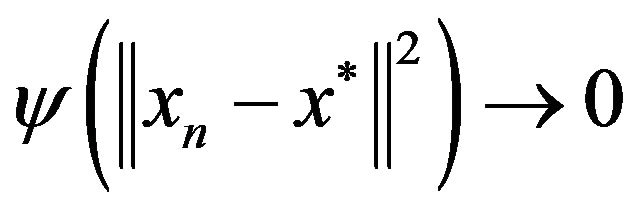 a.s.
a.s.
The proof follows due to the properties of the function 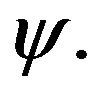 □
□
Remark 5.5. It is clear that all the results remain still valid for self-mappings 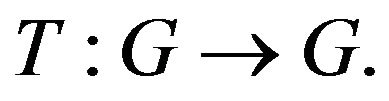 However, in this case, unlike any deterministic situation, the algorithm (1.5)-(1.7) must use the projection operator
However, in this case, unlike any deterministic situation, the algorithm (1.5)-(1.7) must use the projection operator 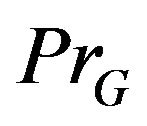 because the vector
because the vector 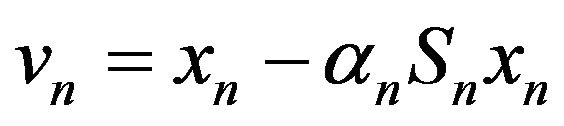 not always belongs to G. If
not always belongs to G. If  for all
for all 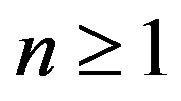 and
and  then (1.5) can be replaced by
then (1.5) can be replaced by

REFERENCES
- M. T. Wasan, “Stochastic Approximation,” Cambridge University Press, Cambridge, 1969.
- M. B. Nevelson and R. Z. Hasminsky, “Stochastic Approximation and Recursive Estimation,” AMS Providence, Rhode Island, 1973.
- Ya. Alber and S. Shilman, “Nonasymptotic Estimates of the Convergence Rate of Stochastic Iterative Algorithms,” Automation and Remote Control, Vol. 42, 1981, pp. 32-41.
- Ya. Alber and S. Shilman, “General Nonasymptotic Estimates of the Convergence Rate of Iterative Stochastic Algorithms,” USSR Computational Mathematics and Mathematical Physics, Vol. 25, No. 2, 1985, pp. 13-20. doi:10.1016/0041-5553(85)90099-0
- K. Barty, J.-S. Roy and C. Strugarek, “Hilbert-Valued Perturbed Subgradient Algorithms,” Mathematics of Operation Research, Vol. 32, No. 3, 2007, pp. 551-562. doi:10.1287/moor.1070.0253
- X. Chen and H. White, “Asymptotic Properties of Some Projection-Based Robbins-Monro Procedures in a Hilbert Space,” Studies in Nonlinear Dynamics & Econometrics, Vol. 6, No. 1, 2002, pp. 1-53. doi:10.2202/1558-3708.1000
- Ya. I. Alber and A. N. Iusem, “Extension of Subgradient Techniques for Nonsmooth Optimization in Banach Spaces,” Set-Valued Analysis, Vol. 9, No. 4, 2001, pp. 315-335. doi:10.1023/A:1012665832688
- Ya. Alber, A. Iusem and M. Solodov, “On the Projection Subgradient Method for Nonsmooth Convex Optimization in a Hilbert Space,” Mathematical Programming, Vol. 81, No. 1, 1998, pp. 23-35. doi:10.1007/BF01584842
- A. P. Dempster, N. M. Laird and D. B. Rubin, “Maximal Likelihood from Incomplete Data via the EM Algorithm,” Journal of the Royal Statistical Society, Vol. 39, No. 1, 1977, pp. 185-197.
- W. Rudin, “Real and Complex Analysis,” McGraw-Hill, New York, 1978.
- Ya. I. Alber and S. Guerre-Delabriere, “Principle of Weakly Contractive Maps in Hilbert Spaces,” Operator Theory, Advances and Applications, Vol. 98, 1997, pp. 7- 22.
- Ya. I. Alber, “Recurrence Relations and Variational Inequalities,” Soviet Mathematics Doklady, Vol. 27, 1983, pp. 511-517.
- Ya. Alber, S. Guerre-Delabriere and L. Zelenko, “The Principle of Weakly Contractive Maps in Metric Spaces,” Communications on Applied Nonlinear Analysis, Vol. 5, No. 1, 1998, pp. 45-68.
- Ya. I. Alber, “New Results in Fixed Point Theory,” Preprint, Haifa Technion, 2000.
- J. Diestel, “The Geometry of Banach Spaces,” Lecture Notes in Mathematics, No. 485, Springer, Berlin, 1975.
- T. Figiel, “On the Moduli of Convexity and Smoothness,” Studia Mathematica, Vol. 56, No. 2, 1976, pp. 121-155.
- Ya. Alber and I. Ryazantseva, “Nonlinear Ill-Posed Problems of Monotone Type,” Springer, Berlin, 2006.
- M. Métivier, “Semimartingales,” De Gruyter, Berlin, 1982. doi:10.1515/9783110845563

