Journal of Environmental Protection
Vol. 4 No. 7A (2013) , Article ID: 34855 , 4 pages DOI:10.4236/jep.2013.47A017
Accounting for Population in an EKC for Water Pollution
![]()
Kansas State University, Manhattan, USA.
Email: alexit@ksu.edu
Copyright © 2013 Alexi Thompson. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 4th, 2013; revised June 13th, 2013; accepted July 5th, 2013
Keywords: Environmental Kuznet’s Curve; Population; Pooled Mean Group Estimation
ABSTRACT
This paper explores the role of population in empirical studies. While panel estimation should control for differences across countries as more populated countries should pollute more, more pollution may not lead to more pollution per capita. Two models are estimated each of which control for population in different ways. One model accounts for population by expressing BOD in per capita terms and the second model regresses BOD on population using the residual in the EKC regression. The Akaike Information Criterion (AIC) reveals the second model is preferred to the first model. In addition, although both models reveal an EKC, the turning points are vastly different. Future EKC studies can benefit by testing EKC models that control for population in different ways.
1. Introduction
This paper takes a look at the role of population in an Environmental Kuznets Curve (EKC) model which describes the relationship between economic growth and pollution as an inverted u-shape. The data concerns water pollution, but the role of population in an empirical EKC model can be extended to various pollutants. The majority of EKC empirical studies utilize panel data [1]. In air pollution studies and water pollution studies, pollution indicators are measured either in total emissions [2-4] or concentrations [5]. If measured in total emissions, air and water pollution indicators are usually expressed in per capita terms [6,7]. In EKC studies where the pollution is measured in concentrations, population density is sometimes included as an explanatory variable [8,9].
This paper does not argue the merits between pollution expressed in total emissions compared to concentration. For a discussion, various published critiques of the EKC are available [7,10].This paper focuses on the studies that express pollution in per capita terms, and offers an alternative method for controlling for population that could be useful in future studies.
Because the majority of EKC studies employ panel data analysis, it is important to control for population across countries. Higher populated countries experience more pollution in total. However, higher population does not necessarily lead to higher pollution per capita. If population increases faster than pollution, increases in population will be associated with lower pollution per capita. Theoretically, the EKC describes the relationship between economic growth and pollution, not economic growth and pollution per capita. Therefore, this paper seeks to reconcile the empirical desire to control for population across panel EKC studies with the theoretical model describing the relationship between pollution and economic growth.
This paper introduces a new way to control for population in EKC studies. Two models are estimated, each of which control for population in different a manner. Estimates are then compared across models. In Model 1, the water pollution indicator biochemical oxygen demand (BOD) is measured in kilograms per day per person. This method is typical in EKC studies. In Model 2, the new method for controlling for population, BOD (measured in kilograms per day) is regressed on population, 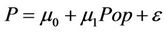 , where
, where 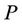 is BOD measured in kilograms per day. The residual from this regression, ε, represents the pollution not explained by population. This residual is then used as the dependent variable BOD in the EKC regression. By Method 2, it is possible to control for population differences across countries in the first step while depicting the EKC relationship between pollution and economic growth in the second step.
is BOD measured in kilograms per day. The residual from this regression, ε, represents the pollution not explained by population. This residual is then used as the dependent variable BOD in the EKC regression. By Method 2, it is possible to control for population differences across countries in the first step while depicting the EKC relationship between pollution and economic growth in the second step.
The results reveal that estimates and EKC turning points vary greatly depending on how population enters into the EKC model. The Akaike Information Criteria (AIC) indicates which model is preferred and results show that Model 2 is preferred to Model 1. This suggests empirical EKC studies should consider other ways to control for population.
2. Data
The dataset includes a balanced panel of 37 countries from 1980 to 2000. BOD data comes from [11]. BOD measures the amount of oxygen required to break down bacteria by organisms. A higher BOD level is equivalent to higher pollution. Income per capita and population data are from [12]. All variables are in natural logarithms.
3. Methods
Evidence of an inverted u-shaped relationship between pollution and income may vary by country, so in empirical EKC studies it may be useful to employ some technique that allows for slope heterogeneity across countries. A recently developed panel estimation technique, pooled mean group (PMG) estimation, is used in this study. PMG is a dynamic panel estimation technique that is more flexible than the panel fixed effects model, allowing short run coefficients to vary across countries and constraining long run coefficients to be the same across countries This method has been employed only recently in EKC studies [1,13-15].
The long run EKC model is
 (1)
(1)
Following [13], the autoregressive distributive lag model (ARDL) follows
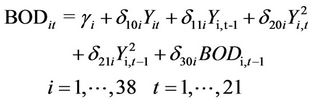 (2)
(2)
It is assumed variables are I(1) and cointegrated within countries. A one period lagged explanatory variable is included in the model.
PMG estimation combines the long run EKC relationship from (1) with the short run ARDL model (2) in the following equation
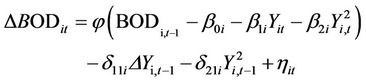 (3)
(3)
where
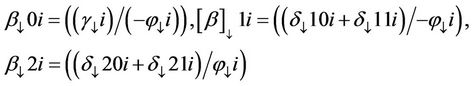
The error corrected coefficients (in parenthesis) represent long run coefficients that are pooled and constrained to be equal across countries. The differenced coefficients represent short run coefficients and are allowed to vary across countries.
Before PMG estimation, the Im, Pesaran, Shin (IPS) panel unit root test tests variables for a unit root because PMG estimation requires variables to be I(1) [16]. The IPS panel unit root test is based on the Dickey-Fuller unit root tests applied in time series studies. Following [17], to perform the IPS test, the following augmented DickeyFuller (ADF) regression is applied to each cross sectional unit
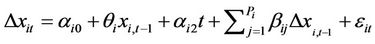 where
where 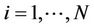 and
and 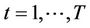
where  is the vector of variables (
is the vector of variables (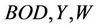 ),
), 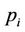 are different lag lengths,
are different lag lengths, 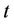 is a time trend, and
is a time trend, and 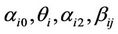 are coefficients to be estimated. The null hypothesis of a unit root for each individual time series is
are coefficients to be estimated. The null hypothesis of a unit root for each individual time series is 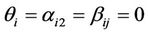 so that
so that 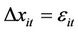 . The t-statistic for the IPS panel unit root test t* takes the individual t-statistic for each series ti and forms the sample mean in the following equation,
. The t-statistic for the IPS panel unit root test t* takes the individual t-statistic for each series ti and forms the sample mean in the following equation, 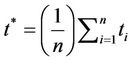 . Results from the panel unit root test reported in Table 1 indicate all variables are I(1).
. Results from the panel unit root test reported in Table 1 indicate all variables are I(1).
To test the long run relationship between the variables, the panel cointegration test developed by [18] is implemented. Many popular cointegration tests such as the [19] test for panel data or the Engle Granger test for time series data are residual based. A shortcoming of residual based cointegration tests are that long run error cointegration and short run dynamics are constrained to be equal [18] referred to as the common factor restriction [20].
The Westerlund panel cointegration technique is structural rather than residual based and does not have a common factor restriction. The Westerlund test calculates four test statistics: Gt, Ga, Pt, and Pa. The first two are group mean statistics the second two are panel statistics. The group mean statistics have a null hypothesis of no
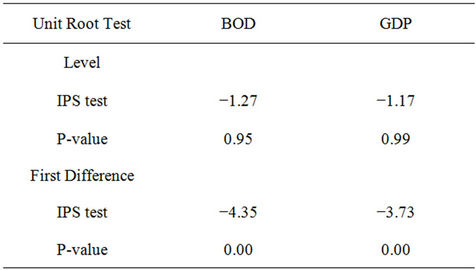
Table 1. Panel unit root tests.
cointegration for all countries against the alternative of cointegration for at least one series. The panel statistics have a null hypothesis of no cointegration for all countries against the alternative of cointegration for the entire panel. Results reported in Table 2 indicate the null of no cointegration can be rejected in the Gt statistic, evidence of cointegration for some series.
4. Results
Results from the two models are in Table 3. Results indicate that the manner in which population is controlled for greatly affects the EKC turning point. From two EKC models, the AIC criterion determines which is preferred. The first model is
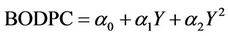
where BODPC is biochemical oxygen demand per capita, Y is income per capita, and α’s are estimated coefficients. Model 2 includes the OLS regression
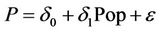
where P is biochemical oxygen demand expressed in cubic kilometers per day, 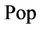 is the yearly population estimates for given countries, δ’s represent coefficients to be estimated, and ε is the error term. The error term ε represents the pollution not explained population, and henceforth is called.
is the yearly population estimates for given countries, δ’s represent coefficients to be estimated, and ε is the error term. The error term ε represents the pollution not explained population, and henceforth is called.
BOD enters the following second stage regression,
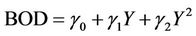
where γ’s are coefficients to be estimated. All variables are expressed in natural logarithms in both models. In the presence of an EKC we should expect a positive α1 and a negative α2 in model 1. In model 2, an EKC would be indicated by a positive γ1 and a negative γ2.
Turning points are
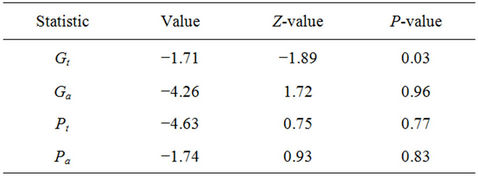
Table 2. Panel cointegration.
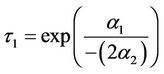
in Model 1 and
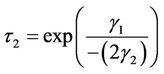
in Model 2.
Results suggest an EKC for the panel of countries with a turning point of $1408 annual per capita income in model 1 and $2631 annual per capita income in Model 2.
The Akaike Information Criterion (AIC) determines which of the two models is preferred. The AIC is based on the log likelihood and follows 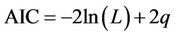 where q is the number of parameters and L is the log likelihood. The lowest AIC is the preferred model. The results for AIC are reported in Table 3 and show that Model 2 is preferred to Model 1.
where q is the number of parameters and L is the log likelihood. The lowest AIC is the preferred model. The results for AIC are reported in Table 3 and show that Model 2 is preferred to Model 1.
Because the models are estimated in natural logarithms, the value and standard error of 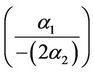 and
and 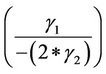 are included in Table 3 (in the column that begins “Value of X”). Statistical significance of these expressions would indicate statistically significant turning points in
are included in Table 3 (in the column that begins “Value of X”). Statistical significance of these expressions would indicate statistically significant turning points in 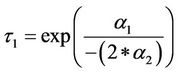 and
and 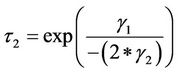 The values
The values  and
and 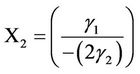 appear to be significant indicating the turning points are statistically significant. 95% Confidence intervals,
appear to be significant indicating the turning points are statistically significant. 95% Confidence intervals,  for
for  are constructed for both models. It cannot be rejected that the turning points are equal to each other as the confidence intervals overlap. Confidence intervals are reported in Table 3.
are constructed for both models. It cannot be rejected that the turning points are equal to each other as the confidence intervals overlap. Confidence intervals are reported in Table 3.

Table 3. Controlling for population Model 1 vs. Model 2.
5. Conclusions
This paper points out the care required in EKC studies to control for population. The majority of EKC studies control for population by expressing the pollution indicator in per capita terms. While controlling for population may be necessary, it may not be theoretically consistent. While more populated countries may pollute more, this does not necessarily translate into higher pollution per capita if population is growing faster than pollution.
Two models are estimated, each controlling for population differently. One model includes BOD in per capita terms and the other model employs a two stage regression where population is initially controlled before the EKC model is estimated. Results indicate EKCs for both models but with very different turning points. The turning point in the two stage model is nearly twice as large as the turning point in the per capita model; $2631 annual per capita income compared to $1408 annual per capita income.
Despite both turning points being relatively low, the GDP per capita of three countries including India, Kenya and Senegal fall between these two turning points for the year 2000 (the last year in the dataset). None of the countries’ GDP per capita is below $1408 annual per capita income in the year 2000. Therefore, if the per capita model was chosen over the two stage model, one would conclude all countries are past the turning point and are experiencing decreasing pollution with economic growth, when India, Kenya, and Senegal would still be facing increasing pollution with economic growth. Although the turning points are not significantly different from each other, the AIC criterion indicates the two stage model is preferred to a BOD per capita model. Future EKC studies may benefit by being wary of how population enters their models, as the present paper indicates the differences in results that may occur.
REFERENCES
- H. Iwata, K. Okada and S. Samreth, “Empirical Study on Environmental Kuznets Curve for CO2 in France: The Role of Nuclear Energy,” Energy Policy, Vol. 38, No. 8, 2010, pp. 4057-4063. doi:10.1016/j.enpol.2010.03.031
- T. M. Selden and D. Song, “Environmental Quality and Development: Is There an Environmental Kuznet’s Curve for Air Pollution?” Journal of Environmental Economics and Management, Vol. 27, No. 2, 1994, pp. 147-162. doi:10.1006/jeem.1994.1031
- J. A. List and C. A. Gallet “The Environmental Kuznets Curve: Does One Size Fit All?” Ecological Economics, Vol. 31, No. 3, 1999, pp. 409-423. doi:10.1016/S0921-8009(99)00064-6
- D. I. Stern and M. S. Common, “Is There an Environmental Kuznets Curve for Sulfur?” Journal of Environmental Economics and Management, Vol. 41, No. 2, 2001, pp. 162-178. doi:10.1006/jeem.2000.1132
- R. K. Kaufman, B. Davisdottir, S. Garnham and P. Pauly, “The Determinants of Atmospheric SO2 Concentrations Reconsidering the Environmental Kuznets Curve,” Ecoogical Economics, Vol. 25, No. 2, 1998, pp. 209-220. doi:10.1016/S0921-8009(97)00181-X
- I. Trabelisi, “Is There an EKC Relevant to the Industrial Emission of Water Pollution for SEMU and EU Countries?” Environmental Management and Sustainable Development, Vol. 1, No. 1, 2012, pp. 31-43.
- D. Stern, “The Rise and Fall of the Environmental Kuznets Curve,” World Development, Vol. 32, No. 8, 2004, pp. 1419-1439. doi:10.1016/j.worlddev.2004.03.004
- H.-C. Hwang, “Water Quality and the End of Communism: Does a Regime Change Lead to a Cleaner Environment,” 2006, in press. doi:10.2139/ssrn.952320
- C. Lee, Y. Chui and C. Sun, “The Environmental Kuznet’s Curve Hypothesis for Water Pollution: Do Regions Matter?” Energy Policy, Vol. 38, No. 1, 2010, pp. 12-23. doi:10.1016/j.enpol.2009.05.004
- S. Dasgupta, B. Laplante H. Wang and D. Wheeler, “Confronting the Environmental Kuznets Curve,” Journal of Economic Perspectives, Vol. 16, No. 1, 2002, pp. 147- 168. doi:10.1257/0895330027157
- World Resources Institute, “Earth Trends: Environmental Information,” 2007. http://earthtrends.wri.org
- A. Heston, R. Summers and B. Aten, “Penn World Table Version 6.3,” Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania, 2009. https://pwt.sas.upenn.edu
- I. Martínez-Zarzosa and A. Bengochea-Morancho, “Pooled Mean Group Estimation of an Environmental Kuznets Curve for CO2,” Economic Letters, Vol. 82, No. 1, 2004, pp. 121-126. doi:10.1016/j.econlet.2003.07.008
- G. Bella, C. I. Massidda and I. Etzo, “A Panel Estimation of the Relationship between Income, Electric Power Consumption and CO2 Emissions,” MPRA Paper No. 26077, 2010. http://mpra.ub.uni-muenchen.de/26077/
- A. Thompson, “Water Abundance and an EKC for Water Pollution,” Economic Letters, Vol. 117, No. 2, 2012, pp. 423-425. doi:10.1016/j.econlet.2012.06.014
- K. M. Im, Pesaran and Y. Shin, “Testing for Unit Roots in Heterogenous Panels,” Journal of Economics, Vol. 115, No. 1, 2003, pp. 53-74.
- W. Enders, “Applied Econometric Time Series,” 2nd Edition, John Wiley and Sons, New York, 2004.
- J. Westurlund, “Testing for Error Correction in Panel Data,” Oxford Bulletin of Economics and Statistics, Vol. 69, No. 6, 2007, pp. 709-748. doi:10.1111/j.1468-0084.2007.00477.x
- P. L. Pedroni, “Panel Cointegration: Asymptotic and Finite Sample Properties of Pooled Time Series Tests with an Application to the Purchasing Power Parity Hypothesis,” Economic Theory, Vol. 20, No. 3, 2004, pp. 597-625. doi:10.1017/S0266466604203073
- J. J. M. Kremers, N. R. Ericson and J. J. Dolado, “The Power of Cointegration Test,” Oxford Bulletin of Economics and Statistics. Vol. 54, No. 3, 1992, pp. 325-348. doi:10.1111/j.1468-0084.1992.tb00005.x

