Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27387,11 pages DOI:10.4236/apm.2013.31017
On a Unification of Generalized Mittag-Leffler Function and Family of Bessel Functions
1Department of Mathematical Sciences, Faculty of Applied Sciences, Charotar University of Science and Technology, Changa, India
2Department of Mathematics, Faculty of Science, The Maharaja Sayajirao University of Baroda, Vadodara, India
Email: jyotindra18@rediffmail.com, bidavemsu@yahoo.co.in, bharti.nathwani@yahoo.com
Received August 27, 2012; revised October 25, 2012; accepted November 7, 2012
Keywords: Generalized Mittag-Leffler Function; Recurrence Relation; Wiman’s Function
ABSTRACT
In the present work, a unification of certain functions of mathematical physics is proposed and its properties are studied. The proposed function unifies Lommel function, Struve function, the Bessel-Maitland function and its generalization, Dotsenko function, generalized Mittag-Leffler function etc. The properties include absolute and uniform convergence, differential recurrence relation, integral representations in the form of Euler-Beta transform, Mellin-Barnes transform, Laplace transform and Whittaker transform. The special cases namely the generalized hypergeometric function, generalized Laguerre polynomial, Fox H-function etc. are also obtained.
1. Introduction
In the present work, we propose an extension of a generalization of the Mittag-Leffler function due to A. K. Shukla and J. C. Prajapati [1], defined as
 (1.1)
(1.1)
where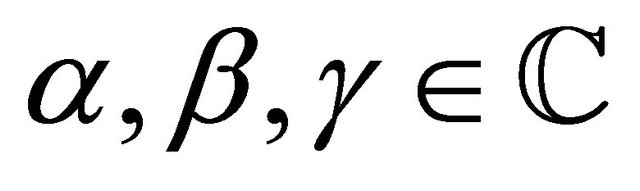 ;
;  and
and 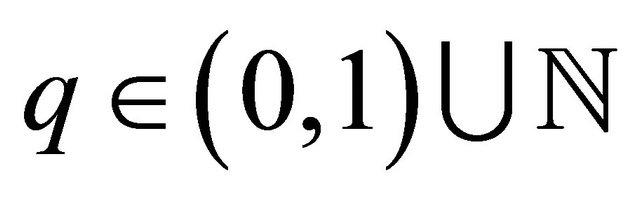 . This is an entire function of order
. This is an entire function of order  if
if 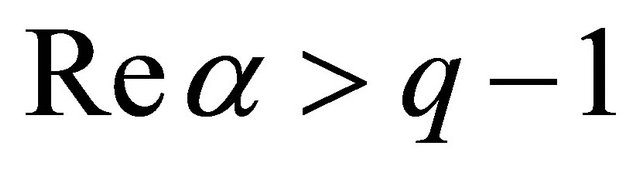 and absolutely convergent in
and absolutely convergent in 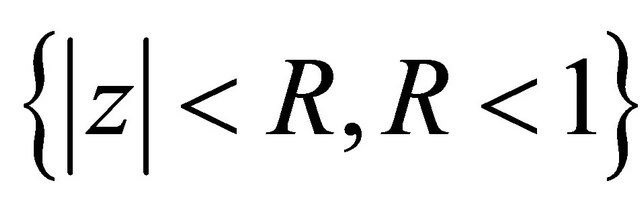 if
if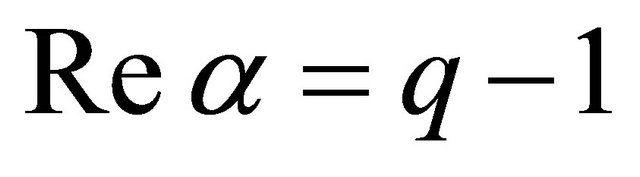 . In fact (1.1) contains the
. In fact (1.1) contains the 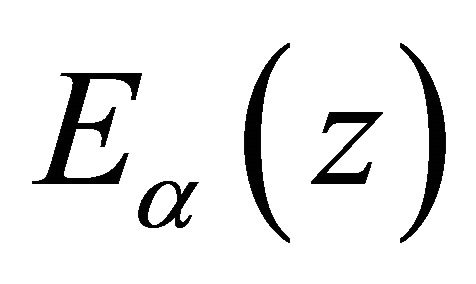 -Mittag-Leffler function [2],
-Mittag-Leffler function [2], 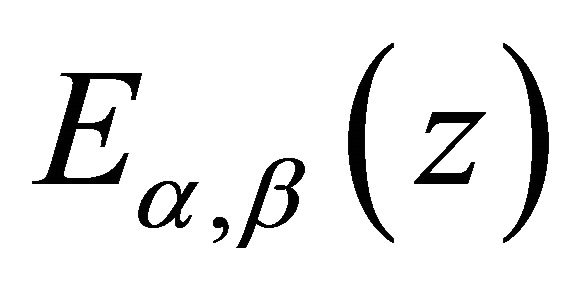 - the generalized Mittag-Leffler function [3] and the function
- the generalized Mittag-Leffler function [3] and the function 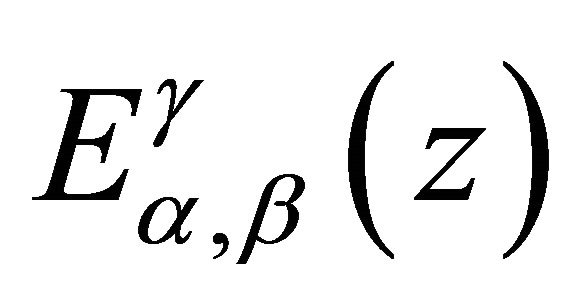 due to Prabhakar [4].
due to Prabhakar [4].
Gorenflo et al. [5], Saigo and Kilbas [6] studied several interesting properties of these functions.
Another generalization of Mittag-leffler function due to T. O. Salim [7], given by
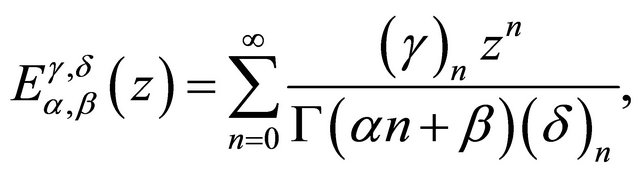 (1.1’)
(1.1’)
where 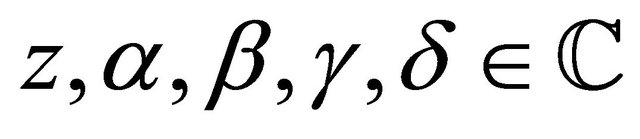 and
and
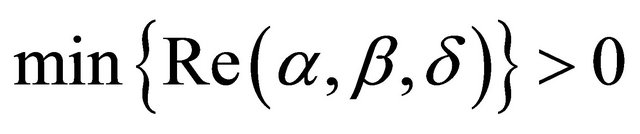 .
.
We state below the extended version in the form:
 (1.2)
(1.2)
where ,
,  ,
,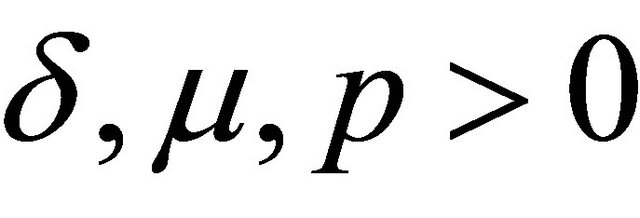 . The function defined by (1.2) reduces to the one in (1.1) and (1.1’) if
. The function defined by (1.2) reduces to the one in (1.1) and (1.1’) if ,
, 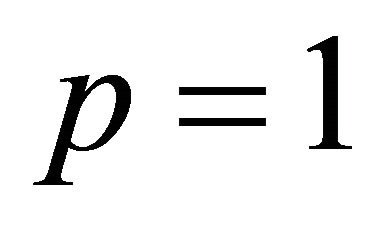 ,
, 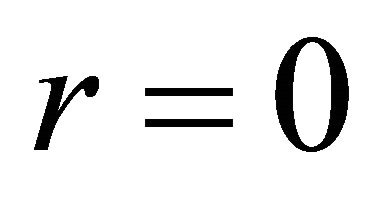 ,
, 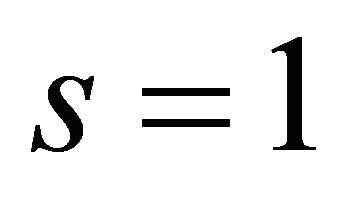 and
and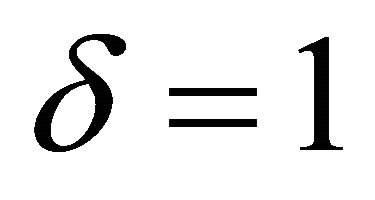 ,
, 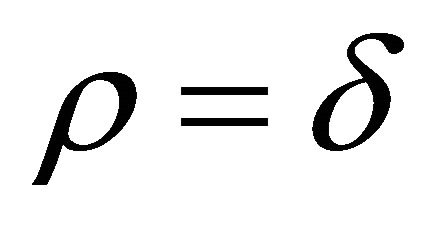 ,
, 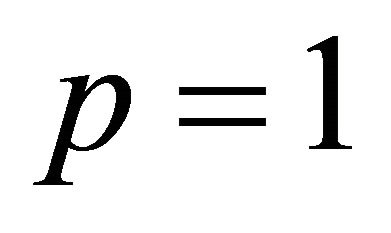 ,
,  ,
, 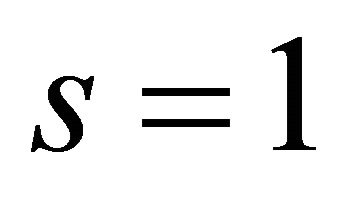 respectively.
respectively.
It is noteworthy that the function in (1.2), besides containing the generalizations of the Mittag-Leffler function, also includes certain functions belonging to the family of Bessel function. To see this, take ,
, 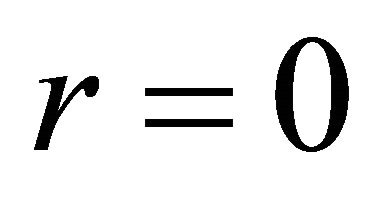 ,
, 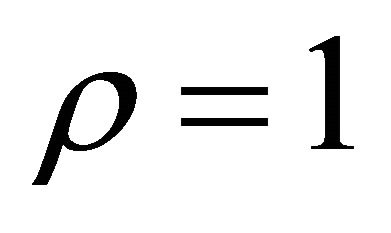 ,
, 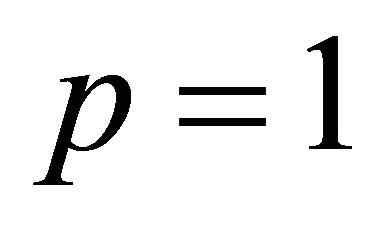 ,
,  ,
, 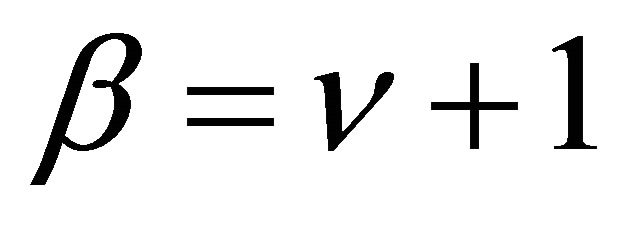 , and replaced z by
, and replaced z by 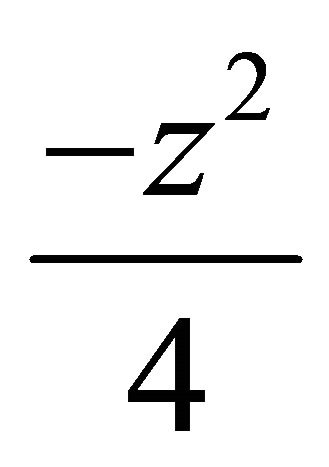 in (1.2), then we find the well known Bessel function [8]:
in (1.2), then we find the well known Bessel function [8]:
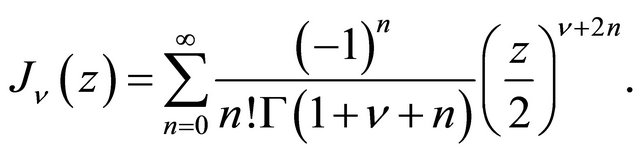
When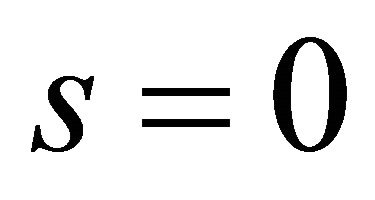 ,
, 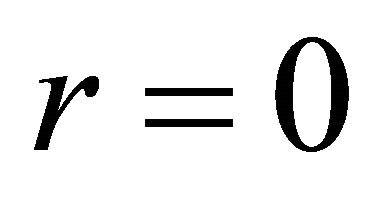 ,
, 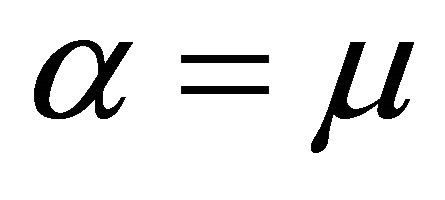 ,
, 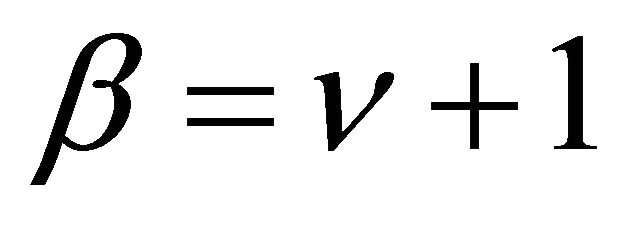 , and z is replaced by
, and z is replaced by 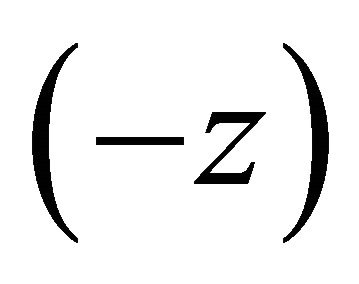 then we get the Bessel Maitland Function [8] given by
then we get the Bessel Maitland Function [8] given by 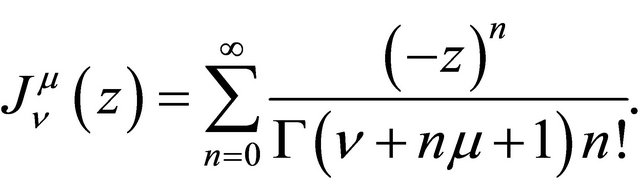 For
For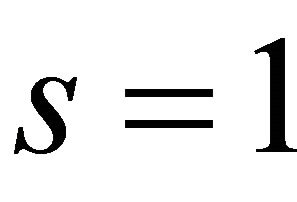 ,
,
 ,
,  ,
, 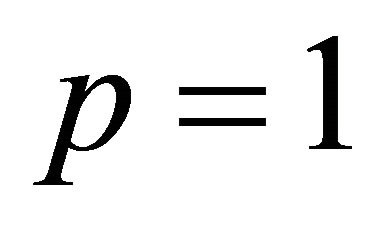 ,
, 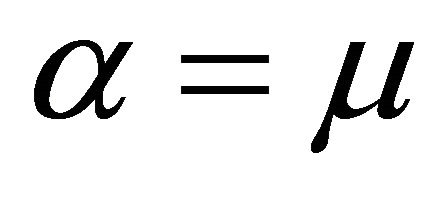 ,
, 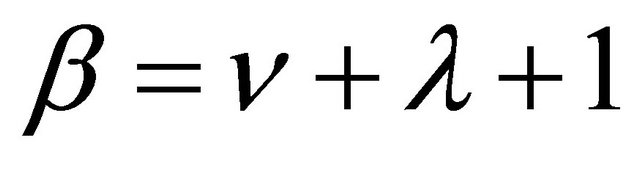 ,
, 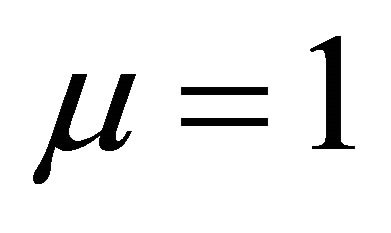 ,
,
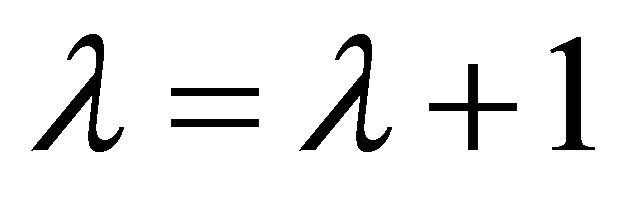 ,
,  ,
, 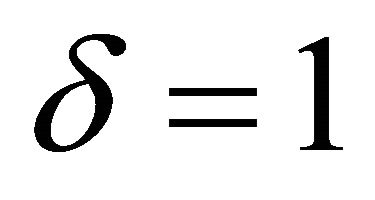 , and z is replaced by
, and z is replaced by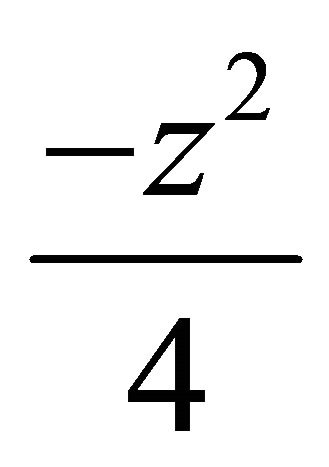 , we obtain the Generalized Bessel Maitland function [8]:
, we obtain the Generalized Bessel Maitland function [8]:

The Dotsenko Function [8]:

occurs by substituting ,
, 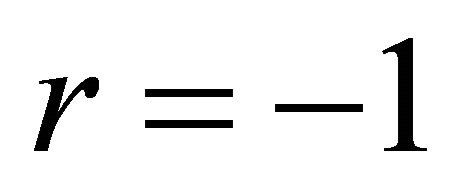 ,
,  ,
, 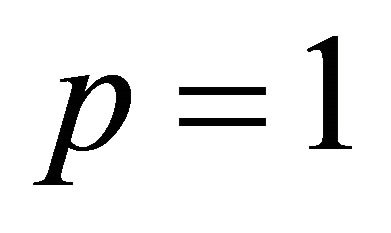 ,
, 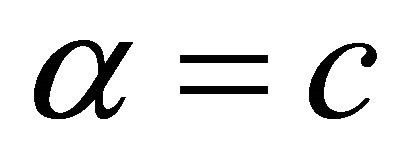 ,
, 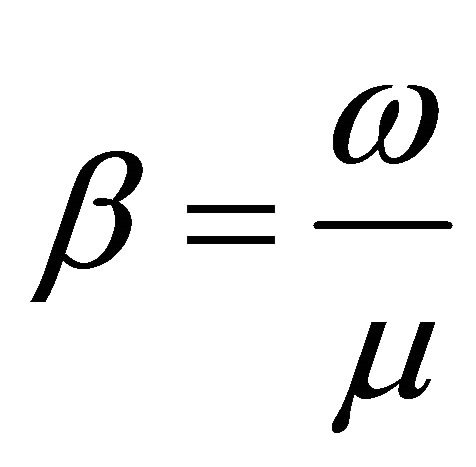 ,
, 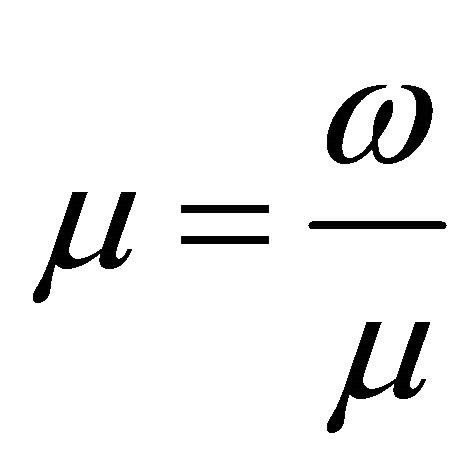 ,
,  ,
, 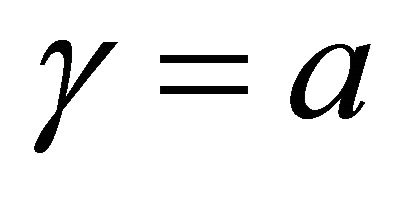 ,
, 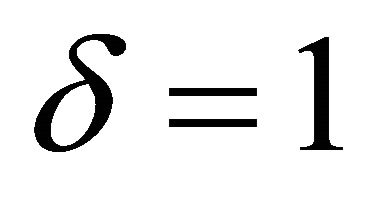 in (1.2).
in (1.2).
The Lommel Function defined by [9]:
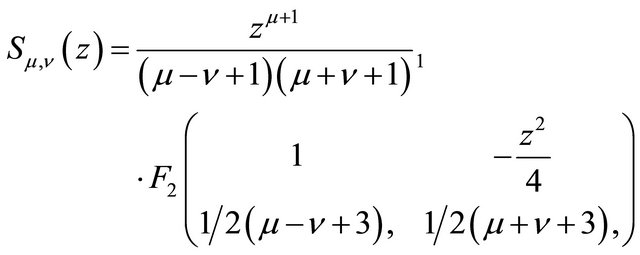
is the special case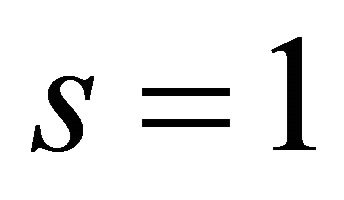 ,
, 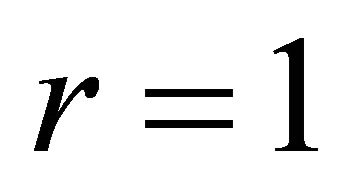 ,
,  ,
, 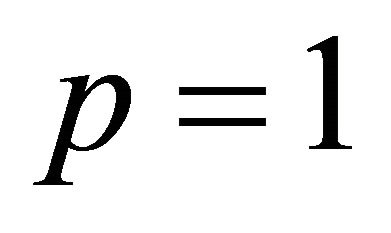 ,
, 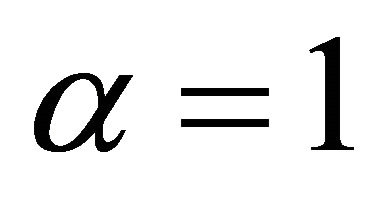 ,
,
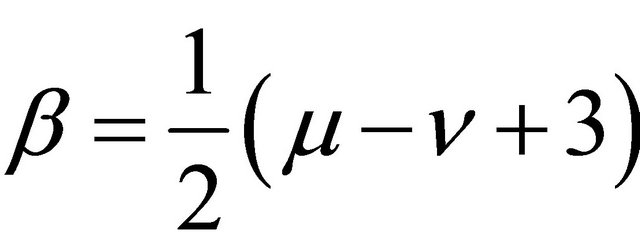 ,
, 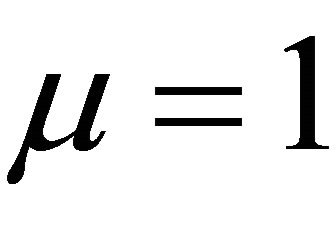 ,
, 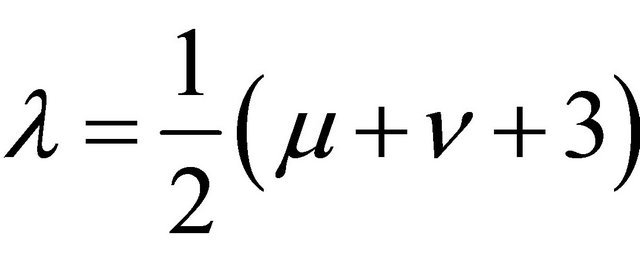 ,
,  ,
, 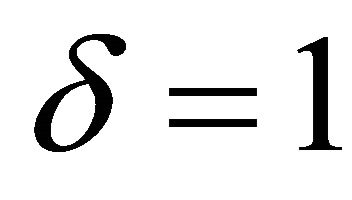 , and z is replaced by
, and z is replaced by  of (1.2). On making substitutions
of (1.2). On making substitutions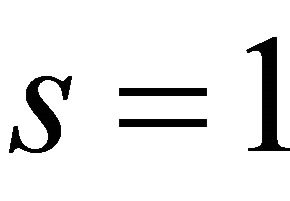 ,
, 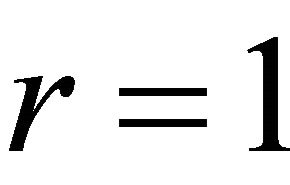 ,
,  ,
,  ,
,  ,
, 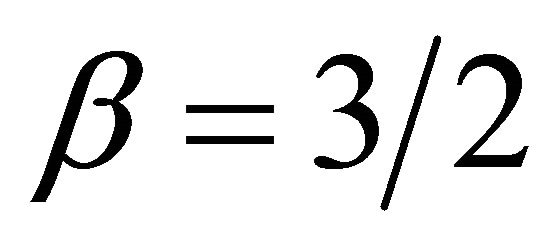 ,
, 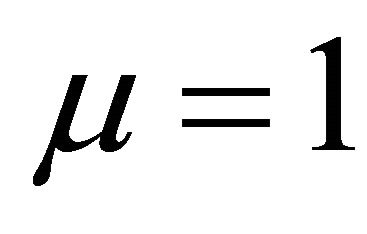 ,
, 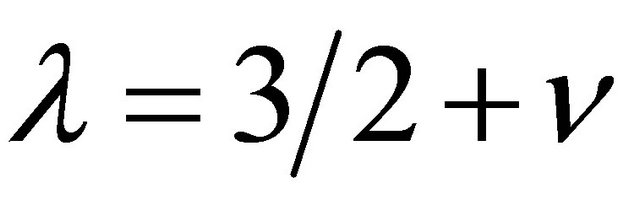 ,
, 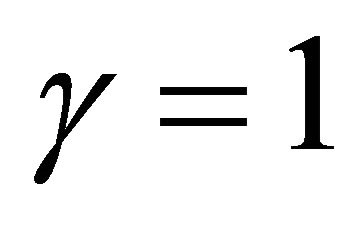 ,
,  , and
, and 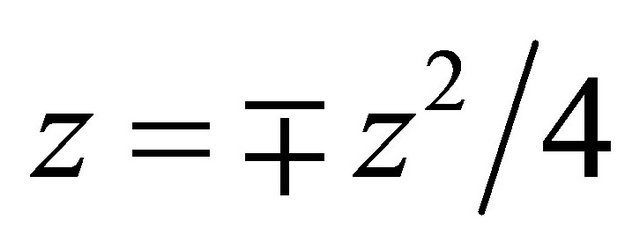 in (1.2), provides us respectively, the Struve Function
in (1.2), provides us respectively, the Struve Function 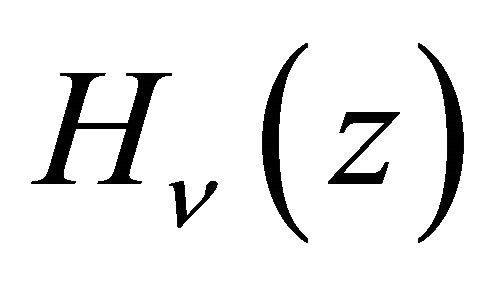 [9] given by
[9] given by
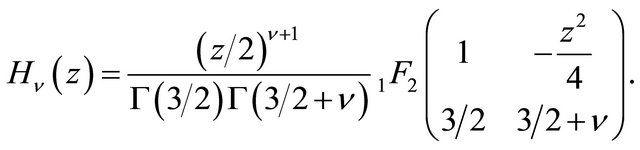
and the Modified Struve Function [9]:
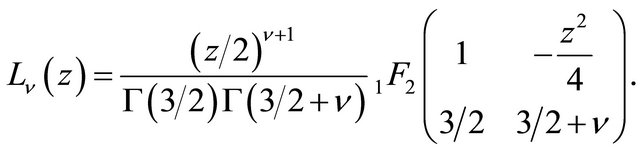
In what follows, we shall use the following definitions and formulas. Euler (Beta) transform [10]:
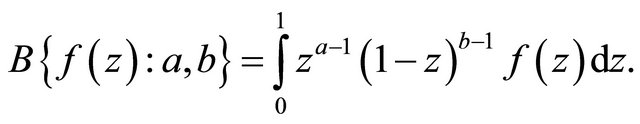 (1.3)
(1.3)
Laplace transform [10]:
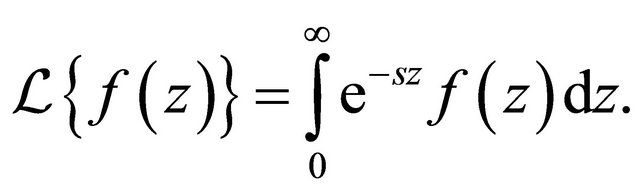 (1.4)
(1.4)
Mellin-Barnes transform [10]:
 (1.5)
(1.5)
then
 (1.6)
(1.6)
Incomplete Gamma function [11]:
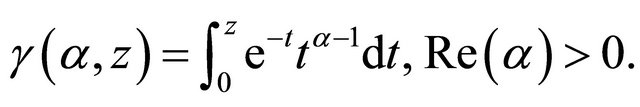 (1.7)
(1.7)
The generalized hypergeometric function is denoted and defined by [11]
 (1.8)
(1.8)
where 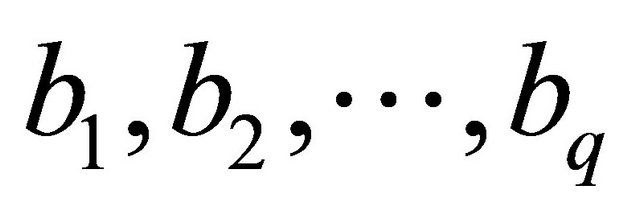 are neither zero nor negative integers, and
are neither zero nor negative integers, and
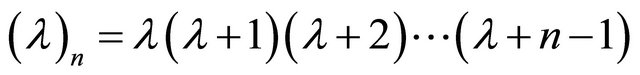 .
.
The series is convergent for 1)  if
if  2)
2) 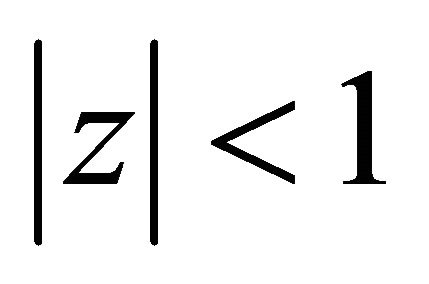 if
if 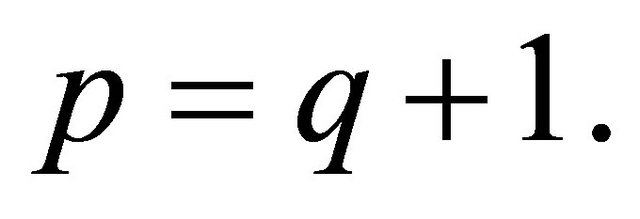
Wright generalized hypergeometric function [12]:
 (1.9)
(1.9)
Laguerre polynomial [12]:
 (1.10)
(1.10)
2. Main Results
In this section, we prove the following results for the function defined in (1.2).
Theorem 2.1. The series represented by the function 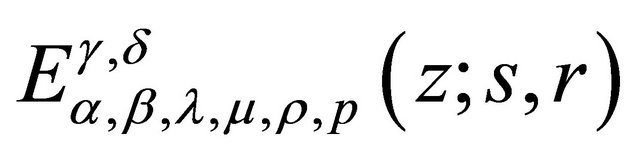 converges absolutely for
converges absolutely for
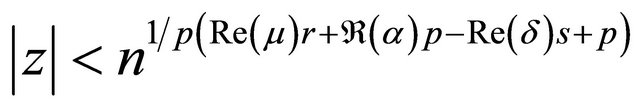 .
.
Proof: Consider,

Take
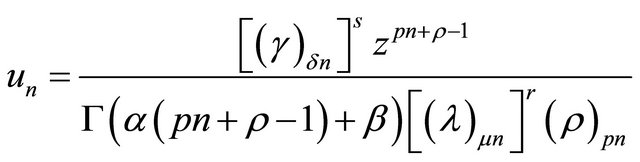
then

Thus,
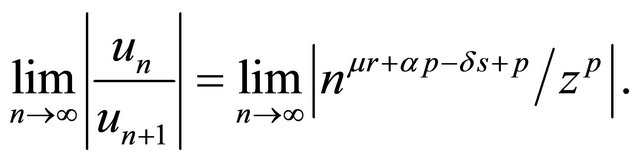
Hence,
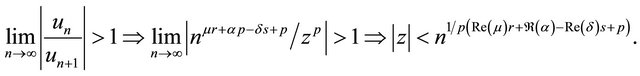
Theorem 2.2. For ;
;  and
and 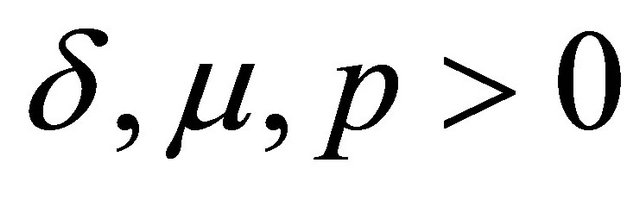 the differential recurrence relation form:
the differential recurrence relation form:
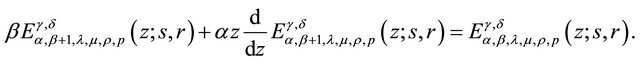
wang#title3_4:spwang#title3_4:spProof.
Consider,
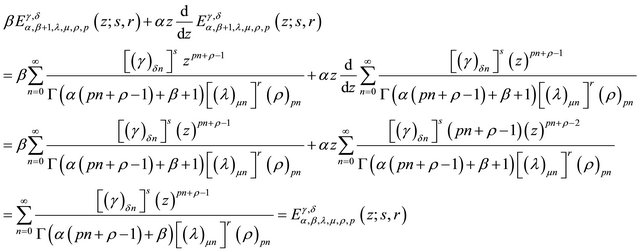
As the series given in (1.2) converges uniformly in any compact subset of , the use of term by term differentiation under the sign of summation leads us to the following theorem.
, the use of term by term differentiation under the sign of summation leads us to the following theorem.
Theorem 2.3. If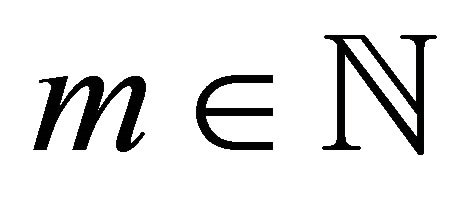 ,
, 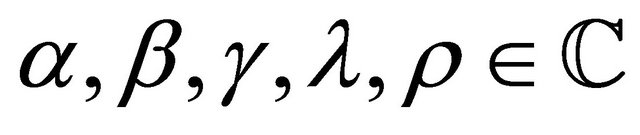 ,
,  and
and 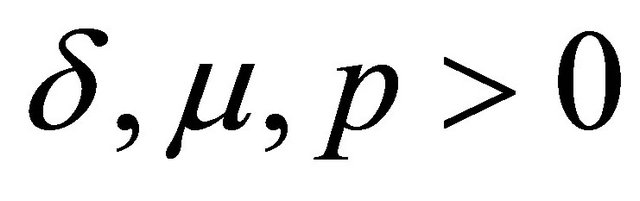 then
then
 (2.3.1)
(2.3.1)
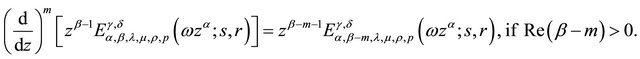 (2.3.2)
(2.3.2)
Proof. Consider

Now consider,
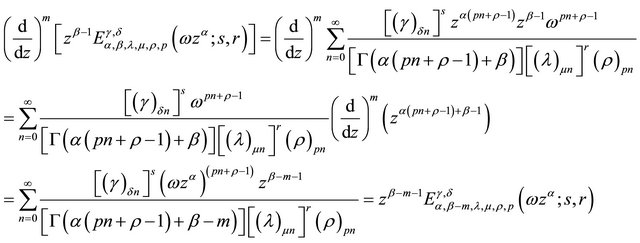
Next, taking  in the Euler (Beta) transform (1.3), one finds the following Theorem 2.4. If
in the Euler (Beta) transform (1.3), one finds the following Theorem 2.4. If ,
, 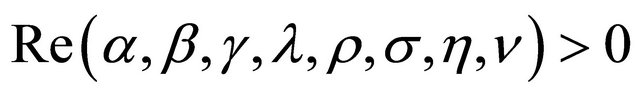 and
and 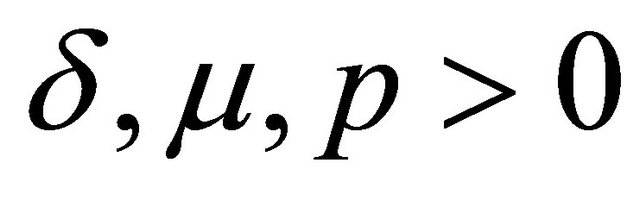 then
then
 (2.4.1)
(2.4.1)
 (2.4.2)
(2.4.2)
 (2.4.3)
(2.4.3)
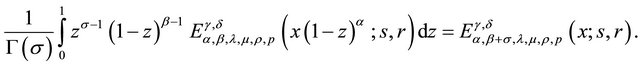 (2.4.4)
(2.4.4)
wang#title3_4:spwang#title3_4:spProof.
In (2.4.1),

Now, denoting the L.H.S. of (2.4.2) by , we have
, we have
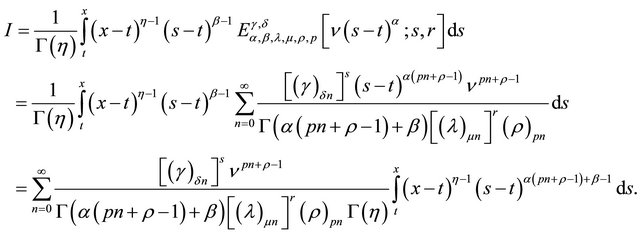
Here, introducing 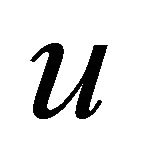 as a new variable of integration, by means of the relation
as a new variable of integration, by means of the relation
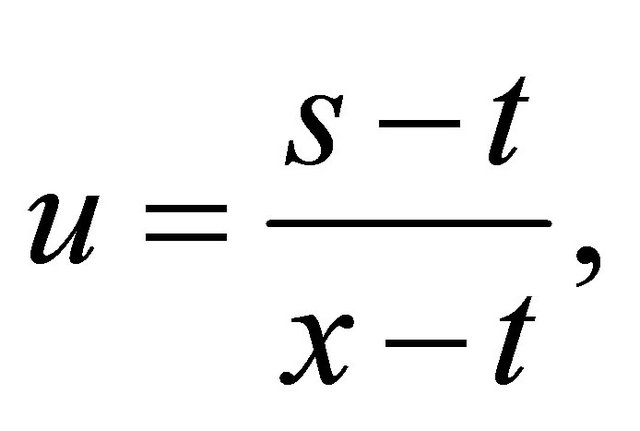
The further simplification gives,
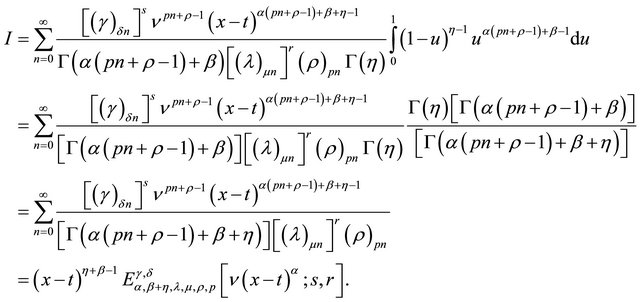
as desired.
To prove (2.4.3) we begin with
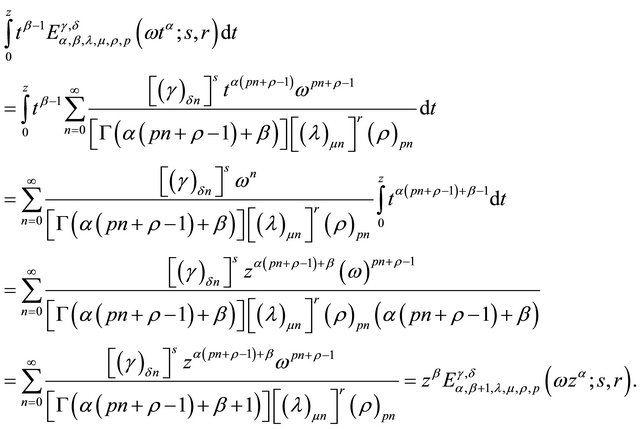
Hence the result.
Now, consider
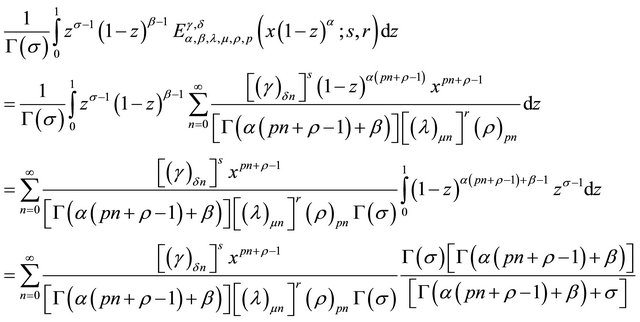
simplification of above series yields (2.4.4).
3. Mellin-Barnes Integral Representation of 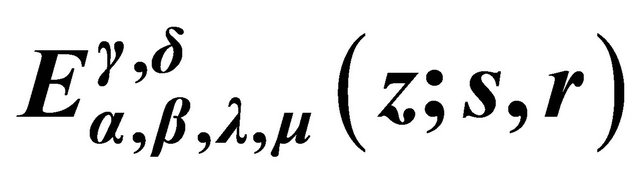
Theorem 3.1. Let ;
; ,
,  and
and ,
,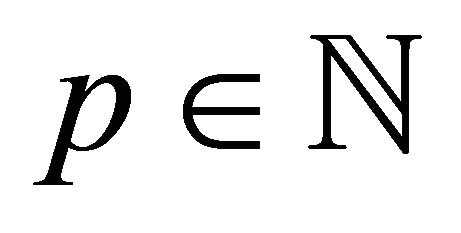 . Then the function
. Then the function  is represented by the Mellin-Barnes integral as
is represented by the Mellin-Barnes integral as
 (3.1.1)
(3.1.1)
where 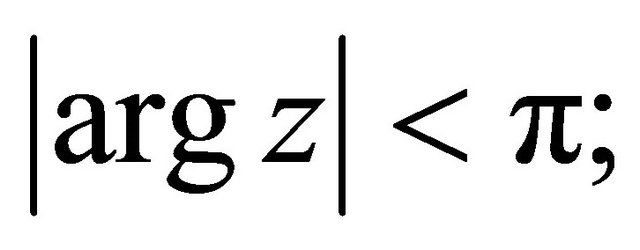 the contour of integration beginning at
the contour of integration beginning at  and ending at
and ending at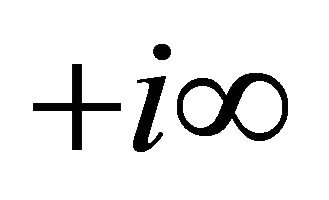 , and indented to separate the poles of integrand at
, and indented to separate the poles of integrand at 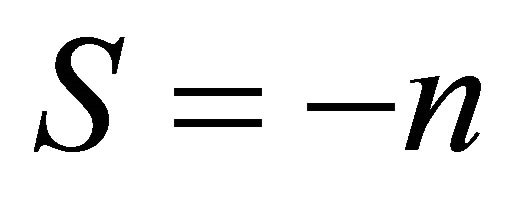 for all
for all  (to the left) from those at
(to the left) from those at  for all
for all  (to the right).
(to the right).
wang#title3_4:spwang#title3_4:spProof.
We shall evaluate the integral on the R.H.S. of (3.1.1) as the sum of the residues at the poles 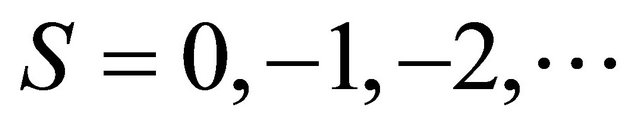 In fact, in view of the definition of residue, we have
In fact, in view of the definition of residue, we have

This gives,

4. Integral Transforms of 
In this section, we discussed some useful integral transforms like Euler transforms, Laplace transforms, Mellin transforms, Whittaker transformsFor the convenience, we introduce the Notation:
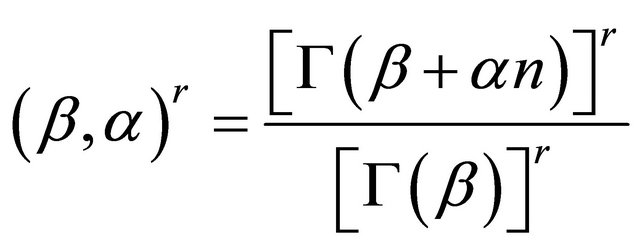
Theorem 4.1. (Euler(Beta) transforms)

where ,
,  and
and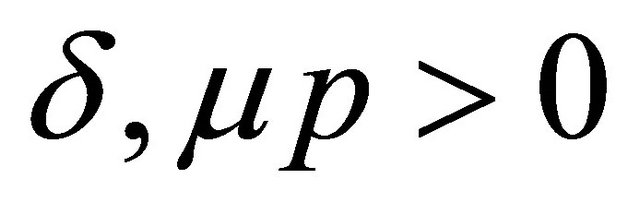 .
.
Proof.

Theorem 4.2. (Laplace transforms)

where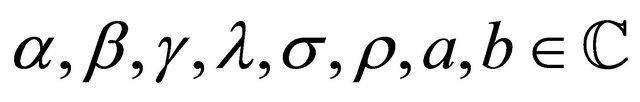 ,
, 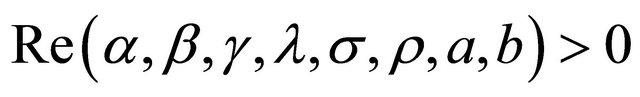 and
and .
.
Proof. We begin with
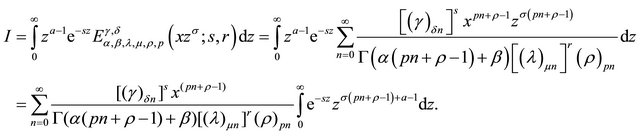
On making substitution , we get
, we get

In proving the following theorem we use the integral formula involving the Whittaker function:
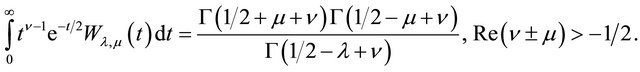
Theorem 4.3. (Whittaker transforms)

where ,
,  and
and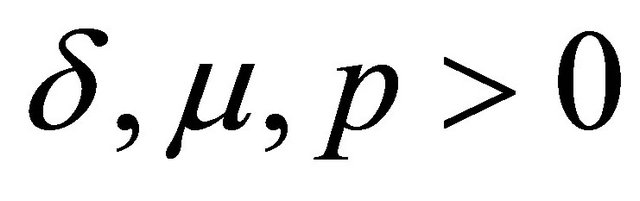 .
.
Proof. Let

then using the substitution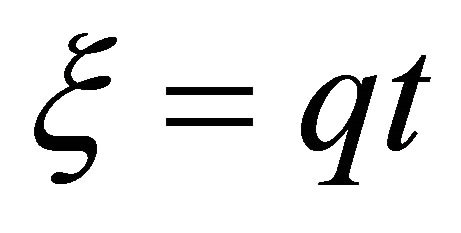 , we get
, we get
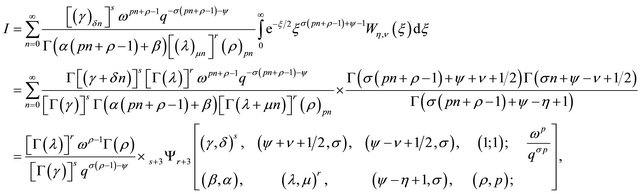
Theorem 4.4. (Mellin transforms)
 (4.4.1)
(4.4.1)
where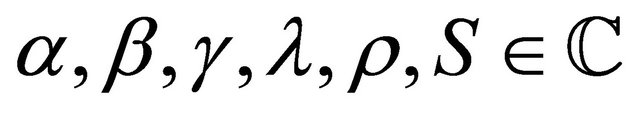 ,
,
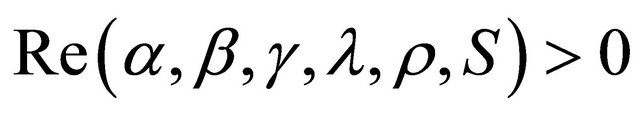 .
.
Proof. Putting 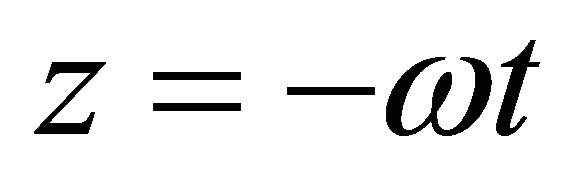 in (3.1.1), we get
in (3.1.1), we get
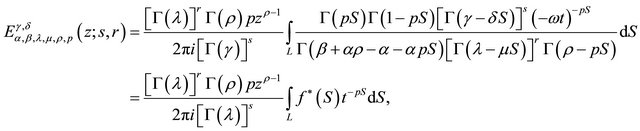 (4.4.2)
(4.4.2)
in which
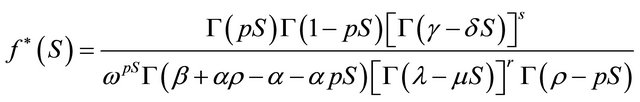
using (1.5) and (1.6) in (4.4.2), immediately leads us to (4.4.1).
5. Generalized Hypergeometric Function Representation of 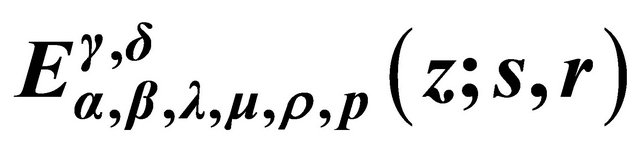
Taking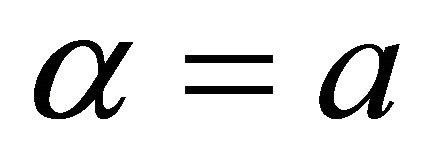 ,
,  ,
,  in (1.2), we get
in (1.2), we get

where  is a n-tuple
is a n-tuple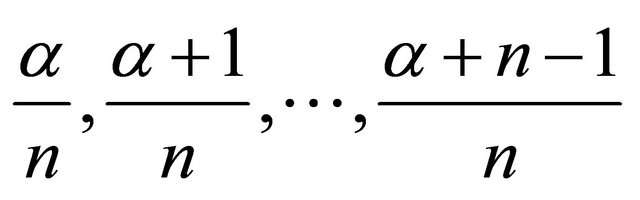 .
.
6. Relationship with Some Known Special Functions (Generalized Laguerre Polynomial, Fox H-Function, Wright Hypergeometric Function)
6.1. Relationship with Generalized Laguerre Polynomials
Putting ,
,  ,
, 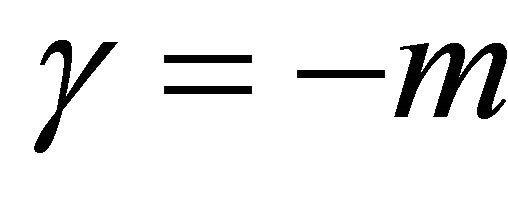 ,
,  ,
,  ,
, 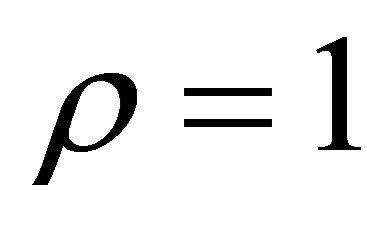 ,
, 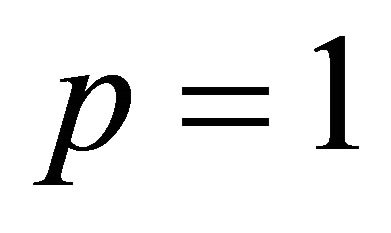 and replacing
and replacing  by
by 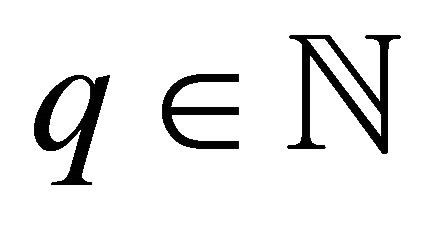 and z by zk in (1.2), we get
and z by zk in (1.2), we get
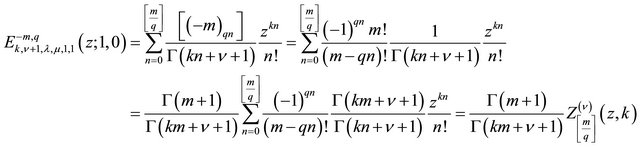 (6.1.1)
(6.1.1)
where 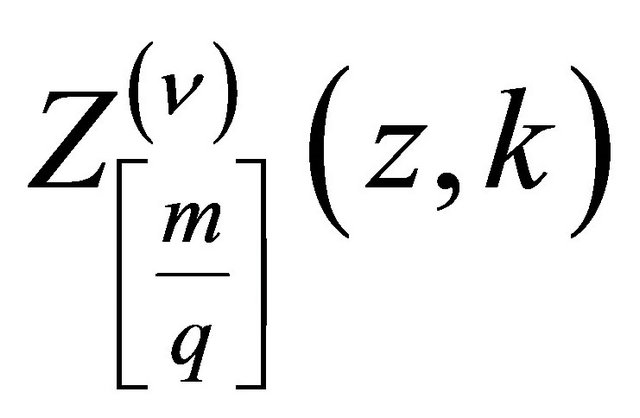 is polynomial of degree
is polynomial of degree  in zk.
in zk.
In particular, 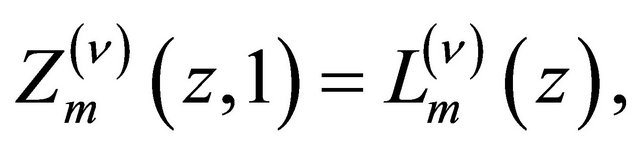 so that
so that
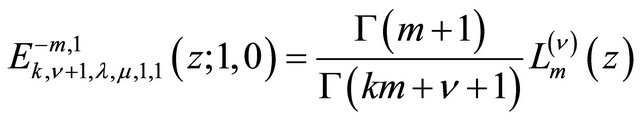 (6.1.2)
(6.1.2)
6.2. Relationship with Fox H-Function
From (3.1.1), we have
 (6.2.1)
(6.2.1)
6.3. Relationship with Wright Function
If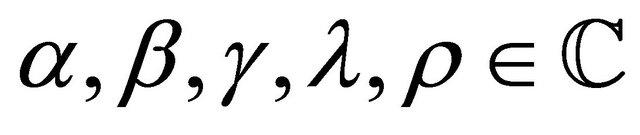 ,
, 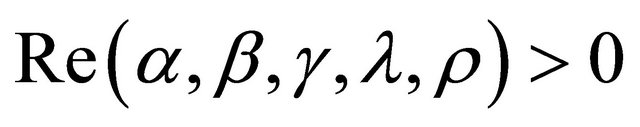 ,
, 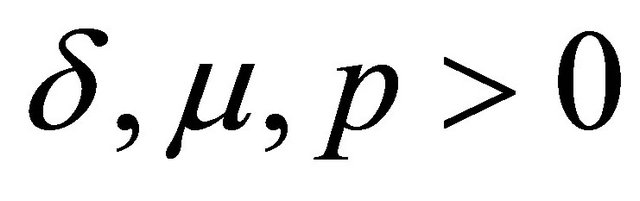 (1.2) can be written as
(1.2) can be written as
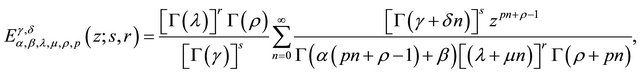 (6.3.1)
(6.3.1)
from (1.9) for (6.3.1), we get
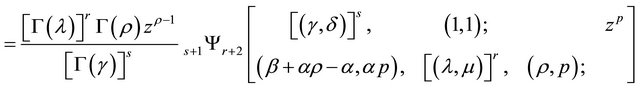
7. Summary
In Section 1, an extended version of Mittag-Leffler function of 10 indices established as an Equation (1.2) including with some necessary information of Bessel function, some well-known integral transforms and generalized hypergeometric functions with their family. Results obtained in Sections 2 to 6 are interesting generalizations of (Shukla and Prajapati [1]) and stimulate the scope of further research in the field of generalization MittagLeffler function.
8. Acknowledgements
This paper dedicated to our beloved great Mathematician Gösta Mittag-Leffler. The authors would like to thank the reviewers for their valuable suggestions to improve the quality of paper.
REFERENCES
- A. K. Shukla and J. C. Prajapti, “On a Generlization of Mittag-Leffler Functions and Its Properties,” Journal of Mathematical Analysis and Applications, Vol. 336, No. 2, 2007, pp. 797-811. doi:10.1016/j.jmaa.2007.03.018
- G. Mittag-Leffler, “Sur la Nouvelle Fonction
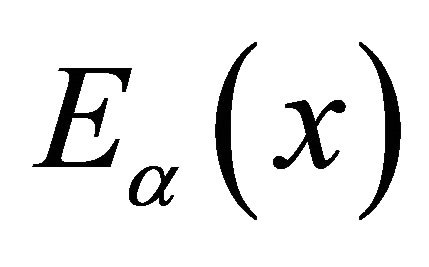 ,” Comptes Rendus de l’Academie des Sciences Paris, Vol. 137, 1903, pp. 554-558.
,” Comptes Rendus de l’Academie des Sciences Paris, Vol. 137, 1903, pp. 554-558. - A. Wiman, “Über die Nullstellen der Funktionen
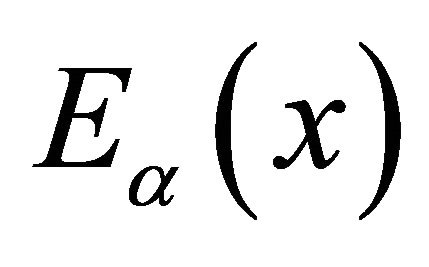 ,” Acta Mathematica, Vol. 29, No. 1, 1905, pp. 217-234. doi:10.1007/BF02403204
,” Acta Mathematica, Vol. 29, No. 1, 1905, pp. 217-234. doi:10.1007/BF02403204 - T. R. Prabhakar, “A Singular Equation with a Generalized Mittag-Leffler Function in the Kernel,” Yokohama Mathematical Journal, Vol. 19, 1971, pp. 7-15.
- R. Gorenflo, A. A. Kilbas and S. V. Rogosin, “On the Generalized Mittag-Leffler Type Function,” Integral Transforms and Special Functions, Vol. 7, No. 3-4, 1998, pp. 215-224. doi:10.1080/10652469808819200
- M. Saigo and A. A. Kilbas, “On Mittag Leffler Type Function and Applications,” Integral Transforms and Special Functions, Vol. 7, No. 1-2, 1998, pp. 97-112. doi:10.1080/10652469808819189
- T. O. Salim, “Some Properties Relating to the Generalized Mittag-Leffler Function,” Advances in Applied Mathematical Analysis, Vol. 4, No. 1, 2009, pp. 21-30.
- H. J. Haubold, A. M. Mathai and R. K. Saxena, “The H-Function: Theory and Applications,” Publication No. 37 of Centre for Mathematical Sciences, Pala Campus, 2008.
- Y. L. Luke, “The Special Functions and their approximations,” Academic Press, New York, London, 1969.
- I. N. Sneddon, “The Use of Integral Transforms,” McGrawHill Book Company, New York, 1972.
- E. D. Rainville, “Special Functions,” Macmillan Co., New York, 1960.
- H. M. Srivastava and H. L. Manocha, “A Treatise on Generating Functions,” Ellis Horwood Ltd., Chichester, 1984.

