ABSTRACT

In this paper we propose a class of non-stationary solutions of Einstein’s field equations describing an embedded Vaidya-de Sitter solution with a cosmological variable function Λ(u). Vaidya-de Sitter solution is interpreted as the radiating Vaidya black hole which is embedded into the non-stationary de Sitter space with variable Λ(u). The energymomentum tensor of the Vaidya-de Sitter black hole may be expressed as the sum of the energy-momentum tensor of the Vaidya null fluid and that of the non-stationary de Sitter field, and satisfies the energy conservation law. We also find that the equation of state parameter w= p/ρ = −1 of the non-stationary de Sitter solution holds true in the embedded Vaidya-de Sitter solution. It is also found that the space-time geometry of non-stationary Vaidya-de Sitter solution with variable Λ(u) is type D in the Petrov classification of space-times. The surface gravity, temperature and entropy of the space-time on the cosmological black hole horizon are discussed.

1. Introduction

The Vaidya solution having a variable mass m(u) with retarded time u is a non-stationary generalization of Schwarzschild black hole of constant mass m [1]. The Schwarzschild solution is regarded as a black hole in an asymptotically flat space. The Schwarzschild-de Sitter solution is interpreted as a black hole in an asymptotically de Sitter space with non-zero cosmological constant Λ [2]. The Schwarzschild-de Sitter solution is also considered as an embedded black hole that the Schwarzschild solution is embedded into the de Sitter space with cosmological constant Λ to produce the Schwarzschildde Sitter black hole [3]. Mallett [4] has introduced Vaidya-de Sitter solution with constant Λ by making the Schwarzschild mass m variable with respect to the retarded time u as m(u) and studied the nature of the spacetime [5].

Here the aim of this paper is to propose an exact solution of Einstein’s field equations describing Vaidya black hole embedded into the non-stationary de Sitter space to obtain Vaidya-de Sitter black hole with variable Λ(u). This Vaidya-de Sitter solution with variable Λ(u) will have the limit m(u) = ± (1/3) Λ(u)^(−1/2) of the Vaidya mass m(u) in the extreme black hole case 9Λ(u)m²(u) = 1, which could not be explained with the constant Λ in [4]. This situation can be seen in the next section of this paper.

Now we introduce the non-stationary de Sitter solution with variable Λ(u) briefly. The line-element describing a non-stationary de Sitter solution of Einstein’s field equations with cosmological function Λ(u) in the null coordinates (u, r, θ, ϕ) is given in [6] as

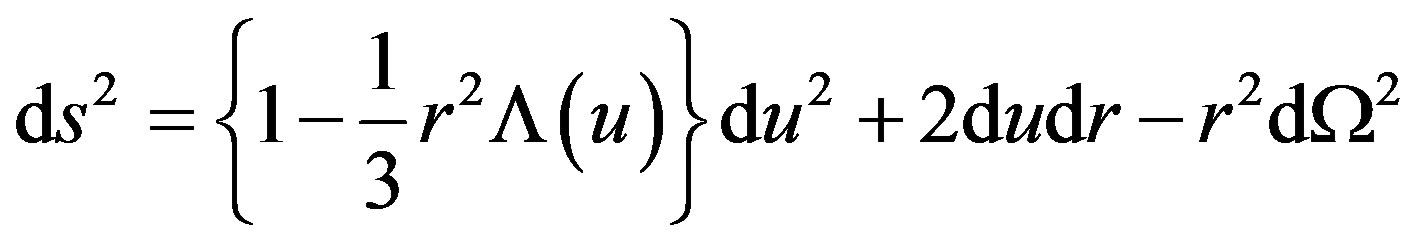(1.1)

where dΩ² = dθ² + sin²θdϕ². Here Λ(u) is an arbitrary non-increasing function of the retarded time coordinate u = t − r. The line-element (1.1) possesses an energy-momentum tensor as

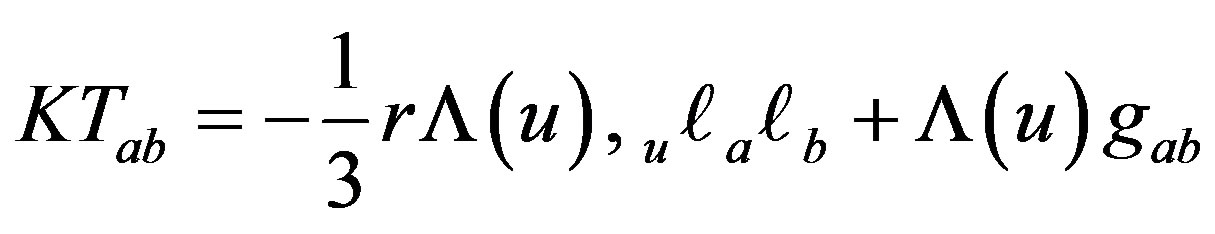(1.2)

where 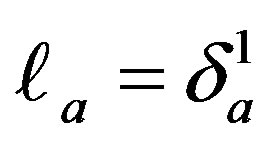is a null vector and the universal constant K = 8πG/c⁴. The trace of the tensor (1.2) is given by KT = 4Λ(u). Here it is worth mentioning that the energymomentum tensor (1.2) involves a Vaidya-like null term, which arises from the non-stationary state of motion of an observer traveling in the nonstationary de Sitter universe (1.1). This non-stationary part of the energy-momentum tensor (1.2) contributes the nature of null matter field present in (1.1) whose energymomentum tensor 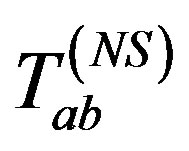has zero trace and will vanish when r → 0. However, it still maintains the non-stationary status that 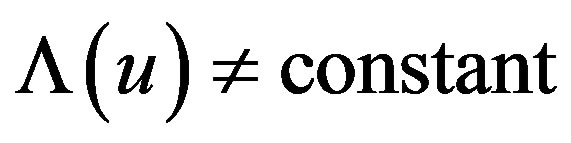and the space-time of the observer are naturally time-dependent even at the origin r → 0. Here “NS” in 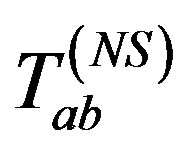stands for non-stationary as it arises from the non-stationary state of the universe.

Using the energy-momentum tenor (1.2) we could write Einstein’s field equations as follows

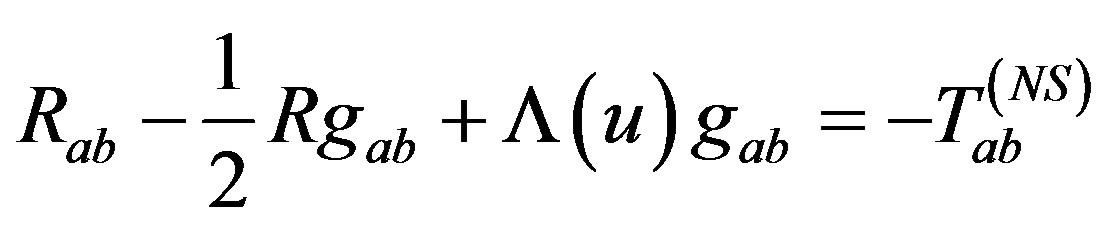(1.3)

where arises from the non-stationary state of  motion depending on the derivative of coordinate u and is given by

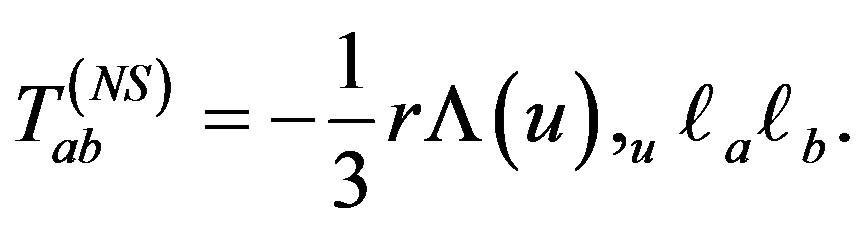
(1.4)

It is noted that the right side of the Equation (1.3) does not involve the universal constant K. The derivation of this non-stationary de Sitter cosmological universe (1.1) is in agreement with the original stationary de Sitter model [7] when Λ(u) takes a constant value Λ.

Now expressing the metric tensor in terms of null tetrad vectors [8] as

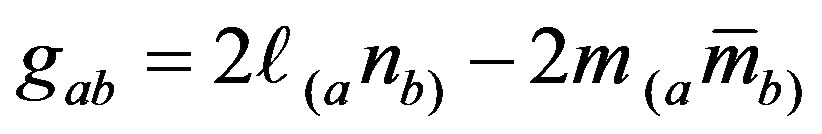, the energy momentum tensor (1.2) takes the form

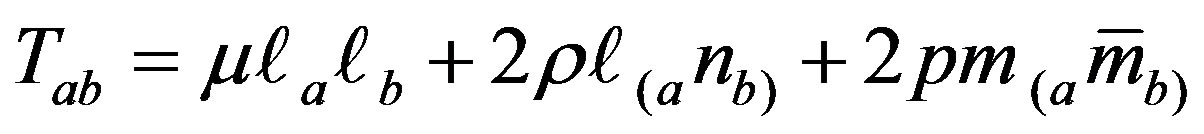, (1.5)

where ρ and p denote the density and the pressure of the non-stationary de Sitter model respectively and are obtained as:

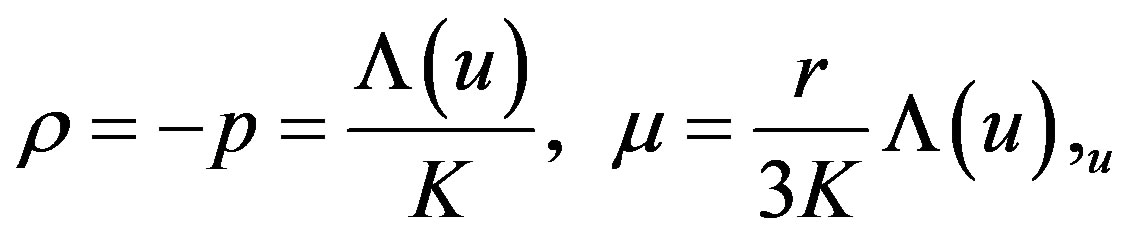. (1.6)

The trace of energy-momentum tensor T_ab (1.5) is given as 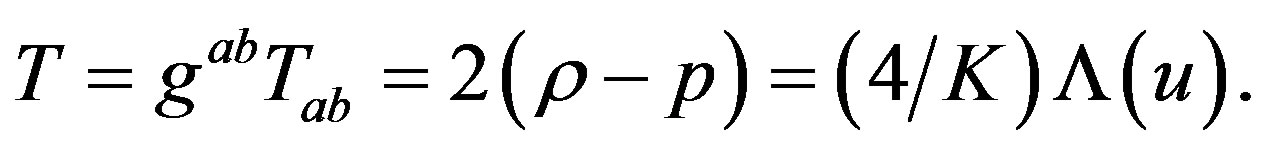Here it is observed that ρ − p > 0 for the non-stationary de Sitter model. From (1.6) we find the equation of state as

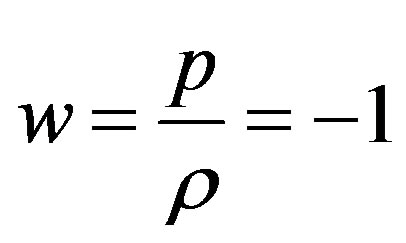(1.7)

with the negative pressure p in (1.6). This shows the fact that the non-stationary de Sitter solution (1.1) is in agreement with the cosmological constant (Λ) de Sitter model possessing the equation of state w = −1 in the dark energy scenario [9-11], when Λ(u) takes a constant value Λ.

The black hole embedded into de Sitter space plays an important role in classical general relativity that the cosmological constant is found present in the inflationary scenario of the early universe in a stage where the universe is geometrically similar to the original de Sitter space [7]. Also embedded black holes can avoid the direct formation of negative mass naked singularities during Hawking’s black hole evaporation process [12].

2. Vaidya in Non-Stationary de Sitter Space

In this section we propose an exact solution describing the Vaidya-de Sitter solution with a non-stationary variable Λ(u), which may be treated as the non-stationary Vaidya-de Sitter black hole or the Vaidya black hole on the non-stationary de Sitter background with variable Λ(u).

Wang and Wu [13] have expressed the mass function as

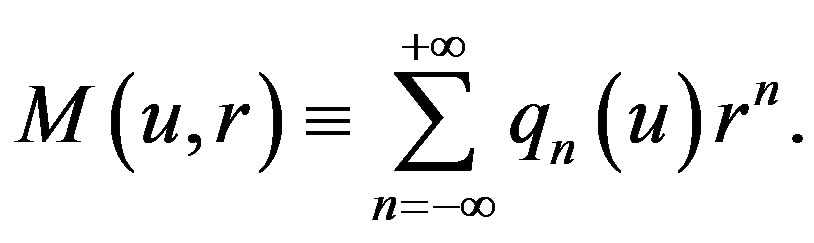(2.1)

Here the u-coordinate is related to the retarded time in flat space-time. The u-constant surfaces are null cones open to the future. The r-constant is null coordinate. The retarded time coordinate is used to evaluate the radiating (or outgoing) energy momentum tensor around the astronomical body [14]. For deriving the Vaidya-de Sitter solution with Λ(u) we consider the Wang-Wu functions q(u) in (2.1) as follows:

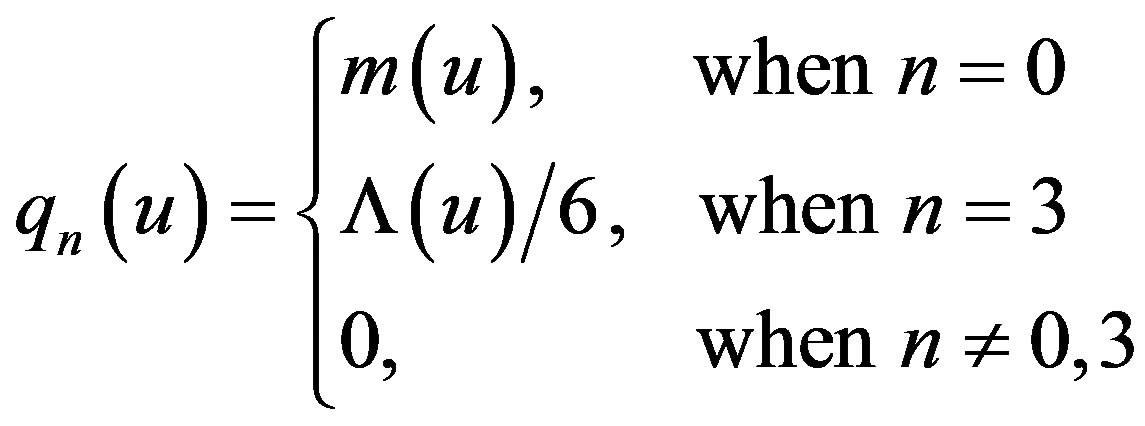(2.2)

such that the mass function (2.1) takes the form

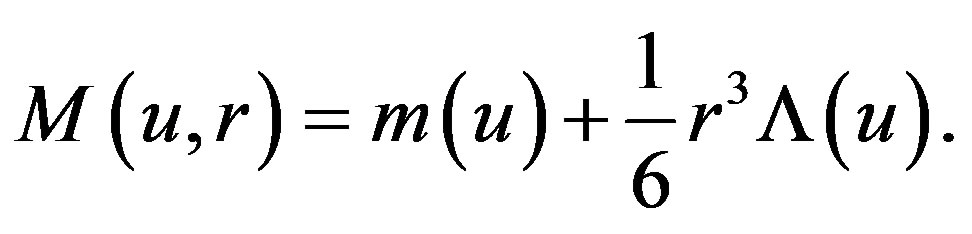(2.3)

Then using this mass function in the Schwarzschildlike metric

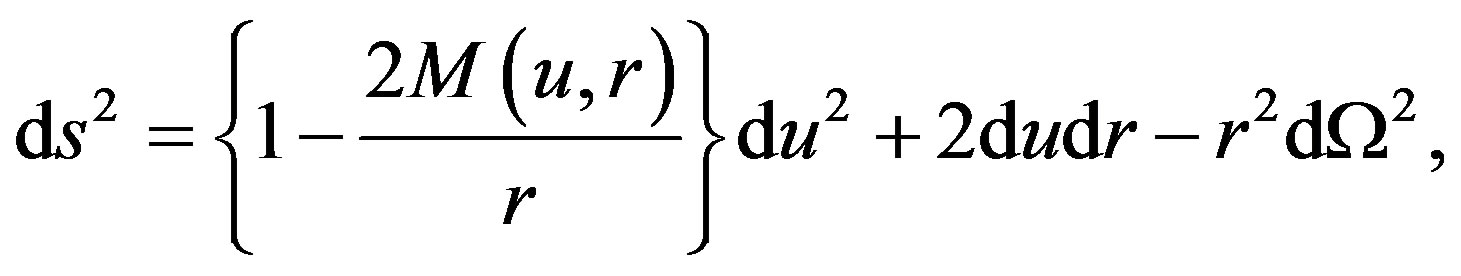(2.4)

with 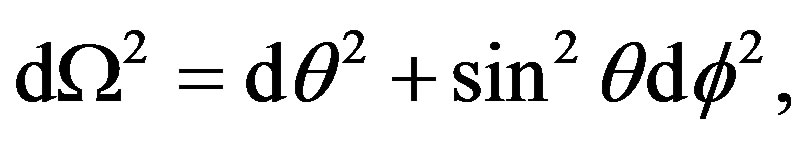we obtain a non-stationary metric, describing the Vaidya metric embedded into the non-stationary de Sitter model to produce Vaidya-de Sitter solution with variable cosmological function Λ(u) as

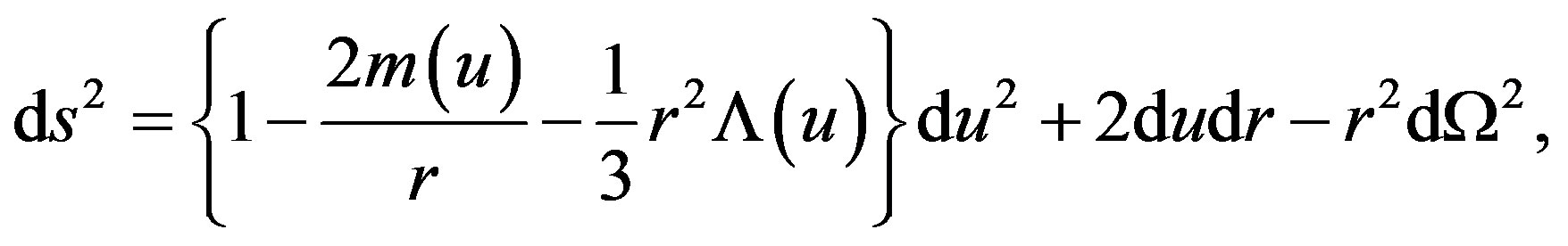(2.5)

where M(u) is the mass of the Vaidya black hole and Λ(u) denotes the de Sitter cosmological function of retarded time coordinate u. When we set the function Λ(u) to be a constant Λ, the line element (2.5) will become the Vaidya de Sitter space-time with cosmological constant. When the Vaidya mass sets to zero, and function Λ(u) to be a constant Λ, the line element will recover the original de Sitter solution. The solution (2.5) may have a singularity when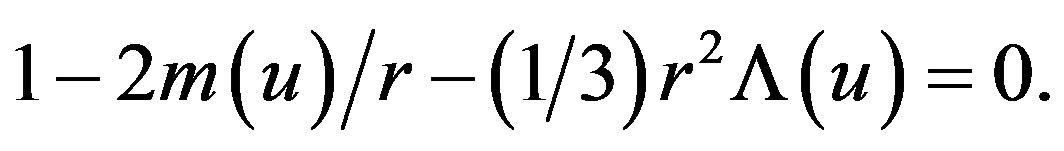

The complex null vectors for the Vaidya-de Sitter solution can be chosen as follows:

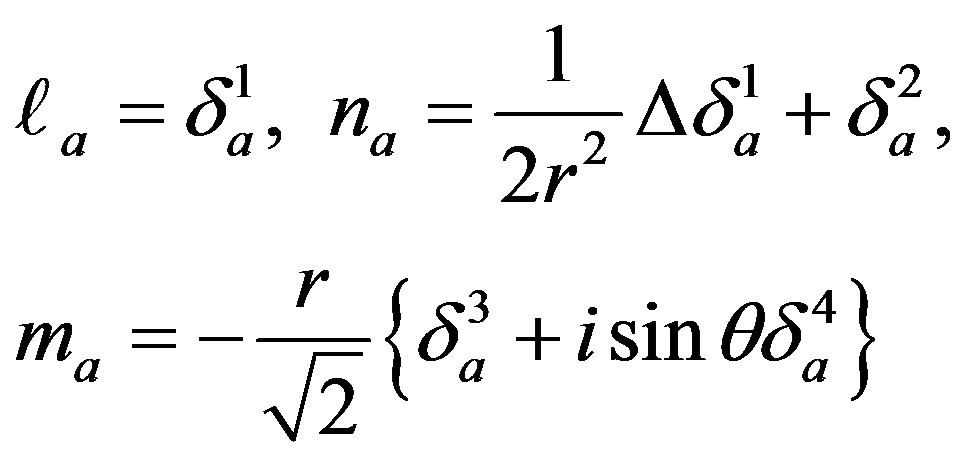(2.6)

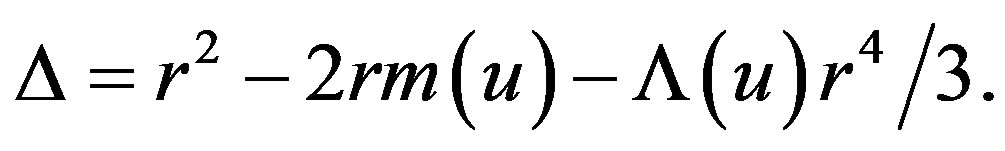where Here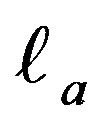, 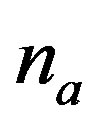are real null vectors and 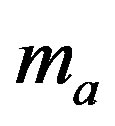is complex with the normalization conditions 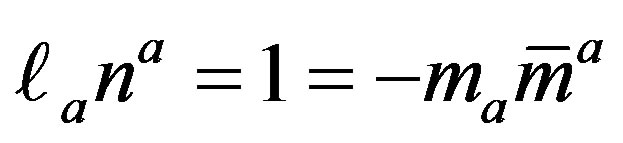and the other inner products of the null vectors are zero. From Einstein’s field equations 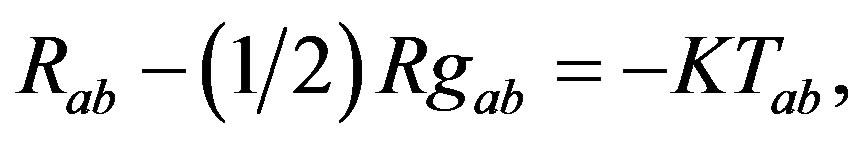we find the energy-momentum tensor describing the matter field for the non stationary space-time (2.5) as

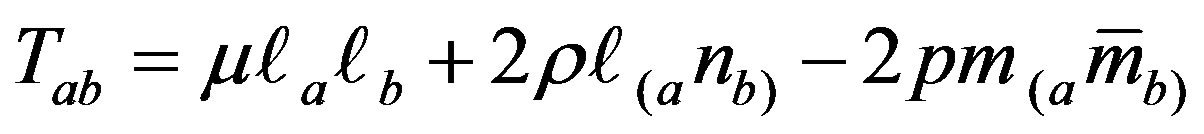(2.7)

where the coefficients ρ, p and μ are the density, the pressure and the null density, respectively and are obtained as:

. (2.8)

The trace of energy-momentum tensor 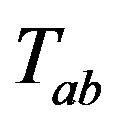(2.7) is given by

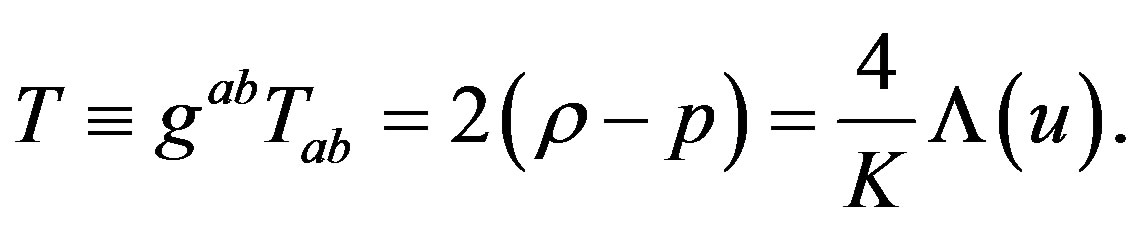(2.9)

Here it is observed that ρ − p > 0 for the non-stationary de Sitter model and the trace T does not involve the Vaidya mass m(u), showing the null fluid distribution of the space-time (2.5). We also find the ratio of the pressure p to the energy density ρ as the equation of state for the solution w = p/ρ = −1, which is one of the important properties of de Sitter space to be regarded as a dark energy candle [9-11] and references there in. The Ricci scalar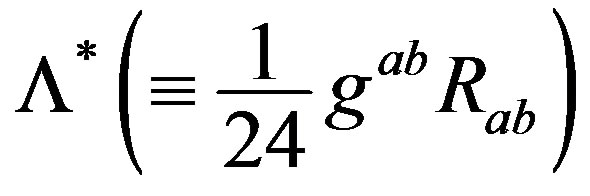, describing matter field takes the form. The energy-momentum tensor

(2.7) satisfies the energy conservation equation

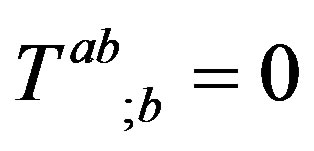(2.10)

As in general relativity the physical properties of a space-time geometry are determined by the nature of the matter distribution in the space, we must express the energy-momentum tensor (2.7) in such a way that one should be able to understand it easily. Thus, the total energy-momentum tensor (EMT) for the solution (2.5) may be written in the following decomposition form as:

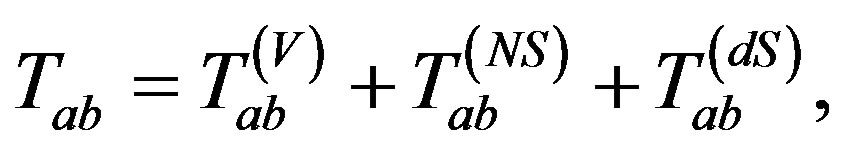(2.11)

where the 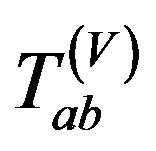for the Vaidya null radiating fluid, 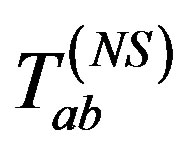the non-stationary contribution of de Sitter field Λ(u) associated with the derivative term and 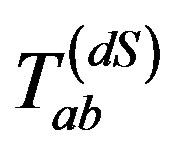the cosmological de Sitter matter are given, respectively

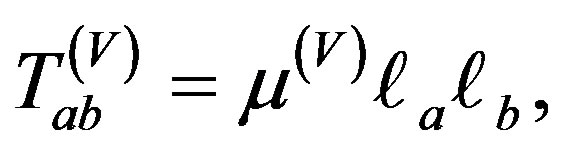(2.12)

(2.13)

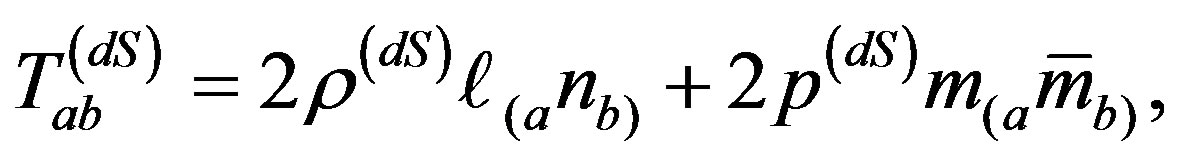(2.14)

with the coefficients

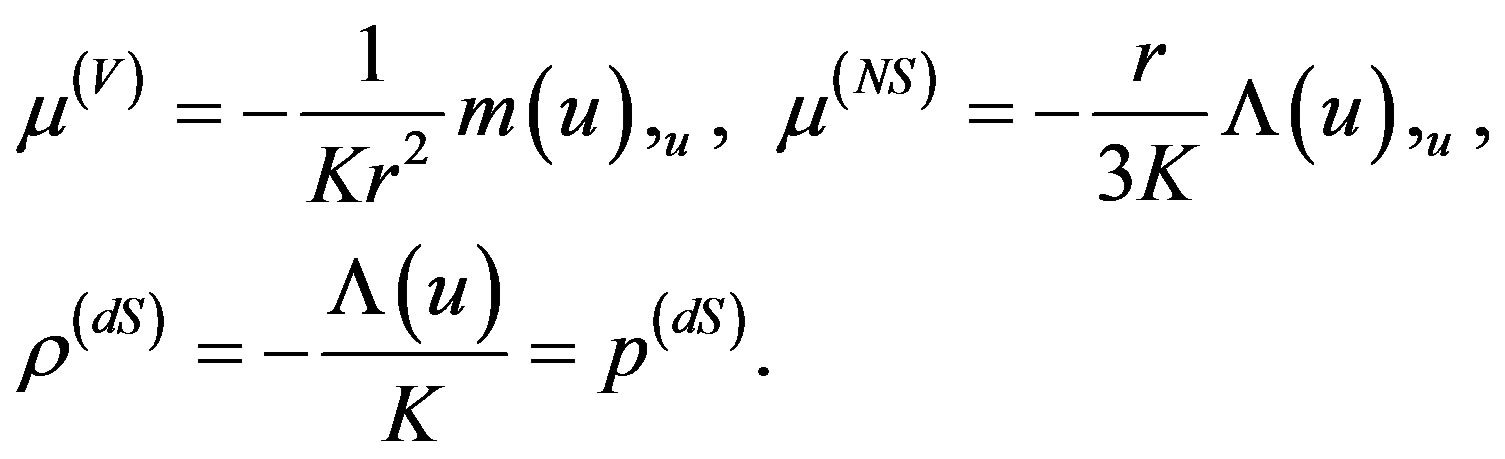(2.15)

Here 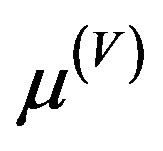is the null density for the Vaidya null fluid 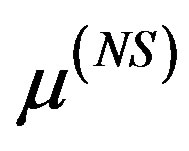the non-stationary null density associated with the derivative of Λ(u), and 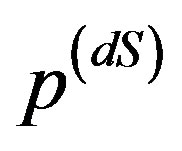are the density and the pressure of de Sitter matter. When the function Λ(u) becomes constant, it will provide

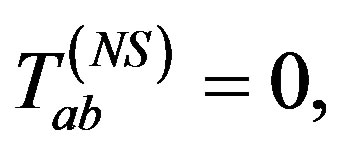then the space-time will be that of the Vaidya-de Sitter with constant Λ. If m(u) = 0,

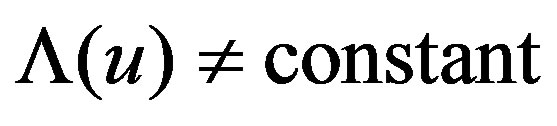we have 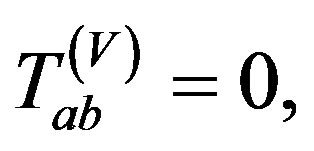then the remaining space-time (2.5) will be the non-stationary de Sitter model with variable Λ(u) [6]. At that time the EMTs and 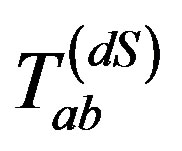will exist indicating the non-stationary de Sitter matter distribution; and for constant Λ, 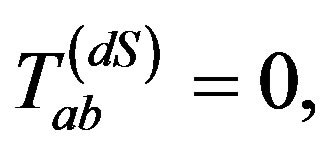then the total energy-momentum tensor (2.11) will reduce to 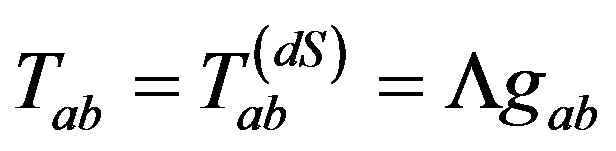for the well-known de Sitter model with constant Λ.

Here, it is interesting to mention that the energy-momentum tensor (2.7) does not satisfy the strong energy condition T_abU^aU^b ≥ (1/2)T, which is equivalent to

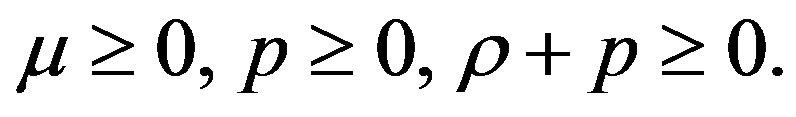(2.16)

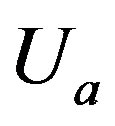is a time-like vector field for an observer in the Vaidya-de Sitter metric. This violation of the strong energy condition is due to the negative pressure in (2.8), and may lead to a repulsive gravitational force of the matter field in the space-time (2.5). The violation of the strong energy condition indicates various properties of the energy-momentum tensor (2.7) or (2.11) which are different from those of the ordinary matter fields, like perfect fluid, electromagnetic field etc., having positive pressures. In particular, it is worth to note that this strong energy condition is satisfied by the energy-momentum tensor of electromagnetic field with 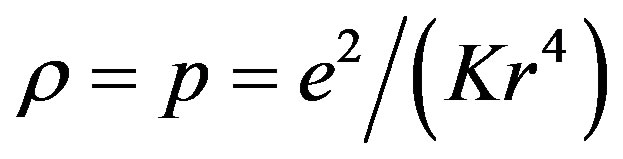of Reissner-Nordstrom space-time. It is also to note that the energy-momentum tensor (2.11) may be written in the form of Guth’s modification of [15] for early inflation of the universe as

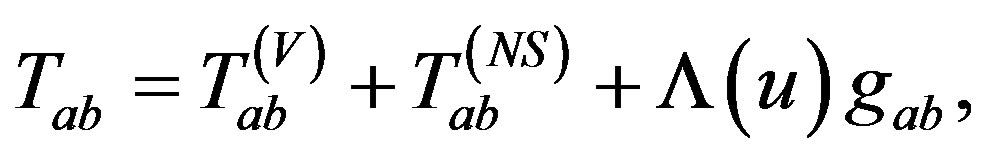(2.17)

where 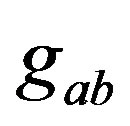is the Vaidya-de Sitter metric. This equation shows the possibility of the inflation of radiating Vaidya space in the non-stationary de Sitter space with cosmological variable Λ(u).

Here we shall justify the nature of the embedded solution in the form of Kerr-Schild ansatze in different backgrounds. The Vaidya-de Sitter metric can be expressed in Kerr-Schild ansatz

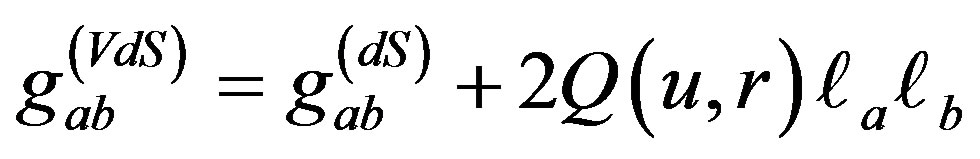(2.18)

where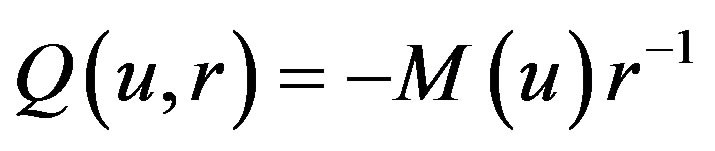. Here, is the nonstationary de Sitter metric given in [6] and 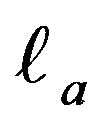is geodesic, shear free, expanding and zero twist null vector for both as well as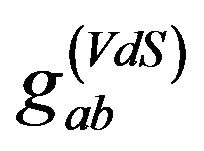. The above Kerr-Schild form can also be recast on the Vaidya background as

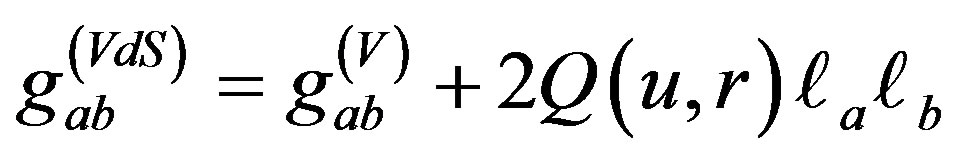(2.19)

where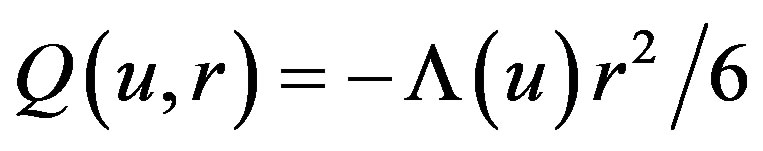. These two Kerr-Schild forms (2.18) and (2.19) support the fact that the nonstationary Vaidya-de Sitter space-time (2.5) with variable Λ(u) is a solution of Einstein’s field equations. They establish the structure of embedded black hole that either “the null radiating Vaidya black hole is embedded into the non-stationary de Sitter cosmological universe to produce Vaidya-de Sitter black hole” or the non-stationary de Sitter universe is embedded into the Vaidya black hole to obtain the de Sitter-Vaidya black hole— both nomenclature possess the same geometrical meaning. That is, we cannot physically predict which space started first to embed into another. When the cosmological function Λ(u) takes a constant value Λ, the line element (2.5) will reduce to the Vaidya-de Sitter black hole [4]. If one sets M(u) and Λ(u) both constant, the metric (2.5) becomes the stationary Schwarzschild-de Sitter black hole.

Surface gravity: The metric (2.5) will describe a cosmological black hole with the horizons at the values of r for which the polynomial equation

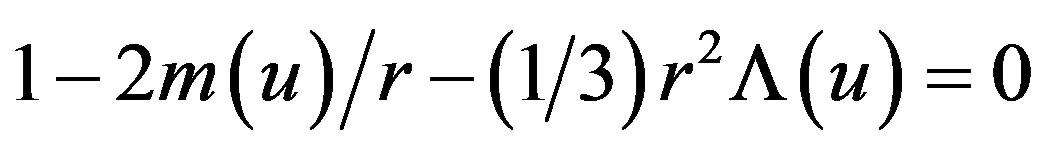has three roots 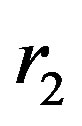and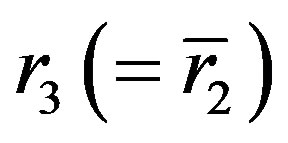. The explicit roots are given as

(2.20)

where

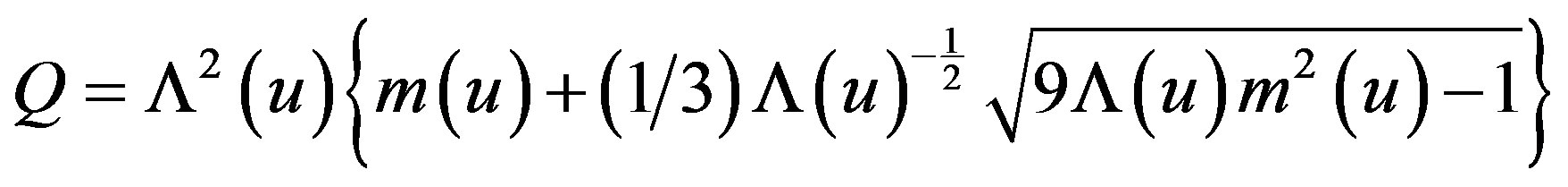(2.21)

These roots satisfy the following relation

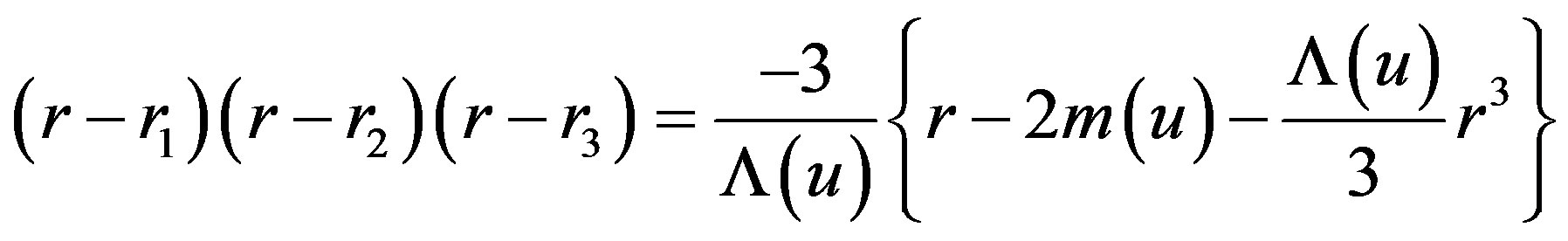(2.22)

Here we are interested only the real root r₁ which may describe the horizon of the Vaidya-de Sitter cosmological black hole, as the complex roots have less physical interpretation.

The surface gravity 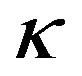of a horizon is defined by the Relation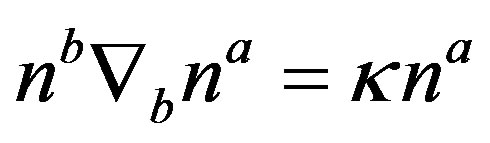, where the null vector n^a is parameterized by the coordinate u, such that [16,17]. 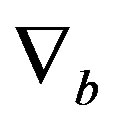is the covariant derivative. The surface gravities at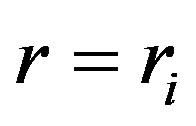, (i = 1, 2, 3) are found as

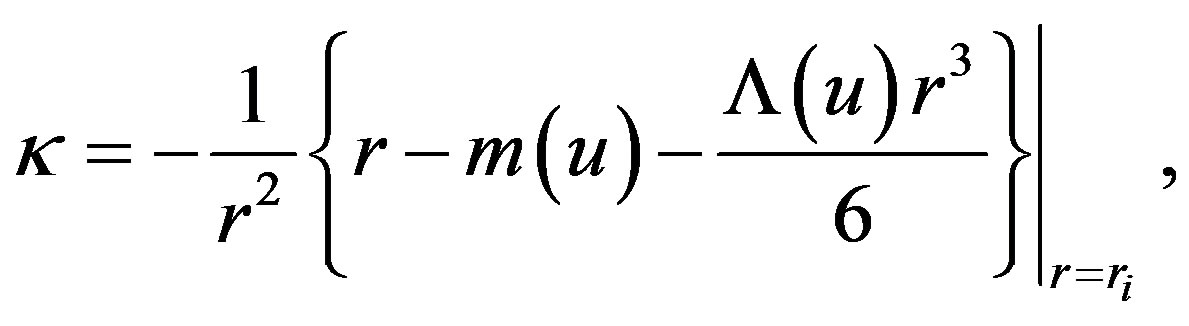(2.23)

and the entropy of the horizon is found as,

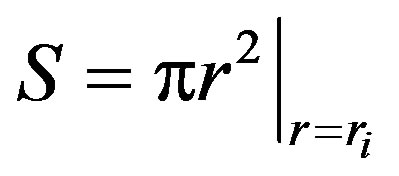(2.24)

Here we consider a case of extreme Vaidya-de Sitter black hole having the mass function

if. This implies that the real root r₁ take the values 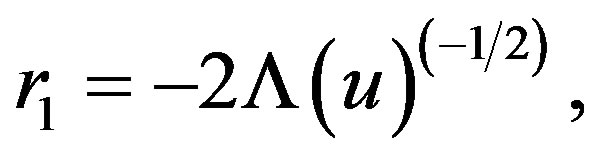and the two complex roots are coincided:

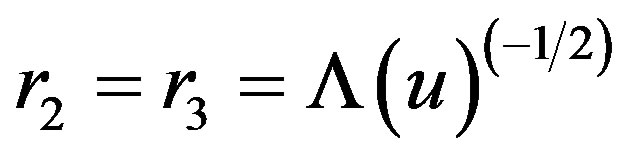. The surface gravity on the cosmological black hole horizon 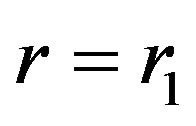takes the form

(2.25)

However, it is vanished at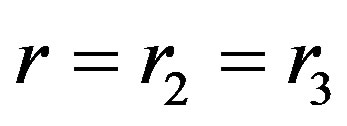. Then we obtain the Hawking’s temperature of the cosmological black hole horizon at 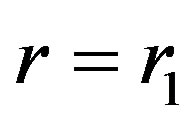from the relation T = κ/2π as

(2.26)

The temperature associated with the real root r₁ in (2.20) will never vanish as long as the de Sitter Λ(u) exists in the space-time geometry of the Vaidya-de Sitter black hole. The condition

of the Vaidya mass m(u) is the non-stationary generalization of the condition 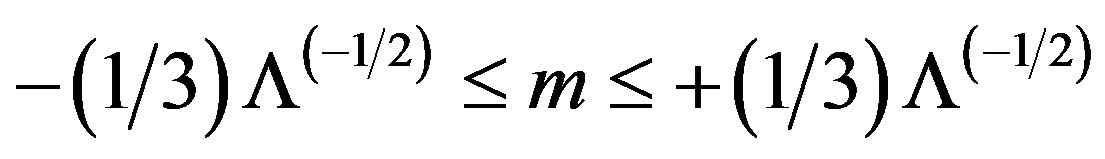of the Schwarzschild-de Sitter black hole with constant mass and Λ [2].

Properties of the time-like vector: The physical properties of the space-time geometry is determined by the motion of a matter field distribution (2.7) whose the time like vector field is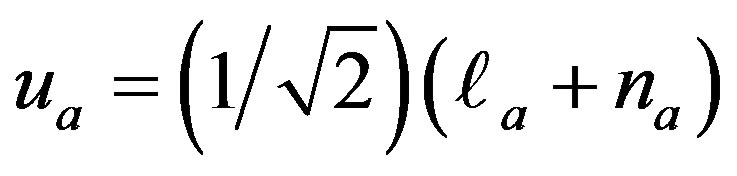. The four velocity vector 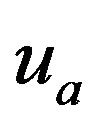measures the kinematical properties of a fluid expansion acceleration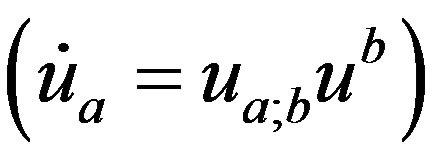, shear and twist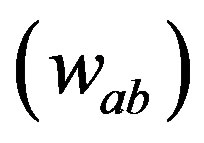. It is found that the fluid flow of the Vaidya-de Sitter model having variable Λ(u) is expanding 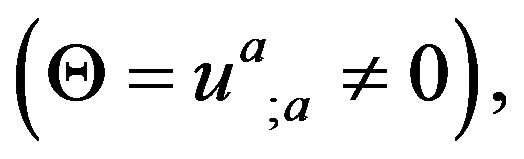accelerating shearing 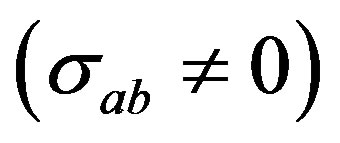and zero twist.

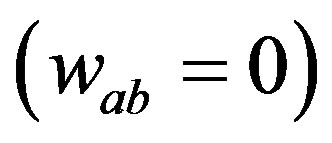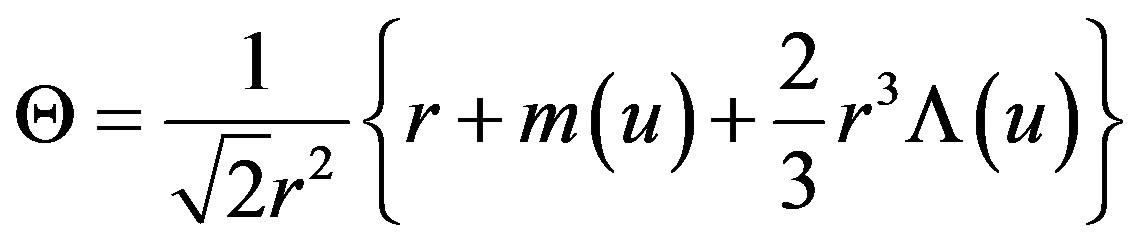(2.27)

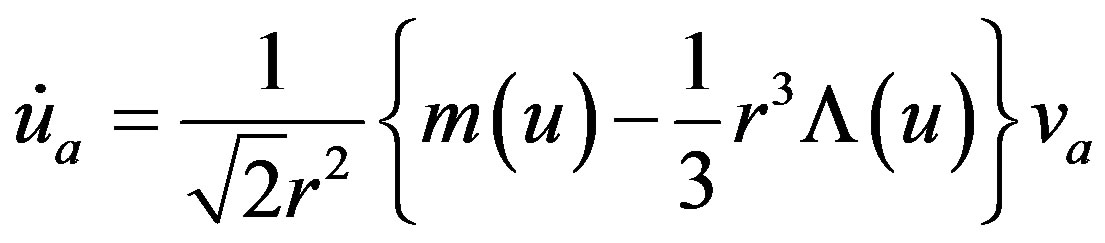(2.28)

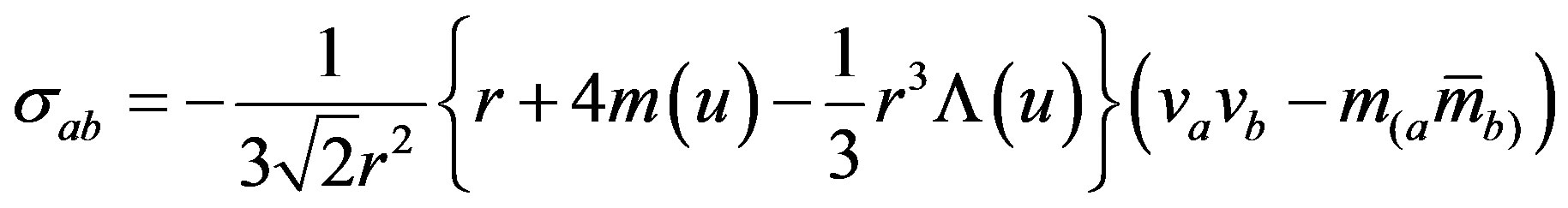(2.29)

where is a space-like vector field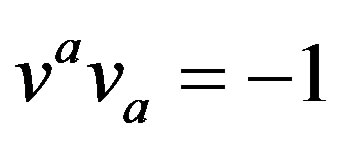. From these we observe that both the mass m(u) and the variable Λ(u) do appear in all the three equations. When m(u) = 0, the remaining equations will be for non-stationary de Sitter space, whereas, if Λ(u) = 0, these will be for Vaidya radiating black hole. This means that the time-like observer in the Vaidya space will have a four velocity vector field which is expanding, accelerating, shearing but zero-twist. This is also true for the observer in non-stationary de Sitter space, when m(u) = 0.

The Vaidya-de Sitter metric (2.5) describes a non-stationary embedded spherically symmetric solution whose Weyl curvature tensor is type D

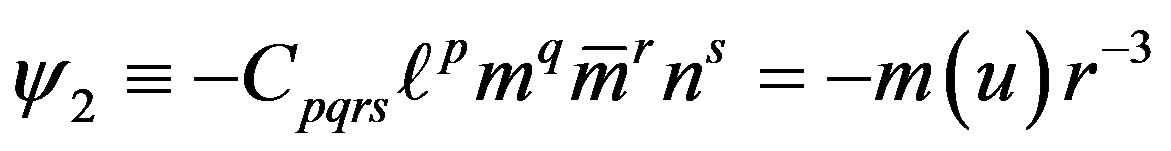(2.30)

in Petrov classification possessing a geodesic, shear free, expanding and zero-twist null vector ℓ_a given in (2.6), as other Weyl scalars are vanished ψ₀ = ψ₁ = ψ₃ = ψ₄ = 0. The Kretschmann scalar for non-rotating Vaidya-de Sitter model (2.5) takes the form

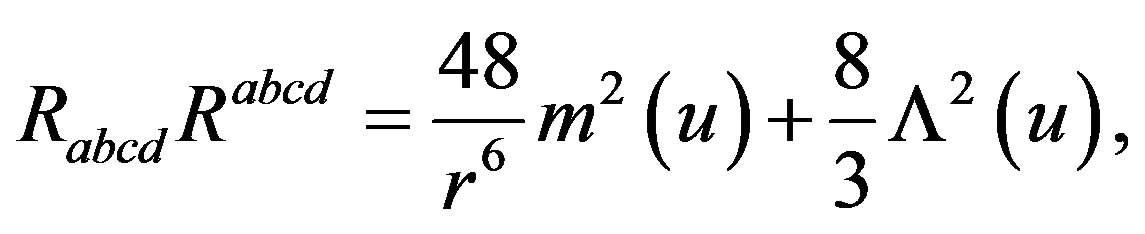(2.31)

which does not involve any derivative term of m(u) and Λ(u), and will not change its form when the mass m(u) and the variable Λ(u) take the constant values. With these constant values the Kretschmann scalar will reduce to that of Schwarzschild-de Sitter solution. This invariant does not diverge at the origin r → 0.

3. Conclusions

We present an exact solution of Einstein field equations for the radiating Vaidya solution embedded in the nonstationary de Sitter background with variable Λ(u) [6]. This solution may be regarded as a generalization of Vaidya-de Sitter solution with constant Λ [4]. The Vaidya-de Sitter solution with mass m(u) and constant Λ is also a generalized form of the Schwarzschild-de Sitter model with constant mass m and constant Λ. The Schwarzschild-de Sitter solution is interpreted as a black hole in asymptotically de Sitter space [3]. Thus, in this regard, our Vaidya-de Sitter solution with variable Λ(u) (2.5) may be interpreted as a black hole in asymptotically non-stationary de Sitter background. We also observe that in the extreme Vaidya-de Sitter black hole, the Vaidya mass m(u) has the limit 

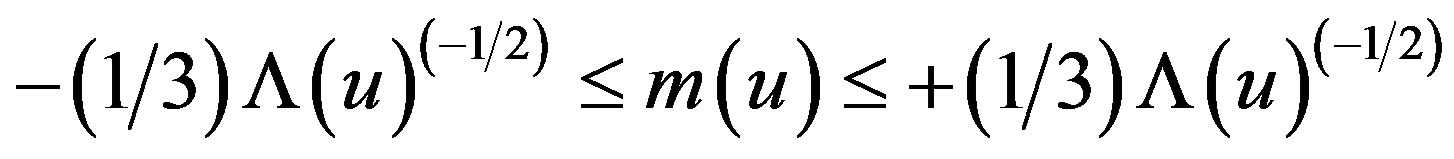
for Λ(u) > 0 as mentioned above. This range of the mass limit is a straightforward generalization of Schwarzschild de Sitter case 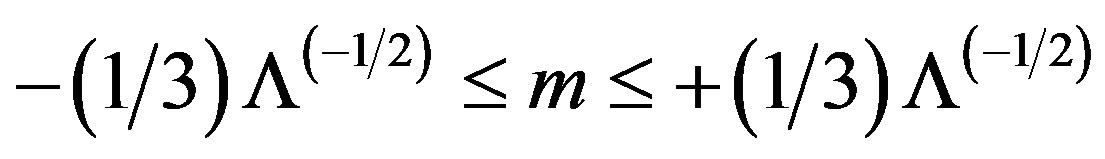associated with constant mass m and Λ(> 0).

We have also observed that the variable Λ(u) does not involve the Weyl scalar ψ₂, which shows the conformally flat property of de Sitter space with variable Λ(u) even in the embedded Vaidya-de Sitter solution (2.5). Also there is no involvement of Vaidya mass m(u) in the expressions of the pressure p and the density ρ (2.8) keeping the equation of state parameter w = p/ρ = −1 unaffected for the embedded solution. We have also seen that the 4-velocity vector u_a of the fluid flow of the Vaidya-de Sitter solution having variable Λ(u) is expanding accelerating, shearing 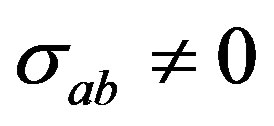and zero twist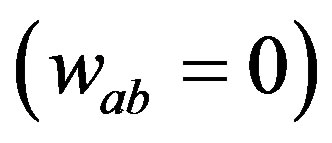. It is emphasized that the embedded Vaidya-de Sitter solution (2.5) discussed here includes the following solutions:

1) non-stationary de Sitter solution,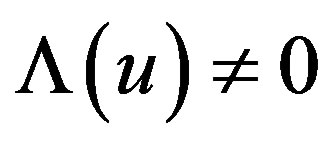

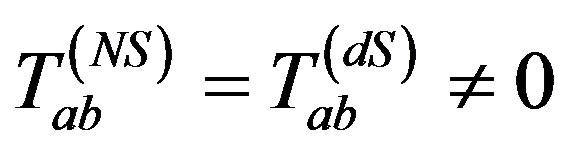when m(u) = 0, [6];

2) Vaidya solution, 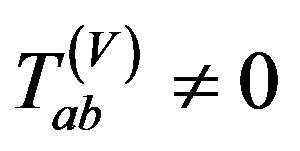when Λ(u) = 0, 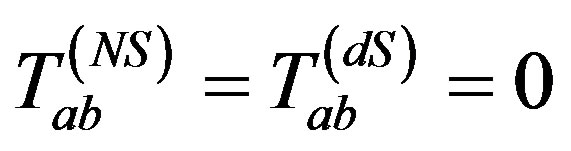[1];

3) Vaidya-de Sitter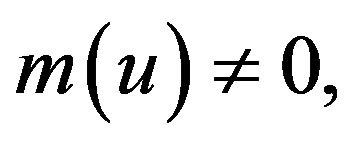

when Λ(u) becomes constant and [4];

4) Schwarzschild-de Sitter when m(u) and Λ(u) are constant with 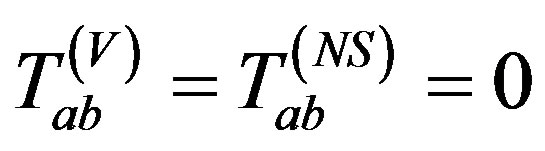[2];

5) de Sitter when m(u) = 0 and Λ(u) is a constant with 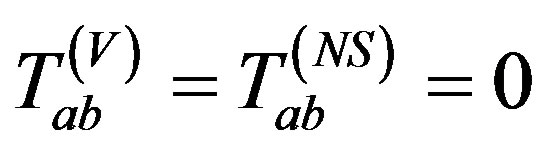[7].

It is noted that all known results with constant Λ may be extended with this variable Λ(u) of the Vaidya-de Sitter space-time.

4. Acknowledgements

The work of Ishwarchandra is supported by the University Grants Commission (UGC), New Delhi, in the form of Rajiv Gandhi National Fellowship for SC/ST.

REFERENCES