International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43662,11 pages DOI:10.4236/ijaa.2014.41017
Bianchi Type-IX Magnetized Dark Energy Model in Saez-Ballester Theory of Gravitation
H. R. Ghate, Atish S. Sontakke
Department of Mathematics, Jijamata Mahaidyalaya, Buldana, India
Email: hrghate@gmail.com, atishsontakke@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 August 2013; revised 16 September 2013; accepted 24 September 2013
ABSTRACT
The Bianchi type-IX cosmological model with variable ω has been studied in the scalar tensor theory of gravitation proposed by Saez and Ballester [Phys. Lett. A 113: 467, 1985] in the presence and absence of magnetic field of energy density ρb. A special law of variation of Hubble’s parameter proposed by Berman [Nuovo Cimento 74 B, 182, 1983] has been used to solve the field equations. The physical and kinematical properties of the model are also discussed.
Keywords:Dark Energy; Magnetic Field; Bianchi Type-IX Universe; Scalar-Tensor Theory

1. Introduction
The recent observations of luminosity of type Ia Supernovae (SNe Ia) [1] -[8] indicate that the universe is currently undergoing an accelerated expansion. The dark energy (DE) with negative pressure is responsible for this scenario. Researchers have developed number of DE models of the universe in general relativity [9] [10] and also in different theories of gravitation [11] -[15] . These models have a lot of significance in theoretical study of the structure of the universe. It is considered that DE is to be the best candidate to explain cosmic acceleration. It is known from the history that our present universe consists of about 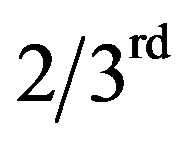 DE and about
DE and about  dark matter (DM) [16] [17] . DE is usually characterized by the EoS parameter defined by the equation of state
dark matter (DM) [16] [17] . DE is usually characterized by the EoS parameter defined by the equation of state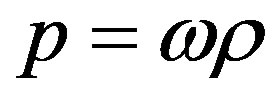 , where
, where 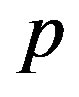 is the fluid pressure and
is the fluid pressure and  is energy density. Usually EoS parameter is assumed to be a constant with the values −1, 0, 1/3 and +1 for vacuum, dust, radiation and stiff matter dominated universe respectively. However, latest observations from SNe Ia data [18] -[20] indicate that
is energy density. Usually EoS parameter is assumed to be a constant with the values −1, 0, 1/3 and +1 for vacuum, dust, radiation and stiff matter dominated universe respectively. However, latest observations from SNe Ia data [18] -[20] indicate that  is not constant. Many authors [21] -[28] have obtained DE models in general relativity with variable EoS parameter.
is not constant. Many authors [21] -[28] have obtained DE models in general relativity with variable EoS parameter.
Magnetic field plays a vital role in the description of the energy distribution in the universe as it contains highly ionized matter. Strong magnetic fields can be created due to adiabatic compression in cluster of galaxies. Large scale magnetic fields give rise to anisotropies in the universe. The magnetic field has the significant role in the dynamics of the universe depending on the direction of the field lines [29] [30] . Many research works have studied the importance of magnetic field for various astrophysical phenomena. Misra and Radhakrishna [31] have obtained the analogous relation between some components of metric and electromagnetic potentials for source free Einstein-Maxwell field described by Einstein-Rosen metric. Thorne [32] , Jacobs [33] [34] , Collins [35] , Roy and Prakash [36] have investigated magnetized cosmological models for perfect fluid distributions in general relativity. Milaneschhi and Fabbri [37] studied the anisotropy and polarization properties of CMB radiations in homogeneous Bianchi type-I cosmological model. Roy et al. [38] investigated Bianchi type-I cosmological models containing perfect fluid and magnetic field directed along x-axis. Adhav et al. [39] have investigated Bianchi type-III model with DE from a wet dark fluid [WDF] in presence and absence of magnetic field in general theory of relativity. Katore et al. [40] have explored Einstein-Rosen cosmological model with magnetized anisotropic DE.
Bianchi type cosmological models are important in the sense that, these are homogeneous and anisotropic, from which the process of isotropization of the universe is studied through the passage of time. Moreover, from the theoretical point of view anisotropic universe has a greater generality than isotropic models. The simplicity of the field equations made Bianchi space-times useful in constructing models of spatially homogeneous and anisotropic cosmologies. Reddy et al. [41] have studied Bianchi-II, VIII and IX models in scale-covariant theory of gravitation. Chakraborty [42] , Raj Bali and Dave [43] , Raj Bali and Yadav [44] have studied Bianchi type-IX string as well as viscous fluid models in general relativity. Pradhan [45] has studied some homogeneous Bianchi type-IX viscous fluid cosmological models with varying . Tyagi et al. [46] have obtained Bianchi type-IX string cosmological models for perfect fluid distribution in general relativity. Rao et al. [47] have obtained Bianchi type-II, VIII and IX DE cosmological models in Saez-Ballester theory of gravitation. Recently, Ghate and Sontakke [48] -[50] have studied Bianchi type-IX cosmological model with anisotropic DE in Lyra geometry, model with binary mixture of perfect fluid and dark energy and DE model in a Brans-Dicke theory of gravitation repectively.
. Tyagi et al. [46] have obtained Bianchi type-IX string cosmological models for perfect fluid distribution in general relativity. Rao et al. [47] have obtained Bianchi type-II, VIII and IX DE cosmological models in Saez-Ballester theory of gravitation. Recently, Ghate and Sontakke [48] -[50] have studied Bianchi type-IX cosmological model with anisotropic DE in Lyra geometry, model with binary mixture of perfect fluid and dark energy and DE model in a Brans-Dicke theory of gravitation repectively.
In the last few decades, alternative theories to Einstein’s theory of gravitation have developed mainly scalar tensor theories proposed by Brans and Dicke [51] , Nordtvedt [52] , Wagoner [53] , Ross [54] , Dun [55] , Saez and Ballester [56] , Barber [57] and La & Steinhardt [58] . Among them Brans-Dicke and Saez-Ballester theories are considered to be viable alternatives to general relativity. Brans-Dicke theory includes a long range scalar field interacting equally with all forms of matter (with the exception of electromagnetism) while in Saez-Ballester theory, metric is coupled with a dimensionless scalar field in a simple manner. This coupling gives satisfactory description of weak fields. This theory suggests a possible way to solve the missing-matter problem in non-flat FRW cosmologies. In earlier literature, cosmological models in Saez-Ballester theory of gravitation have been studied by Singh and Agrawal [59] , Shri Ram and Tiwari [60] , Singh and Shri Ram [61] . In recent years, Reddy and Naidu [62] , Adhav et al. [63] , Katore et al. [64] Pradhan and Singh [65] are some of the authors who have obtained the solutions in Saez-Ballester theory in different contexts.
In this paper, we have studied the solutions of Bianchi type-IX universe with variable 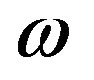 in Saez-Ballester theory of gravitation in the presence and absence of magnetic field of energy density
in Saez-Ballester theory of gravitation in the presence and absence of magnetic field of energy density 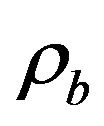 together with constant deceleration parameter. A special law of variation of Hubble’s parameter proposed by Berman [66] is used to solve the field equations. The physical and kinematical properties of the model are also discussed. The out-line of the paper is as follows: In section 2, the model and field equations are described. The solution of field equations are presented in section 3 and section 4 concludes the findings.
together with constant deceleration parameter. A special law of variation of Hubble’s parameter proposed by Berman [66] is used to solve the field equations. The physical and kinematical properties of the model are also discussed. The out-line of the paper is as follows: In section 2, the model and field equations are described. The solution of field equations are presented in section 3 and section 4 concludes the findings.
2. Field Equations
Bianchi type-IX metric is considered in the form
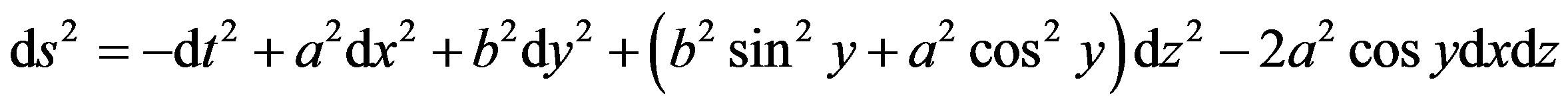 (1)
(1)
where 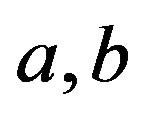 are scale factors and are functions of cosmic time
are scale factors and are functions of cosmic time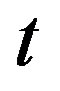 .
.
The model has one transverse direction  and two equivalent longitudinal directions
and two equivalent longitudinal directions  and
and .
.
The field equations in Saez-Ballester theory of gravitation are
 (2)
(2)
and the scalar field satisfies the equation
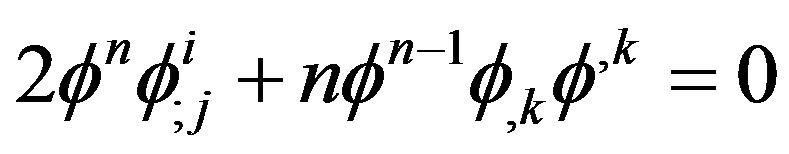 , (3)
, (3)
where 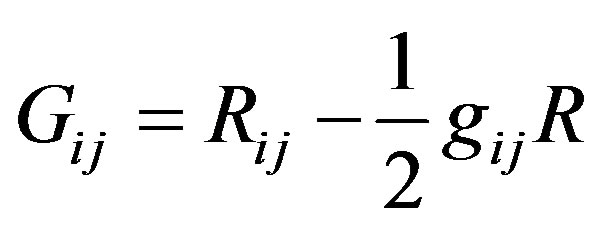 is the Einstein tensor, R is the scalar curvature,
is the Einstein tensor, R is the scalar curvature,  and n are constants,
and n are constants,  is the stress tensor of matter,
is the stress tensor of matter, 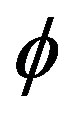 is a dimensionless coupling constant; comma and semicolon denote partial and covariant differentiation respectively.
is a dimensionless coupling constant; comma and semicolon denote partial and covariant differentiation respectively.
Also, we have energy-conservation equation
 , (4)
, (4)
is a consequence of the field equations.
King and Coles [30] and Jacobs [34] used the magnetized perfect fluid energy momentum tensor to discuss the effects of magnetic field on the evolution of the universe filled with perfect fluid.
The energy-momentum tensor for the magnetized anisotropic DE fluid is in the form
 , (5)
, (5)
where 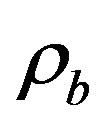 is the energy density of magnetic fluid,
is the energy density of magnetic fluid,  is the energy density of the fluid and
is the energy density of the fluid and ,
, 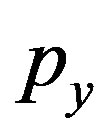 ,
,  are pressures on x, y, z axes respectively.
are pressures on x, y, z axes respectively.
The equation of state for an anisotropic fluid is taken of the form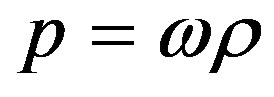 , where
, where  is not necessarily constant (Carroll et al. [67] );
is not necessarily constant (Carroll et al. [67] );
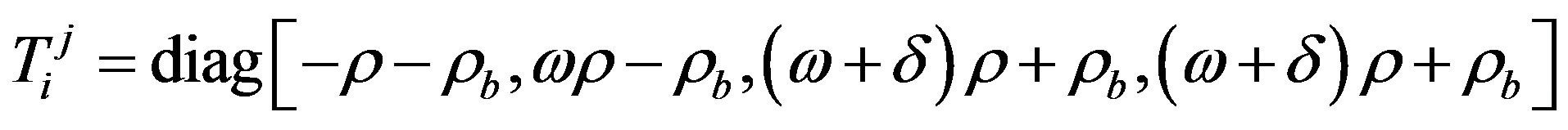 . (6)
. (6)
Here  is the deviation free parameter.
is the deviation free parameter. ,
, 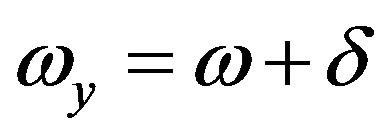 ,
, 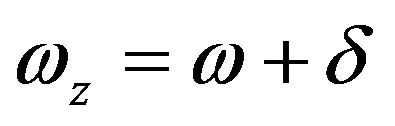 are the directional EoS parameters on
are the directional EoS parameters on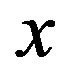 ,
, 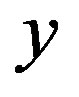 ,
,  axes respectively.
axes respectively.
For Bianchi type-IX metric, using Equation (6), the field Equations (2) and (3) takes the form
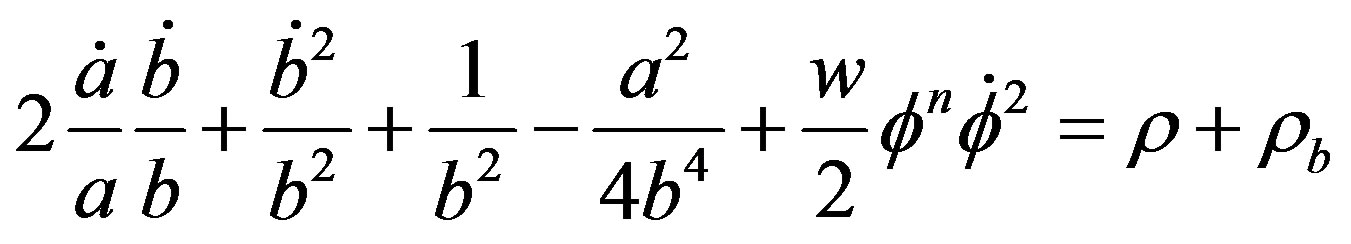 (7)
(7)
 (8)
(8)
 (9)
(9)
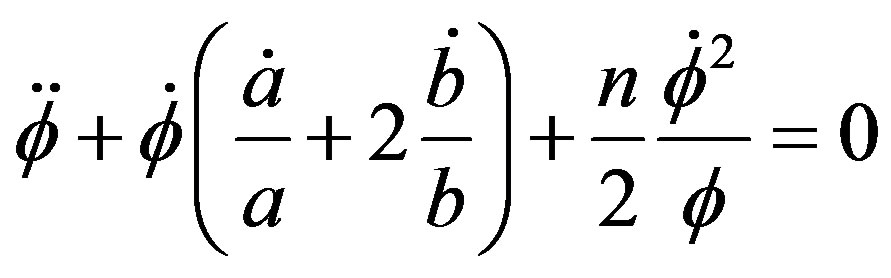 , (10)
, (10)
where over dot  denotes the differentiation with respect to
denotes the differentiation with respect to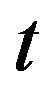 .
.
We have the following equation from the Bianchi identity:
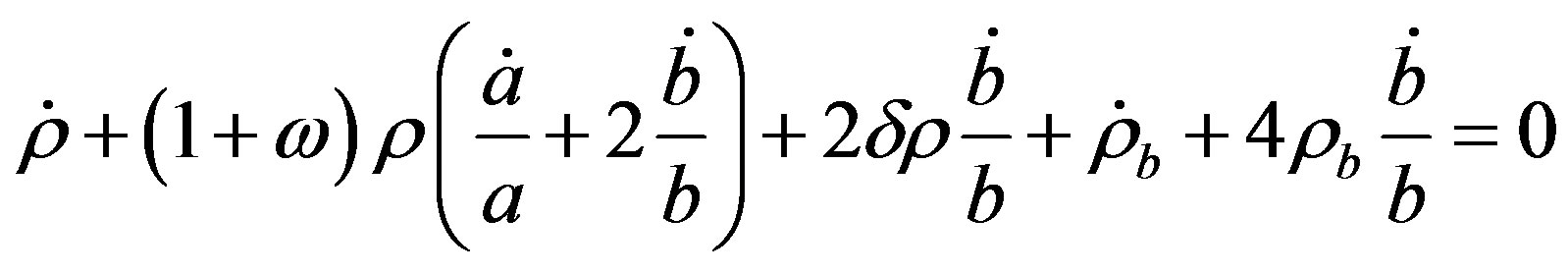 . (11)
. (11)
3. Solution of the Field Equations
The field Equations (7)-(10) are a system of four equations with six unknown parameters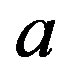 ,
, 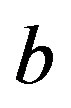 ,
, 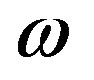 ,
, 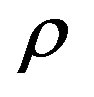 ,
, 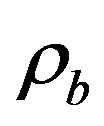 and
and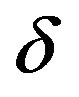 . The system is thus initially undetermined and we need additional constraints to obtain the solution of field equations.
. The system is thus initially undetermined and we need additional constraints to obtain the solution of field equations.
We assumed that the magnetized DE is minimally interacting, hence the Bianchi identity has been split into two separately additive conserved components namely, the conservation of the energy-momentum tensor for the anisotropic fluid and for the magnetic field (King and Coles [30] ).
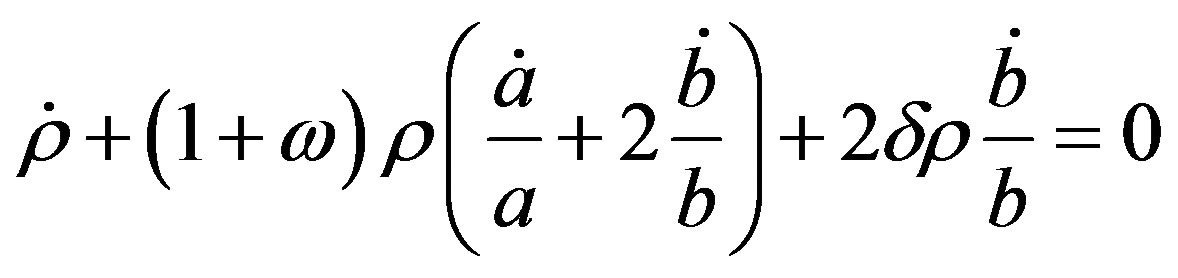 . (12)
. (12)
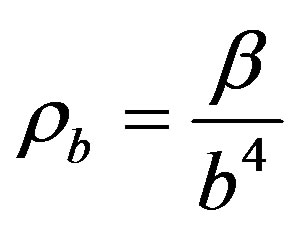 . (13)
. (13)
Finally, we constrain the system of equations with a law of variation for the average Hubble’s parameter that yields a constant value of deceleration parameter. Such types of relation have already been considered by Berman [66] , Berman and Gomide [68] for solving FRW models. Later on many authors (Singh et al. [69] -[71] , Singh and Baghel [72] ) have studied flat FRW and Bianchi type models by using the special law of Hubble parameter that yields constant value of deceleration parameter.
The average scale factor R of Bianchi type-IX metric is given by
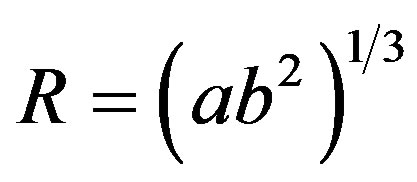 . (14)
. (14)
The proper volume V is defined by
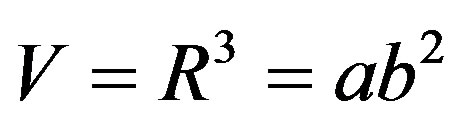 . (15)
. (15)
We defined the generalized mean Hubble’s parameter H as
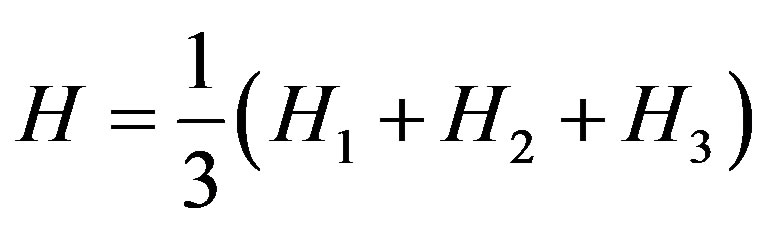 , (16)
, (16)
where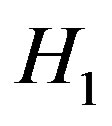 ,
,  and
and  are the directional Hubble parameters in the direction of x, y, z axes respectively.
are the directional Hubble parameters in the direction of x, y, z axes respectively.
From Equations (14) and (16), we obtain
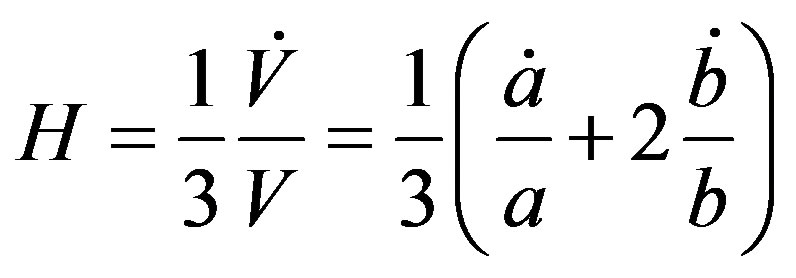 . (17)
. (17)
Since, the line element (1) is completely characterized by Hubble’s parameter H. Therefore, let us consider that, the mean Hubble parameter H is related to the average scale factor by the relation
 , (18)
, (18)
where  and
and  are constants.
are constants.
An important observational quantity is the deceleration parameter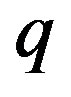 , which is defined as
, which is defined as
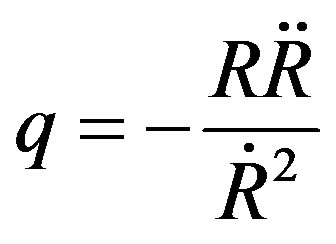 . (19)
. (19)
From Equations (17) and (18), we obtain
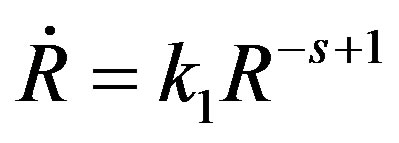 (20)
(20)
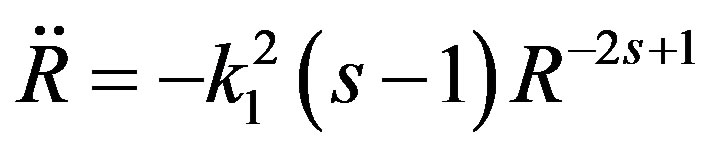 . (21)
. (21)
From Equations (19), (20), (21) we get constant value for the deceleration parameter for the mean scale factor as
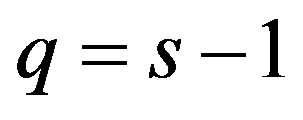 , for
, for
 (22)
(22)
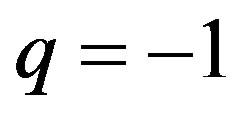 , for
, for
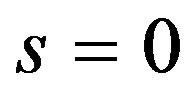 (23)
(23)
The sign of 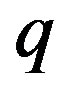 indicates whether the model accelerates or not. The positive sign of
indicates whether the model accelerates or not. The positive sign of  (i.e.
(i.e. ) corresponds to decelerating models whereas the negative sign of
) corresponds to decelerating models whereas the negative sign of  for
for  indicates acceleration and
indicates acceleration and  for
for 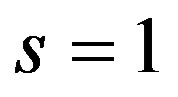 corresponds to expansion with constant velocity.
corresponds to expansion with constant velocity.
Using, Equation (20), we obtain the law of average scale factor as
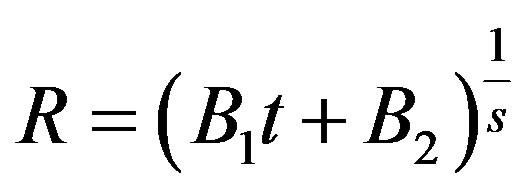 , for
, for
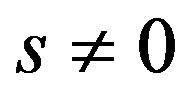 (24)
(24)
 . for
. for
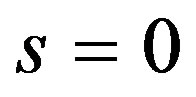 (25)
(25)
where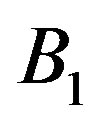 ,
, 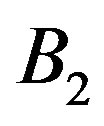 and
and 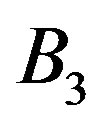 are constants of integration.
are constants of integration.
Case (i): Model for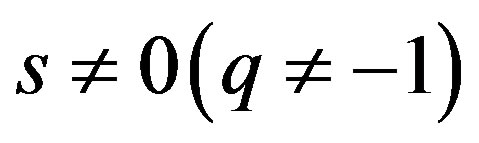 : We consider that, the scalar expansion for
: We consider that, the scalar expansion for  is proportional to the shear scalar for
is proportional to the shear scalar for  i.e.
i.e.  which leads to
which leads to
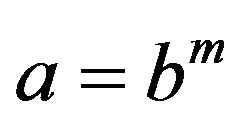 , (26)
, (26)
where m is a positive constant.
From Equations (14) and (24), we get
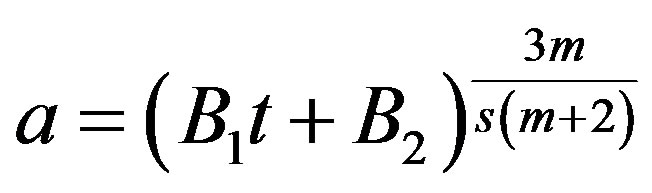 , (27)
, (27)
 . (28)
. (28)
Thus, the Bianchi type-IX magnetized anisotropic DE model in Saez-Ballester scalar-tensor theory can be written as
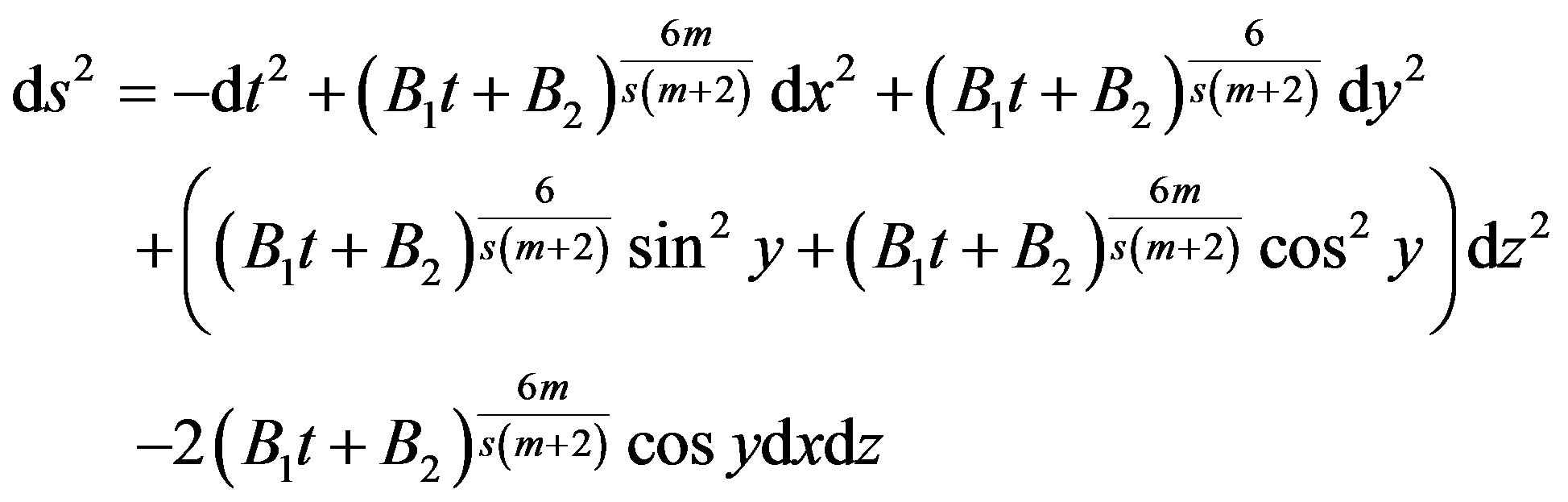 (29)
(29)
The average Hubble’s parameter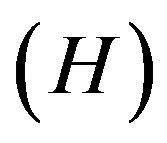 , expansion scalar
, expansion scalar , anisotropic parameter of the expansion
, anisotropic parameter of the expansion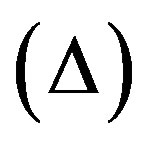 , shear scalar
, shear scalar 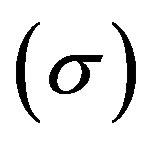 for the model (29) are given by
for the model (29) are given by
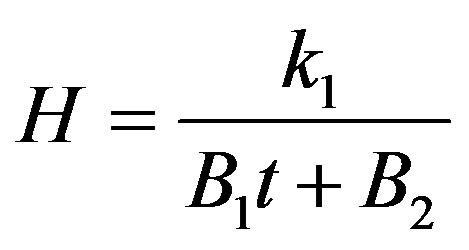 , (30)
, (30)
 , (31)
, (31)
 , (32)
, (32)
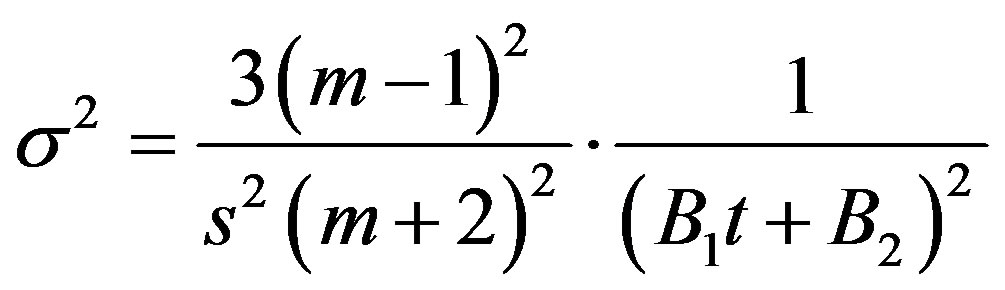 . (33)
. (33)
From Equations (31) and (33), we get
 . (34)
. (34)
Using Equations (13) and (27), we obtain
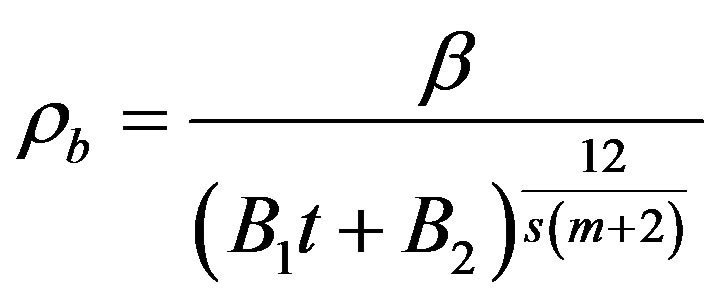 . (35)
. (35)
Using Equations (27) and (28), Equation (10) takes the form
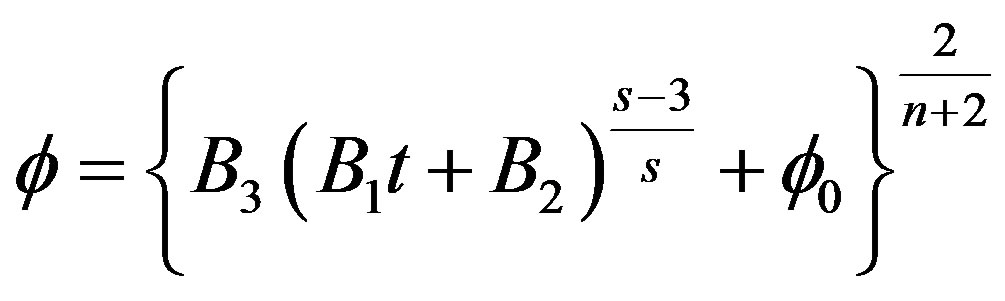 . (36)
. (36)
Using Equations (7), (27), (28), (35) and (36), we obtain energy density for fluid as
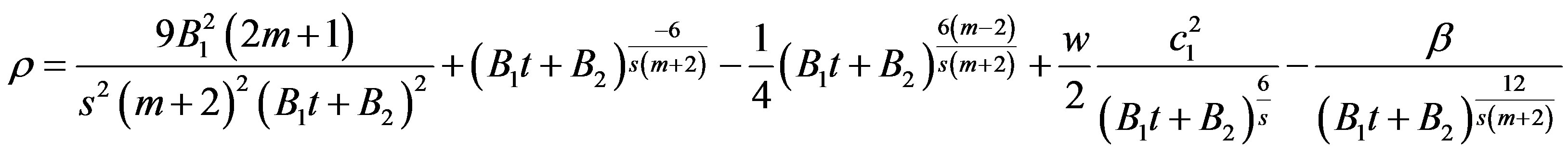 . (37)
. (37)
It is observed that the Hubble parameter , expansion scalar
, expansion scalar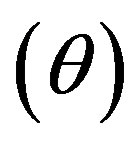 , mean anisotropic parameter of the expansion
, mean anisotropic parameter of the expansion , shear scalar
, shear scalar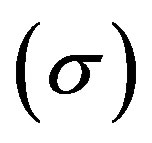 , magnetized DE density
, magnetized DE density 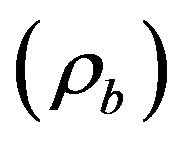 and energy density
and energy density 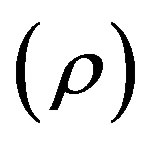 are decreasing functions of time and approaches to 0 as
are decreasing functions of time and approaches to 0 as .
.
Since,  constant
constant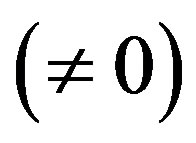 , the model is not isotropic for large values of t.
, the model is not isotropic for large values of t.
Using Equations (8), (27), (28), (35), (36) and (37), the equation of state parameter  is obtained as
is obtained as
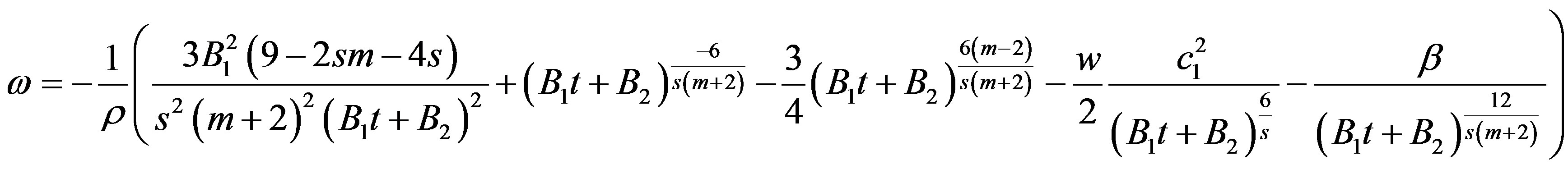 (38)
(38)
It is observed that the equation of state  is time dependent, it can be function of red shift
is time dependent, it can be function of red shift 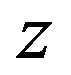 or scale factor R as well.
or scale factor R as well.
Using Equations (9), (27), (28), (35), (36) and (37), the skew-ness parameter  is given by
is given by
 (39)
(39)
In the absence of magnetic field i.e. , the values of the Hubble parameter
, the values of the Hubble parameter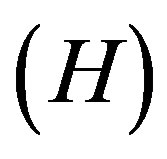 , expansion scalar
, expansion scalar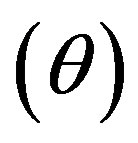 , mean anisotropic parameter of the expansion
, mean anisotropic parameter of the expansion , shear scalar
, shear scalar 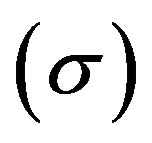 remains as it is whereas magnetized DE density
remains as it is whereas magnetized DE density 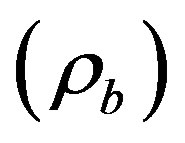 and energy density
and energy density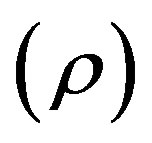 , the EoS parameter
, the EoS parameter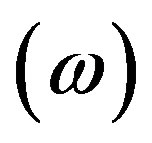 , and the skewness parameter
, and the skewness parameter  are given by
are given by
 . (40)
. (40)
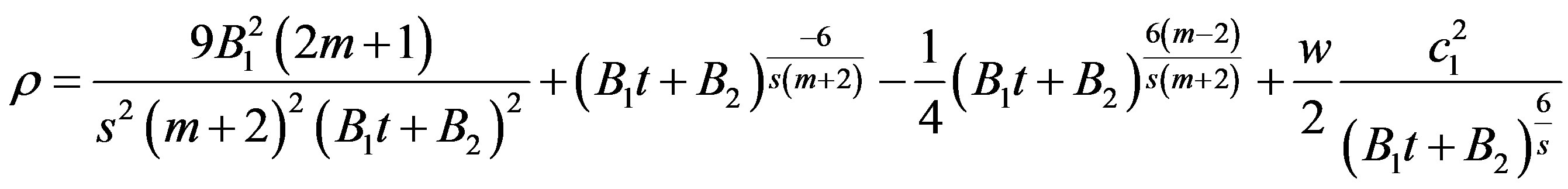 . (41)
. (41)
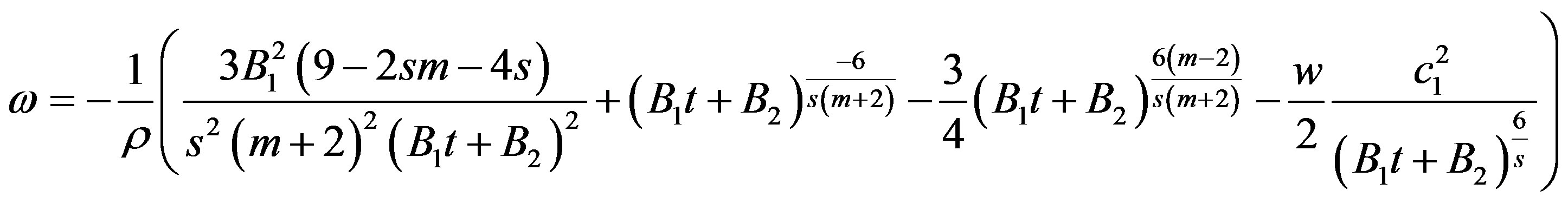 . (42)
. (42)
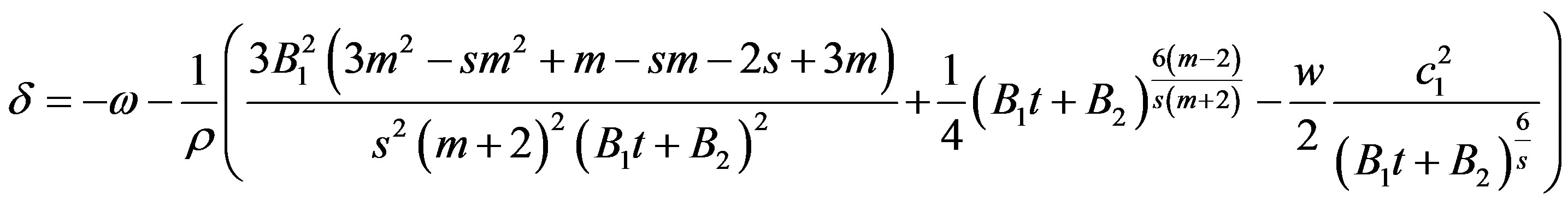 . (43)
. (43)
Case (ii): Model for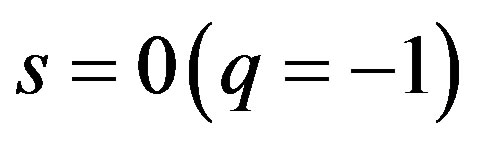 :
:
Using Equations (14) (25) and (26), we get
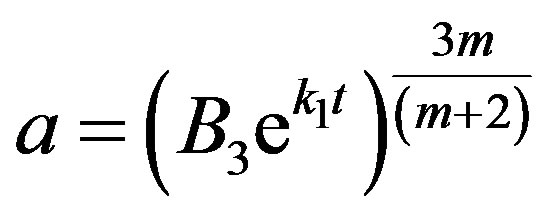 , (44)
, (44)
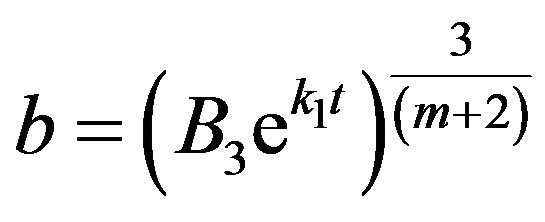 . (45)
. (45)
Thus, the Bianch Type-IX magnetized anisotropic DE model in Saez-Ballester scalar-tensor theory for  can be written as
can be written as
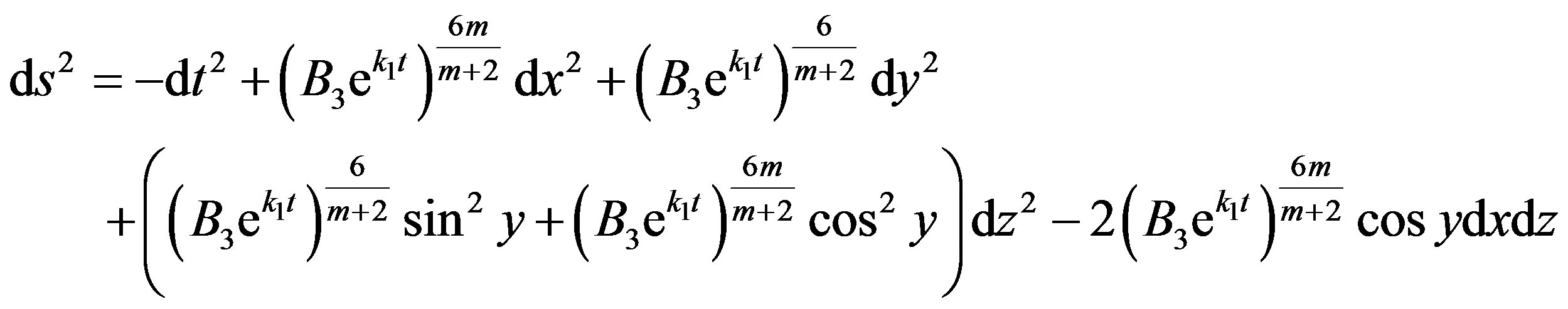 . (46)
. (46)
The expression for kinematical parameters i.e. the average Hubble’s parameter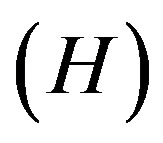 , expansion scalar
, expansion scalar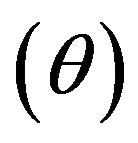 , anisotropic parameter of the expansion
, anisotropic parameter of the expansion , shear scalar
, shear scalar 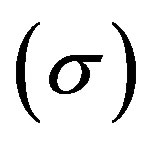 for the model (46) are given by
for the model (46) are given by
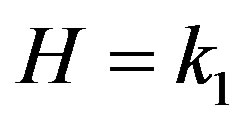 , (47)
, (47)
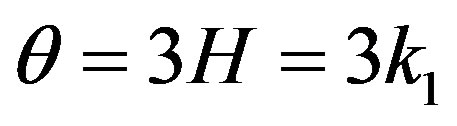 , (48)
, (48)
 , (49)
, (49)
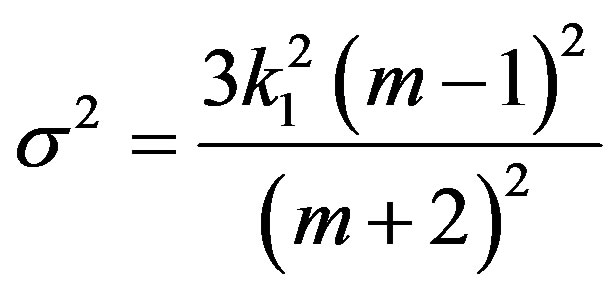 . (50)
. (50)
From Equations (48) and (49),
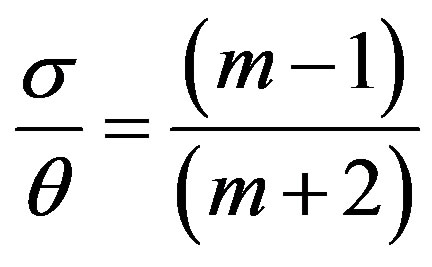 . (51)
. (51)
Using Equations (13) and (45), we obtain
 . (52)
. (52)
Using Equations (44) and (45), Equation (10) takes the form
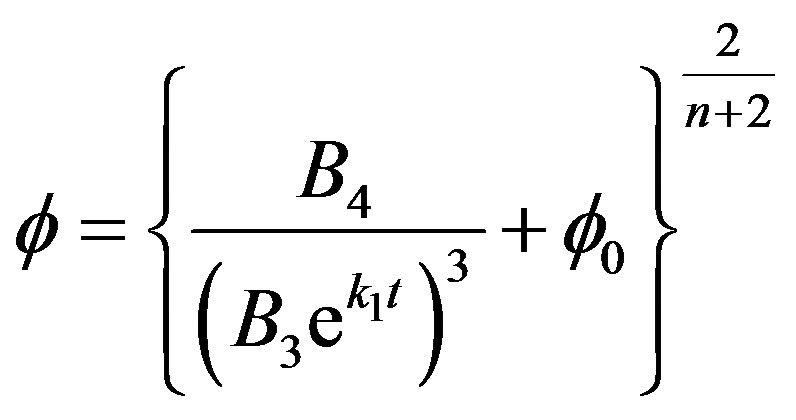 . (53)
. (53)
Using Equations (7), (44), (45), (52) and (53), we obtain energy density for fluid as
 . (54)
. (54)
It is observed that the Hubble parameter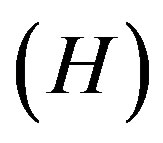 , expansion scalar
, expansion scalar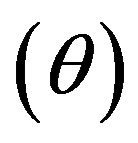 , mean anisotropic parameter of the expansion
, mean anisotropic parameter of the expansion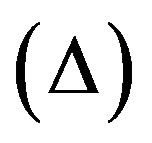 , shear scalar
, shear scalar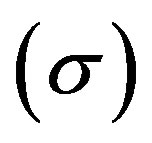 , magnetized DE density
, magnetized DE density 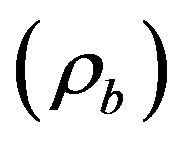 and energy density
and energy density 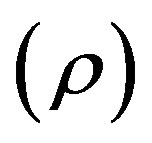 is decreasing function of time and approaches 0 as
is decreasing function of time and approaches 0 as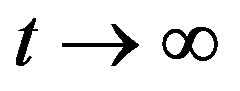 .
.
Since,  the model is not isotropic for large values of t.
the model is not isotropic for large values of t.
Using Equations (8), (44), (45), (52), (53) and (54), the equation of state parameter  is obtained as
is obtained as
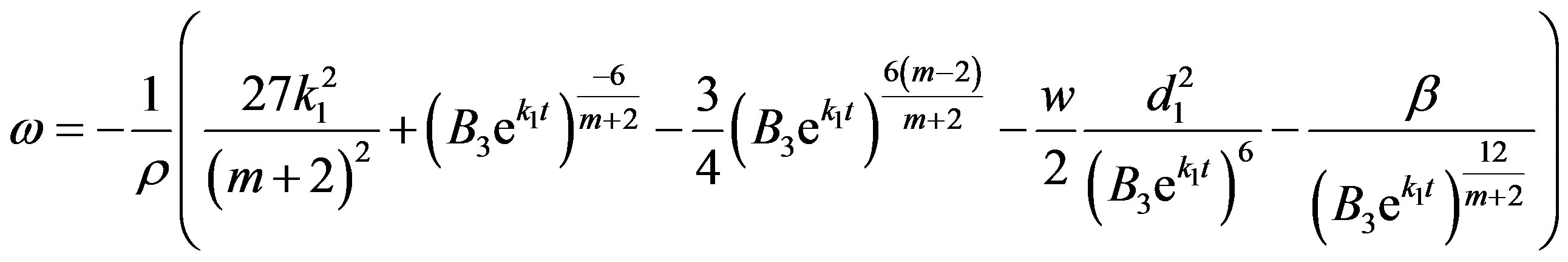 (55)
(55)
It is observed that the equation of state 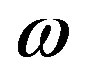 is time dependent, it can be function of red shift z or scale factor R as well.
is time dependent, it can be function of red shift z or scale factor R as well.
Using Equations (9), (44), (45), (52), (53) and (54), the skew-ness parameter 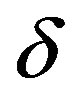 is given by
is given by
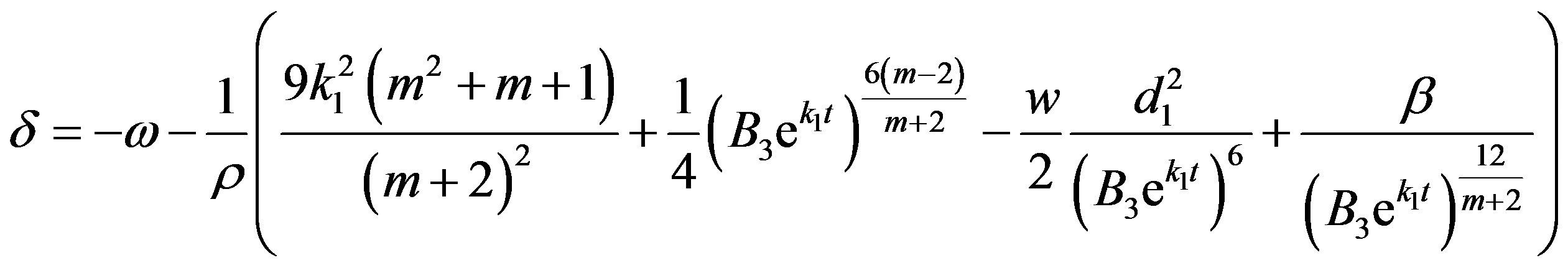 (56)
(56)
In the absence of magnetic field i.e.  , the values of the Hubble parameter
, the values of the Hubble parameter , expansion scalar
, expansion scalar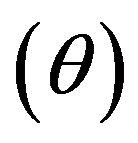 , mean anisotropic parameter of the expansion
, mean anisotropic parameter of the expansion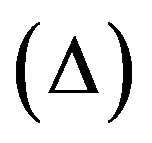 , shear scalar
, shear scalar 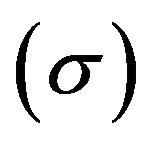 remains as it is whereas magnetized DE density
remains as it is whereas magnetized DE density 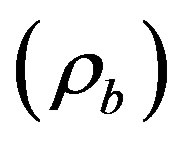 and energy density
and energy density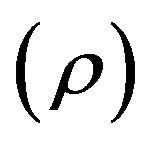 , the EoS parameter
, the EoS parameter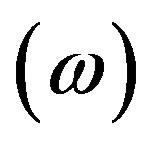 , and the skew-ness parameter
, and the skew-ness parameter 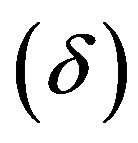 are given by
are given by
 . (57)
. (57)
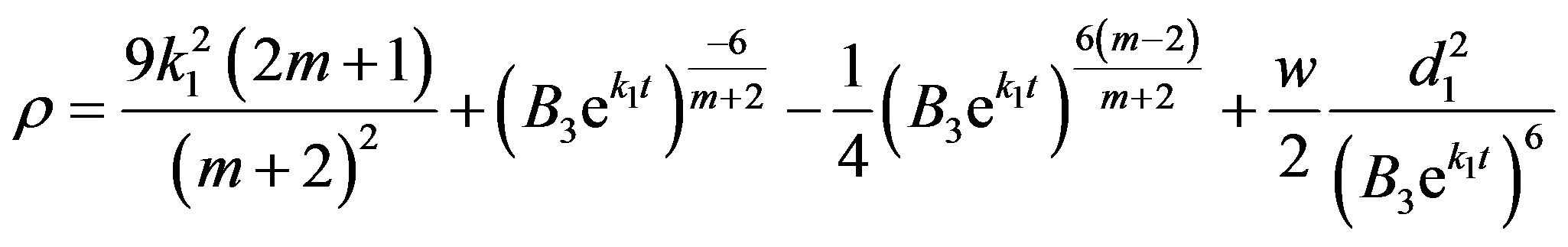 (58)
(58)
 . (59)
. (59)
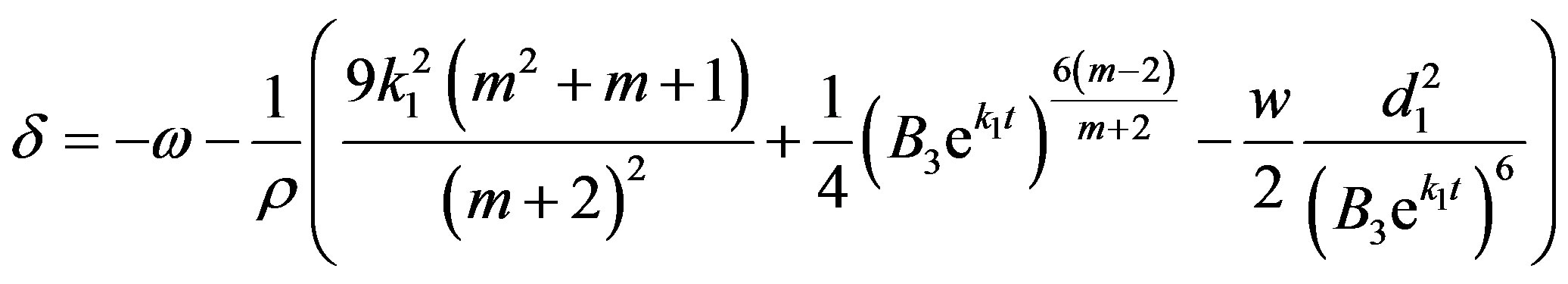 . (60)
. (60)
4. Conclusion
In this paper, we have obtained Bianchi type-IX cosmological model with variable EoS parameter  in Saez-Ballester theory of gravitation in the presence and absence of magnetic field of energy density
in Saez-Ballester theory of gravitation in the presence and absence of magnetic field of energy density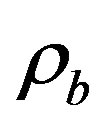 . In this model, the magnetic field used is as in King and Coles [30] . The solution of the field equations is obtained by using special law of variation for Hubble’s parameter proposed by Bermann [66] . We observed that, the model is free from big-bang singularity and the values of Hubble parameter, expansion scalar, shear scalar are constant at the initial epoch and decreases with time approaching to zero as
. In this model, the magnetic field used is as in King and Coles [30] . The solution of the field equations is obtained by using special law of variation for Hubble’s parameter proposed by Bermann [66] . We observed that, the model is free from big-bang singularity and the values of Hubble parameter, expansion scalar, shear scalar are constant at the initial epoch and decreases with time approaching to zero as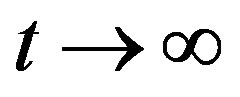 .
.  implies the model does not approach to isotropy i.e. the model is anisotropic throughout the evolution. The values of Hubble parameter, expansion scalar, mean anisotropic parameter of the expansion and the shear scalar remain same in the presence and absence of magnetic field while the component of magnetic field reduces energy density of the anisotropic fluid. It is noted that our investigations resemble with the investigations of Katore [40] .
implies the model does not approach to isotropy i.e. the model is anisotropic throughout the evolution. The values of Hubble parameter, expansion scalar, mean anisotropic parameter of the expansion and the shear scalar remain same in the presence and absence of magnetic field while the component of magnetic field reduces energy density of the anisotropic fluid. It is noted that our investigations resemble with the investigations of Katore [40] .
References
- Perlmutter, S., et al. (1997) Measurement of the cosmological parameters Ω and Λ from the first seven supernovae at z ≥ 0.35. The Astrophysical Journal, 483, 565. http://dx.doi.org/10.1086/304265
- Perlmutter, S., et al. (1998) Discovery of Supernovae Explosion at Half the Age of the Universe. Nature, 391, 51-54. http://dx.doi.org/10.1038/34124
- Perlmutter, S. et al. (1999) Measurement of and 42 high-Redshift Supernovae. The Astrophysical Journal, 517, 565- 586. http://dx.doi.org/10.1086/307221
- Reiss, A.G., et al. (1998) Observational Evidence from super-novae for an Accelerating Universe and a Cosmological Constant. The Astrophysical Journal, 116, 1009-1038.
- Riess, A.G., et al. (2004) Type Ia Supernova Discoveries at z >1 from the Hubble Space Telescope: Evidence for the Past Deceleration and Constraints on Dark Energy Evolution. The Astrophysical Journal, 607, 665-678. http://dx.doi.org/10.1086/383612
- Caldwell, R.R. and Doran, M. (2004) Cosmic Microwave Background and Supernova Constraints on Quintessence: Concordance Regions and Target Models. Physics Review D, 69, 103517. http://dx.doi.org/10.1103/PhysRevD.69.103517
- Huang, Z.Y., Wang, B. and Abdalla, E. (2006) Holographic Explanation of Wide-Angle Power Correlation Suppression in the Cosmic Microwave Background Radiation. Journal of Cosmology and Astroparticle Physics, 2006, 12.
- Daniel, S.F., Caldwell, R.R., Cooray, A. and Melchiorri, A. (2008) Large Scale Structure as a Probe of Gravitational Slip. Physics Review D, 77, 103513. http://dx.doi.org/10.1103/PhysRevD.77.103513
- Copeland, E.J., et al. (2006) Dynamics of Dark Energy. International Journal of Modern Physics D, 15, 1753. http://dx.doi.org/10.1142/S021827180600942X
- Padmanabhan, T. (2008) Dark Energy and Gravity. General Relativity, 40, 529-564. http://dx.doi.org/10.1007/s10714-007-0555-7
- Chandel, P.S., Singh, M.K. and Ram, S. (2012) Bianchi Type-VI Dark Energy Cosmological Model in General Relativity. Global Journal of Science Frontier Research Mathematics and Decision Sciences, 12, 83A05.
- Naidu, R.L., et al. (2012) Bianchi Type-III Dark Energy model in Saez-Ballester Scalar-Tensor Theory. International Journal of Theoretical Physics, 51, 2857-2862. http://dx.doi.org/10.1007/s10773-012-1161-3
- Katore, S.D. and Shaikkh, A.Y. (2012) Plane Symmetric Dark Energy model in Brans-Dicke Theory of Gravity. Bulgarian Journal of Physics, 39, 241-247.
- Katore, S.D. and Shaikkh, A.Y. (2012) Kantowaski-Sachs Dark Energy Model in f(R, T) Gravity. Prespacetime Journal, 3, 1087-1096.
- Ghate, H.R. and Sontakke, A.S. (2013) Bianchi Type-IX Dark Energy Model in Brans-Dicke Theory of Gravitation. Prespacetime Journal, 4, 366-376.
- Spergel, D.N., et al. (2007) Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology. The Astrophysical Journal Supplement Series, 170, 377. http://dx.doi.org/10.1086/513700
- Ratra, B. and Peebles, P.J.E. (2003) The Cosmological Constant and Dark Energy. Reviews of Modern Physics, 75, 559-606. http://dx.doi.org/10.1103/RevModPhys.75.559
- Knop, R.A., et al. (2003) New Constraints on Omega, Lambda and w from an Independent Set of Eleven HighRedshift Supernovae Observed HSTSupernova Cosmology Project Collaboration. Astrophysical Journal, 598, 102. http://dx.doi.org/10.1086/378560
- Tegmark, M., et al. (2004) Cosmological Parameters from SDSS and WMAP. Physics Review D, 69, 103501. http://dx.doi.org/10.1103/PhysRevD.69.103501
- Jimenez, R. (2003) The value of the equation of state of dark energy. New Astronomy Reviews, 47, 761-767. http://dx.doi.org/10.1016/j.newar.2003.07.004
- Sharif, M. and Zubair, M. (2010) Effects of Electromagnetic Field on the Dynamics of Bianchi type-VI0 Universe with Anisotropic Dark Energy. International Journal of Modern Physics D, 19, 1957-1972. http://dx.doi.org/10.1142/S0218271810018165
- Akarsu, O. and Kilinc, C. B. (2010) LRS Bianchi type I models with Anisotropic Dark Energy and Constant Deceleration Parameter. General Relativity and Gravitation, 42, 119-140. http://dx.doi.org/10.1007/s10714-009-0821-y
- Akarsu, O. and Kilinc, C.B. (2010) Bianchi Type-III Models with Anisotropic Dark Energy. General Relativity and Gravitation, 42, 763-775. http://dx.doi.org/10.1007/s10714-009-0878-7
- Rahaman, F., Bhui, B.C. and Bhui, B. (2006) Cosmological Model with a Viscous Fluid in a Kaluza-Klein Metric. Astrophysics and Space Science, 301, 47-49. http://dx.doi.org/10.1007/s10509-006-6304-7
- Usmani, A.A., Ghosh, P.P., Mukhopadhyay, U. and Ray, P.C. (2008) The Dark Energy Equation of State. Monthly Notices of the Royal Astronomical Society: Letters, 386, L92-L95. http://dx.doi.org/10.1111/j.1745-3933.2008.00468.x
- Ray, S., Rahaman, F., Mukhopadhyay, U. and Sarkar, R. (2011) Variable Equation of State for Generalized Dark Energy Model. International Journal of Theoretical Physics, 50, 2687-2696. http://dx.doi.org/10.1007/s10773-011-0766-2
- Pradhan, A., Amirhashchi, H. and Saha, B. (2011) Bianchi Type-I Anisotropic Dark Energy Model with Constant Deceleration Parameter. International Journal of Theoretical Physics, 50, 2923-2938. http://dx.doi.org/10.1007/s10773-011-0793-z
- Pradhan, A. Amirhashchi, H. and Saha, B. (2011) Dark Energy Model in Anisotropic Bianchi Type-III Space-Time with Variable EoS Parameter. Astrophysics and Space Science, 332, 441-448. http://dx.doi.org/10.1007/s10509-010-0539-z
- Madsen, M.S. (1989) Magnetic Fields in Cosmology. Monthly Notices of the Royal Astronomical Society, 237, 109- 117.
- King, E.J. and Coles, P. (2007) Dynamics of a magnetized Bianchi-I Universe with Vacuum Energy. Classical and Quantum Gravity, 24, 2061-2072. http://dx.doi.org/10.1088/0264-9381/24/8/008
- Misra, M. and Radhakrishna, L. (1968) Some Electromagnetic Fields of Cylindrical Symmetry. Proceedings of the National Academy of Sciences, India Section A, 28, 632.
- Thorne, K.S. (1967) Primordial Element Formation, Primordial Magnetic Fields, and the Isotropy of the Universe. Astrophysical Journal, 148, 51. http://dx.doi.org/10.1086/149127
- Jacobs, K.C. (1968) Spatially Homogeneous and Euclidean Cosmological Models with Shear. Astrophysical Journal, 153, 661. http://dx.doi.org/10.1086/149694
- Jacobs, K.C. (1969) Cosmologies of Bianchi Type-I with a Uniform Magnetic Field. Astrophysical Journal, 155, 379. http://dx.doi.org/10.1086/149875
- Collins, C.B. (1972) Qualitative Magnetic Cosmology. Communications in Mathematical Physics, 27, 37-43. http://dx.doi.org/10.1007/BF01649657
- Roy, S.R. and Prakash, S. (1978) An Anisotropic Magnetohydrodynamic Cosmological Model in General Relativity. Indian Journal of Physics, Part B, 52B, 47-52.
- Milaneschi, E. and Fabbri, R. (1985) Polarization of the Microwave Background Radiation in Bianchi Type-I Cosmological Models with a Homogeneous Magnetic Field. Astronomy and Astrophysics, 151, 7-15.
- Roy, S.R., Narain, S. and Singh, J.P. (1985) Bianchi Type-I Cosmological Model with Perfect Fluid and Magnetic Fluid. Australian Journal of Physics, 38, 239-248. http://dx.doi.org/10.1071/PH850239
- Adhav, K.S., Dawande, M.V., Thakare, R.S. and Raut, R.B. (2011) Bianchi Type-III Magnetized Wet Dark Fluid Cosmological Model in General Relativity. International Journal of Theoretical Physics, 50, 339-348. http://dx.doi.org/10.1007/s10773-010-0530-z
- Katore, S.D. (2012) Einstein Rosen Universe with Magnetized Anisotropic Dark Energy. Bulgarian Journal of Physics, 39, 231-240.
- Reddy, D.R.K., Patrudu, B.M. and Venkateswarlu, R. (1993) Exact Bianchi Type-II, VIII and IX Cosmological Models in Scale-Covariant Theory of Gravitation. Astrophysics and Space Science, 204, 155-160. http://dx.doi.org/10.1007/BF00658101
- Chakraborty, S. (1991) A Study on Bianchi-IX Cosmological Model. Astrophysics and Space Science, 180, 293-303. http://dx.doi.org/10.1007/BF00648184
- Bali, R. and Dave, S. (2001) Bianchi Type-IX String Cosmological Model in General Relativity. Pramana: Journal of Physics, 56, 513-518. http://dx.doi.org/10.1007/s12043-001-0100-2
- Bali, R. and Yadav, M.K. (2005) Bianchi Type-IX Viscous Fluid Cosmological Model in General Relativity. Pramana: Journal of Physics, 64, 187-196. http://dx.doi.org/10.1007/BF02704873
- Pradhan, A., Srivastav, S.K. and Yadav, M.K. (2005) Some Homogeneous Bianchi Type IX Viscous Fluid Cosmological Models with a Varying Λ. Astrophysics and Space Science, 298, 419-432. http://dx.doi.org/10.1007/s10509-005-5832-x
- Tyagi, A. and Chhajed, D. (2012) Homogeneous Anisotropic Bianchi Type-IX Cosmological Model for Perfect Fluid Distribution with Electromagnetic Field. American Journal of Mathematics and Statistics, 2, 19-21. http://dx.doi.org/10.5923/j.ajms.20120203.01
- Rao, V.U.M., Santhi, M.V. and Vinutha, T. (2008) Exact Bianchi Type-II, VIII and IX Perfect Fluid Cosmological Models in Saez-Ballester Theory of Gravitation. Astrophysics and Space Science, 317, 27-30. http://dx.doi.org/10.1007/s10509-008-9849-9
- Ghate, H.R. and Sontakke, A.S. (2013) Bianchi Type-IX Cosmological Model with Anisotropic Dark Energy. International Journal of Scientific & Engineering Research, 4, 769-774.
- Ghate, H.R. and Sontakke, A.S. (2013) Bianchi Type-IX Cosmological Models with Anosotropic Dark Energy in Lyra Geometry. Prespacetime Journal, 4, 619-628.
- Ghate, H.R. and Sontakke, A.S. (2013) Binary Mixture of Anisotropic Dark Energy and Perfect Fluid in Bianchi Type-IX Spacetime. Journal of Pioneering Medical Sciences (JPMS), 3, 122-131.
- Brans, H. and Dicke, R.H. (1961) March’s Principle and a Relativistic Theory of Gravitation. Physical Review A, 124, 925-935. http://dx.doi.org/10.1103/PhysRev.124.925
- Nordtvedt Jr., K. (1970) Post-Newtonian Metric for a General Class of Scalar-Tensor Gravitational Theories and Observational Consequences. The Astrophysical Journal, 161, 1059-1067. http://dx.doi.org/10.1086/150607
- Wagoner, R.V. (1970) Scalar-Tensor Theory and Gravitational Waves. Physical Review D, 1, 3209-3216. http://dx.doi.org/10.1103/PhysRevD.1.3209
- Ross, D.K. (1972) Scalar-Tensor Theory of Gravitation. Physical Review D, 5, 284-290. http://dx.doi.org/10.1103/PhysRevD.5.284
- Dunn, K.A. (2007) A Scalar-Tensor Theory of Gravitation. Journal of Mathematical Physics, 15, 2229-2231. http://dx.doi.org/10.1063/1.1666603
- Saez, D. and Ballester, V.J. (1986) A Simple Coupling with Cosmological Implications. Physical Letters A, 113, 467- 470. http://dx.doi.org/10.1016/0375-9601(86)90121-0
- Barber, G.A. (1982) On Two “Self-Creation” Cosmologies. General Relativity and Gravitation, 14, 117-136. http://dx.doi.org/10.1007/s10509-007-9387-x
- La, D. and Steinhardt, P.J. (1989) Extended Inflationary Cosmology. Physical Review Letters, 62, 376-378. http://dx.doi.org/10.1103/PhysRevLett.62.376
- Singh, T. and Agrawal, A.K. (1991) Some Bianchi-Type Cosmological Models in a New Scalar-Tensor Theory. Astrophysics and Space Science, 182, 289-312. http://dx.doi.org/10.1007/BF00645008
- Ram, S. and Tiwari, S.K. (1998) Inhomogeneous Plane Symmetric Models in a Scalar-Tensor Theory. Astrophysics and Space Science, 259, 91-97.
- Singh, C.P. and Ram, S. (2003) Unified Description of Early Universe in Scalar-Tensor Theory. Astrophysics and Space Science, 284, 1199-1206. http://dx.doi.org/10.1023/A:1023637627922
- Reddy, D.R.K. and Naidu, R.L. (2007) Five Dimensional String Cosmological Models in a Scalar-Tensor Theory of Gravitation. Astrophysics and Space Science, 307, 395-398. http://dx.doi.org/10.1007/s10509-007-9387-x
- Adhav, K.S., Ugale, M.R., Kale, C.B. and Bhende, M.P. (2007) Bianchi Type VI String Cosmological Model in SaezBallester’s Scalar-Tensor Theory of Gravitation. International Journal of Theoretical Physics, 46, 3122-3127. http://dx.doi.org/10.1007/s10773-007-9426-y
- Katore, S.D., Adhav, K.S., Shaikh, A.Y. and Sarkate, N.K. (2010) Higher Dimensional LRS Bianchi Type-I Domain Walls in a Scalar-Tensor Theory of Gravitation. International Journal of Theoretical Physics, 49, 2358-2363. http://dx.doi.org/10.1007/s10773-010-0422-2
- Pradhan, A., Kumar Singh, A. and Chouhan, D.S. (2013) Accelerating Bianchi Type-V Cosmology with Perfect Fluid and Heat Flow in Saez-Ballester Theory. International Journal of Theoretical Physics, 52, 266-278. http://dx.doi.org/10.1007/s10773-012-1329-x
- Bermann, M.S. (1983) Special Law of Variation for Hubbles Parameters. IL Nuovo Cimento B, 74, 182-186. http://dx.doi.org/10.1007/BF02721676
- Carroll, S.M., Hoffman, M. and Trodden, M. (2003) Can the Dark Energy Equation-of-State Parameter w be Less than -1? Physical Review D, 68, Article ID: 023509. http://dx.doi.org/10.1103/PhysRevD.68.023509
- Berman, M.S. and Gomide, F.M. (1988) Cosmological Models with Constant Deceleration Parameter. General Relativity and Gravitation, 20, 191-198. http://dx.doi.org/10.1007/BF00759327
- Singh, C.P. (2007) Bianchi Type-II Inflationary Models with Constant Deceleration Parameter in General Relativity. Pramana: Physics and Astronomy, 68, 707-720.
- Singh, C.P. and Kumar, S. (2007) Bianchi Type-III Space-Times with Constant Deceleration Parameter in Self-Creation Cosmology. Astrophysics and Space Science, 310, 31-39. http://dx.doi.org/10.1007/s10509-007-9411-1
- Singh, C.P. and Kumar, S. (2006) Bianchi Type-II Cosmological Models with Constant Deceleration Parameter. International Journal of Modern Physics D, 15, 419-438. http://dx.doi.org/10.1142/S0218271806007754
- Singh, C.P. and Baghel, P.S. (2009) Bianchi Type-V Cosmological Models with Constant Deceleration Parameter in General Relativity. International Journal of Theoretical Physics, 48, 449-462. http://dx.doi.org/10.1007/s10773-008-9820-0

