Journal of Signal and Information Processing
Vol.3 No.1(2012), Article ID:17696,6 pages DOI:10.4236/jsip.2012.31017
Face Recognition Systems Using Relevance Weighted Two Dimensional Linear Discriminant Analysis Algorithm
![]()
Laboratory of Conception and Systems, Faculty of Sciences Agdal, Mohammed V University, Rabat, Morocco.
Email: Hythem0101@hotmail.com, {jedra, zahid}@fsr.ac.ma
Received October 6th, 2011; revised November 15th, 2011; accepted November 29th, 2011
Keywords: LDA; PCA; 2DLDA; RW2DLDA; Extraction; Face Recognition; Small Sample Size
ABSTRACT
Low-dimensional feature representation with enhanced discriminatory power of paramount importance to face recognition systems. Most of traditional linear discriminant analysis (LDA)-based methods suffer from the disadvantage that their optimality criteria are not directly related to the classification ability of the obtained feature representation. Moreover, their classification accuracy is affected by the “small sample size” (SSS) problem which is often encountered in face recognition tasks. In this paper, we propose a new technique coined Relevance-Weighted Two Dimensional Linear Discriminant Analysis (RW2DLDA). Its over comes the singularity problem implicitly, while achieving efficiency. Moreover, a weight discriminant hyper plane is used in the between class scatter matrix, and RW method is used in the within class scatter matrix to weigh the information to resolve confusable data in these classes. Experiments on two well known facial databases show the effectiveness of the proposed method. Comparisons with other LDA-based methods show that our method improves the LDA classification performance.
1. Introduction
Linear Discriminant Analysis [1-5] is a well-known method which projects the data onto a lower-dimensional vector space such that the ratio of the between-class distance to the within-class distance is maximized, thus achieving maximum discrimination. The optimal projection can be readily computed by applying the eigenobjective functions, such as face recognition, all scatter matrices in question can be singular since the data is from a very high-dimensional space, and in general, the dimension exceeds the number of data points. This is known as the under sampled or singularity problem [6].
In recent years, many approaches have been brought to bear on such high-dimensional, under sampled problems, including pseudo-inverse LDA, PCA + LDA, and regularized LDA. More details can be found in [6]. Among these LDA extensions, PCA + LDA, has received a lot of attention, especially for face recognition [3]. In this twostage algorithm, an intermediate dimension reduction stage using PCA is applied before LDA. The common aspect of previous LDA extension is the computation of eigen-decomposition of certain large matrices, which not only degrades the efficiency but also makes it hard to scale them to large datasets.
The objective of LDA is to find the optimal projection so that the ratio of the determinants of the between-class and within-class scatter matrix of the projected samples reaches its maximum. However, concatenating 2D matrices into a 1D vector leads to a very high-dimensional image vector, where it is difficult to evaluate the scatter matrices accurately due to its large size and the relatively small number of training samples. Furthermore, the withinclass scatter matrix is always singular, making the direct implementation of the LDA algorithm an intractable task. To overcome these problems, a new technique called 2- dimensional LDA (2DLDA) was recently proposed. This method directly computes the eigenvectors of the scatter matrices without matrix to vector conversion. Thus, PCA and LDA were developed into the 2-dimensional space methods which are known as 2DPCA and 2DLDA.
The scatter matrices in 2DLDA are quite small compared to the scatter matrices in LDA. The size of the 2DLDA matrix is proportional to the width of the image. 2DLDA evaluates the scatter matrices more accurately and computes the corresponding eigenvectors more efficiently than LDA or PCA. However, the main drawback of 2DLDA is that it needs more coefficients for image representation that the conventional PCA and LDAbased schemes. Moreover, [7] has shown that the class separability criterion that classical LDA maximize is not necessarily representative of classification accuracy and the resulting projection will preserve the distances of already well separated classes while causing unnecessarily overlap of neighbouring classes. To solve this problem Loog et al. [7] have proposed an extended criterion by introducing a weighting scheme in the estimation of between-class scatter matrix. From the similar standpoint [8] has extended this concept to estimate the within-class scatter matrix by introducing the inter-class relationships as relevance weights. He has presented an LDA enhancements algorithm namely relevance weighted LDA (RWLDA) by replacing the un weighted scatter matrices through the weighted scatter matrices in the classical LDA method this was successfully application in face recognition by chogdali [9]. Waiyawut and Yuttapong they are explain efficient face recognition methods called the weighted 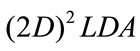 and it incorporating weighted outlier class relationships into the estimation of the overall between-class scatter matrix [10]. However, this algorithm cannot be directly applied for face recognition because of the singularity of the weighted within class scatter matrix.
and it incorporating weighted outlier class relationships into the estimation of the overall between-class scatter matrix [10]. However, this algorithm cannot be directly applied for face recognition because of the singularity of the weighted within class scatter matrix.
2. Subspace LDA Method
The first method in this study is the Subspace LDA method [11-13], which is simply the implementation of PCA by projecting the data onto the eigenface space and then implementing LDA to classify the eigenface space projected data. Projecting the data to the eigenface space generalizes the data, whereas implementing LDA by projecting the data to the classification space discriminates the data. Thus, Subspace LDA approach seems to be a complementary approach to the Eigenface method. Now we described the following steps which summarize the PCA process:
1) Let a face image I be a two dimensional ( ) matrix, pixels is converted to the image vector of size (
) matrix, pixels is converted to the image vector of size ( ) where P= (
) where P= ( ), by adding each column one after the other, we obtain the training set :
), by adding each column one after the other, we obtain the training set :
 (1)
(1)
of image vectors and its size is (P ×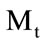 ) where Mt is the number of training images.
) where Mt is the number of training images.
2) Calculate the arithmetic average of the training image vector at each pixel point called mean face and its size:
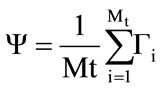 (2)
(2)
3) Find the mean subtracted image is the difference of the training image from the mean image 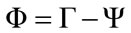 and we obtain the difference Matrix as:
and we obtain the difference Matrix as:
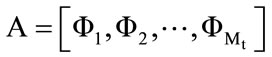 (3)
(3)
is the matrix of all the mean subtracted training image vectors and its size is (P × ).
).
4) Calculate the covariance matrix to represent the scatter degree of all feature vectors related to the average vector. The covariance matrix X of the training image vectors of size (P × P) is defined by:
 (4)
(4)
An important property of the Eigenface method is obtain the eigenvectors of the covariance matrix. For a face image of size ( ) pixels, the covariance matrix is of size (P × P), P being (
) pixels, the covariance matrix is of size (P × P), P being ( ). This covariance matrix is very hard to work with due to its huge dimension causing computational complexity. On the other hand, Eigenface method calculates the eigenvectors of the
). This covariance matrix is very hard to work with due to its huge dimension causing computational complexity. On the other hand, Eigenface method calculates the eigenvectors of the 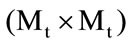 matrix,
matrix, 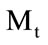 being the number of face images, and obtains (P × P) matrix using the eigenvectors of the
being the number of face images, and obtains (P × P) matrix using the eigenvectors of the  matrix.
matrix.
Initially, a matrix Y is defined as:
 (5)
(5)
5) Compute the eigenvectors and corresponding eigenvalues by:
 (6)
(6)
using (SVD) function, where V is the set of eigenvectors associated with its eigenvalue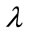 .
.
Also it can be easily observed that the most of generalization power is contained in the first few eigenvectors. For example, 40% of the total eigenvectors have 85% - 90% of the total generalization power .
After this we find the eigenface by projection matrix A into new eigenvector and normalized the eigenface.
6) Each mean subtracted image project into eigenspace using
 (7)
(7)
where k = 1, 2,…, .
.
Finally, we obtain weight Matrix
 (8)
(8)
By performing all these calculations, the training images are projected onto the eigenface space, that is a transformation from P-dimensional space to  dimensional space. This PCA step is achieved to reduce the dimension of the data, also may be referred as a feature extraction step. From this step on, the each image is an (
dimensional space. This PCA step is achieved to reduce the dimension of the data, also may be referred as a feature extraction step. From this step on, the each image is an ( ) dimensional vector in the eigenface space. After de PCA process, we describe the LDA process.
) dimensional vector in the eigenface space. After de PCA process, we describe the LDA process.
With the projected data in hand, a new transformation is performed; the classification space projection by LDA. Instead of using the pixel values of the images (as done in pure LDA), the eigenface projections are used in Subspace LDA method.
Again, as in the case of pure LDA, a discriminatory power is defined as:
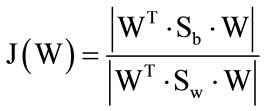 (9)
(9)
where 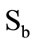 is the between-class and
is the between-class and 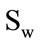 is the withinclass scatter matrix.
is the withinclass scatter matrix.
For c individuals having 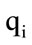 training images in the database, the within-class scatter matrix is computed as:
training images in the database, the within-class scatter matrix is computed as:
 (10)
(10)
The size of  depends on the size of the eigenface space. If
depends on the size of the eigenface space. If  of the eigenface were used, then the size of
of the eigenface were used, then the size of 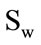 is (
is (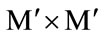 ).
).
Here, eigenface space class mean is defined as:
 (11)
(11)
is the arithmetic average of the eigenface projected training image vector corresponding to the same individual, i = 1, 2,…, c and its size is (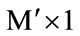 ) .
) .
Moreover, mean face is calculated from the arithmetic average of all the projected training image vector.
 (12)
(12)
Also between-class scatter matrix is computed as:
 (13)
(13)
which represents the scatter of each projection classes mean  around the overall mean vector
around the overall mean vector 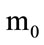 and its size is (
and its size is ( ).
).
The objective is to maximize J(W), that is to find an optimal projection W which maximizes between-class scatter and minimizes within-class scatter .
 (14)
(14)
then, W can be obtained by solving the generalized eigenvalue problem:
 (15)
(15)
Next, the eigenface projections of the training image vectors are projected to the classification space by the dot product of optimum projection W and weight vector
 (16)
(16)
is the projection of the training image vectors eigenface projections to the classification space which is of size ((c-1) ×1) where i = 1, 2,…, .
.
In the testing phase each test image should be mean centered, and projected into the same eigenspace as defined by:
 (17)
(17)
is the projection of a training image on each of the eigenvectors where k = 1, 2, …, . We obtain the weight Matrix:
. We obtain the weight Matrix:
 (18)
(18)
is the representation of the test image in the eigenface space and its size is ( ).
).
After this, the eigenface projection of the test image vector (i.e. weight matrix) is projected to the classification space in the same manner.
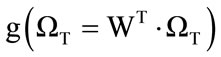 (19)
(19)
which is of size ((c – 1) × 1).
Finally, the distance between the projection is determined by the Euclidean distance between the training and test classification space projection:
 (20)
(20)
is the distance measure which is scalar and calculated for i = 1, 2,…,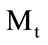 . Is returned the index, which refers to the smallest values of distance measure.
. Is returned the index, which refers to the smallest values of distance measure.
3. Two Dimensional Linear Discriminate Analysis (2DLDA)
Suppose there are C known pattern classes 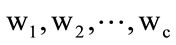 and N training Samples
and N training Samples , i = 12,…, Ic, j = 1, 2,…, c is a set of samples with (m × n) dimension.
, i = 12,…, Ic, j = 1, 2,…, c is a set of samples with (m × n) dimension.  is the number of training samples of class j and satisfies
is the number of training samples of class j and satisfies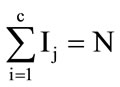 . The following steps summarize the process of 2DLDA:
. The following steps summarize the process of 2DLDA:
1) Calculate the average matrix X of the N training image using:
 (21)
(21)
2) Compute the mean 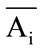 of
of  class by:
class by:
 (22)
(22)
where i=1,2,…, 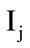
3) Calculate the image between-class scatter matrix by:
 (23)
(23)
4) Calculate the image within-class scatter matrix by:
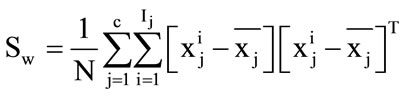 (24)
(24)
We use best eigenvector corresponding to the maximum eigenvalue by:
 (25)
(25)
5) Find the optimal projection W so that the total scatter of the projected samples of the training images is maximized. The objective function of 2DLDA is defined by:
 (26)
(26)
It can be proven that the eigenvector corresponding to the maximum eigenvalue of 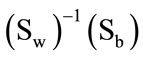 is the optimal projection vectors which maximizes J(W). Generally, as it is not enough to have only one optimal projection vector, we usually look for d projection axes, say
is the optimal projection vectors which maximizes J(W). Generally, as it is not enough to have only one optimal projection vector, we usually look for d projection axes, say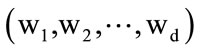 , which are the eigenvectors corresponding to the first d largest eigenvalues of
, which are the eigenvectors corresponding to the first d largest eigenvalues of . In 2DLDA, once these projection vectors are computed, each training image
. In 2DLDA, once these projection vectors are computed, each training image  is then projected onto W to obtain the feature matrix
is then projected onto W to obtain the feature matrix  of size m × d of the training image
of size m × d of the training image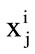 . So, during training, for each training image
. So, during training, for each training image 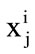 a corresponding feature matrix of size m×d is constructed and sorted for matching at the time of recognition.
a corresponding feature matrix of size m×d is constructed and sorted for matching at the time of recognition.
6) For test image we project the test matrix onto the eigenvectors matrix to fined the new matrix of dimension (m × k):
 (27)
(27)
7) Calculate the face distance between two arbitrary feature matrix  and
and  is defined by:
is defined by:
 (28)
(28)
If  and
and , where
, where 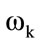 identify the class and B is a test sample, then the resulting decision is
identify the class and B is a test sample, then the resulting decision is .
.
4. Relevance Weighted 2DLDA
To improve the result of the above methods can be modified account of between-class scatter matrix and withinclass scatter matrix on (23) and (24) to find weighted between-class scatter matrix  by:
by:
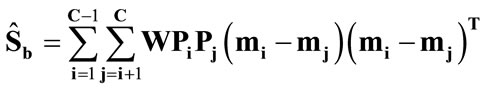 (29)
(29)
where 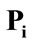 and
and 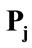 are the class priors, W is the Euclidean distance between the means of class i and class j. The weighting function W is generally a monotonically decreasing function:
are the class priors, W is the Euclidean distance between the means of class i and class j. The weighting function W is generally a monotonically decreasing function:
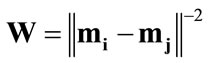 (30)
(30)
Recently, (30) has extended the concept of weighting to estimate a within-class scatter matrix. Thus by introducing a so-called relevance weights, a weighted withinclass scatter matrix 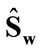 is defined to replace a conventional within-class scatter matrix
is defined to replace a conventional within-class scatter matrix
 (31)
(31)
where 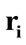 's
's 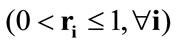 are the relevance based weights defined as:
are the relevance based weights defined as:
 (32)
(32)
To obtains the best result we change Equation (32) to
 (33)
(33)
Using the weighted scatter matrices 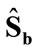 and,
and, 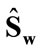 the criterion in (26) is weighted and the resulting algorithm is referred to as relevance weighted 2DLDA.
the criterion in (26) is weighted and the resulting algorithm is referred to as relevance weighted 2DLDA.
5. Experiments
5.1. The Experiments on the ORL Face Base
For showing the effect of PCA + LDA and 2DLDA, we use ORL database [14]. This base contains images from 40 individuals, each providing 40 different images. For some subjects, the images were taken at different times. The facial expressions (open or closed eyes, smiling or non smiling) and facial details (glasses or no glasses) also vary. The images were taken with a tolerance for some titling and rotation of the face of up to 20 degrees. Moreover, there is also some variation in the scale of up to about 10 percent. All images are grayscale and normalized to a resolution of 112 × 92 pixel, Example images are shown in Figure 1.
In an experiment: we use between 9 and 3 image sample per class for training, and the remaining images for the test. We take more than five cases with different input and find the mean of these cases. Table 1 shows the comparisons of methods on recognition accuracy. And we can see from this table most result of testing RW- 2DLDA is better than that of other methods.
It can be seen from Table 2, 2DLDA takes much less time than PCA + LDA and RW2DLDA, because the size of the covariance matrix in 2DLDA is (n × n) and the size of covariance matrix in PCA+LDA is (P × P) where P = (m × n). So, the covariance matrix in 2DLDA is smallest and the computational cost is low also RW2- DLDA take more computational step than 2DLDA.

Figure 1. Examples of ORL database.
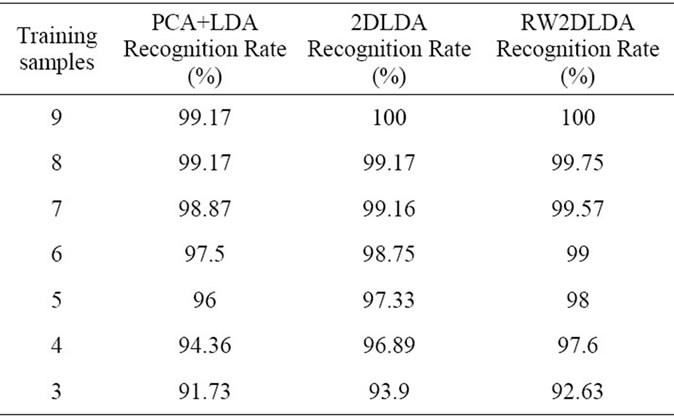
Table 1. Comparison results of mean recognition accuracy of different method on ORL database.

Table 2. Comparison of cup time (s) for feature extraction using the ORL data base.
5.2. Experiment on the Yale Database
The last experiment is performed using the Yale face database [15], which contains 165 images of 15 individuals (each person has 11 different images) under various facial expressions and lighting conditions. Each image is manually cropped and resized 92 × 112 pixel in this experiment. We use between 10 and 3 images sample per class for training, and the remaining images for the test. We take more than five cases with different input and find the mean of these cases. This experimental resulting are listed in Table 3. The recognition rate of RW2DLDA is superior than other methods Example images are shown in Figure 2.

Figure 2. Examples of Yale database.
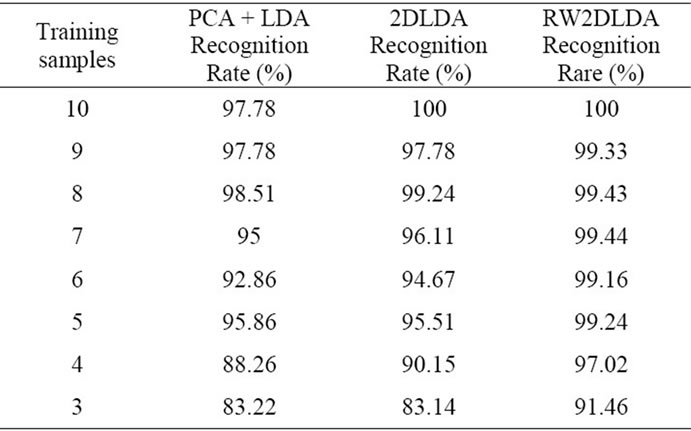
Table 3. Comparison results of mean recognition accuracy of different method on Yale database.
6. Conclusion
In conclusion we came to state the facts the recognition rate of RW2DLDA is better than other methods and the execute time of 2DLDA is less than other methods. Finally we prove that the time depends on the size of the face images and the number of class and relevanceweighted inner class relationships are incorporated into the overall within-class scatter matrix to improve the performance of the 2DLDA method. The faces used during experimentation are ORl face database and Yale B face database demonstrate that proposed method gives a good face recognition rate.
7. Future Work
We plan to apply Kernel Relevance-Weighted 2DLDA and Kernel Weighted Scatter-Difference Based Two Dimensional Discriminant Analysis for Face Recognition in our future work.
REFERENCES
- R. O. Dudo, P. E. Hart and D. Stork, “Pattern Classification,” Wiley, New York, 2000.
- K. Fukunage, “Introduction to Statistical Pattern Classifcation,” Academic Press, San Diego, 1990.
- P. N. Belhumeour, J. P. Hespanha and D. J. Kriegman, “Eienfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 19, No. 7, 1997, pp. 711-720. doi:10.1109/34.598228
- D. L. Swets and J. J. Weng, “Using Discriminant Eigenfeatures for Image Retrieval,” IEEE Transaction on Pattern Analysis and Machine Intelligence, Vol. 18, No. 8, 1996, pp. 831-836. doi:10.1109/34.531802
- S. Dudoit, J. Fridlyand and T. P. Speed, “Comparison of Discrimination Methods for the Classification of Tumors Using Gene Expression Data,” Journal of the American Statistical Association, Vol. 97, No. 457, 2002, pp. 77-87. doi:10.1198/016214502753479248
- W. J. Krzanowski, P. Jonathan, W. V. McCarthy and M. R. Thomas, “Discriminant Analysis with Singular Covariance Matrices: Methods and Applications to Spectroscopic Data,” Applied Statistics, Vol. 44, No. 1, 1995, pp. 101-115. doi:10.2307/2986198
- M. Loog, R. P. W. Duin and R. Hacb-Umbach, “Multiclass Linear Dimension Reduction by Weighted Pair Wise Fisher Criteria,” IEEE Transaction on Pattern Recognition and Machine Intelligence, Vol. 23, No. 7, 2001, pp. 762-766. doi:10.1109/34.935849
- E. K. Tang, P. N. Suganthan, X. Yao and A. K. Qin, “Linear Dimensionality Reduction Using Relevance Weighted LDA,” Pattern Recognition, Vol. 38, No. 4, 2005, pp. 485-493. doi:10.1016/j.patcog.2004.09.005
- K. Chougdali, M. Jedra and N. Zahid, “Kernel Relevance Weighted Discriminant Analysis for Face Recognition,” Pattern Analysis & Application, Vol. 13, No. 2, 2010, pp. 213-221. doi:10.1007/s10044-009-0152-3
- W. Sanayah, et al., “Relevance-Weighted
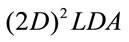 Image Projection Technique for Face Recognition,” ETRI Journal, Vol. 31, No. 4, 2009, pp. 663-667.
Image Projection Technique for Face Recognition,” ETRI Journal, Vol. 31, No. 4, 2009, pp. 663-667. - W. Zhao, A. Krishnaswamy, R. Chellappa, D. L. Swets and J. Weng, “Discriminant Analysis of Principal Components for Face Recognition,” International Conference on Automatic Face and Gesture Recognition, Nara, 14- 16 April 1998, pp. 336-341. doi:10.1109/AFGR.1998.670971
- W. Zhao, R. Chellappa and N. Nandhakumar, “Emprical Performance Analysis of Linear Discriminant Classifiers,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, 23-25 June 1998, pp. 164-169.
- W. Zhao, “Subspace Methods in Object/Face Recognition,” International Joint Conference on Neural Networks, Washington DC, 10-16 July 1999, pp. 3260-3264.
- http://www.cam-orl.co.uk
- ftp://plucky.cs.yale.edu/CVC/pub/images/yalefaceB/TarSets

