International Journal of Geosciences
Vol. 3 No. 3 (2012) , Article ID: 21172 , 10 pages DOI:10.4236/ijg.2012.33063
Neural Network Approach to Response of Buildings Due to Earthquake Excitation
1Department of Civil Engineering, Bengal Engineering and Science University, Howrah, India
2Department of Applied Mathematics, Birla Institute of Technology, Ranchi, India
Email: skcbit@yahoo.co.in
Received February 16, 2012; revised March 17, 2012; accepted April 29, 2012
Keywords: Neural Network; Anisotropic Building; Soft Ground Floor
ABSTRACT
The present article investigates the physical phenomena associated with the wave passage effect into a building considering the ground floor as the soft floor with the conformity of the up-to-date scenario of the construction of high rise buildings, due to shear excitation of the base. The aim of the study is to analyse the post-earthquake situation of the building in respect to its health. With this vision, the ensuing problem on two-dimensional building models, non-incorporating soil-structure interaction, is being tackled by both analytical and neural network approaches. Computational results from both ends (of the approaches) show that the wave energy does not always propagate from the ground into the building, but for lower frequency range it sails to the building without any disturbances. However, for higher frequency range, the computational results show that the building experiences large “torsional” deformations, as a result the building may collapse. Finally, both the approaches maintain a good agreement among themselves. The present investigation may lead to a long way in contributing to better and more rational, simplified design criteria.
1. Introduction
Structural buildings may experience vibrations excited by ground waves, which are generated by earthquakes, by explosions, or by some other vibration sources. Soviet Academy of Sciences, Krivelev [1] suggested several models to study the seismic action on long buildings and presented the shear wave velocities for the equivalent building models (in the range of 300 - 1800 m/s). Kojic et al. [2] analysed the earthquake response of long building like Imperial County Services Building in EI Centro, USA and observed very little damage of the upper part of such buildings during strong earthquake. Gupta and Trifunac [3-6] studied the earthquake response of multidegree-of—freedom system from the stochastic point of view. Kojic et al. [7] also studied earthquake response of arch dams to non-uniform canyon motion. Gupta and Trifunac [8] discussed the earthquake response of simple symmetric buildings due to torsional excitation. Chandler et al. [9] have directed their effort in predicting the amplification behaviour of seismic waves affecting a site for any given earthquake scenario.
For architectural reasons, many buildings possess the ground, or the ground and the first floors with stiffness smaller than the stiffness of the upper floors. These buildings possess typical house stories or various corridors (passages) and open spaces, which can be designated as soft floor, in which the partitions (in the passages) are made of glass, ply-wood etc., rather than that of concrete, steel or masonry. To tackle such type of buildings, it is optimistic to minimise the fundamental frequency of the soil-structure system from the range of large earthquake excitation and in some cases to increase hysteric damping, base-isolation system may be introduced. This type of flexible soft first-storey concept allows the seismic stress resultant throughout the structure to be significantly reduced. Several investigators (Chopra et al. [10]), Lee and Medland [11], Skinner et al. [12] have proposed their thoughts in this respect.
The effects of travelling seismic wave on extended structures, for example long bridges, was studied by Werner et al. [13], Kashefi and Trifunac [14]. However, the effect of seismic waves on buildings has been studied to a very lesser extent. Tzenov and Boncheva [15] and Tzenov [16] noted the need for two-dimensional model of “long-in-plan” buildings to account for the phase difference between the excitation at different points of the foundation. But, they did not consider the excitation to be propagating waves. The nature of the seismic energy transfer from the ground into the foundation of a building, as well as the transport of the energy within the building itself has been discussed by Todorovska et al. [17], Todorovska and Trifunac [18], Todorovska and Lee [19], Todorovska and Trifunac [20]. Hall et al. [21] and Halling and Hall [22] have conducted a series of studies on the effects of near-field ground motion on flexible buildings and base-isolated structures. Todorovska and Trifunac [20] also investigated the propagation of earthquake waves in building considering the first floor as the soft one. Wolf and Obernhuber [23] studied effects of horizontally propagating waves on the response of structures with a soft first storey. They have shown that compared to a conventional structure, travelling-wave effects become more important for R-waves in a structure with a horizontal soft first storey. Chakraborty et al. [24] discussed the frequency-response analysis of shear vibration of long structures due to surface excitation. Their investigation reveals the existence of wave passage effect during the dynamic response of the structure under the optimum conditions on frequencies (low or high) for proper analysis of the resulting deformation of the foundation. Chakraborty and Sarkar [25] also conducted a study on the seismic response of multi-storey buildings on flexible foundation, with soft ground floor, due to seismic excitation. It has been observed from the study that the presence of the flexible foundation influences the propagation of polarised shear motion to such an extent that the motion causing disturbances in the ground floor cannot make headway to the upper part of the building. This effect may be possible as a result of the contribution of an antisymmetric mode of vibration to the overall response.
Over the last two decades, artificial neural networks (ANN) have gradually been established as a powerful tool in pattern recognition, signal processing, control and complex mapping problems, because of their excellent learning capacity and their high tolerance to partially in accurate data. Artificial neural networks have, recently, been further applied to assess damage in structures. Wu et al. [26] used a back-propagation neural network (BPN) to elucidate damage states in a three-storey frame by numerical simulation. Elkordy et al. [27] used a backpropagation neural network with modal shapes in the input layer, to detect the simulated damage of structures. Pandey and Barai [28] detected damage in a bridge truss by applying ANN of multilayer perceptron architectures to numerically simulated data. Using static displacements, natural frequencies and modal shapes, Zhao et al. [29] applied a counter-propagation neural network to locate damage in beams and frames. Masri et al. [30] established a method for detecting damage, based on nonlinear system identification, in which measured displacement, velocity, acceleration responses and input forces were used to train a back-propagation neural network.
The present article investigates the physical phenomena associated with the wave passage effect into a building considering the ground floor as the soft floor with the conformity of the up-to-date situation of the construction of high rise buildings, due to shear excitation of the base. Closed form analytical solutions are obtained for twodimensional building models, non-incorporating soilstructure interaction. It has been shown that the wave energy does not always propagate from the ground into the building, but for frequency ranging from 0.35 Hz - 1.00 Hz it sails to the building without any disturbances. However, for higher frequency range, ranging from 1.50 Hz - 3.50 Hz the computational results show that the buildings experience large “torsional” deformations that result to horizontal stresses. These large torsional deformations may be responsible for failure of the building. Thus, for higher values of frequencies, the whole upper part of the building would rotate almost as a rigid body. As a result of this rotational effect, the building may collapse.
A neural network based-approach is being implemented to the aforesaid model to assess the health monitoring of the building after the earthquake excitation. The issues relating to the design of network and learning paradigm are addressed and network architectures have been developed with reference to different input parameter of buildings. The training patterns are generated for a building and performance of the networks with one hidden layers are examined. A comparative study between analytical and neural-based results has been carried out.
2. Formulation of the Model
Consider a two-dimensional, semi-infinite elastic beam with horizontal discontinuity in the material properties and prescribed displacement at the ground surface z = H. Assume L and H as the length and the height of the building, h1 is the sum of heights of the upper floors, h2 is the height of the ground floor, as shown in Figure 1. The shear moduli and shear wave velocities of the upper floors and ground floor possess nature of anisotropy of orthotropic type i.e. having different values in the xand in the z-directions, e.g., (Q3)i,x, βi,x and (Q1)i,z, βi,z, i = 1, 2. Neglecting floor-foundation interaction, such a model may lead to a closed-form solutions for displacement response to shear motion at the base.
3. Solution
The displacements in the layers, v(i) (x, z, t), i = 1, 2, satisfy the two-dimensional wave equations
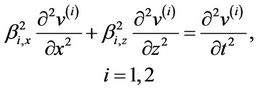 (1)
(1)
in which
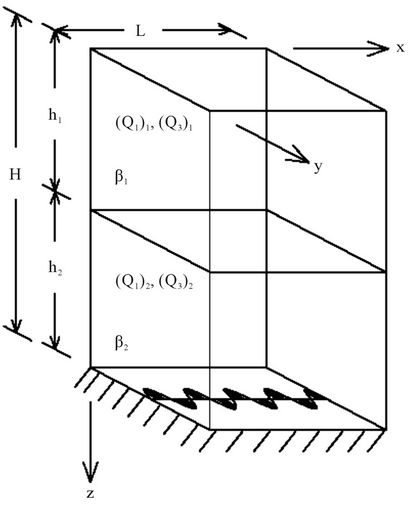
Figure 1. Modelling of building with soft ground floor, subjected to base excitation at z = H.
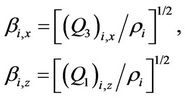 (1a)
(1a)
are the shear wave velocities along xand z-directions respectively.
The eigen function expansion of the displacement in the beam, v, is
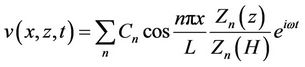 (2)
(2)
where
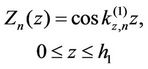 (2a)
(2a)
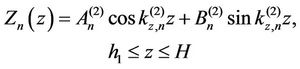 (2b)
(2b)
is the  shape function in the z-direction and
shape function in the z-direction and
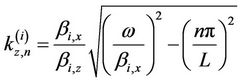 (2c)
(2c)
is the wave number, along z-direction, in the 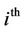 layer.
layer.
The boundary conditions to be satisfied are
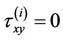 at
at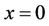 ,
, 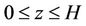 ,
,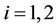 (3a)
(3a)
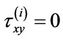 at
at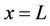 ,
, 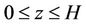 ,
,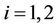 (3b)
(3b)
and
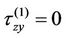 at
at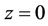 ,
, 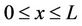 ,(3c)
,(3c)
where
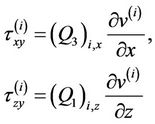 (3d)
(3d)
are the shear stresses in the ith layer. At the interface between the two layers, the continuity conditions are
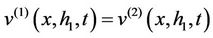 (4a)
(4a)
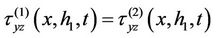 (4b)
(4b)
In addition, the free-field displacement on the surface of the half-space is being considered as
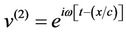 at
at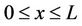 ,
,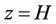 (5)
(5)
when the incident wave possesses frequency w and propagates with phase velocity c in the positive x-direction, following 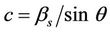 (where
(where 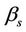 is the shear wave velocity of the soil and q is the angle between the direction of propagation of the incident wave and the normal).
is the shear wave velocity of the soil and q is the angle between the direction of propagation of the incident wave and the normal).
The coefficients 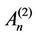 and
and 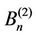 of the nth mode shape are obtained from conditions (4a) and (4b),
of the nth mode shape are obtained from conditions (4a) and (4b),
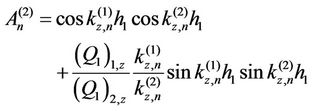 (6a)
(6a)
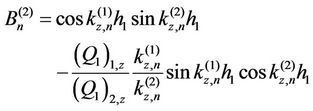 (6b)
(6b)
The coefficients of the expansion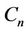 ,
, 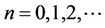 derived from the displacement condition (5) are
derived from the displacement condition (5) are
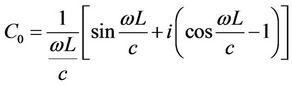 (7a)
(7a)
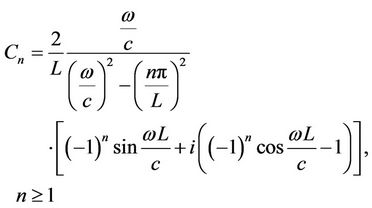 (7b)
(7b)
when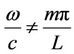 ,
,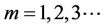 . Under the limiting condition,
. Under the limiting condition, 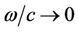 , the coefficients
, the coefficients 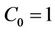 and
and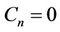 ,
,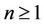 .
.
On application to the model of the type of a “stiff” building with “soft” ground floor, it may be seen from Equaiton (2c) that the wave numbers 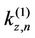 and
and 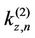 will be real only for finite number of modes. Consequently, the shape functions
will be real only for finite number of modes. Consequently, the shape functions 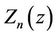 in the layers may be harmonic or exponential functions of z. Thus, such modes may allow the wave energy to be carried only into the soft ground floor from the base. The building will be in resonance with excitation when the denominator in Equation (2)
in the layers may be harmonic or exponential functions of z. Thus, such modes may allow the wave energy to be carried only into the soft ground floor from the base. The building will be in resonance with excitation when the denominator in Equation (2)
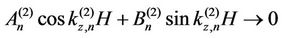 (8)
(8)
as a result of which, the displacements of the model become unbounded.
The displacement of the building can be expressed explicitly in the following fashion,
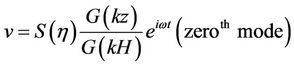 (9)
(9)
where
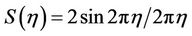 ,
, 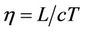
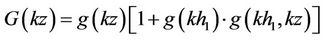
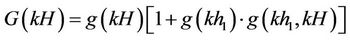
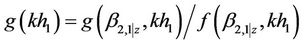
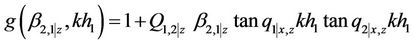
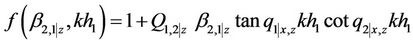
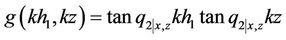
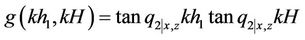
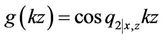 ,
,
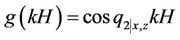
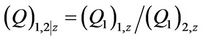 ,
,
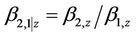
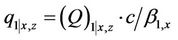 ,
,
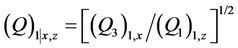
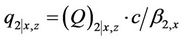 ,
,
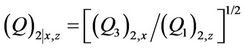 (9a)
(9a)
Similarly, for the other modes, the displacement can also be evaluated.
Next, we will discuss the implementation of Artificial Neural Network to the ensuing model. Finally, a comparative study of the analytical results to the ANN results has been interacted.
4. Artificial Neural Network
Artificial neural networks are modelled on the concept of present understanding of the functioning of the brain thus comprising a massively interconnected network of a large number of artificial neurons or computational units.
Neural network models are specified by the net topology, node (artificial neuron) characteristics and training or learning rules. The function of a neural network is determined by these parameters. The architecture of the network determines the inputs of each node. The node characteristics (threshold, transfer function and weights) determine the output of the node. The training or learning rules determine how the network will react when an unknown input is presented to it.
A neural network is typically characterized by its computational elements, its network topology and the learning algorithm. Among the several different types of ANN, the feed forward, multilayered, supervised neural network with the error Back Propagation Algorithm—the BPN [31]—is by far the most frequently applied neural network learning model, due to its simplicity. The architecture of BP networks, depicted in Figure 2, includes an input layer, one or more hidden layers, and an output layer. The nodes in each layer are connected to each node in the adjacent layer. Notably, Hecht-Nielsen [32] proved that one hidden layer of neurons suffices to model any solution surface of practical interest. Hence, a network with only one hidden layer is considered in this study. Before an ANN can be used, it must be trained from an existing training set of pairs of input-output elements.
5. NARX Neural Network
The most popular type of neural network is the MultiLayer Feed Forward (MLFF). A schematic diagram of a typical MLFF neural network architecture is depicted in Figure 2.
The network usually consists of an input layer, some hidden layers and an output layer. Usually knowledge is stored as a set of connection weights. The process of modifying the connection weights, in some orderly fashion, uses a suitable learning method called training.
The back-error propagation is the most widely used learning algorithm. It is one of the most powerful learning algorithms in neural networks. The back-propagation neural network was proposed by McClelland and Rumelhart [33] in a ground-breaking study originally focused on cognitive computer science. In this paper the structure of neural network includes three layers: the
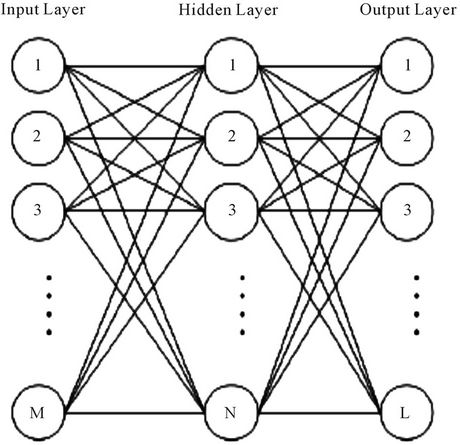
Figure 2. A multi-layer feed forward neural network architecture.
input layer, hidden layer, and output layer. The variable M shows the total neuron number in the input layer, variable N shows the total neuron number in the hidden layer, and the variable L shows the total neuron number in the output layer. Values wMN are the weights between the input and the hidden layer.
The operation of back error propagation is consisting of three steps:
1) Feed-forward step:
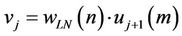 ; (10)
; (10)
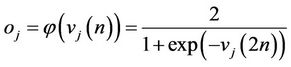 ; (11)
; (11)
where oj is output, vj is input, uj+1 is output of hidden layer and φ is a transfer function.
2) Back-propagation step:
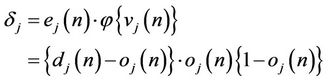 (12)
(12)
where 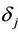 represents the local gradient function, ej shows the error function, oj means the actual output and dj is desired output.
represents the local gradient function, ej shows the error function, oj means the actual output and dj is desired output.
3) Adjust weighted value:
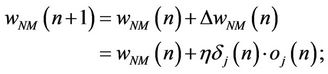 (13)
(13)
where η is the learning rate. Repeating these three steps results to the value of the error function will be zero or a constant value.
In the present model one neural network is employed for desired output. Networks consist of an input layer, a hidden layer and an output layer with 12, 5 and 1 neurons, respectively. In a network, transfer functions for neurons of hidden and output layers are Tansig and Purline, and are defined as Equation (14) and (15) respectively.
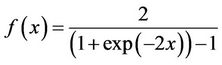 (14)
(14)
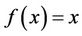 ; (15)
; (15)
6. Numerical Results and Discussions
The transfer of energy of SH-waves from the ground into the building is being illustrated in Figure 3. From Snell’s law,
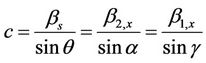 (16)
(16)
(bs, the shear wave velocity of the soil) it may be observed that a will be real, and the wave energy will propagate into the soft layer if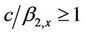 . If
. If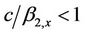 , then a will be purely imaginary and thus g will also be purely imaginary (since
, then a will be purely imaginary and thus g will also be purely imaginary (since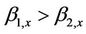 ) and as a result of which the wave energy will not propagate into the upper part of the building. The transfer of wave energy into the upper part of the building depends on the ratio,
) and as a result of which the wave energy will not propagate into the upper part of the building. The transfer of wave energy into the upper part of the building depends on the ratio,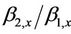 . The energy will propagate into the upper part of the building only if
. The energy will propagate into the upper part of the building only if 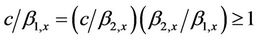 when
when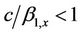 , the displacement in the hard layer will be exponentially decaying towards the top of the building, and it will vibrate as a rigid box welded to the soft layer.
, the displacement in the hard layer will be exponentially decaying towards the top of the building, and it will vibrate as a rigid box welded to the soft layer.
As an example, for numerical calculations, the height of the ground floor is considered to be 1/4 of the total height of the building (H = 12 m), assuming the material properties of the layers of orthotropic type.
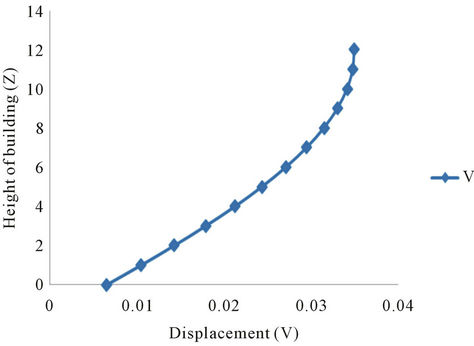
The pattern of energy transfer occurring during the passage of the wave with fundamental mode into the buildings with a soft ground floor has been depicted in Figures 4(a) and (b) (from both analytical and Neural observations). Figure 4 indicate the displacement of an
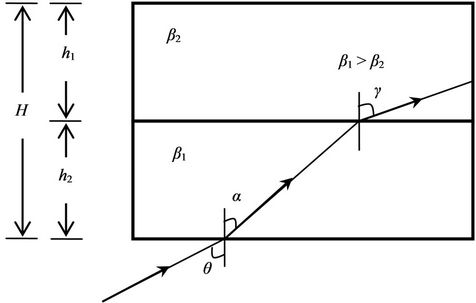
Figure 3. Illustration of transfer of wave energy from below the soft ground floor into the building.
 (a)
(a)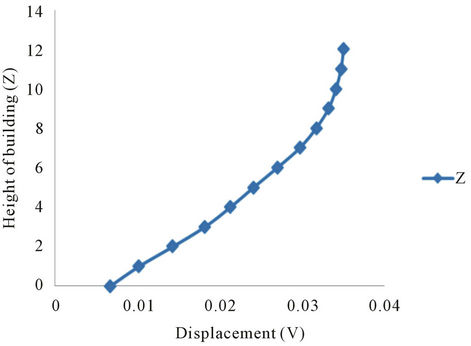 (b)
(b)
Figure 4. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 0.35 Hz). (a) Analytical result; (b) Neural network.
anisotropic building for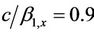 ,
, 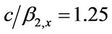 and
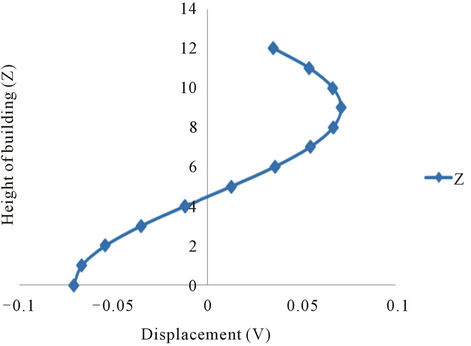
and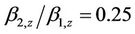 . The Figure 4(a) illustrates the displacements of the anisotropic (orthotropic type) layers in a manner that the energy propagates through the ground floor via the soft floor to the upper floors without any disturbance to the building (for frequency 0.35 Hz). Almost similar is the case with the Figure 4(b) (source, the Neural observation, under the same frequency level). Thus, for the above mentioned frequency of 0.35 Hz, a lesser part of energy of the impulsive wave disturbs the first floor but not the upper part, which is not at all harmful to the whole building. For the frequency of the impulse as close to 1 Hz, the displacement response, v, of the building can be expressed as a summation of the responses to the translational and rotational excitations (may be observed from Figures 5(a) and (b)). The pattern of responses for frequencies 1.60 Hz, 2.25 Hz, 2.85 Hz and 3.20 Hz shows that the buildings experience large “torsional” deformations that result to horizontal stresses
. The Figure 4(a) illustrates the displacements of the anisotropic (orthotropic type) layers in a manner that the energy propagates through the ground floor via the soft floor to the upper floors without any disturbance to the building (for frequency 0.35 Hz). Almost similar is the case with the Figure 4(b) (source, the Neural observation, under the same frequency level). Thus, for the above mentioned frequency of 0.35 Hz, a lesser part of energy of the impulsive wave disturbs the first floor but not the upper part, which is not at all harmful to the whole building. For the frequency of the impulse as close to 1 Hz, the displacement response, v, of the building can be expressed as a summation of the responses to the translational and rotational excitations (may be observed from Figures 5(a) and (b)). The pattern of responses for frequencies 1.60 Hz, 2.25 Hz, 2.85 Hz and 3.20 Hz shows that the buildings experience large “torsional” deformations that result to horizontal stresses
 (a)
(a)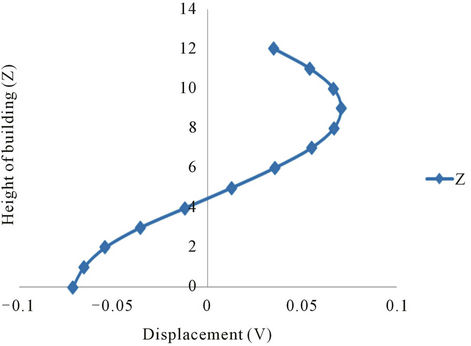 (b)
(b)
Figure 5. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 0.96 Hz). (a) Analytical result; (b) Neural network.
(Figures 6-9). These large torsional deformations may be responsible for failure phenomena of the building. Thus, for higher values of frequencies, the whole upper part of the building would rotate almost as a rigid body. As a result of this rotational effect, the building may collapse.
The following observations are evolved from the trained Artificial Neural Network (ANN) using the input of the structural properties of buildings, such as incremental height of building, height of each floor, orthotropic elastic moduli of soft floor and upper floors, velocity ratios with respect to shear wave etc.
1) Trained network is fruitful to predict the displacement of building.
2) The learning and momentum parameters are assumed as 0.5 and 0.9 respectively.
3) The iterations and other queries like regression coefficient, gradient, mean square error are being dealt by network for distinct values of frequency (ν) in one hidden
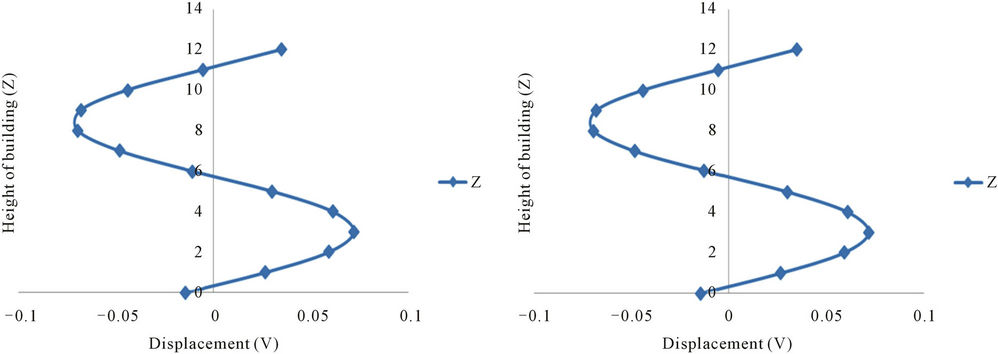 (a) (b)
(a) (b)
Figure 6. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 1.60 Hz). (a) Analytical result; (b) Neural network.
 (a) (b)
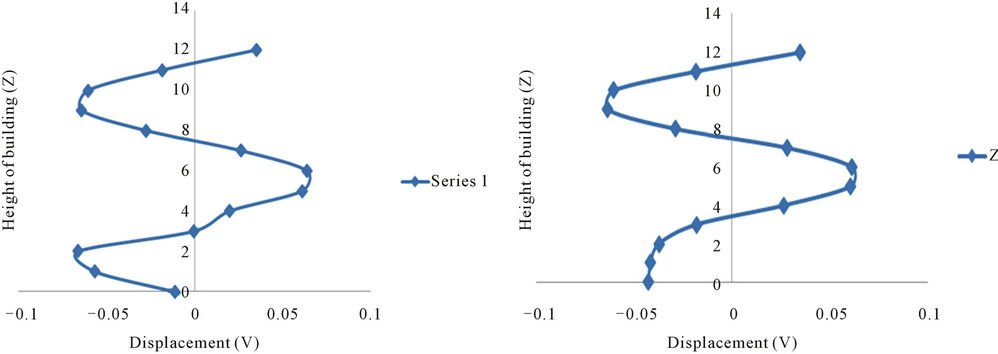
(a) (b)
Figure 7. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 2.25 Hz). (a) Analytical result; (b) Neural network.
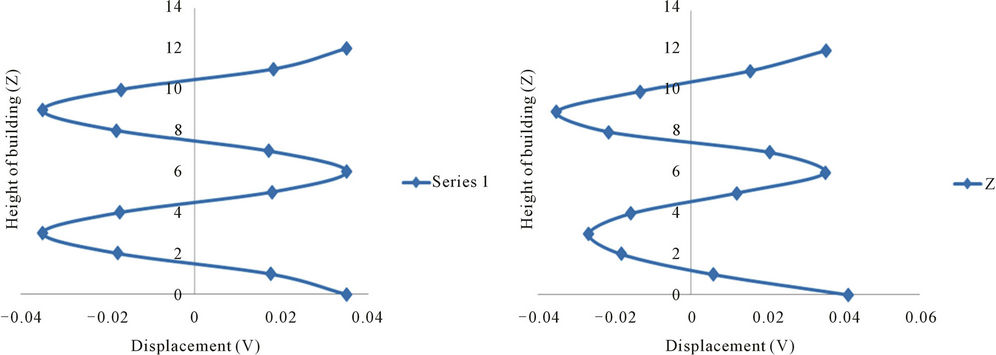 (a) (b)
(a) (b)
Figure 8. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 2.85 Hz). (a) Analytical result; (b) Neural network.
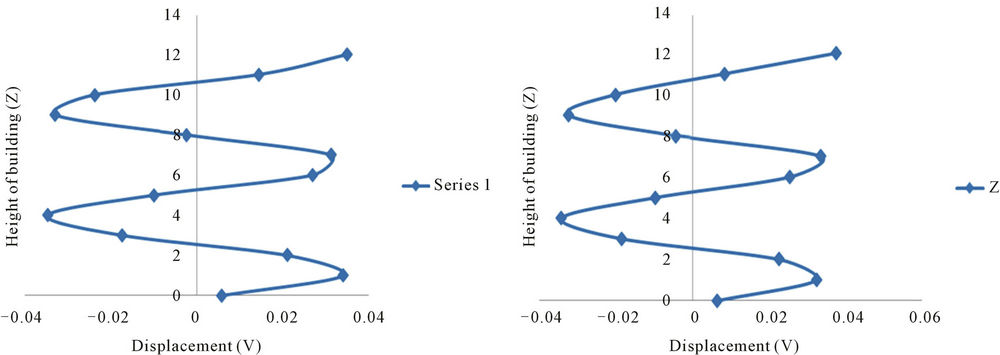 (a) (b)
(a) (b)
Figure 9. Displacement response of building (Anisotropic Model), with soft ground floor, due to propagating SH-wave (c/β2 = 0.05, β1/β2 = 0.25, ν = 3.20 Hz). (a) Analytical result; (b) Neural network.
layer architecture is given in the Table 1.
4) The CPU time required for training the network on MATLAB 7.6.0 (R2008a) is less than 30 minutes in all the exercise undertaken here.
The results obtained from the computational experimentation by ANN approach are quite promising.
The characteristics results for several frequencies obtained from ANN Architecture (12-5-1) (MATLAB) are presented in Table 1.
It has been observed from the computational results of both the analytical and ANN approaches that ANN approach is equally effective as analytical one.
One of the salient features of the investigation is that the “soft” ground floor does not always act as an “isolator” for the upper part of the buildings, and occasionally, for horizontally propagating seismic excitation, the wave energy can propagate into the whole building. These results the vibration of the upper part of the building like a “rigid” box placed over flexible column.
7. Conclusions
If the SH ground motion under buildings with soft ground floor has finite phase velocities in the horizontal direction, then it may happen that: 1) the wave energy does not propagate from the ground into the building; 2) it propagates only into the “soft” ground floor; and 3) it propagates into the whole building. In the case, where it propagates into the soft ground floor, the ground floor may experience very large displacements while the displacement of the upper part of the building are small and there is a possibility of exponentially decaying towards the top of the building.
In conventional earthquake response analyses, which ignore the propagating wave effects, selection of the soft ground floor may reduce the overall design loads on the
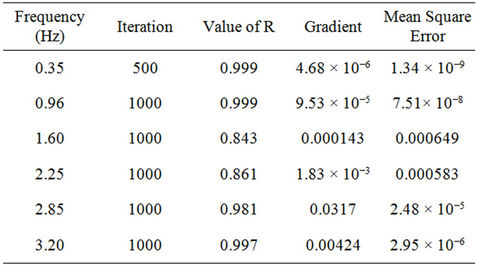
Table 1. Error estimation via ANN.
building. The analysis shows the nature of the additional deformations of the soft floor that should be taken into account in selecting the optimum strength and ductility of the ground floor structural member. Finally, Neural Network approach predicts the displacement at different floors of the building at different frequencies due to earthquake excitation.
REFERENCES
- V. A. Krivelev, Ed., “Volnovie Protcessi V. Konstrukeiah, Zdanii pri Seizmitchaskiih Vozdeistviah,” Nauka, Soviet Academy of Sciences, Moscow, 1987.
- S. Kojic, M. D. Trifunac and J. C. Anderson, “A PostEarthquake Response Analysis of the Imperial County Services Building in EI Centro,” Report No. CE-84-02, Department of Civil Engineering, University of Southern California, Los Angles, 1984.
- I. D. Gupta and M. D. Trifunac, “Order Statistics in Earthquake Response of Multi-Degree-of-Freedom Systems,” Earthquake Engineering and. Engineering Vibration, Vol. 7, No. 4, 1987, pp. 15-50.
- I. D. Gupta and M. D. Trifunac, “Order Statistics of Peaks of Response of Multicomponent Seismic Excitation,” Bulletin of the Indian Society of Earthquake Technology, Vol. 24, No. 3, 1987, pp. 135-139.
- I. D. Gupta and M. D. Trifunac, “Order Statistics of Peaks in Earthquake Response,” Journal of Engineering Mechanics, Vol. 114, No. 10, 1988, pp. 1605-1627. doi:10.1061/(ASCE)0733-9399(1988)114:10(1605)
- I. D. Gupta and M. D. Trifunac, “A Note on Contribution of Rocking Excitation to Earthquake Response of Simple Building,” Bulletin of the Indian Society of Earthquake Technology, Vol. 25, No. 2, 1988, pp. 73-89.
- S. Kojic, M. D. Trifunac and V. W. Lee, “Earthquake Response of Arch Dams to Non-Uniform Canyon Motion,” Report No. CE 84-02, University of Southern California, Los Angles, 1988.
- I. D. Gupta and M. D. Trifunac, “A Note on Contribution of Torsional Excitation to Earthquake Response of Simple Symmetric Buildings,” Earthquake Engineering and Engineering Vibration, Vol. 7, No. 3, 1987, pp. 27-46.
- A. M. Chandler, N. T. K. Lam and H. H. Tsang, “Shear Wave Velocity Modeling in Crustal Rock for Seismic Hazard Analysis,” Soil Dynamics and Earthquake Engineering, Vol. 25, No. 2, 2005, pp. 167-185. doi:10.1016/j.soildyn.2004.08.005
- A. K. Chopra, D. P. Clough and R. W. Clough, “Earthquake Resistance of Buildings with a Soft First Storey,” Earthquake Engineering & Structural Dynamics, Vol. 1, No. 4, 1973, pp. 347-355. doi:10.1002/eqe.4290010405
- D. M. Lee and I. C. Medland, “Base Isolation Systems for Earthquake Protection of Multi-Storey Shear Structures,” Earthquake Engineering & Structural Dynamics, Vol. 7, No. 6, 1979, pp. 555-568. doi:10.1002/eqe.4290070605
- R. I. Skinner, J. L. Beck and G. N. Bycroft, “A Practical System for Isolating Structures from Earthquake Attack,” Earthquake Engineering & Structural Dynamics, Vol. 3, 1975, pp. 297-309. doi:10.1002/eqe.4290030308
- S. D. Werner, et al., “An Evaluation of the Effects of Travelling Seismic Waves on the Three-Dimensional Response of Structures,” Report No. R7720-4514, Agbabian Associates, EI Segundo, 1977.
- I. Kashefi and M. D. Trifunac, “Investigation of Earthquake Response of Simple Bridge Structures,” Report No. CE86-02, University of Southern California, Los Angles, 1986.
- L. Tzenov and H. Boncheva, “Digiv Plan Sgardi s Ogled Sezimichnoto in Osiguriavanic,” Bulgarian Academy of Sciences, Bulgarian Geophysical Journal, Vol. 4, 1979, pp. 61-67.
- L. Tzenov, “Vliane na Dlzinata na Knostruktsiite vrhu Natovaranic,” Journal of Theoretical and Applied Mechanics, Vol. 17, 1981, pp. 97-105.
- M. I. Todorovska, V. W. Lee and M. D. Trifunac, “Investigation of Earthquake Response of Long Buildings,” Report No. CE-88-02, University of Southern California, Ls Angles, 1988.
- M. I. Todorovska and M. D. Trifunac, “Antiplane Earthquake Waves in Long Structures,” Journal of Engineering Mechanics, Vol. 15, No. 12, 1989, pp. 2687-2708. doi:10.1061/(ASCE)0733-9399(1989)115:12(2687)
- M. I. Todorovska and V. W. Lee, “Seismic Waves in Buildings with Shear Walls or Central Core,” Journal of Engineering Mechanics, Vol. 15, No. 12, 1989, pp. 2669- 2686. doi:10.1061/(ASCE)0733-9399(1989)115:12(2669)
- M. I. Todorovska and M. D. Trifunac, “A Note on Excitation of Long Structures by Ground Waves,” Journal of Engineering Mechanics, Vol. 116, No. 4, 1990, pp. 952- 964. doi:10.1061/(ASCE)0733-9399(1990)116:4(952)
- J. F. Hall, T. H. Heaton, M. W. Halling and D. J. Wald, “Near Source Ground Motion and Its Effects on Flexible Buildings,” Earthquake Spectra, Vol. 11, No. 4, 1995, pp. 569-605. doi:10.1193/1.1585828
- M. W. Halling and J. F. Hall, “Analysis of Base-Isolated Structures Utilizing Near-Source Strong Ground Motions,” Proceedings of the Structures Congress, Reston, 1997, pp. 1123-1127.
- J. P. Wolf and P. Obernhuber, “Effects of Horizontally Propagating Waves on the Response of Structures with a Soft First Storey,” Earthquake Engineering & Structural Dynamics, Vol. 9, No. 1, 1981, pp. 1-21. doi:10.1002/eqe.4290090102
- S. K. Chakraborty, S. K. Sarkar and S. P. Bhattacharya, “Frequency-Response Analysis of Shear Vibration of Long Structures Due to Surface Excitation,” International Journal of Acoustics and Vibration, Vol. 12, No. 3, 2007, pp. 109-115.
- S. K. Chakraborty and S. K. Sarkar, “Response Analysis of Multi-Storey Structures on Flexible Foundation Due to Seismic Excitation,” International Journal of Acoustics and Vibration, Vol. 13, No. 4, 2008, pp. 165-170.
- X. Wu, J. Ghaboussi and J. H. Garrett, “Use of Neural Networks in Detection of Structural Damage,” Computers and Structures, Vol. 42, No. 4, 1992, pp. 649-659. doi:10.1016/0045-7949(92)90132-J
- M. F. Elkordy, K. C. Chang and G. C. Lee, “Neural Networks Trained by Analytically Simulated Damage States,” Journal of Computing in Civil Engineering, Vol. 7, No. 2, 1993, pp. 130-145. doi:10.1061/(ASCE)0887-3801(1993)7:2(130)
- P. C. Pandey and S. V. Barai, “Multilayer Perceptron in Damage Detection of Bridge Structures,” Computers and Structures, Vol. 54, No. 4, 1995, pp. 597-608. doi:10.1016/0045-7949(94)00377-F
- J. Zhao, J. N. Ivan and J. T. DeWolf, “Structural Damage Detection Using Arti_Cial Neural Networks,” Journal of Infrastructure Systems, Vol. 4, No. 3, 1998, pp. 93-101. doi:10.1061/(ASCE)1076-0342(1998)4:3(93)
- S. F. Masri, A. W. Smyth, A. G. Chassiakos, T. K. Caughey and N. F. Hunter, “Application of Neural Networks for Detection of Changes in Nonlinear Systems,” Journal of Engineering Mechanics, Vol. 126, No. 7, 2000, pp. 666-676. doi:10.1061/(ASCE)0733-9399(2000)126:7(666)
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning International Representation by Error Propagation,” In: D. E. Rumelhart, et al., Eds., Parallel Distributed Processing, The MIT Press, Cambridge, 1986, pp. 318-362.
- R. Hecht-Nielsen, “Theory of the Back Propagation Neural Network,” Proceedings of International Joint Conference on Neural Networks, IEEE, New York, Vol. 1, 1989, pp. 593-605. doi:10.1109/IJCNN.1989.118638
- J. L. McClelland and D. E. Rumelhart, “Parallel Distributed Processing: Explorations in the Microstructure of Cognition,” Vol. 1-2, MIT Press, Cambridge, 1986.

