Journal of Applied Mathematics and Physics
Vol.03 No.12(2015), Article ID:62458,16 pages
10.4236/jamp.2015.312196
Viscous and Joules Dissipation on MHD Flow past a Stretching Porous Surface Embedded in a Porous Medium
Md. Sharif Uddin
Mathematics Discipline, Khulna University, Khulna, Bangladesh

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 October 2015; accepted 27 December 2015; published 30 December 2015
ABSTRACT
This paper investigates the influence of both viscous and joules dissipation on the problem of magneto-hydrodynamic flow past a stretching porous surface embedded in a porous medium for rotating case. Using similarity approach the system of partial differential equations is transformed into ordinary differential equations which strongly depend on the magnetic parameter, stretching parameter, rotation parameter, permeability parameter and Prandtl number. The coupled differential equations are numerically simulated using the Nactsheim-Swigert shooting technique together with Runge-Kutta six order iteration schemes. The velocity and temperature profiles are discussed and presented graphically. The comparisons for dimensionless skin friction coefficient and local Nusselt number are also taken into account and discussed and presented graphically.
Keywords:
Magneto-Hydrodynamic, Porous Medium, Joules Dissipation, Viscous Dissipation, Rotational Parameter

1. Introduction
Viscous dissipation changes the temperature distributions by playing a role like an energy source, which leads to affected heat transfer rates. The merit of the effect of viscous dissipation depends on whether the plate is being cooled or heated. Apart from the viscous dissipation in MHD flows, the Joules dissipation also acts as a volumetric heat source. Heat transfer analysis over porous surface is of much practical interest due to its abundant applications, such as, heat-treated materials traveling between a feed roll and wind-up roll, materials manufactured by extrusion, glass-fiber and paper production, cooling of metallic sheets, electronic chips and crystal growing. In view of all these aspects, Anjali Devi [1] deals with the effect of viscous and Joules dissipation on MHD flow, heat and mass transfer over a porous surface embedded in a porous medium. An analysis of thermal boundary layer in an electrically conducting fluid over a linearly stretching sheet in the presence of a constant transverse magnetic field with suction or blowing at the sheet was carried out by Chaim [2] . The viscous and joules dissipation and internal heat generation were taken into account in the energy equation. Very recently, the viscous and joules dissipation and internal heat generation were taken into account in the energy equation. Sajid et al. [3] investigated the non-similar analytic solution for MHD flow and heat transfer in a third-order fluid over a stretching sheet. He found that the skin friction coefficient decreased as the magnetic parameter or the third grade parameter increased. A mathematical analysis has been carried out on momentum and heat transfer characteristics in an incompressible, electrically conducting viscoelastic boundary layer fluid flow over a linear stretching sheet by Abel et al. [4] . A numerical reinvestigation of MHD boundary layer flow over a heated stretching sheet with variable viscosity has been analyzed by Pantokratoras [5] . Hence the present study investigates the effect viscous and Joules dissipation on MHD flow, heat and mass transfer over a porous surface embedded in a porous medium for rotating case.
2. Mathematical Analysis
Two-dimensional, nonlinear, steady, MHD laminar boundary layer flow with heat and mass transfer of a viscous, incompressible and electrically conducting fluid over a porous surface embedded in a porous medium in the presence of a transverse magnetic field including viscous and Joules dissipation is considered for investigation. An uniform transverse magnetic field of strength 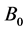 is applied parallel to y-axis. Consider a polymer sheet emerging out of a slit at
is applied parallel to y-axis. Consider a polymer sheet emerging out of a slit at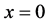 ,
, 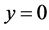 and subsequently being stretched, as in a polymer extrusion process. Let us assume that the speed at a point in the plate is proportional to the power of its distance from the slit and the boundary layer approximations are applicable. In writing the following equations, it is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. Under these conditions, the governing boundary layer equations of momentum, energy and diffusion with viscous and Joules dissipation are
and subsequently being stretched, as in a polymer extrusion process. Let us assume that the speed at a point in the plate is proportional to the power of its distance from the slit and the boundary layer approximations are applicable. In writing the following equations, it is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. Under these conditions, the governing boundary layer equations of momentum, energy and diffusion with viscous and Joules dissipation are
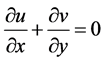 (1)
(1)
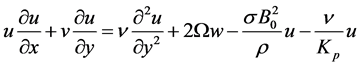 (2)
(2)
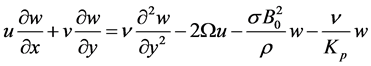 (3)
(3)
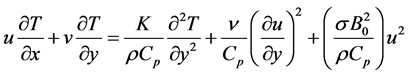 (4)
(4)
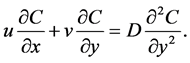 (5)
(5)
The boundary conditions are
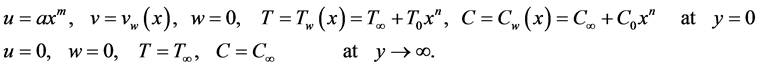 (6)
(6)
Here u, v are components of velocity components in the 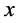 and
and 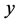 directions,
directions,  is kinematic coefficient of viscosity,
is kinematic coefficient of viscosity, 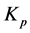 is permeability of the medium,
is permeability of the medium, 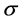 is electrical conductivity of the fluid,
is electrical conductivity of the fluid, 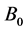 is applied magnetic field,
is applied magnetic field, 













We introduce the following similarity transformations are

where 

The velocity components are given by

It can be easily verified that the continuity Equation (1) is identically satisfied and introduce the non-dimen- sional form of temperature and concentration as

Hence Equations (2)-(5) and boundary conditions (6) reduced to:




The corresponding boundary conditions are

where, 






3. Results and Discussions
In Figure 1, transverse velocity profiles decreases with the increase of









In Figure 11, primary velocity profiles increases with the increase of

























Figure 1. Transverse velocity profiles for β.
Figure 2. Primary velocity profiles for β.
Figure 3. Primary shear stress profile for β.
Figure 4. Secondary velocity profile for β.
Figure 5. Secondary shear stress profile for β.
Figure 6. Temperature profiles for β.
Figure 7. Nusset number profiles for β.
Figure 8. Concentration profiles for β.
Figure 9. Sherwood number profiles for β.
Figure 10. Transverse velocity profiles for Ec.
Figure 11. Primary velocity profile for Ec.
Figure 12. Primary shear stress profile for Ec.
Figure 13. Secondary velocity profile for Ec.
Figure 14. Secondary shear stress profile for Ec.
Figure 15. Temperature profile for Ec.
Figure 16. Nusset number profile for Ec.
Figure 17. Concentration profile for Ec.
Figure 18. Sherwood number profile for Ec.
Figure 19. Transverse velocity profiles for λ.
Figure 20. Primary velocity profiles for λ.
Figure 21. Primary shear stress profiles for λ.
Figure 22. Secondary velocity profiles for λ.
Figure 23. Secondary shear stress profiles for λ.
Figure 24. Temperature profile for λ.
Figure 25. Nusset number profile for λ.
Figure 26. Concentration profile for λ.
Figure 27. Sherwood number profile for λ.
Figure 28. Transverse velocity profiles for λ.
Figure 29. Primary velocity profiles for M2.
Figure 30. Primary shear stress profiles for M2.
Figure 31. Secondary velocity profiles for M2.
Figure 32. Secondary shear stress profiles for M2.
Figure 33. Temperature profile for M2.
Figure 34. Nusset number profile for M2.
Figure 35. Concentration profile for M2.
Figure 36. Sherwood number profile for M2.
4. Conclusion
The effect of viscous and joules dissipation on MHD flow with heat and mass transfer past a stretching porous surface embedded in a porous medium is analyzed in the present study for rotating case. Increasing, decreasing and cross flows occur for the variation of different parameters.
Cite this paper
Md. SharifUddin, (2015) Viscous and Joules Dissipation on MHD Flow past a Stretching Porous Surface Embedded in a Porous Medium. Journal of Applied Mathematics and Physics,03,1710-1725. doi: 10.4236/jamp.2015.312196
References
- 1. Anjali Devi, S.P. and Ganga, B. (2009) Effects of Viscous and Joules Dissipation on MHD Flow, Heat and Mass Transfer past a Stretching Porous Surface Embedded in a Porous Medium. Nonlinear Analysis: Modelling and Control, 14, 303-314.
- 2. Chaim, T.C. (1977) Magnetohydrodynamic Heat Transfer over a Non-Isothermal Stretching Sheet. Acta Mechanica, 122, 169-179.
http://dx.doi.org/10.1007/BF01181997 - 3. Sajid, M., Hayat, T. and Asghar, S. (2007) Non-Similar Analytic Solution for MHD Flow and Heat Transfer in a Third-Order Fluid over a Stretching Sheet. International Journal of Heat and Mass Transfer, 50, 1723-1736.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2006.10.011 - 4. Subhas Abel, M., Sanjayan, E. and Nadeppanvar, M. (2008) Viscoelastic MHD Flow and Heat Transfer over a Stretching Sheet with Viscous and Ohmic Dissipations. Communication in Nonlinear Science and Numerical Simulation, 13, 1808-1821.
http://dx.doi.org/10.1016/j.cnsns.2007.04.007 - 5. Pantokratoras, A. (2008) Study of MHD Boundary Layer Flow over a Heated Stretching Sheet with Variable Viscosity: A Numerical Reinvestigation. International Journal of Heat and Mass Transfer, 51, 104-110.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.04.007





































