Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:60077,7 pages
10.4236/jamp.2015.39149
Exciton Condensates and Superconductors-Technical Differences and Physical Similarities
Henning Soller
Institut für Theoretische Physik, Universität Heidelberg, Heidelberg, Germany
Email: hsoller@googlemail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 July 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
We review several recent theoretical and experimental results in the study of exciton condensates. This includes the present experimental advances in the study of exciton condensates both using layers and coupled bilayers. We will shortly illustrate the different phases of exciton condensates. We focus especially on the Bardeen-Cooper-Schrieffer-like phase and illustrate the similarities to superconductors. Afterwards, we want to illustrate several recent advances and proposals for measuring the different phases of superconductors. In the remainder of this short review, we will provide an outlook for the possibilities and complications for future technical applications of exciton condensates.
Keywords:
Exciton Condensate, Entanglement, Coupled Bilayer, Laser Illuminated, Bardeen-Cooper-Schrieffer, Solar Cells

1. Introduction
Excitons represent one of the most interesting composite particles in modern condensed matter physics. In its simplest form, it is a bound state of an electron and a hole and thus has bosonic properties [1] .
Such bosonic systems have shown a huge variety of different phases including a Bose-Einstein condensate [2] , the Wigner crystal [3] [4] , superconductivity [5] [6] , a gas of particles [1] and even topological phases in reduced dimensions [7] [8] .
In this short review, we want to provide an overview of the recent advances in the generation of exciton condensates and their phase structure. We will especially focus on the superconductor-like phase [1] which allows to generate topological phases [9] -[11] .
We will shortly review the recent experimental advances and results in Section 2 and provide an overview of the different phases of an exciton condensate in Section 3. Section 4 will concentrate on techniques and theoretical proposals for measuring the different phases of an exciton condensate and Section 5 will discuss possible technical applications of exciton condensates in nanoelectronics. We will conclude in Section 6.
2. Recent Advances in the Generation of Exciton Condensates
An exciton is bound pair of an electron and a vacancy (hole) and thus may occur in various circumstances that allow the close proximity of many electrons and holes with some mechanism to forbid immediate recombination [12] [13] . The type of condensation depends on the density [14] : for low densities a Bose-Einstein condensate (BEC) is observed [15] whereas for high densities exciton condensates are assumed to be Barden-Cooper- Schrieffer (BCS) condensates [1] with a density given by
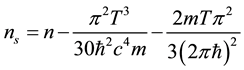 (1)
(1)
where n is the electronic density, T is the temperature and m is the electron mass.
The BEC phase emerges at low densities and low enough temperatures, where the key obstacle is to cool down the excitons to a temperature below the critical temperature [16] . So far this has only been achieved via the generation of indirect excitons in a coupled quantum well structure (AlGaAs). Recombination of the excitons allowed to measure the first order coherence function [15] via a Mach-Zehnder measurement as the proof of condensation in space.
The requirement for BCS condensation being high density and a relatively long lifetime is challenging since typically electron-hole pairs have a very short lifetime [12] . Technically the generation of excitons with long lifetimes in semiconductor heterostructures so far proceeds via three relatively distinct ways:
First, one may use materials for which the direct (dipole) transition for the annihilation of the electron-hole pair is forbidden. The most promising candidate in this respect has been CuO2. In such a setup it is possible to create both direct (electron and vacancy in the same layer) and indirect excitons (electron and vacancy in different layers). However, in spite of several promising results [12] the typical lifetimes of excitons in such materials are still too short to observe the phase structure.
Second, one may use physically separated coupled bilayers which are illuminated by laser at a given frequency. In this case the excitons generated in the separate layers (indirect excitons) have a very long lifetime due to the spatial separation of the layers but have to be generated externally by a laser field. The massively increased lifetime of indirect excitons in layered semiconductor structures and the possible confinement of the electrons in those structures [13] has triggered interest in this specific realization of excitons.
The third candidate are again coupled bilayers which are insulated from each other (e.g. Boroncarbide-hete- rostructure) but still close enough so that the electron and hole can feel their mutual Coulomb interaction. In this case an exciton condensate may emerge without the presence of an applied laser field due to the presence of electrons and holes in both layers very similar to the appearance of superconductivity.
Recently, systems of two graphene layers separated by boron nitride have been realized [17] where two graphene layers are embedded in a boron nitride crystal. The carrier densities in the top and bottom layer can be tunes by top gates and a chemical potential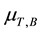 . Drag measurements were performed by applying a drive current in one layer and measuring the induced voltage in the second layer (see Figure 1).
. Drag measurements were performed by applying a drive current in one layer and measuring the induced voltage in the second layer (see Figure 1).
These experimental realizations are compatible with the prediction of the possibility of room-temperature superfluidity in layered graphene systems [18] -[21] and render the assumptions in similar works [22] not adequate for realistic systems.
First results for counterflow transport measurements in a range where condensation is expected have been performed in typical drag configurations, where two Corbino disks are confined in a GaAs/AlGaAs double quantum well structure [23] . The two Corbino disks serve as top and bottom layer of the exciton condensate. In the top Corbino disk a current is induced via a voltage and the induced current in the bottom Corbino disk is measured.
As the first-order coherence function has been shown to be accessible experimentally and shows the typical behavior of a BEC condensate one of the primary theoretical research directions has been to find ways how to
Figure 1. Exciton condensate with two chemical potentials on the different layers and an applied drive-current on the upper layer. A drag voltage can be measured in the lower layer of the two separated layers with a distance d.
investigate the behavior on the BCS side in a similar way.
3. Phases of an Exciton Condensate
Typically we expect to observe a Bose-Einstein condensate (BEC) for low densities whereas for high densities exciton BCS condensates are expected. However, two key characteristics of exciton condensates allow for a richer phase structure.
The first characteristic is the presence of parallel electric dipole moments of indirect excitons due to the separation and different charges of the electron and the vacancy. These become important at intermediate densities. In this case, the electrons can be excited to form excitons but the excitons also feel the repulsion due to the dipole-interaction
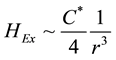 (2)
(2)
We therefore observe a cubic dependence on the inter-exciton distance r.
This inter-exciton exchange leads to the fact that excitons may form Wigner crystals [18] [19] as electrons or Rydberg atoms do [3] .
If the excitons can be observed on a timescale small enough in order to assume that they are fixed in space we should expect the formation of an emergent long-range order of Wigner-crystal type [18] [19] .
The second characteristic is the BCS phase itself. If we discuss one-dimensional systems two topological phases are possible either with all pairs bound or with two particles at the ends being present unpaired [10] [20] . The topological phase can only be reached under certain conditions when the overall systems behaves as the Kitaev model that we will investigate in more detail later [7] .
4. Possible Experiments to Investigate the Phase Structure of Exciton Condensates
Whereas the BEC phase of excitons has been detected the BCS and intermediary phases still remain to be explored experimentally. The more we move away from the BEC phase the less adequate it will become to investigate excitons only in space but we will need to move to transport measurements.
First, transport measurements of excitons did not seem to be an adequate mean to explore excitons since these are neutral particles and therefore will not move once localized in space.
However, as discovered by Su and MacDonald [21] the BCS phase allows the vacancies and electrons to move in separate directions if contacted separately as they are only localized in momentum space [16] . The possibility of superfluid counterflow is a clear prediction to be searched for experimentally.
Theoretically all important features in this BCS-condensed situation are captured by applying an effectively one-dimensional model for an exciton condensate extending from  to
to 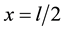 [23]
[23]
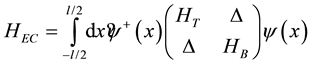 (3)
(3)
where 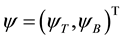 is the two-layer spinor and
is the two-layer spinor and 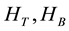 describes the electron (vacancy) single-particle term of the top/ bottom layer. The interlayer interaction is described by an exciton order parameter ∆.
describes the electron (vacancy) single-particle term of the top/ bottom layer. The interlayer interaction is described by an exciton order parameter ∆.
The first and most intriguing prediction from this model is that for voltages below the gap of the exciton condensate the top-current  is equal and opposite to the bottom-current [21] [24] . This feature is remarkably stable upon finite temperature [25] . In spite of the fact that the electron and the vacancy represent a two-particle system the fact that both particles dwell in separate layers gives rise to the fact that the Johnson-Nyquist and shot noise only show one-particle behavior. However, the noise in this configuration is equal and opposite to the cross-correlation of the two currents which again reveals their closely connected nature [25] .
is equal and opposite to the bottom-current [21] [24] . This feature is remarkably stable upon finite temperature [25] . In spite of the fact that the electron and the vacancy represent a two-particle system the fact that both particles dwell in separate layers gives rise to the fact that the Johnson-Nyquist and shot noise only show one-particle behavior. However, the noise in this configuration is equal and opposite to the cross-correlation of the two currents which again reveals their closely connected nature [25] .
The theory described in Equation (3) has also been checked by comparison to the experimental data in [23] and acceptable agreement has been obtained indicating that the experiment in [23] has indeed realized a BCS condensate of excitons [26] .
The investigation of the non-BCS phases becomes less trivial due to the special nature both of the Kitaev phase and the crystalline phase.
The crystalline phase emerges as a consequence of the dipole interaction of excitons. It can be detected in three ways: either by modern spectroscopic techniques measuring the distribution function of generated excitons or the pair correlation function or by a transport measurement using the photoelectric effect.
We will first discuss the two possibilities to measure the phase transition by modern spectroscopic techniques. In this case one focusses on physically separated bilayers and extremely short laser pulses and experimental of τ < 0.1 ns so that the movement of the excitons can be neglected [19] . In this case, the electrons of the underlying system can be effectively regarded as a two-level system (the first level corresponding to typical electrons and the second level corresponding to excitons) [19] in accordance with previous studies of Rydberg atoms [4]
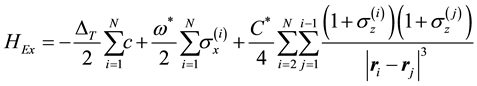 (4)
(4)
where  refers to the transition frequency between the electronic and the exciton state,
refers to the transition frequency between the electronic and the exciton state, 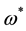 is the Rabi frequency of the system and
is the Rabi frequency of the system and 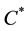 is the dipole interaction strength. The Pauli matrices act on the two-level system of each of the N electrons and
is the dipole interaction strength. The Pauli matrices act on the two-level system of each of the N electrons and 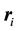 refers to the coordinates of the electron.
refers to the coordinates of the electron.
The Hamiltonian in Equation (4) can be numerically simulated for a finite system of size L. In this case, the correlation function clearly shows the transition from a liquid to a crystalline phase. For weak interactions (blue curve in Figure 2) almost no correlation of the excitons can be observed whereas for strong interaction the system exhibits clear crystalline correlations (red curve in Figure 2). It also exhibits a radius around every electron where no exciton can be formed due to interaction, known as blockade radius due to the repulsive interaction.
Figure 2. Illustrative correlation function in an excitonic bilayer system of size L described by the Hamiltonian in Equation (4). The blue curve refers to weakly interacting excitons and the red curve refers to strongly interacting excitons.
The same behavior can also be extracted by exploring the distribution function or respectively the corresponding moments of the number of excitons. The number of excitons drops by increasing interaction but the variance first increases with increasing interaction whereas for the interaction being larger than a critical value it sharply drops. This change can be associated to the formation of crystalline order [19] .
However, the crystalline phase cannot just be observed by spectroscopic measurements, but also by exploring the photoelectric effect in an exciton bilayer.
If we assume no interaction the Hamiltonian in Equation (4) becomes exactly solvable and the number density of excitons is given by

with 

where 


where 
Indeed Equation (7) allows always for the trivial solution (

If we move to crystalline order the excitons are fixed in space due to their mutual interaction and therefore a photoelectric effect will disappear.
If we therefore find a solution for which the excitons show a photoelectric effect and vary the interaction in order to suppress it, we have clearly shown the transition to the crystalline phase via a transport measurement.
Finally, we want to investigate the Kitaev phase. Typically the Kitaev model can be easily realized in a system involving spin-orbit coupled nanowires coupled to superconductors in a magnetic field or ferromagnetic nanowires coupled to superconductors [27] -[29] .
In the case of exciton condensates, we may also mimick the Kitaev model via coupling a 2D exciton condensate to two p-wave superconductors as shown in Figure 3. The 2D exciton condensate is then proximity-coupled to the p-wave superconductor.
Figure 3. Setup for creation of Majorana fermions in an exciton condensate. The exciton condensate is coupled to four metallic leads and two p-wave superconductors.
In this case, the simplest Hamiltonian describing the exciton condensate in the presence of the p-wave super- conductors is given by [9]

where the states a four-spinors 


and top-bottom space respectively.
The spectrum can be revaled by squaring Equation (8) twice [28] [29] which yields the exciton energies dependent on the momentum. The gap near p = 0 is given by

Consequently, we will observe a level-crossing at 

The appearance of this phase can be easily observed as the Majorana fermions at the ends of the exciton condensate will open perfectly conducting transmitting channels either through the top or bottom part of the exciton condensate. As the top and bottom part will therefore be perfectly conducting transconductance between the layers has to vanish due to unitarity [9] . The vanishing transconductance is therefore the indicator for the topological phase transition.
After this investigation of the different phases of exciton condensates, we want to investigate possible technological applications.
5. Technical Applications of Exciton Condensates in Nanoelectronics
Studying technical applicatios of exciton condensates two properties are of high relevance: the existence of superconducting counterflow and the possibility to excite excitons with light.
The counterflow as such may be used for transformation of current on the nanoscale. In order to do so, one layer of the exciton condensate should not be connected to an outer voltage source but to a nanoelectronical system itself. This means that e.g. the lower layer may directly couple to systems such as quantum point contacts or quantum dots coupled to phonons. Due to the coupling to an additional system the voltage characteristics of the lower layer are changed and the system may be used to transform voltage on the nanoscale [25] .
Furthermore, the availability of a photoelectric effect allows the usage of exciton condensates as solar cells (see Figure 4). However, several shortcomings need to be overcome in order to make exciton condensates a future solar cell. The availability of superconducting counterflow in the layers is a clear advantage compared to traditional silicon-based solar cells. However, the contact resistance remains. Also, here we have only shown solar cells to be applicable for light of a single frequency, whereas sunlight has a wide spectrum of frequencies. Therefore, work remains to be done in order to demonstrate the possibility of exciton-condensate based solar cells with better technical capabilities than silicon-based solar cells.
Figure 4. Exciton condensate illuminated by a laser field.
Finally, the existence of a Kitaev phase and the possible existence of Majorana fermions allow to use exciton condensates as future building blocks of topological quantum computers as discussed in [7] .
6. Conclusions
To conclude, we have reviewed several of the recent experimental and theoretical results for exciton condensates. After the theoretical and experimental exploration of the BEC phase of exciton condensates, the BCS and crystalline phases have attained increasing attention in the last years.
Especially, the possibility of superconducting counterflow in the top and bottom layer starts to be verified experimentally and will in the future be enhanced by the study of the high-order cumulants and cross-correla- tions. Likewise, the study of exciton condensates illuminated by laser light allows to observe crystalline order as in a Wigner crystal and the photoelectric effect in contacted exciton condensates.
Finally, the existence that a rich phase structure allows for several future technological applications of exciton condensates includes the usage in nanotransformers, solar cells and topological quantum computers, which provides a promising future path to explore for exciton condensates.
Acknowledgements
The author would like to thank A. Komnik, S. Maier and D. Breyel for numerous discussions.
Cite this paper
HenningSoller, (2015) Exciton Condensates and Superconductors-Technical Differences and Physical Similarities. Journal of Applied Mathematics and Physics,03,1218-1225. doi: 10.4236/jamp.2015.39149
References
- 1. Lozovik, Y.E. and Berman, O.L. (1996) Phase Transitions in a System of Two Coupled Quantum Wells. Journal of Experimental and Theoretical Physics Letters, 64, 573-579.
http://dx.doi.org/10.1134/1.567264 - 2. Bose, S.N. (1924) Plancks Gesetz und Lichtquantenhypothese. Zeitschrift für Physik, 26, 178-181.
http://dx.doi.org/10.1007/BF01327326 - 3. Breyel, D., Schmidt, T.L. and Komnik, A. (2012) Rydberg Crystallization Detection by Statistical Means. Physical Review A, 86, Article ID: 023405.
http://dx.doi.org/10.1103/PhysRevA.86.023405 - 4. Robicheaux, F., Hernández, J.V., Topçu, T. and Noordam, L.D. (2004) Simulation of Coherent Interactions between Rydberg Atoms. Physical Review A, 70, Article ID: 042703.
http://dx.doi.org/10.1103/PhysRevA.70.042703 - 5. Bardeen, J., Cooper, L.N. and Schrieffer, J.R. (1957) Theory of Superconductivity. Physical Review, 108, 1175.
http://dx.doi.org/10.1103/PhysRev.108.1175 - 6. Onnes, H.K. (1911) The Resistance of Pure Mercury at Helium Temperatures. Commun. Phys. Lab. Univ. Leiden, 12, 1.
- 7. Kitaev, A.Y. (2001) Unpaired Majorana Fermions in Quantum Wires. Physics-Uspekhi, 44, 131.
http://dx.doi.org/10.1070/1063-7869/44/10S/S29 - 8. Altland, A. and Zirnbauer, M.R. (1997) Nonstandard Symmetry Classes in Mesoscopic Normal-Superconducting Hybrid Structures. Physical Review B, 55, 1142.
http://dx.doi.org/10.1103/PhysRevB.55.1142 - 9. Soller, H. and Breyel, D. (2013) Signatures in the Conductance for Phase Transitions in Excitonic Systems. Modern Physics Letters B, 27, Article ID: 1350185.
http://dx.doi.org/10.1142/S0217984913501856 - 10. Seradjeh, B. (2012) Majorana Edge Modes of Topological Exciton Condensate with Superconductors. Physical Review B, 86, Article ID: 121101.
http://dx.doi.org/10.1103/physrevb.86.121101 - 11. Budich, J.C., Trauzettel, B. and Michetti, P. (2014) Time Reversal Symmetric Topological Exciton Condensate in Bilayer HgTe Quantum Wells. Physical Review Letters, 112, Article ID: 146405.
http://dx.doi.org/10.1103/PhysRevLett.112.146405 - 12. Snoke, D. (2002) Spontaneous Bose Coherence of Excitons and Polaritons. Science, 298, 1368-1372.
http://dx.doi.org/10.1126/science.1078082 - 13. Gärtner, A., Prechtel, L., Schuh, D., Holleitner, A.W. and Kotthaus, J.P. (2007) Micropatterned Electrostatic Traps for Indirect Excitons in Coupled GaAs Quantum Wells. Physical Review B, 76, Article ID: 085304.
http://dx.doi.org/10.1103/PhysRevB.76.085304 - 14. Comte, C. and Nozieres, P. (1982) Exciton Bose Condensation: The Ground State of an Electron-Hole Gas-I. Mean Field Description of a Simplified Model. Journal de Physique, 43, 1069-1081.
http://dx.doi.org/10.1051/jphys:019820043070106900 - 15. High, A.A., Leonard, J.R., Hammack, A.T., Fogler, M.M., Butov, L.V., Kavokin, A.V., et al. (2012) Spontaneous Coherence in a Cold Exciton Gas. Nature, 483, 584-588.
http://dx.doi.org/10.1038/nature10903 - 16. Zwierlein, M.W., Stan, C.A., Schunck, C.H., Raupach, S.M.F., Kerman, A.J. and Ketterle, W. (2004) Condensation of Pairs of Fermionic Atoms near a Feshbach Resonance. Physical Review Letters, 92, Article ID: 120403.
http://dx.doi.org/10.1103/PhysRevLett.92.120403 - 17. Gorbachev, R.V., Geim, A.K., Katsnelson, M.I., Novoselov, K.S., Tudorovskiy, T., Grigorieva, I.V., et al. (2012) Strong Coulomb Drag and Broken Symmetry in Double-Layer Graphene. Nature Physics, 8, 896-901.
http://dx.doi.org/10.1038/nphys2441 - 18. Astrakharchik, G.E., Boronat, J., Kurbakov, I.L. and Lozovik, Y.E. (2007) Quantum Phase Transition in a Two-Dimensional System of Dipoles. Physical Review Letters, 98, Article ID: 060405.
http://dx.doi.org/10.1103/PhysRevLett.98.060405 - 19. Breyel, D., Soller, H., Schmidt, T.L. and Komnik, A. (2014) Detecting an Exciton Crystal by Statistical Means. Physica B: Condensed Matter, 441, 33-36.
http://dx.doi.org/10.1016/j.physb.2014.01.042 - 20. Su, J.J. and MacDonald, A.H. (2008) How to Make a Bilayer Exciton Condensate Flow. Nature Physics, 4, 799-802.
http://dx.doi.org/10.1038/nphys1055 - 21. Min, H., Bistritzer, R., Su, J.J. and MacDonald, A.H. (2008) Room-Temperature Superfluidity in Graphene Bilayers. Physical Review B, 78, Article ID: 121401.
http://dx.doi.org/10.1103/PhysRevB.78.121401 - 22. Kharitonov, M.Y. and Efetov, K.B. (2008) Electron Screening and Excitonic Condensation in Double-Layer Graphene Systems. Physical Review B, 78, Article ID: 241401.
http://dx.doi.org/10.1103/PhysRevB.78.241401 - 23. Nandi, D., Finck, A.D.K., Eisenstein, J.P., Pfeiffer, L.N. and West, K.W. (2012) Exciton Condensation and Perfect Coulomb Drag. Nature, 488, 481-484.
http://dx.doi.org/10.1038/nature11302 - 24. Dolcini, F., Rainis, D., Taddei, F., Polini, M., Fazio, R. and MacDonald, A.H. (2010) Blockade and Counterflow Supercurrent in Exciton-Condensate Josephson Junctions. Physical Review Letters, 104, Article ID: 027004.
http://dx.doi.org/10.1103/PhysRevLett.104.027004 - 25. Soller, H., Dolcini, F. and Komnik, A. (2012) Nanotransformation and Current Fluctuations in Exciton Condensate Junctions. Physical Review Letters, 108, Article ID: 156401. http://dx.doi.org/10.1103/PhysRevLett.108.156401
- 26. Soller, H. and Komnik, A. (2013) Current Noise and Higher Order Fluctuations in Semiconducting Bilayer Systems. Fluctuation and Noise Letters, 12, Article ID: 13400014.
http://dx.doi.org/10.1142/S0219477513400014 - 27. Oreg, Y., Refael, G. and von Oppen, F. (2010) Helical Liquids and Majorana Bound States in Quantum Wires. Physical Review Letters, 105, Article ID: 177002.
http://dx.doi.org/10.1103/PhysRevLett.105.177002 - 28. Gangadharaiah, S., Braunecker, B., Simon, P. and Loss, D. (2011) Majorana Edge States in Interacting One-Dimensional Systems. Physical Review Letters, 107, Article ID: 036801.
http://dx.doi.org/10.1103/PhysRevLett.107.036801 - 29. Soller, H. and Komnik, A. (2014) Charge Transfer Statistics of Transport through Majorana Bound States. Physica E: Low-Dimensional Systems and Nanostructures, 63, 99-104.
http://dx.doi.org/10.1016/j.physe.2014.05.020





