Received 23 February 2015; accepted 26 May 2015; published 29 May 2015

ABSTRACT

This paper presents theoretical modeling for predicting the optimum twist angle on yarn made by open end rotor spinning machine in textile industry. Fiber movement on yarn can be used for predicting the optimum twist angle which can be used to reduce yarn breaking in spinning process. In this research the twist angle has been found and the result of this research shows the twist angle around 45˚ and the theoretical result of the ratio of rotor diameter to fiber length is.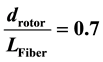

Keywords:

Twist Angle, Open End Spinning, Yarn Movement

1. Introduction

In textile industry the study of the fiber movement inside yarn has been researched of many researchers. According to Rohlena [1] , Lawrence [2] and Hearle [3] , fiber movement on yarn will influence the yarn breakage. Fiber migration is the change in the distance of a fiber (along its length) from the axis of a yarn, which occurs during production spinning yarn. According to Lawrence [2] , the characteristic of spun yarn can be determined by the fiber movement and yarn structure as Figure 1.

Rohlena [1] said that breakage rate is influenced by the twist. The lower the twist is, the higher the breakage rate is. According to Hearle [3] and Lawrence [2] , fiber migration can be shown as the relation of as relative

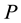measure of radial position against the yarn length and the probability, , of the fiber being resided into the yarn depends on the ratio of the sum of elemental length (yarn length) to the fiber length 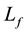(Figure 2). Hearle [3] and Rohlena [1] developed mathematical relationship of fiber migration as below

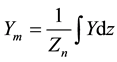(1)

where is mean fiber migration, is yarn length and as relative measure of radial position. According to Lawrence [2] , for the probability can be written as

(2)

Thus, for the probability 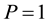then the full length of the fiber will be spun in and for the probability, then fiber is laid on the surface, as it’s called hair. According to Furter [4] , the higher of twist is, the lower the hairiness is. If part of the fiber length is spun in and the rest protrudes from the yarn, then. The trace of fiber inside the yarn can be shown as Figure 2.

Yarn properties can be analyzed and determined from the fiber movement which is shown by the ratio of yarn length to fiber length, , as below

(3)

where the sum of fiber length which is projected to the yarn length and is the angle of yarn length against fiber trace. According to Lawrence [2] and Rohlena [1] , the ratio of yarn length to fiber length, , will influence the strength. The higher value of the more strength of yarn will increase. According to Musa [5] , Penava [6] and Prenzova [7] the relationship of yarn strength is proportional to the diameter of yarn, the wider the diameter of the yarn the higher the strength of the yarn. According to Trommer [8] , the value of tenacity on winding (yarn package) must be around 20% R_o (tenacity of take off roller) which makes the yarn will not break during the spinning process. By extensive experiment, Trommer [8] has found that the limitation of the ratio of rotor diameter to fiber length is more than 0.7. The influence of ratio to the properties of yarn such as diameter of yarn, angle twist, strength, hairiness, yarn delivery, and also yarn twist will be discussed and derived in this paper looking from the fiber-yarn movement on cylindrical coordinate and using Lagrange methods.

2. Predicting Twist Angle of Fiber Movement Using Lagrange Methods

Suppose a fiber moves in cylindrical coordinate and twist is defined as turns per unit yarn length H (in unit m).

Suppose a cotton fiber with length inside yarn (radius) moves along l-axis as in Figure 3 by an external force and an twist angle. It can be used Lagrange methods to analyze the moving of individual fiber which moves by angular speed [rpm] and by ignoring the influenced of yarn mass, hence

(4)

(5)

(6)

Suppose that the acceleration of fiber accelerates

(7)

(8)

(9)

(10)

Twist is defined as turns per unit length, hence

(11)

(12)

(13)

(14)

is defined as twist coefficient

(15)

Another way to derive the relation of twist and the yarn number is by using this formula

(16)

(17)

(18)

(19)

(20)

substitute Equation (17) to Equation (9)

(21)

(22)

(23)

(24)

Suppose the angle twist

(25)

Taking

(26)

(27)

According to Trommer [8] , the value of must be around 20% R_o which makes the yarn will not break during the spinning process, hence Equation (24) is agree with the experimental result. Using the twist angle 45˚ it can be explained and determined the relationship of fiber movement inside yarn and also the limitation of the ratio of rotor diameter to fiber length is more than 0.7 and the fiber substansce strength (the ratio of yarn strength to fiber strength is 50%).

3. Development of Fiber Movement Model

A simple model of fiber movement would be a made in a cylindrical coordinate. Pretend that a fiber moves inside a yarn in a cylindrical coordinate which can be written as below

(28)

During a certain time, a length of a fiber moves inside the yarn whose length is. The fiber is rotated about this axis through an angle. A fiber moves toward or away from the yarn axis with a distance. The geodesic equation of the square of length of fiber can be measured as below

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

Let in the equation above, we have

(40)

(41)

(42)

(43)

Hence

(44)

(45)

(46)

which has solutions

(47)

(48)

For then

(49)

(50)

For in one full rotation, then

(51)

(52)

Let, then

(53)

Defined that, we have

(54)

Hence Equation (28) can be written as

(55)

(56)

(57)

(58)

(59)

For the value of, then

(60)

Based on Figure 4 then

(61)

(62)

The prediction of the theoretical model is appropriate enough comparing the experimental having done by Trommer [8] . It has found that the limitation of the ratio of rotor diameter to fiber length is more than 0.7. The value of can be measured as

(63)

The value of depends on (the angle of twist). According to Lawrence [2] and Rohlena [8] , the ratio of yarn length to fiber length, , will influence the strength. The higher value of the more strength of yarn will increase.

4. Results and Discussion

The prediction of fiber movement and the influence of the kinematic inside of yarn which is worked by a fiber has been derived and determined accurately according to the experimental data of Trommer [8] . According to Trommer [8] , the value of tenacity on winding on yarn package must be around 20% R_o (tenacity of take off roller) which makes the yarn will not break during the spinning process. By extensive experiment, Trommer [8] has found that the limitation of the ratio of rotor diameter to fiber length is more than 0.7. The prediction of the theoretical model is accurate enough comparing the experimental having done by Trommer [8] . It has found that the limitation of the ratio of rotor diameter to fiber length is more than 0.7. the value of can be measured as

(64)

The value of depends on (the angle of twist). According to Lawrence [2] and Rohlena [1] , the ratio of yarn length to fiber length, , will influence the strength. The higher value of the more strength of yarn will increase. The value of twist angle is 45˚ using this value the value, then the tenacity on winding (yarn package) must be around 20% R_o (tenacity of take off roller) which makes the yarn will not break during the spinning process.

5. Conclusion

It has been shown via classical mechanics (Lagrange and geodesic methods) that fiber movement on yarn can be

used for predicting the optimum angle twist which can be used to reduce yarn breaking in spinning process. In this research the angle twist has been found and the result of this research shows the angle twist around 45˚ and

the theoretical result of the ratio of rotor diameter to fiber length is.

References