Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:59192,5 pages
10.4236/tel.2015.54068
Should a New Good Replace Existing Ones? A Network Approach*
Tomohiko Konno
Institute of Advanced Study, Waseda University, Tokyo, Japan
Email: tomo.konno@aoni.waseda.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 July 2015; accepted 24 August 2015; published 27 August 2015
ABSTRACT
We study goods (or service) with network effect. Social network services are examples. An existing service has an advantage over new one because of the network effect. We study the condition that new goods (or service) replace the existing one, and show that the condition depends on the underlying network structures. For this purpose, we study a coordination game with network structure. If more than half of the players change their strategies, then new strategy beats the existing one in regular networks. On the other hand, if very small number of players with large degree changes their strategies, then the new strategy beats the existing one in scale-free networks.
Keywords:
Local Social Interaction, Network Effect, Network Heterogeneity, Scale-Free Networks, Games on Networks, Coordination Games

1. Introduction
There are goods and service which have network effects. People obtain benefits if neighbors use it. The social local interaction can be represented by a network. Social network services and programming languages are examples of such goods with network effect. An existing goods has an advantage over new goods. The existing one is already in there and has network externality.
How can new goods beat the existing one under which condition(s), if any, new goods can beat existing ones? Does the structure of social network matter? We will address these questions. The goods and service with network effects can be modeled by a coordination game on networks. The networks are the social networks. Each player plays games with adjacent players only and derives payoff from each game. In a coordination game, a player obtains payoff if the player chooses the same strategy as that of the opponent. Such a coordination game on networks is the model for goods and service with network effects through social local interaction. We denote that a strategy prevails in the network if the strategy is chosen by more than half of the players. We study a coordination game with two strategies, A and B on networks. Suppose that all the players have the strategy B in the beginning and then we will show the condition for strategy A to beat the strategy B and to prevail in the network. The condition depends on the underlying network structures. If more than half of the players change their strategies, then new strategy beats the existing one in regular networks. On the other hand, if very small number of players with large degree change their strategies, then the new strategy beats the existing one in scale-free networks. More specifically, we will investigate the following problem.
1. In the beginning, all the players choose strategy B.
2. Then, the strategies of a fraction of players are changed from B to A.
3. After enough time steps, the state will arrive at either of the two distinct stable states.
(a) More than half of the players still take strategy B. The strategy B still prevails;
(b) More than half of the players change to the strategy A. The strategy A beats strategy B.
This situation is illustrated in Figure 1.
We will address the following questions:
1. What is the ratio of players who should change their strategies from B to A so that strategy A will prevail in the stable state?
2. Is the ratio dependent on network structure? Are they different between regular networks and scale-free networks in particular?
We will show that the network structure matters and that only small number of hub players determine whether new goods beat the existing strategy in scale-free networks. Scale-free networks are typical networks in reality. While more than half of the players must change their strategies from A to B for strategy A to prevail in regular networks, if small number of hub players change their strategies, then the strategy A prevails in scale-free networks.
This research is partly motivated by complex network researches. An academic interest in scale-free networks arose in late 1990’s (see the paper [1] ). Now it is recognized that outcomes of models including games on networks are dependent on network structures. In particular, interesting outcomes happen in scale-free networks because they have great network heterogeneity, which is the variance of degree distribution. One example is an epidemic spread model studies by [2] that investigates a contact network of an infectious disease. In regular networks, an epidemic spread occurs if and only if a certain condition is satisfied. On the other hand, it always breaks out in scale-free networks.
Figure 1. A blue vertex indicates strategy B, while a red vertex indicates strategy A. Initially, all the players choose strategy B and then strategies of a fraction of players are changed from B to A. In the next time step, two cases can occur by the network effect. In one case, some players return to strategy B, and strategy B prevails again. In the second case, other players choose strategy A, and strategy A prevails. Which occurs depends on the network structure and the fraction of changed players as we will show later.
2. Model
A player is on each vertex on a network. They play games with adjacent players only and derive payoff from each game. We will consider a pure coordination game, which means payoff from choosing the same strategy with adjacent player are the same regardless of the strategy A and B. We derive an average payoff from social interactions in some cases and we derive payoff from each social interaction in orther cases. We will study the latter case. To study this pure coordination game on networks is a good idea in order to investigate the condition that new goods beats the existing goods if they have network effect.
Let 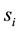 denote the strategy of player i. We assume that
denote the strategy of player i. We assume that 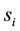 takes either
takes either  or
or  without loss of generality. The
without loss of generality. The  corresponds to strategy A and
corresponds to strategy A and 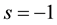 to B. The payoff of the player i from the game with adjacent player j is given by
to B. The payoff of the player i from the game with adjacent player j is given by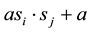 . The payoff from choosing the same strategy is 2a and the payoff is 0 otherwise. Let
. The payoff from choosing the same strategy is 2a and the payoff is 0 otherwise. Let 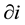 denote the set of all players adjacent to player i. The payoff
denote the set of all players adjacent to player i. The payoff 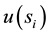 of the player i is given by
of the player i is given by
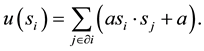 (1)
(1)
A randomly chosen player updates the strategy in each time step. We assume that player i chooses the strategy with the following Logit probability:
 (2)
(2)
where 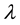 is the payoff responsiveness parameter which can be understood as rationality. Such a functional form (2) has been used by several well-known papers, for example, [3] - [6] . We have a method to study network problem with this functional form. The mathematical structure itself is the same as that of the Ising model (see references such as [7] - [10] ). We solve the model by the method developed in order to solve the Ising model. Moreover, [6] solved the model by the same method that was developed earlier. After a while, the probability distribution of the strategy will be stable. This state is called stable state and we will focus on it.
is the payoff responsiveness parameter which can be understood as rationality. Such a functional form (2) has been used by several well-known papers, for example, [3] - [6] . We have a method to study network problem with this functional form. The mathematical structure itself is the same as that of the Ising model (see references such as [7] - [10] ). We solve the model by the method developed in order to solve the Ising model. Moreover, [6] solved the model by the same method that was developed earlier. After a while, the probability distribution of the strategy will be stable. This state is called stable state and we will focus on it.
3. Beating the Existing Strategy
If the mean strategy of all the players is positive , strategy A prevails in the network; in other words, strategy A beats the existing strategy B. Degree is a number of links a vertex has. Let
, strategy A prevails in the network; in other words, strategy A beats the existing strategy B. Degree is a number of links a vertex has. Let  denote the fraction of players with degree
denote the fraction of players with degree  whose strategies were changed from B to A,
whose strategies were changed from B to A, 



where


Therefore, we have the following result.
Proposition 1: New strategy A will beat the existing strategy B if and only if 
3.1. Two Ways of Changing the Strategy
The existing strategies are changed in either of following two ways.
Random replacement: Players change strategies from B to A randomly irrespective of the degree. If a fraction 


Selective replacement: Players change strategies from B to A according to a descending order of degree. We have

meaning if the degree of a vertex is larger than



3.2. Regular Network
Every vertex has the same degree in regular networks, so elective replacement cannot be considered. We consi- der random replacement. Because of the condition 
Proposition 2: For new strategy A to beat the existing strategy B more than half of the players must change their strategies from B to A in random replacement for regular networks.
What does this imply? The best strategy for players to get the biggest payoff is to choose the strategy chosen by most of the neighbors. In random replacement, the strategies of more than half of the players are changed so that more than half of the neighbors of any player choose strategy A. This is not an effective way to beat the existing strategy since we must change the strategies of more than half of the players. From other respect, regular networks is robust.
3.3. Scale-Free Network
In random replacement, the condition remains the same as Proposition 2.
Proposition 3: For new strategy A to beat the existing strategy B more than half of the players must change their strategies from B to A in random replacement for scale-free networks.
Strategies of more than half of the players must be changed from B to A in scale-free networks. We will discuss selective replacement, wherein we have

We also have


We will calculate

Suppose a fraction 

which yields

The condition 

Proposition 4:
In scale-free networks and in selective replacement, if more than a fraction 
An example: Suppose we have a scale-free network with





From one respect, scale-free networks are weak to selective replacement. If very small number of hub players changes their strategies, then most of the players change their strategies. On the other hand, scale-free networks are as robust as regular network in random replacement.
3.4. Numerical Simulations
We confirm the claims by numerical simulations. The payoff parameter



scale-free network for fair comparison. The simulation for regular network was done in the following way. In the beginning all the players are B-player meaning


Figure 2. The x axis indicate 

Figure 3. The x axis indicate 

4. Concluding Remarks
We study goods and service with network effect. For this purpose, we study a coordination game with network structure. We study the condition that new goods and service replace the existing strategy. In regular networks, half of the players must be changed their strategies. On the other hand, it is enough for the new strategy to replace the existing strategy if small number of players with large degree changes their strategies. If
Cite this paper
TomohikoKonno, (2015) Should a New Good Replace Existing Ones? A Network Approach. Theoretical Economics Letters,05,584-589. doi: 10.4236/tel.2015.54068
References
- 1. Barabasi, A. and Albert, R. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512. http://dx.doi.org/10.1126/science.286.5439.509
- 2. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Spreading in Scale-Free Networks. Physical Review Letters, 86, 3200. http://dx.doi.org/10.1103/PhysRevLett.86.3200
- 3. Blume, L. (1993) The Statistical Mechanics of Strategic Interaction. Games and Economic Behavior, 5, 387-424.
- 4. Arthur, W., Durlauf, S. and Lane, D. (1997) The Economy as an Evolving Complex System II. Addison-Wesley Reading, Boston.
- 5. Young, H. (2001) Individual Strategy and Social Structure: An Evolutionary Theory of Institutions. Princeton University Press, Princeton.
- 6. Brock, W. and Durlauf, S. (2001) Discrete Choice with Social Interactions. The Review of Economic Studies, 68, 235-260.
- 7. Baxter, R. (1982) Exactly Solved Models in Statistical Mechanics. Academic Press, London.
- 8. Kubo, R. (1965) Statistical Mechanics: An Advanced Course with Problems and Solutions. North-Holland Publishing Company.
- 9. Greiner, W., Neise, L. and Stocker, H. (1995) Thermodynamics and Statistical Mechanics. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0827-3
- 10. Ising, E. (1925) Beitrag zur theorie des ferromagnetismus. Zeitschrift fur Physik A Hadrons and Nuclei, 31, 253-258.
- 11. Dorogovtsev, S., Mendes, J. and Samukhin, A. (2000) Structure of Growing Networks with Preferential Linking. Physical Review Letters, 85, 4633-4636.
NOTES
*Publication was supported by a grant-in-aid from Zengin foundation for studies on Economics and Finance.





