Theoretical Economics Letters
Vol.4 No.6(2014), Article
ID:47480,7
pages
DOI:10.4236/tel.2014.46063
Note on Fully Modified Estimation for Three-Regime Threshold Cointegration Model
Chien-Ho Wang
Department of Economics, National Taipei University, New Taipei City, Taiwan
Email: wangchi3@mail.ntpu.edu.tw
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 April 2014; revised 14 May 2014; accepted 22 June 2014
Abstract
In this paper we consider a three-regime threshold cointegration model. The fully modified ordinary least squares (FM-OLS) regression of Phillips and Hansen [1] is used to develop new methods for estimating cointegrating coefficients. After we remove the second-order biases of parameter estimates from the three-regime threshold cointegration model, FM-OLS estimates have a limit distribution that is mixed normal for all the nonstationary coefficients.
Keywords
Fully Modified Regression, Nonlinearity, Threshold Cointegration

1. Introduction
Since the breakthrough paper by Balke and Fomby [2] , nonlinear cointegration has become one of the most important research areas in time series analysis, and a strand of econometric literature has concentrated on estimating and testing for threshold cointegration. The early works in these directions include the studies by Choi and Saikkonen [3] , Hansen and Seo [4] , Gaul [5] , Gonzalo and Pitarakis [6] [7] , Kiliç [8] , Li and Lee [9] , and Seo [10] among others. Numerous contributions apply the threshold cointegration concept in empirical studies. Lo and Zivot [11] and Bec and Rahbek [12] have provided comprehensive reviews of the topic.
Although there are numerous research papers in the literature, only a few of those papers focus on the estimation of multi-regime threshold cointegration. Hansen and Seo [4] developed a maximum likelihood-based estimation and testing theory for a two-regime threshold cointegration model, while Seo [10] , Gonzalo and Pitarakis [6] , and Li and Lee [9] constructed tests for cointegration in the presence of possible threshold effects. Gaul [5] provided a Wald test against threshold effects in a three-regime threshold vector error correction model1. Moreover, all of the theories proposed before require the assumption of i.i.d. residuals. Only rare studies have discussed the efficiency of estimation when the error sequence is under weakly stationaryThe main purpose of this paper is to develop an approach estimating for cointegrated parameters in three-regime threshold models. We use the fully modified ordinary least squares (FM-OLS) regression by Phillips and Hansen [1] to provide the optimal estimates of threshold cointegration. An asymptotic theory for FM-OLS is derived. From the asymptotic theory for three-regime threshold cointegration regression, the FM-OLS principle may be used to eliminate the possible second-order biases from weakly dependent residuals. The estimates of FM-OLS for threshold cointegration are free for possible endogeneity.
The remainder of the paper is organized as follows. Section 2 introduces the basic assumptions and asymptotic distributions of fully modified threshold cointegration estimators. Section 3 provides a conclusion, and the Appendix provides all the proofs of the theorems discussed.
2. Assumptions and Parameter Estimation
This study considers the following cointegrating relationship with three-regime threshold effects.
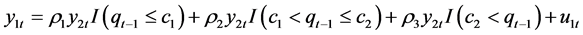 (1)
(1)
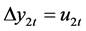 (2)
(2)
where 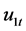 and
and 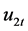 are scalar and p vector-valued stationary disturbances,
are scalar and p vector-valued stationary disturbances, 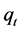 is the stationary threshold variable,
is the stationary threshold variable, 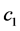 and
and 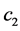 are threshold parameters,
are threshold parameters,  is indicator function. For convenience, we rewrite Equation (1) in matrix format as
is indicator function. For convenience, we rewrite Equation (1) in matrix format as
 (3)
(3)
where 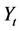 stacks
stacks 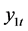 and
and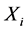 ,
, 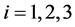 stacks on the regressors of Equation (1) for different indicators. Asymptotic properties of FM-OLS estimates are determined by the joint error process of
stacks on the regressors of Equation (1) for different indicators. Asymptotic properties of FM-OLS estimates are determined by the joint error process of , Throughout this paper, we will derive the limit distributions under following assumptions.
, Throughout this paper, we will derive the limit distributions under following assumptions.
Assumption 1. The sequence  is weakly stationary, ergodic and strong mixing with mixing coefficients
is weakly stationary, ergodic and strong mixing with mixing coefficients 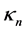 satisfying
satisfying
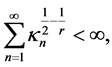
for some .
.
Assumption 2. 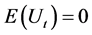 and
and 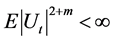 for some
for some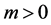 .
.
Assumption 3.
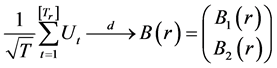
where 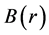 is a p-dimensional Brownian motion with a long-run covariance matrix given by
is a p-dimensional Brownian motion with a long-run covariance matrix given by
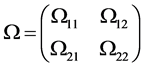
with 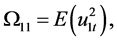

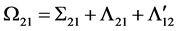 and
and 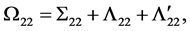 where
where 
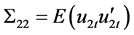
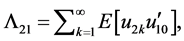

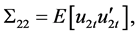
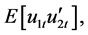 and
and
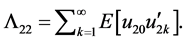
Assumption 4. The threshold variable 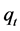 is strictly stationary and independent of the process
is strictly stationary and independent of the process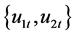 , and has a distribution function
, and has a distribution function 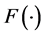 that is continuous and strictly increasing.
that is continuous and strictly increasing.
Assumption 5. The threshold parameter 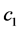 and
and  are such that
are such that 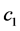 and
and 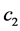
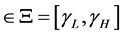 a closed and bounded subset of the sample space of the threshold variable.
a closed and bounded subset of the sample space of the threshold variable.
Assumption 6. 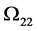 is nonsingular, i.e. the p-dimensional I (1) vector
is nonsingular, i.e. the p-dimensional I (1) vector 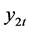 are not cointegrated each other.
are not cointegrated each other.
Assumption 1 is fairly general and covers a variety of weakly stationary posses. It also allows for the endogeneity of 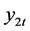 and the serial correlation in
and the serial correlation in  in Equation (1). This treatment of the serial correlation in
in Equation (1). This treatment of the serial correlation in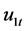 , like that in the study by de Jong [13] and Gonzalo and Pitarakis [7] , a more general assumption in threshold cointegration regression. Assumption 2 provides some moment conditions imposed on
, like that in the study by de Jong [13] and Gonzalo and Pitarakis [7] , a more general assumption in threshold cointegration regression. Assumption 2 provides some moment conditions imposed on 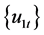 and
and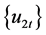 . Assumption 3 is a multivariate invariance principle for the partial sum process. Assumption 1 - 3 are used for establishing the limit theory for partial sum process like
. Assumption 3 is a multivariate invariance principle for the partial sum process. Assumption 1 - 3 are used for establishing the limit theory for partial sum process like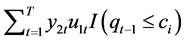 . Assumption 4 and 5 are standard assumptions for threshold literatures. Assumption 4 excluded the possibility that that the threshold variable
. Assumption 4 and 5 are standard assumptions for threshold literatures. Assumption 4 excluded the possibility that that the threshold variable 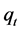 is correlated with
is correlated with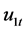 . Assumption 5 ensures that there are enough observations in each regime. Assumption 6 rules out the possibility that the components of
. Assumption 5 ensures that there are enough observations in each regime. Assumption 6 rules out the possibility that the components of 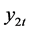 will themselves be cointegrated.
will themselves be cointegrated.
Our estimation of threshold estimators of  and
and 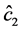 for Equation (1) is based on the nonlinear least squares regression. Let
for Equation (1) is based on the nonlinear least squares regression. Let
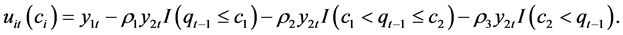
The authors consider
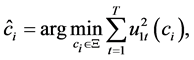 (4)
(4)
where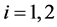 . Once
. Once 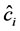 is obtained, the
is obtained, the 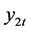 can be separated by indictors. Because the regressors of Equation (1) are orthogonal each other. For given threshold value
can be separated by indictors. Because the regressors of Equation (1) are orthogonal each other. For given threshold value 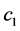 and
and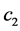 , it can be estimated by using OLS procedure
, it can be estimated by using OLS procedure
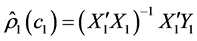 (5)
(5)
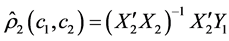 (6)
(6)
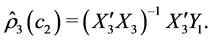 (7)
(7)
Although NLS procedure may be consistent, the limits of estimated parameters may contain second-order bias. Phillips and Hansen [1] propose a fully modified estimation methods which can eliminate these bias effects. Following the spirit of Phillips and Hansen [1] , we suggest the FM-OLS principle for threshold cointegrating regression. From the cointegration model of Equation (3), the residuals  are weakly dependent.
are weakly dependent. 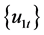 may be correlated with
may be correlated with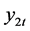 . It will cause efficiency loss.
. It will cause efficiency loss.
Consider 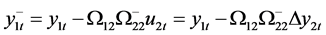 and
and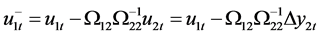 . Redefine
. Redefine
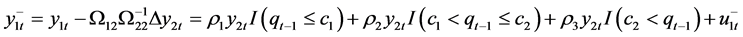 (8)
(8)
Define a transformation matrix:
 (9)
(9)
The vector 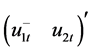 can be written as
can be written as
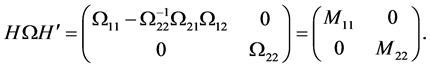 (10)
(10)
Lemma 1. Under Assumption 1 - 3, for Equation (8) we have
 (11)
(11)
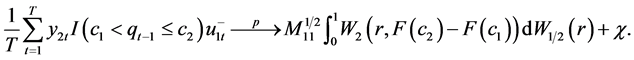 (12)
(12)
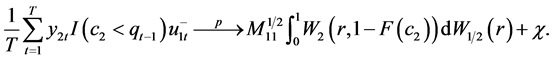 (13)
(13)
where  denotes a Brownian sheet,
denotes a Brownian sheet, 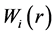 ,
, 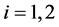 , is a p-dimensional standard Brownian motion,
, is a p-dimensional standard Brownian motion, 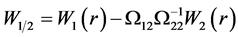 and
and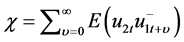 .
.
Lemma 2. Under Assumption 1 - 3, for Equation (8) we have
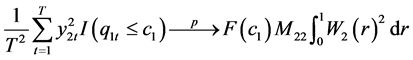 (14)
(14)
 (15)
(15)
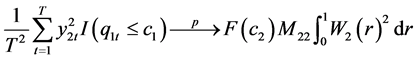 (16)
(16)
The following theorem shows the limit distribution of FM-OLS estimators.
Theorem 1. Under Assumption 1 - 3, for Equation (8) we have
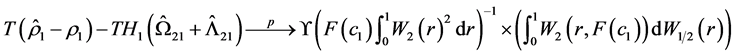 (17)
(17)
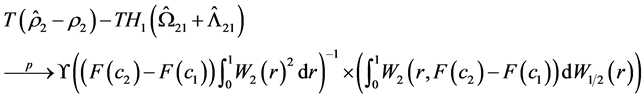 (18)
(18)
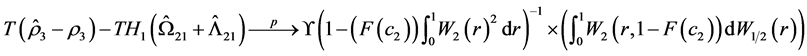 (19)
(19)
where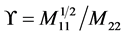 .
.
In the formulae for the bias correction terms in Equation (17)-(19), 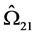 and
and 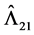 are the kernel estimates of long run covariance matrices, which can be found in Phillips [14] . From the Theorem 1, the limit distribution is free of second order bias.
are the kernel estimates of long run covariance matrices, which can be found in Phillips [14] . From the Theorem 1, the limit distribution is free of second order bias.
3. Conclusions
In this paper, we have established the asymptotics of fully modified ordinary least squares cointegrating estimators for three-regime threshold cointegration regression. Our results may be used under the condition that residuals with weakly dependency exist. These results improve the estimation methods available in threshold cointegration literatures.
There are a variety of potential topics for future research related to this study. First, it is possible to extend our results to more than one cointegrating relationship, although a single threshold cointegrating relationship is often used in economics and international finance. Second, testing for threshold cointegration based on the FM-OLS principle is not yet available. The authors hope to further study these issues in the future.
Acknowledgements
The author thanks financial support from Ministry of Science and Technology of Taiwan under grant NSC 95- 2415-H-305-010 and Shu-Yu Lin and Yi-Ting Tsai for excellent research assistants.
References
- Phillips, P. and Hansen, B. (1990) Statistical Inference in Instrumental Variables Regression with I(1) Processes. Review of Economic Studies, 57, 99-125. http://dx.doi.org/10.2307/2297545
- Balke, N. and Fomby, T. (1997) Threshold Cointegration. International Economic Review, 38, 627-645. http://dx.doi.org/10.2307/2527284
- Choi, I. and Saikkonen, P. (2004) Testing Linearity in Cointegrating Smooth Transition Regressions. The Econometrics Journal, 7, 341-365. http://dx.doi.org/10.1111/j.1368-423X.2004.00134.x
- Hansen, B. and Seo, B. (2002) Testing for Two-Regime Threshold Cointegration in Vector Error Correction Models. Journal of Econometrics, 110, 293-318. http://dx.doi.org/10.1016/S0304-4076(02)00097-0
- Gaul, J. (2006) Estimation and Testing in a Three Regime Vector Error Correction Model. University of Bonn, Bonn.
- Gonzalo, J. and Pitarakis, J.-Y. (2006) Threshold Effects in Multivariate Error Correction Models. In: Mills, T. and Patterson, K., Eds., Palgrave Handbook of Econometrics: Econometric Theory Volume 1, Palgrave MacMillan, New York, 578-609.
- Gonzalo, J. and Pitarakis, J.-Y. (2006) Threshold Effects in Cointegration Relationships. Oxford Bulletin of Economics and Statistics, 68, 813-833. http://dx.doi.org/10.1111/j.1468-0084.2006.00458.x
- Kilic, R. (2011) Testing for Co-Integration and Nonlinear Adjustment in a Smooth Transition Error Correction Model. Journal of Time Series Analysis, 32, 647-660. http://dx.doi.org/10.1111/j.1467-9892.2011.00722.x
- Li, J. and Lee, J. (2010) ADL Tests for Threshold Cointegration. Journal of Time Series Analysis, 31, 241-254.
- Seo, M. (2006) Bootstrap Testing for the Null of No Cointegration in a Threshold Vector Error Correction Models. Journal of Econometrics, 134, 129-150.
http://dx.doi.org/10.1016/j.jeconom.2005.06.018 - Lo, M. and Zivot, E. (2001) Threshold Cointegration and Nonlinear Adjustment to the Law of One Price. Macroeconomic Dynamics, 5, 533-576.
- Bec, F. and Rahbek, A. (2004) Vector Equilibrium Correction Models with Non-Linear Discontinuous Adjustments. The Econometrics Journal, 7, 628-651.
http://dx.doi.org/10.1111/j.1368-423X.2004.00147.x - De Jong, R. (2002) Nonlinear Minimization Estimators in the Presence of Cointegrating Relationships. Journal of Econometrics, 110, 241-259. http://dx.doi.org/10.1016/S0304-4076(02)00093-3
- Phillips, P. (1995) Fully Modified Least Squares and Vector Autoregression. Econometrica, 63, 1023-1078. http://dx.doi.org/10.2307/2171721
Mathematical Appendix
Proof of Lemma 1
Let 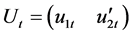 and
and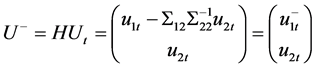 . The asymptotic distribution follows directly from Phillips [14] and Gonzalo and Pitarakis [6]
. The asymptotic distribution follows directly from Phillips [14] and Gonzalo and Pitarakis [6]
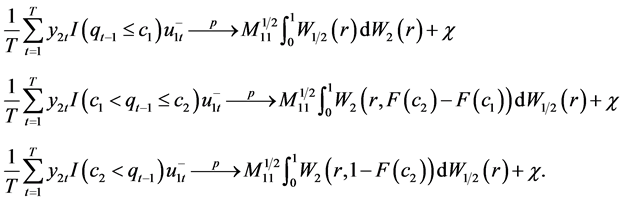
Proof of Lemma 2
From the Proposition 2 in Gonzalo and Pitarakis [7], Lemma A3 in Gonzalo and Pitarakis [7] and the continuous mapping theorem give
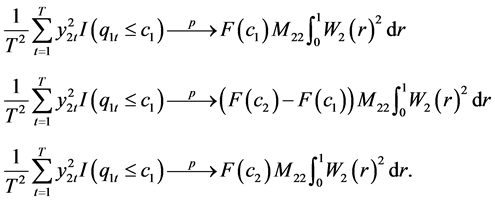
Proof of Theorem 1
Consider fully modified estimator .
.
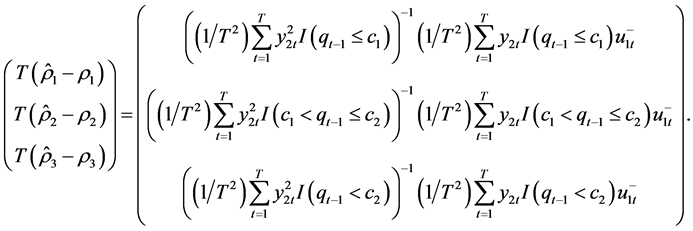
For denominator,
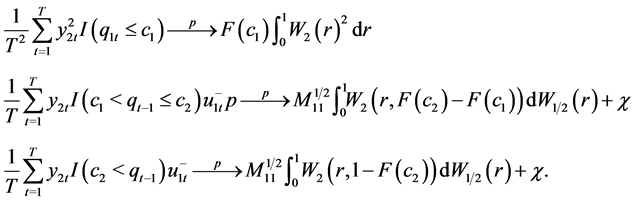
by Lemma 2 For numerator, by virtue of Lemma 1
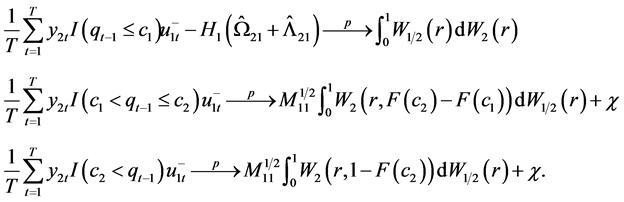
According to the continuous mapping theorem and functional central limit theorem, it follows that

where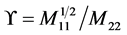 .
. 
NOTES

1Hansen and Seo and Gonzalo and Pitarakis consider MLE methods, but they need normality for residuals.

