Theoretical Economics Letters
Vol.2 No.2(2012), Article ID:19326,3 pages DOI:10.4236/tel.2012.22037
Playing the Deficit Gamble Easily*
School of Commerce, Meiji University, Tokyo, Japan
Email: tamegawa@kisc.meiji.ac.jp
Received February 2, 2012; revised March 14, 2012; accepted March 23, 2012
Keywords: Deficit Gamble; Government Debt
ABSTRACT
In this paper, we attempt to obtain the exact probability distribution of the debt-to-GDP ratio in T years, assuming that 1) the primary balance is zero and 2) the interest rate and the GDP growth rate are given as exogenous random variables. With this approach, researchers can play the “Deficit Gamble” without conducting a Monte Carlo simulation. Calculating the distribution of the debt-to-GDP ratio would be useful for policy planning.
1. Introduction
Recently, many countries provided fiscal stimulus packages to cope with the economic recession arising from the financial crisis. As a result, these governments’ debt increased, and the fiscal crisis became a very important issue, especially in the EU countries. Therefore, it is important to predict the future path of government debt. This paper provides a useful formula to obtain the probability distribution of the debt-to-GDP ratio in T years, assuming that (1) the primary balance is zero and (2) the interest rate and the GDP growth rate are given as exogenous random variables.
Given assumptions (1) and (2), the debt-to-GDP ratio in T years is a random variable. Thus, the time path of the debt-to-GDP ratio exceeding a target level given an initial condition is purely random. Therefore, this “game” is referred to as the “Deficit Gamble”. Ball et al. [1] have shown the probability of the debt deficit gamble failing in T years in the US, where the deficit gamble is considered to have failed if the debt-to-GDP ratio exceeds some target level. In Ball et al. [1], this probability has been calculated using a Monte Carlo simulation. However, as shown below, the exact distribution of the debt-to-GDP ratio can be easily obtained and thus we can calculate this probability without a simulation analysis. We only need the standard normal distribution table and a simple OLS estimation. Using this simplification, one can easily play the deficit gamble.
The rest of the paper is organized as follows: Section 2 derives a distribution of the debt-to-GDP ratio, Section 3 states a useful statistic for the debt-to-GDP ratio, and finally, Section 4 concludes our paper.
2. Literature Review
The deficit gamble has been suggested in Ball et al. [1] and recently has been applied to the Japanese economy in Oguro [2]. As stated above, these studies use the Monte Carlo simulation to obtain the distribution of debt-to-GDP ratio. On the other hand, with the approach developed in this paper, researchers need not use the Monte Carlo simulation, and deficit gamble analysis becomes very simple.
The deficit gamble approach does not require any economic theory and, therefore, one can mechanically obtain information for debt accumulation path. However, an analysis using a micro-founded economic model is also important for considering how debt accumulates through an economic structure. In line with this, Sakuragawa and Hosono [3] have used a dynamic stochastic general equilibrium model in order to calculate the debt accumulation path.
Our approach would be quite useful for supporting an argument for the sustainability of government debt. Related to this issue, Bohn [4], Trehan and Walsh [5], and Hakkio and Rush [6] have analyzed the sustainability of government debt given the economic data. Using our approach, one can calculate a counter factual debt accumulation distribution if the primary balance would have been zero at certain past periods. An analysis such as this would become another approach for dealing with the sustainability issue.
3. Distribution of the Debt-to-GDP Ratio
Suppose that government debt is accumulated as follows:
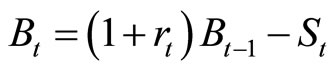 , (1)
, (1)
where 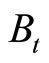 denotes the nominal government debt at the end of term,
denotes the nominal government debt at the end of term,  denotes the nominal interest rate, and
denotes the nominal interest rate, and  denotes the primary balance, which is the government spending minus tax. From Equation (1), we get
denotes the primary balance, which is the government spending minus tax. From Equation (1), we get
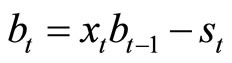 where, defining
where, defining  as GDP,
as GDP, 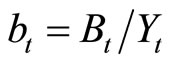 ,
, 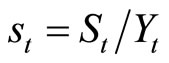 , and
, and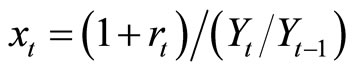 . Our goal is to obtain the probability distribution of the debt-to-GDP ratio in T years with zero primary balance. Assuming that the current period is zero and that
. Our goal is to obtain the probability distribution of the debt-to-GDP ratio in T years with zero primary balance. Assuming that the current period is zero and that 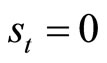 for all
for all , the debt-to-GDP ratio in T years is as follows:
, the debt-to-GDP ratio in T years is as follows:
 . (2)
. (2)
Following Ball et al. [1], we assume
 where
where 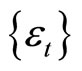 is a normally distributed random variable with mean zero and variance
is a normally distributed random variable with mean zero and variance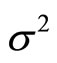 . Taking the logarithm of Equation (2), we get
. Taking the logarithm of Equation (2), we get
 . (3)
. (3)
Since 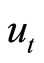 can be expressed as the following MA representation
can be expressed as the following MA representation

Equation (3) can be written as follows:1
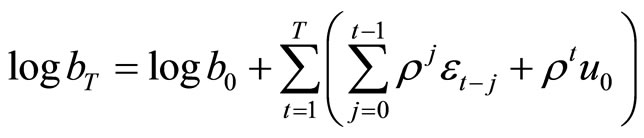 .
.
The above equation can be simplified as follows:
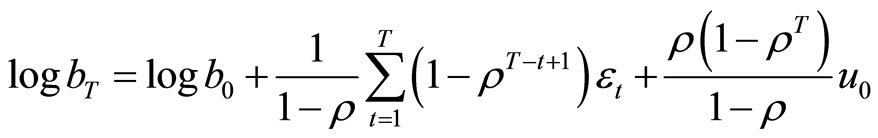 . (4)
. (4)
Note that the distribution we want to obtain is conditional on the current period’s information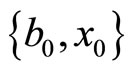 . Equation (4) implies that the distribution of
. Equation (4) implies that the distribution of 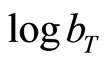 conditional on
conditional on  is normal with mean
is normal with mean
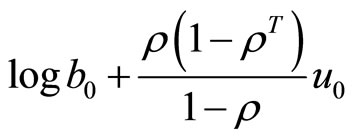 and variance
and variance
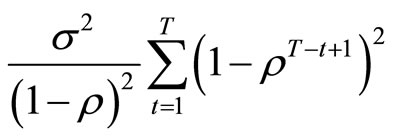 .
.
Noting that
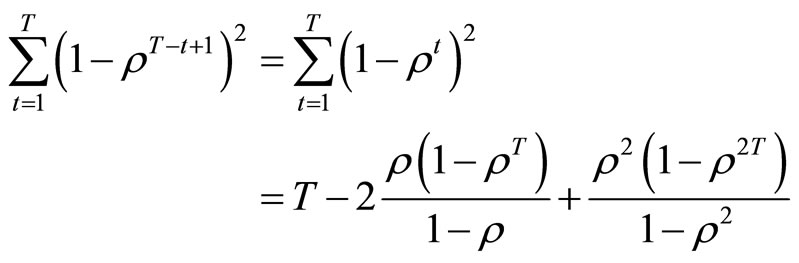
and defining z as

We have the following proposition Proposition. If 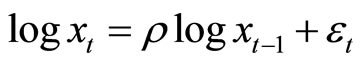 and
and 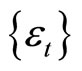 is a sequence of independently normal distributed random variables with mean zero and variance
is a sequence of independently normal distributed random variables with mean zero and variance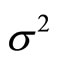 , then
, then 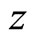 as conditional on
as conditional on 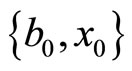 follows the standard normal distribution.
follows the standard normal distribution.
In practice, 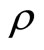 and
and 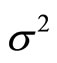 are not known a priori and they have to be estimated on the basis of the available information. Regardless, since the estimates of
are not known a priori and they have to be estimated on the basis of the available information. Regardless, since the estimates of 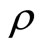 and
and 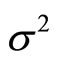 are fixed for
are fixed for 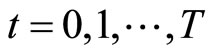 years as non-random variables, the proposition still holds.
years as non-random variables, the proposition still holds.
4. Deficit Gamble Statistic
In this section, we define a useful statistic for the deficit gamble. Suppose that the deficit gamble fails if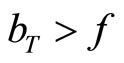 , where
, where 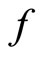 is some target level of the debt-to-GDP ratio that is set manually by researchers. Now define
is some target level of the debt-to-GDP ratio that is set manually by researchers. Now define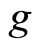 , which we call the “Deficit Gamble Statistic”, as follows:
, which we call the “Deficit Gamble Statistic”, as follows:

In this setting, the probability of the debt deficit gamble failing in T years is calculated as , where
, where  denotes the standard normal distribution function. Here is an example.
denotes the standard normal distribution function. Here is an example.
Example. Assume 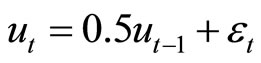 with
with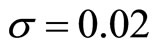 ,
,  ,
, 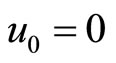 , and T = 25. Setting the target level f = 1.5, we obtain g = 2.6173. In this case, the probability of the debt deficit gamble failing in 25 years is 0.005.
, and T = 25. Setting the target level f = 1.5, we obtain g = 2.6173. In this case, the probability of the debt deficit gamble failing in 25 years is 0.005.
5. Concluding Remarks
In this paper, we obtain the exact distribution of the debt-to-GDP ratio in T years and further develop the formula for calculating the probability of the deficit gamble, wherein the debt-to-GDP ratio exceeds some target level, without conducting a Monte Carlo simulation. Calculating the distribution of the debt-to-GDP ratio would prove useful for policy planning.
REFERENCES
- L. D. Ball, D. W. Elmendorf and N. Mankiw, “The Deficit Gamble,” Journal of Credit, Money, and Banking, Vol. 30, No. 4, 1998, pp. 699-720. doi:10.2307/2601125
- K. Oguro, “A Study of Government Deficit in Terms of a Gamble: Under Uncertainty for GDP Growth Rate and Interest Rate,” JCER Journal, No. 60, 2009, pp. 19-35.
- M. Sakuragawa and K. Hosono, “Fiscal Sustainability of Japan: A Dynamic Stochastic General Equilibrium Approach,” Japanese Economic Review, Vol. 61, No. 4, 2010, pp. 517-537. doi:10.1111/j.1468-5876.2009.00503.x
- H. Bohn, “The Behaviour of US Public Debt and Deficits,” Quarterly Journal of Economics, Vol. 113, No. 3, 1998, pp. 949-963. doi:10.1162/003355398555793
- B. Trehan and C. E. Walsh, “Common Trends, the Government Budget Constraint, and Revenue Smoothing,” Journal of Economic Dynamics and Control, Vol. 12, No. 2-3, 1988, pp. 425-444. doi:10.1016/0165-1889(88)90048-6
- C. S. Hakkio and M. Rush, “Is the Budget Deficits ‘Too Large’,” Economic Inquiry, Vol. 29, 1991, pp. 429-445. doi:10.1111/j.1465-7295.1991.tb00837.x
- F. Hayashi, “Econometrics,” Princeton University Press, Princeton, 2000.
NOTES
*I am grateful to an anonymous referee and Shin Fukuda for their helpful comments. This work was supported by a Grant-in-Aid for Scientific Research (No. 22330090) from the Ministry of Education, Culture, Sport, Science and Technology, Japan.
1This expression can also be obtained from the Beveridge-Nelson decomposition. For example, see Hayashi [7].

