Journal of Mathematical Finance
Vol.06 No.05(2016), Article ID:72445,27 pages
10.4236/jmf.2016.65064
Valuating New Product Development Project with a Stochastic Volatility Model
Chengru Hu1, Chulhee Jun2, Maggie Foley3
1State University of New York at Canton, Canton, NY, USA
2University of Macao, Macao, China
3Jacksonville University, Jacksonville, FL, USA
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 19, 2016; Accepted: November 26, 2016; Published: November 30, 2016
ABSTRACT
In this study, we develop an option-based model to valuate New Product Development (NPD) projects in which management has the flexibility to abandon the project upon completion if the value of the established product falls below the required investment outlay. In the analysis, we explicitly consider the fact that the level of product volatility changes across development stages, as well as the stochastic nature of competition erosion. A closed-form solution is derived under a simplifying assumption of independence between product volatility and other stochastic processes considered in the model. The complete model is solved numerically by using Monte Carlo simulation. Our result indicates that ignoring the stochastic natures of product development uncertainty and competition erosion introduces a severe undervaluation bias. Such a bias worsens when 1) current product value is close to the required investment cost (so that the NPD project is nearly “at-the-money”); 2) development duration lengthens; 3) competition is intense; 4) the window of profitable opportunity lengthens, and 5) the market and the developing firm are more risk-prone (less risk-averse).
Keywords:
Real Option, Strategic Flexibility, New Product Development, Stochastic Volatility

1. Introduction
New Product Development (NPD) is fundamental to stimulating economic growth for business organizations. Successful NPDs not only support important business activities that over time contribute to long-run business profitability, but also provide firms with sufficient cutting edges in competitive battles.
Recognition of the importance of NPD to business prosperity has triggered considerable research interests from a variety of domains including marketing, strategic management and economics. Of all widely studied research topics, none is more challenging and has received more attention than the valuation of NPD investments. When corporate resources are limited, competition is intense, and the cost associated with NPD investment is significant; therefore, the accuracy with which NPD investments can be evaluated becomes critically important.
Traditionally, the Net Present Value (NPV) rule is recommended for analyzing investment decisions. The NPV rule helps decision makers choose between two alternatives: accepting or rejecting an investment opportunity. However, it is widely accepted that the majority of the investments firms make are dynamic in that decision makers do more than just accept or reject an investment opportunity using information available at the time of the decision. Upon arrival of additional information, decision makers update their beliefs about the profitability of the investment and may choose to defer, expand, contract, or shut down temporarily and later restart the investment project (Trigeorgis and Mason [1] ; Trigeorgis [2] ; among others). Flexibility to revise actions based on future events enables management to amplify future gain or mitigate loss in face of favorable or unfavorable events, and thus carries real value. Standard NPV analysis places investment analysis into a static framework and totally ignores the value of strategic flexibilities; consequently it will result in an undervaluation of investment pro- jects (Myers [3] ; Kester [4] ; Amram and Kulatilaka [5] ; etc).
Alternatively, academic researchers adopt the principles of option pricing in analyzing investment decisions. Strategic flexibilities that allow decision makers to alter the course of investment at later dates resemble options written upon the underlying assets (Caballero [6] ; Kulatilaka [7] ; Baldwin and Clark [8] and [9] ; etc). Therefore the option-based approach, or the real option approach, provides more appropriate representations of investment dynamics and will effectively mitigate the documented undervaluation problems.
In this study, we develop an option-based model to evaluate a NPD project that allows management to abandon the project upon completion. NPD is a risky process. Previous studies document high product failure rates and significant costs to sponsoring company upon product failure (Booz-Allen and Hamilton [10] ; Mansfield [11] ; Panne, Beers, and Kleinknecht [12] ). Flexibility to abandon the project given unfavorable outcomes effectively reduces downside loss, and is a valuable strategic tool. Ignoring it would lead to a significant undervaluation problem.
Our model differs from other real option models in two ways. Previously, literature generally assumed that uncertainty associated with product development remained constant throughout the development process. However, there exists abundant evidence, from both marketing and economic literature, that suggests NPD uncertainty varies across development stage progresses (Sahal [13] ; Nelson and Winter [14] ; Fahey and Narayanna [15] ; Contractor and Narayanan [16] ; etc.). We extend previous literature and allow the level of product volatility to change randomly (i.e. stochastic). Secondly, we explicitly consider the stochastic nature of industrial competition on NPD valuation. Industrial competition erodes the value of NPD projects, long before the establishment of a product. Previous studies on the impact of competition erosion assume the rate of erosion to be either constant or take a deterministic functional form. We recognize that competition erosion depends on stochastic competitor arrivals and uncertainty about the future investment environment. Consequently, we allow the rate of competition erosion to be random in our NPD valuation model.
The dynamics underneath our stochastic (product) volatility with stochastic competition model (SVSCM) is very general in which previously studied project dynamics are special cases of ours. For example, by assuming a constant level of product volatility, our model reduces to a stochastic competition with Constant (product) Volatility Model (CVM). By further restricting that change in the rate of competition erosion to zero, our model is further reduced to the Constant Competition with constant product volatility Model (CCM).
We derive a closed-form solution to SVSCM under a simplifying assumption that a change in product volatility is independent of changes in new product value and competition erosion. We further provide a numerical solution to the full-scale SVSCM using Monte Carlo simulations. We design a control variate methodology to obtain accurate (as measured by standard deviation of simulation results) estimations of project value with low computation cost (as measured by the number of simulation repetitions). We then examine the valuation benefit of admitting the stochastic nature of development uncertainty and industrial competition based on simulation results. Our results suggest valuation under SVSCM is much higher than those under CVM and CCM under various scenarios. We find that the undervaluation bias in CVM and CCM becomes severe when 1) current product value is close to required investment cost (so that the NPD project is nearly “at-the-money”); 2) development duration lengthens; 3) competition is intense; 4) the window of profitable opportunities lengthens, and 5) markets and developing firms are more risk-averse.
The major contribution of this study is that it highlights the importance of additional volatility from changing project uncertainty and competition erosion in the valuation of NPD projects. Previous studies assume constant product uncertainty and/or constant competition erosion. We argue that these assumptions are inadequate to capture the dynamic nature of NPD development. Real option theory suggests that under dynamic management the value of an NPD project increases with the uncertainty. Changing competition erosion and product volatility adds to a project’s uncertainty, which increases the likelihoods of both significant gain and loss. The option to abandon effectively limits downside losses, but allows a developing firm to reap potential gains; consequently additional uncertainty implies higher valuation. Our results indicate that ignoring the stochastic nature of competition erosion, and especially changing level product volatility will introduce severe undervaluation bias, and lead to an underinvestment problem.
The study is structured as follows. Section 2 briefly reviews real option literature. Section 3 describes the dynamics of the NPD project, derives a valuation model, and provides a solution to under risk-neutral representation. In Section 4, a closed-form solution is provided assuming independence between change in product volatility and other stochastic variables. Section 5 utilizes a Monte Carlo simulation technique to numerically solve the value of the NPD project. We also examine the marginal contribution of our derived model under various scenarios. We then conclude our study in Section 6.
2. Literature Review
The conventional (static) DCF technique assumes that an investment, once started, will be operated continuously until the end of its expected useful life. The valuation criterion is based on present values of expected outputs/inputs discounted at a risk-adjusted rate, i.e.
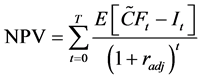 (1)
(1)
where 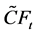 is period t cash flow from the investment;
is period t cash flow from the investment; 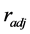 is a discount rate adjusted for risk associated with the investment; T is expected useful life of the investment (it is the required investment outlay required at time t); and E[・] is the expectation operator. Investments with positive (negative) NPVs increase (decrease) the wealth of a firm’s owners; therefore should be accepted (rejected).
is a discount rate adjusted for risk associated with the investment; T is expected useful life of the investment (it is the required investment outlay required at time t); and E[・] is the expectation operator. Investments with positive (negative) NPVs increase (decrease) the wealth of a firm’s owners; therefore should be accepted (rejected).
Standard NPV analysis suffers from several limitations. First, it assumes a static operating strategy. NPV analysis recommends either acceptance or rejection of an investment based on information available at the time of the initial decision, but it fails to consider that management may act upon the arrival of new information in the future of the project’s operating life to defer, expand, contract, or abandon investment. These flexibilities enable management to amplify future gain or reduce loss upon favorable or unfavorable future events; consequently, they create real value. NPV fails to account for these flexibilities and may result in an undervaluation problem. Secondly, NPV analysis relies on estimates of future cash flow distribution that is inherently subjective. Investors hold heterogeneous beliefs about cash flow perspectives. The heterogeneity of expectations can generate significant variations in project valuations among market participants. Consequently, NPV analysis usually results in inconsistent valuations across users. Finally, consistent estimation of the risk-adjusted discount rate may also be difficult to reach in NPV analysis. The most popular technique used is the CAPM. However, it has been pointed out that an asset’s true beta depends on the asset’s growth opportunities (Myers and Turnbull [17] ). A related point is that it may not be proper to infer the discount rate from observed systematic risk even if non-systematic risk is fully diversifiable. As flexibilities to alter investment decisions restrain investment losses while allowing product specific benefit to accrue to the firm, they effectively change a firm’s growth opportunities (Brennan [18] ) and introduce measurement errors into NPV analysis.
Since seminal work by Myers [3] , the option-pricing framework has been applied to value investment decisions and contractual claims on corporate assets. Managerial flexibilities to alter the investment course at later stages resemble options written upon the underlying real assets (Myers [3] ; Kester [4] ). Table 1 suggests that there exist striking similarities between “options” on real assets (thereafter, real options) and financial options. As a result, it has been suggested that financial option-pricing theories could be utilized to measure values of managerial flexibilities.
The problems with static NPV easily can be solved with a real option approach. First of all, the real option approach relies on contingent claim analysis, and replicates future cash flows from a potential investment using those of a portfolio of existing assets. This “cash flow equivalent” portfolio has the same payoff as the investment under consideration. In the absence of arbitrage opportunities, the value of investment is the value of this replicating portfolio. All individuals, regardless of their subjective estimates of future cash flow distributions, agree on the valuation. Secondly, as future cash flow estimates are independent of individual risk preference, risk-neutral probabilities and a risk-free rate are used in the valuation. Finally, operating flexibilities are models as a set of boundary conditions, so that initial investment strategies (and investment outcomes) can be altered upon realization of future events.
So far, the real option approach has been adopted in the valuation of various types of managerial flexibilities. Examples include (but not limited to) 1) option to defer (Paddock, Siegel and Smith [19] ; McDonald and Siegel [20] [21] ; etc.); 2) time to build (Majd and Pindyck [22] ; Trigeorgis [23] ; etc.); 3) option to expand (contract) (Brennan and Schwartz [24] ; McDonald and Siegel [21] ; etc.); 4) option to switch (Kensinger [25] ); and 5) option to abandon (Myersand Majd [26] ); etc.
Option to abandon a project at a later stage is an important strategic tool especially when project development faces high level of uncertainty and severe competition, for example a NPD project. A NPD project typically involves technology whose future is virtually unknown. As evidenced by unexceptionally high failure rates among NPD projects (Mansfield et al. [11] ; Booz, Allen and Hamilton [10] ; etc.), product constructions are usually unstable with low confidence in the product’s success. Industry competition erodes the value of a NPD project long before the establishment of a product, as potential consumers waiting for the new product are diverted to competing products
Table 1. Comparison of financial and real options.
of similar technologies, reducing the potential market for the new product. The ability to abandon the project when product value at a future time (e.g. upon completion) falls below required thresholds would effectively curb downside loss but enable firms to reap upside potential gain if the product turns out to be a success; consequently, the ability to abandon represents real value. Intuitively, the value of this strategic tool increases with uncertainty.
Chen, Ho, Ik and Lee [27] are among the first to adopt real option approach into NPD evaluation. Chen et al consider the flexibility to abandon in the valuation of a NPD project. They take into consideration the effect of industrial competition on the value of the new product. Schwartz [28] uses real option approach to value patents and patent- protected R & D projects in pharmaceutical industry. His model implicitly considers uncertainty in cost-to-completion, uncertainty in cash flows to be generated, and possibility of catastrophic events. In both studies, volatility of innovative project are assumed to be constant during development period. However, there exists abundant evidence, from both marketing and economic literature, that suggest risk levels associated with NPDs vary as product development progresses (Contractor and Narayanan [16] ; Fahey and Narayanna [15] ; Nelson and Winter [14] ; Sahal [13] ; etc.). A typical NPD involves seeding, startup, breakthrough, and new product commercialization phases. A firm’s focus changes across development stages. The early stage involves idea testing with a major source of uncertainty being the feasibility of the innovation concept. In later phases (e.g. start-up, breakthrough), a firm focuses on materializing the concept. Consequently, most uncertainties come from finding technical solutions. Finally, during product commercialization, the firm’s major concern shifts to competitions and especially the demands of the market. Cash flows resulting from the new product are less dependent on the firm’s technological capability. As uncertainty levels across phases vary with shifting development focuses, assuming constant product volatility in project valuation is apparently inappropriate. Such assumption will under-es- timate NPD uncertainty and under-value both the strategic ability to abandon NPD projects.
3. New Product Development Valuation Model
In this section, we propose an option-based valuation model to capture the value of flexibility to abandon NPD projects at later stage. We explicitly consider the impacts of varying project volatility and stochastic competition on values of NPD projects.
Suppose the firm under consideration is developing a new product. The development will last T months. Upon product completion, if value of the established product falls below required production costs K, the firm will choose to abandon the project. The value of NPD project at time t, 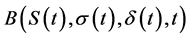 , is a function of the value of product under development,
, is a function of the value of product under development,  , and the loss in value (from sales reduction) due to competition
, and the loss in value (from sales reduction) due to competition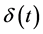 .
.
3.1. Product Value
Donate time t (t ≤ T) value of the new product as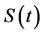 . We assume
. We assume 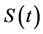 follows a Geometric Brownian motion with the following form:
follows a Geometric Brownian motion with the following form:
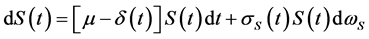 (2)
(2)
where μ is the expected value appreciation for the product; 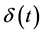 is time t rate of competition erosion;
is time t rate of competition erosion; 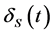 is time t instantaneous product volatility; and
is time t instantaneous product volatility; and  is the increment of a standard Wiener process with
is the increment of a standard Wiener process with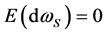 , and
, and 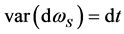
3.2. Product Volatility
We model instantaneous product volatility,  , with a stochastic process to capture the fact that the level of uncertainty changes as the NPD project progresses. Firms tend to develop products in their existing business line; consequently, product volatility normally reverts to the risk of firm’s existing assets in the long-run (Chung and Charoenwong [29] ; Miles [30] ). We therefore use the following process to model instantaneous product volatility
, with a stochastic process to capture the fact that the level of uncertainty changes as the NPD project progresses. Firms tend to develop products in their existing business line; consequently, product volatility normally reverts to the risk of firm’s existing assets in the long-run (Chung and Charoenwong [29] ; Miles [30] ). We therefore use the following process to model instantaneous product volatility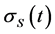 :
:
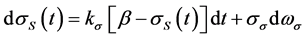 (3)
(3)
where 






3.3. Competition Erosion
Loss in value due to competition represents value outflows that will not accrue to the developing firm. This resembles dividend-like convenience yield on real assets (Fama and French [31] [32] ; Gibson and Schwartz [33] ). In the long-run, competition tends to move back towards an equilibrium level due to factors such as marginal production costs (Gibson and Schwartz [33] ; Demers [34] ; Bjerksund and Ekern [35] ). Consequently, we model rate of erosion due to industrial competition, 

where 






It is assumed competition erosion is positively correlated with product value, i.e.

3.4. Boundary Condition
Managers have the flexibility to abandon the investment if the value of developed product falls below the required investment outlay, K, upon product complete at time T. Project value upon considering this flexibility can be modeled as:

where 
Risk neutral representation of NPD dynamics (2), (3) and (4) could be established by adjusting the actual movements of underlying state variables with corresponding risk premiums (Cox, Ingersoll and Ross [36] ). Value movements governed by stochastic processes (2), (3) and (4), the corresponding risk neutralized processes are given as:



where r is the risk free rate; 



With Ito’s Lemma, it can be shown that in the absence of arbitrage opportunities NPD value following the risk-adjusted processes (2)*, (3)* and (4)* must satisfy the following partial differential equation (for simplicity, we drop the “^” from the notation):

subject to boundary condition (5).
Equation (6) doesn’t depend on investor risk preference. Therefore, its solution has a risk-neutral representation (Cox and Ross [37] ). For simplicity, we evaluate NPD value at time t = 0. The value of NPD project at time 0 is:

where 
NPD value at evaluation can be calculated by determining the time T distribution 

Equation (8) implies that with a stochastic process governed by a risk adjusted pro- cess (2)*, (3)* and (4)*, NPD value 

4. Closed-Form Solution under Simplifying Assumption
1That is, 
2Note 
3This is based on the fact that
With movement of project value governed by processes specified in Section 3, there exists no closed-form solution to Equation (8). However, under the simplifying solution that volatility change is independent of NPD change (therefore
Define Θ as the point in the probability space that labels the stochastic path. For each
path Θ, we define 
Under the assumptions that NPD volatility is independent of both NPD value change and industrial competition defined in (2)* and (4)*, (8) can be expressed as3:

where 





trality, where
will use 

The inner integral in (9) represents NPD value under a path Θ. It represents solution to the following partial differential equation (Cox, Ingersoll and Ross [36] , Theorem 3):

with boundary condition
Appendix A shows that with a selected sample path, the resulting distribution of new product’s value at time T is log-normal distributed, with a density function given by:
in which 

Given that the NPD value at time T under each sample path of 


In Appendix B, we show that NPD value distribution (11) is given by:

where
With time T product value distribution

5. Numerical Solution
Even under the simplifying assumption, the closed-form solution given in (13) requires integration with imaginary functions; therefore the calculations are very complex and time-consuming. To solve for NPD value under the full model (8), we implement a Monte Carlo simulation to numerically find its solution. There are two major concerns to any Monte Carlo simulation, namely accuracy (as measured by standard deviation of estimates) and computational cost (as measured by number of simulation repetitions). In order to improve the accuracy of Monte Carlo estimates while reducing the number of simulation repetitions performed, a control variate methodology is adopted. The basic idea is to replace the integration Equation (8) with one that has an analytic solution, under the assumption that product volatility, 
5.1. Base Case Result
We first present the base case simulation results. Table 2 lists the parameter values used in the simulation, which follow those used in Chen et al. [27] and Schwartz [28] . For the base case, it is assumed the current value of the product, S(0), is $120 million. A new product requires 12 months to develop (i.e. T = 12). Upon product completion, if the firm intends to continue with the production, an additional $100 million (K) is required for subsequent construction. The firm may choose to abandon the project, if the completed product’s value falls below $100 million. The annual risk-free interest rate (r) is assumed to be 8%. The initial value for competition erosion is set to be zero, 
Table 2. Summary of base case simulation parameters.
Parameter values are based on the simulations by Chen et al. (2001) and Schwartz (2004).
and its long-term level, α, is set to be 12%. Initially, the product volatility, 










Table 3 reports simulated NPD values with the control variate methodology introduced in the Appendix C with 1000 replications. Increasing the number of replications by a factor of 100 reduces the standard deviation of the estimates by a factor of 10 (i.e. 1001/2); consequently 1000 replications offer an accurate result at reasonable computation cost. Panel A indicates that when the development duration increases from 3 months to 24 months (S(0) = $120 million), standard deviations for simulated NPD values increase from 0.0162 to 0.0372. Consistent with previous studies (Boyle [39] ), we observe in Panel B that standard deviations of estimates increase (from 0.0193 to 0.0348) with current product value (from $120 million to $180 million, or S(0)/K ratio from 1.2 to 1.8). In summary, our simulation provides more reliable results at 1) shorter project duration and 2) lower S(0)/K ratio.
In Panel A, we observe that NPD value decreases as development duration lengthens. Intuitively, the longer it takes to establish the final product, the more potential customers will be diverted to products of competitors. Our result suggests being able to bring out products faster will provide companies with significant competitive advantage over competitors.
In the next section, we explore the marginal contribution of our SCSVM model (i.e. Stochastic Competition with Stochastic Volatility model) relative to CCM (i.e. Constant Competition Model) and CVM (Constant Volatility Model). We allow several parameters that govern dynamic processes (1), (2) and (3) to vary, and examine changes in the marginal contribution of SCSVM over CCM and CVM.
Table 3. NPD base case value estimates: 1,000 replications.
5.2. Model Comparison
In CCM, we set competition erosion (δ) and product volatility (


5.2.1. Current Product Value, S(0)
In Table 5, we change the current value of a new product within a range between $80 and $160 million, while keeping other parameters at their base case values. Given the cost of investment remains at $100 million, Table 4 provides the values of a full list of “out-of-the-month” (OTM), “at-the-money” (ATM) and “in-the-money” (ITM) pro- jects.
For the base case, with the current value of the new product at $120 million and investment cost at $100 million, the value of the NPD project under SVSCM is $20.27 million, which is $3.38 million and $2.34 million(correspond to increases of 20.01% and 13.06%, respectively) higher than that under CVM and CCM, respectively. Within the range of current product values, SCSVM consistently outperforms CCM and CVM. The result indicates that failure to capture the stochastic nature of competition and product volatility will undervalue the NPD project, and will introduce an undervaluation bias.
Table 4. Models comparison. This table lists differences in assumptions under CCM (Constant Competition Model), CVM (Constant Volatility Model), and SCSVM (Stochastic Competition with Stochastic Volatility Model).
Table 5. Impact of current product value, S(0). This table reports NPD values under CCM, CVM and SCSVM models, given different initial product values, S(0). Simulation uses 1,000 replications. Parameters are defined as in Table 2. All values are in millions.
*VSCSVM, VCCM, VCVM are NPD values derived under SCSVM, CCM and CVM, respectively.
We compute the differences in values estimated under SCSVM and those under CVM and CCM. We plot value differences against current product value S(0) in Figure 1. Dashed (solid) line represents differences in values simulated under SCSVM and CVM (CCM). Figure 1 indicates, for out-of-the-money (OTM) projects (i.e. S(0) is well below K), value difference increases with S(0); while for in-the-money (ITM) projects (i.e. S(0) is well above K), difference in values decreases with S(0). One explanation is that high current product value makes it more likely that a completed product’s value will surpass investment cost; consequently the firm is less likely to abandon the project ?the value of strategic flexibility to abandon is low. At the same time, chance that product value will move higher diminishes; therefore increased volatility (due to added uncertainties associated with competition erosion and changing product volatility) more likely results in value reduction, making the difference in value between SCSVM and CVM/CCM shrink. At a low current product value, strategic flexibility to abandon
Figure 1. This figure plots the differences in values under 1) SVSCM and CVM and 2) SVSCM and CCM against initial product value, S(0). Value differences are based on simulation results reported in Table 5. All values are in millions.
protects firms from downside loss when product volatility increases; therefore, it carries more value. In the meantime, increasing volatility is more likely to result in an increase in project value. Consequently, the difference between values derived from SCSVM and CVM/CCM will widen, and will peak when project is at the money (ATM) (i.e. S(0) is nearly equal to K).
5.2.2. Investment Outlay, K
Increasing the required investment outlay K reduces project value. In Table 6, project values derived from all models decrease when development cost K rises from $60 million to $150 million. Values of NPD projects under the CCM are the lowest and those derived from SCSVM are highest.
Figure 2 exhibits a similar pattern with Figure 1. At low (high) development cost K, a NPD project is deeply in the money (out of the money). High (low) probability of accepting the project implies low (high) strategic value of abandonment. In the meantime, it is more likely that product value becomes lower (higher) at higher uncertainty. Consequently value difference between SCSVM and CVM/CCM shrinks (widens).
5.2.3. Development Duration, T
The effect of development duration, T, on NPD value is two-folded. On one hand, information accumulates with time. Firms gradually adjust product developments by the arrival of information over time, therefore would benefit from a high learning effect. Also lengthened development duration carries more flexibility. It is argued that managerial flexibility is more valuable for investment of longer duration (Teisberg [40] ), and
Table 6. Impact of investment outlay, K. This table reports NPD values under CCM, CVM and SCSVM models, given different product development cost, K. Simulation uses 1,000 replications. Parameters are defined as in Table 2. All values are in millions.
Figure 2. This figure plots the differences in values under 1) SVSCM and CVM and 2) SVSCM and CCM against development cost, K. Value differences are based on simulation results reported in Table 6. All values are in millions.
that growth opportunities of longer duration are more valuable and a firm should avoid to exercise them sooner than necessary (Kester [4] ). All else the same, NPD value should increase with T. We call it the “value increasing effect” of T. On the other hand, competition erodes the value of a NPD project. Loss in value increases as the product development process lengthens. All else the same, longer product development time will result in higher competition erosion and lower the product value. We name this the “competition erosion effect” of T.
We at first vary only the development duration T within 3 to 24 months, but leave all other parameters at their base case values. Table 7 indicates that, in this scenario, “competition erosion effect” dominates the “value increase effect” - NPD values generated by all three models decrease uniformly when development duration T lengthens. This highlights the importance of speeding up the product development process. It has been documented that Japanese companies shorten the product development process by overlapping investment phases(Takeuchi and Nonaka [41] ); that firms accommodate rapid product introductions by increasing spending to product development (Stalk [42] ); and that firms implement multi-task processing and operations implification to accelerate the product development process (Millson, Raj and Wilemon [43] ). Our result is consistent with these findings. Being early in the market provides a firm with unique advantages to set barriers in pricing, technology and production cost (Day and Wensley [44] ).
The marginal contribution of SCSVM over CCM/CVM increases with development duration. For example, when T = 3 months, project value under SCSVM exceeds those under CCM and CVM by $2.35 million and $1.11 million, respectively. However, when T = 24 months, the differences widen to $4.07 million and $3.25 million respectively. This is not surprising, as the marginal contribution by SCSVM comes from additional uncertainty being recognized. As project uncertainty increases as development duration lengthens, so do the value differences.
We then allow current product value to vary within a range (thus create a full list of ITM, ATM, and OTM projects) while development duration T varies at the same time. It is interesting to note that the relation between “competition erosion effect” and “value increase effect” varies with project moneyness. In Table 8, when NPD projects are out-of-the-money, “value increase effect” dominates; when investment duration lengthens, NPD values by all three models increase. However, for in-the-money NPD
Table 7. Impact of development duration, T. This table reports NPD values under CCM, CVM and SCSVM models, given different product development duration, T. Simulation uses 1,000 replications. Parameters are defined as in Table 2. All values are in millions.
projects, “competition erosion effect” dominates. This suggests competition intensifies when underlying innovation becomes more profitable.
5.2.4. Project Uncertainty
Project uncertainty comes from two sources, namely, competition uncertainty and uncertainty associated with the product under development. The essence of real option literature is that uncertainty creates value (Trigeorgis [2] ; Amram and Kulatilaka [5] ). Therefore the values of the investment opportunity will increase when project uncertainty increases.
Consistent with real option literature, Table 9 suggests that the values of NPD pro- jects increase as competition volatility and the level of project uncertainty increase. Product values estimated with SCSVM are higher than those obtained from CVM and
Table 8. Impact of current product value, S(0), and development duration, T.
Table 9. Impact of project uncertainty*.
*NPD value under CCM remains at $16.89 in all scenarios.
CCM, and value difference increases as volatility becomes higher. Also, the marginal contribution of SCSVM increases as uncertainty associated with competition, sδ, and with product, ss, increase. This is consistent with the fact that the marginal contribution of SCSVM comes from added uncertainty recognized.
5.2.5. Adjustment Speed, kd and ks
Adjustment rates kd and ks determine the average time needed to absorb random shocks generated by changes in competition and product uncertainty. Table 10 indicates that when it takes less time to absorb a shock from either source, project values tend to decrease. High levels of kd imply that competition is more intense. Increased competitive activities tend to devour more product value, making NPD values low. Increase in ks, on the other hand, suggests shorter windows of opportunities opened by unexpected changes in project uncertainty. As profitable investment opportunities disappear quickly, the value of projects tends to be lower.
The marginal contribution of SCSVM over CCM/CVM increases with kd. The value differences between SCSVM and CCM/CVM is $3.69 million and $2.36 million, respectively, at kd = 6.0, but rise to $4.05 million and $3.33 million when kd is 6.0. The result suggests that the importance of uncertainty to value creation strengthens as more value is devoured by competition. The marginal contribution of SCSVM decreases with ks. High ks value implies shorter windows of opportunities opened by project uncertainty; consequently reducing the advantage of SCSVM over CCM and CVM.
5.2.6. Investor Risk Aversion
Prices of risk, ld and ls, represent prices developing firms would be willing to pay to reduce uncertainty associated with competition erosion and changing product volatility. They also measure levels of risk aversion: when developing firms are more risk-averse, they would accept a higher risk premium, resulting in higher values for ld and ls.
Table 10. Impact of rate of adjustment, kd and ks*.
*NPD value under CCM remain at $16.89 in all scenarios.
Varying ld and ls allows us to examine the effect of firms’ risk altitudes towards NPD valuations.
Notice that competition erosion represents value outflows. As competitors erode the value of the product, they simultaneously bear part of a product’s risk. Consequently competition erosion represents risk sharing. To developing companies, an increase in competition erosion reduces the risk they eventually bear; therefore risk premium requested for competition erosion is negative, i.e. developing firms get paid by competitors to reduce part of a project’s risk.
Table 11 indicates that when investors and developing firms become more risk- averse, they tend to depress the value of the NPD projects. Risk aversion makes developing firms less willingly to take risk. Because uncertainty is a major source of value creation under the real option approach, we observe a decrease (increase) in project value and a reduced (increased) marginal contribution by SVSCM, as firms are more risk averse (risk prone).
6. Conclusion
We develop a stochastic volatility real option model to value NPD projects that carry managerial flexibility to abandon the project if upon completion, product value falls below the required development cost. Real option theory suggests uncertainty is important to value creation under dynamic management. We explicitly consider the stochastic nature of competition erosion and changing project uncertainty across development stages. We derive a close-form solution under a simplifying assumption of independence between product development uncertainty and other stochastic processes considered in the model. We then solve the full-scale model numerically with Monte
Table 11. Impact of price of risk, ld and ls*.
*NPD value under CCM remain at $16.89 in all scenarios
Carlo simulation. Our result is consistent with real option theory. We find a significant undervaluation bias if uncertainties association with competition and changing project volatility are ignored. We examine the marginal contribution (therefore the size of undervaluation bias) of our stochastic volatility with stochastic competition model. We find undervaluation bias is more severe when 1) The NPD project is either out-of-the- money or at-the-money; 2) when development duration lengthens; 3) when competition is more intense; 4) when the window of profitable opportunity shortens; and 5) when developing firms are more risk-prone.
Cite this paper
Hu, C.R., Jun, C. and Foley, M. (2016) Valuating New Product Development Project with a Stochastic Volatility Model. Journal of Mathematical Fi- nance, 6, 975-1001. http://dx.doi.org/10.4236/jmf.2016.65064
References
- 1. Trigeorgis, L. and Mason, S.P. (1987) Valuing Managerial Flexibility. Midland Corporate Finance Journal, 5, 14-21.
- 2. Trigeorgis, L. (1996) Real Options: Managerial Flexibility and Strategy in Resource Allocation. MIT Press, Cambridge, MA.
- 3. Myers, S.C. (1977) Determinants of Corporate Borrowing. Journal of Financial Economics, 5, 147-175.
https://doi.org/10.1016/0304-405X(77)90015-0 - 4. Kester, W.C. (1984) Today’s Options for Tomorrow’s Growth. Harvard Business Review, 62, 153-165.
- 5. Amram, M. and Kulatilaka, N. (1999) Real Options: Managing Strategic Investment in an Uncertain World. Oxford University Press, Oxford.
- 6. Caballero, R.J. (1991) On the Sign of the Investment-Uncertainty Relationship. American Economic Review, 81, 279-288.
- 7. Kulatilaka, N. (1993) The Value of Flexibility: The Case of a Dual-Fuel Industrial Steam Boiler. Financial Management, 22, 271-280.
- 8. Baldwin, C.Y. and Clark, K.B. (2000) Design Rules: The Power of Modularity. MIT Press, Cambridge, MA.
- 9. Baldwin, C.Y. and Clark, K.B. (2002) The Option Value of Modularity in Design. Working Paper, Harvard Business School, Boston.
- 10. Booz, A.H. (1980) Management of New Products. Booz, Allen and Hamilton, New York.
- 11. Mansfield, E.D. (1972) Research and Innovation in the Modern Corporation. W.W. Norton & Co., New York.
- 12. Van der Panne, G., van Beers, C. and Kleinknecht, A. (2003) Success and Failure of Innovation: A Literature Review. International Journal of Innovation Management, 7, 306-337.
- 13. Sahal, D. (1981) Patterns of Technological Innovation. Addison-Wesley, Reading, MA.
- 14. Nelson, R.R. and Winter, S.G. (1982) An Evolutionary Theory of Economic Change. Harvard University Press, Cambridge, MA.
- 15. Fahey, L. and Narayanan, V.K. (1986) Macroenvironmental Analysis for Strategic Management. West Publishing, Minnesota.
- 16. Contractor, F.J. and Narayanan, V.K. (1990) Technology Development in the Multinational Firm: A Framework for Planning and Strategy. R&D Management, 20, 305-322.
https://doi.org/10.1111/j.1467-9310.1990.tb00720.x - 17. Myers, S.C. and Turnbull, S.M. (2002) Capital Budgeting and the Capital Asset Pricing Model: Good News and Bad News. The Journal of Finance, 32, 321-333.
https://doi.org/10.1111/j.1540-6261.1977.tb03272.x - 18. Brennan, M.J. (1973) An Approach to the Valuation of Uncertain Income Streams. The Journal of Finance, 28, 661-674.
https://doi.org/10.1111/j.1540-6261.1973.tb01387.x - 19. Paddock, J.L., Siegel, D.R. and Smith, J.L. (1988) Option Valuation of Claims on Real Assets: The Case of Offshore Petroleum Leases. The Quarterly Journal of Economics, 103, 479-508.
https://doi.org/10.2307/1885541 - 20. McDonald, R. and Siegel, D. (1984) Option Pricing When the Underlying Asset Earns a Below-Equilibrium Rate of Return: A Note. The Journal of Finance, 39, 261-265.
https://doi.org/10.1111/j.1540-6261.1984.tb03874.x - 21. McDonald, R. and Siegel, D. (1986) The Value of Waiting to Invest. The Quarterly Journal of Economics, 101, 707-727.
https://doi.org/10.2307/1884175 - 22. Majd, S. and Pindyck, R.S. (1987) Time to Build, Option Value, and Investment Decisions. Journal of Financial Economics, 18, 7-27.
https://doi.org/10.1016/0304-405X(87)90059-6 - 23. Trigeorgis, L. (1993) The Mature of Option Interactions and the Valuation of Investments with Multiple Real Options. The Journal of Financial and Quantitative Analysis, 28, 1-20.
https://doi.org/10.2307/2331148 - 24. Brennan, M.J. and Schwartz, E.S. (1985) Evaluating Natural Resource Investments. The Journal of Business, 58, 135-157.
https://doi.org/10.1086/296288 - 25. Kensinger, J. (1987) Adding the Value of Active Management into the Capital Budgeting Decision. Midland Corporate Finance Journal, 5, 31-42.
- 26. Myers, S.C. and Majd, S. (1987) Abandonment Value and Project Life. Advances in Futures and Options Research, 4, 1-21.
- 27. Chen, S.S., Ho, K.W., Ik, K.H. and Lee, C.F. (2003) The Valuation of New Product Introductions under Uncertain Competition: A Real Option Approach. Advances in Financial Planning and Forecasting, 11, 23-43.
- 28. Schwartz, E.S. (2004) Patents and R&D as Real Options. Economic Notes, 33, 23-54.
https://doi.org/10.1111/j.0391-5026.2004.00124.x - 29. Chung, K.H. and Charoenwong, C. (1991) Investment Options, Assets in Place, and the Risk of Stocks. Financial Management, 20, 21-32.
- 30. Miles, J.A. (1986) Growth Options and the Real Determinants of Systematic Risk. Journal of Business Finance and Accounting, 13, 95-105.
https://doi.org/10.1111/j.1468-5957.1986.tb01175.x - 31. Fama, E.F. and French, K.R. (1988) Commodity Futures Prices: Some Evidence on Forecast Power, Premiums and the Theory of Storage. The Journal of Business, 60, 55-73.
https://doi.org/10.1086/296385 - 32. Fama, E.F. and French, K.R. (1988) Business Cycles and the Behavior of Mental Prices. The Journal of Finance, 43, 1075-1093.
https://doi.org/10.1111/j.1540-6261.1988.tb03957.x - 33. Gilson, R. and Schwartz, E.S. (1990) Stochastic Convenience Yield and the Pricing of Oil Contingent Claims. The Journal of Finance, 45, 959-976.
https://doi.org/10.1111/j.1540-6261.1990.tb05114.x - 34. Demers, M. (1991) Investment under Uncertainty, Irreversibility and the Arrival of Information Over Time. The Review of Economic Studies, 58, 333-350.
https://doi.org/10.2307/2297971 - 35. Bjerksund, P. and Ekern, S. (1995) Contingent Claims Evaluation of Mean-Reverting Cash Flows in Shipping. In: Trigeorgis, L., Ed., Real Options in Capital Investment: Models, Strategies, and Applications, Greenwood Publishing Group, Connecticut, 207-219.
- 36. Cox, J.C., Ingersoll, J.E. and Ross, S.A. (1985) An Intertemporal General Equilibrium Model of Asset Prices. Econometrica, 52, 363-384.
https://doi.org/10.2307/1911241 - 37. Cox, J.C. and Ross, S.A. (1976) The Valuation of Options for Alternative Stochastic Processes. Journal of Financial Economics, 3, 145-166.
https://doi.org/10.1016/0304-405X(76)90023-4 - 38. Stein, E.M. and Stein, J.C. (1991) Stock Price Distributions with Stochastic Volatility: An Analytic Approach. The Review of Financial Studies, 4, 727-752.
https://doi.org/10.1093/rfs/4.4.727 - 39. Boyle, P.P. (1977) Options: A Monte Carlo Approach. Journal of Financial Economics, 4, 323-338.
https://doi.org/10.1016/0304-405X(77)90005-8 - 40. Teisberg, E.O. (1995) Methods for Evaluating Capital Investment Decisions under Uncertainty. In: Trigeorgis, L., Ed., Real Options in Capital Investment: Models, Strategies, and Applications, Greenwood Publishing Group, Connecticut, 31-45.
- 41. Takeuchi, H. and Nonaka, I. (1986) The New New Product Development Game. Harvard Business Review, 64, 137-146.
- 42. Stalk, G.J. (1984) Time—The Next Source of Competitive Advantage. Harvard Business Review, 66, 41-52.
- 43. Millson, M.R., Raj, S.P. and Wilemon, D. (1992) A Survey of Major Approaches for Accelerating New Product Development. The Journal of Product Innovation Management, 9, 53-69.
https://doi.org/10.1111/1540-5885.910053 - 44. Day, G.S. and Robin, W. (1988) Assessing Advantage: A Framework for Diagnosing Competitive Superiority. Journal of Marketing, 52, 1-20.
https://doi.org/10.2307/1251261 - 45. Duffie, D. (2010) Dynamic Asset Pricing Theory. Princeton University Press, Princeton.
- 46. Karatzas, I. and Steven S. (2012) Brownian Motion and Stochastic Calculus. Springer Science & Business Media, Berlin.
Appendex A
To owner (i.e. the firm) of the new product, competition erosion creates a dividend-like value outflow. Upon product completion, firm obtains spot new product value. Assume there exists a contract F, which requires the transfer of completed new product to contract owner upon product completion. Under a risk-neutral economy, future payment streams from these two positions are identical, therefore values of the contract and NPD project must be the same.
Donate F as the value of the contract. By construction, it should be the function of time t, new product value




with a deterministic continuous sample path of

where 

It can be shown (Cox, Ingersoll and Ross [36] , Theorem 3) that the value of the contract on NPD project must satisfy the following partial differential equation:

with boundary condition given in (A.1).
Duffie [45] and Karatzas and Shrev [46] demonstrated that solution to Equation (A.3) with boundary condition (A.1) is given as:

with Ito’s lemma, given selected stochastic volatility path and risk-neutral processes described in (2)* and (4)*, instantaneous value change of the contract is:

Denote:

with (A.4) and (A.6), (A.5) can be simplified as:

Since 



Denote:

(A.6a) could be simplified to:

It is obvious that change in contract value 

The resulting distribution of the contract value at time T is given by:

with 
Appendix B
We follow Stein and Stei [38] to derive the exact distribution of NPD value at time T.
Define 




Apply the Fourier transformation to (B.1)

Using definition in (A.6b), 
And (B.2) can be re-expressed as:

where 

Apply Fourier inversion formula to (B.3) to get:

Now make the change of variables of


Appendix C
A Simplified Solution
In this section, we derive a closed-form solution under the assumption that NPD volatility follows a deterministic process.
Assume σσ = 0. Partial deferential Equation (6) becomes

Solution to Equation (C.1), with the boundary condition (5), admits the following special representation (Duffi [45] ; Karatzas and Shreve [46] ):

where


and

Our estimate of the NPD project (7) can be rewritten as:

Control Variate Methodology
Starting with time 0, for a small time interval (0, 0 + Δt), we randomly generate values for, dωS, dωδ and dωσ, from a joint normal distribution such that

and
and

We then simulate incremental changes


We repeat the above operation for all the following intervals

By time T, a sample path for S(T), δ(T), and σ(T) can be generated, respectively. A value of the project upon time T, as defined by boundary condition (5), can be computed.
We utilize the same series of dωS, dωδ and dωσ values generated in the above simulation and repeat the above procedure to simulate sample paths of S(T) and δ(T). However, we restrict σσ = 0 in (3)* when simulating δ(T) (such that δ(T) is actually deterministic). We compute the value of the project upon time T using boundary condition (5), based on the value of the project simulated under the restriction σσ = 0.
We compute the difference between the project values obtained from these two simulations. We repeat the above process. Givena large quantity of repetitions, time T distributions of S(T), δ(T), and σ(T), with and without the assumption σσ = 0, as well as a sample of the differences between project values under these assumptions, can be obtained.
We compute B*[S(0), δ(0), σ(0)] with solutions provided by (C.3) to (C.5). The value of the integral on the right-hand-side of (C.6) is computed as the present value (discounted at risk-free rate r) of the sample average of the differences obtained from above simulations. Based on the law of large numbers, when a number of repetitions is large enough, the value of the integral should converge to its true value, regardless of the true distribution 

Because the value of the integral on the right-hand-side of (C.6) is simulated using the same random variable series of dωS, dωδ and dωσ, and the underlying dynamics are similar except we assume σσ = 0 in the second round of simulation, the value of project from both simulations should be closely correlated. By utilizing only their differences, the control variate methodology should achieve a significant variance reduction.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmf@scirp.org










