Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21195,11 pages DOI:10.4236/jmp.2012.37086
Energetic Nature of Rigidity
Faculty of Mechanical Engineering, Politechnika Koszalińska, Koszalin, Poland
Email: *Tadeusz.Hryniewicz@tu.koszalin.pl
Received February 21, 2012; revised April 20, 2012; accepted May 12, 2012
Keywords: Rigidity; Coefficient of Stiffness; Stiffness Energy; Proper Stiffness Energy; Gained Stiffness Energy; Potential Field; Proper Stiffness Potential; Gained Stiffness Potential; Rigidity Work; Rigidity Force; Deflection
ABSTRACT
The work is to present the energetic nature of the rigidity. It starts with the definition by introducing the notion of sensual magnitudes with the pyramidal structure of all surrounding magnitudes known by a human being. Next the selection of the subject is provided in view of a smooth categorization of magnitudes describing the reality. The adequate description of the considered mechanical phenomenon is presented by formulating general stiffness characteristics. There are several characteristics analyzed, both functional and parametric. An essential, quite a new one is the characteristic of stiffness energy measure which is the stiffness potential. The proper and gained stiffness potentials situated on stable and unstable potential fields have been analyzed. An example of using of this theory to practice is given. It has been referred to a cylindrical grinder case. The presented theory allowed describing the entire stiffness characteristics, including its initial very essential course which has been usually, though inequitably, extrapolated by a straight line segment coming out of zero point with zero coordinates.
1. Introduction
The rigidity of solid or a material body system is the resistance to its deformation. In case of shape deformations the shape stiffness is considered; whereas in case of contact strains it should be referred to the contact stiffness.
Thus the stiffness is the magnitude which may be determined qualitatively by engaging senses (of touch and sight), forming in fact sensual, not a physical magnitude. Therefore the stiffness may be determined as small, big, very big, or immense. A determined measure may be ascribed to this sensual magnitude/stiffness. That measure is the coefficient of stiffness and it is a physical magnitude. It may be determined by measuring the component magnitudes and then calculating in accordance to a proper formula.
That physical magnitude, the coefficient of stiffness k, is defined as the first derivative (derivative of the first order) of the rigidity force S against the deflection f, then
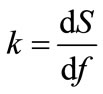 (1)
(1)
This work determines generally the stiffness, by introducing the notion of the coefficient of stiffness; it does not divide it into springy, flexible, elastic, and plastic rigidity, or just flexibility, elasticity, plasticity. The considerations are provided with the load of system where no firm deformations occur.
Until now three categories of magnitudes have been separated, namely: sensual, physical, and material. There are also intellectual magnitudes, and the considered stiffness energy has such a character.
One should admit that right order/arrangement of all these magnitudes is of importance. It was considered also in the previous works [1-3]. The structure of these magnitudes: intellectual I, sensual S, physical P, and material M, is significant. It may be presented in the form of a pyramid (Figure 1), as this kind of lump presents terminological stratification in the best way. One could say this figure presents pyramidal, laminar structure of magnitudes of the external human world.
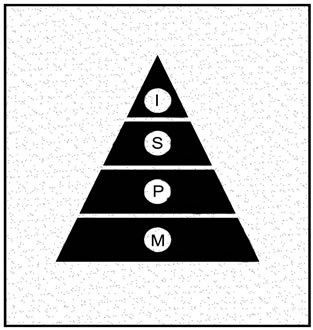
Figure 1. Pyramidal structure of magnitudes of the external human world [1-3].
2. The Subject of Formulation
The selection of the subject is fully justified. First of all there is no correct terminological description of the phenomenon of shape deformation. To perform it in a right way, first a separation of all magnitudes is needed, i.e. intellectual, sensual, physical, and material, providing to: stiffness energy, rigidity, and stiffness measure of the described material system. One may refer now to the examples of material objects concerning their rigidity.
The stiffness (reversal to flexibility) is an essential feature of the system material elements, their connections, joints (kinematic pairs), as well as of each separate element. Dependent on the use of such a system (device), its stiffness is in different value ranges. The proper (initial) rigidity, with the force as a measure, is of importance for a link, node, and all material system.
Let us focus on the machine tools to evaluate their resistance to deformation of the component assemblies. This resistance, covering the rigidity, should be as high as possible. It is of special attention in the machine tools to be used for fine machining.
In [4] the rigidity of the working spaces of machining centres was assessed. The indexes determining the effect of the carrying machine tool system on the machining accuracy, related to the changing localization of cutting zone, were given. The evaluation results, as mentioned there, may be used to introduce changes in the design and technological process, to improve the rigidity of the machine tool in its working space.
The work [5] reveals that there are some methods to eliminate negative effect of the machine tool flexibility and particular its elements. They are: 1) selection of such a machining scheme which does not require a big rigidity of the technological system, 2) using some compensational systems which allow to decrease or compensate deformations of the machine tool elements, and 3) increasing the proper rigidity of the design components.
The contact rigidity in the grinding zone is a very important feature of grinders. The work [6] presents results of the studies of dependence of that feature on the quotient of velocities (ratio of the grinding wheel velocity to the workpiece velocity).
The study results presented in [7] show that the real thickness of the cut layer, while in-depth turning with the traverse feed, depends on the deformation of carrying assemblies of a machine tool. A mathematical model, to determine the cut layer regarding the flexibility of the machine tool, was derived.
The work [8] presents a theoretical model, describing the influence of a grinder rigidity on the cohesion of ground elements made of sintered Si3N4. The described verifying actions showed that there is a critical rigidity while grinding that material, distinctly dependent on the depth of grinding.
An extremely essential feature of a machine tool is its proper rigidity. It was shown in [9] that a high proper rigidity may be even replaced by a foundation. That idea was realized in relation to the machining centre to machine the workpieces of big overall dimensions (1600 ´ 1600 ´ 1200 mm). One should add that the machining on this centre is possible under one fixed position from five sides/ directions at the same time.
Some more certificates of exemplary studies of rigidity of the component elements of the machine tools may be added to this analysis. The work [10] provides the study results of this feature in reference to the needle segments of the rolling guides of machine tools, the bedways made by 1NA-HYDREL Company. It was found that the rigidity of the bedways plays an important role in modeling and analysis of dynamics of the slide systems of machine tools, especially regarding the non-linearity.
The presented literature references show that the need to describe the mechanical phenomenon of deformation of the material systems is still of importance and valid. The necessity exists to describe this phenomenon more adequately and precisely. The resistance to deformations (rigidity) and the tendency to deformations (deformability) of these systems are their reverse features characterizing the considered phenomenon. The rigidity is, however, the feature which is more often introduced to evaluate the technological systems. It appears that also due to the exploitational reasons they should be more resistant to deformations. Thus the rigidity is to be the subject of considerations of this work.
Furthermore, at first the general indicative rigidity characteristics will be given as the basis to explain the title energetic nature of the rigidity. Its adequate presentation in the form of dependence of the rigidity force on the deflection results from the source differential description of the magnitude in the interstate spaces.
3. Adequate Description of the Considered Mechanical Phenomenon
At the source of cognitive way of all physical phenomena which occur with variable rate/intensity or velocity between the neighbouring energetic states there is a general differential equation, namely:
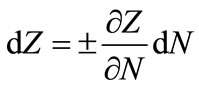 (2)
(2)
where: dZ—total differential of magnitudes forming dependent variables, dN—total differential of magnitudes forming independent variables, —partial derivative of dependent magnitudes against independent ones. The symbols (±) are the algebraic operators with a determined function. The operator (+) fulfills a formal function, just confirming the physical significance of the described phenomenon, whereas the sign (–) provides a physical sense to a determined description. That general source differential equation has been presented in [11], referred to the real determined technological conditions with different initial conditions. These initial conditions determine a detail solution of this type of equation. They refer to the initial conditions of a phenomenon or process but not those connected with the beginning of measure of determined physical magnitudes. The measurement of these magnitudes is a necessary though not a sufficient condition. The sufficient condition is ascribed to their measurement at the very beginning of a phenomenon.
—partial derivative of dependent magnitudes against independent ones. The symbols (±) are the algebraic operators with a determined function. The operator (+) fulfills a formal function, just confirming the physical significance of the described phenomenon, whereas the sign (–) provides a physical sense to a determined description. That general source differential equation has been presented in [11], referred to the real determined technological conditions with different initial conditions. These initial conditions determine a detail solution of this type of equation. They refer to the initial conditions of a phenomenon or process but not those connected with the beginning of measure of determined physical magnitudes. The measurement of these magnitudes is a necessary though not a sufficient condition. The sufficient condition is ascribed to their measurement at the very beginning of a phenomenon.
The record of the equation (2), applied to the considered phenomenon, possesses the following configuration:
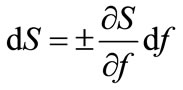 (3)
(3)
where the sign (+) concerns the progressively rising changes of the rigidity force, and (–) is considered in describing degressively rising changes of this magnitude. In the first case the rate of force changes rises with the increase of deflection, whereas the second one informs that the rate of changes will be decreasing respectively. One should add that the rate of changes of the considered magnitude is just the coefficient of stiffness defined by the formula (1).
4. General Rigidity Characteristics
The rigidity characteristics, being the dependence of the rigidity force on deflection (Figure 2), has a progressive exponential course in the direction of the system loading (Figure 2(a)); whereas the degressive course of this kind takes place in the direction of de-loading system (Figure 2(b)); as it results from the joining of these curves (Figure 2(c)) and they do not overlap forming a sort of the rigidity hysteresis loop.
These courses occur in a deformation-force space/zone (dotted area) limited by the deformation and force potential field. To say more strictly, it concerns the stable deformation potential field  and unstable potential field of this type
and unstable potential field of this type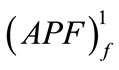 . They are the fields limiting the mentioned space in the direction of deflection.
. They are the fields limiting the mentioned space in the direction of deflection.
In the force direction it is more complex in character and requires some extended explanations. Two energetic bands appear here (the spaces filled with horizontal lines). One of them concerns the proper rigidity energy (Figure 2(a)) and is limited by the bottom stable force potential field 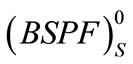 and the upper stable force potential field
and the upper stable force potential field , whereas the second one refers to the gained rigidity energy (Figure 2(b)) and is limited by the upper/top unstable force potential field
, whereas the second one refers to the gained rigidity energy (Figure 2(b)) and is limited by the upper/top unstable force potential field  and the bottom stable force potential field
and the bottom stable force potential field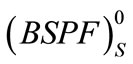 .
.
The introduced notions of the rigidity energy are in full agreement with the definition of energy; the definition is not respected until now with the evidence being the actions of aliasing the energy with work. It is not necessary to develop many references in the field to support or confirm the existing notion gap. It is enough to mention some recent books covering this energetic quest [12-16].
The proper rigidity energy of the system is its readiness to perform the rigidity work whereas the gained rigidity energy of this system, in turn, is the ability to perform the rigidity work over it. At this stage, while defining both these energies, one may state that the proper energy is lesser than the gained energy. One should admit that they are intellectual magnitudes (see Figure 1), and not the physical ones. This is why these energies may be evaluated qualitatively only, indicating that: the first one (proper) is lesser than the second one (gained), or the second one being bigger than the first one.
A need for possessing measures of both these intellecttual magnitudes exists. These measures will be the physiccal magnitudes. The measure of the proper rigidity energy is the proper rigidity potential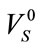 , being the product of the initial proper rigidity force
, being the product of the initial proper rigidity force  and the distance between the deformation potential fields, that is
and the distance between the deformation potential fields, that is . Thus
. Thus
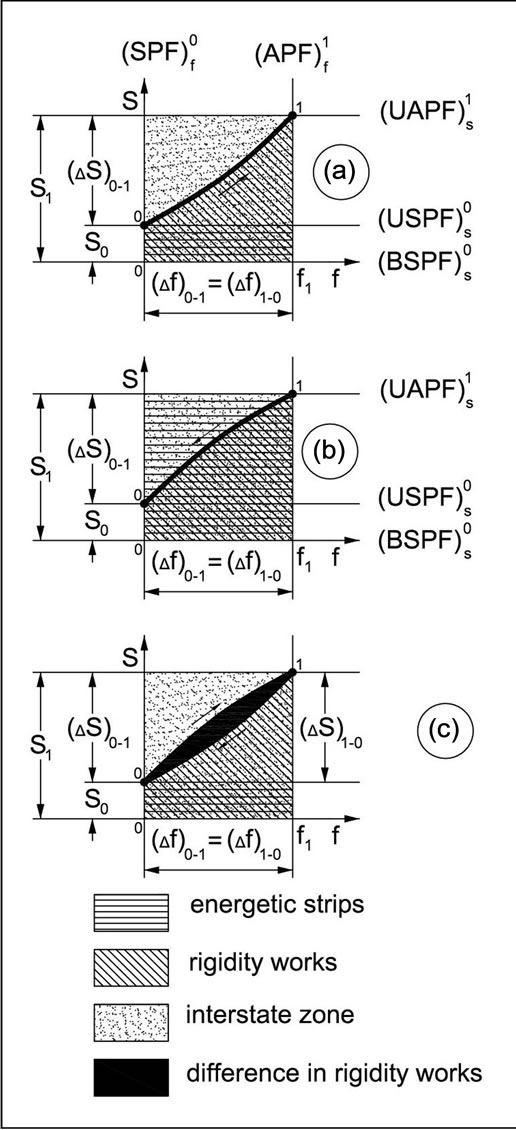
Figure 2. Indicative courses of the rigidity curves related to the directions of: loading (a), and de-loading (b) of the system; as well as to the both directions (c).
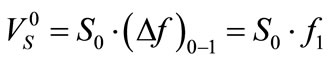 (4)
(4)
That corresponds with the field of horizontally dashed area (see Figure 2(a)), i.e. the proper energetic band, or the band of the proper energy. One should add that the magnitude 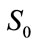 is at the same time the intensity of stable deformation potential field
is at the same time the intensity of stable deformation potential field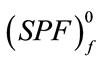 . Thus the potential is the product of the intensity of the mentioned potential field and the distance between the deformation potential field, with the distance being the measure of deformation resistance of the deformation-force space. (Here, the analogy to the Ohm’s law may be noticed.)
. Thus the potential is the product of the intensity of the mentioned potential field and the distance between the deformation potential field, with the distance being the measure of deformation resistance of the deformation-force space. (Here, the analogy to the Ohm’s law may be noticed.)
And now, getting to the gained rigidity energy: its measure is the gained rigidity potential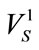 , being the product of the gained rigidity force
, being the product of the gained rigidity force 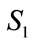 and the distance between the deformation potential fields, that is
and the distance between the deformation potential fields, that is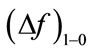 . Therefore
. Therefore
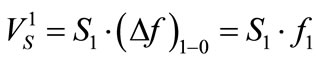 (5)
(5)
It may be noticed, the band of the gained energy is considerably bigger than the band of the proper energy and it covers the entire deformation-force zone. The notion of the rigidity tension  is introduced now, being the potential difference of
is introduced now, being the potential difference of  and
and . Thus, after taking into account the formulae (4) and (5), one obtains
. Thus, after taking into account the formulae (4) and (5), one obtains
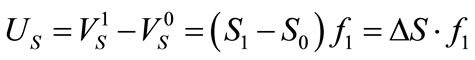 (6)
(6)
It results evidently from these considerations that the energy measure (the more to say the energy, being the intellectual magnitude) is not the same as the work, although both these magnitudes have the same measure unit. The contents of these both magnitudes are generous and much differentiated.
The oblique dashed fields (see Figure 2) present the areas referred to the rigidity works. In the direction of the system loading (Figure 2(a)) this kind of work is bigger than the rigidity measure of the proper energy. However, in the direction of de-loading of the system (Figure 2(b)) there is a reverse situation, because the gained energy measure is greater than the work. The difference of the rigidity works (Figure 2(c)), corresponding with the blackened area, denotes the rigidity hysteresis, as resulting mainly from the fact that in the direction of the system loading a determined external stimulus acts, whereas in the reverse direction, the direction of return of the system into the stable state, this stimulus (due to sufficiently big the gained energy) does not work. In other words, at first the system collected/cumulated the energy, and then it was giving it out.
5. Creation of the Rigidity Characteristics
At first the rigidity characteristics will be described, corresponding with the direction of the system loading. That is an exponential, progressively rising curve which illustrates the dependence of the rigidity force S on the deflection f (Figure 3).
This curve is the envelope of right-angled triangles of which the deformation leg is constant and equals to the so called deformation constant , with the force leg varying respectively. The initial point of the curve is on the intersection of the stable potential fields of: the stable deformation potential field
, with the force leg varying respectively. The initial point of the curve is on the intersection of the stable potential fields of: the stable deformation potential field 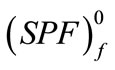 and the upper/top stable force potential field
and the upper/top stable force potential field . The final point of this curve is situated on the intersection of the unstable potential fields of: the first unstable deformation potential field
. The final point of this curve is situated on the intersection of the unstable potential fields of: the first unstable deformation potential field 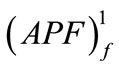 and the first upper/top unstable force potential field
and the first upper/top unstable force potential field . The mentioned potential fields are the limits of the deformation-force space of which the dimension in the deformation direction is
. The mentioned potential fields are the limits of the deformation-force space of which the dimension in the deformation direction is , and in the force direction is
, and in the force direction is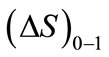 .
.
The force leg of this moving/shifting right-angled triangle is, as it was mentioned, respectively variable that results from the changing position of tangent to the curve of rigidity force. For 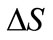 the length of this leg equals
the length of this leg equals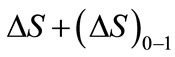 .
.
Now one may come up to the integration of equation (3), denoting limits of the integrals from the total differentials. It means that
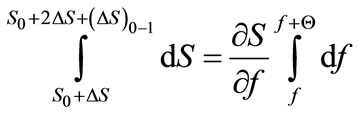 (7)
(7)
and
 (8)
(8)
or
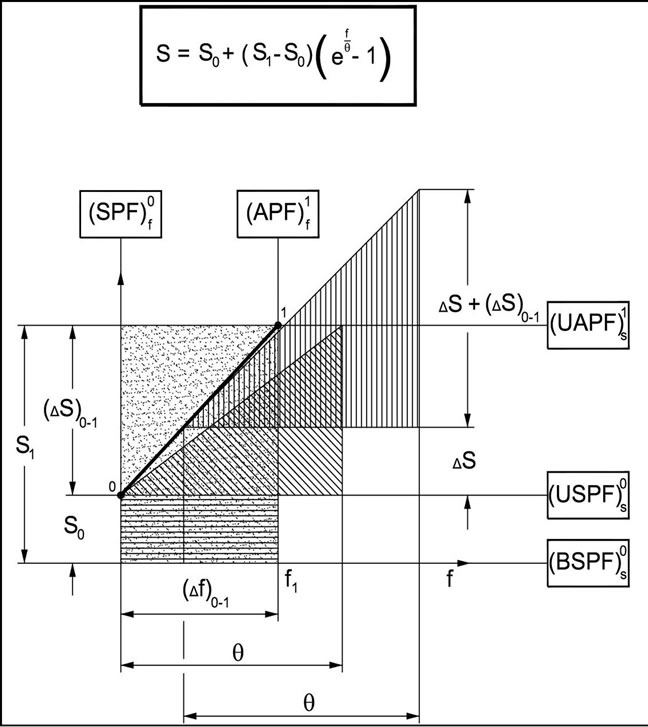
Figure 3. Illustration of scheme of creation of the rigidity characteristics in the direction of the system loading.
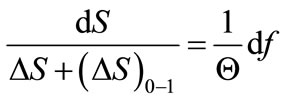 (9)
(9)
One may notice the partial derivative was substituted by the quotient of the total differentials. One could do that as the total differentials have been clearly determined by introducing the limits of their integrals. It is worthy admitting that the sign (+), the positive algebraic operator, has been regarded because the changes in the rigidity force are rising progressively.
Furthermore, by integrating both sides of the equation (9), one obtains the result
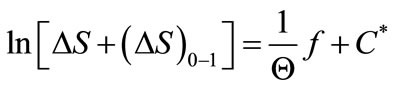 (10)
(10)
that is
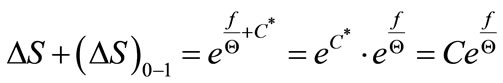 (11)
(11)
After regarding that for 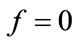 the magnitude
the magnitude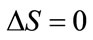 , one obtains
, one obtains
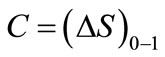 (12)
(12)
and after substituting (12) to (11)
 (13)
(13)
that is (see Figure 3)
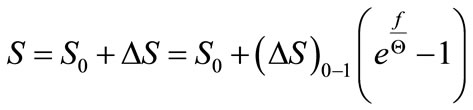 (14)
(14)
or
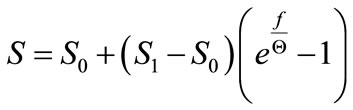 (15)
(15)
One may determine now the second coordinate of the point 1, that is the deflection corresponding with the end of the phenomenon of the system deformation. That result is obtained by introducing the force 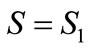 and deflection
and deflection 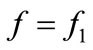 to the equation (15). Therefore
to the equation (15). Therefore
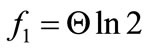
The characteristics of the rigidity system, corresponding with the direction of its de-loading (Figure 4), is degressively rising in the nature. This curve is the envelope of right-angled triangles of which the deformation leg is constant and equals to the so called the deformation constant  (introduced above), and the force leg varies respectively.
(introduced above), and the force leg varies respectively.
The deformation constant  is on the nominal potential field (NPF), being the asymptote to which the second, apparent part of the curve (dashed line) is tending. Along this field the mentioned triangle with its leg is moving.
is on the nominal potential field (NPF), being the asymptote to which the second, apparent part of the curve (dashed line) is tending. Along this field the mentioned triangle with its leg is moving.

Figure 4. Illustration of scheme of creation of the rigidity characteristics description in the direction of the system de-loading.
Now one may start integrating the equation (3), marking the limits of integrals from the total differentials and regarding with this the negative sign of the algebraic operator. Therefore
 (16)
(16)
and further
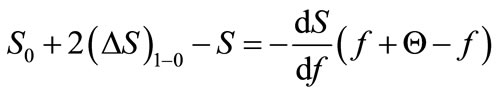 (17)
(17)
which is
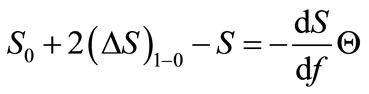 (18)
(18)
or
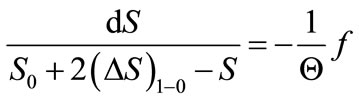 (19)
(19)
By integrating both sides of the equation (19) one obtains the following solution
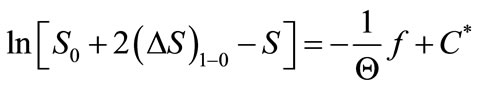 (20)
(20)
that is
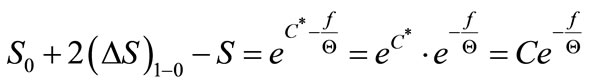 (21)
(21)
After taking into account the initial conditions, meaning that for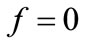 ,
, 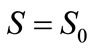 , one obtains
, one obtains
 (22)
(22)
and after substituting (22) to (21)
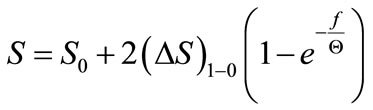 (23)
(23)
Regarding further that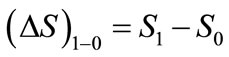 , the equation (23) may be recorded as follows
, the equation (23) may be recorded as follows
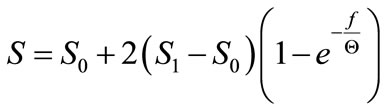 (24)
(24)
Thus two basic functional characteristics have been introduced, corresponding with the directions of: the loading (15), and de-loading (24) of the system. Now further characteristics, being the formulae on the coefficient of stiffness k and the rigidity work/labour , may be determined.
, may be determined.
6. Further Characteristics of the Rigidity System
The consecutive functional characteristics are formed by the dependences of the coefficient of rigidity k on the deflection f, being the first derivatives (derivatives of the first order) of the rigidity force S against the latter parameter that has been reflected by the definition formula (1) given above. Therefore that kind of characteristics, referred to the direction of loading, takes the form
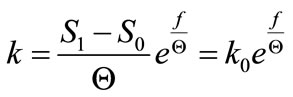 (25)
(25)
and in reference to the direction of de-loading of the system
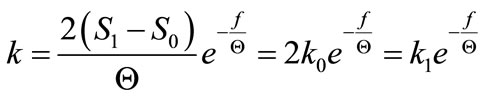 (26)
(26)
The illustration of both of these dependences (Figure 5) indicates that for a determined deflection f* that coefficient takes uniform, the same value k*.
That deflection may be determined by comparing the formulae (25) and (26), respectively, that is
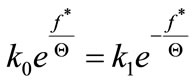 (27)
(27)
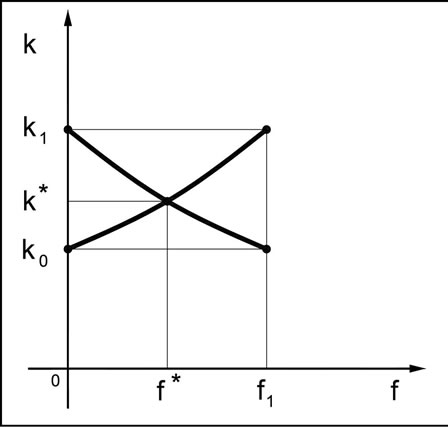
Figure 5. Courses of dependences of the rigidity coefficients k0, k1 on the deflection f.
The solution of that equation with one unknown f* takes the following form
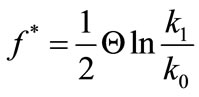 (28)
(28)
By substituting to the equation, for instance (25), one obtains
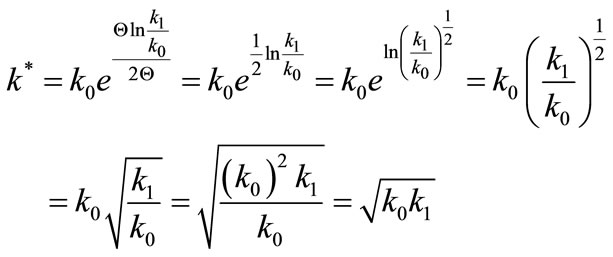 (29)
(29)
Thus the coefficient of rigidity k* is the square root of the product of coefficients k0 and k1, that is the geometrical mean of these coefficients. Furthermore, by regarding , one obtains
, one obtains
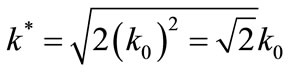 (30)
(30)
Now let us consider the following functional characteristics, being the formulae on the rigidity work
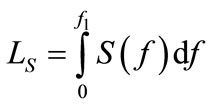 (31)
(31)
Therefore the rigidity work in the direction of the system loading is expressed by the formula
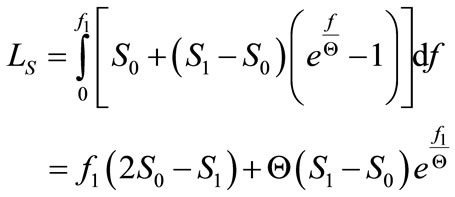 (32)
(32)
and in the direction of the system de-loading
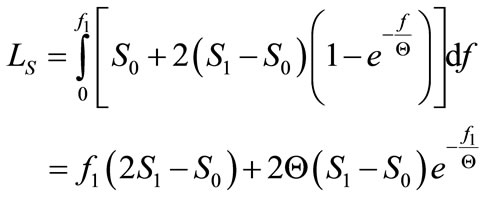 (33)
(33)
7. Example of Using the Presented Theory
The presented theory has been used to the adequate description of the rigidity characteristics of the tailstock (loose headstock) and the fixed headstock of the workpiece with the assemblies being the design links of the system of thread grinder of type MM-582. In Table 1, there are the measurement results of the rigidity force S and the deflections of these links of the grinder, i.e. yw, zw, yk, zk; they have been excerpted from the work [17]. The measurements of deflections, related to the particular rigidity forces, have been performed in the planes perpendicular to the workpiece axes, in the directions: vertical z, and horizontal y; thus the above markings the
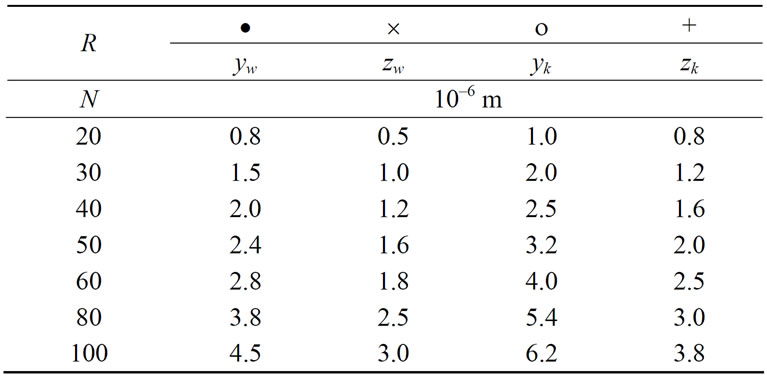
Table 1. Results of measurements of rigidities and deflections of the loose headstock and fixed headstock of thread grinder of type MM-582 [17].
deflections of: yw—the deflection of the fixed headstock in horizontal direction, zw—the deflection of the fixed headstock in vertical direction, yk—the deflection of the loose headstock in horizontal direction, zk—the deflection of the loose headstock in vertical direction. One should add that all these results are to determine the characteristics of links of the system in the direction of its loading.
The graphical illustration of the set of experimental points (Figure 6) has been substituted by the straight lines coming out of one, zero point of the coordination system: the rigidity force—deflection. One may notice here very simplified data handling of measurements of all these magnitudes. Position of the lines did not result from a statistical handling of the material, but was determined approximately. That way (approximate) was treated also the approximation and the extrapolation of the phenomenon of deformation of both these links of the grinder.
It appears the set of experimental points indicates distinctly that the courses of deflections are exponential in their character and rising degressively. In the coordination system: deflection—rigidity force, the system which should be considered, the courses of the rigidity force will be exponential and rising progressively.
In the next part of the work the latter system was adopted as in this system the rigidity coefficients may be determined, being the derivative of the rigidity force against the deflection, and defined analytically by the formula (1). The first system (see Figure 6) allows to determine the reversal matter to the rigidity force k, which is the coefficient of flexibility c, namely

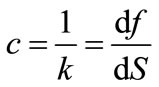 (34)
(34)
Taking advantage of the presented theory, first of all the values of coordinates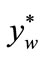 ,
,  ,
, 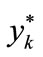 ,
, 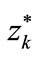 , should be determined. These coordinates determine the position of straight line, tangent to this searched, adequate course of the rigidity force. These coordinates result from the formula (16), then
, should be determined. These coordinates determine the position of straight line, tangent to this searched, adequate course of the rigidity force. These coordinates result from the formula (16), then
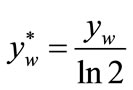 (35)
(35)
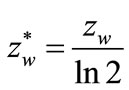 (36)
(36)
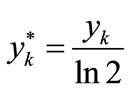 (37)
(37)
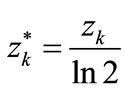 (38)
(38)
The results of calculations of these coordinates (Table 2) indicate that they are bigger as to their values than the experimental coordinates. The values of coordinates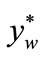 ,
,  ,
, 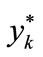 ,
, 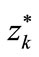 , should be now handled statistically, by approximating them in accordance to the following dependences:
, should be now handled statistically, by approximating them in accordance to the following dependences:
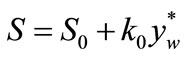 (39)
(39)
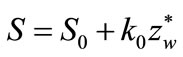 (40)
(40)
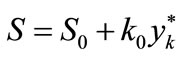 (41)
(41)
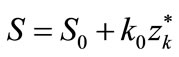 (42)
(42)
For generally recorded that kind of the linear dependence
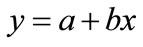 (43)
(43)
the coefficients a and b are determined in accordance to the following formulae:
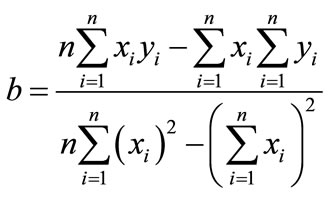 (44)
(44)
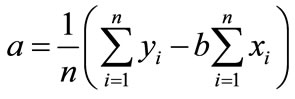 (45)
(45)
which are the result of using the rule of the least sum square of deviations of the experimental values from
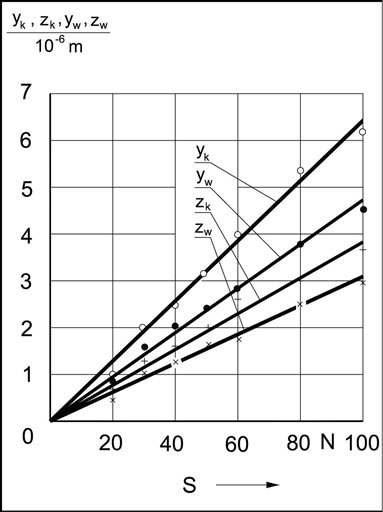
Figure 6. Graphical illustration of the set of experimental points [17].
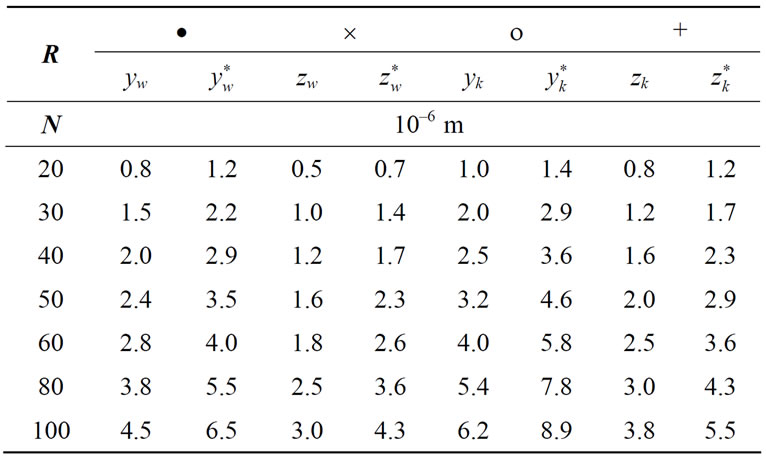
Table 2. Results of measurements and calculations of magnitudes characterizing the design links of the investigated grinder.
theoretical ones, resulting from the position of the linear regression function. That rule has been described in detail in references, such as [18-21].
Comparison of the magnitudes needed for calculation of the coefficients of linear regression, the initial rigidity force 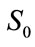 and the initial coefficient of stiffness k0 in the formulae (39), (40), (41), and (42), has been presented in Table 3.
and the initial coefficient of stiffness k0 in the formulae (39), (40), (41), and (42), has been presented in Table 3.
For example, for the rigidity force S and deflection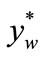 , that is the tangent shifted on the direction of tangent to the searched curve, tangent in the initial point, with the coefficients S0 and k0 described by the formulae
, that is the tangent shifted on the direction of tangent to the searched curve, tangent in the initial point, with the coefficients S0 and k0 described by the formulae
 (46)
(46)
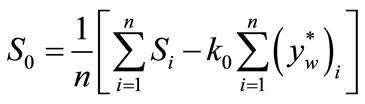 (47)
(47)
Therefore
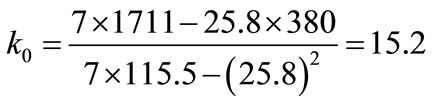 N×mm–1 (48)
N×mm–1 (48)
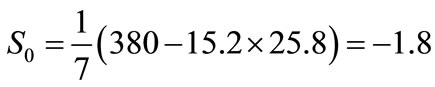 N(49)
N(49)
Thus
 (50)
(50)
One may notice, the initial rigidity force S0 has a negative value. The regression line (Figure 7) crosses the axis of abscissae, that is the axis of deflections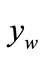 ,
, 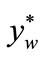 , in a determined point.
, in a determined point.
The coordinate of this point 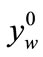 may be calculated by substituting the rigidity force
may be calculated by substituting the rigidity force 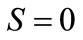 to (50). Therefore
to (50). Therefore
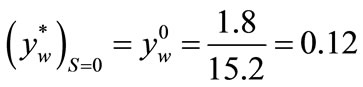 mm(51)
mm(51)
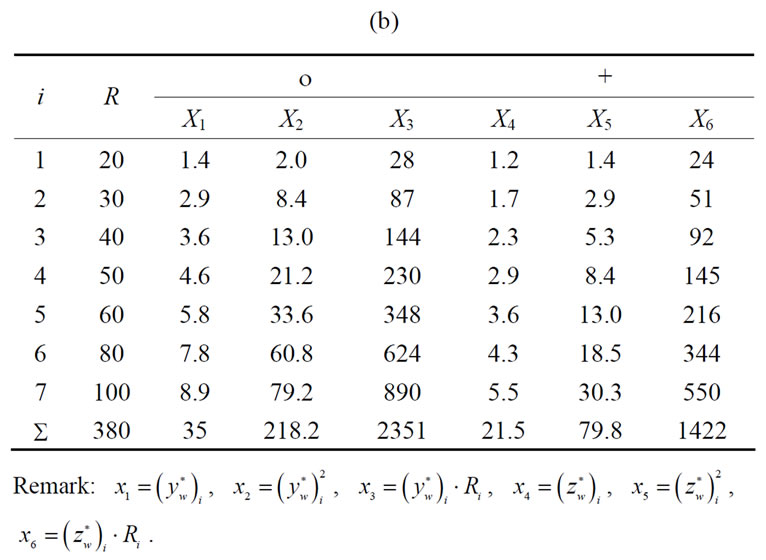
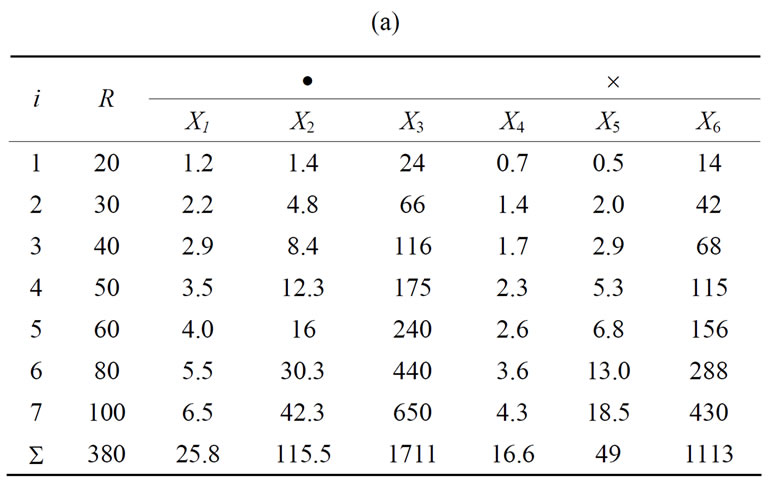
Table 3. Comparison of magnitudes needed to calculate the values of the coefficients of linear regression.
The following conclusion arises that the considered node of the grinder, which is the fixed headstock, has a determined clearance in horizontal direction. Thus for the described curve to possess the physical significance, not having negative values, it should be presented in a reverse coordinates system, that is the deflection—rigidity force, and then elaborate/handle the experimental results in accordance with other theory, adopted to the description of the degressive exponential curve. The essence of this theory has been presented above in this work.
The authors have focused the attention on the adequate description of the dependence  for the sets of experimental points of which the statistical handling reveals the positive initial rigidity force, reflecting the initial tension of the design link. This is why the course of further actions is neglected and it is connected with handling the results revealing lack of a physical meaning/ sense
for the sets of experimental points of which the statistical handling reveals the positive initial rigidity force, reflecting the initial tension of the design link. This is why the course of further actions is neglected and it is connected with handling the results revealing lack of a physical meaning/ sense  in the system the rigidity force—deflecttion. That mentioned phenomenon is inordinate anyway and at least this is why its description has none a practical justification.
in the system the rigidity force—deflecttion. That mentioned phenomenon is inordinate anyway and at least this is why its description has none a practical justification.
Coming to the description of the effects of loading of the link (the fixed headstock) in the vertical direction (Figure 8), one may calculate the coefficients S0 and k0
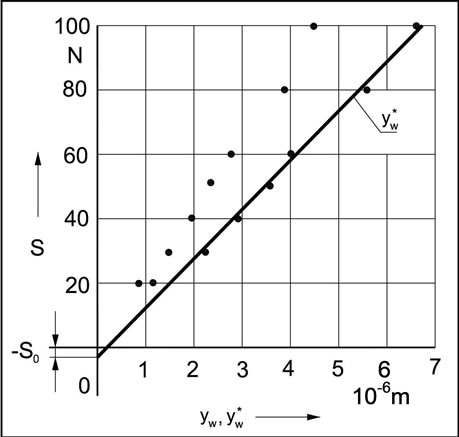
Figure 7. Dependence of the rigidity force S on the deflections yw,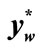 .
.
Figure 8. Dependence of the rigidity force S on the deflections zw and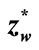 .
.
occurring in the formula (40).
These coefficients are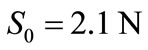 , and
, and 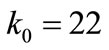 N×mm–1, respectively. Therefore
N×mm–1, respectively. Therefore
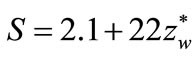 (52)
(52)
The deformation constant  corresponds with the coordinate
corresponds with the coordinate 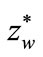 for
for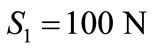 , so
, so
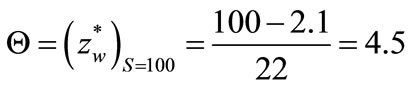 mm(53)
mm(53)
Now substituting the values of parameters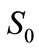 ,
, 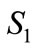 , and
, and  to the formula (15), one obtains the following configuration of the dependence
to the formula (15), one obtains the following configuration of the dependence 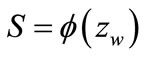
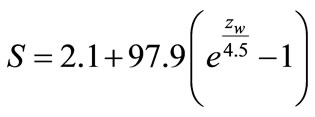 (54)
(54)
where, as may be noticed, the symbol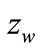 , relating to the deflection of spindle in the vertical direction has been introduced in the place of general denotation of the deflection f.
, relating to the deflection of spindle in the vertical direction has been introduced in the place of general denotation of the deflection f.
The coordinate 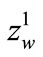 (see Figure 8) may be calculated from the formula (16), substituting with this symbol the deflection
(see Figure 8) may be calculated from the formula (16), substituting with this symbol the deflection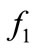 . Therefore
. Therefore
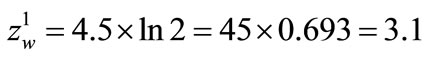 mm (55)
mm (55)
The measure of the proper rigidity energy, that is the rigidity potential , is calculated according to the formula (4), with
, is calculated according to the formula (4), with 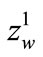 substituted instead of
substituted instead of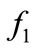 . Therefore
. Therefore
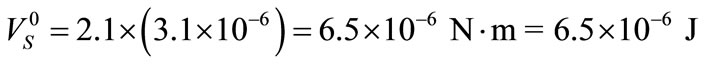 (56)
(56)
The measure of the gained rigidity energy, that is the gained rigidity potential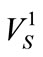 , is described by the formula (5). Thus, regarding that
, is described by the formula (5). Thus, regarding that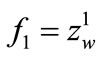 , one obtains
, one obtains
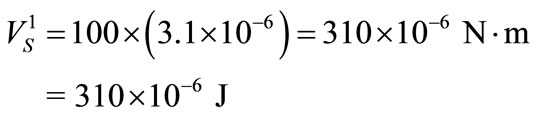 (57)
(57)
The coefficient of stiffness k is described by the formula (25). Therefore
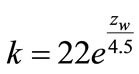 N×mm–1(58)
N×mm–1(58)
It appears that after substituting 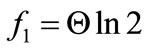 to it, that is
to it, that is 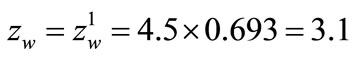 the following relation occurs
the following relation occurs
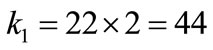 N×mm–1(59)
N×mm–1(59)
then
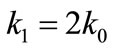 (60)
(60)
One may also calculate the rigidity work, in accordance to the formula (32), then
 (61)
(61)
By handling the results of measurements (Figure 9) of the rigidity forces S and deflections of the loose headstock in the horizontal direction, that is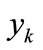 , one obtains
, one obtains 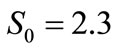 N,
N, 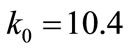 N×mm–1, then
N×mm–1, then
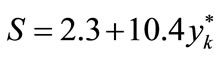 (62)
(62)
The deformation constant 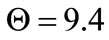 mm. Therefore
mm. Therefore
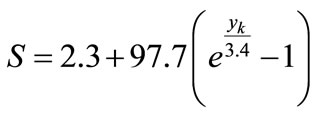 (63)
(63)
The values of further parameters of the characteristics of this design node are equal: 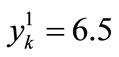 mm,
mm,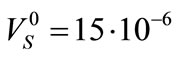 J,
J, 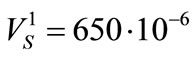 J coefficients of stiffness k are described by the formula
J coefficients of stiffness k are described by the formula
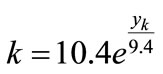 N×mm–1 (64)
N×mm–1 (64)
and the rigidity work equals 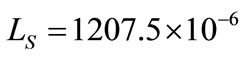 J.
J.
The results of measurement of the rigidity force S and the deflection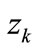 , as well as the results of calculation of the magnitude
, as well as the results of calculation of the magnitude 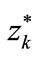 (Figure 10), handled in accordance to the above presented scheme, have led to the following
(Figure 10), handled in accordance to the above presented scheme, have led to the following
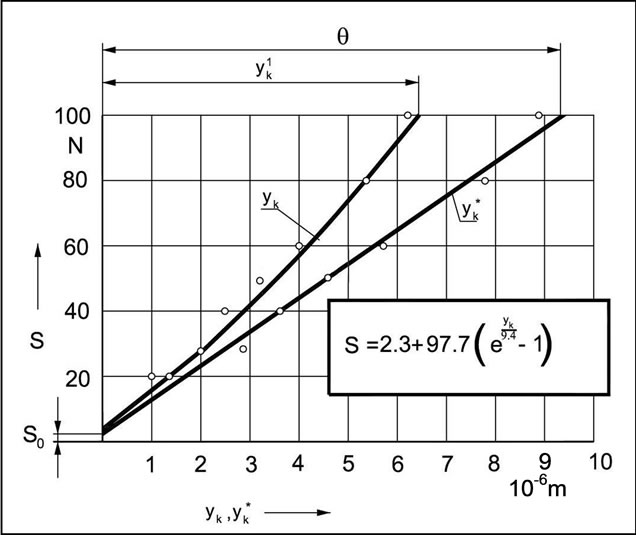
Figure 9. Dependence of the rigidity force S on the deflections yk and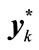 .
.
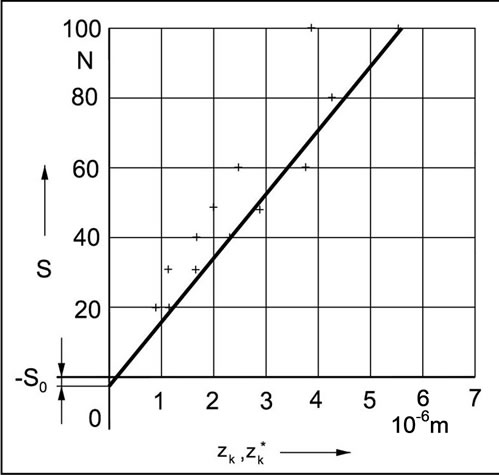
Figure 10. Dependence of the rigidity force S on the deflections zk and .
.
results: 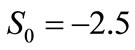 N,
N, 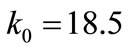 N×mm–1. The regression line for the set of points of coordinates
N×mm–1. The regression line for the set of points of coordinates 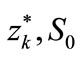 takes the following form:
takes the following form:
 (65)
(65)
Here also, as it appears, the initial rigidity force has a negative value, that means the occurrence of a clearance in this design link, that is in the loose headstock. Further handling of the results, similar like before (see Figure 7), has none a practical justification. That statistic handling of the experimental material/matter made it possible to reveal the clearance occurring in this subjective link. Any further actions should be directed rather to stiffen this link.
8. Summary
In the frames of the summary it is worthy indicating that simplification of a description of the real systems leads to the hiding of some valuable information.
The rigidity problems, referred to the essential nodes of the grinder, have been analysed thoroughly. That approach made it possible to disclose the adequate rigidity characteristics of nodes both on the side of fixed headstock as well as of the loose headstock. It was found these characteristics possess the configuration of exponential curves. The phenomenon of deformation of these nodes has been considered in detail; that made it possible to obtain some valuable utilitarian information. In the light of the cognitive approach it appears any aspiration to linearise the real non-linear characteristics is not justified. To say more, the tendency to substitute them by a straight line, coming through zero point, is incorrect.
Moreover, in this work it was stated that the rigidity has the energetic nature. An adequate notion of the rigidity energy has been introduced, by determining its measures for the initial and final energetic states of the studied design nodes. They are the notions of the proper rigidity potential and the gained potential of this kind. It has been clarified the essential and fundamental difference between the energy and work, here in reference to the rigidity energy and work. De facto it has a broader meaning and refers to each kind of energy. The identifying the energy with work is erroneous and should not have place on the ground of science. Also the energy measures, as stated, also cannot be identified with the work.
The method of the rigidity investigation presented in this work has values both cognitive and utilitarian. It may be used to study the effect of the rigidity on the course and results of machining, as well as the exploitational properties of tools cutting determined materials on determined machine tools. This method may be used also for the assessment of technical condition of the machine tools, concerning their rigidity. Also the research on the recipient’s request and/or the reliability compliance tests could be related to the rigidity aspect.
REFERENCES
- Z. Pluta, “Return to the sources (Powrót do źródeł),” Forum Akademickie, Vol. 6, No. 3, 1999, pp. 58-60.
- T. Hryniewicz and Z. Pluta, “Understanding the Teaching Process or the Lost Essence of Energy,” Proceedings of the 8th World Conference on Continuing Engineering Education, Theme A: Knowledge, Skills, and Competency, Toronto, 12-16 May 2001, pp. 25-31.
- Z. Pluta, “Lost Essence of Energy. Some Terminological Quests (Zagubiona Istota Energii. Niektóre Kwestie Terminologiczne),” Energetyka, Vol. 59, No. 7, 2005, pp. 496-501.
- P. Ugrinov, “Ocenjavane na stabilnost’ v Rabotnom Prostranstve na Obrabotauščim Centri,” Mašinostroenie, Vol. 44, No. 4, 1995, pp. 124-125.
- V. V. Bušuev, “Žestkost’ stankov,” Stanki i instrument (STIN), Vol. 61, No. 8, 1996, pp. 26-32.
- J. C. Ramos, J. Vinolas and F. J. Nieto, “A Simplified Methodology to Determine the Cutting Stiffness and the Contact Stiffness in the Plunge Grinding Process,” International Journal of Machine Tools and Manufacture, Vol. 48, No. 1, 2001, pp. 33-48.
- V. M. Skiba and S. M. Obidin, “Vlijanie Uprugoj Sistemy Stanka na Process Rezanija,” Mašinostroenie, Vol. 50, No. 2-3, 2001, pp. 92-98.
- doi:10.1115/1.1371928
- H. Klewenhagen, “Hohe Eigensteifigkeit ersetzt Fundament. Fahrständer-Bearbeitungszentrum mit Drehtisch Bearbeitet Grossvolumige Wekstücke an Fünf Seiten,” Maschinenmarkt, Vol. 110, No. 5, 2004, pp. 26-27.
- K. Grudziński and K. Konowalski, “Investigations of the Contact Deformations in the Rolling Guideway Connections of Machine Tools under Static Loads,” Advanced Manufacturing Science and Technology, Vol. 28, No. 3, 2004, pp. 41-56.
- Z. Pluta, “Fundamentals of Surface Smoothing by Elastic Grinding Wheels (Podstawy Wygładzania Powierzchni Ściernicami Elastycznymi),” Wydawnictwo Politechniki Koszalińskiej, Koszalin, 2007.
- P. M. Harman, “Energy, Force, and Matter: The Conceptual Development of Nineteenth Century Physics,” Cambridge University Press, Cambridge, 1982. doi:10.1017/CBO9780511665394
- C. Smith, “The Science of Energy: A Cultural History of Energy Physics in Victorian Britain,” Athlone Press, London, 1998.
- J. R. Taylor, “Classical mechanics (Mechanika klasyczna),” Wydawnictwo Naukowe PWN SA, Warszawa, 2006.
- L. W. Landau and J. M. Lifszyc, “Theoretical Physics Mechanics (Fizyka Teoretyczna. Mechanika),” 4th edition, Wydawnictwo Naukowe PWN SA, Warszawa, 2006.
- P. Atkins, “Galileo Finger (Palec Galileusza),” Dom Wydawniczy REBIS, Poznań, 2006.
- W. Kacalak, “Theoretical and Experimental Bases of Grounding of Helical Surfaces by Disk Wheels (Teoretyczne i Doświadczalne Podstawy Szlifowania Powierzchni Śrubowych Ściernicami Krążkowymi),” Wydawnictwo Wyższej Szkoły Inżynierskiej w Koszalinie, Koszalin, 1977.
- K. Mańczak, “Technique of Experiment Planning,” Technika Planowania Eksperymentu, Warszawa, 1976.
- H. Szydłowski, “Theory of measurements (Teoria pomiarów),” PWN, Warszawa, 1978.
- E. B. Wilson, “An Introduction to Scientific Studies (Wstęp Do Badań Naukowych),” 2nd edition, PWN, Warszawa, 1968.
- W. E. Deming, “Statistical Adjustment of Data,” Wiley, New York, 1938.
NOTES
*Corresponding author.

