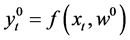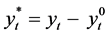Open Journal of Statistics
Vol.06 No.01(2016), Article ID:63994,14 pages
10.4236/ojs.2016.61017
Predictive Modeling of Gas Production, Utilization and Flaring in Nigeria using TSRM and TSNN : A Comparative Approach
Olugbenga Falode1, Christopher Udomboso2
1Department of Petroleum Engineering, University of Ibadan, Ibadan, Nigeria
2Department of Statistics, University of Ibadan, Ibadan, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 February 2014; accepted 26 February 2016; published 29 February 2016
ABSTRACT
Since the discovery of oil and gas in Nigeria in 1956, much gas has been flared because the operators pay little or no concern to its utilization, and as such, trillions of dollars have been lost. In this paper, a model is proposed using Time Series Regression Model (TSRM) and Time Series Neural Network (TSNN) to model the production, utilization and flaring of natural gas in Nigeria with the ultimate aim of observing the trend of each activity. The results show that TSNN has better predictive and forecasting capabilities compared to TSRN . It is also observed that the higher the hidden neurons, the lower the error generated by the TSNN .
Keywords:
Natural Gas, Production, Utilization, Flaring, TSRM , TSNN , Model Selection

1. Introduction
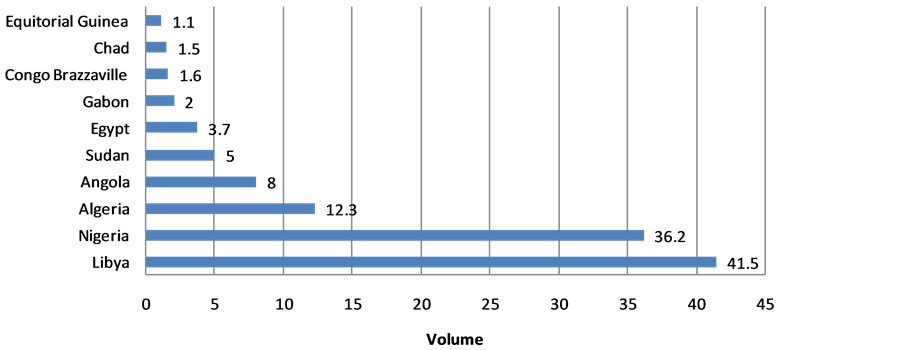
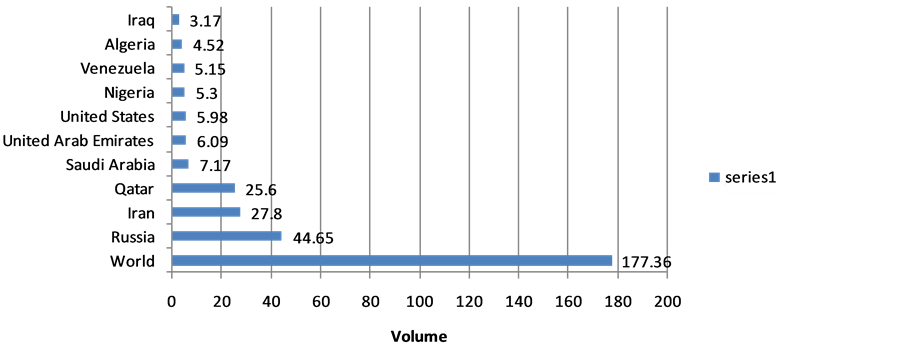
Natural gas was first discovered in Nigeria in 1956, at Afam, Rivers State, in association with oil during the drilling of Oloibiri well (now in Bayelsa State), which was the first commercial oil discovery in the country. However, Nigeria’s natural gas development is still at its infancy, but with very high potential for growth. Various literatures cite that Nigeria is more endowed with natural gas reserves than oil. Nigeria has been considered an oil rich nation in Africa as shown in Figure A1 nevertheless currently, the country is Africa’s largest natural gas holder with a proven reserve of 186.99 tcf and the 7th as shown in Figure A2 and has been described as a gas province with oil pockets. Unfortunately, the Multinational Oil Company at the time of discovery―Shell BP, paid little or no attention to the utilization of this resource since it was not their primary drilling objective. At this early stage of development, there was no legislation governing the utilization of natural gas in the country, while, at the same time, there was little or no market for the commodity. A recent study conducted by the World Bank revealed that developing countries account for more than 85% of gas flaring and venting worldwide, with Nigeria being the largest [1] . The first utilization of gas could be traced to 1963 when Shell BP sold and supplied the resource obtained from fields in Aba and Ughelli to industries around the areas. Later, the company started supplying the commodity to the then Electricity Corporation of Nigeria (ECN), later named National Electricity Power Authority (NEPA), and now known as Power Holding Corporation of Nigeria (PHCN) at its Afam plant in Rivers State. The commodity was also supplied to the River State Utility Board in Port Harcourt, capital of Rivers State.
Gas flaring refers to the burning of natural gas that is associated with crude oil when it is pumped up from the ground. This is a means of disposal either because there is no market for the gas or the operator does not elect (or cannot use) the gas for a non-wasteful purpose. On the other hand, venting is the release of natural gas that cannot be processed for sale or use because of technical or economic reasons. Gas flaring in Nigeria dated back to the onset of oil production in Oloibiri in 1958 with the flaring of about 4.5 million scf/day of associated gas. An average of 1000 scf of associated gas is produced for every barrel of oil produced. The amount of associated gas flared increased in proportion to the volume of oil produced and rose progressively to about 2.6 billion scf/day in 1996 when crude oil production averaged 2.4 million barrels per day. The volume of associated gas flared has only decreased slightly to 2.3 billion scf/day in subsequent years despite various regulations and measures put in place to discourage the flaring of gas associated with oil production.
Natural gas flares cause various degrees of pollution such as variations in the chemistry, meteorological, biological, and chemical parameters of the air and atmosphere, as well as soil conditions in the immediate environment of the flare. Local farmers have complained about retardation of growth and productivity of farm crops around gas flares, as well as scarcity of animals around the gas flare environment.
The problem is that in Nigeria, not much has been done in predicting and forecasting the production, utilization and flaring of the natural gas. In this paper, we seek to use a combination of two statistical models―Time Series Regression and Artificial Neural Network in solving this problem.
1.1. Gases Associated with Gas Flaring
When natural gas is flared, a combustion reaction takes place in the form stated below [2] :
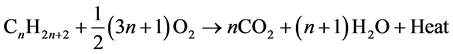
Presented below, as an example, is the combustion reaction of propane.
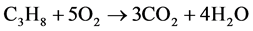
During a combustion reaction, several intermediate products are formed, and eventually, most are converted to CO2 and water. Some quantities of stable intermediate products such as carbon monoxide, hydrogen, and hydrocarbons will escape as emissions.
For a complete reaction, carbon (IV) oxide and water vapour are formed. However, when the reaction is incomplete, carbon (II) oxide is formed alongside carbon (IV) oxide and water vapour .
Depending on the location, impurities such as sulphur, nitrogen and hydrogen sulphide are also found with natural gas. These gases undergo a combustion reaction to form acid gases such as oxides of nitrogen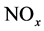 , oxides of sulphur
, oxides of sulphur 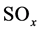 and hydrogen sulphide H2S.
and hydrogen sulphide H2S.
Complete combustion requires sufficient combustion air and proper mixing of air and gas. Smoke may result from combustion, depending upon gas components and the quantity and distribution of combustion air. Gases containing methane, hydrogen, CO, and ammonia usually burn without smoke. Gases containing heavy hydrocarbons such as paraffins above methane, olefins, and aromatics, cause smoke.
1.2. Application of Artificial Neural Network in Petroleum Engineering
Artificial Neural Network (ANN) have been used to address some of the fundamental problems in petroleum engineering that conventional predictive models have been unable to solve, especially when engineering data for design, interpretations and calculations have been less adequate. Also, with recent advances in pattern recognition, classification of noisy data, nonlinear feature detection, market forecasting, sickness recognition in human blood in medicine, and process modeling, ANN technology is very well suited for solving problems in the petroleum industry. Several authors have developed ANN models to solve several problems in the petroleum industry. Juniardi and Irashagi [3] developed ANN model to predict permeability and skin factor of faulted Reservoir. Arehart [4] developed a 3-layer back propagation neural network model to determine the grade of a drill bit while it is drilling. Ashenayi et al. [5] used a hybrid 3-layer back propagation neural network model to identify beam pump malfunctioning from down hole pump cards. Erahaghi et al. [6] used a multiple ANN to train and recognize patterns (CD, PD, tD, S, dD…) for specific conceptual reservoir model. Kumoluyi [7] discussed the general application of neural networks and their potential uses in some areas of petroleum engineering. They found that one advantage of feed forward networks in pattern recognition is their ability to recognize patterns regardless of position, rotation and scaling. The application of pattern recognition is essential in well log interpretation of multiphase flow and in seismic data processing. Mohagheh et al. [8] used a 3-layered forward back propagation neural network model to estimate the heterogeneity of some reservoirs. Briones et al. [9] developed a 3-layer radial basis neural network (RBFNN) model to relate gas-oil ratio (GOR) and API gravity to the corresponding molar composition (C1, C2, C3, C4, C5, C6, C7 and CO2) . Mc Vay et al. [10] used a feed forward back propagation neural network model to train the actual refracture treatment design, basic well information, and well performance in order to determine the Sand Volume, Fluid Type, Injection Rate and Acid Volume as the majoring factors that influence the well deliverability during hydraulic fracturing. Manmath et al. [11] used ANN model to predict fluid distribution taking oil, water, and gas production as input data. Wong et al. [12] developed a back propagation neural network (BPNN) model to estimate formation permeability in the RAVVA oil and gas field offshore in India. Garrmouch and Smaoul [13] developed a 3-layered back propagation neural network model to estimate formation permeability of tight gas reservoir. Soto et al. [14] used a neural network model to predict the permeability and porosity of zone C of the Cantagallo field in Colombia. Shelley et al. [15] developed two separate neural network models for well completion analysis and optimization to identify the factors that affect production and measure their contributions to the production result. Nikravesh et al. [16] developed several neural network models for water flood management in fractured reservoir to predict the wellhead pressure and future production in quarterly basis.
Application of neural networks in time series forecasting [17] -[20] is based on the ability of neural networks to approximate nonlinear functions. The most popular treatment of input data is feeding the neural networks with either the data at each observation, or the data from several successive observations. Denote the data at instant k as y(k), where y may be a vector, then the above treatment can be described as
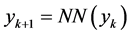
or
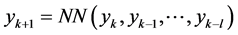
respectively, where NN() stands for the neural network forecaster and l is the number of successive observations. This treatment considers the time series as a nonlinear time series and tends to generate a nonlinear “auto- regression” model to fit the series. So far, there have been few papers describing how to choose inputs for the neural network forecaster in order to achieve better forecasting performance. It is our belief that the performance of a neural network forecaster is much affected by input data patterns.
Autocorrelation analysis has been often used in time series forecasting using statistical approaches such as ARMA models. This analysis is mainly used in detecting the autocorrelations between successive observations of time series, and used in the well-known ARIMA models with Box-Jenkins methods that are very efficient in forecasting linear time series [21] .
Autocorrelation analysis can be used to determine the correct input patterns for nonlinear time series fore- casting with a neural network. The scheme contains three phases: detection of input patterns, determination of the number of neurons in hidden layer(s), and construction of the neural network forecaster. In the detection phase, autocorrelation analysis is used to identify input patterns of time series for training. Determination of the number of neurons in hidden layer(s) is done with Baum-Haussler rules [22] . The neural network forecaster is then constructed with the determined input patterns and the number of neurons in hidden layer(s).
2. Materials and Methods
2.1. Time Series Regression Model (TSRM)
We recall the linear regression model (LRM ) given as:
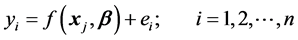 (1)
(1)
which is made up of the predicted part and the residual part. The residual is the difference between the observed and the predicted values which is ascribed to unknown sources. n is the number of observations, yi is the ith observation, 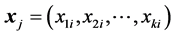 is the predictor variable vector related to yi,
is the predictor variable vector related to yi, 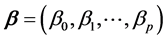 is the parameter vector, and ei is the error associated with ith observation.
is the parameter vector, and ei is the error associated with ith observation.
Writing (1) in time series notation, we have
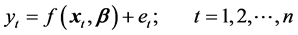 (2)
(2)
Explicitly, this is written as
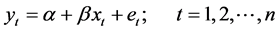 (3)
(3)
where yt is the dependent variable, xt is the independent variable (in this case, the “years” ), α is the intercept, β is the parameter associated with the independent variable, xt , and et is the stochastic term or error associated with the model.
We minimize (3) with respect to α and β , 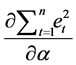 and
and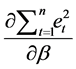 , to obtain two normal equations respec-
, to obtain two normal equations respec-
tively. Solving the normal equations, we obtain the estimates of the parameters 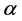 and
and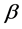 :
:
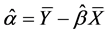
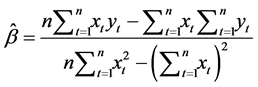
The predicted model becomes
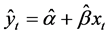
and the residual is given as
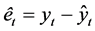
2.2. The Time Series Neural Network (TSNN) Model
The statistical neural network (SNN) model structurally is composed of two parts: the predictive and the residual, as is in classical regression, given as
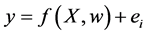
where 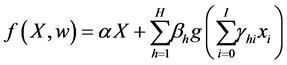
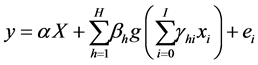
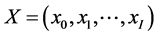
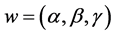
We propose a simple time series neural network model,
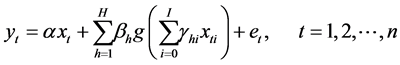
The terms and symbols are as explained in the SNN model, except that t refers to “time” or “period” .
The weights are estimated using Taylor’s first order approximation,
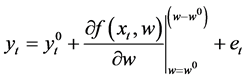
where
If 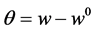
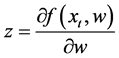
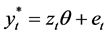
where
The least squares estimate of the parameter 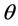
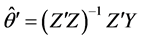
and the estimated model is
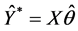
while the network error is given as
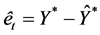
In this paper, we used the symmetric saturated linear transfer function,
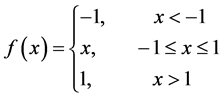
The data used in this study are annual data on natural gas production, utilization and flared in Nigeria from 1958-2006, obtained from the Annual Abstract of Statistics of the Nigeria Bureau of Statistics (NBS) , formerly Federal Office of Statistics (FOS) -(1970-1990), Ministry of Petroleum Resources (MPR) -(1991-1994) and NAPIMS -(1995-2006). This makes a total of 49 data set. In each case (production, utilization and flared), the TSNN model formulation is:
1-2-1, 1-5-1, 1-10-1.
All input variables were standardized, that is, converting them to the range (0, 1) before feeding them into the network. This is to avoid the application of extremely small weighting factors in the case of large input values.
Similarly, the output values are “destandardized” to provide meaningful results since all values leaving the network are automatically output in a standardized format. This is done by simply reversing the standardization algorithm used on the input nodes.
We used SPSS for the TSRM part of the analysis, while a neural code was written for the analysis of the TSNN using MATLAB R2009a, and interesting results were obtained.
2.3. Model Selection Criteria
Here we discuss several criteria that have been used to choose between the two models. Several criteria are used for this purpose. In particular, we discuss these criteria: (i) R2 ; (ii) adjusted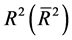
3. Results and Discussions
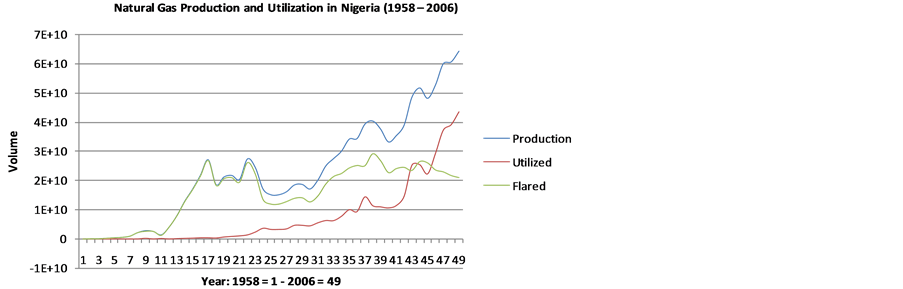
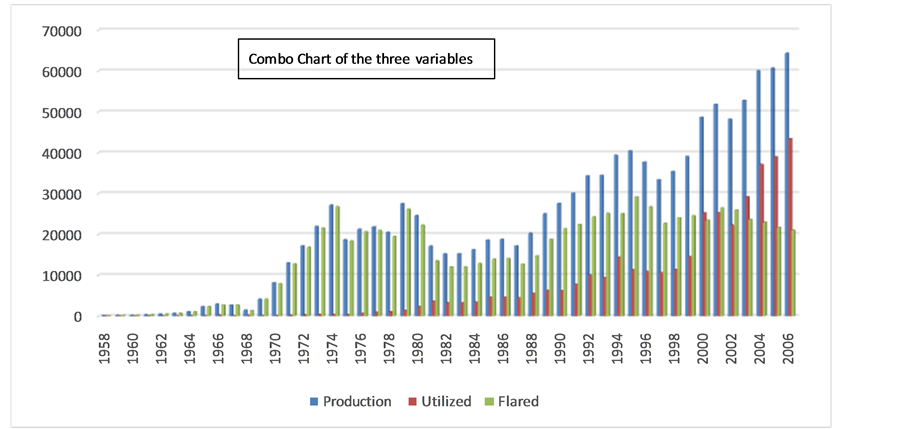
Figure 1 is a time plot of the production, utilization and flared natural gas in Nigeria oil and gas industry. The time plot of all the variables that are of interest in the study shows that gas utilization and production rate steadily accelerated upward from the base year till the end. More so, flared gas also had an upward trend except that it is an oscillatory trend. At times it rises and fall but later maintained the upward trend. The plot shows that
Figure 1. Time plot of Nigeria’s natural gas.
during the first ten years of production, there was zero gas utilized and a geometrical increase in the produced and flared gas. Following this period, a steady increase in the amount of gas utilized while a gradual decline was observed for produced and flared gas for about ten years. However, the plot flattens during the last ten years showing that the volume flared remained constant whereas there was a corresponding sharp increase in the volume utilized with production. Some spikes on the plot at points 16, 23 and 38 corresponding to 1974, 1981 and 1996 represent the highest volume of gas flared. The amount of gas flared was higher than those utilized until 2004.
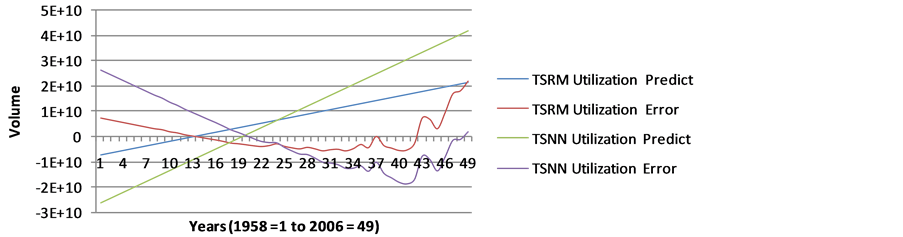
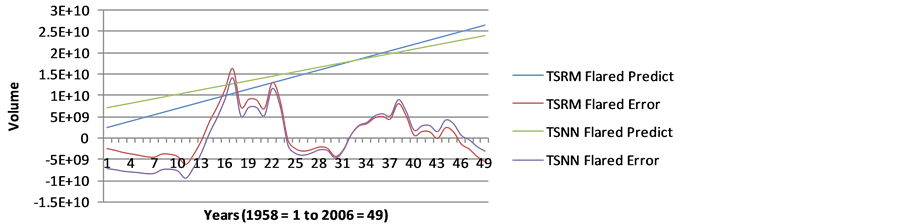
Figures A3-A5 show the prediction of natural gas in Nigeria. The graph show that TSNN have a higher prediction than TSRM, while their errors are in the reverse.
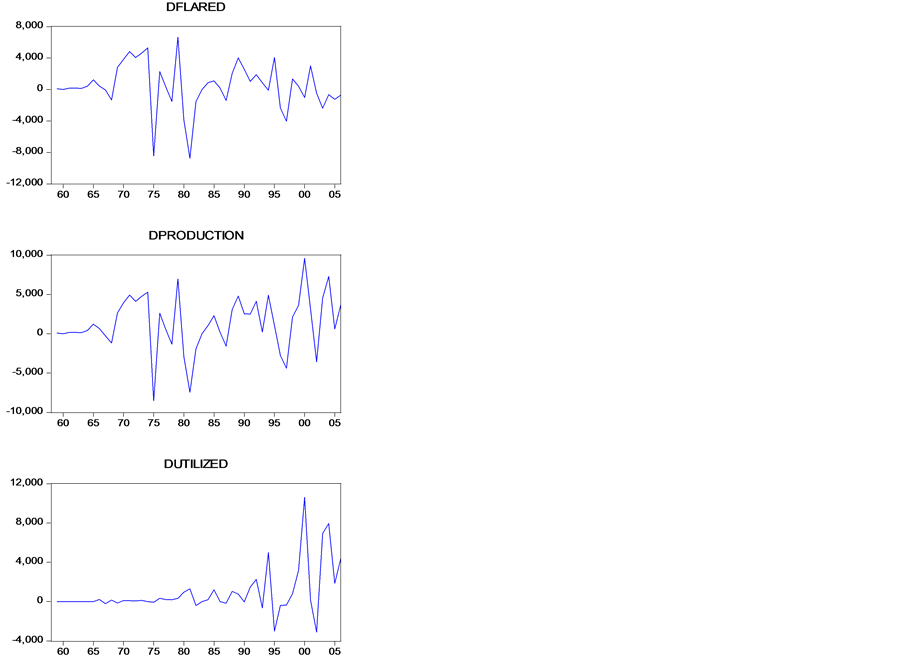
4. Time Plot of the Stationarized Variables
Correlogram of the data shows that the variables are non-stationarized since their respective lag value is zero and autocorrelation values are big (Figure 2). This necessitated the need to check for the unit root test of the respective variables. However, Using Augmented Dickey Fuller Unit root test trend and intercept authenticates the proof that the initial data of the variables has a unit root since their respective P-value are greater than 5%. Meanwhile at first difference, the three variables seems to be okay as it has been stationarized since both time plots seem to have constant means, their respective correlogram have none of its P-value to be zero and smaller autocorrelation values. Figure 2 shows the time plot of the stationarized variables
Furthermore, ADF result below illustrates that the variable can now be used for time series model since their respective P-values are less than 5% which shows to be normal.
Table below shows the descriptive statistics of the variables which vividly indicates that the differencing variable were shown to be positively symmetric as their respective mean values (436.0625, 1339.313 and 9903.2500) are bigger than their median values (258.5000, 1058.000 and 116.0000), flared and production are negatively skewed as their respective skewness value is less than zeros, kurtosis of the three variables are mesokurtic since their respective K-value > 3.
5. Descriptive Statistics of the Stationarized Variables
Figure 2. Time plot of the stationarized variables.
However, the regression result below indicates that the model is of best perfect fit as the coefficient of determination = 1 (one). Furthermore, flared and utilized has a positive joint contribution to the production of gas as it’s P-value is < zero (significant).
6. Regression Result
Figure 3 is a combo chart which helps us to see the relationship among production, utilized and flared gas during the period of investigation.
Tables 1-3 summarizes the results of the model adequacy of the two models. The MSE compares the variations in the errors generated by the different models. The model with the smallest MSE is considered a better
Figure 3. Combo Chart of Production, Utilized and Flared Gas.
Table 1. Estimated model adequacy for gas production.
Table 2. Estimated model adequacy for gas utilization.
Table 3. Estimated model adequacy for gas flared.
model. R2 measures the fit of each of the models. Since more than one model is involved, R2 will not be adequate for comparison.
Thus for model fit, 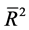
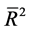
The results of the analysis in Tables 1-3 shows that the MSE s of the TSNN are by far smaller than the MSE of the TSRM . Hence, from Table 4, all the models of the TSNN are preferred than the TSRM .
Table 5 and Table 6 summarize the results for model adequacy and selection. The percentages of the 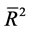
Table 4. Model selection based on MSE.
Table 5. (a) Model selection based on R2 and 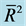
Table 6. Hidden neuron inequality based on model selection criteria.
Table 7. Comparison of parameter esimates obtained by TSRM, TSNN.
The result of the entire analysis shows that as the hidden neurons increases, the values of the MSE, AIC and SIC decreases, while those of 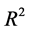
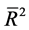
7. Model Description
This section describes the model formulation based on the estimates of the parameters; the parameter estimates obtained by TSRM and TSNN are presented in Table 7.
The results of 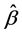
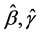
8. Concluding Remarks
We have compared the Time Series Regression Model (TSRM) and the Time Series Statistical Neural Network (TSNN) to estimate the production, utilization and flaring of natural gas in Nigeria from 1958 to 2006. Both me- thods attempt to minimize the error sum of squares between observations and predicted values. Regression requires an explicit function to be defined before the least squares parameter estimates can be computed, while a neural network depends more on training data and the learning algorithm. Neural networks have been shown to be an efficient methodology to estimate natural gas production, utilization and flaring. Comparing model prediction in both cases show that TSNN performs better than TSRM.
Cite this paper
OlugbengaFalode,ChristopherUdomboso, (2016) Predictive Modeling of Gas Production, Utilization and Flaring in Nigeria using TSRM and TSNN: A Comparative Approach. Open Journal of Statistics,06,194-207. doi: 10.4236/ojs.2016.61017
References
- 1. World Bank (2000/2001) Regulation of Associated Gas Flaring and Venting. A Global Overview and Lessons from International Experience. World Development Report, Washington.
- 2. Omole, O. and Falode, A.O. (1998) Analysis of Petroleum Pollution Incidents in the Nigerian Petroleum Industry. Journal of Science Research, 4, 25-33.
- 3. Juniardi, I.R. and Ershaghi, I. (1993) Complexities of Using Neural Network in Well Test Analysis of Faulted Reservoirs. SPE, 26106.
- 4. Arehart, R.A. (1989) Drill Bit Diagnosis Using Neural Network. SPE, 19558.
- 5. Ashenayi, K., Nazi, G.A., Lea, J.F. and Kemp, F. (1994) Application of an Artificial Neural Network to Pump Card Diagnosis. SPE, 25420.
- 6. Erahaghi, I., Xuchai, L., Mahnaz, H. and Yusuf, S.A. (1993) Robust Neural Network Model for Pattern Recognition of Pressure Transient Test Data. SPE, 26427.
- 7. Kumoluyi, A.O. and Daltaban, T.S. (1993) Higher Order Neural Networks in Petroleum Engineering. SPE, 27905.
- 8. Mohagheh, S., Reza, A., Ameri, S. and Hefner, M.H. (1994) A Methodological Approach for Reservoir Heterogeneity Characterization Using Artificial Neural Networks. SPE, 28394.
- 9. Briones, M.F., Rojas, G.A. and Martinez, E.R. (1994) Application of Neural Network in the Prediction of Reservoir Hydrocarbon Mixture Composition from Production Data. SPE, 28598.
- 10. McVay, D.S., Mohagheh, S., Aminian, K. and Ameri, S. (1995) Identification of Parameters Influencing the Response of Gas Storage Wells to Hydraulic Fracturing with the Aid of Neural Network. SPE, 29159.
- 11. Manmath, P.N., Zaucha, D.E., Perez, G., Anilk, C. and Plano, W. (1995) Application of Neural Networks to Modeling Fluid Contacts in Prudhoe Bay. SPE 30600.
- 12. Wong, P.M. and Henderson, D.J. (1997) Reservoir Permeability Determination from Well Log Data Using Artificial Neural Networks—An Example from the RAVVA Field, Offshore India. SPE 38034.
- 13. Garrmouch, A. and Smaoul, N.H. (1998) Artificial Neural Network Model for Estimating Tight Gas Sand Permeabilty. SPE 39703.
- 14. Soto, R.B., Ardila, J.F., Femeyness, H. and Berano, A. (1997) Use of Neural Networks to Predict the Permeability and Porosity of Zone C of the Cantagallo Field in Colombia. SPE Petroleum Computer Conference, Dallas, 8-11 June 1997, SPE 38134.
http://dx.doi.org/10.2118/38134-ms - 15. Shelley, R., Stephenson, S., Haley, W. and Craig, E. (1998) Red Fork Completion Analysis with the Aid of Artificial Neural Networks. SPE 39963.
- 16. Nikravesh, M., Kovscek, A.R., Murer, A.S. and Patzek, T.W. (1996) Neural Networks for Fieldwise Water Flood Management in Low Permeability Fractured Oil Reservoir. SPE 35721.
- 17. Wang, H.A. and Chan, A.K.-H. (1993) A Feed Forward Neural Network Model for Hang Seng Index. Proceedings of 4th Australian Conference on Information Systems, Brisbane, 28-30 September 1993, 575-585.
- 18. Windsor, C.G. and Harker, A.H. (1990) Multi-Variate Financial Index Prediction—A Neural Network Study. Proceedings of International Neural Network Conference, Paris, 9-13 July 1990, 357-360.
- 19. White, H. (1988) Economic Prediction Using Neural Networks: The Case of the IBM Daily Stock Returns. Proceedings of IEEE International Conference on Neural Networks, San Diego, 24-27 July 1988, 451-458.
http://dx.doi.org/10.1109/ICNN.1988.23959 - 20. Rao, V.B. and Rao, H.V. (1993) C++Neural Networks and Fuzzy Logic. MIS Press, New York.
- 21. Jarrett, J. (1991) Business Forecasting Methods. Basil Blackwell, Oxford.
- 22. Baum, E.B. and Haussler, D. (1988) What Size Net Gives Valid Generalization? Neural Computation, 1, 151-160.
http://dx.doi.org/10.1162/neco.1989.1.1.151
Appendix
Figure A1. Africa’s Oil Reserve Ranking as at 2007.
Figure A2. Top Ten World Natural Gas Proven Reserves as at 2007.
Figure A3. Prediction and Error of Natural Gas Production in Nigeria (1958 - 2006) using TSRM and TSNN. Source: Journal of Oil and Gas.
Figure A4. Prediction and Error of Natural Gas Utilization in Nigeria (1958-2006) using TSRM and TSNN.
Figure A5. Prediction and Error of Natural Gas Flared in Nigeria (1958-2006) using TSRM and TSNN.
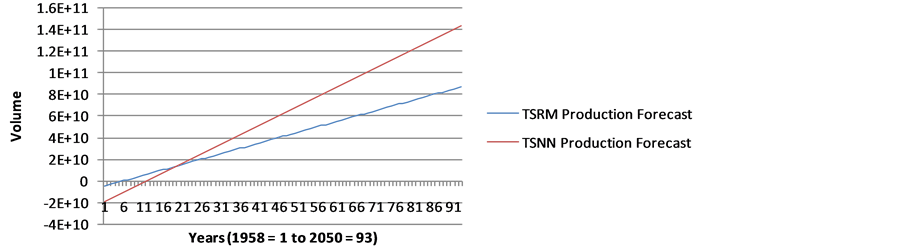
Figure A6. Forecast of Natural Gas Production in Nigeria (1958-2050) using TSRM and TSNN.
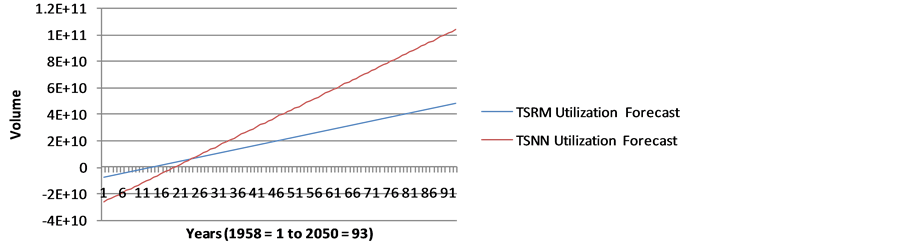
Figure A7. Forecast of Natural Gas Utilization in Nigeria (1958-2050) using TSRM and TSNN.
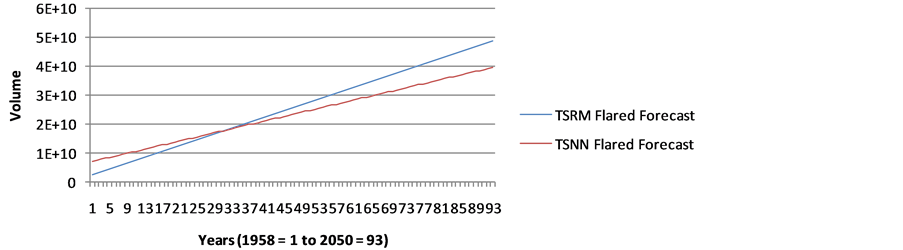
Figure A8. Forecast of Natural Gas Flared in Nigeria (1958-2050) using TSRM and TSNN.
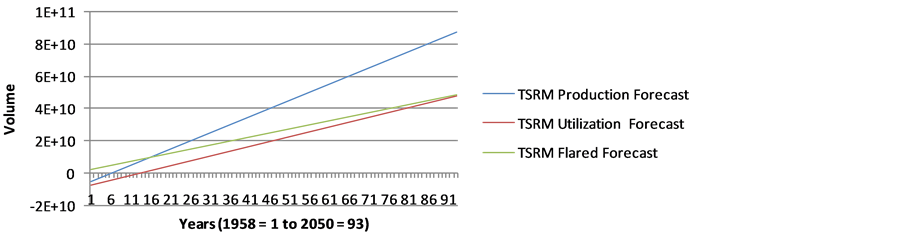
Figure A9. Forecast of Natural Gas Production, Utilization and Flared in Nigeria (1958- 2050) using TSRM.
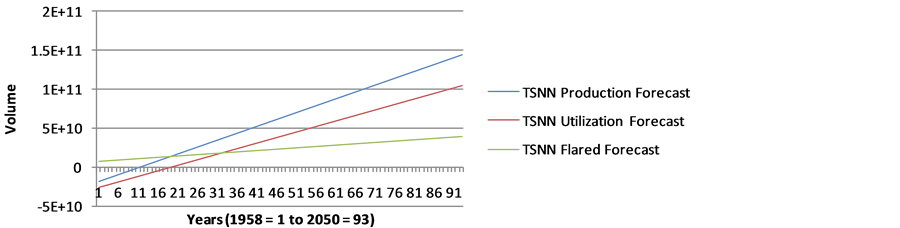
Figure A10. Forecast of Natural Gas Production, Utilization and Flared in Nigeria (1958- 2050) using TSNN.