Engineering, 2010, 2, 220-227
doi:10.4236/eng.2010.24032 Published Online April 2010 (http://www.SciRP.org/journal/eng)
Algorithms for Masking Pixel Defects at Low Exposure
Conditions for CMOS Image Sensors
**Vinesh Sukumar, Jason Tanner, Atif Sarwari, **Herbert L Hess
** Microelectronics Resear ch and Communications Institut –MRCI, University of Idaho, Moscow, U.S.A.
Received November 20, 2009; revised January 27, 2010; accepted Febr uary 4, 2010
Abstract
This paper introduces certain innovative algorithms to mask for pixel defects seen in image sensors. Pixel
defectivity rates scale with pixel architecture and process nodes. Smaller pixel and process nodes introduce
more defects in manufacturing. Brief introduction to causes for pixel defectivity at lower pixel nodes is ex-
plained. Later in the paper, popular defect correction schemes used in image processing applications are dis-
cussed. A new approach for defect correction is presented and evaluated using images captured from an 8M
Bayer image sensor. Experimentation for threshold evaluation is done and presented with practical results for
better optimization of proposed algorithms. Experimental data shows that proposed defect corrections pre-
serves a lot of edge details and corrects for bright and hot pixels/clusters, which are evaluated using histo-
gram analysis.
Keywords: Hot Pixels, Pixel Clusters, Defect Correction, Cluster Correction
1. Introduction
Digital imaging systems (including digital still camera,
digital video camera etc) capture the spectrum or color
information of physical stimuli by filtering the object
image through color filters with different spectral trans-
mittances, and transform the photon signal into elec-
tronic signal which finally is quantized into digital
counts with electronic sensors [1]. Electronic sensors
generally are based on Char ge-Cou pled Device (CCD) or
Active Pixel Sensor (APS) Complimentary MOS tech-
nology. This digital information produced by these elec-
tronic sensors, ignoring all non-idealities of CMOS/CCD
imager optics and pixels, must undergo some image
processing functions prior to display on any visual media
or data storage in Red Green Blue (RGB) format. The
resolving power of the imaging system to present details
of the viewing object can be presented in terms of system
MTF (Modulat ion Transfer Functi o n ) [1] .
Pixel architecture is always a crucial element of any
imaging system design, which can be quantified in MTF
terms. Pixel designers always have to make a fundamen-
tal tradeoff when choice comes to selecting a pixel size.
Reducing pixel size improves the imaging system per-
formance by increasing spatial resolution for fixed sensor
die size. Increasing pixel size improves the imaging sys-
tem performance by increasing dynamic range and sig-
nal-to-noise ratio. Pixel scaling has been very aggressive
in the APS CMOS domain when compared to that of
CCD as illustrated in Figure 1. These solid-state image
sensors develop in-field defects in all common APS
CMOS manufacturing environments. This is more chal-
lenging for smaller pixel geometries. Many experiments
have demonstrated the gro wth of significant quantities o f
pixel defects that degrade the dynamic range of an image
sensor and potentially limit low-light imaging perform-
ance. Existing image processing techniques used in sev-
eral imaging applications used for suppressing hot-pixels
are inadequate because these defective pixels saturate at
relatively low illumination levels.
In this paper, an 8M CMOS APS sensor, which has
plenty of hot-pixels, is used for analysis. A correction
algorithm repairs the final image by certain unique proc-
essing algorithms which are discussed in this paper. Per-
formance metrics and tradeoffs are pr esented in the latter
half of the paper .
2. Hot Pixel Characteristics
As pixels are made smaller to improve on image resolu-
tion, pixel elements get located closer together, resulting
in increased risk of cross-talk between adjacent pixels.
Shallow trench isolation (STI) regions, which may be
dielectric-filled trenches formed in the substrate of the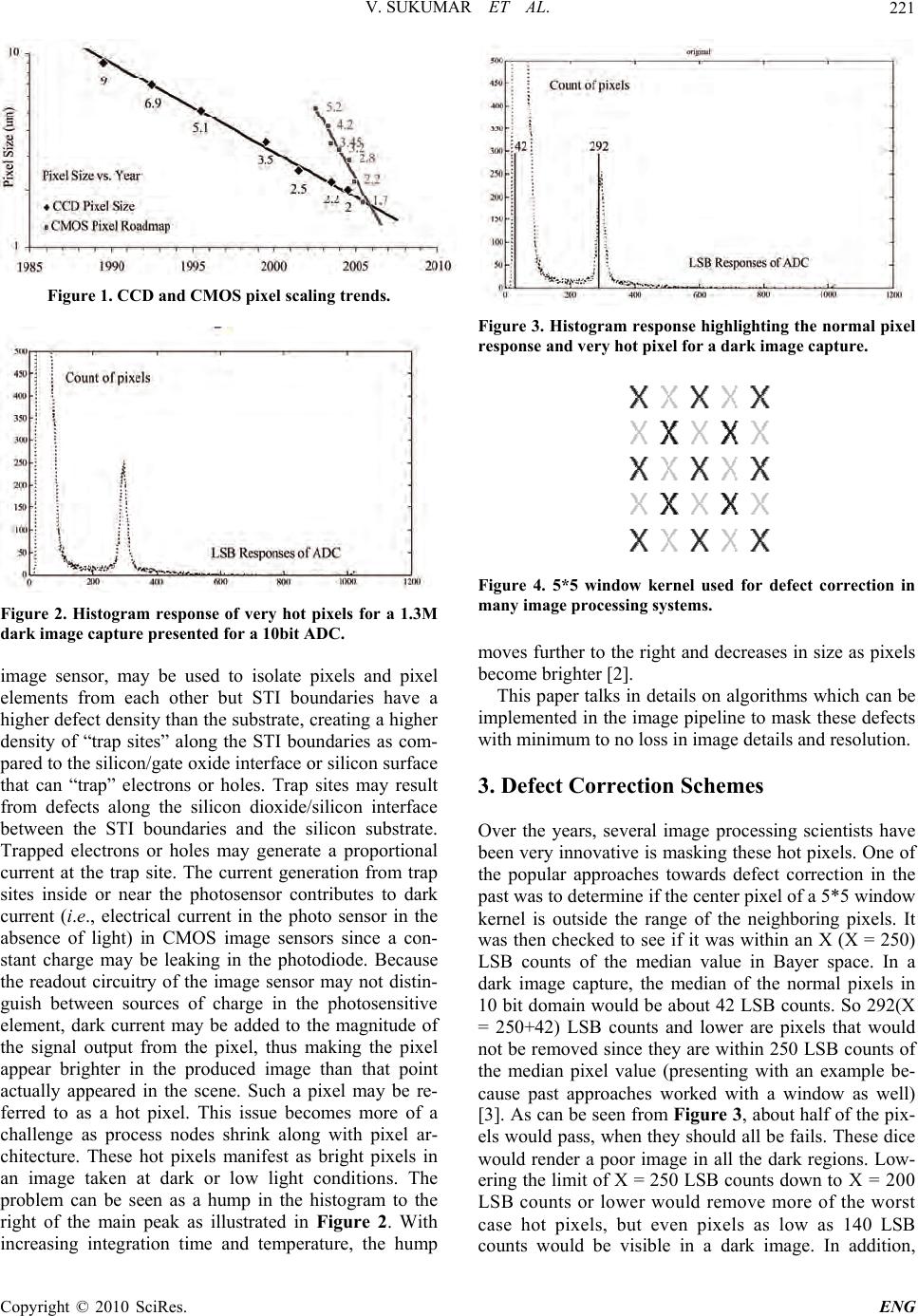

V. SUKUMAR ET AL. 221
Figure 1. CCD and CMOS pixel scaling trends.
Figure 2. Histogram response of very hot pixels for a 1.3M
dark image capture presented for a 10bit ADC.
image sensor, may be used to isolate pixels and pixel
elements from each other but STI boundaries have a
higher defect density than the substrate, creating a higher
density of “trap sites” along the STI boundaries as com-
pared to the silicon/gate oxide in terface or silicon su rface
that can “trap” electrons or holes. Trap sites may result
from defects along the silicon dioxide/silicon interface
between the STI boundaries and the silicon substrate.
Trapped electrons or holes may generate a proportional
current at the trap site. The current generation from trap
sites inside or near the photosensor contributes to dark
current (i.e., electrical current in the photo sensor in the
absence of light) in CMOS image sensors since a con-
stant charge may be leaking in the photodiode. Because
the readout circuitry of the image sensor may not distin-
guish between sources of charge in the photosensitive
element, dark current may be added to the magnitude of
the signal output from the pixel, thus making the pixel
appear brighter in the produced image than that point
actually appeared in the scene. Such a pixel may be re-
ferred to as a hot pixel. This issue becomes more of a
challenge as process nodes shrink along with pixel ar-
chitecture. These hot pixels manifest as bright pixels in
an image taken at dark or low light conditions. The
problem can be seen as a hump in the histogram to the
right of the main peak as illustrated in Figure 2. With
increasing integration time and temperature, the hump
Figure 3. Histogram response highlighting the normal pixel
response and very hot pixel for a dark image capture.
Figure 4. 5*5 window kernel used for defect correction in
many image processing sy ste ms.
moves further to the right and decreases in size as pixels
become brighter [2].
This paper talks in details on algorithms which can be
implemented in the image pipeline to mask these defects
with minimum to no loss in image details and resolution.
3. Defect Correction Schemes
Over the years, several image processing scientists have
been very innovative is masking th ese hot pixels. One of
the popular approaches towards defect correction in the
past was to determine if the center pixel of a 5*5 window
kernel is outside the range of the neighboring pixels. It
was then checked to see if it was within an X (X = 250)
LSB counts of the median value in Bayer space. In a
dark image capture, the median of the normal pixels in
10 bit domain would be about 42 LSB counts. So 292(X
= 250+42) LSB counts and lower are pixels that would
not be removed since they are within 250 LSB counts of
the median pixel value (presenting with an example be-
cause past approaches worked with a window as well)
[3]. As can be seen from Figure 3, about half of the pix-
els would pass, when they should all be fails. These dice
would render a poor image in all the dark regions. Low-
ering the limit of X = 250 LSB counts down t o X = 2 0 0
LSB counts or lower would remove more of the worst
case hot pixels, but even pixels as low as 140 LSB
counts would be visible in a dark image. In addition,

V. SUKUMAR ET AL. 222
removing clusters is important since the likelihood of
failing pixels in the same window is more likely as pixel
size shrink in lower process nodes. Better solutions to
resolve this issue are presented below.
Approach 1: In earlier implementations, if the pixel
of a 5*5 window kernel as presented in Figure 4 lies
within the range of the six nearest neighbors, the pixel
under test was automatically considered a good pixel. In
this new approach, if it is assumed that any two red pix-
els are completely exposed to maximum 1023 LSB
counts (for a 10 bit ADC domain) and are located nex t to
each other. Other assumption is that the rest of the pixels
have a response portfolio of 100 LSB counts. Checking
one of the 1023LSB count pixel would show that it does
lie within the range of 1023 LSB coun ts and pass quality
monitor before being checked to be within a threshold of
the median. This new approach allows an indicated
number of pixels to be removed from the 5*5 window
kernel before the range is checked.
In MATLAB simulations, two thresholds are used:
200 and 150 LSB counts. In these simulations, (one at
150 and one at 200 LSB counts) the highest pixel of the
six neighbors was removed from the list of eligible pixels.
Several dice from the different production lots were
tested. From the data below, throwing out the high pixel
from the nearest neighbors removed more bright pixels.
At the same time, the lower threshold replaced more pix-
els [4].
The option of removing defective pixels from any de-
fect analysis kernel is essential to eliminate any pixel
clusters. During experimental analysis, using images
with known defects, the visually best images removed
only one defective pixel. Removing two defective pixels
created false colors in some images and noticeably re-
moved detail. This approach also removed the most de-
fects. The test image used in this study is presented in
Figure 5, which is captured using a digital SLR. Image
5a shows none of the brightest pixels from the analysis
kernel being removed. Image 5b is with one pixel re-
moved from the kernel. Image 5b is with two pixels and
lastly Image 5c is with three pixels removed from the
defect correction kernel. It is clear that when more pixels
are removed from the analysis kernel, borders tend to
become more blurred leading to loss of fine detail. This
would be unacceptable in many high end mobile camera
applications where importance is given to preserving
details.
A potential improvement to Approach 1 will be to use
a dynamic distance option rather than a static distance
option from the median of the kernel. This option creates
a dynamic threshold by calculating the difference from
the MAX pixel value (with an option of removing certain
number of pixels from the window of analysis) and then
multiplying it by a set constant. A MIN and MAX value
is set for this threshold. For example, if the threshold Td
< 50 LSB counts, the value is automatically set to 50 and
Figure 5. Effect of eliminating different amount of defective
pixels from the defect analysis kernel on a digital SLR cap-
tured test image [5].
if Td > 400 LSB counts, the value is set to the difference
from the MAX to the median. This allows flat areas of
the image to be flat and to check for edges of the image.
Experimental analysis using this improved Approach 1 is
preserved fo r future analysis.
Approach 2: In this approach, instead of comparing
the center pixel to its neighb ors, this app ro ach ch eck ed to
see if the center pixel has any neighbors within its range.
The pixels from the analysis kernel are also forced to
have two of their neighbors in that threshold. The
neighbors were forced to lie within a group of predeter-
mined shapes as illustrated in Figure 6 (three horizontal
rows, three vertical rows, two diagonals, and four cor-
ners-only one is illustrated for simplic ity).
This approach forced regions to have context with re-
lation to the area under test. So if no shape is found in
the neighborhood, the center pixel failed and was as-
signed the median value. If any shape(s) is to be found,
the pixels lying with in the shape(s) were summed to find
the mean. The center pixel has to be within a set thresh-
old of the mean to be valid. This way multiple pixels can
be ignored to identify a defective pixel. The image re-
gions, where the kernel passes over edges or other shapes
can judge a pixel by the context of the pixels in its
neighborhood rather than all eight surrounding pixels
from the kernel. For example in Figure 7, if there is a
vertical edge in an image, where the transition happens
from black to white. All of the horizontal shap es will fail
as none of the thr ee pixe ls are on th e black plane . For the
vertical shapes, the first column will pass as while the
last column will not as they are not in the neighborhood
of the center pixel. In a similar fashion, the diagonal
shapes test will both fail and two of the four corner shap e
tests will pass. So all the pixels in the two columns and

V. SUKUMAR ET AL. 223
Figure 6. Predetermined shapes used in Approach 2 defect
correction analysis.
Figure 7. A 3*3 kernel showing transition from white to
black region in a test image. This is done to gauge per-
formance of Approach 2.
two corner shapes will be u sed to compute an average. If
the center pixel is found to lie within a threshold of the
Approach 2 – 310 Approach 2 – 351 Approach 2 – 251
Approach 2 – 310: First th reshold of 300 and a second thres hol d o f 100.
Approach 2 – 351: First th reshold of 300 and a dynam ic second threshold of 50.
Approach 2 – 251: First th reshold of 200 and a dynam ic second threshold of 50.
Figure 8. Different versions of Approach 2 are tested on an 8M captured image to visually understand improvements expected. The
red box image indicates the region being tested from the original image. Note the ability of the different implementations to remove
the noise in the upper left corner of the checkerboard pattern. Approach 2 clearly does the best job of presenting details and not
mixing together the square with the neighboring white regions. Definitions for each of the approaches are presented below.

V. SUKUMAR ET AL. 224
Approach 2 – 310 Approach 2 – 351 Approach 2 – 251
Approach 2 – 310: First th reshold of 300 and a second thres hol d o f 100.
Approach 2 – 351: First th reshold of 300 and a dynam ic second threshold of 50.
Approach 2 – 251: First th reshold of 200 and a dynam ic second threshold of 50.
Figure 9. Different versions of Approach 2 are tested on a different section of the image to understand detail preservation.
ach of the approaches used does a good job with elimination of defects and avoid any smearing artifacts. E
computed value, the pixel und er test is a good pixel. If it
is to be a defectiv e pixel, the computed average value of
the neighbors o r the median o f the n eighb ors will now b e
the new pixel value. In this test case, five pixels instead
of eight pixels will compute the new value of the pixels
in the analysis kernel [6 ].
This algorithm will be able to handle anything lower
than three pixel clusters that lay within one of the
pre-defined shapes. Also, this approach takes advantage
of the random noise patterns. There is always a point,
where the noise overrides the ability to d etect any shapes.
Such die would be failed as gross fails [7]. As a minor
adjustment to Approach 2, the threshold of the neighbors
in the analysis kernel is also dynamically adjusted. This
is based on the number of pixels that are coun ted to be as
neighbors. If a given pixel has all eight neighbors, it is
considered a possibility that the pixel under test lies
within a region of subtle transition. This expanded the
threshold by a set factor. This approach is tested by mul-
tiplying by scale two if there are more than three pixels
and multiplied by scale three if there are more than six
pixels.
4. Experimental Results
In the experimental test results section, multiple versions
of Approach 2 are tested to narrow down the optimal
thresholds and other settings. Unless otherwise men-
tioned, all test images used are taken from an 8M CMOS
image sensor. This sensor supports 1.75um pixel, 4WS

V. SUKUMAR ET AL. 225
Histogram response: Original imag e Histogram response: Appr oach 2 – 310
Histogram response: Appr oach 2 – 351 Histogram response: Appr oach 2 – 251
Figure 10. Using a statistical analysis tool, it was found that the region highlighted in the red box of the test image has the
highest number of pixel defectivities or response deviation from the ideal pixel mean. Using different implementations of Ap-
proach 2, histogram responses are computed to understand pixel responses. Approach 2-251 does show the lowest second
peak response and as expected the first peak response has shifted toward the right because of more averaging done on the
riginal image. o
architecture and cropped to the center 1M region. All test images are BAYER 10 data to apply the correction

V. SUKUMAR ET AL. 226
Figure 11. Log plot presenting the dark current data in
electrons/second for the original image (red window in Fig-
ure 10) to processed image (Approach 2-251).
Figure 12. SNR plots for original image (red window in
Figure 10) to processed image (Approach 2-251).
schemes and then interpolated to RGB color space using
a simple bilinear algorithm. Region of analysis used in
each of the image used for evaluation is highlighted for
convenience to the reader.
From the results provided above, it is very evidently
seen that dark current or defectivity counts of the proc-
essed image has significantly gone down. This is clearly
reflected on test images, which are presented in Figure 8
and 9. In order to narrow down the optimal threshold
usage for Approach 2, histogram analysis is done on se-
lect dark regions of the test image. The region chosen for
analysis has the maximum pixel defectivity count. This is
done to better understand shift in histogram response.
Histogram profiles pre and post correction are presented
for comparison in Figure 10. In Figure 10, using Ap-
proach 2, the second peak of the histogram plot for each
of the thresholds is much lower in comparison with the
original image. This highlights that the pixels of varying
amplitudes are much lower in occurrence and get faded
into the normal distribution. This helps maintain a tight
mean value and sigma deviation for the entire statistical
window of analysis. Approach 2–251 is optimal in
threshold usage leading to good masking of pixel defects
with little to no loss in resolution details. This is also
better presented in Figure 11 using dark current analysis.
Figure 11 shows that the dark current distribution (met-
ric using in the imaging world to present pixel defectivity
behavior) has moved left post processing making the
image visually more appealing.
All versions of Approach 2 are also able to remove
noise and elevate Signal to Noise Ratio’s (SNR) as the
computed from the window of analysis used in Figure 10 .
Figure 13. MTF charts captured using the original image to processed image (Approach 2-251 used on original image). Row
profile illustrates details along the x-axis.

V. SUKUMAR ET AL. 227
This is done for both the original image and processed
image (Approach 2-251). The data indicates that the
SNR for the processed image has increased by 7% for
the same signal strength of the image. This indicates that
Approach 2- 2 5 1 is bet t e r.
Sharpness score is also captured using Modulation
Transfer Function (MTF) charts to gauge preservation of
details. In this test, the original 8M CMOS image sensor
is used to capture the sharpness chart and Approach
2-251 code is used on the entire frame of the original
image to understand sharpness details. As illustrated in
Figure 13, little to no loss in transitional details is seen.
This further validates Approa ch 2- 2 51 usa ge .
5. Conclusions and Future Work
In conclusion, Approach 2 preserves shapes and edges
and gives a greatly improved final image. As seen from
the analysis done on the test image, Approach 2 is capa-
ble of catching most of the true fails. The false fails cor-
rected by Approach 2 do not leave any visible defects.
The different variations of Approach 2 are capable of
being scaled to fit the ap propriate imagin g app lication . In
the case study conducted by the author, Approach 2-251
gives in optimal results. As pixel size decreases, correc-
tion for hot pixels and clusters will become very critical.
As part of future work, this research work will be ex-
tended to consider potential dynamic calculation of the-
multiplier used in Approach 2. At the same time, explore
possibilities of extending the range used for dynamic
threshold or shrink by a percentage ratio.
5
. References
[1] R. C. Gonzalez and R. E. Woods, “Digital Image Proc-
essing,” Addison-Wesley, MA, 1992.
[2] H. Wach et al., “Noise Modeling for Design and Simula-
tion of Computational Imaging Systems,” Optical Patte rn
Recognition, XVI, Proceedings of SPIE, Vol. 5438, No.
159, 2004, pp. 159-170.
[3] Jean-Marc, Leger, Dominique et al., “Modulation Trans-
fer Function Measurement Using Non Specific View,”
Optical Engineering, Vol. 43, 2004, pp. 1355-1365.
[4] O. Hadar, M. Huber, R. Huber and A. Stern, “MTF as A
Quality Measure for Compressed Images Transmitted
Over Lossy Packet Network,” Optical Engineering, Vol.
40, No. 10, 2001, pp. 2134-2142.
[5] J. S. Lee and R. I. Hornsey, “Photoresponse of Photodi-
ode Arrays for Solid State Image Sensors,” Journal of
Vacuum Science and Technology, Vol. 18, No.2, 2000, pp.
621-625.
[6] Yadid-Pecht, “Geometrical Modulation Transfer Function
for Different Pixel Active Area Shapes,” Optical Engi-
neering, Vol. 39, No. 4, 2000, pp. 859-865.
[7] G. D. Boreman and A. Plogstedt, “Spatial Filtering by a
Nonrectangular Detector,” Applications of Optical Engi-
neering, Vol. 28, No. 6, 1994, pp. 3063-3071.