Paper Menu >>
Journal Menu >>
 Engineering, 2010, 2, 205-211 doi:10.4236/eng.2010.24030 Published Online April 2010 (http://www. SciRP.org/journal/eng) Copyright © 2010 SciRes. ENG 205 A Finite Element Study of Elastic-Plastic Hemispherical Contact Behavior against a Rigid Flat under Varying Modulus of Elasticity and Sphere Radius Prasanta Sahoo*, Biplab Chatterjee Department of Mechanical Engineering, Jadavpur University, Kolkata, India E-mail: psjume@gmail.com Received November 18, 2009; revised January 28, 2010; accepted February 4, 2010 Abstract The present study considers a finite element analysis of elastic-plastic axi-symmetric hemispherical contact for a frictionless deformable sphere pressed by a rigid flat. The material of the sphere is modeled as elastic perfectly plastic. Analysis is carried out to study the effect of varying modulus of elasticity and sphere radius in wide range of dimensionless interference until the inception of plasticity as well as in plastic range. Re- sults are compared with previous elastic-plastic models. It is found that materials with Young’s modulus to yield strength (E/Y) ratio less than and greater than 300 show strikingly different contact phenomena. The dependency of E on dimensionless interference at which the plastic region fully covers the surface is ob- served. However with different radius, finite element study exhibits similar elastic-plastic phenomena. Keywords: Elastic-plastic Contact, Sphere against Flat, ANSYS, Modulus of Elasticity, Sphere Radius 1. Introduction Contact is necessary in any engineering application to transfer force and power hence it is almost an indispen- sable field of study. The elastic-plastic contact of a hemisphere with a rigid surface is a fundamental prob- lem to study the major characteristics like localized de- formation, the variation in the contact area, the contact force, displacement and the stress distribution in the de- formable body. Much interest is devoted in the literature to the reverse case of indentation loading where a rigid sphere penetrates an elasto-plastic half space. It is worthy to emphasize that indentation and hemispherical defor- mation (this work) are significantly different in the elasto-plastic and fully plastic regimes. One of the earli- est models of elastic asperity contact is that of Green- wood and Williamson [1]. This model uses the solution of the frictionless contact of an elastic hemisphere and a rigid flat plane, otherwise known as the Hertz contact solution [2]. Some works are restricted to pure plastic deformation of the contacting sphere, based on Abbott and Firestone [3]. The works on either pure elastic or pure plastic deformation of the contacting sphere over- look a wide intermediate range of interest where elas- tic-plastic contact prevails. An attempt to bridge this gap was made by Chang et al [4]. Zhao et al [5] used mathe- matical manipulation to smooth the transition of the con- tact load and contact area expressions between the elastic and elastic-plastic deformation regimes. Mathematical models are replaced using finite element model (FEM) concepts recently. Kogut and Etsion (KE) [6] used FEM concept and analyzed the evolution of the elastic-plastic contact with increasing interference revealing three dis- tinct stages that ranges from fully elastic, elastic-plastic up to fully plastic (0 < * 110). The model provides dimensionless expression for contact area, contact load and mean contact pressure covering a large range of in- terference values. They inferred that their analysis is normalized in such a way that allowed a general solution, which is independent of specific material and radius of the sphere. A change in the behavior of the mean contact pressure was observed in their analysis at *=6, which marks the elastic limit of the contact area. To generalize their solution, the numerical solutions were normalized with respect to their corresponding critical values at yielding inception, c. The validity of this normalization was tested by solving the problem for several different material properties (100 < E/Y < 1000, = 0.3) and sphere radii (0.1 mm < R < 10 mm). Their results show that the entire contact zone is plastic when the dimen- sionless interference ratio (/c = *) is 68 and the rate of its radial expansion increases substantially. Moreover  P. SAHOO ET AL. 206 when /c = 110, the dimensionless mean contact pres- sure (p/Y) approaches the value of 2.8. This is identical to the ratio between the hardness and yield strength found experimentally for many materials as indicated by Tabor [7]. Kogut and Etsion [8] studied the maximum tangential load that can be supported by a normally preloaded elas- tic perfectly plastic spherical contact at the inception of sliding using an approximate semi analytical solution. Sliding inception was interpreted as a failure of the con- tact. They found that when the normal load is less than the Hertzian critical load the failure occurs on the contact surface. If the normal load exceeds that critical one, the failure occurs below the contact surface. Brizmer et al. [9] analyzed and compared the ductile material yielding in- ception and the brittle material failure inception for two different contact conditions between a smooth elastic sphere and rigid flat and the effect of contact condition and material properties on the termination of elasticity. Jackson and Green (JG) [10] extended the KE model to account for the geometry and the material effects in the analysis. They used finer mesh than the KE model and solved for five different yield strengths. Their analysis showed markedly different behavior for the materials with different strengths in the transition from elas- tic-plastic to fully plastic deformations. For calculating the critical interference, they used material yield strength (Y) directly in their expressions. Their results show that the dimensionless mean contact pressure does not reach 2.8 for most of the yield strength values. The JG solution used E/Y ratio of 952.4, 356.6, 219, 158.1 and 137.74 by varying the values of ‘Y’ with constant E = 200 GPa. They also analyzed the interference when plastic defor- mation first reaches the contacting surface at the far right end and the contact surface first becomes entirely plastic for yield strength of 1.619, 1.2653, 0.9115 GPa. Quick- sall et al. [11] have taken five hypothetical material properties and studied the error of formulation for KE and JG models. The first test generated contact area and contact force data for five hypothetical metals with Poisson’s ratio, yield strength and elastic modulus typi- cal of aluminum, bronze, copper, titanium and malleable cast iron. Non-dimensional interference between *=5 and *=250 were used to generate data in both the elas- tic-plastic and the plastic regimes except for aluminum at *=250 and malleable cast iron above *=10. Second set of tests generated non-dimensional contact area and con- tact force data for a generic material in which the elastic modulus and Poison’s ratio were independently varied with yield strength held constant at 200 MPa. Firstly Poisson’s ratio was varied between 0.28 and 0.36 with the elastic modulus held constant at 200 GPa. Then the elastic modulus was varied between 160 and 240 GPa with Poisson’s ratio held constant at 0.32. The dimen- sionless interference was set at *=20, 80 and 250 for each test iteration. Jackson et al. [12] used the mesh size same as that of JG model and presented results for a range of normalized interference *, from 0.571 to 171. Then the contact force, stress tensor, von mises stresses and the displacement in both the radial and axial direc- tions were recorded. After loading conditions had been simulated; the solution was then restarted and unloaded completely to simulate the residual stresses and the dis- placements. In order to measure the effect of the material properties on the hemispherical deformation, both alu- minum and steel sphere unloaded from *=135; they inferred that the deformation of the hemisphere is de- pendent on the properties of the material and the inter- ference. Shankar and Mayuram (SM) [13] studied the evolution of elastic core and the plastic region within the asperity for different Y/E ratios. They varied the yield strength from 250 N/mm2 to 2250 N/mm2. E equals to 2.07 x 105 N/mm2. The range of E/Y is from 83.333 to 500. It was revealed from their analysis that higher dimensionless interference, * is required for the plastic region to just touch the contact surface when E/Y > 166.66 and this * is varied with E/Y ratio. For E/Y< 166.667, this * is constant and equals to 6. Same trend was observed for the entire contact surface to be in plastic. For E/Y > 166.66, the value of /c decreases with decrease of E/Y ratio. When E/Y ratio is less than 166.66, the fully plastic contact condition exists at a constant interference ratio of 54. They studied the variation of mean contact pressure (p/Y) as a function of dimensionless interference ratio and observed that materials having low yield strength (i.e. when E/Y>300) produces results similar to the KE model but p/Y ratio never reaches 2.8. Malayalamurti and Marappan (MM) [14] analyzed the elastic-plastic behav- ior of a sphere loaded against a rigid flat in two region. One is when E/Y > 300, another when E/Y < 300. They observed that when E/Y<300, the fully plastic average contact pressure or hardness is not constant. However, the hardness and interference at the inception of fully plastic condition are constant for materials with E/Y>300. The present work aims to study the qualitative and quan- titative contact characteristics of single asperity contact using commercial FEM software ANSYS. Analysis is carried out to study the effect of varying modulus of elasticity and sphere radius in wide range of dimen- sionless interference until the inception of plasticity as well as in plastic range. 2. Finite Element Model and Procedure To improve upon the efficiency of computation, an axi-symmetric 2-D model is used. The present study utilizes the commercial program ANSYS. The hemi- sphere is modeled by a quarter of a circle, due to its axi- symmetry. A line models the rigid flat. The model re- Copyright © 2010 SciRes. ENG  P. SAHOO ET AL. Copyright © 2010 SciRes. ENG 207 fines the element mesh near the region of contact to al- low the hemisphere’s curvature to be captured and accu- rately simulated during deformation. The model uses quadrilateral, four node elements to mesh the hemisphere. The resulting ANSYS mesh is presented in Figure 1. The nodes on the axis of symmetry are fixed in radial direction. Likewise the nodes on the bottom of the hemisphere are fixed in both axial and radial direction. This boundary condition is valid for the modeling of as- perity contacts for two reasons: first, the asperities are connected to a much larger bulk material at the base; second, since the high stress region occurs near the con- tact, the boundary condition at the base of the hemi- sphere will not greatly affect the solution because of Saint Venant’s principle. The bilinear isotropic harden- ing (BISO) option in the ANSYS program is chosen to account the elastic-plastic material response for the sin- gle asperity model. The rate independent plasticity algo- rithm incorporates the von Mises criterion. Tangent modulus is assumed as zero for validating the results with other elastic perfectly plastic models. The KE model uses a maximum of 2944 nodes and JG model uses a constant of 11,101 elements for their analysis. However the present work uses a maximum of 11069 elements for the radius of 1 mm. The mesh density is iteratively increased until the contact force and contact area differed by less than 1% between iterations. In addi- tion to mesh convergence, the model also compares well with the Hertz elastic solution at interferences below the critical interference. The contact force of the model dif- fers from the Hertzian solution by no more than 2% while the contact radius differs by less than 10%. The smaller error in the contact force is due to overall force balance enforced by ANSYS. But, the contact radius is obtained from a discrete mesh which has a finite resolu- tion. Apart from this, the magnitude of the contact ele- ment stiffness also has some effect on such contact radii, although not on the overall force balance. This work uses Lagrangian multiplier method. The tolerance of current work is set to 1% of the element width. There are two ways to simulate the contact problem. The first applies a force to the rigid body and then com- putes the resulting displacement. The second applies a displacement and then computes the resulting contact force. In both methods, the displacement, stress, and strain can be determined as well as the contact pressure. In this work the latter approach is used. This method is used because the resulting solution converges more rap- idly than the former. In this work contact parameters are normalized using the JG model’s expression for critical interference (c), critical load (Pc) and critical contact area (Ac) to form dimensionless parameters. The critical interference (c) is expressed as [10] c = (CY/2E/)2R (1) Where C=1.295 exp(0.736). The Poisson’s ratio, , to be used here is that of the material which yields first. The critical load, Pc, is then may be calculated as [10] Pc = (4/3)(R/E/) 2.(CY/2) 3 (2) Figure 1. Finite element mesh of a sphere generated by ANSYS. 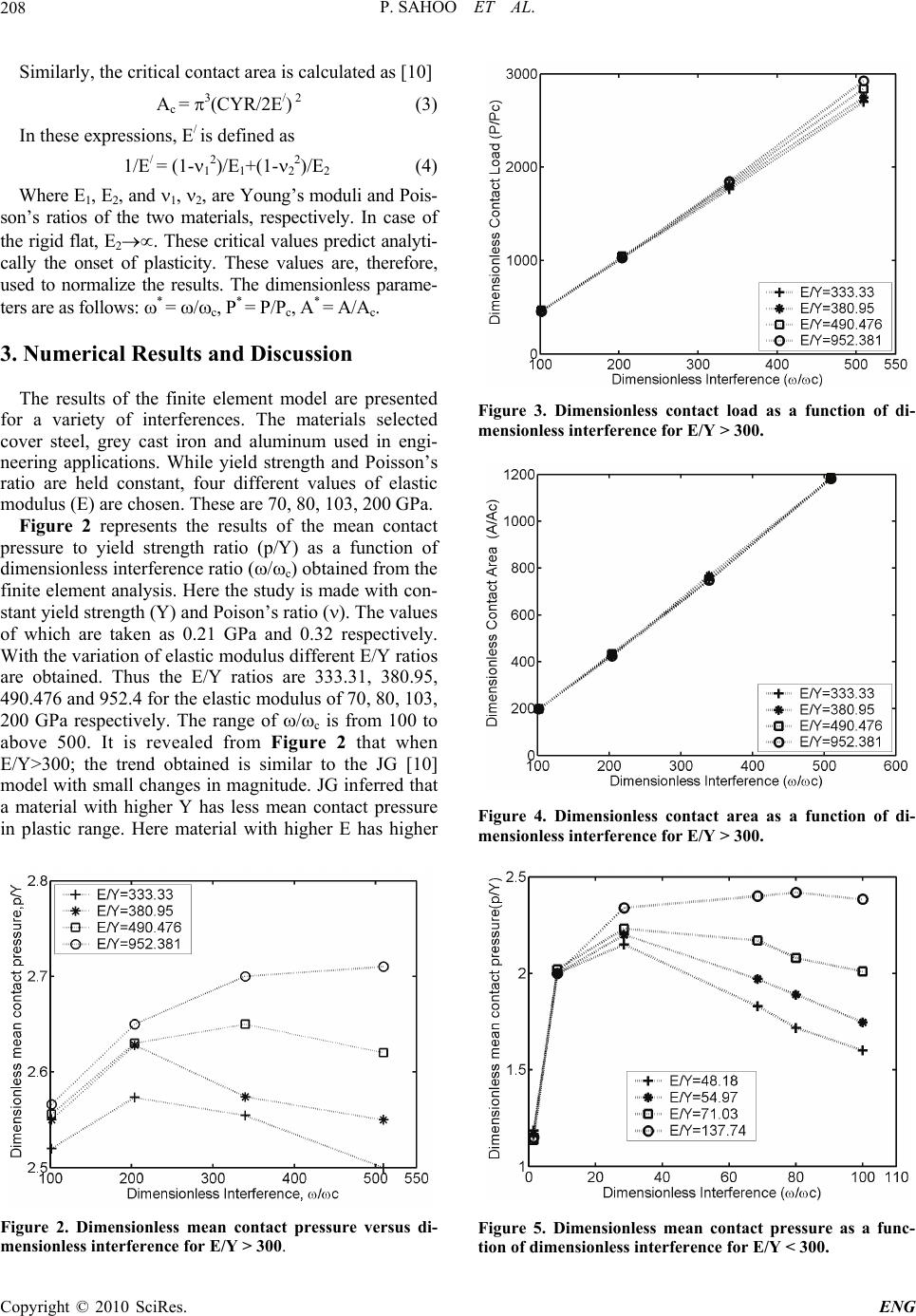 P. SAHOO ET AL. 208 Similarly, the critical contact area is calculated as [10] Ac = 3(CYR/2E/) 2 (3) In these expressions, E/ is defined as 1/E/ = (1-1 2)/E1+(1-2 2)/E2 (4) Where E1, E2, and 1, 2, are Young’s moduli and Pois- son’s ratios of the two materials, respectively. In case of the rigid flat, E2. These critical values predict analyti- cally the onset of plasticity. These values are, therefore, used to normalize the results. The dimensionless parame- ters are as follows: * = /c, P* = P/Pc, A* = A/Ac. 3. Numerical Results and Discussion The results of the finite element model are presented for a variety of interferences. The materials selected cover steel, grey cast iron and aluminum used in engi- neering applications. While yield strength and Poisson’s ratio are held constant, four different values of elastic modulus (E) are chosen. These are 70, 80, 103, 200 GPa. Figure 2 represents the results of the mean contact pressure to yield strength ratio (p/Y) as a function of dimensionless interference ratio (/c) obtained from the finite element analysis. Here the study is made with con- stant yield strength (Y) and Poison’s ratio (). The values of which are taken as 0.21 GPa and 0.32 respectively. With the variation of elastic modulus different E/Y ratios are obtained. Thus the E/Y ratios are 333.31, 380.95, 490.476 and 952.4 for the elastic modulus of 70, 80, 103, 200 GPa respectively. The range of /c is from 100 to above 500. It is revealed from Figure 2 that when E/Y>300; the trend obtained is similar to the JG [10] model with small changes in magnitude. JG inferred that a material with higher Y has less mean contact pressure in plastic range. Here material with higher E has higher Figure 2. Dimensionless mean contact pressure versus di- mensionless interference for E/Y > 300. Figure 3. Dimensionless contact load as a function of di- mensionless interference for E/Y > 300. Figure 4. Dimensionless contact area as a function of di- mensionless interference for E/Y > 300. Figure 5. Dimensionless mean contact pressure as a func- tion of dimensionless interference for E/Y < 300. Copyright © 2010 SciRes. ENG  P. SAHOO ET AL.209 mean contact pressure as the dimensionless interference increases in the plastic range. MM [14] concluded the material independent behavior for E/Y > 300. They had- taken the average results of four materials. Moreover they modeled the material of the sphere as an elastic lin- ear hardening material. A 1% linear hardening was se- lected for their work. The present work modeled the ma- terial of the sphere as an elastic perfectly plastic material and the results entirely deviate from their result as mean contact pressure to yield strength ratio (p/Y) never reaches 2.8. Figure 3 shows the variation of dimen- sionless contact load as a function of dimensionless in- terference, when E/Y is greater than 300. The result in- dicates the similarity with Quicksall et al. [11] findings. With the increased modulus of elasticity (E), the value of dimensionless load increases in the plastic range. Dimensionless contact area as a function of * (di- mensionless interference) is plotted in Figure 4. The values for dimensionless contact area continue to in- crease with interference even past fully plastic condition. For the contact area, all the models follow the same gen- eral trend, but they differ only in magnitude. The result shows that the dimensionless contact area is independent of E when E/Y > 300. Study is also made for the materials of E/Y < 300. For this case Y is taken as 1.619 GPa, with constant Pois- son’s ratio of 0.32.With four E values of 70, 80, 103 and 200 GPa the corresponding E/Y ratios are 48.178, 54.972, 71.0315 and 137.739 respectively. These values are well below 300. The behaviors of these materials in elastic as well as in elastic-plastic ranges are also analyzed. The average contact pressure to yield strength ratio is plotted in Figure 5 as a function of dimensionless interference (*). It is clearly evident from the plot that dimensionless mean contact pressure does not reach the value of 2.8 even if for steel with E = 200 GPa. There is a decrease in mean contact pressure after reaching its peak value, though the peak value is dependent on E. As the value of E increases, peak mean contact pressure also increases. There is a similarity of the trend with the findings of MM [14]. But MM inferred that peak value would reach after the dimensionless interference of 90 only. Present work observed that the peak value of mean contact pressure in all the cases occurred well below the dimensionless in- terference of 90. It can be seen from Figure 5, the loca- tion at which the mean pressure attain its peak value and its magnitude is entirely dependent on modulus of elas- ticity (E) of the material. Figure 6 represents the plot of dimensionless load (P*) versus *. It is clear from the figure that for different value of E up to the inception of fully plastic contact the trend is linear with marginal change in magnitude. This is similar to the prediction of KE [6]. This trend is not observed in higher interference ratio. Figure 7 represents the plot of dimensionless contact area with * when E/Y < 300. The FEM results from this study indicate that dimensionless contact area decreases slightly with in- creased elastic modulus of elasticity. Same trend was observed by Quicksall et al. [11]. When interference increases, the elastic core com- pletely disappears and the fully plastic region reaches the contact surface as shown in Figure 8, thus the transition to the fully plastic state occurs. KE model predicted this transition limited to specific dimensionless ratio of 68. JG [10] and SM [13] predicted that this ratio at which this transition occurs is not constant. In the present work it is observed that this ratio is dependent on E. As the value of E increases the dimensionless ratio at which the transition occurs is also increasing. There is no indication of constant value for the present four E/Y ratio though SM also observed a constant value of 54 when E/Y < 166.66. Figure 9 is the plot of * versus E/Y where it is clear that in the present domain of work SM overesti- mates the interferences marginally. The present work also studied the values of dimensionless contact load, Figure 6. Dimensionless contact load versus dimension- less interference for E/Y < 300. Figure 7. Dimensionless contact area versus dimension-less interference for E/Y < 300. Copyright © 2010 SciRes. ENG  P. SAHOO ET AL. 210 Figure 8. Inception of fully plastic contact. Figure 9. End of elastic-plastic region based on the disap- pearance of elastic core. contact area and mean contact pressure with different sphere radii, the study is made with radii of 1, 2, and 3 mm. No significant deviation is observed. Thus it can be inferred that earlier mentioned dimensionless contact characteristics are independent of the sphere radius. 4. Conclusions The present work considers 2D axi-symmetric finite element model of an elastic perfectly plastic hemisphere in contact with a rigid flat surface. A comparison is also made with other existing models. The material is mod- eled as elastic perfectly plastic, and yielding occurs ac- cording to the Von Mises criterion. It has been clearly shown that the dimensionless mean contact pressure ratio is not constant at 2.8 in the plastic range but depends on modulus of elasticity whether E/Y is greater or lesser than 300. But the peak value (i.e. maximum mean con- tact pressure ratio), the dimensionless interference at which this value occurs, the trend of variation are all dependent on E/Y ratio. Dimensionless contact area, contact load also depends on modulus of elasticity. But dimensionless contact load, contact area and mean con- tact pressure is independent of the radius of sphere. The development of the elastic core and the transition to the plastic region within the surface for the wide range of interference is studied using Von Mises stress. It is ob- served that the dimensionless interference ratio at the instance when the plastic region fully covers the surface is dependent on the values of modulus of elasticity when Copyright © 2010 SciRes. ENG  P. SAHOO ET AL.211 other properties are kept constant. 5. Nomenclature Symbol Meaning Unit P Contact load N R Radius of the sphere mm p Pressure GPa Interference m A Contact area m2 E Modulus of Elasticity GPa Y Yield strength of sphere GPa Poison’s ratio 5.1 Subscripts c = critical values 5.2 Superscripts / = equivalent * = dimensionless 6. References [1] J. A. Greenwood and J. B. P. Williamson, “Contact of Nominally Flat Surfaces,” Proceedings of the Royal So- ciety of London, Vol. A295, 1966, pp. 300-319. [2] S. Timoshenko and J. N. Goodier, “Theory of Elasticity,” McGraw-Hill, New York, 1951. [3] E. J. Abbott and F. A. Firestone, “Specifying Surface Quality-A Method Based on Accurate Measurement and Comparison,” Journal of Mechanical Engineering, No. 55, 1933, pp. 569-572. [4] W. R. Chang, I. Etsion and D. B. Bogy, “An Elas- tic-plastic Model for the Contact of Rough Surfaces,” Journal of Tribology, Vol. 109, No. 2, 1987, pp. 257-263. [5] Y. Zhao, D. M. Maietta and L. Chang, “An Asperity Mi- cro Contact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow”, Journal of Tribology, Vol. 122, No. 1, 2000, pp. 86-93. [6] L. Kogut and I. Etsion, “Elastic-plastic Contact Analysis of a Sphere and a Rigid Flat,” Journal of Applied Me- chanics, Vol. 69, No. 5, 2002, pp. 657-662. [7] D. Tabor, “The Hardness of Metals,” Clarendon Press, Oxford, 1951. [8] L. Kogut and I. Etsion, “A Semi-analytical Solution for the Sliding Inception of a Spherical Contact,” Journal of Tribology, Vol. 125, No. 3, 2003, pp. 499-506. [9] V. Brizmer, Y. Kligerman and I. Etsion, “The Effect of Contact Conditions and Material Properties on the Elas- ticity Terminus of a Spherical Contact,” International Journal of Solids and Structures, Vol. 43, 2005, pp. 5736-5749. [10] R. L. Jackson and I. Green, “A Finite Element Study of Elasto-plastic Hemispherical Contact against a Rigid Flat,” Journal of Tribology, Vol. 127, No. 2, 2005, pp. 343-354. [11] J. J. Quicksall, R. L. Jackson and I. Green, “Elasto- plastic Hemispherical Contact Models for Various Me- chanical Properties,” Journal of Engineering Tribology, Vol. 218, No. 4, 2004, pp. 313-322. [12] R. L. Jackson, I. Chusoipin and I. Green, “A Finite Ele- ment Study of the Residual Stress and Deformation in Hemispherical Contacts,” Journal of Tribology, Vol. 127, No. 3, 2005, pp. 484-493. [13] S. Shankar and M. M. Mayuram, “A Finite Element Based Study on the Elastic-plastic Transition Behavior in a Hemisphere in Contact with a Rigid Flat,” Journal of Tribology, Vol. 130, 2008, pp. 1-6. [14] R. Malayalamurthi and R. Marappan, “Elastic-plastic Contact Behavior of a Sphere Loaded against a Rigid Flat,” Mechanics of Advanced Materials and Structures, Vol. 15, No. 5, 2008, pp. 364-370. Copyright © 2010 SciRes. ENG |

