Open Journal of Ap pli e d Sci e nce , 20 1 1, 1, 1-7
doi:10.4236/ojapps.2011.11001 Published Online December 2011 (http://www.SciRP.org/journal/ojapps)
Ultrasonic Wave Propagation in Californium
Monopnictides
Rajkumar1,*, Devraj Singh2 and Giridhar Mishra2
1Department of Physics, Nims University, Jaipur, India
2Department of Applied Physics, Amity School of Engineering and Technology, Bijwasan, New Delhi, India
*E-mail:
Received November 12, 2011; revised December 15, 2011; accepted December 30, 2011
Abstract
In this paper, theoretical computations have been made for the investigations of temperature dependence of
the ultrasonic parameters like ultrasonic velocities and Grüneisen parameters in californium monopnictides
CfY (Y: N, As and Sb) for longitudinal and shear waves along <100>, <110> and <111> crystallographic
directions in the temperature range 100–500K. For the same evaluation the second- and third- order elastic
constants have also been computed for these monopnictides using Coulomb and Born-Mayer potential upto
second nearest neighborhood. The mechanical properties and stability of CfN is best, because of its high va-
lued elastic constants. Ultrasonic velocity is found to be highest for CfAs along all chosen directions, so
CfAs will be most suitable compound for wave propagation. The obtained results of present investigation are
discussed in along with identified thermophysical properties.
Keywords: Californium monopnictides; Coulomb and Born-Mayer potential; Elastic constants;
Ultrasonic velocity; Grüneisen parameters
1. Introduction
Ultrasonic non-destructive testing (NDT) is a useful
technique that can be applied to a range of materials for
the characterization of their microstructures, the appraisal of
defects and the determination of physical properties such
as density, thermal conductivity and electrical resistivity.
The Grüneisen parameter is of considerable importance
to Earth’s scientists, because it sets limitations on the
thermoelastic properties of lower mantle [1]. The study
of Grüneisen parameters for a solid enables us to describe
and discuss the various physical properties of a system,
such as high temperature specific heats of lattice, thermal
expansion, thermal conductivity and temperature varia-
tion of the elastic constants. The Grüneisen parameters
play a significant role in the study of thermoelastic prop-
erties. It has its fundamental importance to the equation
of state of a system and related thermodynamic proper-
ties of the solids [2]. The calculation of anharmonic ef-
fects in solids such as thermal expansion or the interac-
tion of acoustic and thermal phonons involves Grüneisen
parameters, which describe the volume and strain de-
pendence of the lattice vibrational frequencies. In the
Debye model, these vibrations are replaced by standing
wave modes of a dispersionless elastic continuum. The
Grüneisen parameters are then no longer frequency dep-
endent and can be expressed in terms of second- and
third- order elastic constants [3]. Wave velocity is the
key parameter in ultrasonic characterization and can pro-
vide information about crystallographic texture. The ul-
trasonic velocity (V) is related to the elastic constant by
the relation V = (C/), where C is the relevant elastic
constant and  is the density of that particular material.
The elastic constant, in particular provides valuable in-
formation on the stability and stiffness of the materials.
The elastic constants of solids also provide a link be-
tween the mechanical and dynamical behaviours of crys-
tals and give important information concerning the na-
ture of forces operating in solids [4]. To the best of our
knowledge, the studies of californium monopnictides
have not been found in detail and we hope the ultrasonic
study can be of potential interest. We found few studies
of californium monopnictides in literature [5-8]. Haire et
al. [5] and Damien et al. [6] studied the crystal structure
and lattice parameters of Cf monopnictides and also
proved semimetallic nature of CfY. Magnetism of cali-
fornium Monopnictides has been discussed by Nave et al.
[7-8]. No experimental and theoretical result on ultra-

RAJKUMAR ET AL.
2
sonic velocity and Grüneisen parameters on these mate-
rials has been found in the literature. Moreover the tem-
perature dependent elastic constants have not been com-
puted and measured, which stimulates us to execute
theoretical analysis of elastic constants, ultrasonic ve-
locities and Grüneisen parameters in californium mo-
nopnictides along <100>, <110> and <111> directions at
temperature range 100 K - 500 K.
2. Theory
The second and third order elastic constants (SOEC and
TOEC) have been calculated following Brugger’s
definition of elastic constants [9-10] at absolute zero
(0
I
J
Cand 0
I
JK
C). The SOEC and TOEC at different higher
temperatures are obtained by the method developed by
Leibfried and Haln [11], Ludwig [12] and Hiki [13] for
NaCl-type crystals as the chosen semimetallics have
well-developed structures of the NaCl-type crystals. The
lattice parameters are very close to those in literature
[6-8,14].
When sound wave propagates through a solid medium,
there are three modes of propagation one longitudinal
acoustical and two transverse acoustical. Hence, there
exist three types of velocities, as one longitudinal (VL)
and two shear (VS1 and VS2) that depend on the direction
of propagation of wave [15]. The direction dependent
ultrasonic velocities for a cubic crystal are expressed as
given below
Along <100> crystallographic direction;


11
S1 244
;
V
L
S
VCρ
VC
ρ



 

(1)
Along <111> crystallographic direction;


11 1244
S1211 1244
243;
V
L
S
VCCCρ
VCCC3
ρ

 

  
(2)
Along <110> crystallographic direction;
11 1244
4411 12
S1 2
2 ;
2
V;
L
S
CC C
Vρ
CC
V
ρρ








C
(3)
where CIJ are particular elastic constant of the material
and ρ is the density. The Debye average velocity (VD) is
useful for information of Debye temperature and thermal
relaxation time of the materials. The following expres-
sions have been used for evaluation of Debye average
velocity [12].
1/3
33
1
1/3
33 3
12
11 2;
3
along 100 , 111 directions
11 11
;
3
along 110 direction
m
LS
LS S
VVV
VVV







 












 






 
(4)
A number of anharmonic properties of solids are fre-
quently expressed in terms of Grüneisen parameters,
which are expressed, in quasiharmonic approximation, as
diverse weighted averages of Grüneisen tensor of the
first order: 1()
j
αβ ii αβ
γωωqη


 . For example, the ther-
mal expansivity is relative to the specific heat weighted
,,
,,qi
j
αβ qi αβ qi
qi
γCγC

,which is thermal Grüneisen
parameters ; and the (shear) ultrasonic attenuation’s
Grüneisen parameter can be suitably expressed [16] by
thermal conductivity weighted averages of the product
j
j
αβ γδ
γγ . Brugger [17] derived expressions for the com-
ponents of Grüneisen tensor in terms of SOEC and
TOEC of an anisotropic elastic continuum. These relations
permit the above weighted average to be reliably calcu-
lated from elastic and thermal data to give ultrasonic att-
enuation and non-linear parameters, which compares very
well with measured results [18]. Formulae of Grüneisen
parameters along different crystallographic directions are
given in literature [19].
3. Results and Discussion
The elastic constants of materials are directly related to
their microstructure and are used to obtain the Debye
average velocity, Grüneisen parameter and other physical
properties; and therefore, these are of great interest in
applications where the mechanical strength and dura-
bility are important. The SOEC and TOEC have been
evaluated using two basic parameters i.e., lattice para-
meter and hardness parameter. The lattice parameters [6,
7, 14] for CfN, CfAs and CfSb are 4.95 Å, 5.809 Å, and
6.165 Å and the value of hardness parameters [20] are
0.313 Å,0.303 Å and 0.311 Å respectively. The computed
results of temperature dependent SOEC and TOEC are
given in Tables 1. No experimental/theoretical result of
SOEC and TOEC of these materials was found directly
in existing literature. So our achieved results have been
compared with gadolinium monopnictides GdY [21].
These compared results are available in Table 1. It is
clear from Table 1 that out of nine elastic constants, four
(i.e., C11, C44, C112 and C144) are increasing and four (i.e.,
C12, C111, C166 and C123) are decreasing with the
temperature while C456 is found to be unaffected. This
trend of elastic constants in chosen materials at higher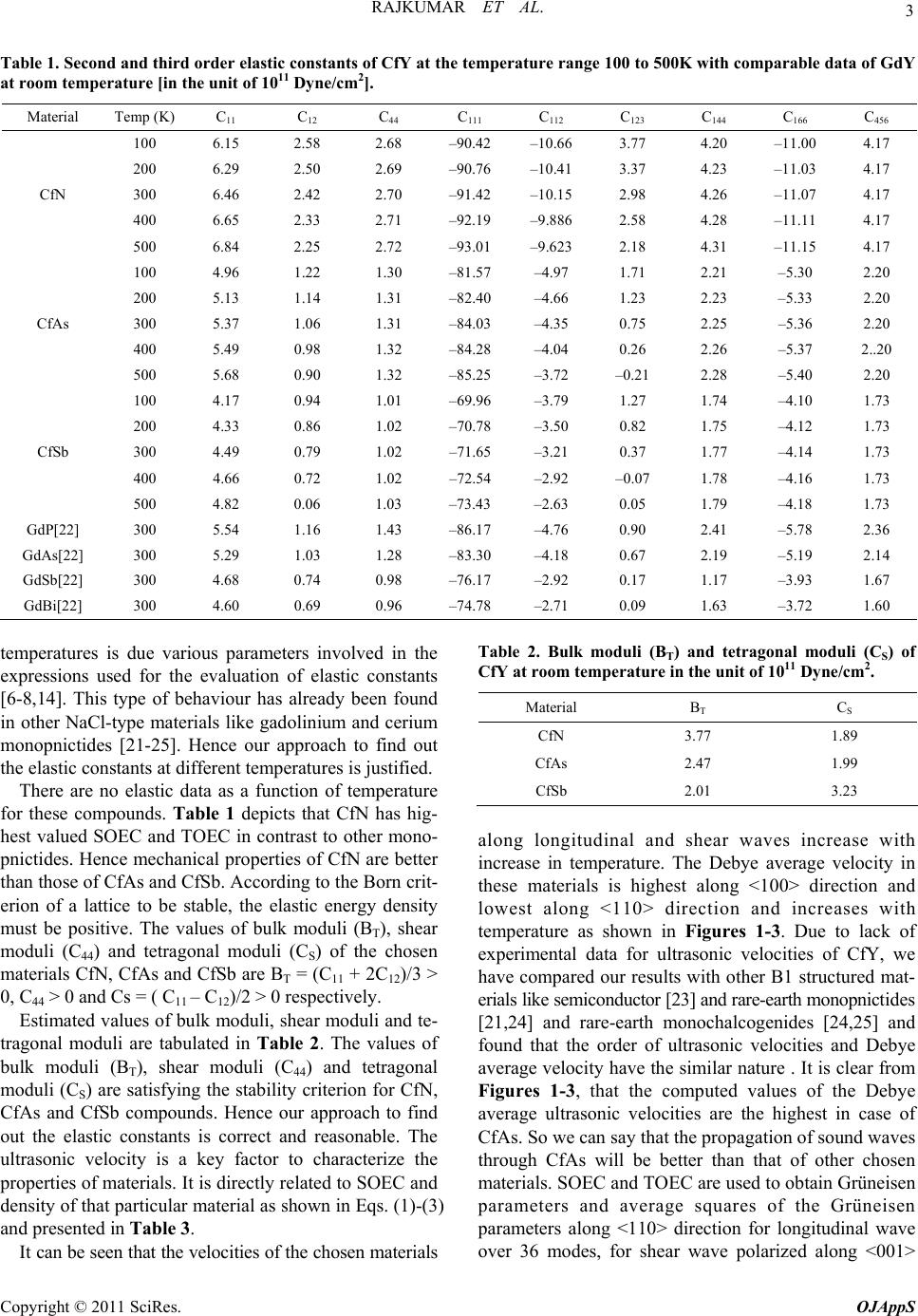

RAJKUMAR ET AL.
3
Table 1. Second and third order elastic constants of CfY at the temperature range 100 to 500K with comparable data of GdY
at room temperature [in the unit of 1011 Dyne/cm2].
Material Temp (K) C11 C
12 C 44 C 111 C 112 C 123 C 144 C 166 C 456
100 6.15 2.58 2.68 –90.42 –10.66 3.77 4.20 –11.00 4.17
200 6.29 2.50 2.69 –90.76 –10.41 3.37 4.23 –11.03 4.17
300 6.46 2.42 2.70 –91.42 –10.15 2.98 4.26 –11.07 4.17
400 6.65 2.33 2.71 –92.19 –9.886 2.58 4.28 –11.11 4.17
CfN
500 6.84 2.25 2.72 –93.01 –9.623 2.18 4.31 –11.15 4.17
100 4.96 1.22 1.30 –81.57 –4.97 1.71 2.21 –5.30 2.20
200 5.13 1.14 1.31 –82.40 –4.66 1.23 2.23 –5.33 2.20
300 5.37 1.06 1.31 –84.03 –4.35 0.75 2.25 –5.36 2.20
400 5.49 0.98 1.32 –84.28 –4.04 0.26 2.26 –5.37 2..20
CfAs
500 5.68 0.90 1.32 –85.25 –3.72 –0.21 2.28 –5.40 2.20
100 4.17 0.94 1.01 –69.96 –3.79 1.27 1.74 –4.10 1.73
200 4.33 0.86 1.02 –70.78 –3.50 0.82 1.75 –4.12 1.73
300 4.49 0.79 1.02 –71.65 –3.21 0.37 1.77 –4.14 1.73
400 4.66 0.72 1.02 –72.54 –2.92 –0.07 1.78 –4.16 1.73
CfSb
500 4.82 0.06 1.03 –73.43 –2.63 0.05 1.79 –4.18 1.73
GdP[22] 300 5.54 1.16 1.43 –86.17 –4.76 0.90 2.41 –5.78 2.36
GdAs[22] 300 5.29 1.03 1.28 –83.30 –4.18 0.67 2.19 –5.19 2.14
GdSb[22] 300 4.68 0.74 0.98 –76.17 –2.92 0.17 1.17 –3.93 1.67
GdBi[22] 300 4.60 0.69 0.96 –74.78 –2.71 0.09 1.63 –3.72 1.60
temperatures is due various parameters involved in the
expressions used for the evaluation of elastic constants
[6-8,14]. This type of behaviour has already been found
in other NaCl-type materials like gadolinium and cerium
monopnictides [21-25]. Hence our approach to find out
the elastic constants at different temperatures is justified.
There are no elastic data as a function of temperature
for these compounds. Table 1 depicts that CfN has hig-
hest valued SOEC and TOEC in contrast to other mono-
pnictides. Hence mechanical properties of CfN are better
than those of CfAs and CfSb. According to the Born crit-
erion of a lattice to be stable, the elastic energy density
must be positive. The values of bulk moduli (BT), shear
moduli (C44) and tetragonal moduli (CS) of the chosen
materials CfN, CfAs and CfSb are BT = (C11 + 2C12)/3 >
0, C44 > 0 and Cs = ( C11 – C12)/2 > 0 respectively.
Estimated values of bulk moduli, shear moduli and te-
tragonal moduli are tabulated in Table 2. The values of
bulk moduli (BT), shear moduli (C44) and tetragonal
moduli (CS) are satisfying the stability criterion for CfN,
CfAs and CfSb compounds. Hence our approach to find
out the elastic constants is correct and reasonable. The
ultrasonic velocity is a key factor to characterize the
properties of materials. It is directly related to SOEC and
density of that particular material as shown in Eqs. (1)-(3)
and presented in Table 3.
It can be seen that the velocities of the chosen materials
Table 2. Bulk moduli (BT) and tetragonal moduli (CS) of
CfY at room temperature in the unit of 1011 Dyne/cm2.
Material BT C
S
CfN 3.77 1.89
CfAs 2.47 1.99
CfSb 2.01 3.23
along longitudinal and shear waves increase with
increase in temperature. The Debye average velocity in
these materials is highest along <100> direction and
lowest along <110> direction and increases with
temperature as shown in Figures 1-3. Due to lack of
experimental data for ultrasonic velocities of CfY, we
have compared our results with other B1 structured mat-
erials like semiconductor [23] and rare-earth monopnictides
[21,24] and rare-earth monochalcogenides [24,25] and
found that the order of ultrasonic velocities and Debye
average velocity have the similar nature . It is clear from
Figures 1-3, that the computed values of the Debye
average ultrasonic velocities are the highest in case of
CfAs. So we can say that the propagation of sound waves
through CfAs will be better than that of other chosen
materials. SOEC and TOEC are used to obtain Grüneisen
parameters and average squares of the Grüneisen
parameters along <110> direction for longitudinal wave
over 36 modes, for shear wave polarized along <001>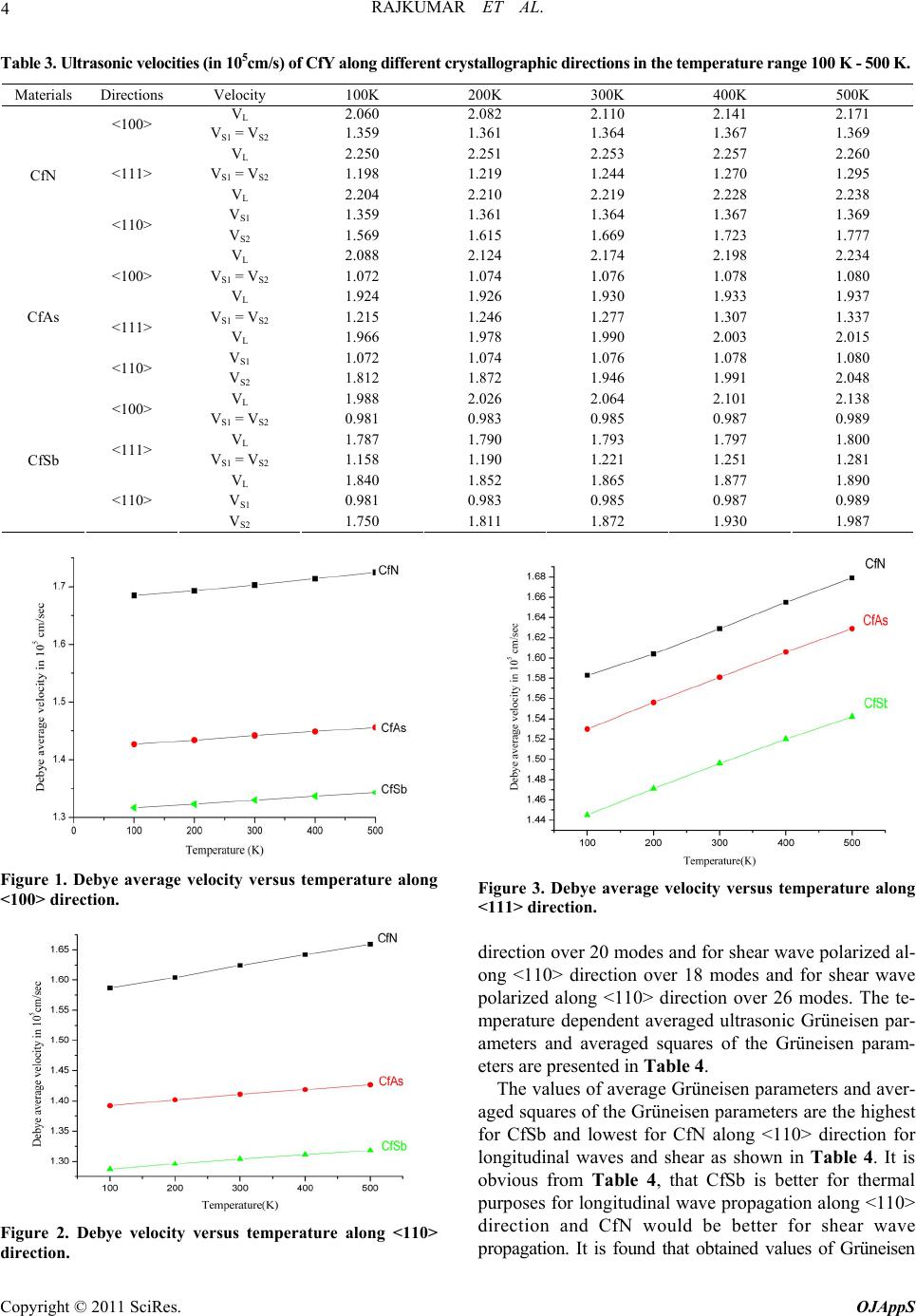

RAJKUMAR ET AL.
4
Table 3. Ultrasonic velocities (in 105cm/s) of CfY along different crystallographic directions in the temperature range 100 K - 500 K.
Materials Directions Velocity 100K 200K 300K 400K 500K
VL 2.060 2.082 2.110 2.141 2.171
<100> VS1 = VS2 1.359 1.361 1.364 1.367 1.369
VL 2.250 2.251 2.253 2.257 2.260
VS1 = VS2 1.198 1.219 1.244 1.270 1.295 <111>
VL 2.204 2.210 2.219 2.228 2.238
VS1 1.359 1.361 1.364 1.367 1.369
CfN
<110> VS2 1.569 1.615 1.669 1.723 1.777
VL 2.088 2.124 2.174 2.198 2.234
VS1 = VS2 1.072 1.074 1.076 1.078 1.080 <100>
VL 1.924 1.926 1.930 1.933 1.937
VS1 = VS2 1.215 1.246 1.277 1.307 1.337
<111> VL 1.966 1.978 1.990 2.003 2.015
VS1 1.072 1.074 1.076 1.078 1.080
CfAs
<110> VS2 1.812 1.872 1.946 1.991 2.048
VL 1.988 2.026 2.064 2.101 2.138
<100> VS1 = VS2 0.981 0.983 0.985 0.987 0.989
VL 1.787 1.790 1.793 1.797 1.800
<111> VS1 = VS2 1.158 1.190 1.221 1.251 1.281
VL 1.840 1.852 1.865 1.877 1.890
VS1 0.981 0.983 0.985 0.987 0.989
CfSb
<110>
VS2 1.750 1.811 1.872 1.930 1.987
Figure 1. Debye average velocity versus temperature along
<100> direction.
Figure 2. Debye velocity versus temperature along <110>
direction.
Figure 3. Debye average velocity versus temperature along
<111> direction.
direction over 20 modes and for shear wave polarized al-
ong <110> direction over 18 modes and for shear wave
polarized along <110> direction over 26 modes. The te-
mperature dependent averaged ultrasonic Grüneisen par-
ameters and averaged squares of the Grüneisen param-
eters are presented in Table 4.
The values of average Grüneisen parameters and aver-
aged squares of the Grüneisen parameters are the highest
for CfSb and lowest for CfN along <110> direction for
longitudinal waves and shear as shown in Table 4. It is
obvious from Table 4, that CfSb is better for thermal
purposes for longitudinal wave propagation along <110>
direction and CfN would be better for shear wave
propagation. It is found that obtained values of Grüneisen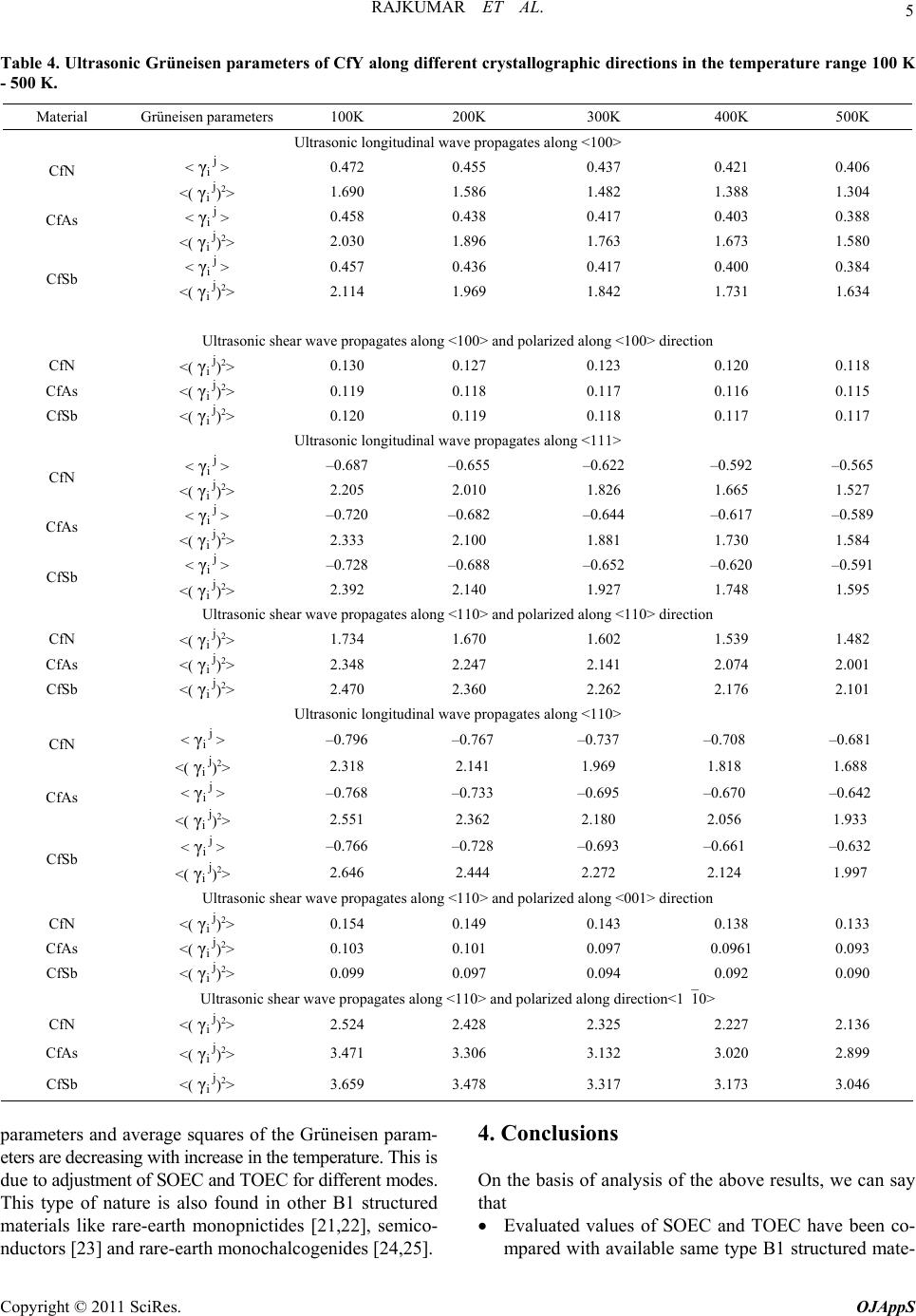

5 RAJKUMAR ET AL.
Table 4. Ultrasonic Grüneisen parameters of CfY along different crystallographic directions in the temperature range 100 K
- 500 K.
Material Grüneisen parameters 100K 200K 300K 400K 500K
Ultrasonic longitudinal wave propagates along <100>
< γi j > 0.472 0.455 0.437 0.421 0.406
CfN
<( γi j)2> 1.690 1.586 1.482 1.388 1.304
< γi j > 0.458 0.438 0.417 0.403 0.388
CfAs
<( γi j)2> 2.030 1.896 1.763 1.673 1.580
< γi j > 0.457 0.436 0.417 0.400 0.384
CfSb <( γi j)2> 2.114 1.969 1.842 1.731 1.634
Ultrasonic shear wave propagates along <100> and polarized along <100> direction
CfN <( γi j)2> 0.130 0.127 0.123 0.120 0.118
CfAs <( γi j)2> 0.119 0.118 0.117 0.116 0.115
CfSb <( γi j)2> 0.120 0.119 0.118 0.117 0.117
Ultrasonic longitudinal wave propagates along <111>
< γi j > –0.687 –0.655 –0.622 –0.592 –0.565
CfN <( γi j)2> 2.205 2.010 1.826 1.665 1.527
< γi j > –0.720 –0.682 –0.644 –0.617 –0.589
CfAs <( γi j)2> 2.333 2.100 1.881 1.730 1.584
< γi j > –0.728 –0.688 –0.652 –0.620 –0.591
CfSb <( γi j)2> 2.392 2.140 1.927 1.748 1.595
Ultrasonic shear wave propagates along <110> and polarized along <110> direction
CfN <( γi j)2> 1.734 1.670 1.602 1.539 1.482
CfAs <( γi j)2> 2.348 2.247 2.141 2.074 2.001
CfSb <( γi j)2> 2.470 2.360 2.262 2.176 2.101
Ultrasonic longitudinal wave propagates along <110>
< γi j > –0.796 –0.767 –0.737 –0.708 –0.681
CfN
<( γi j)2> 2.318 2.141 1.969 1.818 1.688
< γi j > –0.768 –0.733 –0.695 –0.670 –0.642
CfAs
<( γi j)2> 2.551 2.362 2.180 2.056 1.933
< γi j > –0.766 –0.728 –0.693 –0.661 –0.632
CfSb <( γi j)2> 2.646 2.444 2.272 2.124 1.997
Ultrasonic shear wave propagates along <110> and polarized along <001> direction
CfN <( γi j)2> 0.154 0.149 0.143 0.138 0.133
CfAs <( γi j)2> 0.103 0.101 0.097 0.0961 0.093
CfSb <( γi j)2> 0.099 0.097 0.094 0.092 0.090
Ultrasonic shear wave propagates along <110> and polarized along direction<110>
CfN <( γi j)2> 2.524 2.428 2.325 2.227 2.136
CfAs <( γi j)2> 3.471 3.306 3.132 3.020 2.899
CfSb <( γi j)2> 3.659 3.478 3.317 3.173 3.046
parameters and average squares of the Grüneisen param-
eters are decreasing with increase in the temperature. This is
due to adjustment of SOEC and TOEC for different modes.
This type of nature is also found in other B1 structured
materials like rare-earth monopnictides [21,22], semico-
nductors [23] and rare-earth monochalcogenides [24,25].
4. Conclusions
On the basis of analysis of the above results, we can say
that
 Evaluated values of SOEC and TOEC have been co-
mpared with available same type B1 structured mate-

RAJKUMAR ET AL.
6
rials, which are in agreement; hence our approach to
compute elastic constants is justified.
 SOEC and TOEC of CfN are highest so mechanical
properties will be better than other CfY.
 All the chosen materials follow the Born criterion of
stability. So they all are stable.
 SOEC and TOEC have been used to find out the ul-
trasonic velocities for longitudinal and shear waves,
Debye average velocity and Grüneisen parameters in
CfY.
 Ultrasonic velocity is found to be the highest for
CfAs along all chosen directions, so CfAs will be the
most suitable compound for wave propagation.
 CfSb is better for longitudinal wave propagation
along <110> direction and CfN would be better for
thermal purposes, because Grüneisen parameters are
the most sensitive to temperature.
Hence, we conclude that current approach is justified
and obtained results will be useful for finding various
theoretical, experimental investigations like ultrasonic
attenuation, non-linearity parameters, ultrasonic measu-
rements, polarizing microscopy, solid state NMR, SEM,
TEM.
5. Acknowledgements
The authors are thankful to Prof. Dr. R.R. Yadav, De-
partment of Physics, University of Allahabad for his sti-
mulating discussion and encouragement for the work.
6. References
[1] A.K. Pandey, B.K. Pandey and Rahul, “Theoretical predi-
ction of Grüneisen parameters for bulk metallic glasses”,
Journal of Alloys and Compounds, Vol. 509, No.11, 2011,
pp. 4191-4197.
[2] V.P. Singh and M.P. Hemkar, “Dynamical theory for
Grüneisen parameters in fcc metals”, Journal of Physics F
and Metal Physics, Vol. 7, No. 5, 1977, pp. 761-769.
[3] D.N. Joharpurkar and M.A. Breazeale, “Nonlinearity
parameters, nonlinearity constant and frequency depend-
ence of ultrasonic attenuation in GaAs”, Journal of Ap-
plied Physics, Vol. 67, No. 1, 1999, pp. 76-80.
[4] D. Singh, D.K. Pandey, D.K. Singh and R.R. Yadav,
“Propagation of ultrasonic waves in neptunium mono-
chalcogenides”, Applied Acoustics, Vol.72, No. 10, 2011,
[5] R.G. Haire and R.D. Gand Baybarz, “Crystal structure
and melting point of metal”, Journal of Inorganic and
Nuclear Chemistry, Vol. 36, No. 6, 1974, pp. 1295-1302.
[6] D. Damien, R.G. Haire and J.R. Peterson, “Cf-249
monoarsenide and monoantimonide”, Inorganic and Nu-
clear Chemistry Letters, Vol. 16, No. 9-12, 1980,
pp.537-41.
[7] S.E. Nave, J.R. Moore, M. T. Spaar, R.G. Haire and P.G.
Huray, “Magnetic susceptibility of Cf oxides”, Physica B,
Vol. 130, No. 1-3, 1985, pp. 225-227.
[8] S.E. Nave, J. R Moore, R.G Haire, J.R Peterson, D.A.
Damien and P.G Huray, “Magnetic susceptibility of CfN ,
CfAs and CfSb” , Journal of Less Common Metals, Vol.
121, 1986, pp. 319-24.
[9] M. Born and J. E. Mayer, “Zur Gittertheorie der Ionenk-
ristalle”, Zeitschrift für Physik, Vol. 75, No. 1-21931, pp.
1-18.
[10] K. Brugger, “Thermodynamic definition of higher elastic
coefficients”, Physical Review, Vol. 133, No. 6A, 1964,
pp. A1611-A1612.
[11] G. Leibfried and H. Haln, “Zur temperaturabhangigkeit
der elastischen konstantaaen von al-halihalogenidkris-
tallen”, Zeitschrift für Physik, Vol. 150, 1958, pp. 497-
525.
[12] G. Leibfried and W. Ludwig, “Theory of anharmonic
effect in crystal”, Solid State Physics XII, in: F. Seitz, D.
Turnbull (Eds.). Academic Press, New York 1961, pp.
276-444.
[13] S. Mori and Y. Hiki, “Calculations of third order elastic
constants and forth order elastic constants of alkali hal-
ides crystals”, Journal of Physical Society of Japan, Vol.
45, 1978, pp. 1449-1456.
[14] R.W.F. Wyckoff, Crystal Structure, Interscience Publica-
tion, New York, 1963.
[15] D. Singh, Rajkumar, D.K. Pandey, “Temperature and
orientation dependence of ultrasonic parameters in am-
ericium monopnictides”, Advances in Materials Physics
and Chemistry, Vol.1, No. 2, 2011, pp. 31-38.
[16] R. Nava and J. Romero, “Ultrasonic Grüneisen parame-
ters for non conducting cubic crystals”, Journal of Acous-
tical Society of America, Vol. 64, No. 2, 1978, pp. 529-
532.
[17] K. Brugger, “Generalized Grüneisen parameters in ani-
sotropic Debye model”, Physical Review, Vol. 137, No.
6A, 1965, pp. A1826-A1827.
[18] S.D. Lambade, G.G. Sahasrabudhe and S. Rajagopalan,
“Temperature dependence of acoustic attenuation in sili-
con”, Physical Review B, Vol. 51, No. 22, 1995, pp.
15861-158866.
[19] W.P. Mason, “Effect of impurities and phonon processes
on the ultrasonic attenuation in germanium crystal quartz
and silicon”, Physical Acous-tics IIIB, Academic Press,
New York, 1965, pp. 237-285.
[20] M.P. Tosi, Cohesion of ionic solids in Born model, in:
Solid State Physics, Vol.16, F. Seitz, D. Turnbull (Eds.),
(Academic Press, New York, 1964) pp. 1-120.
[21] D. Singh, S. Tripathi, D.K. Pandey, A.K. Gupta, D.K.
Singh and J. Kumar, “Ultrasonic wave propagation in
semimetallic single crystals”, Modern Physics Letters B,
Vol. 25, No. 31, 2011, pp. 2377-2390.
[22] R.R. Yadav, A.K. Tiwari and D. Singh, “Effect of pres-
sure on ultrasonic attenuation in Ce-monopnictides at low

RAJKUMAR ET AL.
7
temperature”, Journal of Materials Science, vol. 40, No.
19, 2005, pp. 5319-5321.
[23] D. Singh, R.R. Yadav and A.K. Tiwari, “Ultrasonic at-
tenuation in semiconductors”, Indian Journal of Pure and
Applied Physics, Vol. 40, No. 12, 2002, pp. 845-849.
[24] D. Singh, D.K. Pandey and P.K. Yadawa, “Ultra-sonic
wave propagation in rare-earth monochalcogenides”,
Central European Journal of Physics, Vol. 7, No. 1, 2009,
pp. 198-205.
[25] R.R. Yadav and D. Singh, “Effect of thermal
con-ductivity on ultrasonic attenuation in praseodymium
monochalcogenides”, Acoustical Physics, Vol. 49, No. 5,
2005, pp. 595-604.