 Advances in Materials Physics and Chemistry, 2011, 1, 86-90 doi:10.4236/ampc.2011.13014 Published Online December 2011 (http://www.SciRP.org/journal/ampc) Copyright © 2011 SciRes. AMPC Band Gaps and Single Scattering of Phononic Crystal* Xiaoyi Huang1#, Jingcui Peng2, Huanyou Wang1, Gui Jin1 1Department of Physics, Xiangnan University, Chenzhou, China 2Department of Applied Physics, Hunan University, Changsha, China E-mail: #jghxy@126.com Received August 28, 2011; revised September 29, 2011; accepted October 11, 2011 Abstract A method is introduced to study the transmission and scattering properties of acoustic waves in two-dimen- sional phononic band gap (PBG) materials. First, it is used to calculate the transmission coefficients of PBG samples. Second, the transmitted power is calculated based on the far field approach. We have also calcu- lated the scattering cross section, the results indicate that phononic band gap appear in frequency regions between two well separated resonance states. Keywords: Phononic Crystal, Band Gap, Single Scattering 1. Introduction The acoustic properties of a locally homogeneous and isotropic composite material is characterized by a set of parameters varying in space: mass densityρ, Lamé coef- ficients λ, and μ. In this paper we focus on the composite materials, which consist of homogeneous particles dis- tributed periodically in a host medium. They are charac- terized by different mass densities and Lamé coefficients. When identical particles are distributed periodically in a host medium, the composite material may be referred to as a phononic crystal. Recently the propagation of elastic or acoustic waves (EL or AC wave) in a phononic crystal has received much renewed attention [1-9]. These new materials can be of real interest since a large contrast between the elastic parameters is allowed. For example, systems composed of very soft rubber [10] are more likely to obtain the low-frequency gaps with a structure of small dimension. This can lead to promising applica- tions such as a low-frequency vibration/noise devices such as lenses and acoustic interferometers [11]. On the other hand, more sophisticated combinations such as fluids infiltrated in a drilled solid [5] or solid-solid sys- tems [7] have been demonstrated to produce a full pho- nonic band gap for ultrasounds. Phononic crystal make possibility of the achievement of complete frequency band gaps that are useful to prohibit specific vibrations in accurate technologies such as transducers and sonar. In the plane-wave expansion method, the finite differ- ence time domain and the multiple-scattering theory are commonly used in order to study the elastic response of phononic crystal [12-15]. In this work, in order to study the propagation of acoustic waves in phononic crystal, we consider a two-dimensional periodic system consist- ing of finite cylinders of circular cross section. The sys- tem is periodic in the x-y plane and within it there is a translational invariance in the direction (z) parallel to the cylinders. The intersection of the cylinders with a trans- verse plane makes a square lattice. We treated finite PBG samples as scattering objects in open geometry, The ra- diation boundary condition was naturally imposed. Con- sidering the far-field approach, we have independently adopted this method to study the transmission and scat- tering properties of finite PBG samples. In the case of transmission, a generalized transmission coefficient can be defined in terms of the far-field total scattering am- plitude, from the total scattering amplitude we can re- trieve the dispersion relations and the decay length inside a gap. By adopted this method, the incident field, scat- tered field and the total scattering amplitude become very simple form, the calculating can be extremely sim- plified. We explicitly demonstrate that this method can produce transmission results that are in excellent quanti- tative agreements with the available experimental data. 2. Model and Formula The displacement vector ,tUr in a homogeneous elastic medium of mass density ρ and Lamé coefficients λ, μ satisfies the following equation: *Supported by the Key Project of Education Department of Hunan Province (09A086), Science and Technology Project of Chenzhou.  X. Y. HUANG ET AL.87 2 20 t UUU it (1) In the case of a harmonic elastic wave with angular frequency ω, we have ,Re expt Ur Ur, (2) and Equation (1) was reduced to the following time-in- dependent form 2 2 uu0u. (3) Defining ulmn, (4) where l, (5) m Z Z , (6) n, (7) where is the unit vector along the z-axis. Z , χ and ψ are the displacement potential functions of longitudinal and two transverse waves respectively. The displacement potential function of the incident longitudinal waves can be expanded in terms of the cylindrical Bessel Function [16] exp exp n inczn lr jk zjJkrjn , (8) where 12 22 lrl z kkk is the radial component of the incident wave vector, Jn is the Bessel function of the first kind of order n, kz is the z-axis component of the incident wave vector; kl is the longitudinal wave numbers, r is the normal distance of the field spot away from z-axis; and θ is the angle of direction. The displacement potential functions of the longitudi- nal and transverse scattered waves can also be expanded: exp exp sczn nlr n jkzA Hkrjn , (9) exp exp sczn nlr n jkzBHkrjn , (10) exp exp sczn nlr n jk zC Hkrjn , (11) where Hn is the Hankel function. Using the same method we can expand the displacement potential functions of the incident transverse waves in terms of the cylindrical Bessel functions. Therefore the displacement potential functions of the incident transverse waves inside the cyl- inders are expanded as: 0 0 exp exp inznnlrn n n nn trnn jkzA HkrD BJ k rEjn (12) 0 0 exp exp inznnlrn n n nn trnn jkzA JkrD BJ k rEjn (13) 0 exp exp inznnlrn n n jk zC JkrFjn (14) where nn F are coefficients and 12 22 trt z kkk . In the following we consider a sample of the two-di- mensional periodic arrays system. The sample was made of d-radius rods with lattice constant a. The position of the rod with index j corresponds to , jj r r. What are around this rod are incident waves involving external sources and scattered waves from other rods. The total field around this rod is inc scatt uu u . The coefficients nn F are defined depending on the boundary conditions. In the light of the continuity of the displacements, there are :,, inc scin iii rd rdrd uuu ir z , (15) Due to the continuity of the stresses, there exists: :,, inc scin iii rd rdrd pppir z z , (16) where ,: ,, iijj j pnijr and 222 22,,: ijt ijttijll l cuccui jlrz ,,. where σij are the stress tensor elements and uij are the strain tensor elements that result from the components of the displacement vector. The superscripts inc, sc, in, de- note the incident, the scattered and the inner field respec- tively. In the far field, when , 1 lt kr kr exp scatt s uf rikrr. The total scattering amplitude of the longitudinal waves from Equations (9)-(11) is 2exp π nN sn n l fjA kjn . (17) For acoustic wave transmission, a slit with width w along the y direction is put between a source and the sample. Acoustic waves propagate along x direction. In this case, the incident field can be obtained from the Kirchoff integral formula [17]: 2 01 2 ,d 4 w l incl l w kx uxy yHkriHkr r , (18) where 2 2 rxyy , in the case of far field, Copyright © 2011 SciRes. AMPC  X. Y. HUANG ET AL. 88 when , Equation (18) becomes rw 0 ua exp inc l ikrr r with π42 0 2sin2 sin ecos2 2πsin l il l kw k ak . (19) The vector of energy flux density is: Im 8πl cuu k rrr. (20) Therefore the far-field energy flux has the form 0 ,8π s ca fr rS r r Sr . (21) So we define a transmission coefficient as the ratio of transmission energy flux to that of the incident wave at 0 . Therefore: 2 2 π4 2 0 02π 11e 0 si s l f T akw 0f. (22) According to Equation (17) and the definition of scat- tering cross section, the dimensionless scattering cross sections of the longitudinal and transverse scattered waves have the form: 2 2 1 0 1 1 ˆt lnn n ll c a kd c 2 n b (23) 2 22 1 0 1 1 ˆl tnn n tt cab kd c n (24) where ˆl and ˆt are the scattering cross sections for longitudinal and transverse incident wave respectively, kl and kt are the longitudinal and transverse wave numbers for the host, cl1 and ct1 are the longitudinal and transverse wave velocities for the host, d is the diameter of cylinder, an and bn are the longitudinal and transverse scattered wave coefficients. For elastic media, there is a reasonable amount of cal- culations for infinite systems [18-20]. However, systems are finite and there are boundaries. Therefore under a proper choice of parameters, states sliding and propagat- ing along the surface and localized in the normal to the surface, i.e., should appear, these are analogous to elec- tronic surface in crystals [21] and to those calculated for photonic systems [22]. According to M. Torres et al. that surface state solutions are consubstantial with finite sys- tems and exist for sonic propagation in finite elastic me- dia. They deal with several realizations of structures for ultrasonic propagation in elastic media to observe such surface state modes and localization phenomena in linear and point defects [3]. 3. Numerical Results In this paper, the finite-sized PBG sample used in the calculation consisted of 6 rows along the x axis, 36 col- umn rods with steel rods arranged in air host as square with the lattice constant a, with filling fraction of f = 0.55, rod radius mains = 0.35a, and a room of temperature 25˚C. The mass density of phononic crystal is ρ = 7800 g/cm3, longitudinal wave velocity cl = 5940 m/s, trans- verse wave velocity ct = 3220 m/s [23], width of slit w = 3.5a, and is placed at a distance of l = 2.1a. From Equa- tion (22) we have calculated the transmission coefficient and total transmitted power as π 2 0 2 T Psd . Figure 1 shows the calculated results of transmission coefficient and total transmitted power, in dimensionless frequency region (1.75 to 2.25). Acoustic wave propaga- tion is inhibited forming frequency band gaps. The transmission coefficient curve is finite and total trans- mitted power becomes zero. The results are in excellent agreement with previous results from Ref. [1]. Taking T ≈ 0 in Equation (22) which gives 0 s afwa inside the bands 0 s f show large variations in frequency. This is related to the phase shift of the scattered waves, if we assuming 1T 0 002sin2exp s fa ii 2 and 02sin2 s af wa , where Φ is the phase difference between outgoing and incoming waves. Φ changes rapidly near band edges. The derivative of Φ(f) gives information on group velocity vg. At band edge, dΦ/df diverges and vg approaches zero. Therefore from fs(0) we are able to extract the effective elastic constant for frequencies inside a band and the decay length for frequencies inside a gap. (a) (b) 6 5 4 3 2 1 0 Figure 1. Acoustic band structure and transmission coeffi- cients and total transmitted power for a square array of rigid stainless steel cylinders in air host. The filling fraction is f = 0.55. (a) The band structures reproduced from Ref. [1]; (b) Solid curves: transmission coefficients. Dashed curves: total transmitted power. Copyright © 2011 SciRes. AMPC 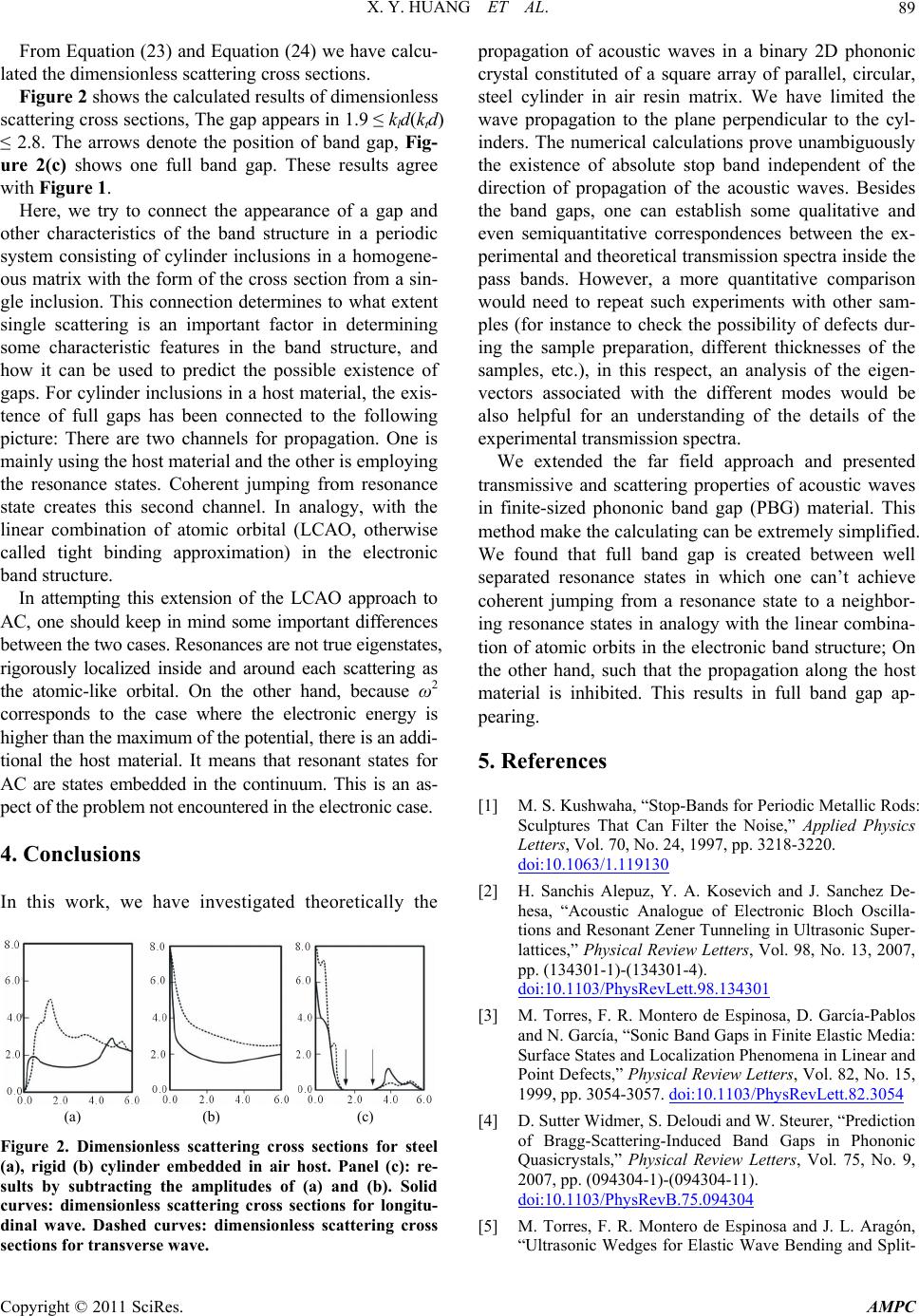 X. Y. HUANG ET AL.89 From Equation (23) and Equation (24) we have calcu- lated the dimensionless scattering cross sections. Figure 2 shows the calculated results of dimensionless scattering cross sections, The gap appears in 1.9 ≤ kld(ktd) ≤ 2.8. The arrows denote the position of band gap, Fig- ure 2(c) shows one full band gap. These results agree with Figure 1. Here, we try to connect the appearance of a gap and other characteristics of the band structure in a periodic system consisting of cylinder inclusions in a homogene- ous matrix with the form of the cross section from a sin- gle inclusion. This connection determines to what extent single scattering is an important factor in determining some characteristic features in the band structure, and how it can be used to predict the possible existence of gaps. For cylinder inclusions in a host material, the exis- tence of full gaps has been connected to the following picture: There are two channels for propagation. One is mainly using the host material and the other is employing the resonance states. Coherent jumping from resonance state creates this second channel. In analogy, with the linear combination of atomic orbital (LCAO, otherwise called tight binding approximation) in the electronic band structure. In attempting this extension of the LCAO approach to AC, one should keep in mind some important differences between the two cases. Resonances are not true eigenstates, rigorously localized inside and around each scattering as the atomic-like orbital. On the other hand, because ω2 corresponds to the case where the electronic energy is higher than the maximum of the potential, there is an addi- tional the host material. It means that resonant states for AC are states embedded in the continuum. This is an as- pect of the problem not encountered in the electronic case. 4. Conclusions In this work, we have investigated theoretically the (a) (b) (c) Figure 2. Dimensionless scattering cross sections for steel (a), rigid (b) cylinder embedded in air host. Panel (c): re- sults by subtracting the amplitudes of (a) and (b). Solid curves: dimensionless scattering cross sections for longitu- dinal wave. Dashed curves: dimensionless scattering cross sections for transverse wave. propagation of acoustic waves in a binary 2D phononic crystal constituted of a square array of parallel, circular, steel cylinder in air resin matrix. We have limited the wave propagation to the plane perpendicular to the cyl- inders. The numerical calculations prove unambiguously the existence of absolute stop band independent of the direction of propagation of the acoustic waves. Besides the band gaps, one can establish some qualitative and even semiquantitative correspondences between the ex- perimental and theoretical transmission spectra inside the pass bands. However, a more quantitative comparison would need to repeat such experiments with other sam- ples (for instance to check the possibility of defects dur- ing the sample preparation, different thicknesses of the samples, etc.), in this respect, an analysis of the eigen- vectors associated with the different modes would be also helpful for an understanding of the details of the experimental transmission spectra. We extended the far field approach and presented transmissive and scattering properties of acoustic waves in finite-sized phononic band gap (PBG) material. This method make the calculating can be extremely simplified. We found that full band gap is created between well separated resonance states in which one can’t achieve coherent jumping from a resonance state to a neighbor- ing resonance states in analogy with the linear combina- tion of atomic orbits in the electronic band structure; On the other hand, such that the propagation along the host material is inhibited. This results in full band gap ap- pearing. 5. References [1] M. S. Kushwaha, “Stop-Bands for Periodic Metallic Rods: Sculptures That Can Filter the Noise,” Applied Physics Letters, Vol. 70, No. 24, 1997, pp. 3218-3220. doi:10.1063/1.119130 [2] H. Sanchis Alepuz, Y. A. Kosevich and J. Sanchez De- hesa, “Acoustic Analogue of Electronic Bloch Oscilla- tions and Resonant Zener Tunneling in Ultrasonic Super- lattices,” Physical Review Letters, Vol. 98, No. 13, 2007, pp. (134301-1)-(134301-4). doi:10.1103/PhysRevLett.98.134301 [3] M. Torres, F. R. Montero de Espinosa, D. García-Pablos and N. García, “Sonic Band Gaps in Finite Elastic Media: Surface States and Localization Phenomena in Linear and Point Defects,” Physical Review Letters, Vol. 82, No. 15, 1999, pp. 3054-3057. doi:10.1103/PhysRevLett.82.3054 [4] D. Sutter Widmer, S. Deloudi and W. Steurer, “Prediction of Bragg-Scattering-Induced Band Gaps in Phononic Quasicrystals,” Physical Review Letters, Vol. 75, No. 9, 2007, pp. (094304-1)-(094304-11). doi:10.1103/PhysRevB.75.094304 [5] M. Torres, F. R. Montero de Espinosa and J. L. Aragón, “Ultrasonic Wedges for Elastic Wave Bending and Split- Copyright © 2011 SciRes. AMPC  X. Y. HUANG ET AL. Copyright © 2011 SciRes. AMPC 90 ting without Requiring a Full Band Gap,” Physical Re- view Letters, Vol. 86, No. 19, 2001, pp. 4282-4285. doi:10.1103/PhysRevLett.86.4282 [6] D. Garcia-Pablos, F. R. Montero de Espinosa, M. Torres, M. Kafesaki and N. García, “Theory and Experiments on Elastic Band Gaps,” Physical Review Letters, Vol. 84, No. 19, 2000, pp. 4349-4352. doi:10.1103/PhysRevLett.84.4349 [7] J. O. Vasseur, P. A. Deymier, B. Djafari-Rouhani, L. Dobrzynski and D. Prevost, “Experimental and Theoreti- cal Evidence for the Existence of Absolute Acoustic Band Gaps in Two-Dimensional Solid Phononic Crys- tals,” Physical Review Letters, Vol. 86, No. 14, 2001, pp. 3012-3015. doi:10.1103/PhysRevLett.86.3012 [8] S. X. Yang, J. H. Page, Z. Y. Liu, M. L. Cowan, C. T. Chan and P. Sheng, Physical Review Letters, Vol. 88, No. 10, 2001, pp. (104301-1)-(104301-4). [9] S. X. Yang, J. H. Page, Z. Y. Liu, M. L. Cowan, C. T. Chan and P. Sheng, Physical Review Letters, Vol. 93, No. 2, 2004, pp. (024301-1)-(024301-4). [10] Z. Y. Liu, X. X. Zhang, Y. W. Mao, Y. Y. Zhu, Z. Y. Yang, C. T. Chan and P. Sheng, “Locally Resonant Sonic Materials,” Science, Vol. 289, No. 8, 2000, pp. 1734- 1736. doi:10.1126/science.289.5485.1734 [11] F. Cervera, L. Sanchis, J. V. Sánchez-Pérez, R. Martínez- Sala, C. Rubio, F. Meseguer, C. López, D. Caballero and J. Sánchez-Dehesa, Physical Review Letters, Vol. 88, No. 2, 2002, pp. (023902-1)-(023902-4). [12] M. S. Kuswaha, Applied Physics Letters, Vol. 2, 1999, pp. 743-755. [13] C. Goffaux and J. Sanchez-Dehesa, “Two-Dimensional Phononic Crystals Studied Using a Variational Method: Application to Lattices of Locally Resonant Materials,” Physical Review B, Vol. 67, No. 14, 2003, pp. (144301- 1)-(144301-10). doi:10.1103/PhysRevB.67.144301 [14] Y. Y. Chen and Z. Ye, “Theoretical Analysis of Acoustic Stop Bands in Two-Dimensional Periodic Scattering Ar- rays,” Physical Review E, Vol. 64, No. 3, 2001, pp. (036616-1)-(036616-6). doi:10.1103/PhysRevE.64.036616 [15] Y. Tanaka, Y. Tomoyasu and S. I. Tamura, Physical Re- view B, Vol. 62, 2000, pp. 7383-7395. [16] R. M. White, Journal of the Acoustical Society of Amer- ica, Vol. 30, No. 8, 1958, pp. 771-785. [17] J. D. Jackson, “Classica Electrodynamics,” Wiley, New York, 1975. [18] M. M. Sigalas and E. N. Economou, Journal of Sound and Vibration, Vol. 158, No. 2, 1992, pp. 377-382. [19] E. N. Economou and M. M. Sigalas, “Classical Wave Propagation in Periodic Structures: Cermet versus Net- work Topology,” Physical Review B, Vol. 48, No. 18, 1993, pp. 13434-13438. doi:10.1103/PhysRevB.48.13434 [20] M. M. Sigalas and E. N. Economou, “Attenuation of Multiple-Scattered Sound,” Europhysics Letters, Vol. 36, No. 4, 1996, pp. 241-246. doi:10.1209/epl/i1996-00216-4 [21] C. Kittel, “Introduction to Solid State Physics,” Wiley, New York, 1971. [22] R. D. Meade, K. D. Brommer, A. M. Rappe and J. D. Joannopoulos, “Electromagnetic Bloch Waves at the Sur- face of a Photonic Crystal,” Physical Review B, Vol. 44, No. 19, 1991, pp. 10961-10964. doi:10.1103/PhysRevB.44.10961 [23] M. Kafesaki and E. N. Economou, “Interpretation of the Band-Structure Results for Elastic and Acoustic Waves by Analogy with the LCAO Approach,” Physical Review B, Vol. 52, No. 18, 1995, pp. 13317-13331. doi:10.1103/PhysRevB.52.13317
|