Applied Mathematics, 2011, 2, 1479-1485
doi:10.4236/am.2011.212210 Published Online December 2011 (http://www.SciRP.org/journal/am)
Numerical Solution of Nonlinear Klein-Gordon Equation
Using Lattice Boltzmann Method
Qiaojie Li1, Zong Ji2, Zhoushun Zheng1, Hongjuan Liu1
1School of Mathematical Science and Computing Technology, Central South University, Changsha, China
2Modern Service and Trade College, Yunnan University of Finance and Economics, Kunming, China
Received October 24, 2011; revised November 24, 2011; accepted December 1, 2011
Abstract
In this paper, in order to extend the lattice Boltzmann method to deal with more nonlinear equations, a one-
dimensional (1D) lattice Boltzmann scheme with an amending function for the nonlinear Klein-Gordon
equation is proposed. With the Taylor and Chapman-Enskog expansion, the nonlinear Klein-Gordon equa-
tion is recovered correctly from the lattice Boltzmann equation. The method is applied on some test exam-
ples, and the numerical results have been compared with the analytical solutions or the numerical solutions
reported in previous studies. The L2, L∞ and Root-Mean-Square (RMS) errors in the solutions show the effi-
ciency of the method computationally.
Keywords: Lattice Boltzmann, Chapman-Enskog Expansion, Nonlinear Klein-Gordon Equation
1. Introduction
Nonlinear phenomena modeled by partial differential
equation appear in many areas of scientific fields such as
solid state physics, plasma physics, fluid dynamics, ma-
thematical biology and chemical kinetics. The nonlinear
Klein-Gordon equation has attracted much attention in
studying solutions and condensed mater physics, in in-
vestigating the interaction of solitons in a collisionless
plasma, the recurrence of initial states, and in examining
the nonlinear wave equations [1,2]. In the last few de-
cades, many powerful methods, such as the inverse sca-
ttering method, Baklund transformation, the auxiliary
equation method [3,4], the Wadati trace method, Hirota
bilinear forms, the tanh-sech method, the sine-cosine me-
thod, Jacobi elliptic functions, and the Riccati equation
expansion method were used to investigate these types of
equations (see [5] and references therein). A variety of
finite difference scheme have been presented (see [6] and
references therein) and the alternative approaches using
spectral and pseudo-spectral methods have recently been
presented [7,8]. To avoid the mesh generation, meshless
techniques have attracted the attention of researchers in
recent years. The radial basis function (RBF) as a truly
meshless method was used to solve nonlinear Klein-Gor-
don equation in [9].
Recently, unlike convectional numerical methods which
search for the macroscopic equation, the lattice Boltzmann
method (LBM) has achieved much success in studying
nonlinear equations and the evolution of complex systems
[10,11]. By choosing appropriate collision or equilibrium
distribution, the lattice Boltzmann model is able to recover
the PDE of interest. This method is a new technique based
on a mesoscopic kinetic equation for the particle distri-
bution functions. Compared with the conventional nume-
rical methods, the LBM provides many of the advantages,
including geometrical flexibility, clear physical pictures,
ease in incorporating complex boundary conditions, simpli-
city of programming and numerical efficiency. Recently, it
has been developed to simulate linear and nonlinear PDE
such as Laplace equation [12], Poisson equation [13,14],
the shallow water equation [15], Burgers equation [16],
Korteweg-de Vires equation [17], Wave equation [18,19],
reaction-diffusion equation [20,21], convection-diffusion
equation [22-24].
In this paper, the initial-value problem of the one-dimen-
sional nonlinear Klein-Gordon equations is given by the
following equation,
() (,)
tt xx
uugufxt


 (1)
where (,)uuxt

represents the wave displacement at
position x and time t,

is a known constant and ()
g
u
is the nonlinear force.
The present work is motivated by the desire to extend

Q. J. LI ET AL. 1480
the lattice Boltzmann method to deal with evolution
models characterized by nonlinear wave dispersion. By
using Taylor expansion and the Chapman-Enskog expan-
sion, the second-order nonlinear Klein-Gordon equation
can be recovered from the present model correctly. The
local equilibrium distribution function and the amending
function are obtained. To make a comparison between
numerical solutions and analytical ones, four Klein-Gor-
don equations with quadratic or cubic nonlinearity are
considered. From the simulations, we find that the nu-
merical results are in excellent agreement with the ana-
lytical solutions. This indicates that the present method is
an efficient and flexible approach for practical applica-
tion.
The organization of the paper as follows. In Section 2,
the lattice Boltzmann model is described. Numerical
examples are simulated in Section 3. Summary and con-
clusion are presented in Section 4.
2. The Lattice Boltzmann Model
The lattice Boltzmann model used on this study is the
three-velocity lattice Bhatnagar-Gross-Krook (LBGK)
model. The directions of the discrete velocity are defined
as ()
i
c0,1, 2i
012
[,, ][0,,]ccc cc.
where c is a constant. The lattice Boltzmann equation
with an amending function is given as follow

,(,)
1(,) (,)(,)
ii i
eq
ii i
fxcttt fxt
f
xtfxttF xt

 

 

(2)
where (,)
i
f
xt and i(,)
eq
f
xt are defined as the distri-
bution and equilibrium distribution function, respectively.
i(,)
F
xt is an amending function and

is the dimen-
sionless relaxation time. i
x
ct  and are the
lattice spacing and time step, respectively.
t
Unlike for the normal LBM, the first derivative of the
macroscopic variable meets the following con-
servation laws
(,)uxt
(,)
(,) (,)
i
eq
i
ii
uxt
fxtf xtt



 (3)
Then, through choosing appropriate local equilibrium
distributions, we can retrieve the corresponding macro-
scopic equation correctly.
Indeed, applying the Taylor expansion to left-hand
side of Equation (2) and retaining terms up to 3
()t

,
we get

2
2
3
2
1
() i
iii
eq
ii
t
tcf cf
xt xt
tfft

 

 

 

 
The macroscopic equation can be recovered in the
multi-scale analysis using a small expansion parameter

which is proportional to the ration of the lattice spac-
ing to the characteristic macroscopic length. To do this,
the Chapman-Enskog expansion in time and space is
applied:
(1)2(2)2(2)
2
12 1
,
,
eq
iiii ii
f
ff fFF
tt txx
 
 
 
 
 
 
(5)
where ()k
i
f
and (2)
i
F
are the non-equilibrium distribu-
tion functions and non-equilibrium amending function,
which satisfy the solvability conditions
()
(2) (2)
0( 1)
k
i
i
i
i
fk
FF



 (6)
Substituting Equation (5) into (4), we have



2(1)2(2)
11 2
2
2(1)
11 2
(1)2( 2 )2( 2 )
2
1
eq
iii
eq
iii
ii i
cfff
xt t
tcff
xt t
ff F


 


 
 

 





 

 
2(2)
i
i
f (7)
Comparing the two sides of Equation (7) and treating
terms in order of

and 2

gives
(1)
11
1
():ii
eq
i
cf
xt t





 

f (8)
2(
211
2
(2) (2)
11
():
1
2
iii
ii
q
eq
ii
e
fc f
txt
tcff
xt t












 

1)
F
(9)
Applying Equation (8) to the left side of Equation (9),
we can rewrite Equation (9) as
(1)
21
(2) (2)
1
12
1
ii
q
ii
e
1
i
f
cf
tx
fF
t





 





 

t



(10)
In order to recover Equation (1), we must give appro-
priate local equilibrium distribution function. We choose
q
i
e
f
such that,
(,)
i
eq
i
uxt
ft



i
F



(4)
2
0,(, )
eq eq
iii
ii
isi
cfccf cuxt

 (11)

Q. J. LI ET AL.1481
where 22
3
s
cc is called the lattice Boltzmann sound
speed. Equation (11) leads to three linear equations for
(,)
i
eq
f
x
t. Solving these equations determines the equi-
librium distribution functions
0
1
2
(,) (,)
(,) 3
(,)
(,) 6
(,)
(,) 6
eq
eq
eq
uxt uxt
fxtt
uxt
fxt
uxt
fxt





(12)
Meanwhile, the amending function (,)
i
F
xt is taken
as

(,)(,)(,) ()
ii i
F
xtF xtfxtgu    (13)
such that (,) (,)
i
i
F
xtF xt
. For simplicity, only one
case is given here



0
1
2
2
(,)(,) ()
3
1
(,)(,) ()
6
1
(,)(,)()
6
F
xtf xtgu
F
xtf xtgu
F
xtf xtgu



(14)
Summing Equation (8) and Equation (10) over i, and
using Equation (6) and (11), we obtain
1
0
u
tt





 (15)
(1) (2)
21
1
12i
i
i
ucf F
tt x 
  
 
 
 
 
 
 (16)
Using Equation (8) and (11), we get
(1)
11
11
2
1
()(
()
eq
ii
ii
eq eq
i
ii
ii ii
i
s
cftccf
xt
t ccfcf
xt
tcu
x





 




 





 

)
i

(17)
Then substituting Equation (17) into Equation (16), we
have
2
21
1
2
s
uu
ct F
tt xx


 
 
 

 
 

(2)
1
(18)
When Equation 2
(15) (18)

  is applied, the fi-
nal nonlinear Klein-Gordon equation is recovered as
22
22
(,)(,) ()
uu
F
xtf xtgu
tx



 (19)
where 21
2
s
ct







In the computational process, in order to obtain u(x,t),
we can apply backward difference to the item (,)uxt
t


(,)(,)(,)uxtuxtuxtt
tt




(20)
3. Numerical Simulation Results
In this section, we present the result of our LBM numeri-
cal experiments for the relevant equations. In comparison
with the analytical solutions and results derived by exist-
ing literature, the efficiency of proposed model is vali-
dated. The distribution function (,)
i
f
xt is initialized
with i(,)
eq
f
xt
(,uxt
for all nodes at . The macroscopic
variable is initialized by the initial condition and
the non-equilibrium extrapolation scheme proposed by
Guo [25] is used for boundary treatment. The following
error norms are used to measure the accuracy
0t
)
1) L2-error
1
2
2
2
1
n
i
i
L errore






2) L∞-error
Max ,1
i
Lerrorei n




3) The root mean square (RMS) error
1
22
1
n
i
i
e
RMS errorn






where (,) (,)
ii i
euxtuxt
, and
are the numerical solution and analytical one.
(,)
i
ux t(,)
i
uxt

Example 1. The Klein-Gordon equation with quadratic
nonlinearity in the interval 11
x
 
22
cos cos
tt xx
uux txtu
2


The initial conditions are given by
(,0),(,0) 0
t
uxx u x


The exact solution is given in [9]
(,) cosuxt xt
We extract the boundary condition from the exact so-
lution. In Table 1, the L∞, L
2 and RMS errors are ob-
tained for 1,3, 5,7,10t

. The graph of analytical and
LBM solution for 1t

and are given in Figure
1 and the space-time graph of the LBM solution is given
in Figure 2.
10t
Example 2. Consider the nonlinear Klein-Gordon equ-
ation with quadratic nonlinearity in interval 01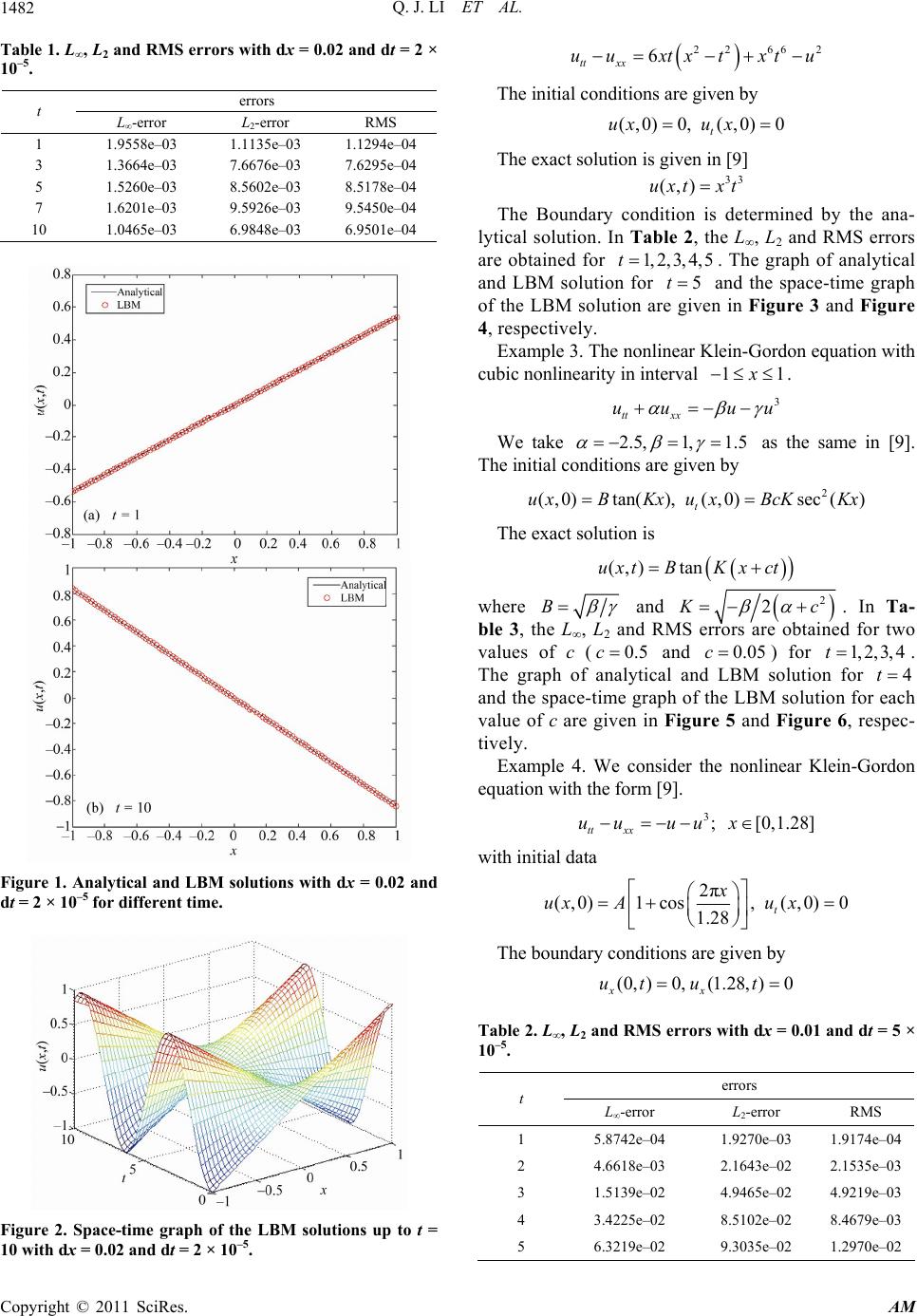
x

.

Q. J. LI ET AL. 1482
Table 1. L∞, L2 and RMS errors with dx = 0.02 and dt = 2 ×
10–5.
errors
t L∞-error L
2-error RMS
1 1.9558e–03 1.1135e–03 1.1294e–04
3 1.3664e–03 7.6676e–03 7.6295e–04
5 1.5260e–03 8.5602e–03 8.5178e–04
7 1.6201e–03 9.5926e–03 9.5450e–04
10 1.0465e–03 6.9848e–03 6.9501e–04
Figure 1. Analytical and LBM solutions with dx = 0.02 and
dt = 2 × 10–5 for different time.
Figure 2. Space-time graph of the LBM solutions up to t =
10 with dx = 0.02 and dt = 2 × 10–5.


22 66
6
tt xx
uxtxtxut 2 u


The initial conditions are given by
(,0) 0,(,0)0
t
uxu x


The exact solution is given in [9]
33
(,)uxt xt
The Boundary condition is determined by the ana-
lytical solution. In Table 2, the L∞, L2 and RMS errors
are obtained for 1, 2,3, 4,5t

. The graph of analytical
and LBM solution for 5t

and the space-time graph
of the LBM solution are given in Figure 3 and Figure
4, respectively.
Example 3. The nonlinear Klein-Gordon equation with
cubic nonlinearity in interval 11
x
 .
3
tt xx
uu uu

 
We take 2.5,1, 1.5



 as the same in [9].
The initial conditions are given by
2
( ,0)tan(),( ,0)sec()
t
uxBKxu xBcKKx
The exact solution is


(,) tanuxtBKxct
where B

 

and

2
2
K
c   . In Ta-
ble 3, the L∞, L2 and RMS errors are obtained for two
values of c (0.5c

and ) for 0.05c1,2,3,4t

.
The graph of analytical and LBM solution for 4t

and the space-time graph of the LBM solution for each
value of c are given in Figure 5 and Figure 6, respec-
tively.
Example 4. We consider the nonlinear Klein-Gordon
equation with the form [9].
3;[0,1.28]
tt xx
uu uux 
with initial data
2π
( ,0)1cos,( ,0)0
1.28 t
x
uxAu x








The boundary conditions are given by
(0, )0,(1.28,)0
xx
ut ut


Table 2. L∞, L2 and RMS errors with dx = 0.01 and dt = 5 ×
10–5.
errors
t L∞-error L
2-error RMS
1 5.8742e–04 1.9270e–03 1.9174e–04
2 4.6618e–03 2.1643e–02 2.1535e–03
3 1.5139e–02 4.9465e–02 4.9219e–03
4 3.4225e–02 8.5102e–02 8.4679e–03
5 6.3219e–02 9.3035e–02 1.2970e–02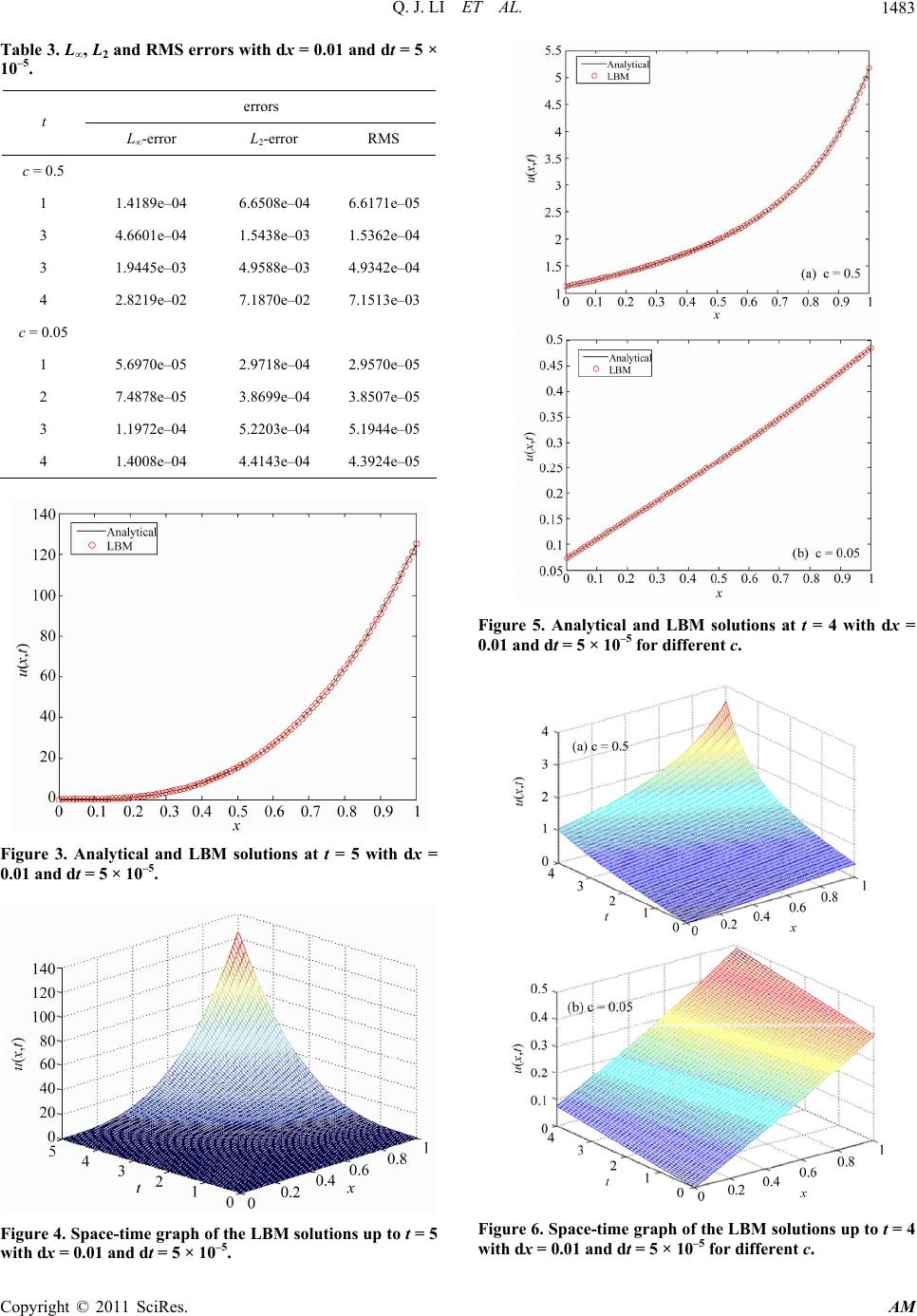

Q. J. LI ET AL.1483
Table 3. L∞, L2 and RMS errors with dx = 0.01 and dt = 5 ×
10–5.
errors
t
L∞-error L
2-error RMS
c = 0.5
1 1.4189e–04 6.6508e–04 6.6171e–05
3 4.6601e–04 1.5438e–03 1.5362e–04
3 1.9445e–03 4.9588e–03 4.9342e–04
4 2.8219e–02 7.1870e–02 7.1513e–03
c = 0.05
1 5.6970e–05 2.9718e–04 2.9570e–05
2 7.4878e–05 3.8699e–04 3.8507e–05
3 1.1972e–04 5.2203e–04 5.1944e–05
4 1.4008e–04 4.4143e–04 4.3924e–05
Figure 3. Analytical and LBM solutions at t = 5 with dx =
0.01 and dt = 5 × 10–5.
Figure 4. Space-time graph of the LBM solutions up to t = 5
–5
Figure 5. Analytical and LBM solutions at t = 4 withx = d
0.01 and dt = 5 × 10–5 for different c.
Figure 6. Space-time graph of the LBM solutions up to t = 4
with dx = 0.01 and dt = 5 × 10–5 for different c.
with dx = 0.01 and dt = 5 × 10.

Q. J. LI ET AL. 1484
boundary
co
7
. Conclusions
the current study, a new lattice Boltzmann model is
his work was supported by the National Natural Sci-
For the above problem due to the periodic
nditions, the continuous solutions remain always
symmetric with respect to the center of the spatial in-
terval. Authors of [26] also studied this problem and
found undesirable characteristics in some of the nu-
merical schemes, in particular a loss of spatial symme-
try and the onset of instability for larger values of the
parameter A (amplitude) in the initial condition of the
equation. We solved the above problem using lattice
Boltzmann method for several values of A. In Figure 7,
we show the approximate solutions for A = 1 with
0.0128x and 5 1.8286 10t . Figure 8 pre-
roxima 100 with
0.0128x and 5 1.8286 10t  Figure
, we cpatial symmetry is
kept for different amplitude A. It indicates that the
present lattice Boltzmann method is comparable with
other numerical schemes.
sents the app
and Figure 8
te solutions for A
an find that the s
. From
4
In
proposed to solve 1D nonlinear Klein-Gordon equation.
The efficiency and accuracy of the proposed model are
validated through detail numerical simulation with
quadratic and cubic nonlinearity. It can be found that the
LBGK results are in excellent agreement with the ana-
lytical solution. It should be point out that in order to
attain better accuracy the lattice Boltzmann model re-
quires a relatively small time step tand the proper
range is form 10–4 to 10–6. Detailed stability analysis of
present model is needed in further study.
5. Acknowledgements
T
Figure 7. LBM solution at t = 0, 3, 50 with A = 1, dx =
0.0128 and dt = 1.8286 × 10–5.
Figure 8. LBM solution with A = 100 at different time t
nce Foundation of China (50874123, 51174236) and
. References
] P. J. Caudrey, I. C. Eilbeck and J. D. Gibbon, “The Sine-
rris,
uxiliary Equation Method and New Solu-
.
e
National Basic Research Program of China (2011CB60-
6306).
6
[1
Gordon Equation as a Model Classical Field Theory,”
Nuovo Cimento, Vol. 25, No. 2, 1975, pp. 497-511.
[2] R. K. Dodd, I. C. Eilbeck, J. D. Gibbon and H. C. Mo
“Solitons and Nonlinear Wave Equations,” Academic,
London, 1982.
[3] Sirendaoreji, “A
tions of Klein-Gordon Equations,” Chaos, Solitons &
Fractals, Vol. 31, No. 4, 2007, pp. 943-950.
doi:10.1016/j.chaos.2005.10.048
[4] Sirendaoreji, “A New Auxiliary Equation and Exact Tra-
velling Wave Solutions of Nonlinear Equation,” Physics
Letters A, Vol. 356, No. 2, 2006, pp. 124-130.
doi:10.1016/j.physleta.2006.03.034
[5] A. M. Wazwaz, “New Travelling Wave Solutions to the
Boussinesq and Klein-Gordon Equations,” Communica-
tions in Nonlinear Science and Numerical Simulation,

Q. J. LI ET AL. 1485
Vol. 13, No. 5, 2008, pp. 889-901.
doi:10.1016/j.cnsns.2006.08.005
[6] M. A. Lynch, “Large Amplitude Instability in Finite Dif-
ference Approximates to the Klein-Gordon Equation,”
Applied Numerical Mathematics, Vol. 31, No. 2, 1999, pp.
173-182. doi:10.1016/S0168-9274(98)00128-7
[7] X. Li, B. Y. Guo and L. Vazquez, “A Legendre Sp
A Legendre Spectral Method for
n and A. Shokri, “Numerical Solution of the
ectral
Method for Solving the Nonlinear Klein-Gordon Equa-
tion,” Mathematics Applied and Computation, Vol. 15,
No. 1, 1996, pp. 19-36.
[8] X. Li and B. Y. Guo, “
Solving Nonlinear Klein-Gordon Equation,” Journal
Computation of Mathematics, Vol. 15, No. 2, 1997, pp.
105-126.
[9] M. Degha
Nonlinear Klein-Gordon Equation Using Radial Basis
Functions,” Journal of Computational and Applied
Mathematics, Vol. 230, No. 2, 2009, pp. 400-410.
doi:10.1016/j.cam.2008.12.011
[10] R. Benzi, S. Succi and M. Vergassola, “The Lattice
Boltzmann Equation: Theory and Application,” Physics
Reports, Vol. 222, No. 3, 1992, pp. 145-197.
doi:10.1016/0370-1573(92)90090-M
[11] S. Y. Chen and G. D. Doolen, “Lattice Boltzmann
Method for Fluid Flows,” Annual Review of Fluid Me-
chanics, Vol. 30, No. 1, 1997, pp. 329-364.
doi:10.1146/annurev.fluid.30.1.329
[12] J. Y. Zhang, G. W. Yan and Y. F. Dong, “A New Lattice
Boltzmann Model for the Laplace Equation,” Applied
Mathematics and Computation, Vol. 215, No. 2, 2009, pp.
539-547.doi:10.1016/j.amc.2009.05.047
[13] Z. H. Chai and B. C. Shi, “A Novel Lattice Boltzmann
Model for the Poisson Equation,” Applied Mathematical
Modelling, Vol. 32, No. 10, 2008, pp. 2050-2058.
doi:10.1016/j.apm.2007.06.033
[14] M. Hirabayashi, Y. Chen and H. Ohashi, “The Lattice
BGK Model for the Poisson Equation,” JSME Interna-
tional Journal Series B, Vol. 44, No. 1, 2001, pp. 45-52.
doi:10.1299/jsmeb.44.45
[15] J. G. Zhou, “Lattice Boltzmann Method for Shallow Wa-
oltzmann
ter Flows,” Springer Verlag, New York, 2004.
[16] Z. Shen, G. Yuan and L. Shen, “Lattice B
Method for Burgers Equation,” Chinese Journal of Com-
putational Physics, Vol. 175, No. 1, 2000, pp. 172-177.
[17] J. Y. Zhang and G. W. Yan, “A Lattice Boltzmann Model
for the Korteweg-de Vries Equation with Two Conserva-
tion Laws,” Computer Physics Communications, Vol. 180,
No. 7, 2009, pp. 1054-1062.
doi:10.1016/j.cpc.2008.12.027
[18] G. W. Yan, “A Lattice Boltzmann Equation for Waves,”
Journal of Computational Physics, Vol. 161, No. 1, 2000,
pp. 61-69. doi:10.1006/jcph.2000.6486
[19] J. Y. Zhang, G. W. Yan and X. Shi, “Lattice Boltzmann
Model for Wave Propagation,” Physics Review E, Vol. 80,
2009, Article ID 026706.
doi:10.1103/PhysRevE.80.026706
[20] S. P. Dawson, S. Chen and G. D. Doolen, “Lattice Boltz-
mann Computations for Reaction-Diffusion Equation,”
Journal of Chemical Physics, Vol. 98, No. 2, 1993, pp.
1514-1523. doi:10.1063/1.464316
[21] X. Yu and B. C. Shi, “A Lattice Boltzmann Model for
Reaction Dynamical Systems with Time Delay,” Applied
Mathematics and Computation, Vol. 181, No. 2, 2006, pp.
958-965. doi:10.1016/j.amc.2006.02.020
[22] S. R. Vander and M. Ernst, “Convection-Diffusion Lat-
tice Boltzmann Scheme for Irregular Lattice,” Journal of
Computational Physics, Vol. 160, No. 2, 2000, pp. 766-
782. doi:10.1006/jcph.2000.6491
[23] Z. L. Guo, B. C. Shi and N. C. Wang, “Fully Lagrangian
and Lattice Boltzmann Method for the Advection-Diffu-
sion Equation,” Journal of Scientific Computing, Vol. 14,
No. 3, 1999, pp. 291-300.
doi:10.1023/A:1023273603637
[24] B. C. Shi and Z. L. Guo, “Lattice Boltzmann Model for
Nonlinear Convection-Diffusion Equations,” Physics Re-
view E, Vol. 79, 2009, Article ID 016701.
doi:10.1103/PhysRevE.79.016701
[25] Z. L. Guo, C. G. Zheng and B. C. Shi, “Non-Equilibrium
Extrapolation Method for Velocity and Pressure Bound-
ary Conditions in the Lattice Boltzmann Method,” Chi-
nese Physics, Vo. 11, No. 4, 2002, pp. 366-374.
doi:10.1088/1009-1963/11/4/310
[26] S. Jiminez and L. Vazquez, “Analysis of Four Numerical
Scheme for a Nonlinear Klein-Gordon Equation,” Ap-
plied Mathematics and Computation, Vol. 35, No. 1,
1990, pp. 61-94. doi:10.1016/0096-3003(90)90091-G