 Applied Mathematics, 2011, 2, 1469-1478 doi:10.4236/am.2011.212209 Published Online December 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM The Analytical and Numerical Solutions of Differential Equations Describing of an Inclined Cable Subjected to External and Parametric Excitation Forces Mohamed S. Abd Elkader1,2 1Department of Mathematics and Statistics, Faculty of Science, Taif University, El-Taif, Kingdom of Saudi Arabia 2Department of Engineering Mathematics, Faculty of Electronic Engineering, Menoufia University, Menouf, Egypt E-mail: moh_6_11@yahoo.com Received October 21, 2011; revised November 22, 2011; accepted November 30, 2011 Abstract The analytical and numerical solutions of the response of an inclined cable subjected to external and para- metric excitation forces is studied. The method of perturbation technique are applied to obtained the periodic response equation near the simultaneous principal parametric resonance in the presence of 2:1 internal reso- nance of the system. All different resonance cases are extracted. The effects of different parameters and worst resonance case on the vibrating system are investigated. The stability of the system are studied by us- ing frequency response equations and phase-plane method. Variation of the parameters α2, α3, β2, γ2, η2, γ3, η3, f2 leads to multi-valued amplitudes and hence to jump phenomena. The simulation results are achieved using MATLAB 7.6 programs. Keywords: Perturbation Method, Resonance, Chaotic Response, Stability 1. Introduction Cable structures play an important role in many engi- neering fields, such as civil, ocean and electric engineer- ing. Arafat and Nayfeh [1] studied the motion of shallow suspended cables with primary resonance excitation. The method of multiple scales is applied to study nonlinear response of this suspended cables and its stability and the dynamic solutions. Some interesting work on the nonlin- ear dynamics of cables to the harmonic excitations can be found in the review articles by Rega [2,3]. Nielsen and Kierkegaard [4] investigated simplified models of inclined cables under super and combinatorial harmonic excitation and gave analytical and purely numerical re- sults. Zheng, Ko and Ni [5] considered the super-har- monics and internal resonance of a suspended cable with almost commensurable natural frequencies. Zhang and Tang [6] investigated the chaotic dynamics and global bifurcations of the suspended inclined cable under com- bined parametric and external excitations. Nayfeh et al. [7] investigated the nonlinear nonplanar responses of suspended cables to external excitations. The equations of motion governing such systems contain quadratic and cubic nonlinearities, which may result in 2:1 and 1:1 in- ternal resonances. Chen and Xu [8] investigated the glo- bal bifurcations of the inclined cable subjected to a har- monic excitation leading to primary resonances with the external damping by using averaging method. Kamel and Hamed [9], studied the nonlinear behavior of an inclined cable subjected to harmonic excitation near the simulta- neous primary and 1:1 internal resonance using multiple scale method. Abe [10] investigated the accuracy of non- linear vibration analyses of a suspended cable, which possesses quad ratic and cub ic nonlinearities, with 1:1 in - ternal resonance. The nonlinear dynamics of suspend cable structures have been studied with 2:1 internal reso- nances by the authors [11,12]. Experimental studies of this problem have been conducted by Alaggio and Rega [13] and Rega and Allagio [14], however explicit stabil- ity regions for t he semi-triv i al sol ut i on h ave not be en cal - culated analytically. Here, we use a modal model to com- pute the insta b i li t y b o un d a ry f or a range of excitati on fre- quencies close to the 2:1 resonance for an inclined cable, including nonlinear modal interaction. The out-of-plane  M. S. ABD ELKADER 1470 dynamic stability of in clined cables subj ected to in-plane vertical support excitation is investigated by Gonzalez- Buelga et al. [15]. Perkins [16] examined the effect of one support motion on the three-dimensional nonlinear response. Using the Galerkin method, he constructed a two-degree-of-freedom model to analyze the 2:1 internal resonance. Lee and Perkins [17] extended the work to in- clude second-order perturbations and multiple internal resonances. Still, the focus was on the 2:1 internal reso- nance, whereas the excitation was changed to a harmoni- cally varying load per unit length acting in the static equilibrium plane. Lee and Perkins [18] also used a three-degree-of-freedom model to simulate non-linear response of suspended, inclined cables driven by planar excitation and determined the existence and stability of four classes of periodic solutions. Eissa and Sayed [19-21] and Sayed [22], studied the effects of different active controllers on simple and spring pendulum at the primary resonance via negative velocity feedback or its square or cubic. Sayed and Hamed [23] studied the response of a two-degree-of-freedom system with quadratic coupling under parametric and harmonic excitations. The method of multiple scale perturbation technique is applied to solve the non-linear differential equations and obtain approximate solutions up to and including the second-order approximations. Sayed and Kamel [24,25] investigated the effects of different con- trollers on the vibrating system and the saturation control to reduce vibrations due to rotor blade flapping motion. The stability of the ob tained numerical solution is inves- tigated using both phase plane methods and frequency response equations. Amer and Sayed [26], studied the response of one-degree-of freedom, non-linear system under multi-parametric and external excitation forces simulating the vibration o f the cantilever beam. Variation of some parameters leads to multi-valued amplitudes and hence to jump phenomena. Sayed et al. [27], investigated the non-linear dynamics of a two-degree-of freedom vi- bration system including quadratic and cubic non-lin- earities subjected to external and parametric excitation forces. The stability of the system is investigated using both frequency response curves and phase-plane trajecto- ries. The effects of different parameters of the system are studied numerically. This work deals with model having two-degree-of- freedom nonlinear system subjected to external and pa- rametric excitation forces describes the vibrations of an inclined cable. The method of multiple scales perturba- tion is applied to obtain modulation response equations near the simultaneous principal parametric resonance in the presence of 2:1 internal resonance (22 2 and 12 2 ). The stability of the proposed analytic nonlin- ear solution near the above case is studied and the stabil- ity condition is determined. The effect of different pa- rameters on the steady state response of the vibrating system is studied and discussed from the frequency re- sponse curves. The numerical solution and chaotic re- sponses of the nonlinear system of an inclined cable for some different parameters are also studied. A compari- son with previously published work is included. 2. Mathematical Analysis Our attention is focused on an elastic-sag hanging at fixed supports and excited by harmonic and parametric distributed vertical forcing in plane. The two-degree-of- freedom describing the nonlinear dynamics of cable shown in Figure 1, can be written as: 22232 11 222 2 20xcxx xyxxy (1) 23 2233 3 112 2 2 cos cos ycyy xyyx ftyf t 2 y (2) where and denote in-plane and out-of-plane dis- placements, respectively, and dots denote derivatives with respect to the time t. The parameters 1 and 2 are the viscous damping coefficients, 1 y c c and 2 are the natural frequencies associated with in-plane and out-of- plane modes 1 and 2 are the excitation frequencies, f1 and f2 are the excitation forces amplitude, 222 ,,, 233 ,, and 3 are the coefficients of nonlinear pa- rameters. The linear viscous damping forces, the exciting forces and nonlinear parameters are assumed to be 22 222 112 2 22 ˆˆˆ ˆ ˆˆ ,, , , ˆ ˆˆ , 1, 22, 3 nnsss ss ccc cff ns , s where is a small perturbation parameter and 0 1. For the convenience of the analysis of Equa- tions (1)-(2), the non-dimensional parameter is in- troduced. We ca n obt ai n 22 2 112 2 23 2 22 ˆ ˆ ˆ 2( ˆˆ ()0 2 ) cx xxy xxy (3) 22 232 2233 3 2112 2 ˆˆˆ ˆ 2( ˆˆ (coscos ) ) cy yxyyxy ftyf t (4) The parameters 23 2 ˆ ˆˆ ,, ˆˆˆ ˆˆ ,,,,cc are of the order of 1 and the parameters 12232312 are of the order of 2. The approximate solution of Equations (3)-(4) can be obtained using the method of multiple scales [28]. Let ˆˆ ˆ ,,,f f 0012 1012 22012 (;) (,,)(,,) (,,) txTTT xTTT xTTT (5) Copyright © 2011 SciRes. AM  M. S. ABD ELKADER1471 Figure 1. A schematic of inclined cable under combined excitations. 0012 1012 22012 (;)(,,)(,,) (,,) yty TTTyTTT yTTT (6) where, n n Tt (n = 0, 1, 2) are the fast and slow time scales respectively. In terms of 0 and , the time derivatives transform according to 1 ,TT 2 T 2 012 2222 00110 2 d d d2(2 d DD D t DDDDDD t 2 ) (7) where nn . Substituting Equations (5)-(6) and (7) into Equations (3)-(4) and equating the coefficients of similar powers of in both sides, we obtain the differen- tial equations as follo ws: DT Order 0 () : 22 010 ()Dx 0 0 (8) 22 020 ()Dy (9) Order 1 () : 22 2 011 010202 ˆ ˆ ()2DxDDxx 2 0 y 0 y (10) 22 02101030 ˆ ()2DyDDyx 2 (11) Order () : 22 2 01210011 020 00201 201 32 20 200 1 ()2 2 ˆ ˆ ˆ 222 ˆˆ DxDxDDxDDx cDxxxyy xxy (12) 22 2 02210 011 020 3 2003 010130 2 300 110 0220 ()2 2 ˆˆ ˆ 2() ˆˆ ˆcos cos DyDyDDyDDy cDyxyyxy yxfTyfT (13) The solution of Equations (8)-(9) can be expressed in the complex form: 01210 ( ,)exp() AT Ti Tcc (14) 012 20 ( ,)exp()yBTTiTc where cc denotes the complex conjugate of the preceding terms and , are complex functions in 1 and 2 T which determined through the elimination of secular and small-divisor terms from the first and second-order of approximations. BT In this case, we analyze the case where 22 2 and 12 2 . To describe quantitatively the nearness of the resonances, we introduce the detuning parameters 1 and 2 according to 221 ˆ 2 , 2 12 ˆ 2 . Substituting Equations ( 14)-( 15) into Equations (10)-(11) and eliminating the secular terms leads to the solvability conditions for the first-order expansion as: 2 12 21 1ˆˆ 2exp( iDA BiT )0 (16) 21 321 ˆˆ 2exp(iDB AB iT )0 (17) After eliminating the secular terms, the particular solu- tions of Equations (10)-(11) a re given by : 2 222 110 222 111 ˆ ˆˆ exp(2 ) 3 AiT AABB cc (18) 3 10 2 2 212 12 ˆexpyABi Tcc (19) Now substituting Equations (14)-(15) and Equations (18)-(19) into Equations (12)-(13), the following are ob- tained 22 012 22 1112121 1 () ˆ (22)exp( ) Dx DA icA iDAABBAAiT NSTcc 0 (20) 22 022 22 122223 42 2220 () ˆ 22 exp( 1ˆexp( ()) 2 Dy DB icB iDBAABBBiT fBiTNSTcc 0 ) (21) where 23 22 12 222 212 1 ˆˆ ˆˆ 24ˆ 2, () 2 2 22 2 1 ˆ 10 ˆ 3 3 , 2 323 33 2 22 21 21 ˆˆˆ 2ˆ 2, () 23 43 2 1 ˆˆ 2ˆ 3 c (15) and NST stands for non-secular terms. Eliminating the Copyright © 2011 SciRes. AM  M. S. ABD ELKADER 1472 secular terms leads to the solvability conditions for the second-order expansion 22 2111 2 11 ˆ 22 iDADA icAABBAA (22) 2 22 13 2 42 22 ˆ 22 1ˆˆ exp( ) 2 iDBDBicBAAB BBf BiT 11 (23) Stability Analysis of Nonlinear Solutions From Equation (7), multiplying both sides be 1 2,i 2 2i we get 2 1111 d 22 2 d A iiDAi t 2 DA (24) 2 221 d 22 2 d B iiDBi t 22 DB (25) To analyze the solutions of Equations (16)-(17) and Equations (22)-(23), we express and in the polar form B 12 12 12 (, )(2),(, )(2) ii TTae BTTbe (26) where a , b and (1,2 ss) are the steady state ampli- tudes and phases o f the motion respectively. Substituting Equations (26), (16)-(17) and Equations (22)-(23) into Equations (24)-(25) and equating the real and imaginary parts we obtain the following equations describing the modulation of the amplitudes and phases: 2 222 1 2 1 1 sin 48 acab 2 (27) 2 222 12 2 11 23 523 6 2 11 12 cos 48 88 16 ab ab a (28) 23 32 21 2 222 2 sin sin 44 8 f bcbab b (29) 2 323 22 2 2 32 10 1 2 2 cos 48 cos 4 bab f bb 9 ab ( 30) where 2 37 238 910 32 22 2 22 22 56781234 11122 2112 1 , 88 32 32 ,,,, , , ˆˆ and2 ,2 TT Form the system of Equations (27)-(30) to have sta- tionary solutions, the following conditions must be satis- fied: 12 0ab (32) It follows from Equation (31) that 2111 1, 22 (33) Hence, the steady state solutions of Equations (27)-(30) are given by 2 222 12 2 11 sin 0 48 ca b (34) 23 6 222 12 2 2 11 2 523 2 12 1 1 () cos 48 8 0 816 ab ab a (35) 23 32 2 222 2 21 sinsin 0 44 8 f cbab b (36) 2 23 3 12 2 32 10 1 2 2 2 1cos 24 8 cos 0 4 bab f bb 9 ab (37) Solving the resulting algebraic equations for the fixed points of the practical case where , that is non-planar motions, we obtain the following frequency response equations 0, 0ab 2222224264 12 1123 22 6 121 122 42 12 () 2( )2( ) 20 acaabab ab a ab (38) 2222 242 2622 12910 91 2 42422 2 10 19 1042 2 2 42 12 2 1 4 216 cos()0 2 bcbabbba f babab fab 2 b (39) where 2 5236 222 123 22 11 1 1 12 ,, 884 16 8 (31) and 23 3 422 24 8 . The stability of the obtained fixed points for the simul- Copyright © 2011 SciRes. AM  M. S. ABD ELKADER1473 taneous primary, principal parametric and 2:1 internal resonance case is determined and studied as follows: one lets 101110 11 01 , and ss s aaabbb (40) where a 10, b 10 and 0 are the solutions of Equations (34)-(37) and a 11, b11, 1 are perturbations which are assumed to be small compared to a10, b10 and 0 . Sub- stituting Equation (40) into Equations (27)-(30), using Equations (34)-(37) and keeping only the linear terms in a11, b11, 1 we obtain: 2 113 102021 31020 11 111cos 2sin acaKb Kb b (41) 21 2 1106 10 21 4209 1011 10 10 2 310 410202021 10 310 410 1201 1020 10 1010 2 6102 10 101011 10 2 2 2 1 3 () cos 2 8 sin sin 2cos 2cos 2 3cos 4 si 2 ba aa aa b aa ba b ba b af bb b f 10 11 n (42) 114102011 2 24102011 2 2 4101020 211010 11 10 2 sin sin sin 4 cos cos 4 bb a f ca b f ab b (43) 4 2091011 4102021 2 410910 1 2010 1011 10 10102 2 11 10 10 11 2 cos 2sin cos3 cos 2 sin 2 aa a aaf b bb b f 2 4 b (44) The system of Equations (41)-(44) are first order autonomous ordinary differential equations and the sta- bility of a particular fixed point with respect to an infini- tesimal disturbance proportional to exp( )t is deter- mined by eigenvalues of the Jacobian matrix of the right hand sides of Equations (41)-(44). The zeros of the char- acteristic equation are given by 432 1234 0LL LL (45) where, and are functions of the parameters (1 23223232112 212 123 ,,LLL ,, ,cc 4 L ,,,,,,,,, ,, ,,ab f ). According to the Routh-Hurwitz criterion the necessary and sufficient conditions for all the roots of Equation (45) to possess negative real parts are: 2 11233123144 0,0,0, 0LLLLLLLL LLL (46) The system is stable if the eigenvalues have negative real parts, otherwise is unstable. In the frequency re- sponse curves, solid/dotted lines denote stable/ unstable periodic responses, respectively. 3. Results and Discussion The response of the two-degree-of-freedom nonlinear system under both parametric and external excitations is studied. The solution of this system is determined up to and including the second order approximation by apply- ing the multiple time scale perturbation. The steady state solution and its stability are determined and representa- tive numerical results are included. The stability zone and effects of the different parameters are discussed us- ing frequency response curve. The stability of the nu- merical solution is studied also using the phase-plane method. Some of the resulting resonance cases are con- firmed applying well-known numerical techniques. The effects of the some different parameters on the vibrating system behavior are investigated and discussed. 3.1. Numerical Solution Figure 2 shows that the response of the inclined cable for the non-resonant at the practical values of the pa- rameters c1 = 0.0002, c2 = 0.03, α2 = 0.2, β2 = 0.5, γ2 = 0.3, η2 = 0.5, α3 = 0.03, η3 = 0.05, γ3 = 0.04, 1 = 2, 2 = 0.01, 1 = 2.75, 2 = 3.2, 1 = 1.2, 2 = 1.5. It can be seen from this figure that the steady state amplitude is about 0.005 with dynamic chaotic behavior for the in- plane mode and about 0.18 with multi-limit cycle for the out-of-plane mode. The amplitudes decreasing with in- creasing time and tend to steady state motion and have stable solution. The worst resonance case is also con- firmed numerically as shown in Figure 3. From this fig- ure, it can be notice that the maximum steady state am- plitude of the in-plane mode is about 130 times that of basic case with multi-limit cycle, while the maximum amplitude of out-of-plane mode is about 4 times of the basic case with chaotic motion. Effects of external and parametric excitation forces f1 and f2. Copyright © 2011 SciRes. AM 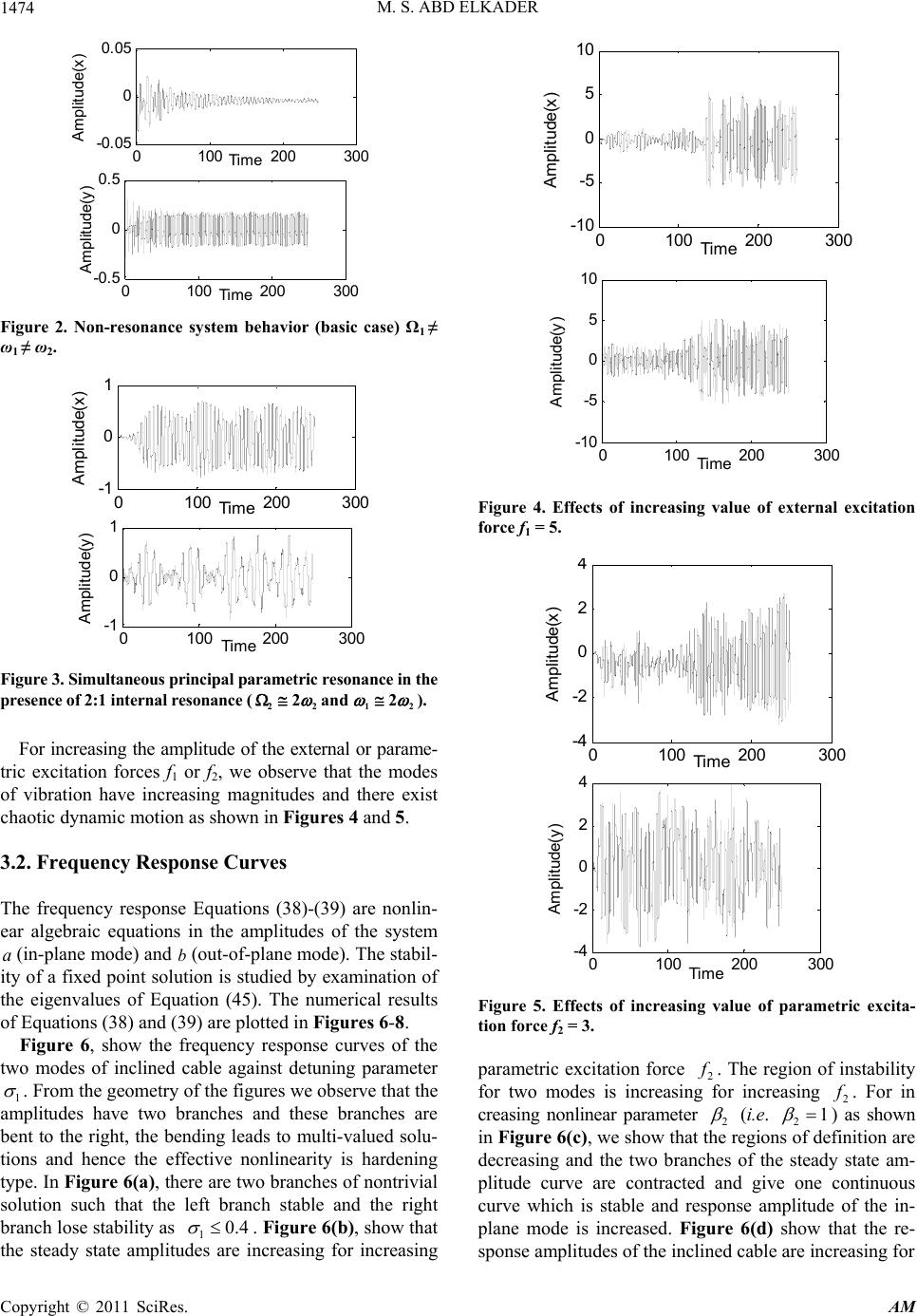 M. S. ABD ELKADER 1474 0100 200 300 -0.05 0 0.05 Time A mpli tude(x) 0100 200 300 -0.5 0 0.5 Time Am plitude(y) Figure 2. Non-resonance system behavior (basic case) Ω1 ≠ ω1 ≠ ω2. 0100 200 300 -1 0 1 Time Amplitude(x) 0100 200 300 -1 0 1 Time Am plitude(y ) Figure 3. Simultaneous principal parametric resonance in the presence of 2:1 internal resonance (221 2and 2 2 ). For increasing the amplitude of the external or parame- tric excitation forces f1 or f2, we observe that the modes of vibration have increasing magnitudes and there exist chaotic dynamic motion as shown in Figures 4 and 5. 3.2. Frequency Response Curves The frequency response Equations (38)-(39) are nonlin- ear algebraic equations in the amplitudes of the system (in-plane mode) and b(out-of-plane mode). The stabil- ity of a fixed point solution is studied by examination of the eigenvalues of Equation (45). The numerical results of Equations (38) and (39) are plotted in Figures 6-8. a Figure 6, show the frequency response curves of the two modes of inclined cable against detuning parameter 1 . From the geometry of the figures we observe that the amplitudes have two branches and these branches are bent to the right, the bending leads to multi-valued solu- tions and hence the effective nonlinearity is hardening type. In Figure 6(a), there are two branches of nontrivial solution such that the left branch stable and the right branch lose stability as 10.4 . Figure 6(b), show that the steady state amplitudes are increasing for increasing 0100 200 300 -10 -5 0 5 10 Time Ampli tude(x) 0100 200 300 -10 -5 0 5 10 Time Amplitude(y) Figure 4. Effects of increasing value of external excitation force f1 = 5. 0100 200300 -4 -2 0 2 Time Amplitude(x) 0100 200 300 -4 -2 0 2 4 Time Amplitude(y) Figure 5. Effects of increasing value of parametric excita- tion force f2 = 3. parametric excitation force 2. The region of instability for two modes is increasing for increasing 2. For in creasing nonlinear parameter 2 f f (i.e. 21 ) as shown in Figure 6(c), we show that the regions of definition are decreasing and the two branches of the steady state am- plitude curve are contracted and give one continuous curve which is stable and response amplitude of the in- plane mode is increased. Figure 6(d) show that the re- sponse amplitudes of the inclined cable are increasing for Copyright © 2011 SciRes. AM 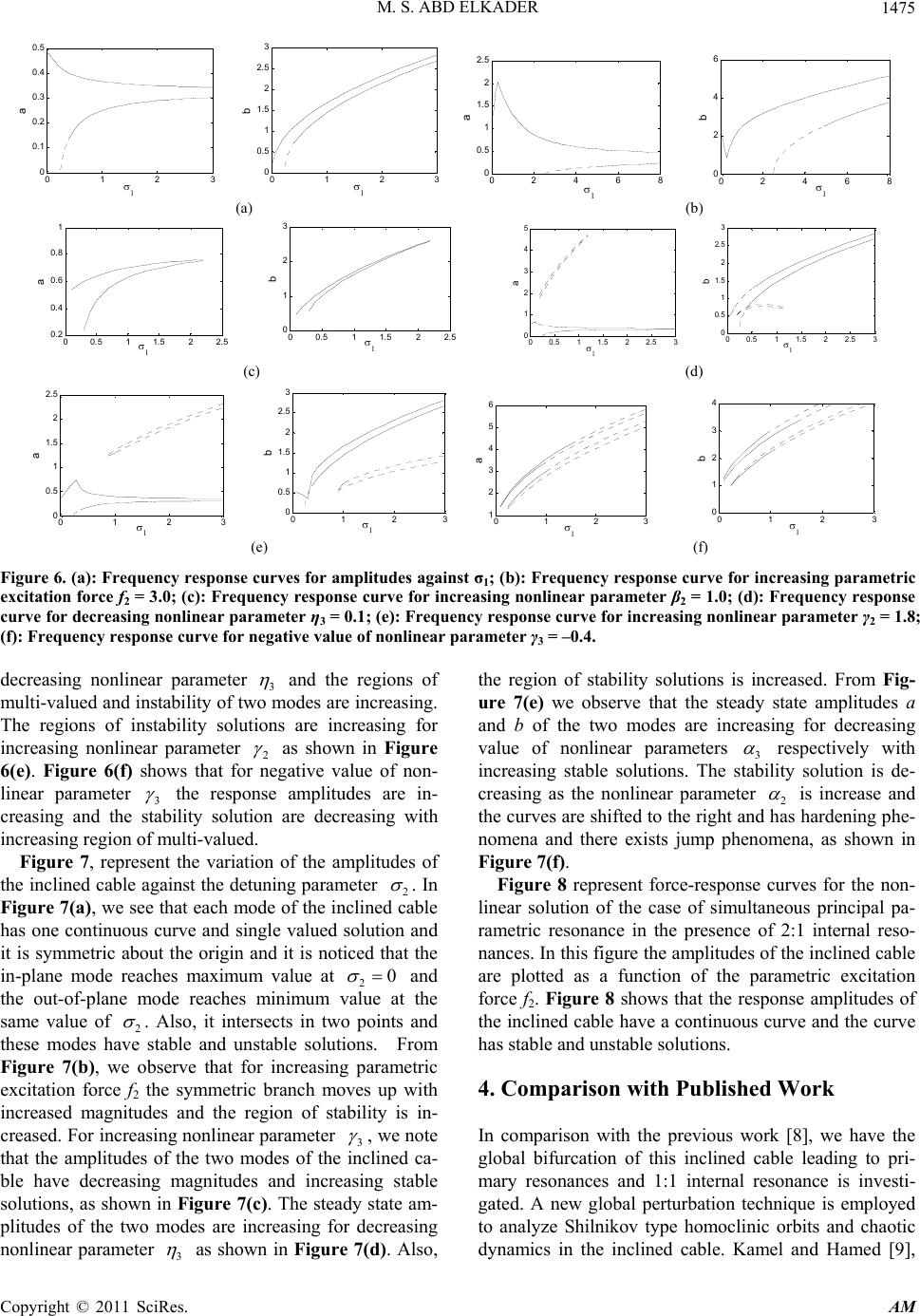 M. S. ABD ELKADER Copyright © 2011 SciRes. AM 1475 0 1 23 0 0.1 0.2 0.3 0.4 0.5 a 0 1 2 3 0 0. 5 1 1. 5 2 2. 5 3 b 02468 0 0.5 1 1.5 2 2.5 a 02468 0 2 4 6 b (a) (b) 00.5 11.5 22.5 0.2 0.4 0.6 0.8 1 a 00.5 11.5 22.5 0 1 2 3 b 00.5 11.5 22.5 3 0 1 2 3 4 5 a 00.5 11.5 22.5 3 0 0.5 1 1.5 2 2.5 3 b (c) (d) 0 1 2 3 0 0.5 1 1.5 2 2.5 a 0 123 0 0.5 1 1.5 2 2.5 3 b 0123 1 2 3 4 5 6 a 0 123 0 1 2 3 4 b (e) (f) Figure 6. (a): Frequency response curves for amplitudes against σ1; (b): Frequency response curve for increasing parametric excitation force f2 = 3.0; (c): Frequency response curve for increasing nonlinear parameter β2 = 1.0; (d): Frequency response curve for decreasing nonlinear parameter η3 = 0.1; (e): Frequency response curve for increasing nonlinear parameter γ2 = 1.8; (f): Frequency response curve for negative value of nonlinear parameter γ3 = –0.4. decreasing nonlinear parameter 3 and the regions of multi-valued and instability of two modes are increasing. The regions of instability solutions are increasing for increasing nonlinear parameter 2 as shown in Figure 6(e). Figure 6(f) shows that for negative value of non- linear parameter 3 the response amplitudes are in- creasing and the stability solution are decreasing with increasing region of multi-valued. Figure 7, represent the variation of the amplitudes of the inclined cable against the detuning parameter 2 . In Figure 7(a), we see that each mode of the inclined cable has one continuous curve and single valued solution and it is symmetric about the origin and it is noticed that the in-plane mode reaches maximum value at 20 and the out-of-plane mode reaches minimum value at the same value of 2 . Also, it intersects in two points and these modes have stable and unstable solutions. From Figure 7(b), we observe that for increasing parametric excitation force f2 the symmetric branch moves up with increased magnitudes and the region of stability is in- creased. For increasing nonlinear parameter 3 , we note that the amplitudes of the two modes of the inclined ca- ble have decreasing magnitudes and increasing stable solutions, as shown in Figure 7(c). The steady state am- plitudes of the two modes are increasing for decreasing nonlinear parameter 3 as shown in Figure 7(d). Also, the region of stability solutions is increased. From Fig- ure 7(e) we observe that the steady state amplitudes a and b of the two modes are increasing for decreasing value of nonlinear parameters 3 respectively with increasing stable solutions. The stability solution is de- creasing as the nonlinear parameter 2 is increase and the curves are shifted to the right and has hardening phe- nomena and there exists jump phenomena, as shown in Figure 7(f). Figure 8 represent force-response curves for the non- linear solution of the case of simultaneous principal pa- rametric resonance in the presence of 2:1 internal reso- nances. In this figure the amplitudes of the inclined cable are plotted as a function of the parametric excitation force f2. Figure 8 shows that the response amplitudes of the inclined cable have a continuous curve and the curve has stable and unstable solutions. 4. Comparison with Published Work In comparison with the previous work [8], we have the global bifurcation of this inclined cable leading to pri- mary resonances and 1:1 internal resonance is investi- gated. A new global perturbation technique is employed to analyze Shilnikov type homoclinic orbits and chaotic dynamics in the inclined cable. Kamel and Hamed [9],  M. S. ABD ELKADER Copyright © 2011 SciRes. AM 1476 Amplitudes a b -2 -1 0 1 2 0 0.2 0.4 0.6 0.8 a -1 -0.500.5 1 0.2 0.4 0.6 0.8 1 1.2 b f 2 =0.3 f 2 =0.3 f 2 =0.6 f 2 =0.6 f 2 =0.15 f 2 =0.15 (a) (b) -1.5 -1 -0.5 00.5 11.5 0 0.1 0.2 0.3 0.4 0.5 a -1.5 -1 -0.5 00.5 11.5 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 b -0.4 -0.200.2 0.4 0.6 0.1 0.2 0.3 0.4 0.5 0.6 a -0.4 -0.200.2 0.4 0.2 0.4 0.6 0.8 b eta3=1.6 eta3=1.6 eta3=0.6 eta3=0 .6 eta3=0.2 eta3=0.2 (c) (d) -0.2 -0.100.1 0.2 0.3 0 0.2 0.4 0.6 0.8 a -0.2 -0.1 00.1 0.2 0.3 0. 2 0. 4 0. 6 0. 8 b -2 -1 0 123 0 0.5 1 1.5 a -2 -1 0 1 23 0.2 0.3 0.4 0.5 0.6 0.7 0.8 b 2 (e) (f) Figure 7. (a): Frequency response curves for simultaneous principal parametric resonance in the presence of 2:1 internal resonance 22 1 2and 2 ; (b): Frequency response curve for parametric excitation force f2; (c): Frequency response curve for nonlinear parameter γ3; (d): Frequency response curve for nonlinear parameter η3; (e): Frequency response curve for nonlinear parameter α3; (f): Frequency response curve for nonlinear parameter α2. 0246810 12 0 0. 5 1 1. 5 f 2 a 0246810 0 1 2 3 4 5 f 2 b Figure 8. Force response curves for (221 2,2 2 ). studied the nonlinear behavior of an inclined cable sub- jected to harmonic excitation near the simultaneous pri- mary and 1:1 internal resonance by using multiple scale method. In this paper, periodic and chaotic response of a dis- cretization two-degree-of-freedom model of a suspended inclined cable, containing a 2:1 internal resonance, sub- ject to harmonic external and parametric excitation are obtained. The stable/unstable periodic solutions are de- termined using the method of multiple scale and are pre- sented through frequency response plots. Chaotic re- sponses are determined by numerical integration of the governing ordinary differential equations of motion. Var- iation of the parameters 23222 ,, ,,, 332 ,,f leads  M. S. ABD ELKADER1477 to multi-valued amplitudes and hence to jump phenom- ena. 5. Conclusions Cables are very efficient structural members and hence have been widely used in many long-span structures, including suspension, roofs and guyed towers. The nonlinear dynamic response of the nonlinear system sub- jected to external and parametric excitations is investi- gated. The method of multiple scales is applied to obtain the solution of the considered system up to second order approximation. The numerical solutions and chaotic re- sponse of this nonlinear system are investigated. The stability of the proposed analytic nonlinear solution is studied at worst resonance case which is the simultane- ous principal parametric resonance in the presence of 2:1 internal resonances. The modulation equations of the amplitudes and phases are obtained and steady state solu- tions are determined. The effects of some nonlinear pa- rameters on the steady state response of the vibrating cable leading to multi-valued solutions. From the analy- sis the following may be concluded. 1) For the resonance case 2212 2, 2 we note that the steady state amplitude is increased to about 130% compared to basic case with multi-limit cycle, and it is better to avoid this resonance case as working condi- tions for the system. 2) The steady state amplitude of the system are in- creasing for increasing external or parametric excitation force, and for large values of the system become unsta- ble. 3) Variation of α2, α3, β2, γ2, η2, γ3, η3, f2 leads to multi-valued amplitudes and hence jump phenomena. 4) For increasing parametric excitation force f2 or negative value of the nonlinear parameter γ3 we observe that the steady state amplitudes of the two modes are increasing with increasing instability solutions. 5) Increasing of the nonlinear parameters η3 or γ3 can reduce the amplitude of the system and obtain the effect of reduction of the amplitude. 6) Variation of the parameter α2 leads to multi-valued amplitudes and hence to jump phenomena. 7) For increasing parametric excitation force f2 or de- creasing nonlinear parameter α3 we show that the steady state amplitudes of the two modes are increasing. For increasing nonlinear parameter η3 we note that the steady state amplitudes of the two modes are decreasing with decrease of the stability solutions. 6. References [1] H. N. Arafat and A. H. Nayfeh, “Non-Linear Responses of Suspended Cables to Primary Resonance Excitations,” Journal of Sound and Vibration, Vol. 266, No. 2, 2003, pp. 325-354. doi:10.1016/S0022-460X(02)01393-7 [2] G. Rega, “Non-Linear Vibrations of Suspended Cables; Part I: Modeling and Analysis,” Journal of Applied Me- chanics Review, Vol. 57, No. 6, 2004, pp. 443-478. doi:10.1115/1.1777224 [3] G. Rega, “Non-Linear Vibrations of Suspended Cables; Part II: Deterministic Phenomena,” Journal of Applied Mechanics Review, Vol. 57, No. 6, 2004, pp. 479-514. doi:10.1115/1.1777225 [4] S. R. Nielsen and P. H. Kirkegaard, “Super and Combi- natorial Harmonic Response of Flexible Inclined Cables with Small Sag,” Journal of Sound and Vibration, Vol. 251, No. 1, 2002, pp. 79-102. doi:10.1006/jsvi.2001.3979 [5] G. Zheng, J. M. Ko and Y. O. Ni, “Super-Harmonic and Internal Resonances of a Suspended Cable with Nearly Commensurable Natural Frequencies,” Nonlinear Dy- namics, Vol. 30, No. 1, 2002, pp. 55-70. doi:10.1023/A:1020395922392 [6] W. Zhang and Y. Tang, “Global Dynamics of the Cable under Combined Parametrical and External Excitations,” International Journal of Non-Linear Mechanics, Vol. 37, No. 3, 2002, pp. 505-526. doi:10.1016/S0020-7462(01)00026-9 [7] A. H. Nayfeh, H. Arafat, C. M. Chin and W. Lacarbonara, “Multimode Interactions in Suspended Cables,” Journal of Vibration and Control, Vol. 8, No. 3, 2002, pp. 337- 387. doi:10.1177/107754602023687 [8] H. Chen and Q. Xu, “Bifurcation and Chaos of an In- clined Cable,” Nonlinear Dynamics, Vol. 57, No. 2-3, 2009, pp. 37-55. doi:10.1007/s11071-008-9418-3 [9] M. M. Kamel and Y. S. Hamed, “Non-Linear Analysis of an Inclined Cable under Harmonic Excitation,” Acta Mechanica, Vol. 214, No. 3-4, 2010, pp. 315-325. doi:10.1007/s00707-010-0293-x [10] A. Abe, “Validity and Accuracy of Solutions for Nonlin- ear Vibration Analyses of Suspended Cables with One- to-One Internal Resonance,” Nonlinear Analysis: Real World Applications, Vol. 11, No. 4, 2010, pp. 2594-2602. doi:10.1016/j.nonrwa.2009.09.006 [11] N. Srinil, G. Rega and S. Chucheepsakul, “Two-yo-One Resonant Multi-Modal Dynamics of Horizontal/Inclined Cables. Part I: Theoretical Formulation and Model Vali- dation,” Nonlinear Dynamics, Vol. 48, No. 3, 2007, pp. 231-252. doi:10.1007/s11071-006-9086-0 [12] N. Srinil and G. Rega, “Two-To-One Resonant Multi- Modal Dynamics of Horizontal/Inclined Cables. Part II: Internal Resonance Activation Reduced-Order Models and Nonlinear Normal Modes,” Nonlinear Dynamics, Vol. 48, No. 3, 2007, pp. 253-274. doi:10.1007/s11071-006-9087-z [13] R. Alaggio and G. Rega, “Characterizing Bifurcations and Classes of Motion in the Transition to Chaos through 3D-Tori of a Continuous Experimental System in Solid Mechanics,” Physica D, Vol. 137, No. 1, 2000, pp. 70-93. doi:10.1016/S0167-2789(99)00169-4 [14] G. Rega and R. Alaggio, “Spatio-Temporal Dimensional- Copyright © 2011 SciRes. AM  M. S. ABD ELKADER Copyright © 2011 SciRes. AM 1478 ity in the Overall Complex Dynamics of an Experimental Cable/Mass System,” International Journal of Solids and Structures, Vol. 38, No. 10-13, 2001, pp. 2049-2068. doi:10.1016/S0020-7683(00)00152-9 [15] A. Gonzalez-Buelga, S. A. Neild, D. J. Wagg and J. H. G. Macdonald, “Modal Stability of Inclined Cables Sub- jected to Vertical Support Excitation,” Journal of Sound and Vibration, Vol. 318, No. 3, 2008, pp. 565-579. doi:10.1016/j.jsv.2008.04.031 [16] N. C. Perkins, “Modal Interactions in the Non-Linear Response of Inclined Cables under Parametric/External Excitation,” International Journal of Non-linear Me- chanics, Vol. 27, No. 2, 1992, pp. 233-250. doi:10.1016/0020-7462(92)90083-J [17] C. L. Lee and N. C. Perkins, “Nonlinear Oscillations of Suspended Cables Containing a Two-to-One Internal Resonance,” Nonlinear Dynamics, Vol. 3, 1992, pp. 465- 490. [18] C. L. Lee and N. C. Perkins, “Three-Dimensional Oscil- lations of Suspended Cables Involving Simultaneous In- ternal Resonance,” Proceedings of ASME Winter Annual Meeting AMD-14, 1992, pp. 59-67. [19] M. Eissa and M. Sayed, “A Comparison be tween Passive and Active Control of Non-Linear Simple Pendulum Part-I,” Mathematical and Computational Applications, Vol. 11, No. 2, 2006, pp. 137-149. [20] M. Eissa and M. Sayed, “A Comparison be tween Passive and Active Control of Non-Linear Simple Pendulum Part-II,” Mathematical and Computational Applications, Vol. 11, No. 2, 2006, pp. 151-162. [21] M. Eissa and M. Sayed, “Vibration Reduction of a Three DOF Non-Linear Spring Pendulum,” Communication in Nonlinear Science and Numerical Simulation, Vol. 13, No. 2, 2008, pp. 465-488. doi:10.1016/j.cnsns.2006.04.001 [22] M. Sayed, “Improving the Mathematical Solutions of Nonlinear Differential Equations Using Different Control Methods,” Ph.D. Thesis, Menofia University, Egypt, No- vember 2006. [23] M. Sayed and Y. S. Hamed, “Stability and Response of a Nonlinear Coupled Pitch-Roll Ship Model under Para- metric and Harmonic Excitations,” Nonlinear Dynamics, Vol. 64, No. 3, 2011, pp. 207-220. doi:10.1007/s11071-010-9841-0 [24] M. Sayed and M. Kamel, “Stability Study a nd Control of Helicopter Blade Flapping Vibrations,” Applied Mathe- matical Modelling, Vol. 35, No. 6, 2011, pp. 2820-2837. doi:10.1016/j.apm.2010.12.002 [25] M. Sayed and M. Kamel, “1:2 and 1:3 Internal Resonance Active Absorber for Non-Linear Vibrating System,” Ap- plied Mathematical Modelling, Vol. 36, No. 1, 2012, pp. 310-332. doi:10.1016/j.apm.2011.05.057 [26] Y. A. Amer and M. Sayed, “Stability at Principal Reso- nance of Multi-Parametrically and Externally Excited Mechanical System,” Advances in Theoretical and Ap- plied Mechanics, Vol. 4, No. 1, 2011, pp. 1-14. [27] M. Sayed, Y. S. Hamed and Y. A. Amer, “Vibration Re- duction and Stability of Non-Linear System Subjected to External and Parametric Excitation Forces under a Non- linear Absorber,” International Journal of Contemporary Mathematical Sciences, Vol. 6, No. 22, 2011, pp. 1051 - 1070. [28] A. H. Nayfeh, “Non-Linear Interactions,” Wiley/Inter- Science, New York, 2000.
|