Int. J. Communications, Network and System Sciences, 2011, 4, 778-789
doi:10.4236/ijcns.2011.432096 Published Online December 2011 (http://www.SciRP.org/journal/ijcns)
Biometric Signature of Private Key by Reliable Iris
Recognition Based on Flexible-ICA Algorithm
Aissa Boukhari, Salim Chitroub, Imen Bouraoui
Signal and Image Processing Laboratory, Telecommunication Department,
Electronics and Computer Science Faculty, University of Science and Technology of
Houari Boumedienne (USTHB), Algiers, Algeria
Received September 29, 2011; revised November 7, 2011; accepted November 20, 2011
Abstract
The numerical world is under a fast development generating facilities and threats. The recommended solu-
tions are especially the protection of information in all its states. The levels of protection show a discrepancy
from an application to another; governmental, commercial or even cybercriminal. The infrastructure used in
modern cryptography is based on public key cryptosystem. The problem is how to make safe the private key
and to memorize it without difficulties and damages. This paper introduces a biometric solution of owner
signature generating an encryption of the key using the iris recognition kept in a smart card. Several precau-
tions were taken to guarantee the safety and the availability of the use of the private key. They are two essen-
tial goals to attest: the quality of the service and the robustness of suggested safety. Being the quality of the
service, the used iris recognition is based on a new emerging method founded on Flexible-ICA algorithm.
This method offers a better Equal Error rate compared to other methods previously used. This quality of
recognition was also reinforced by an encoding of error using a flag and finally Reed Solomon encoder. For
recommended safety, a scheme based on block encryption is used. The proposed scheme is Propagating Ci-
pher Block chaining which offers a very propagation of a high level of confusion and diffusion. Indeed, the
robustness of this cryptographic process was studied by setting up strict criteria of safety.
Keywords: Image Processing, Cryptosystem, Public Key, Iris Recognition, Code Reed Solomon,
Independent Component Analysis (ICA)
1. Introduction
The current world of the data security lived a very im-
portant jump. The scopes of application are the crucial
factors requiring of the complex, robust and especially
owners schemes.
Nowadays, the E-commerce, E-banking, E-voting, and
so on became part of the daily people’s life. However,
the kind of cryptographic system used is of public keye.g.
RSA [1,2].The problematic of the human being is di-
vided in two parts. The first part is the robustness of the
private key. The second part is the manner of storage. In
the first part, the requirement implies that not only the
private key satisfy the criteria’s security of the concep-
tion of the public key cryptosystem, but also the length
of the key. As example of RSA, a public key of 2048 bits,
generated from the big primer numbers, is strongly rec-
ommended [3]. In the second part, some problems are
born following the realization of the first part. Indeed,
how could a human being remember such a large key e.g.
2048 bits?
Secure storage solutions have been proposed. The sub-
scription in a file easily accessible was avoided [4]. Also,
the passwords, that are typically short, are breakable and
susceptible to the dictionaries attacks [4] in which the
attacker tried several passwords lists to decrypt the cryp-
togram containing the private key.
In order to thwart these problems, we propose a bio-
metric signature method using the irises. This will achieve
three goals: Avoid the memorization of a short password.
By the way, the owner confidentiality and the authenti-
cation of the users are assured by a specific system to
each person. Finally, the no repudiation is related to the
user’s biometric features. No one can deny to have used
his or her specific biometric mean [5].
In the literature, several considerable approaches of

A. BOUKHARI ET AL.
779
security using the biometric data were proposed. There
are those that generate key’s encryption directly from the
biometric measures as Tomko et al. [6] using the finger-
prints. Gohand Ngo [7] used a random projection of
user’s face as source of keys generation. In 2001 Mon-
roses et al. [8] propose a combination of password with
the user’s voice. This last method has been compromised
by the small entropy of the biometric key which is about
46 bits [8]. An approach using the irises was proposed by
Hao et al. [9]. They used the smart card and a coding
chain achieved around the Reed Solomon and Hamming
encoder in order to procure a key of 140 bits.
Otherwise, the biometric systems have their own prob-
lems. For example the iris’s features scan of the same
person is almost always different e.g. from 10% to 20%
according to [10]. The second problem is the irrevocabil-
ity of the biometric signatures. Indeed, no one can store
the biometric features in the free spaces. This proves to
be dangerous because the attacker or the robber can take
the complete user’s identity.
In this work, we propose some solutions to these con-
straints. For the first constraint, we will use a new man-
ner of recognition of iris. It is Flexible-ICA algorithm for
reliable iris recognition. This method carried out recently
by giving a FFR (False Features rejection) which tends
towards zero.
Many researchers have worked on iris recognition in-
cluding image databases, and human iris authentication
process basically consists of four steps as follows: 1) iris
segmentation, where the iris is localized and isolated
from the noise due to sclera, pupil, eyelids and eyelashes;
2) normalization, where iris is mapped from rectangular
representation to domain polar representation; 3) feature
extraction, where a feature vector is formed which con-
sists of the ordered sequence of the features extracted
from the various representation of the iris images; 4) and
matching, where the feature vectors are classified through
different techniques such as Hamming Distance, weight
vector and winner selection, dissimilarity function, etc.
In our work, we first use Canny edge detection and
Hough transform for iris localization. Then, the extracted
iris region is normalized into a rectangular block with
constant dimensions to account for imaging inconsisten-
cies of Daugman’s model. We apply Flexible-ICA algo-
rithm to extract efficient feature vectors. Then, each iris
feature vector is encoded into an iris code. Finally, a
Hamming distance is used, for the matching process. We
demonstrate our experimental results using two different
subsets of CASIA-V3 iris image database and some
mathematical criteria, in order to compare this technique
against some other existing methods in order to assess its
usefulness.
For the second constraint, we propose to use a joint
solution. The first one was proposed in [11]. It is sum-
marized in the creation of a flag vector to correct the
features’ iris. The use of the flag will be distinctly more
efficient compared to the gotten results in [11]. In the
previous works one used the Daugman’s method [10]
having a bigger FFR in relation to the Flexible-ICA
method used in this paper. Also the complexity in the
works of Sheikh Ziauddin and Matthew N. Dailey [11] is
of 9600 bits for the features and 9600 bits for the masks.
In this paper the proposed method based on the Flexible-
ICA algorithm gives a FRR about 4% for a complexity
of 960 bits for the features. These results reduce strongly
the rejected bits by the vector flag. Thus, there will be an
effective features vector of about 960 bits on the one
hand and on the other hand a low FRR. Indeed, in the
jointed solution we propose to use an Error Encoder
Correction (EEC) of Reed Solomon to correct the errors.
With the good performances acquired by using Flexible-
ICA and the flag we will have an effective correction of
error at 100%.
To summarize the security of the private key, the user
enrolls himself to create his own public data, namely: a
vector flag and EEC code. These data will be store in a
smart card. The same smart card will contain the en-
crypted private key with a cipher block cryptosystem
using features of the iris like key encryption. The cipher
block cryptosystem used is Propagating Cipher Block
Chaining (PCBC). This mode of encryption was used in
Kerberos protocol conceived by MIT (Massachusetts
Institute of Technology) [12] which has given a strong
authentication client/server. In this paper we will show
the use of this mode PCBC assembled around standard
AES with 256 bits key for encrypting the user’s private
key.
2. Flexible-ICA for Features Extraction
2.1. Image Pre-Processing
The iris is an annular part between the pupil (inner
boundary) and the sclera (outer boundary). Therefore, a
captured image cannot be expected to have only the iris
part, it contains some non-useful part e.g. sclera, eyelid
and pupil, therefore the iris region should be located in
captured eye image, and normalized to polar array.
2.2. Iris Localization
Iris localization by definition means to isolate the actual
iris region in a digital eye image by detecting the inner
and outer boundaries of the iris. The eyelids and eye-
lashes normally occlude the upper and lower parts of the
iris region. To detect the iris and pupil boundaries,

780 A. BOUKHARI ET AL.
Hough transform is used by involving Canny edge detec-
tion to generate an edge map. The gradients are biased in
the vertical direction for the outer iris/sclera boundary
while the vertical and horizontal ones are weightede-
qually for the inner iris/pupil boundary, as suggested in
[13] and [14].
The Hough transform locates contours in an n-dimen-
sional parameter space by examining whether they lie on
curves of a specified shape. For the iris outer or pupillary
boundaries and a set of recovered edge points

,1
ii
x
yi n, a Hough transform is defined by
 
1
,, ,,,,
n
cc iicc
i

H
xyr hxyxyr

 (1)
where

,,
cc

H
xyr
,,
cc
shows a circle through a point, the
coordinates
x
yr define a circle by the following
equation
222
0
cc
xyr (2)
In the case of edge detection for iris boundaries, the
above equation becomes

22
20
ic ic
xxyy r (3)
The eyelids are then isolated by first fitting a line to
the upper and lower eyelid parts using a linear Hough
transform. A second horizontal line is then drawn, which
intersects with the first line at the iris edge that is closest
to the pupil. The second horizontal line allows a maxi-
mum isolation of eyelid regions while a threes holding
operation is used to isolate eyelashes.
2.3. Iris Normalization
Normalization refers to preparing a localized iris image
for the feature extraction process. The process involves
unwrapping iris image and converting it into its polar
equivalent. It is carried out by using Daugman’s Rubber
sheet model [15,16] as shown in Figure 1. The center of
the pupil is considered as the reference point and a re-
mapping formula is used to convert the points on the
Cartesian scale to the polar scale.
The remapping of iris image

,
x
y
I
from raw Carte-
sian coordinates to polar coordinates

,r


can be rep-
resented as
θ
θ
1
r r
0
Figure 1. Daugman’s rubber sheet model.






,,, ,

I
xr yrIr

   (4)
where r is on the interval [0, 1] and θ is angle [0, 2π],
with



 
 
,1
,1
PI
PI
xrrx rx
yrr yry





 

 



(5)
where
 

  
cos
sin
PPP
PPP
xOxr
yOyr









(6)
And
  
 

cos
sin
III
III
xOxr
yOyr









(7)
The centre of the pupil is denoted by

,
P
p
Ox Oy and


,
I
I
Ox Oy is the center of the iris; rP is the radius of
the pupil and
I
r is the radius of the iris; and


,
P
p
x
y
and


,
I
I
x
y are the coordinates of points bordering the
pupil’s radius and iris’ radius respectively along the di-
rection

.
2.4. Feature Extraction by ICA
The iris has an interesting structure and presents rich
texture information. The distinctive spatial characteris-
tics of the human iris are available at a variety of scales
[17]. As such, a well-known subspace analysis technique
such as Independent Component Analysis (ICA) is used
to capture local distinctive information in an iris and cre-
ates a set of compact features for an effective recognition
task.
2.4.1. Indepe ndent Compon ent Analysis
ICA represents a novel and powerful statistical method
for subspace analysis, with applications in computational
neuroscience and engineering. It consists of automati-
cally identifying the underlying components in a given
data set. It requires that at least as many simultaneously
recorded mixtures as there are components and each
mixture is a combination of components that are inde-
pendent and nongaussian. However, like all methods, the
success of ICA in a given application depends on the
validity of the assumptions on which ICA is based and
the results should be treated with caution. So, much
theoretical work remains to be done on precisely how
ICA fails when its assumptions, i.e. linear mixing and
statistical independence, are severely violated [18,19].
Generally, the most popular noising—free linear mo-
del of ICA is expressed as follows
X
AS

(8)

A. BOUKHARI ET AL.
781
where X is a vector variable, of dimension N, in which
each variable is an observed signal mixture and S is a
vector variable, of dimension M, in which each variable
is a source signal. We assume that N > M. The mixing
matrix A defines a linear transformation on S, which can
usually be reversed in order to recover an estimate U of S
from X, i.e.
SyWX (9)
where the separating matrix is the inverse of
A. However, A is an unknown matrix and cannot there-
fore be used to find W. Instead, many iterative algorithms
are used to approximate W in order to optimize inde-
pendence of S. In this paper, the Flexible-ICA algorithm
[20] is deployed.
1
WA


Since mutual information is the natural informa-
tion-theoretic measure of the independence of random
variables, it could be used as the criterion for finding the
ICA transform. In this approach, which is an alternative
to the model estimation approach, the ICA of a random
vector X is defined as an invertible transformation as in
(9), where the matrix W is determined so that the mutual
information of the transformed components of S is
minimized.
Mutual information is a natural measure of the de-
pendence between random variables. It can be inter-
preted by using the concept of differential entropy H of a
random vector y with density (.)
f
as follows [21]
 
log d
H
yfyfy
y
i
(10)
Entropy is considered as the coding length of the ran-
dom variable . In fact, it is defined as
,1
i
yi N
 
log
ii
i
H
yPyP
y (11)
However, mutual information I between the N (scalar)
random variables [22,23], is defined as
,1
i
yi N
 
12
,,, N
Ni
i
I
yyyHy Hy

 (12)
Using the invertible linear transformation presented in
(9). Mutual information [22], [21] is given by
 
12
,,,logdet
Ni
i
I
yyyHy HxW

 (13)
To search space of separating matrix or Stiefelmani-
fold W, let us consider that yi have been uncorrelated and
have unit variance. This means
TTT
EyyWExxWI
 

 
T
(14)
which implies
det1 detdetdetdet
TT T
I
WE xxWWE xxW
 
 

(15)
This implies that (det W) must be constant. In this case,
the minimization of mutual information leads to the fol-
lowing loss function

 
log ii LWp y (16)
The gradian of loss function (16) is given by
  
T
LW
LWy x
W


 
 (17)
where
 
11
,, T
NN
yy y  

 


 (18)
and
 
dlog
d
ii
i
i
py
yy   (19)
The natural Reimannian gradient in Stiefel Manifold
was calculated by [24] and it can be written as follows
 
 
T
TT
LWLW WLWW
yx yyW 
 

 (20)
With this, the learning algorithm for W takes the form
[25,26]


TT
WLWyyWyx 


 

 (21)
where η is a learning rate (small positive constant) and


y

is non-linear function, noted by
  
1
1
1log coshy
a
 

a y
2
(22)
where 1 1a

 is some suitable constant.
In the learning process, the increment should
satisfy the constraint
W
0
TT
WWW W

  (23)
2.4.2. Feature E xtraction
Image representations are often based on discrete linear
transformations of the observed data. Consider a black-
and-white image whose gray-scale value at the pixel in-
dexed by x and y, denoted by


,
I
xy . Many basic mod-
els in image processing express the image


,
I
xy as a
linear superposition of some features or basis functions


,
i
axy, that is
 
1
,
M
i
i,
i
I
xya xys

 (24)
where i
s
are feature coefficients. These basis functions,


y,
i
ax , are able to capture the inherent structure of the
iris texture. This, particularity allows us to apply ICA
and thus create a set of compact features for an effective
recognition task. Alternatively, we can just collect all the
pixel values in a single vector X, in which case we can
express the representation as in (8) for ICA model. We
assume here that the number of transformed components

782

A. BOUKHARI ET AL.
is equal to the number of observed variables. This type of
a linear superposition model gives a useful description
on a low level support where we can ignore such higher-
level nonlinear phenomena such as occlusions. For the
sake of simplicity, let us restrict ourselves here to the
simple case where the variables form an in-
vertible linear system, that is, the matrix A is square.
Then we can invert the system as:

,
i
axy

,

,,
ii
xy
s
wxyIxy (25)
where the wi denote the inverse filters of ICA.
In practice, we cannot model a whole image using the
model in (24). Rather, we apply it on image patches or
windows [18]. Thus we partition the image into patches
of n × n pixels and model the patches with the model in
(24). However, care must then be taken to avoid border
effects.
Before extracting the iris features, we note that the
ICA application is greatly simplified if the vector X of all
iris images is first whitened or sphered. There are two
common pre-processing steps. The first step is to center
the images as,

X
XEX in order to make their
local mean equal 0. The next step is to apply a whitening
transform B to the data such that
12 T
BDE

 (26)
with E corresponds to the eigenvectors of the covariance
matrix of X and the diagonal matrix D contains the re-
lated eigenvalues. The whitening process helps to uncor-
relate the data so that Principal Component Analysis
(PCA) can work with a unit variance. The whitened data
are used as the input for the Flexible-ICA algorithm [20],
demonstrated above, which computes a set of basis vec-
tor, wi from a set of iris images, and the images are pro-
jected into the compressed subspace to obtain a set of
coefficients, si. New test images are then matched to
these known coefficients by projecting them onto the
basis vectors and finding the closest coefficients in the
subspace.
2.5. Matching
It is very important to present the obtained feature vector
in a binary code because it is easier to determine the dif-
ference between two binary code-words than between
two number vectors. In fact, Boolean vectors are always
easier to compare and to manipulate. We have applied a
Hamming Distance matching algorithm for the recogni-
tion of two samples. It is basically an exclusive OR (XOR)
function between two bit patterns. Hamming Distance is
a measure, which delineates the differences of iris codes.
Every bit of a presented iris code is compared to the
every bit of referenced iris code, if the two bits are the
same, e.g. two 1’s or two 0’s, the system assigns a value
“0” to that comparison and if the two bits are different,
the system assigns a value “1” to that comparison. The
formula for iris matching is shown as follows
1
ii
H
DP
NQ


 (27)
where N is the dimension of feature vector, Pi is theith-
component of the presented feature vector, while Qi is
the ith component of the referenced feature vector.
3. Biometric Signature of Pri va te K ey
Process
3.1. User Enrollment
In this section one exposes the enrollment phase of the
owner user data. The data are: the flag vector, the EEC
code resulting from Reed Solomon encoding of the reli-
able iris features. The Figure 2 shows this enrollment
phase and the flag creation learning.
We note that the public key, mentioned in this figure,
is delivered to a certificate authority in order to generate
the certificate that contains their relative data. This part
won’t be studied in this paper. Our goal is to secure the
private key with an owner signature.
3.1.1. Vector Flag Generati o n
In practice, some iris areas of the same person are reli-
able than others. This is due to the pupil-irises boundary
and the irises-sclera boundary. The imperfection of de-
tection is present in the inner and outer circles. Because
of these difficulties, a user, wanting to be enrolled, pre-
sents n iris scan. In our case of experimentation n = 3.
For each iris scan one generates a template of 960 bits
of features. To create a single unify iris template T, the
flag is used. Indeed, to create the flag we detect in the
template iris scan the reliable bits which correspond to
the identical bits along n templates. To these positions
one assigns the value “1” for the vector flag if not the
assigned value is “0”. In this way the vector flag F was
build with 960 bits.
On the whole of the reliable bits, we take the first 523
bits. Finally the vector flag generated F is stored in a
smart card. The following gives an example for 3 tem-
plates of iris.
1010100111010101 The flag vector F is:
1111 0111 0111111 0
1010000101010100 The template unique T is:
1010001101010
1010100111010100

A. BOUKHARI ET AL.
783
Figure 2. Biometric signature of private key proce ss.
3.1.2. Template Encoding Using Reed Solomon
Encoder
3.1.2.1. Reed Solomon Encoder
Reed Solomon encoder, noted [27] is a cy-
clic encoder allowing the detection and the correction of
the errors per payload.This encoder is represented on the
Galois field of and consequently it transforms
a word of N symbols of m bits by adding

,RSNK


2m GF
RSN K


symbols of redundancies.
The length of the code word checks the following
equation [28]:

21 and 3
m
Nm (28)
The capacity of correction Reed Solomon encoder is
related to the minimal distance within the meaning of
Hamming. In other word, the smallest distance
min between two distinct code words from
the code.
1dNK
This shows that the encoder can correct


min 1
2
d
t


symbols of m bits.
3.1.2.2. The Template Encoding
During the enrollment one uses a flag vector that was
generated to select features of a common template called
T. This template was the result of the application of the
flag vector. And finally the first 523 bits were selected.
In this phase, a Reed code is generated by the encod-
ing T. In order to carry out this process, in Reed Solomon
encoding, important parameters will be given, namely: N,
K and t.
In our experiment, the length of the RS code is like
that adopted in [29].
This work followed the results found by Sim et al. [29]
in the recognition and the reduction of FRR from 26% to
2,9%. In this paper we propose the use of the Flexible-
ICAmethod which with its low level competitor FFR
with all the old methods. Like summary, the parameters
are: , 211023 bits
m
N250 bit
s
t, and
523 bitsK

. At the end of this phase, the RS code is
recorded in the smart card. See the Figure 2.
3.2. Private Key Encryption
In this second phase, the user’s smart card will receive
the essential data that is the encrypted private key. The
process of the private key encryption follows the scheme
represented in Figure 3. In this figure one notices that
the first 512 bits of the template T have been used like
encryption key.
The encryption scheme is a Propagating cipher block
chaining (PCBC) gone up around the standard AES (Ad-
vanced Encrypted Standard) of 256 bits key [25,26]. In
our work we use two initialization vectors VI1 and VI2 of
128 bits each taken from the two first 128 bits of the
template. As unique key of the blocks, we will use the
256 bits that follow the initialization vectors. The plain
text, in our case is the private key, will be shared in
blocks of 128 bits each for the encryption process.
The personalization of the PCBC scheme as using two
initialization vectors is justified as follow: The first VI1
vector is used classically to initialize the encryption of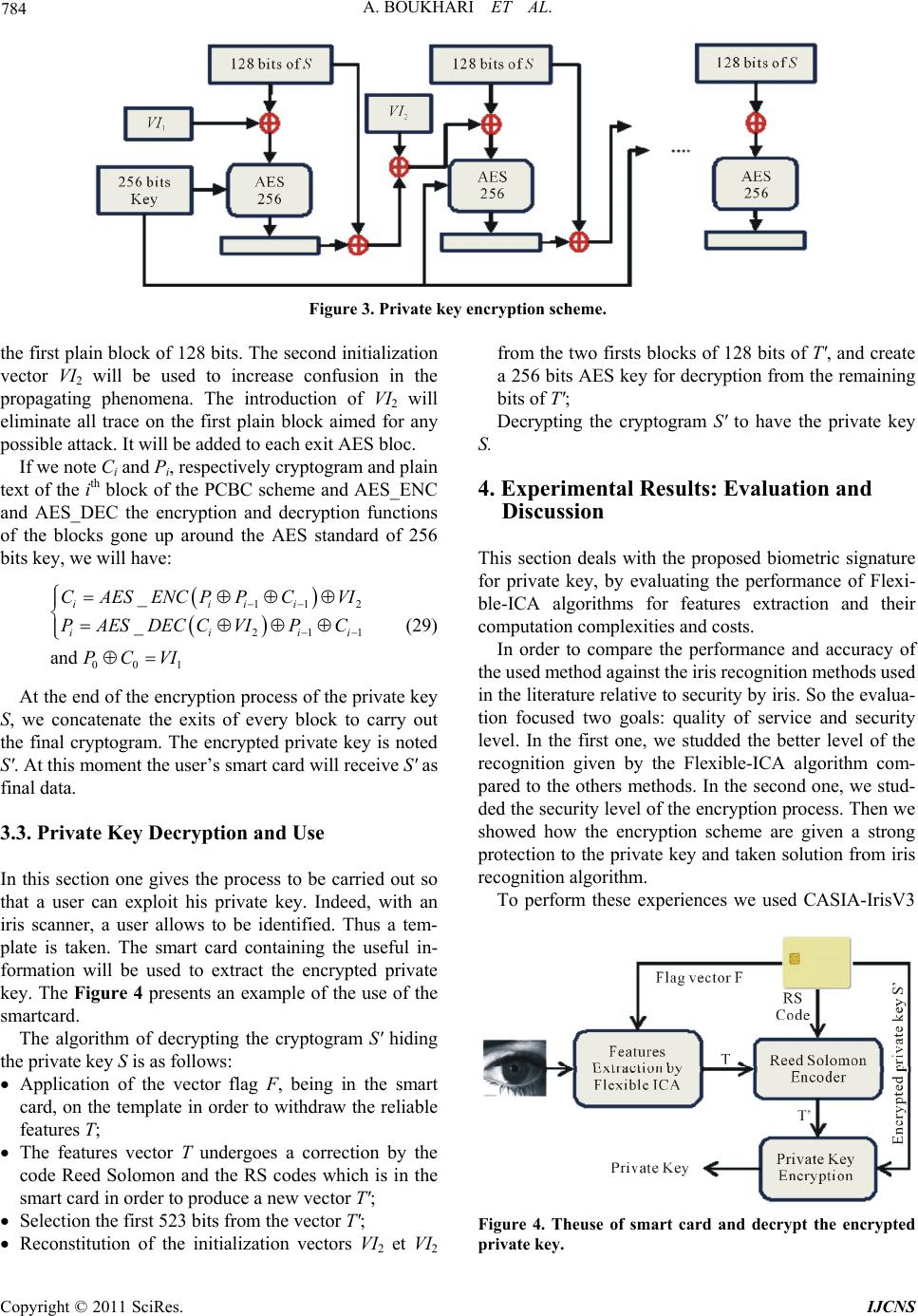

784 A. BOUKHARI ET AL.
Figure 3. Private key encryption scheme.
the first plain block of 128 bits. The second initialization
vector VI2 will be used to increase confusion in the
propagating phenomena. The introduction of VI2 will
eliminate all trace on the first plain block aimed for any
possible attack. It will be added to each exit AES bloc.
If we note Ci and Pi, respectively cryptogram and plain
text of the ith block of the PCBC scheme and AES_ENC
and AES_DEC the encryption and decryption functions
of the blocks gone up around the AES standard of 256
bits key, we will have:


11
21
00 1
_
_
and
iiii
iii
CAESENC PPCVI
PAESDECCVIPC
PCVI








2
1i


(29)
At the end of the encryption process of the private key
S, we concatenate the exits of every block to carry out
the final cryptogram. The encrypted private key is noted
S'. At this moment the user’s smart card will receive S' as
final data.
3.3. Private Key Decryption and Use
In this section one gives the process to be carried out so
that a user can exploit his private key. Indeed, with an
iris scanner, a user allows to be identified. Thus a tem-
plate is taken. The smart card containing the useful in-
formation will be used to extract the encrypted private
key. The Figure 4 presents an example of the use of the
smartcard.
The algorithm of decrypting the cryptogram S' hiding
the private key S is as follows:
 Application of the vector flag F, being in the smart
card, on the template in order to withdraw the reliable
features T;
 The features vector T undergoes a correction by the
code Reed Solomon and the RS codes which is in the
smart card in order to produce a new vector T';
 Selection the first 523 bits from the vector T';
 Reconstitution of the initialization vectors VI2 et VI 2
from the two firsts blocks of 128 bits of T', and create
a 256 bits AES key for decryption from the remaining
bits of T';
Decrypting the cryptogram S' to have the private key
S.
4. Experimental Results: Evaluation and
Discussion
This section deals with the proposed biometric signature
for private key, by evaluating the performance of Flexi-
ble-ICA algorithms for features extraction and their
computation complexities and costs.
In order to compare the performance and accuracy of
the used method against the iris recognition methods used
in the literature relative to security by iris. So the evalua-
tion focused two goals: quality of service and security
level. In the first one, we studded the better level of the
recognition given by the Flexible-ICA algorithm com-
pared to the others methods. In the second one, we stud-
ded the security level of the encryption process. Then we
showed how the encryption scheme are given a strong
protection to the private key and taken solution from iris
recognition algorithm.
To perform these experiences we used CASIA-IrisV3
Figure 4. Theuse of smart card and decrypt the encrypted
private key.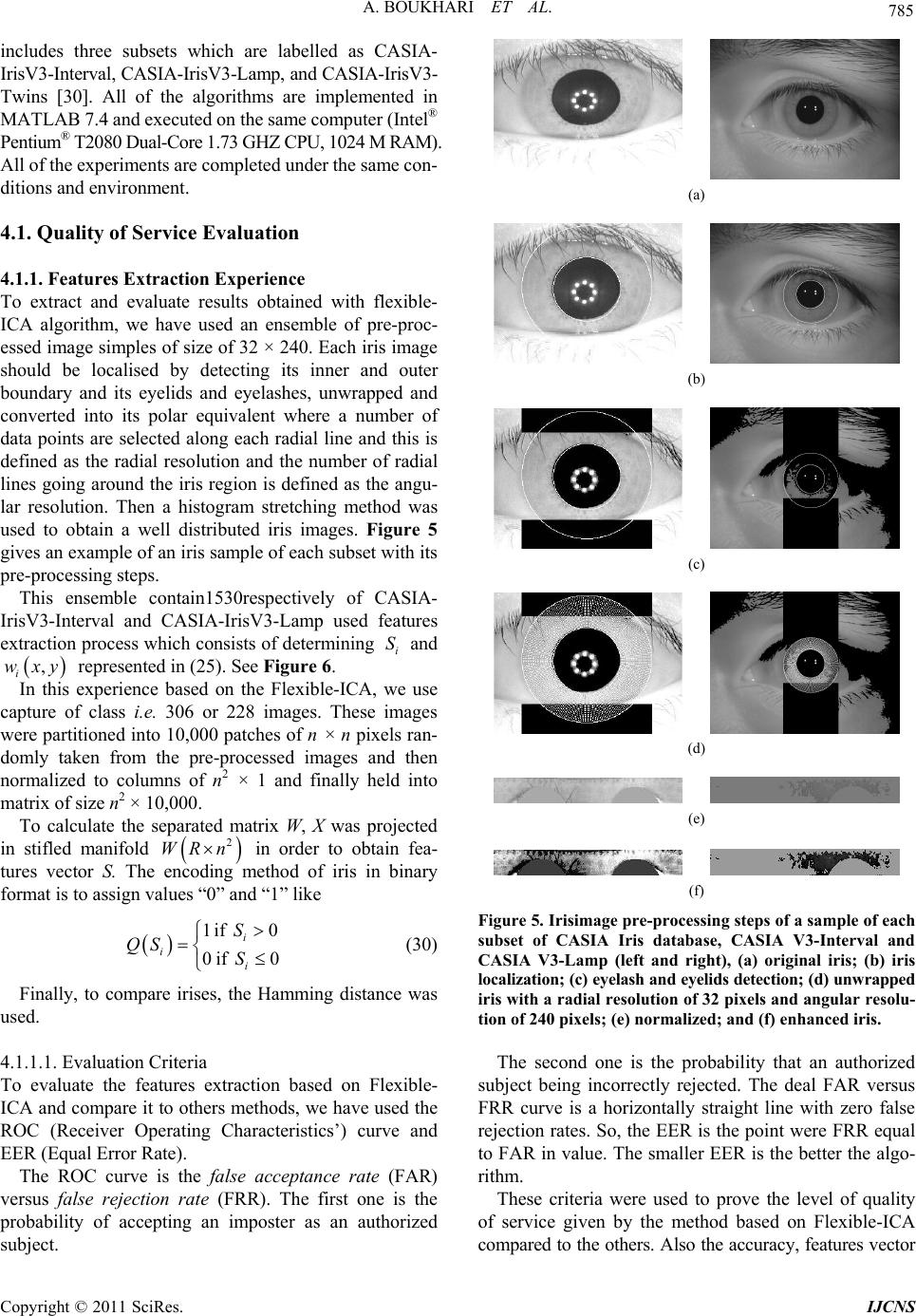

A. BOUKHARI ET AL.
785


includes three subsets which are labelled as CASIA-
IrisV3-Interval, CASIA-IrisV3-Lamp, and CASIA-IrisV3-
Twins [30]. All of the algorithms are implemented in
MATLAB 7.4 and executed on the same computer (Intel®
Pentium® T2080 Dual-Core 1.73 GHZ CPU, 1024 M RAM).
All of the experiments are completed under the same con-
ditions and environment.
4.1. Quality of Service Evaluation
4.1.1. Features Extraction Experience
To extract and evaluate results obtained with flexible-
ICA algorithm, we have used an ensemble of pre-proc-
essed image simples of size of 32 × 240. Each iris image
should be localised by detecting its inner and outer
boundary and its eyelids and eyelashes, unwrapped and
converted into its polar equivalent where a number of
data points are selected along each radial line and this is
defined as the radial resolution and the number of radial
lines going around the iris region is defined as the angu-
lar resolution. Then a histogram stretching method was
used to obtain a well distributed iris images. Figure 5
gives an example of an iris sample of each subset with its
pre-processing steps.
This ensemble contain1530respectively of CASIA-
IrisV3-Interval and CASIA-IrisV3-Lamp used features
extraction process which consists of determining and
represented in (25). See Figure 6.
i
S

,
i
wxy
In this experience based on the Flexible-ICA, we use
capture of class i.e. 306 or 228 images. These images
were partitioned into 10,000 patches of n × n pixels ran-
domly taken from the pre-processed images and then
normalized to columns of n2 × 1 and finally held into
matrix of size n2 × 10,000.
To calculate the separated matrix W, X was projected
in stifled manifold in order to obtain fea-
tures vector S. The encoding method of iris in binary
format is to assign values “0” and “1” like

2
WR n

1if 0
0if 0
i
i
i
S
QS S



 (30)
Finally, to compare irises, the Hamming distance was
used.
4.1.1.1. Evaluation Criteria
To evaluate the features extraction based on Flexible-
ICA and compare it to others methods, we have used the
ROC (Receiver Operating Characteristics’) curve and
EER (Equal Error Rate).
The ROC curve is the false acceptance rate (FAR)
versus false rejection rate (FRR). The first one is the
probability of accepting an imposter as an authorized
subject.
(a)
(b)
(c)
(d)
(e)
(f)
Figure 5. Irisimage pre-processing steps of a sample of each
subset of CASIA Iris database, CASIA V3-Interval and
CASIA V3-Lamp (left and right), (a) original iris; (b) iris
localization; (c) eyelash and eyelids detection; (d) unwrapped
iris with a radial resolution of 32 pixels and angular resolu-
tion of 240 pixels; (e) normalized; and (f) enhanced iris.
The second one is the probability that an authorized
subject being incorrectly rejected. The deal FAR versus
FRR curve is a horizontally straight line with zero false
rejection rates. So, the EER is the point were FRR equal
to FAR in value. The smaller EER is the better the algo-
rithm.
These criteria were used to prove the level of quality
of service given by the method based on Flexible-ICA
compared to the others. Also the accuracy, features vector

A. BOUKHARI ET AL.
786
X

ˆ
X
Figure 6. Block diagram of feature extraction process.
Table 1. Performance evaluation according to numbers of
independent component and image patches sizes of CASIA
V3-Interval and CASIA V3-Lamp.
size and complexity are given in the next section.
4.1.1.2. Results Study
For assess of the Flexible-ICA algorithm in its recogni-
tion, each iris is compared to all other irises at intra or
inter class of CASIA used subset. A total of 49,725 and
34,086 comparisons were executed respectively in CA-
SIA-V3-Interval and CASIA-V3-Lamp.
Database CASIA-V3-Interval CASIA-V3-Lamp
Win. size 8 × 8 16 × 16 8 × 8 16 × 16
56 0.10% 0.03% 15.69%12.48%
40 0.03% 0.10% 16.89%12.34%
32 0.16% 0.03% 16.88%15.54%
24 0.10% 0.34% 16.22%13.62%
20 0.14% 0.86% 16.19%18.09%
16 0.04% 0.45% 16.82%17.08%
12 0.16% 3.95% 19.93%20.83%
10 0.13% 3.72% 16.76%19.28%
ICs
8 0.13% 2.25% 18.34%23.96%
Figure 7 shows the large distribution of the distance
between the intra and inter class. Figure 7 reveals the
variation of visible illumination makes the distribution of
distance of CASIA-V3-Lamp is larger than the intra
class distance distribution of CASIA-V3-interal. This is
caused by bad results of phase localization and normali-
zation.
To evaluate the EERs, Table 1 shows results for R =
{56, 40, 32, 24, 20, 16, 12, 10, 8} and image patches size
of 16 × 16 or 8 × 8 pixels. We see that CASIA-V3-interval
gives EERs lower than 0.2%because of its good quality
resulting in extremely clear iris textures details. Like
general remark, we see that ERRs increase when ICA
coefficients decrease but when the information is strongly
affected by noise according some coefficients the per-
formance does not always decrease with reduction of
ICA coefficients.
features. These methods are: Daugman [16,31], Ma et al.
[32] and Tan et al. [33] using the CASIA-V3-interval iris
image database [30]. So, we only analyze and compare
the accuracy, efficiency and computational complexity.
Daugman represent the local shape of the iris details
by phase information and projected each small local re-
gion onto bank of Gabor filters, then he quantize the re-
sulting phase, denoted by complex valued coefficients, to
one of the four quadrants in the complex plane. The di-
mensionality of the features vector is 2048 components.
This observation is studded by results obtained with
CASIA-V3-Lamp. This is the same remark like accuracy
showed in Figure 6. To compare our results to others in
the next section we take the better value in Table 1.
Ma et al. method [32] constructs a set of intensity sig-
nals to contain the most important details of the iris and
makes use of stable and reliable local variations of the
4.1.1.3. Quality Service Study
In this section we present a comparison between three
methods, used in the literature, like security based on iris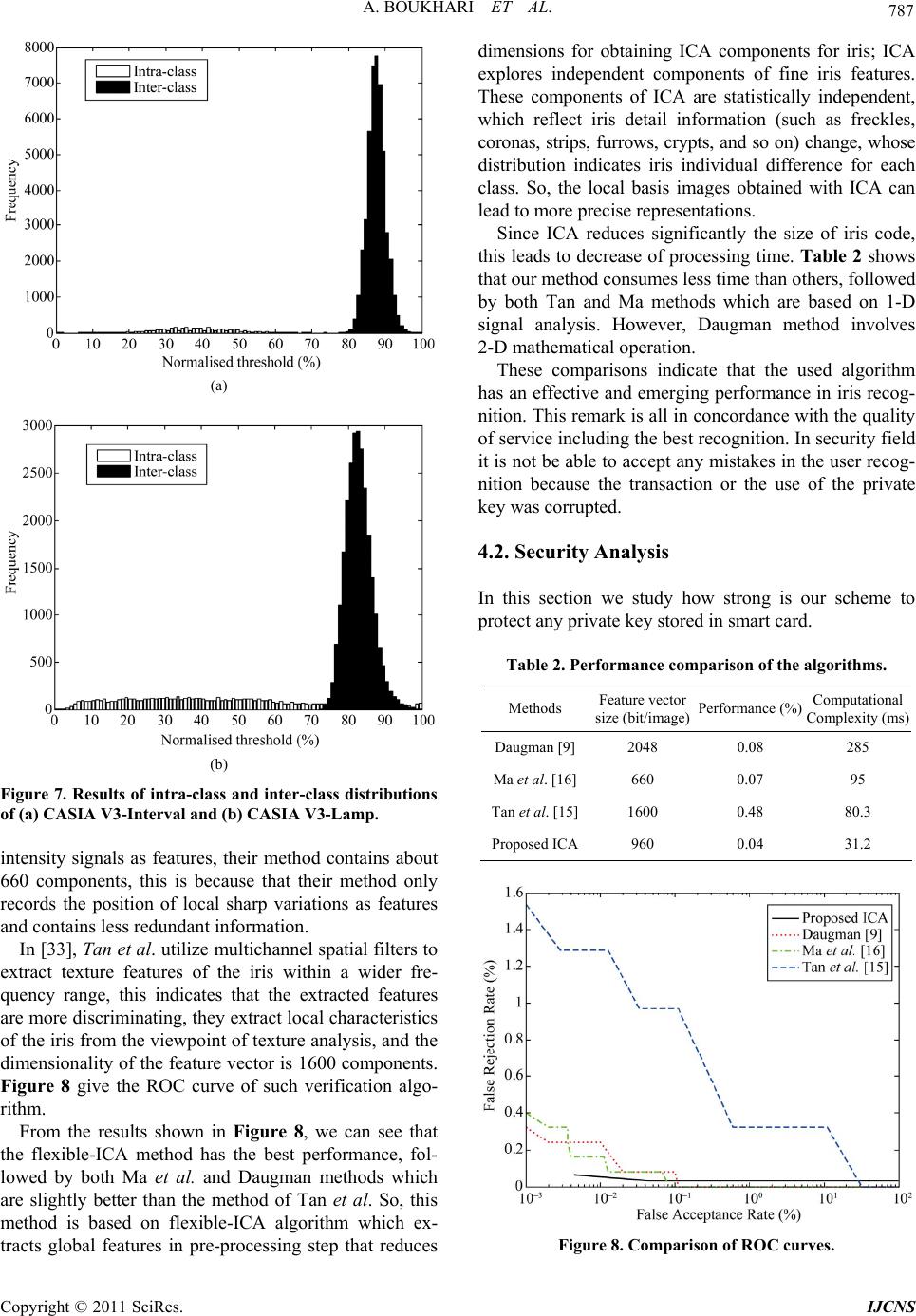

A. BOUKHARI ET AL.
787
(a)
(b)
Figure 7. Results of intra-class and inter-class distributions
of (a) CASIA V3-Interval and (b) CASIA V3-Lamp.
intensity signals as features, their method contains about
660 components, this is because that their method only
records the position of local sharp variations as features
and contains less redundant information.
In [33], Tan et al. utilize multichannel spatial filters to
extract texture features of the iris within a wider fre-
quency range, this indicates that the extracted features
are more discriminating, they extract local characteristics
of the iris from the viewpoint of texture analysis, and the
dimensionality of the feature vector is 1600 components.
Figure 8 give the ROC curve of such verification algo-
rithm.
From the results shown in Figure 8, we can see that
the flexible-ICA method has the best performance, fol-
lowed by both Ma et al. and Daugman methods which
are slightly better than the method of Tan et al. So, this
method is based on flexible-ICA algorithm which ex-
tracts global features in pre-processing step that reduces
dimensions for obtaining ICA components for iris; ICA
explores independent components of fine iris features.
These components of ICA are statistically independent,
which reflect iris detail information (such as freckles,
coronas, strips, furrows, crypts, and so on) change, whose
distribution indicates iris individual difference for each
class. So, the local basis images obtained with ICA can
lead to more precise representations.
Since ICA reduces significantly the size of iris code,
this leads to decrease of processing time. Table 2 shows
that our method consumes less time than others, followed
by both Tan and Ma methods which are based on 1-D
signal analysis. However, Daugman method involves
2-D mathematical operation.
These comparisons indicate that the used algorithm
has an effective and emerging performance in iris recog-
nition. This remark is all in concordance with the quality
of service including the best recognition. In security field
it is not be able to accept any mistakes in the user recog-
nition because the transaction or the use of the private
key was corrupted.
4.2. Security Analysis
In this section we study how strong is our scheme to
protect any private key stored in smart card.
Table 2. Performance comparison of the algorithms.
Methods Feature vector
size (bit/image)Performance (%) Computational Complexity (ms)
Daugman [9] 2048 0.08 285
Ma et al. [16]660 0.07 95
Tan et al. [15]1600 0.48 80.3
Proposed ICA 960 0.04 31.2
Figure 8. Comparison of ROC curves.

788 A. BOUKHARI ET AL.
4.2.1. Iris Key Space Analysis
If an attacker try to break our key used in encryption of
private key, he would be systematically search the 523
bits key space for the correct iris code. So, we see that as
long as, the iris code is kipped private and the brute force
or more sophistical attack on the cryptosystem used the
iris code is the best an attacker can do. In this focus, we
consider that the powerful attacker who has complete
knowledge on the correlation present between iris tem-
plate space as well as complete knowledge of the Reed
Solomon codeword space.
In the literature Daugman [10] has estimated the de-
gree of freedom in iris template to be 249 bits. It means
that these 249 bits are sufficient to reconstruct a valid iris
template for one person, and likewise, are capable of rep-
resenting the eyes of more than 2249 unique individuals.
In our case, if an attacker has complete knowledge of
the structure of the iris template space, he could simply
search 249 bits iris code. At each time a valid iris tem-
plate for an individual is checked the correctness from
Reed Solomon codeword. So this codeword can, in the
worse correction, recovery 250 bits or the iris code used
by the cryptosystem is equal to 523 bits. Then the at-
tacker by all that, he has to complete 24 bits.
To estimate the complexity attack time we assumed
that the time recovery of any code bit search is about 1
second then we have

249 24
Time BFA2Time RSseconds

 (31)
where, Time BFA is the time brute force attack and Time
RS the time Reed Solomon recovery. Well, it is long
time to do a best attack like this!
4.2.2. Aval a nche Effect
The avalanche effect is the desirable property of crypto-
system. It means that if an input changed slightly e.g.
flipping a single bit, the out put changes significantly e.g.
a half of out bits flip. So, in our work, we use an AES-
256 bit like a bloc cipher system, then the avalanche ef-
fect is obtained from the security of this standard [34].
Since we use a Propagating Cipher bloc Chaining
(PCBC), if a bit changed in ith bloc all flowed block
changed for more than half of bits. It could arrive to
change completely. For example at i = 1 (first block), if
the private key S, subject to encryption, changed at any
bit from the first bloc of 128 bits the encrypted form of S'
would change at most completely. This property is guar-
anteed by the propagating phenomena and this change
from bloc to other gives a best avalanche effect.
4.2.3. Confusion and Diffu sio n
Like avalanche effect, these two properties guaranteed a
statistical security means. Indeed, confusion is to avoid
any relationship between key and cipher text and diffu-
sion is to illuminate any redundancy in the plain text by
dissipate it in the statistic of cipher text.
At each bloc, of the used PCBC, the confusion and
diffusion are guaranteed systematically by AES-256 bit
in first. Then each block of 128 bits of private key S un-
dergone if own appropriate transformations. However,
our PCBC is mad by using two initialization vector vec-
tors VI1 and VI2. The first one mad a complete transfor-
mation in the first block of S before the encryption proc-
ess. Also the second block, of S, accepts its own com-
plete transformation by the second initialization vector
VI2 and the XOR of the first block and its encryption
form.
The phenomena of propagating use for the rest of
block a transformation of their block of S the XOR of the
plain and its encryption form of the previous block. All
those give transformed plain bloc to each block of used
AES. This is a guaranty of higher confusion and diffu-
sion mad in the private key before and after the encryp-
tion process.
5. Conclusions and Future Works
In this paper we have given a complete system for en-
crypt and secure the private key of any public key infra-
structure. Our contribution is to avoid any weak secure
scheme previously proposed to a secure storage of pri-
vate key. Our scheme is based on the use of biometric
signature by reliable iris recognition. The originality is in
the use of the Flexible-ICA for feature extraction with
partition of iris images into patches, and hamming dis-
tance for matching. Two iris image subsets of CASIA
iris V3 database have been used to evaluate the per-
formance of our system. Flexible-ICA algorithm, which
improves the quality of separation introducing a better
density matching and allows a faster learning, has been
adopted for computing the ICs.
Best results have been obtained. In the first, the quality
of recognition, given by the way a high quality of service
to recovery the private key without any error in the key
encryption. To eliminate any probability of error, a joint
flag and Reed Solomon encoder have used. Secondly, the
proposed scheme has been evaluated to prove its robust-
ness.
Like future works, we propose to use the Noisy-ICA
algorithm for features extraction. This method avoids
any problems made by the multiplicative and additive
noise in iris scan.
6. References
[1] W. Stallings, “Cryptography and Network Security: Prin-

A. BOUKHARI ET AL.
789
ciples and Practice,” 3rd Edition, Prentice Hall, Saddle
River, 2003.
[2] R. F. Churchhouse, “Codes and Ciphers,” Cambridge Uni-
versity Press, Cambridge, 2004.
[3] C. Paar and J. Pelzl, “Understanding Cryptography,” Sprin-
ger-Verlag, Berlin, Heidelberg, 2010, p. 173.
[4] B. Schneier, “Applied Cryptography—Protocols, Algo-
rithms, and Source Code in C,” 2nd Edition, John Wiley
& Sons, Inc., New York, 1996.
[5] D. R. Stinson, “Cryptography: Theory and Practice,” 2nd
Edition, CRC Press, Boca Raton, 2002.
[6] G. Tomko, C. Soutar and G. Schmidt, “Biometric Control-
led Key Generation,” United States Patent No. 5680460,
1997.
[7] A. Goh and D. Ngo, “Computation of Cryptographic Keys
from Face Biometrics,” Proceedings of International Con-
ference on Communications and Multimedia Security,
Torino, 2-3 October 2003, pp. 1-13.
[8] F. Monrose, M. K. Reiter, Q. Li and S. Wetzel, “Crypto-
graphic Key Generation from Voice,” Proceedings of the
IEEE Symposium on Security and Privacy, Oakland, 14-
16 May 2001, pp. 202-213.
[9] F. Hao, R. Anderson and J. Daugman, “Combining Cry-
pto with Biometrics Effectively,” IEEE Transactions on
Computers, Vol. 55, No. 9, 2006, pp. 1081-1088.
doi:10.1109/TC.2006.138
[10] J. Daugman, “The Importance of Being Random: Statis-
tical Principles of Iris Recognition,” Pattern Recognition,
Vol. 36, No. 2, 2003, pp. 279-291.
doi:10.1016/S0031-3203(02)00030-4
[11] S. Ziauddin and M. N. Dailey, “Robust Iris Verification
for Key Management,” Pattern Recognition Letters, Vol.
31, No. 9, 2009, pp. 926-935.
doi:10.1016/j.patrec.2009.12.028
[12] Massachusetts Institute of Technology, “Kerberos: The
Network Authentication Protocol,” august 2011.
http://www.web.mit.edu/kerberos/
[13] C. Tisse, L. Martin, L. Torres and M. Robert, “Person Iden-
tification Technique Using Human Iris Recognition,” Pro-
ceedings of 15th International Conference on Vision In-
terface, Calgary, 27-29 May 2002, pp. 294-299.
[14] R. P. Wildes, “Iris Recognition: An Emerging Biometric
Technology,” Proceedings of the IEEE, Vol. 85, No. 9,
1997, pp. 1348-1363. doi:10.1109/5.628669
[15] S. Sanderson and J. Erbetta, “Authentication for Secure
Environments Based on Iris Scanning Technology,” IEEE
Colloquium on Visual Biometrics, London, 2 March 2000,
pp. 8/1-8/7.
[16] J. G. Daugman, “How Iris Recognition Works,” IEEE
Transsctions on Circuits and Systems for Video Techno-
logy, Vol. 14, No. 1, 2004, pp. 21-30.
doi:10.1109/TCSVT.2003.818350
[17] J. Wayman, A. Jain, D. Maltoni and D. Maio, “Biometric
Systems, Technology, Design and Performance Evalua-
tion,” Springer, London, 2005.
[18] Hyvarinen, J. Karhunen and E. Oja, “Independent Com-
ponent Analysis,” John Wiley, Hoboken, 2001.
doi:10.1002/0471221317
[19] J. V. Stone, “Independent Component Analysis,” MIT Press,
Cambridge, 2004.
[20] S. Choï, A. Cichocki and S. Amari, “Adaptative Blind Sig-
nal and Image Processing: Learning Algorithms Applica-
tions,” John Wiley & Sons, Hoboken, 2002.
[21] A. Papoulis, “Probability, Random Variables, and Stochas-
tic Processes,” 3rd Edition, McGraw-Hill, Boston, 1991.
[22] T. M. Cover and J. A. Thomas, “Elements of Information
Theory,” Wiley, Hoboken, 1991.
doi:10.1002/0471200611
[23] P. Comon, “Independent Component Analysis—A New
Concept?” Signal Processing, Vol. 36, No. 3, 1994, pp. 287-
314. doi:10.1016/0165-1684(94)90029-9
[24] S. Amari, “Natural Gradient for Over- and Under-Com-
plete Bases in ICA,” Neural Computation, Vol. 11, No. 8,
1999, pp. 1875-1883. doi:10.1162/089976699300015990
[25] National Institute of Standards and Technology (NIST),
“Advanced Encryption Standard,” NIST, FIPS PUB 197,
US Department of Commerce, 2001.
http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[26] M. Dworkin, “Recommendation for Block Cipher Modes
and Operations,” NIST Special Publication 800-38A, 2001.
[27] C. Berrou, “Codes et Turbo Codes,” Springer-Verlag, Paris,
2007. ISBN 13: 978-2-287-32739-1
[28] J. Proakis and M. Salehi, “Digital Communications,” 5th
Edition, McGraw-Hill, Boston, 2007.
ISBN-13: 978-0072957167
[29] S. H. Moi, P. Saad, N. A. Rahim and S. Ibrahim, “Error
Correction on IRIS Biometric Template Using Reed So-
lomon Codes,” IEEE 4th Inernationnal Conference on Ma-
thematical/Analytical Modelling and Computer Simula-
tion (AMS), Kota Kinabalu, 26-28 May 2010, pp. 209-214.
doi10.1109/AMS.2010.50
[30] Download the Application form at the Website:
http://www.cbsr.ia.ac.cn/IrisDatabase.html
[31] J. Daugman, “High Confidence Visual Recognition of Per-
sons by a Test of Statistical Independence,” IEEE Tran-
sactions on Pattern Analysis and Machine Intelligence, Vol.
15, No. 11, 1993, pp. 1148-1161. doi:10.1109/34.244676
[32] L. Ma, T. Tan, Y. Wang and D. Zhang, “Efficient Iris Re-
cognition by Characterizing Key Local Variations,” IEEE
Transactions on Image Processing, Vol. 13, No. 6, 2004,
pp. 739-750. doi:10.1109/TIP.2004.827237
[33] L. Ma, T. Tan, Y. Wang and D. Zhang, “Personal identi-
fication based on iris texture analysis,” IEEE Transac-
tions on Pattern Analysis and Machine Intelligence, Vol.
25, No. 12, 2003, pp. 1519-1533.
doi:10.1109/TPAMI.2003.1251145
[34] C. E. Shannon, “Communication Theory of Secrecy Systems,”
Bell System Technical Journal, Vol. 28, No. 4, 1949, pp.
656-715.