Int. J. Communications, Network and System Sciences, 2011, 4, 761-769
doi:10.4236/ijcns.2011.432094 Published Online December 2011 (http://www.SciRP.org/journal/ijcns)
LDPC-Coded OFDM Transmission Based on Adaptive
Power Weights in Cognitive Radio Systems
Seyed Eman Mahmoodi, Bahman Abolhassani
School of Electrical Engineering, Iran University of Science and Technology (IUST), Tehran, Iran
Received October 9, 2011; revised November 17, 2011; accepted November 30, 2011
Abstract
In this paper, we propose a new scheme to improve the performance of an LDPC-coded OFDM based cogni-
tive radio (CR) link by applying adaptive power weights. To minimize estimation errors of detected signals
in all the CR subcarriers, power weights are allocated to the CR subcarriers at the secondary transmitter.
Some constraints for the power weights are considered, such as keeping the interference power introduced by
the CR to primary users below a given interference threshold and also keeping sum of transmission powers
in all CR subcarriers within a total transmission power. The LDPC decoder applies these power weights in
the Log Likelihood Ratios (LLRs) used in message passing scheme at the secondary receiver to achieve
more reliable communications. So, the received signal in each CR subcarrier will be decoded with the
knowledge of transmission power weights, which come from the cognitive feedback channel without addi-
tional cost. Simulation results demonstrate that our proposed scheme achieves a lower bit error rate and a
higher transmission rate compared with those of the same scheme without applying power weights.
Keywords: Cognitive Radio, OFDM, LDPC, Interference, Power Weighting
1. Introduction
Transmission of data over wireless communication sys-
tems grows rapidly. Cognitive Radio (CR) systems have
made it feasible to utilize the frequency spectrum, dy-
namically and efficiently. A CR system allows coexist-
ing of an unlicensed secondary user (SU) with a licensed
primary user (PU) on the same frequency spectrum.
However, CR systems should consider the mutual inter-
ference introduced by these two groups of users to each
other. If this mutual interference is not considered or is
considered inaccurately, the spectrum efficiency of both
systems could be corrupted. So, one of the main goals for
a cognitive radio is to provide a reliable besides high
data rate transmission in coexistence with a PU [1].
On the other hand, Low Density Parity Check (LDPC)-
coded Orthogonal Frequency Division Multiplexing
(OFDM) systems have many advantages, which provide
both reliability and high data rate communications for
CR systems. OFDM transmission makes it feasible to
null the subcarriers whose frequency bandwidths are oc-
cupied by PUs. As well, applying FFT in this modula-
tion provides an ease of implementation for analysis of
the spectrum in other tasks of CR [2]. Moreover, LDPC
codes can improve bit error rate (BER), considerably in
fading channels by applying appropriate decoders [3].
So far, performances analysis of LDPC-coded OFDM
systems have been discussed in different communication
environments [3-9]. In [3], the authors study the BER of
LDPC codes in block fading channels. They consider
that channel state information (CSI) is known in both
transmitter and receiver. As well, the use of iterative
message passing technique is considered as an efficient
approach and is used for decoding in these error correc-
tion codes [4]. The utilization of Log Likelihood Ratio
(LLR) during this iterative decoding as the reliability
factor is investigated and it is shown that the BER is im-
proved [5]. Moreover, use of message passing scheme
for decoding of LDPC codes is considered jointly with
cooperative spectrum sensing, which is discussed in [6].
Applying LDPC codes in a CR is considered in [7], too.
The authors in [7] show that how much improvement in
BER can be made by different LDPC decoding algo-
rithms.
Throughput maximization of an LDPC-coded OFDM
system is also very important, specifically for high data
rate wireless transmission [8]. In [8], the authors derive
the optimal power allocation for an LDPC coded system

762 S. E. MAHMOODI ET AL.
to improve the throughput of the system. However, the
problem of mutual interference introduced by different
systems to each other is a high priority constraint for
throughput maximization in CR systems. In [9], the au-
thors analyze the performances of LDPC-coded OFDM
systems while users are experiencing the mutual inter-
ference. However, in this paper, we consider these sys-
tems in cognitive environment. In [10], effect of noise
plus interference power introduced by PUs to the CR
system is investigated, and the interference power intro-
duced by SUs to the Pus is considered as a constraint.
However, this paper does not consider throughput maxi-
mization of the CR system. In our paper, we propose an
iterative scheme for message passing in the LDPC de-
coder, while in the secondary transmitter, power weights
for each OFDM subcarrier is considered to improve both
BER and throughput of the CR. Moreover, since there is
a cognitive feedback channel between secondary trans-
mitter and secondary receiver, we apply these power
weights in the LDPC decoder as used in the secondary
transmitter. This causes improvement in the performance
of the CR for error corrections.
The rest of this paper is organized as follows. Section
2 describes the system model. In Section 3, we propose
our new scheme in two subsections. First, we achieve the
power weights and then apply LDPC coding by these
power weights. Section 4 discusses simulation results by
comparing with classical scheme. Finally, Section 5 con-
cludes the paper.
2. System Description
We consider a single link between a secondary transmit-
ter and a secondary receiver while there are many PUs,
which have occupied M OFDM subchannels. This single
CR communication link uses LDPC-coded OFDM whose
block diagram is shown in Fi gu r e 1.
As it can be observed from Figure 1, there is a cogni-
tive feedback channel in CR systems, which provides the
information related to spectrum sensing, estimation of
interference threshold and channel state information (CSI)
to the secondary transmitter [1]. This information is pro-
vided by secondary receiver or cognitive sensors, which
usually sense the spectrum cooperatively and then inform
the secondary transmitter by a fusion center. In addition
to dynamic spectrum decision, the secondary transmitter
in the system model applies this information for power
allocation. We consider that this feedback channel is
perfect (no error in received information).
Using the Shannon capacity formula for the CR sys-
tem, and considering an ideal coding scheme, the trans-
mission rate at the OFDM subcarrier i is given by:




2
2
2
1
,log1
ss
ii
ss
iii Mm
wi
m
hP
RPh f
J 




 





, (1)
where the frequency spacing between CR subcarriers is
f

Hz, 2
w

denotes the variance of thermal noise and
i
P denotes the transmission power of the CR subcarrier
i. As well,

2
ss
i
h is the instantaneous channel gain of
the subcarrier i between SU’s transmitter and receiver
and

m
i
J
shows the interference power introduced by
PU’s subchannel m to the CR subcarrier i. There are M
subchannels which are occupied by PUs. Since, the CR
system has no information about instantaneous channel
gains between PUs’ transmitters and the secondary re-
Channel model
Cognitive Feedback
Channel
Transmitted
data streamLDPC EncoderOFDM Modulator Channel (Hss)
Thermal noise
Adaptive Power
weighting 
Interference introduced
by primary users
OFDM
Demodulator
LDPC Decoder
Received Data
Stream
Detector and
Spectrum Sensors
CSI & Interference
Threshold Estimator

Secondary Receiver
Secondary Transmitter
Figure 1. Block diagram of LDPC-coded OFDM in a cognitive radio link.

S. E. MAHMOODI ET AL.
763
ceiver and modulation strategy of PUs, precise calcula-
tion of the interference power introduced by PUs is in-
feasible for the CR. On the other hand, estimation of
these interference powers,

m
i
J
(for all ),
is possible at the SU’s transmitter. However, for consid-
ering PUs’ activities, the CR needs to update the estima-
tion of the interference powers, periodically. This is im-
practical for large number of OFDM subchannels, which
consists of CR subcarriers and the subchannels occupied
by PUs. This makes the CR very slow to perform estima-
tion at the secondary receiver and then feedback to the
SU’s transmitter for transmission power weighting.
1, 2,,mM
Since, we consider an imperfect spectrum sensing and
we cannot estimate noise variance plus the sum interfere-
ence power introduced by PUs accurately, applying
LDPC coding seems an efficient solution to have a CR
system with an acceptable performance. To make this
LDPC coding even more efficient, using message pas-
sing scheme, power weights are passed to the LDPC de-
coder to be used for a more efficient decoding.
We assume a linear model for the received voltage
signal, as


 
,
ss
i
yiwhixini=+ (2)
where denotes the signal weight of CR subcarrier i.
Also,
i
w

x
i and

y
i are the transmitted and received
voltage signals in CR subcarrier i, respectively and


ni
denotes total power of interference generated by M sub-
channels of PUs and received by the CR receiver in sub-
carrier i and thermal noise, which is AWGN with zero
mean and variance 2
w

. The receiver should estimate

ˆ
x
i, the transmitted signal in each subcarrier. Using
[11], the LS estimation of

ˆ
x
i is given by
 

  


0, 0,
ˆ,
ss ss
ii ii
yi ni
xi xi
wPhiwPhi
 (4)
where 0,i denotes the initial power of CR subcarrier i,
which has equal value for all N subcarriers, that is
P
0, 1, 2,,.
T
i
P
Pi
N
N (5)
In Equation (4), noise and the interference coming
from PUs are included in wi. Also, from Equation (4), the
variance of the LS estimation of

ˆ
x
i is given by



2
1
2
0,
1.
Mm
wi
m
iss
ii
J
wP hi



 
2
(6)
This equation shows that to minimize Δi, for small
values of the ratio of the channel gain to noise plus in-
terference, weight of transmission power should be
increased.
2
i
w
3. Proposed Scheme
In this section, we propose our new scheme which con-
sists of two important phases. In the first phase, we
achieve transmission power weights in all CR subcarriers
at the secondary transmitter. Then, using these power
weights in the LDPC decoder of the CR receiver, we
improve system performance of the CR in the second
phase. In the following two subsections, we explain these
two phases.
3.1. Phase I: Calculations of Power Weights
Knowledge on the summation of interference powers
introduced by PUs is infeasible in this system model, and
applying Equation (1) for rate maximization in LDPC-
coded system is inefficient. So, we consider the objective
function proposed in [12], to achieve power weights. We
write the summation of estimation errors of


ˆ
x
i,
1, 2,, iN

, for all N subcarriers of the CR system as




2
11
1
12 2
2
00
0,
,,,. (7)
Mm
wi
NN
m
Ni ss
ii
ii
J
ww w
wP hi

 


 


By considering Equation (7) normalized to the noise
variance plus summation of interference powers intro-
duced by PUs as the objective function, we solve opti-
mization problem to allocate adaptive transmission po-
wer weights for each secondary subcarrier. Then, we use
these weights in the LDPC decoding.
By minimizing Δ, signal estimation errors decrease. In
other words, by maximizing inverse of Δ, actually, we
consider the maximization of the total signal to interfere-
ence plus noise (SINR) in all CR subcarriers. However,
as was expressed in system description, the CR is un-
aware of the transmission power levels of the PUs and
their channel gains to the secondary receivers, so calcu-
lation of the interference introduced by PUs is infeasible.
So, we normalize the sum of estimation errors (Δ) to
noise plus sum interference. This normalization results in
calculation of suboptimum transmission power weights


2.
i
ws However, the optimization problem would be
feasible without knowing the noise plus interference
power. Also, the optimization problem has some con-
straints, which should be noted for reliable communica-
tions in the primary system and total transmission power
of the SU. This optimization problem could be mathe-
matically written as,


12
2
0,
0
max ,
i
Nss
ii
wi
wP hi


 (8)

S. E. MAHMOODI ET AL.
764
,
t
h
subject to,


 2
,
10
,
MN m
iimi
mi
I
dw I


 (9)
2
0,
0
,
N
ii T
i
wP P


 (10)
where


2
,,
m
iimi

I
dw represents the interference power
introduced by CR subcarrier i to the primary subchannel
m, which is a function of power weight in that subcarrier
and the spectral distance between the CR subcarrier i and
primary subchannel m, written by ,im [13]. By nor-
malizing Equation (7) to noise plus sum interference and
d
inversing


2
2
0,
1ss
ii
wP hi






, 1, 2,,kN

, we maxi-
mize total received signal powers in all CR subcarriers
using Equation (8), instead of minimizing Equation (7).
It’s notable that in this optimization problem the inter-
ference powers introduced to the PUs should be kept
below an interference threshold, I(th) (Inequality (9)).
Also, Inequality (10) represents that the sum value of the
weighted transmission powers in N secondary subcarriers
should be PT, at maximum. Although, the objective func-
tion in Equation (8) causes increasing the transmission
power, both Inequalities (9) and (10) prevent increasing
transmission powers to meet threshold interference (I(th))
and peak transmit power (PT).
By applying convex optimization for this problem, de-
fining the cost function by Equation (8), applying La-
grange multipliers (α and β) for two constraints in Ine-
qualities (9) and (10) and considering Karush-Kahn-Tuc-
ker (KKT) Conditions [14], we have


 4
0,
2
1
0,
10.
Mm
iii
ss m
i
IPw
Ph i


 

 



(11)
From Equation (11), can be derived as
2
i
w
 

2
2
0, 0,
1
1.
iMms
iki
m
w
IPPhi





 



s
(12)
To obtain α and β, we use a similar algorithm pro-
posed in [12]. We consider the two constraints expressed
in Inequalities (9) and (10). By setting power weights
obtained using Equation (12) into Inequalities (9) and
(10) and applying an iterative algorithm, which is men-
tioned below in two steps, these parameters would be
obtained.
1) With respect to the definition of

for the con-
straint of total power, we first set 0

 in Equation
(12) to obtain α by Inequality (9), as




2
1
1
1.
Mm
i
Nm
T
th ss
i
I
P
NIhi













(13)
2) Using α obtained from Equation (13) and assuming
initial β, we check the total power constraint given by
Inequality (10). Iteratively, we add to previous β until the
total power constraint in (10) is satisfied.
Since by applying Step 2, all the power weights de-
crease, so the interference constraint given by Inequality
(9) would not be violated in iterations. Therefore, by ob-
taining the two Lagrange multipliers, power weights are
obtained. Moreover, we observe that these power weight
are independent from noise plus sum interference.
3.2. Phase II: LDPC Decoding Using Power
Weights
In the first phase, we used power weights of OFDM sig-
nals in CR subcarriers at the secondary transmitter to
reduce the estimation errors of detected signals. Use of
error correction codes, by applying Low-Density Parity
Check (LDPC) codes, which is one of the most efficient
coding schemes in wireless communications, is investi-
gated in the second phase by applying the power weights
obtained in Phase I. Since, we have applied a blind
scheme to transmit signals without knowledge on the
interference power of PUs to each CR subcarrier; use of
wireless channel coding schemes, such as LDPC codes
improves efficiency of the CR system against the noise
plus interference. So far, we have assumed ideal coding
in our power loading schemes. However, by encounter-
ing unsteady noise plus interference power, use of LDPC
codes in the CR system could be considered for error
correction to recover the variance of noise plus interfere-
ence uncertainty. It’s notable that by applying LDPC
codes, transmission rate and error rate of the CR system
is improved against interference and noise. In the LDPC
decoder, we use message passing scheme to correct bit
errors as an iterative solution. The power weights ob-
tained in Phase I of the proposed algorithm and Equation
(12) could be considered in the Log Likelihood Ratio
(LLR) of iterative message passing scheme in the LDPC
decoder to reduce error rates or increase the transmission
rate of the CR system. So, the error rate performance of
the LDPC coded OFDM system with an iterative decoder
is totally characterized without knowledge on the inter-
ference power of PUs on the CR receiver.
We assume a sparse parity check matrix with coding
rate of 1/2. As shown in [5], the log-likelihood ratio
(LLR) with BPSK modulation is given by

S. E. MAHMOODI ET AL.
765





2
12
ln ,
1
1, 2,,,
dem dem
nn n
ndem
nn
pr syy
L
pr sy
nK





(14)
where n
s
and are n’th transmitted and received
bit streams among K bits in each packet and

dem
n
y
2

de-
notes the AWGN noise plus interference power.
Considering the power weights obtained by Equation
(12) and the iterative algorithm mentioned in 3.1, we set
the LLRs based on these power weights. Since, we have
no knowledge about interference powers in CR subcar-
rier i; we consider noise variance, 2
w

, instead of noise
plus interference. So, for the variance of transmitted sig-
nals in CR subcarrier i, we write


2
2
2
0,
,1,2,,
w
iss
ii
i
wP hi

 
.N (15)
Theorem: the LLR in CR subcarrier i for n’th bit
stream by received signal can be set as

,
dem
ni
y
 2
,
,2
2,1,2, ,,1,2, ,.
dem
ini
ni
w
wy
LnKi

 N (16)
which causes to improve the error rate performance in
the new scheme.
proof: The conditional probability density function
(pdf) of received bit stream n in this system model can be
considered as

2
,0,
2
,2
1exp .
2
2π
niii n
yni
yPws
p














(17)
By assuming uniform distribution of probability in BPSK
modulation (pr (sn = 1) = pr (sn = –1) = 0.5), and consid-
ering (14), obtained LLR from the channel is written as




 2
,0, ,
,2
,
12
ln ,
1
1, 2,,,1, 2,,,
dem dem
nni iini
ni dem
nni
pr syww Py
L
pr sy
nKiN




 
(18)
On the other hand, we should consider the value of
noise plus the interference power introduced by PUs to
the CR (σ2). Since, we have no information to estimate
the interference power introduced by PUs; this could be
estimated as AWGN variance [15]. So, we have
 2
1
,
Mm
wi
m
J2



 (19)
where σ2 is the variance of normal distribution. So, by
considering the normalized variance of transmitted sig-
nals in CR subcarrier i (Equation (15)), the variance of
LLR could be written based on 2
w

. Therefore Equation
(16) is concluded from Equation (18). It’s notable that
the achieved LLR is normalized to the fix value of .
0,i
We observe that the LLR given by Equation (16) relies
on demodulated signal bits, noise variance and the trans-
mission power weights in each CR subcarrier, which is a
function of the channel gain between SU’s transmitter
and SU’s receiver, and interference introduced to the
PUs by CR subcarriers. Therefore, by comparing the
received signals decoded by the usual message passing
scheme with the one decoded by the new scheme (ap-
plying weighted LLRs in the decoder), better error rate
performance for the new scheme is achieved.
P
Thus, we have an adaptive weighted LDPC-coded
OFDM system. By this channel coding in the CR system,
we use the power weights and derive the proposed
scheme to reduce the error rate of the LDPC-coded CR
system based on OFDM. It is notable that in this coded
system model; transmission rate in unit of bits/sub-
channel can be given by [9]
,
s
NI
RB

 (20)
where N denotes the number of CR subcarriers, Is repre-
sents number of information bits per subcarrier, and B
denotes number of subcarrier bits per OFDM symbol.
In summary, we illustrate the two phase proposed
scheme in a flowchart, which is shown in Figure 2 . In the
CR, we initialize transmit power of CR subcarriers with
uniform distribution. From the cognitive feedback chan-
nel, we have the CSI between secondary transmitter and
secondary receiver and sum interference power, which is
introduced by CR to the PUs. Due to power weights cal-
culations, we use a loop. By initialization of Lagrange
multiplier β and satisfying Constraint (9) in the optimiza-
tion problem, we obtain Lagrange multiplier α. So, we
calculate power weights by Equation (12). Now, if these
power weights satisfy Constraint (10), desired power
weights are achieved. Else, by adding appropriate ε to β,
power weights are decreased to finally satisfy Constraint
(10). So, power weights for all CR subcarriers are
achieved and used for CR transmission. We apply these
power weights in LLRs of the LDPC decoder for each bit
stream for all CR subcarriers to improve the system per-
formance. As we illustrated in this section and we ob-
serve in the next section, by applying Equation (16) in-
stead of Equation (14) in message passing, error rate
decreases and transmission rate of the CR system in-
creases.
4. Simulation Results
In this section, BER and transmission rate of the pro-

766 S. E. MAHMOODI ET AL.
Calculate α by Equation (13)
Calculate power weights
by Equation (12)
Yes
No
0,
/1,2,, & =0 ,
iT
PPNi N


,
Applying the obtained power weights in
LLRs of decoder based on Equation (16)
for each bit stream in all CR subcarriers
, 1,2,...,,1,2,...,.
ni
LiNn K 
End
Initialize transmit powers in all CR subcarriers
& Lagrange multiplier () 
2
(, =1,2,...,)
i
wi N
2
,
1
Is ?
N
ioi T
i
wP P



Set

 
()
()
1
() Update CSI () and interference
introduced by CR (), =1,2,...,
ss
Mm
i
m
i
I
h
iN



Figure 2. Flowchart of the proposed scheme.
posed two phase scheme is evaluated by using simulation
results. Here, we consider the system model, which is
discussed in Section 2 by simulation parameters as shown
in Table 1. We consider a weighted LDPC coded-OFDM
based CR system coexisting with a number of PUs with
M occupied subchannels. SU’s receiver senses spectrum
and feedbacks data to the SU’s transmitter. In simula-
tions, we consider a uniform distribution for spectral
situations of OFDM subchannels which have been occu-
pied by PUs. Then, by considering the value of false
alarm probability and detection of occupied subchannels,
spectrum sensing is done. By knowing the CSI between
secondary transmitter and receiver, and the sum inter-
ference introduced to PUs by CR, power weighting is
performed. According to the flowchart, which is shown
in Figure 2, the power weights are obtained and sent to
Table 1. Simulation parameters.
Parameter Value
# of CR subcarriers (N) 40
# of occupied PUs’ subchannels (M) 24
False alarm probability 0.15
Symbol duration (Ts) 0.4 μs.
Coding rate 1/2
PU’s transmit power in each occupied subchannel 2 × 10–4 W
the decoder. In the second phase, LDPC decoding is per-
formed by applying the obtained power weights in the
LLRs, which is obtained and proved in the previous sec-
tion. By using these new LLRs in each demodulated bit
stream, and comparing the received bit stream to the
transmitted bit stream, error rate can be calculated. As
well, transmission rate is presented in terms of total
transmission power and the interference power intro-
duced by CR to the PUs. In these simulations N which is
the number of subcarriers allocated to the CR and M are
40 and 24, respectively. We assume that 30% of PUs
occupies the specified frequency bandwidth of the pri-
mary system. False alarm probability is 0.15. In the CR
system, sampling time is 0.4 μs; 5 bits are used in each
frame and 20000 frames are applied for each packet. As
well, we consider a 20 × 10 parity check matrix made by
using sparse LU decomposition method [16]. Channel
model between SU’s transmitter and receiver, and chan-
nel model between SU’s transmitter and each of PUs’
receivers are assumed to be Rayleigh fading and average
channel gain of these channels is –10 dB.
We consider our proposed scheme, which applies mes-
sage passing for the LDPC decoding with the LLRs re-
lied on the power weights of the transmitted signal in
each CR subcarrier and we compare its performance with
the same LDPC coded-OFDM based CR system without
applying power weights in the message passing scheme
for decoding.
Figure 3 shows bit error rate (BER) of the proposed
scheme versus received SINR for our proposed scheme
and the same scheme without using power weights, both
experiencing CR environment. In this figure, the inter-
ference threshold introduced to the PUs is assumed to be
2 × 10–4 W. We observe that our proposed scheme achi-
eves lower error rates by increasing SINR, so that BER
of our proposed scheme is 4 × 10–4 at SINR = 10 dB,
while BER of the same system without using power
weights increases to 5 × 10–4, which is more than ten
times higher.
In Figure 4, we plot the transmission rate of the CR
system in Megabits/seconds versus total transmission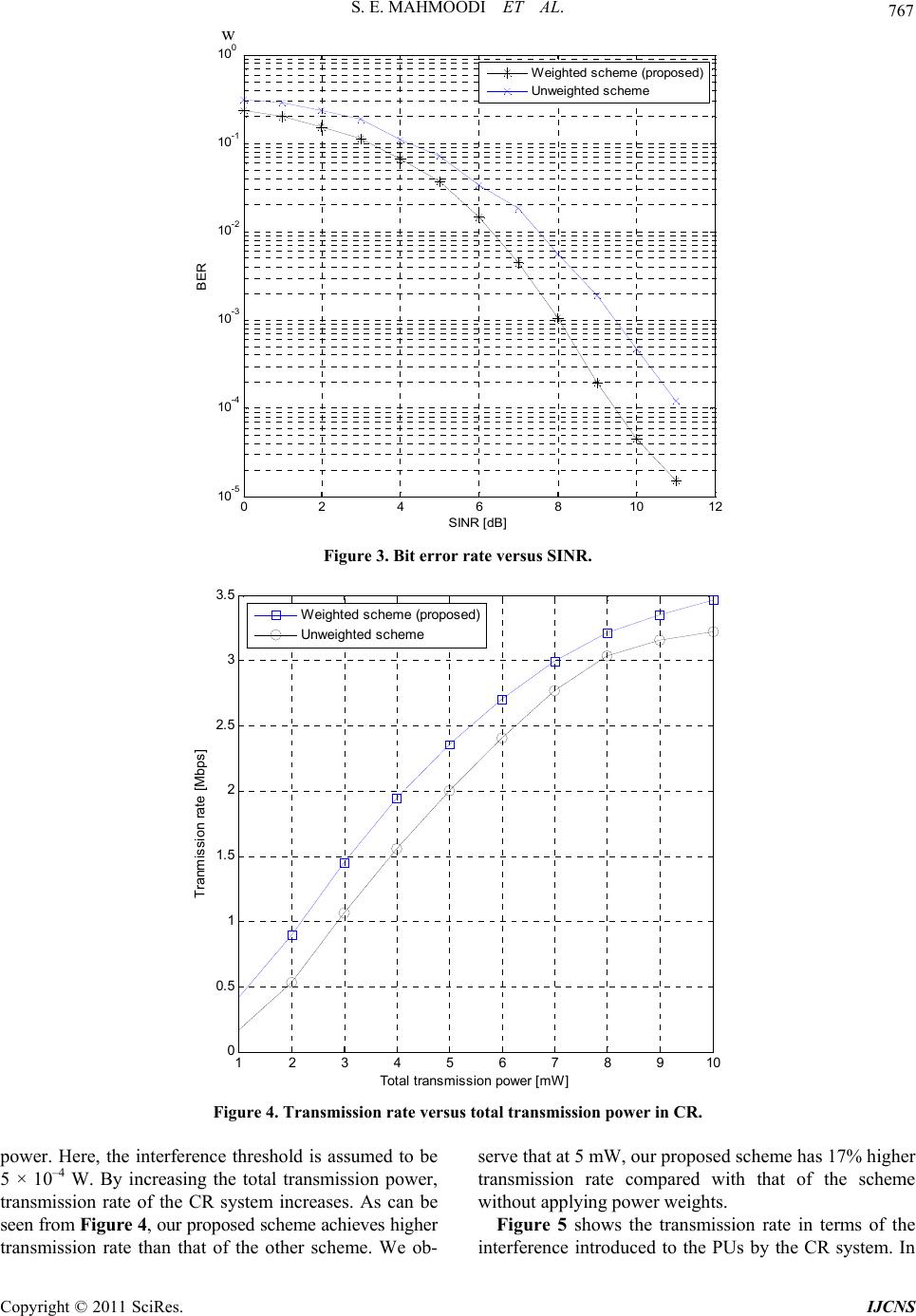

S. E. MAHMOODI ET AL.
767
w
02 4 6 810 12
10-5
10-4
10-3
10-2
10-1
100
SINR [dB]
BER
Wei ghted sc hem e (propos ed)
Unweight ed scheme
Figure 3. Bit error rate versus SINR.
12 3 4 5 6 7 8 910
0
0. 5
1
1. 5
2
2. 5
3
3. 5
Total transmission power [mW]
Tranmission rate [Mbps]
Weight ed s cheme (propos ed)
Unweighted scheme
Figure 4. Transmission rate versus total transmission power in CR.
power. Here, the interference threshold is assumed to be
5 × 10–4 W. By increasing the total transmission power,
transmission rate of the CR system increases. As can be
seen from Figure 4, our proposed scheme achieves higher
transmission rate than that of the other scheme. We ob-
serve that at 5 mW, our proposed scheme has 17% higher
transmission rate compared with that of the scheme
without applying power weights.
Figure 5 shows the transmission rate in terms of the
interference introduced to the PUs by the CR system. In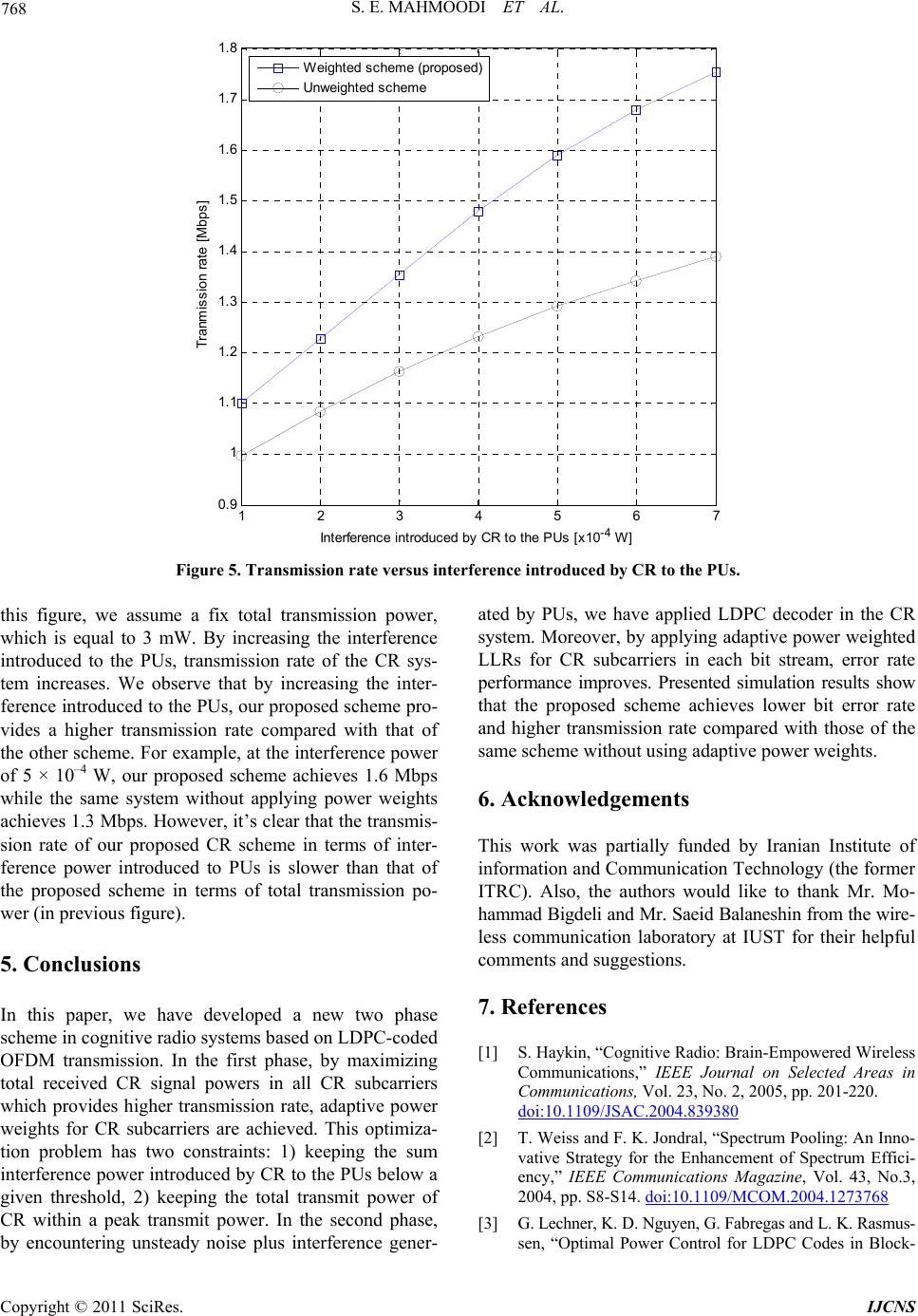

768 S. E. MAHMOODI ET AL.
1234567
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
Int erferenc e introduced by CR t o t he P Us [x10
-4
W]
Tranmi ss ion rat e [Mbps ]
Weight ed s cheme (proposed)
Unweighted sc heme
Figure 5. Transmission rate versus interference introduced by CR to the PUs.
this figure, we assume a fix total transmission power,
which is equal to 3 mW. By increasing the interference
introduced to the PUs, transmission rate of the CR sys-
tem increases. We observe that by increasing the inter-
ference introduced to the PUs, our proposed scheme pro-
vides a higher transmission rate compared with that of
the other scheme. For example, at the interference power
of 5 × 10–4 W, our proposed scheme achieves 1.6 Mbps
while the same system without applying power weights
achieves 1.3 Mbps. However, it’s clear that the transmis-
sion rate of our proposed CR scheme in terms of inter-
ference power introduced to PUs is slower than that of
the proposed scheme in terms of total transmission po-
wer (in previous figure).
5. Conclusions
In this paper, we have developed a new two phase
scheme in cognitive radio systems based on LDPC-coded
OFDM transmission. In the first phase, by maximizing
total received CR signal powers in all CR subcarriers
which provides higher transmission rate, adaptive power
weights for CR subcarriers are achieved. This optimiza-
tion problem has two constraints: 1) keeping the sum
interference power introduced by CR to the PUs below a
given threshold, 2) keeping the total transmit power of
CR within a peak transmit power. In the second phase,
by encountering unsteady noise plus interference gener-
ated by PUs, we have applied LDPC decoder in the CR
system. Moreover, by applying adaptive power weighted
LLRs for CR subcarriers in each bit stream, error rate
performance improves. Presented simulation results show
that the proposed scheme achieves lower bit error rate
and higher transmission rate compared with those of the
same scheme without using adaptive power weights.
6. Acknowledgements
This work was partially funded by Iranian Institute of
information and Communication Technology (the former
ITRC). Also, the authors would like to thank Mr. Mo-
hammad Bigdeli and Mr. Saeid Balaneshin from the wire-
less communication laboratory at IUST for their helpful
comments and suggestions.
7. References
[1] S. Haykin, “Cognitive Radio: Brain-Empowered Wireless
Communications,” IEEE Journal on Selected Areas in
Communications, Vol. 23, No. 2, 2005, pp. 201-220.
doi:10.1109/JSAC.2004.839380
[2] T. Weiss and F. K. Jondral, “Spectrum Pooling: An Inno-
vative Strategy for the Enhancement of Spectrum Effici-
ency,” IEEE Communications Magazine, Vol. 43, No.3,
2004, pp. S8-S14. doi:10.1109/MCOM.2004.1273768
[3] G. Lechner, K. D. Nguyen, G. Fabregas and L. K. Rasmus-
sen, “Optimal Power Control for LDPC Codes in Block-

S. E. MAHMOODI ET AL.
769
Fading Channels,” IEEE Transactions on Communica-
tions, Vol. 59, No. 7, 2011, pp. 1759-1765.
doi:10.1109/TCOMM.2011.051311.090238
[4] H. Futaki and T. Ohtsuki, “Performance of Low-Density
Parity-Check (LDPC) Coded OFDM Systems,” IEEE In-
ternational Conference on Communications (ICC), Vol. 3,
2002, pp. 1696-1700. doi:10.1109/ICC.2002.997138
[5] M. Jiang, C. Zhao, E. Xu and L. Zhang, “Reliability-
Based Iterative Decoding of LDPC Codes Using Likeli-
hood Accumulation,” IEEE Communications Letters, Vol.
11, No. 8, 2007, pp. 677-679.
doi:10.1109/LCOMM.2007.070450
[6] J. Lei, R. Yates, P. Spasojevic and L. Greenstein, “Coop-
erative Sensing of Primary Users in Cognitive Radio Net-
works Based on Message Passing,” 43th Annual Confer-
ence on Information Sciences and Systems (CISS), Balti-
more, 18-20 March 2009, pp. 568-573.
doi:10.1109/CISS.2009.5054784
[7] A. Baker, S. Soumik Ghosh, A. Kumar and M. Bayoumi,
“LDPC Decoder: A Cognitive Radio Perspective for Next
Generation (XG) Communication,” IEEE Circuits and
Systems Magazine, Vol. 7, No. 3, 2007, pp. 24-37.
doi:10.1109/MCAS.2007.904180
[8] B. Lu, Y. Guosen and W. Xiaodong, “Performance Ana-
lysis and Design Optimization of LDPC-coded MIMO
OFDM Systems,” IEEE Transactions on Signal Process-
ing, Vol. 52 , No. 2, 2004, pp. 348-361.
[9] Y. Li and W. E. Ryan, “Mutual-Information-Based Adap-
tive Bit-Loading Algorithms for LDPC-Coded OFDM,”
IEEE Transactions on Wireless Communications, Vol. 6,
No. 5, 2007, pp. 1670-1680.
doi:10.1109/TWC.2007.360369
[10] A. Jovicic and P. Viswanath, “Cognitive Radio: An In-
formation-Theoretic Perspective,” IEEE Transactions on
Information Theory, Vol. 55, No. 9, 2009, pp. 3945-3958.
[11] W. Lingfan, E. K. S. Au, P. W. C. Chan, R. D. Murch, R.
S. Cheng, H. M. Wai and V. K. N. Lau, “Effect of Carrier
Frequency Offset on Channel Estimation for SISO/MIMO
OFDM Systems,” IEEE Transactions on Wireless Com-
munications. Vol. 6, No. 5, 2007, pp. 1854-1863.
doi:10.1109/TWC.2007.360387
[12] S. E. Mahmoodi and B. Abolhassani, “Two New Power
Allocation Schemes for an OFDM Cognitive Radio with
No Knowledge on Primary Users’ Interference,” submit-
ted to the International Journal of Communication Sys-
tems, 2011.
[13] T. Weiss, J. Hillenbrand, A. Krohn and F. K. Jondral,
“Mutual Interference in OFDM-based Spectrum Pooling
Systems,” Proceeding of IEEE 59th Vehicular Technol-
ogy Conference, Milan, 17-19 May 2004, pp. 1873-1877.
[14] S. Boyd and L. Vandenberghe, “Convex Optimization,”
Cambridge University Press, Cambridge, 2004.
[15] G. Bansal, M. J. Hossain and V. K. Bhargava, “Optimal
and Suboptimal Power Allocation Algorithms for OFDM-
Based Cognitive Radio Systems,” IEEE Transaction on
Wireless Communications, Vol. 7, No. 11, 2008, pp. 4710-
4718. doi:10.1109/T-WC.2008.07091
[16] S. Xiangran and Sh. Dongxin, “Design and Optimization
of LDPC Encoder Based on LU Decomposition with Si-
mulated Annealing,” International Conference on Com-
puter Science and Service System (CSSS), Nanjing, 27-29
June 2011, pp. 2181-2184.
doi:10.1109/CSSS.2011.5974805