Int. J. Communications, Network and System Sciences, 2010, 3, 406-412
doi:10.4236/ijcns.2010.34052 blished Online April 2010 (http://www.SciRP.org/journal/ijcns/)
Pu
Unified Performance and Availability Model for Call
Admission Control in Heterogeneous Wireless Networks
Ramesh Babu H. Siddamallaiah1, Gowrishankar Subramanian2, Piriyapatna S. Satyanarayana3
1Department of Information Science and Engineering, Acharya Institute of Technology, Bangalore, India
2Department of Computer Science and Engineering, B.M.S. College of Engineering, Bangalore, India
3Department of Electronics and Communication Engineering, B.M.S. College of Engineering, Bangalore, India
Received January 31, 2010; revised February 27, 2010; accepted March 25, 2010
Abstract
The system capacity of wireless networks varies temporally. This may be due to the dynamic allocation of
the channels and also the mobility of the users. The change in capacity will create greater impact on the sys-
tem performance parameters. This variation of capacity particularly poses a greater challenge to the research
community to ensure the Quality of Service (QoS) as it affects the call blocking probability which is one of
the important QoS parameters. This paper proposes a performance model for call admission control and the
availability model for a heterogeneous wireless network environment. The proposed model is able to handle
three types of traffic considered for the study includes conversation traffic, interactive traffic and background
traffic. The unified performance-availability model is developed using the Stochastic Area Networks (SAN).
The performance of both analytical models and the SAN based performance-capacity models are verified by
taking the call blocking probabilities for all the three types of traffics.
Keywords: Call Admission Control, Call Blocking Probability, Heterogeneous Wireless Networks, Stochastic
Activity Networks, Quality of Service
1. Introduction
There is tremendous increase in the growth of wireless
communication technologies which is evidently indicated
by exponential increase in the wireless communication
technologies usage. This popularity obviously demands
the next stage beyond third-generation (3G) networks to
include multiple wireless access technologies, all of wh-
ich will coexist in a heterogeneous wireless access net-
work environment [1,2] and use a common IP core to
realize user-focused service delivery. The coexistence of
Heterogeneous radio access technologies (RATs) is be-
coming mandatory to fulfill the needs of the growing
users’ community of wireless technologies. This in turn
will noticeably amplify the intensity in development of
different high-speed multimedia services, such as video
on demand, mobile gaming, Web browsing, video strea-
ming, voice over IP and e-commerce etc. Seamless in-
tersystem roaming across heterogeneous wireless access
networks will be a major feature in the architecture of
next generation wireless networks [3]. It is very well
evident that no single RAT can provide ubiquitous cov-
erage and continuously high quality service (QoS), the
mobile users may have to roam among various radio ac-
cess technologies to keep the network connectivity active
to meet the applications/users requirements. With the
increase in offered services and access networks, effi-
cient user roaming and management of available radio
resources becomes decisive in providing the network
stability and QoS provisioning. The future users of mobi-
le communication look for always best connected (ABC)
anywhere and anytime in the Complementary access
technologies like Wireless Local Area Networks (WL-
AN), Worldwide Inter operability for Microwave Access
(WiMAX) and Universal Mobile Telecommunication
Systems (UMTS) which may coexist with the satellite
networks [4-6].
With this prevalent scenario of user mobility, ensuring
the required radio resources to the users is a highly chal-
lenging task. In spite of failures in hardware, software, or
combination of these two may still make the wireless
networks to work and support the users. But there will be

R. B. H. SIDDAMALLAIAH ET AL. 407
a definite effect on the system capacity, i.e., the number
of channels available and number of users that can be
accommodated by the wireless networks may decrease
and the throughput of the system will come down. This is
an important aspect concerned to performance modelling.
There is a strong need of performance modelling which
should be able to take care of not only the pure perform-
ance but also the availability and reliability model of the
system. But most of the performance models will con-
sider this contention and generally over estimate the sit-
uation and will not consider the failure–recovery of the
systems resources in turn the traditional availability mo-
dels are not considering the performance metrics. There
is a need for a composite model which will work on fail-
ure recovery model.
Researchers have achieved success in developing tech-
niques for modelling the performance, availability and
reliability of communication systems in a unified way.
There are good number of approaches that have proved
the need of unified performance model and availability
models of any stochastic system under study. In this pa-
per we have proposed composite Performance and Avai-
lability models and are evaluated using the stochastic
petrinet.
The further sections of the paper are organized as fol-
lows. The Section 2 presents the performance model for
call admission control. Section 3 focuses on the Avail-
ability model. The Section 4 represents SAN based per-
formance-availability of the CAC system and Section 5
is devoted to discuss the simulation results and Section 6
concludes the paper.
2. Performance Model
In this paper we propose a novel analytic performance
model admission control mechanism for reducing the call
blocking probability there by increasing the resource
utilization. This would achieve the objective of guaran-
teeing the user QoS requirements. The proposed model is
able to handle three types of traffic considered for the
study includes conversation traffic, interactive traffic and
background traffic. All of this traffic represents different
QoS service class of traffic with the following QoS pa-
rameters.
The conversational traffic is sensitive to transfer delay
and jitter. It demands guaranteed bit rate and low bit er-
ror rate. The examples of the applications belonging to
this category are video-conferencing and audio confer-
encing. The interactive traffic is a QoS class that is not
sensitive to transfer delay and Jitter but demands low bit
error rate. The applications of this QoS class do not need
guaranteed bit rate for example web browsing, interac-
tive chats and interactive games. The background traffic
QoS class is not sensitive to transfer delay and jitter but
needs low bit error rate from the network and these ap-
plications do not depend on guaranteed bit rate. The ex-
amples belonging to this group are e-mail, SMS applica-
tions. The assumption made for the design and develop-
ment of analytical CAC model was type3 traffic would
require three channels to be assigned in the system and
type2 traffic demands two channels and type1 traffic
needs one channel.
The proposed model is developed keeping in mind the
WCDMA, WiFi, and WiMax. The CAC mechanism
proposed is focused only on the system’s ability to ac-
commodate newly arriving users in terms of the total
channel capacity which is needed for all terminals after
the inclusion of the new user. In the case when the chan-
nel load with the admission of a new call was precom-
piled (or computed online) to be higher than the capacity
of the channel the new call is rejected, if not, the new
call could be admitted. The decision of admitting or re-
jecting a new call in the network will be made only based
on the capacity needed to accommodate the call.
We consider a heterogeneous network which com-
prises a set of RATs Rn with co-located cells in which
radio resources are jointly managed. Cellular networks
such as Wireless LAN and Wi-Max can have the same
and fully overlapped coverage, which is technically fea-
sible, and may also save installation cost. H is given as H
{RAT 1, RA T 2, RAT k} where k is the total number of
RATs in the heterogeneous cellular network. The het-
erogeneous cellular network supports n-classes of calls,
and each RAT in set H is optimized to support certain
classes of calls.
The analytical model for call admission control mec-
hanism in heterogeneous wireless networks is modelled
using higher order Markov model and is as shown in
Figure 1. In the proposed model it is assumed that,
whenever a new user enters the network will originate
the network request at the rate λi and is assumed to fol-
low a poisson process. The service time of the different
class of traffic and types of calls is µi .The mean service
time of all types of users were assumed to follow nega-
tive exponential distribution with the mean rate 1/µ.
Since voice traffic is Erlang distributed, the condition
that is considered for simulation is negative exponential
distribution. The total number of virtual channels in the
system are N. When the numbers of available channels
are below the specified threshold the system will drop
the calls. The threshold limit is determined by three posi-
tive integers A1, A2 and A3. These are called as utilization
rates, where A is represented as
Figure 1. Analytical model for CAC.
C opyright © 2010 SciRes. IJCNS

R. B. H. SIDDAMALLAIAH ET AL. 408
A = λ / μ
Similarly,
1
1
1
A


, 2
2
2
A


, 3
3
3
A


(1)
are the utilisation rate of type1 traffic, type2 traffic and
type3 traffic respectively. In general the values of the
utilisation rate in a steady state system will be with in 1.
When the available number of channels falls below the
threshold A3 the proposed system will accept only the
voice calls and web browsing. When the available num-
ber of channels falls below the threshold A2 the proposed
system will accept only the voice calls. If the available
number of channels falls below the threshold A1 the pro-
posed system will not accept any calls as it reaches the
stage where there will be no channels available to allo-
cate to the incoming calls and leads to system blocking.
The P(0) is the probability that there are no allocated
channels in the designated system. The parameters of
analytical performance model are also called as Per-
formance model parameters. The parameters are number
of virtual channels (N), user arrival rate (λ), arrival rate
of type1 call (λ1), arrival rate of type2 call (λ2) arrival
rate of type3 call (λ3) and service time of the calls is
taken as µ1 , µ2 and µ3.
Assuming that the arrival time of all the types of traf-
fic are equal i.e., 123 

 and the service time
for the types of traffic are equal i.e., 123 

 ,
the call blocking probability for type1 traffic could be
expressed as
-12 -3
(
3
nnnn
a
PPPP

) (2)
where a = λ / μ which should be generally less than one
for the system stability. Similarly, the call blocking
probability for type2 traffic Pn-1 is
1-23
(
3
nnn
a
PPPP


-4
)
n
(3)
And the call blocking probability for type3 traffic Pn-2
is represented as
2-34
(
3
nnn
a
PPPP


-5
)
n
(4)
The call blocking probability for the overall system
traffic Pnb can be expressed as
1-2
(
3
nbn nn
a
PPPP

) (5)
3. System Availability Model
The system availability model indicates the availability
of the channels in the proposed system. When all N
channels are failed then the system is unavailable for
data transmission. Here the system is modelled as inde-
pendent failure - repair model [7] which is also iterated
in our previous work [8]. Each virtual channel is sub-
jected to time and frequency selective fading and multi-
path fading then the virtual channel will be unavailable
for data transmission. The individual channel is available
for use by changing the mobile terminal position or by
channel equalization technique [7]. The channel recovery
model is developed as independent repair facility [9]. The
failure rate of the channel is Poisson distribution with the
rate γ. The channel recovery is exponential repair time
distribution of parameter distribution with the parameter
τ. The N independent channel failure and recovery can be
represented as a single dimension Markov Chain. The
system availability can be modelled as Markov chain.
The steady state probability P(i), where i is the number
of available channel in the system and given by

1
0
!
() (0)
i
i
j
i
pi p
Nj










(6)
The steady state unavailability P(0) of the system is
given by
1
1
0
!
(0)
()
i
N
i
i
jo
i
P
Nj
























(7)
The important observations from Performance-avai-
lability model is, increasing the number of channels will
decrease the call blocking probability Pnb. The system
availability model is as shown in Figure 2.
4. Composite Performance and Availability
Model
The performance-availability model is based on Stochas-
tic Activity Networks (SAN). The SAN is a stochastic
extension of Stochastic Petri Networks (SPN) in which
the capacity to define temporary characteristics with sta-
tistical parameters has been added. The SAN exhibits the
Figure 2. System availability model.

R. B. H. SIDDAMALLAIAH ET AL. 409
innovative graphics which allows the researchers to rep-
resent a model with a high level of formal specification,
expression of behaviour and dependency of the system in
an uncomplicated and straightforward way. SPNs can be
in general considered to constitute a method to model di-
stributed, asynchronous concurrent systems, which have
parallel characteristics. It is possible to study the per-
formance and evolution of the system easily using Petri
nets as Petri Nets combine graphic design and extensive
mathematical theory to represent a system model.
A SAN performance model for CAC is represented in
Figure 3 as channel usage model and the channel avail-
ability model which is also called as system capacity
model is represented in Figure 4 for the aggregate traffic.
The performance model of the proposed system is shown
in Figure 5 and primitive components used in the pro-
posed model are shown in Table 1. The activities tr_t1,
tr_t2 and tr_t3 represents the new user arrival/call arrival
of traffic type1, traffic type2 and traffic type3 respec-
tively which are timed activities and the firing distribu-
tion is a Poisson distribution. The new traffic arrivals
have an inhibitory input from the input gate ig_nt1, ig_nt2
and ig_nt3 when the number of virtual channels is less
than A1 channels, A
2 and A3 respectively. The transition
tr_sr1, tr_sr2 and tr_sr3 represent user Service requests
from traffic type1, type2 and type3 to system. Service
requests are hyper-exponential distribution. The places
AC and OC in the channel usage model indicate avail-
able channels and occupied channels /used channels.
The activity tr_t1 represents the call arrival of traffic
type1 on firing of transition tr_t1, the output gate og_nt1
shown in the Traffic type1 SAN performance model will
function and removes single token from place AC and
deposit a single token in place OC as shown in Figure 3.
The transition tr_sr1 represents user Service requests
from traffic type1 to system. Service requests are hy-
per-exponential distribution. After the call is serviced the
channel is released to the timed activity tr_sr1 through
input gate ig_sr1. On firing tr_sr1 the output gate og_sr1
will draw a token from OC and deposit the token in place
AC.
Figure 3. Channel usage model.
Figure 4. Channel availability/ fading model.
Figure 5. Performance-availability model.
Table 1. Structural components of traffic models.
SymbolSAN objectDescription
AC Place Available Virtual Channels
OC Place Used / Consumed Virtual Channels
tr_t1
tr_t2
tr_t3
Transitions Type1 call arrival, type2 call arrival,
type3 call arrival respectively
tr_sr1
tr_sr2
tr_sr3
Transitions
Service completion of type1 call/traffic,
Service completion of type2 call/traffic,
Service completion of type3 call/traffic
ig_nt1
ig_nt2
ig-nt3
Input gate
Input predicate for type1 Traffic arrival,
Input predicate for type2 Traffic arrival,
Input predicate for type3 Traffic arrival,
og_nt1
og_nt1
og_nt1
Output gate
Output function for type1 traffic arrival,
Output function for type2 traffic arrival,
Output function for type3 traffic arrival
ig_sr1
ig_sr2
ig-sr3
Input gate
Input predicate for type1 Traffic ser-
vice, Input predicate for type2 Traffic
service, Input predicate for type3 Traf-
fic service,
og_sr1
og_sr1
og_sr3
Output gate
Output function for type1 traffic ser-
vice, Output function for type2 traffic
service, Output function for type3 traf-
fic service
C opyright © 2010 SciRes. IJCNS

R. B. H. SIDDAMALLAIAH ET AL. 410
The performance model for type2 call is represented in
Figure 2. On firing of transition tr_t2 the output gate
og_nt2 of the traffic type2 SAN performance model will
function and removes single token from place AC and
deposit a single token in place OC. The transition tr_sr 2
represents user Service requests from traffic type2 to
system. Service requests are hyper-exponential distribu-
tion. After the call is serviced the channel is released to
the timed activity tr_sr2 through input gate ig_sr 2. On
firing tr_sr2 the output gate og_sr2 will draw a token
from OC and deposit the token in place AC.
The activity tr_nt3 in Figure 3 represents the call arri-
val of traffic type3 and on firing of transition tr_t3 the
output gates og_nt3 in of the traffic type3 SAN perform-
ance will function and removes single token from place
AC and deposit a single token in place OC. The transition
tr_sr3 represents user Service requests from traffic type3
to system. Service requests are hyper-exponential distri-
bution. After the call is serviced the channel is released
to the timed activity tr_sr3 through input gate ig_sr3. On
firing tr_sr3 the output gate og_sr3 will draw a token
from OC and deposit the token in place AC.
The transition tr_t1 represents an event of call arrival
of type1 traffic to the system. The transition new call/
user arrival of traffic type1 has an inhibitory input from
the input gate ig_ nt 1, when the total numbers of available
channels are less than A1 the transition tr_t1 is disabled.
The transition tr_t2 represents an event of call arrival of
type2 traffic to the system. The transition new user arri-
val of traffic type2 has an inhibitory input from the input
gate ig_nt2, when the total numbers of available channels
are less than A2 the transition is tr_t2 is disabled. The
tr_t3 is timed transition that represents the event of arri-
val of type3 traffic to the system. The transition tr_nt3 is
disabled when the available channel falls below A3.
The Figure 4 represents the fading model of the chan-
nel which gives the availability of the channel which
represents the system capacity. The AC and UAC are the
places in fading model and will represent channel avail-
ability and channel non-availability respectively in the
proposed system. The transition tr_fad represent the fad-
ing rate in wireless network and fading rate generally
follows Weibull distribution. The transition tr_ fad is fir-
ed if and only if the tokens are available in the place AC
and this condition is implemented through input gate
ig_fad. Transition tr_rel is the channel recovery process
and is assumed to be exponential distribution. When the
Timed activity tr_rel is fired the output gate og-rel will
draw a token from the place UAC and send it to AC.
This is nothing but when a channel fades then the chan-
nel will be in UAC state and when channel comes out of
fading state it will trigger the transition tr_rel and place
the token in AC. In other words the channel after coming
out of fading state UAC will enter the available channel
state AC.
The SAN based performance-capacity model is repre-
sented in Figure 5. which is a composite architecture of
the composite performance-availability model developed
by combining the channel usage model and channel
availability model/channel fading model.
5. Simulation Results and Discussion
In this section, we present the numerical results and com-
pare the call blocking probabilities of the different types
of traffic. A set of experiments were conducted varying
the number of channels and the call blocking probability
was compared for SAN performance-Availability model
and the analytical models for all three types of traffic.
The parameters of analytic performance-capacity mo-
del are divided into performance model parameters and
availability model parameters. Performance model pa-
rameters are number of channels (N), total user arrival
rate of type1 traffic (λ1), total user arrival rate of type2
traffic (λ2), total user arrival rate of type3 traffic (λ3) and
service time of the users (µ).
The system capacity model parameters are channel fai-
lure rate (γ) and channel recovery rate (τ). Parameters
Values are 50(N), 7(λ1), 3(λ2), 1(λ3), 2(µ), 3(γ) and 2(τ).
The Parameters of SAN Performance-capacity model
is divided into channel usage model parameters and cha-
nnel fading model parameters. The channel usage param-
eters are number of virtual channels represented by num-
ber of tokens in place AC, firing rate of type1 traffic ar-
rival transition (tr_t1), firing rate of type2 traffic arrival
transition (tr_t2), firing rate of type3 traffic arrival tran-
sition (tr_t3) and channel usage service rates for type1,
type2, type3 traffic are tr_sr 1, tr_sr 2, tr_ sr 3 respec-
tively. The channel usage rate is hyper-exponential dis-
tribution and classified into three types of usage such as
low, medium and high with the service rate µL, µM and
Table 2. Fading model structural components.
Symbol SAN objectDescription
AC Place Channel Availability
UAC Place Unavailability of Channel
tr_fad Transition Channel fading Rate
tr_rel Transition Channel recover y/release rate
ig_fad Input gate Input predicate for channel fading
ig_rel Input Gate Service completion
og_fad Output gate Output function for fading transition
og_rel Output gate Output function for recovery transi-
tion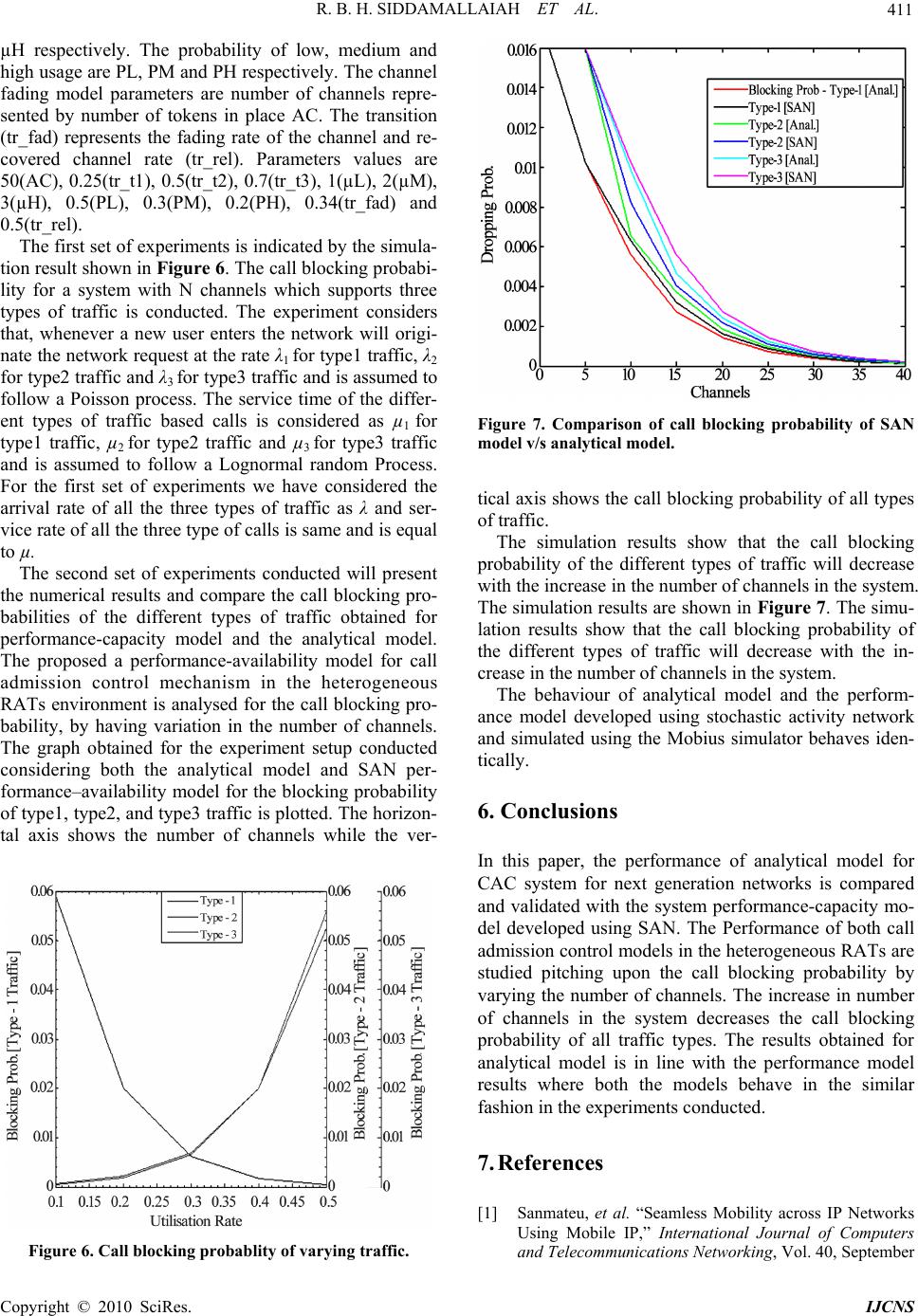

R. B. H. SIDDAMALLAIAH ET AL. 411
µH respectively. The probability of low, medium and
high usage are PL, PM and PH respectively. The channel
fading model parameters are number of channels repre-
sented by number of tokens in place AC. The transition
(tr_fad) represents the fading rate of the channel and re-
covered channel rate (tr_rel). Parameters values are
50(AC), 0.25(tr_t1), 0.5(tr_t2), 0.7(tr_t3), 1(µL), 2(µM),
3(µH), 0.5(PL), 0.3(PM), 0.2(PH), 0.34(tr_fad) and
0.5(tr_rel).
The first set of experiments is indicated by the simula-
tion result shown in Figure 6. The call blocking probabi-
lity for a system with N channels which supports three
types of traffic is conducted. The experiment considers
that, whenever a new user enters the network will origi-
nate the network request at the rate λ1 for type1 traffic, λ2
for type2 traffic and λ3 for type3 traffic and is assumed to
follow a Poisson process. The service time of the differ-
ent types of traffic based calls is considered as µ1 for
type1 traffic, µ2 for type2 traffic and µ3 for type3 traffic
and is assumed to follow a Lognormal random Process.
For the first set of experiments we have considered the
arrival rate of all the three types of traffic as λ and ser-
vice rate of all the three type of calls is same and is equal
to µ.
The second set of experiments conducted will present
the numerical results and compare the call blocking pro-
babilities of the different types of traffic obtained for
performance-capacity model and the analytical model.
The proposed a performance-availability model for call
admission control mechanism in the heterogeneous
RATs environment is analysed for the call blocking pro-
bability, by having variation in the number of channels.
The graph obtained for the experiment setup conducted
considering both the analytical model and SAN per-
formance–availability model for the blocking probability
of type1, type2, and type3 traffic is plotted. The horizon-
tal axis shows the number of channels while the ver-
Figure 6. Call blocking probablity of varying traffic.
Figure 7. Comparison of call blocking probability of SAN
model v/s analytical model.
tical axis shows the call blocking probability of all types
of traffic.
The simulation results show that the call blocking
probability of the different types of traffic will decrease
with the increase in the number of channels in the system.
The simulation results are shown in Figure 7. The simu-
lation results show that the call blocking probability of
the different types of traffic will decrease with the in-
crease in the number of channels in the system.
The behaviour of analytical model and the perform-
ance model developed using stochastic activity network
and simulated using the Mobius simulator behaves iden-
tically.
6. Conclusions
In this paper, the performance of analytical model for
CAC system for next generation networks is compared
and validated with the system performance-capacity mo-
del developed using SAN. The Performance of both call
admission control models in the heterogeneous RATs are
studied pitching upon the call blocking probability by
varying the number of channels. The increase in number
of channels in the system decreases the call blocking
probability of all traffic types. The results obtained for
analytical model is in line with the performance model
results where both the models behave in the similar
fashion in the experiments conducted.
7. References
[1] Sanmateu, et al. “Seamless Mobility across IP Networks
Using Mobile IP,” International Journal of Computers
and Telecommunications Networking, Vol. 40, September
C opyright © 2010 SciRes. IJCNS

R. B. H. SIDDAMALLAIAH ET AL. 412
2002, pp. 181-190.
[2] G. Wu, et al. “MIRAI Architecture for Heterogeneous
Networks,” IEEE Communications, Vol. 40, No. 2, 2002,
pp. 126-134.
[3] S. Y. Hui and K. H. Yeung, “Challenges in the Migration
to 4G Mobile Systems,” IEEE Communications, Vol. 41,
No. 12, 2003, pp. 54-59.
[4] X. G. Wang, J. E. Mellor and G. Min, “A QoS-Based
Bandwidth Management Scheme in Heterogeneous Wire-
less Networks,” International Journal of Simulation Sys-
tems, Science and Technology, Vol. 5, No. 1-2, 2004, pp.
9-17.
[5] E. Vanem, S. Svaet and F. Paint, “Effects of Multiple
Access Alternatives in Heterogeneous Wireless Net-
works,” IEEE Wireless and Networking, Vol. 3, 2003, pp.
1696-1700.
[6] K. Murray, R. Mathur and D. Pesch, “Network Access
and Handover Control in Heterogeneous Wireless Net-
works for Smart Space Environments,” First Interna-
tional Workshop on Management of Ubiquitous Commu-
nications and Services, MUCS ,Waterford, Ireland, De-
cember 11, 2003.
[7] Gowrishankar, H. S. R. Babu, G. T. Raju and P. S. Sat-
yanarayana, “Performability Model of Vertical Handoff
in Wireless Data Networks,” 4th IEEE International Con-
ference on Wireless and Mobile Communication (ICW-
MC2008), Athens, Greece, 27 July-1 August 2008, pp.
309-314.
[8] K. S. Trevedi, “Probability and Statistics with Reliability,
Queuing and Computer Science Application,” 2nd Edi-
tion, John Wiley and Sons, New York, 2001.
[9] Mulgrw, “Applying Radial Basis Functions,” IEEE Signal
Processing Magazine, Vol. 13, No. 2, 1996, pp. 50-65.