Int. J. Communications, Network and System Sciences, 2010, 3, 369-379
doi:10.4236/ijcns.2010.34047 blished Online April 2010 (http://www.SciRP.org/journal/ijcns/)
Pu
A Novel Approach towards Cost Effective Region-Based
Group Key Agreement Protocol for Ad Hoc Networks
Using Elliptic Curve Cryptography
Krishnan Kumar1, J. Nafeesa Begum1, V. Sumathy2
1Government College of Engineering, Bargur, India
2Government College of Technology, Coimbatore, India
Received January 12, 2010; revised February 19, 2010; accepted March 20, 2010
Abstract
This paper addresses an interesting security problem in wireless ad hoc networks: the dynamic group key
agreement key establishment. For secure group communication in an ad hoc network, a group key shared by
all group members is required. This group key should be updated when there are membership changes (when
the new member joins or current member leaves) in the group. In this paper, we propose a novel, secure,
scalable and efficient region-based group key agreement protocol for ad hoc networks. This is implemented
by a two-level structure and a new scheme of group key update. The idea is to divide the group into sub-
groups, each maintaining its subgroup keys using group elliptic curve diffie-hellman (GECDH) Protocol and
links with other subgroups in a tree structure using tree-based group elliptic curve diffie-hellman (TGECDH)
protocol. By introducing region-based approach, messages and key updates will be limited within subgroup
and outer group; hence computation load is distributed to many hosts. Both theoretical analysis and experi-
mental results show that this Region-based key agreement protocol performs well for the key establishment
problem in ad hoc network in terms of memory cost, computation cost and communication cost.
Keywords: Ad Hoc Network, Region-Based Group Key Agreement Protocol, Elliptic Curve Diffie-Hellman,
Tree-Based Group Elliptic Curve Diffie-Hellman
1. Introduction
Wireless networks are growing rapidly in recent years.
Wireless technology is gaining more and more attention
from both academia and industry. Mostly wireless net-
works are used today e.g. the cell phone networks and
the 802.11 wireless LAN, are based on the wireless net-
work model with pre-existing wired network infrastruc-
tures. Packets from source wireless hosts are received by
near-by base stations, then injected into the underlying
network infrastructure and then finally transferred to
destination hosts.
Another wireless network model, which is in active
research, is the ad-hoc network. This network is formed
only by mobile hosts and requires no pre-existing net-
work infrastructure. Hosts with wireless capability form
an ad-hoc network, some mobile hosts work as routers to
relay packets from source to destination. It is very easy
and economic to form an ad-hoc network in real time.
Ad-hoc network is ideal in situations like battlefield or
rescuer area where fixed network infrastructure is very
hard to deploy.
A mobile ad hoc network is a collection of autono-
mous nodes that communicate with each other. Mobile
nodes come together to form an ad hoc group for secure
communication purpose. A key distribution system re-
quires a trusted third party that acts as a mediator between
nodes of the network. Ad-hoc networks characteristically
do not have a trusted authority. Group key agreement
means that multiple parties want to create a common se-
cret key to be used to exchange information securely.
Furthermore, group key agreement also needs to address
the security issue related to membership changes due to
node mobility. The membership change requires frequent
changes of group key. This can be done either periodi-
cally or updating every membership changes. The
changed group key ensures backward and forward se-
crecy. With frequent changes in group memberships, the

K. KUMAR ET AL. 370
recent researches began to pay more attention on the ef-
ficiency of group key update. Recently, collaborative and
group–oriented applicative situations like battlefield,
conference room or rescuer area in mobile ad hoc net-
works have been a current research area. Group key
agreement is a building block in secure group communi-
cation in ad hoc networks. However, group key agree-
ment for large and dynamic groups in ad hoc networks is
a difficult problem because of the requirements of scal-
ability and security under constraints of node available
resources and node mobility.
We propose a communication and computation effi-
cient group key agreement protocol in ad-hoc network.
In large and high mobility ad hoc networks, it is not pos-
sible to use a single group key for the entire network
because of the enormous cost of computation and com-
munication in rekeying. So, we divide the group into
several subgroups; let each subgroup has its subgroup
key shared by all members of the subgroup. Each group
has sub group controller node and gateway node, in
which the sub group controller node is controller of sub-
group and gateway node is controller among subgroups.
Let each gateway member contributes a partial key to
agree with a common outer group key among the sub-
groups.
The contribution of this work includes
1) In this paper, we propose a new efficient method
for solving the group key management problem in ad-
hoc network. This protocol provides efficient, scalable
and reliable key agreement service and is well adaptive
to the mobile environment of ad-hoc network.
2) We introduce the idea of subgroup and subgroup
key and we uniquely link all the subgroups into a tree
structure to form an outer group and outer group key.
This design eliminates the centralized key server. Instead,
all hosts work in a peer-to-peer fashion to agree on a
group key. We use region-based group key agreement
(RBGKA) as the name of our protocol. Here we propose
a region based group key agreement protocol for ad hoc
networks using elliptic curve cryptography called re-
gion-based GECDH and TGECDH protocol.
3) We design and implement region-based group key
agreement protocol using Java and conduct extensive
experiments and theoretical analysis to evaluate the per-
formance like memory cost, communication cost and
computation cost of our protocol for Ad-Hoc network.
The rest of the paper is as follows, Section 2 presents
the elliptic curve cryptography schemes. Section 3 pre-
sents the proposed schemes. Section 4 describes the per-
formance analysis and finally Section 5 concludes the
paper.
2. Elliptic Curve Cryptography
ECC [1-3] has become the cryptographic choice for ad
hoc networks and communication devices due to its size
and efficiency benefits. Elliptic curve cipher uses very
small keys and is computationally very efficient, which
makes it ideal for the smaller, less powerful devices be-
ing used today by majority of individuals to access net-
work services. The elliptic curve cryptosystem (ECCS) is
a crypto-algorithm method of utilizing a discrete loga-
rithm problem (DLP) over the points on an elliptic curve.
An elliptic curve is usually defined over two finite
fields: the prime finite field Fp containing p elements and
the characteristic finite field containing 2m elements. This
paper focuses on the prime finite field. Let Fp be a prime
finite field, p is an odd prime number, and a,b ε Fp satis-
fy 4a3 + 27b2 ≠ 0(mod p), then an elliptic curve E(Fp)
over Fp defined by the parameters a,b ε Fp consists of the
set of solutions or points P = (x, y) for x, y ε F
p to the
equation:
y2 = x3 + ax + b(mod p) (1)
The equation y2=x3+ax+b (mod p) is called the defin-
ing equation of E(Fp). For a given point P = (xP , yP ), xP
is called the x-coordinate of P, and yP is called the
y-coordinate of P.
Cryptographic schemes based on ECC rely on scalar
multiplication of elliptic curve points. Given an integer k
and a point P ε E(Fp), scalar multiplication is the process
of adding P to itself k times. The result of this scalar
multiplication is denoted k * P or kP. Scalar multiplica-
tion of elliptic curve points can be computed efficiently
using the addition rule together with the double-and-add
algorithm or one of its variants.
2.1. Two Parties Elliptic Curve Diffie-Hellman
Protocol
Similar to DLP-based Diffie-Hellman key exchange agr-
eement, a key exchange between users A and B using
elliptic curve Diffie-Hellman (ECDH) [2,3] can be ac-
complished as follows:
1) A selects an integer nA less than p, this is A’s private
key. A then generates a public key PA = nA * G; the pub-
lic key is a point in Ep(a, b).
2) B similarly selects a private key nB and computes a
public key PB = nB * G.
3) A and B generates the secret key K = nA*PB, K = nB
*PA respectively.
The two calculations in step 3 produce the same result
because
nA*PB = nA* (nB * G) = nB * (nA * G) = nB * PA.
The secret key K is a point in the elliptic curve.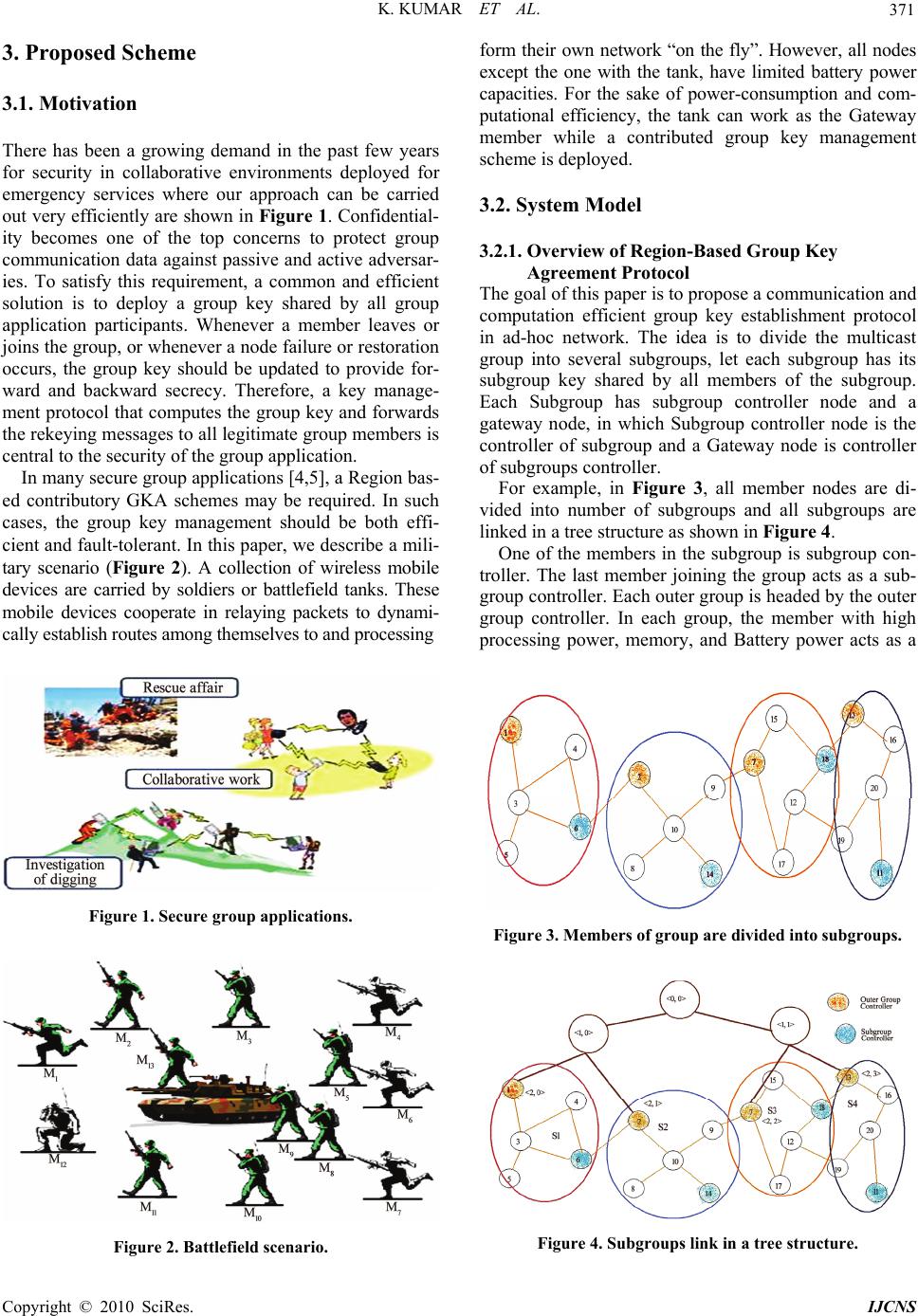

K. KUMAR ET AL. 371
3. Proposed Scheme
3.1. Motivation
There has been a growing demand in the past few years
for security in collaborative environments deployed for
emergency services where our approach can be carried
out very efficiently are shown in Figure 1. Confidential-
ity becomes one of the top concerns to protect group
communication data against passive and active adversar-
ies. To satisfy this requirement, a common and efficient
solution is to deploy a group key shared by all group
application participants. Whenever a member leaves or
joins the group, or whenever a node failure or restoration
occurs, the group key should be updated to provide for-
ward and backward secrecy. Therefore, a key manage-
ment protocol that computes the group key and forwards
the rekeying messages to all legitimate group members is
central to the security of the group application.
In many secure group applications [4,5], a Region bas-
ed contributory GKA schemes may be required. In such
cases, the group key management should be both effi-
cient and fault-tolerant. In this paper, we describe a mili-
tary scenario (Figure 2). A collection of wireless mobile
devices are carried by soldiers or battlefield tanks. These
mobile devices cooperate in relaying packets to dynami-
cally establish routes among themselves to and processing
Figure 1. Secure group applications.
Figure 2. Battlefield scenario.
form their own network “on the fly”. However, all nodes
except the one with the tank, have limited battery power
capacities. For the sake of power-consumption and com-
putational efficiency, the tank can work as the Gateway
member while a contributed group key management
scheme is deployed.
3.2. System Model
3.2.1. Overview of Region-Based Group Key
Agreement Protocol
The goal of this paper is to propose a communication and
computation efficient group key establishment protocol
in ad-hoc network. The idea is to divide the multicast
group into several subgroups, let each subgroup has its
subgroup key shared by all members of the subgroup.
Each Subgroup has subgroup controller node and a
gateway node, in which Subgroup controller node is the
controller of subgroup and a Gateway node is controller
of subgroups controller.
For example, in Figure 3, all member nodes are di-
vided into number of subgroups and all subgroups are
linked in a tree structure as shown in Figure 4.
One of the members in the subgroup is subgroup con-
troller. The last member joining the group acts as a sub-
group controller. Each outer group is headed by the outer
group controller. In each group, the member with high
processing power, memory, and Battery power acts as a
Figure 3. Members of group are divided into subgroups.
Figure 4. Subgroups link in a tree structure.
C opyright © 2010 SciRes. IJCNS

K. KUMAR ET AL. 372
gateway member. Outer group messages are broadcast
through the outer group and secured by the outer group
key while subgroup messages are broadcast within the
subgroup and secured by subgroup key.
Let N be the total number of group members, and M
be the number of the subgroups in each subgroup, then
there will be N/M subgroups, assuming that each sub-
group has the same number of members.
There are two shared keys in the Region-Based Group
Key Agreement Scheme:
1) Outer Group Key (KG) is used to encrypt and de-
crypt the messages broadcast among the subgroup con-
trollers.
2) The Subgroup Key (KR) is used to encrypt and de-
crypt the Sub Group level messages broadcast to all sub
group members.
In our Region-Based Key Agreement protocol shown
in Figure 5. a Subgroup Controller communicates with
the member in the same region using a Regional key (i.e.
Subgroup key ) KR. The Outer Group key KG is derived
from the Outer Group Controller. The Outer Group Key
KG is used for secure data communication among sub-
group members. These two keys are rekeyed for secure
group communications depending on events that occur in
the system. The layout of the network is as shown in
below Figure 5.
Assume that there are total N members in Secure
Group Communication. After sub grouping process (al-
gorithm 1), there are S subgroups M1, M2… Ms with n1,
n2 …ns members.
Figure 5. Region based group key agreement.
A Regional key KR is used for communication be-
tween a subgroup controller and the members in the
same region. The Regional key KR is rekeyed whenever
there is a membership change event and subgroup joins/
leaves and member failure. The Outer Group key KG is
rekeyed whenever there is a join/leave subgroup control-
lers and member failure to preserve secrecy.
The members within a subgroup use Group Elliptic
Curve Diffie-Hellman (GECDH) Contributory Key
Agreement. Each member within a subgroup contributes
his share in arriving at the subgroup key. Whenever
membership changes occur, the subgroup controller or
previous member initiates the rekeying operation.
The gateway member initiates communication with
the neighboring member belonging to another subgroup
and mutually agree on a key using Tree-Based Group
Elliptic Curve Diffie-Hellman (TGECDH) Contributory
Key Agreement protocol to be used for inter subgroup
communication between the two subgroups. Any mem-
ber belonging to one subgroup can communicate with
any other member in another subgroup through this
member as the intermediary. In this way adjacent sub-
groups agree on outer group key. Whenever membership
changes occur, the outer group controller or previous
group controller initiates the rekeying operation.
Algorithm 1. Region-Based Key Agreement
Protocol
1) The Subgroup Formation
The number of members in each subgroup is
N / S < 100.
where,
N – is the group size. and
S – is the number of subgroups.
Assuming that each subgroup has the same
number of members.
2) The Contributory Key Agreement protocol
is implemented among the group members. It
consists of three stages.
a. To find the Subgroup Controller for
each subgroups.
b. GECDH protocol is used to generate
one common key for each subgroup headed by the
subgroup controller.
c. Each subgroup gateway member con-
tributes partial keys to generate a one common
backbone key (i.e. Outer group Key (KG)) headed
by the Outer Group Controller using TGECDH
protocol.
3) Each Group Controller (sub /Outer) distrib-
utes the computed public key to all its members.
Here, we prefer the subgroup key to be different from
the key for backbone. This difference adds more freedom
of managing the dynamic group membership. In addition
by using this approach can potentially save the commu-
nication and computational cost.
3.3. Network Dynamics
The network is dynamic in nature. Many members may
join or leave the group. In such case, a group key man-
agement system should ensure that backward and for-
ward secrecy is preserved.
3.3.1. Member Join
When a new member joins, it initiates communication
with the subgroup controller. After initialization, the sub-
group controller changes its contribution and sends pub-
lic key to this new member. The new member receives
the public key and acts as a group controller by initiating
the rekeying operations for generating a new key for the
subgroup. The rekeying operation is as follows.

K. KUMAR ET AL. 373
Join request
N
ew node ubgroup ControllerS
change its contribution and send public key to
ubgroup ControllerNew Node S
Acts as
N
ew Node New Subgroup Controller
puts its contribution to all the public key value &
Multicast this public key value to
New Subgroup Controllerthe entire member in the subgroup
put is contribution to the public value & Compute
Each Member New Subgroup Key
3.3.2. Member Leave
3.3.2.1. When a Subgroup member Leaves
When a member leaves the Subgroup Key of the sub-
group to which it belongs must be changed to preserve
the forward secrecy. The leaving member informs the
subgroup controller. The subgroup controller changes its
private key value, computes the public value and broad-
casts the public value to all the remaining members.
Each member performs rekeying by putting its contribu-
tion to public value and computes the new Subgroup Key.
The rekeying operation is as follows.
Leaving Message
Leaving Node Subgroup Controller
changes its private key value, compute the public key value and
Multicast the public key value to
Subgroup Controller All the remaining Member
Performs Rekeying and Compute
Each Member New Subgroup Key
previous subgroup controller now acts as a Subgroup
controller. This Subgroup controller changes its private
contribution value and computes all the public key val-
ues and broadcasts to all the remaining members of the
group. All subgroup members perform the rekeying op-
eration and compute the new subgroup key. The rekeying
operation is as follows.
3.3.2.2. When Subgroup Controller Leaves
When the Subgroup Controller leaves, the Subgroup key
used for communication among the subgroup controller
needs to be changed. This Subgroup Controller informs
the previous Subgroup Controller about its desire to leave
the subgroup which initiates the rekeying procedure. The
Leaving Message
Leaving Subgroup Controller Old Subgrou
p
Controller
change its private value,compute the all
public key value and Multicast
Old Subgroup Controller Remaining Member in the group
Perform Rekeying and Compute
Subgroup Member New Subgroup Key
3.3.2.3. When Outer Group Controller Leaves
When the Outer group Controller leaves, the Outer group
key used for communication among the Outer group
need to be changed. This Outer group Controller informs
the previous Outer group Controller about its desire to
leave the Outer group which initiates the rekeying pro-
cedure. The previous Outer Group controller now be-
comes the New Outer group controller. This Outer group
controller changes its private contribution value and
computes the public key value and broadcast to the entire
remaining member in the group. All Outer group mem-
bers perform the rekeying operation and compute the
new Outer group key. The rekeying operation is as fol-
lows.
Leaving Message
Leaving Outer group Controller Old Outer group Controller
change its private value,compute the all
public key value and Multicast
Old Outer group Controller Remaing Member in the Outer group

K. KUMAR ET AL. 374
Perform Rekeying and Compute
Outer group Member New Outer group Key
3.3.2.4. When Gateway Member Leaves
When a gateway member leaves the subgroup, it dele-
gates the role of the gateway to the adjacent member
having high processing power, memory, and Battery
power and acts as a new gateway member. Whenever the
gateway member leaves, all the two keys should be
changed. These are
i. Outer group key among the subgroup.
ii. Subgroup key within the subgroup.
In this case, the subgroup controller and outer group
controller perform the rekeying operation. Both the Con-
troller leaves the member and a new gateway member is
selected in the subgroup, performs rekeying in the sub-
group. After that, it joins in the outer group. The proce-
dure is same as joining the member in the outer group.
3.4. Communication Protocol
The members within the subgroup have communication
using subgroup key. The communication among the sub-
group members takes place through the gateway mem-
ber.
3.4.1. Communication within the Subgroup
The sender member encrypts the message with the sub-
group key (KR) and multicasts it to all member in the
subgroup. The subgroup members receive the encrypted
message, perform the decryption using the subgroup key
(KR) and get the original message. The communication
operation is as follows.
KR
E[Message] & Multicast
Source Member Destination Member


KR KR
DE [Message]
Destination Member Original Message
3.4.2. Communication among the Subgroup
The sender member encrypts the message with the sub-
group key (KR) and multicasts it to all members in the
subgroup. One of the members in the subgroup acts as a
gate way member. This gateway member decrypts the
message with subgroup key and encrypts with the outer
group key (KG) and multicast to the entire gateway
member among the subgroup. The destination gateway
member first decrypts the message with outer group key.
Then encrypts with subgroup key and multicast it to all
members in the subgroup. Each member in the subgroup
receives the encrypted message and performs the decryp-
tion using subgroup key and gets the original message. In
this way the region-based group key agreement protocol
performs the communication. The communication opera-
tion is as follows.
KR
E[Message] & Multicast
Source Member Gateway Member


KR KR
DE [Message]
Gateway Member Original Message
KG
E[Message] & Multicast
Gateway Member Gateway Member [ Among Subgroup]


KG KG
DE [Message]
Gateway Member Original Message
KR
E[Message] & Multicast
Gateway Member Destination Member


KR KR
DE [Message]
Destination Member Original Message
3.5. Applying Elliptic Curve Based
Diffie-Hellman Key Exchange
3.5.1. Member Join
User A and user B are going to exchange their keys (Fig-
ure 6): Take p = 211, Ep = (0,-4), which is equivalent to
the curve y2 = x3 – 4 and G = (2,2). A’s private key is nA
= 47568, so A’s public key PA = 47568(2,2) = (206, 121),
Figure 6. User-A and User –B join the group.

K. KUMAR ET AL. 375
B’s private key is nB = 13525,so B’s public key PB =
13525(2,2) = (29,139). The group key is computed (Fig-
ure 6) as User A sends its public key (206,121) to user B,
then user B computes their Subgroup key as nB (A’s
Public key) = 13525(206,121) = (155,1 15). User B sends
its public key (29,139) to User A, then User A compute
their Subgroup key as nA (B’s Public key) =
47568(29,139) = (12 0,180)
When User C is going to join in the group, C’s private
key becomes nC = 82910. Now, User C becomes a Sub-
group Controller. Then, the key updating process will
begin as follows: The previous Subgroup Controller User
B sends the intermediate key as (B’s Public key $ A’s
Public Key $ Group key of A&B) = ((29,139) $ (206,121)
$ (155,115)) User C separates the intermediate key as
B’s Public key, A’s Public Key and Group key of A&B
= (29,139), (206,121) and (155,115). Then, User C gen-
erates the new Subgroup key as nC (Subgroup key of
A&B) = 82910(155,115) = (12 0,31). Then, User C
broadcasts the intermediate key to User A and User B.
That intermediate key is ((Public key of B & C) $ (Public
key of A & C)) = ((131,84) $ (147, 97)). Now, User B
extracts the value of public key of A & C from the value
sent by User C. Then User B compute the new Subgroup
key as follows: nB (Public key of A&C) = 13525 (147,97)
= (120, 31). Similarly, User A extracts the value of pub-
lic key of B & C from intermediate key, sent by User C.
Then User A compute the new Subgroup key as follows:
nA (public key of B&C) = 47568(131,84) = (120,31).
Therefore, New Subgroup Key of A, B and C = (120, 31)
as shown in the Figure 7.
The same procedure is followed when User D joins as
shown in the Figure 8.
3.5.2. Member Leave
When a user leaves (Figure 9) from the Subgroup, then
the Subgroup controller changes its private key. After
that, it broadcasts its new public key value to all users in
the Subgroup. Then, new Subgroup key will be gener-
ated. Let us consider, User B is going to leave, then the
Subgroup Controller D changes its private key nD’ =
43297, so public key of User A & User C = (198,139)
$(136,11). Then the new Subgroup Key generated is =
43297(198,139) = (207,115). Then, User A & User C
Figure 7. User - C joins in the group.
Figure 8. User-D joins in the group.
Figure 9. User –B leaves from the group.
computes the new Subgroup Key by using new public
key. Therefore, the new Subgroup Key is (207,115).
3.5.3. Group Controller Leave
When a Subgroup controller leaves (Figure 10) from the
group, then the previous Subgroup controller changes its
private key. After that, it broadcasts its new public key
value to all users in the group. Then, new Subgroup key
will be generated. Let us consider, Subgroup Controller
User D going to leave, then the previous Subgroup con-
troller User C act as Subgroup Controller and changes its
private key nC’ = 52898, and computes the public key of
B&C $ A&C = (16,111)$(181,2). Then the new Sub-
group Key generated is = 52898(21,103) = (198,139).
Then, User A & User B compute the new Subgroup Key
by using new public key. Therefore, the new Subgroup
Key is (198,139).
Figure 10. Group controller leaves from the group.
C opyright © 2010 SciRes. IJCNS

K. KUMAR ET AL. 376
3.6. Tree-Based Group Elliptic Curve
Diffie-Hellman Protocol
The proposed protocol (Figure 11), Tree-based group
Elliptic Curve Diffie-Hellman (TGECDH), is a variant of
TGDH based on ECDLP. In TGECDH, a binary tree is
used to organize group members. The nodes are denoted
as <l, v>, where 0 <= v <= 2l. – 1 since each level l hosts
at most 2l. nodes. Each node <l, v> is associated with the
key K<l,v> and the blinded key BK<l,v> = F(K<l,v>)
where the function F() is scalar multiplication of elliptic
curve points in prime field. Assuming a leaf node <l, v>
hosts the member Mi, the node <l, v> has Mi’s session
random key K<l,v>. Furthermore, the member Mi at
node <l. v> knows every key in the key-path from <l, v>
to <0, 0>. Every key K<l,v> is computed recursively as
follows:
,1,21,21
mod
lvl vl v
K
KBK
  
p
1,2 11,2mod
lv lv
K
BK p
  

1,21,2 1mod
lv lv
K
KG
 
p
1,21,2 1
()
lv lv
FK K
  

It is not necessary for the blind key BK<l,v> of each
node to be reversible. Thus, simply use the x-coordinate
of K<l,v> as the blind key. The group session key can be
derived from K<0,0>. Each time when there is member
join/leave, the outer group controller node calculates the
group session key first and then broadcasts the new blind
keys to the entire group and finally the remaining group
members can generate the group session key.
Figure 11. Key tree.
Figure 12. User M1 and M2 join the group.
3.6.1. When Node M1&M2 Join the Group
User M1 and User M2 are going to exchange their keys:
Take p = 751, Ep = (1,188), which is equivalent to the
curve y2 = x3 + x + 188 and G = (0,376). User M1’s pri-
vate key is 1772, so M1’s public key is (290,638). User
M2’s private key is 1949, so M2’s public key is (504,163).
The Outer Group key is computed (Figure 12) as User
M1 sends its public key (290,638) to user M2, the User
M2 computes their group key as PV(0,0) = Xco (PV(1,0)
*PB(1,1)) and PB(0,0) = PV(0,0)*G = (540, 111). Simi-
larly, User M2 sends its public key (504,163) to user M1,
and then the user M1 computes their group key as
(540,111). Here, Outer Group controller is User M2.
3.6.2. When 3rd Node Join
When User M3 joins the group, the old Outer group con-
troller M2 changes its private key value from 1949 to
2835 and passes the public key value and tree to User M3.
Now, M3 becomes new Outer group controller. Then, M3
generates the public key (623, 52) from its private key as
14755 and computes the Outer group key as (664,736)
shown in Figure 13. M3 sends Tree and public key to all
users. Now, user M1 and M2 compute their group key.
The same procedure is followed by joining the User M4
as shown in Figure 14.
Figure 13. User M3 joins the group.
Figure 14. User M4 joins the group.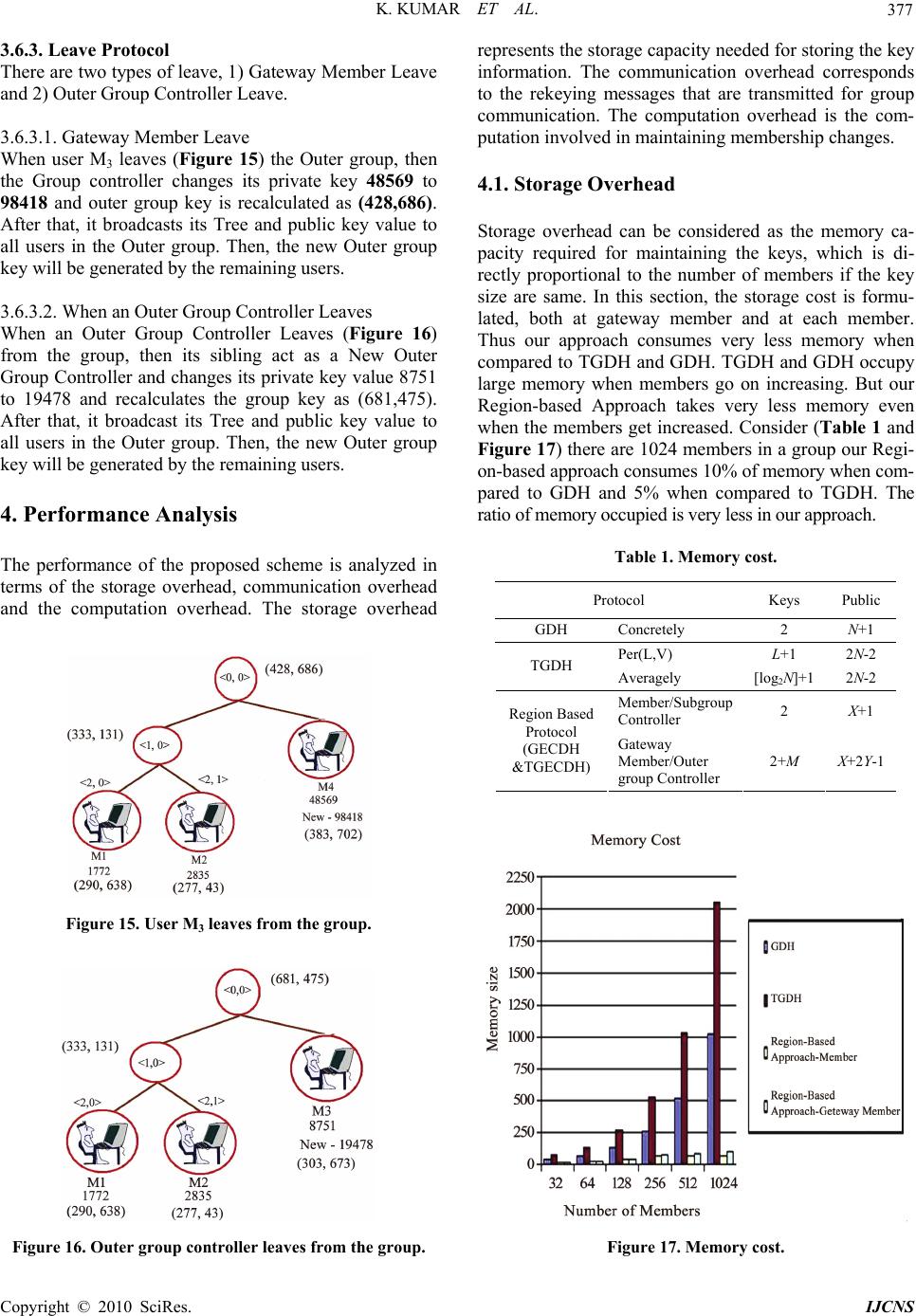

K. KUMAR ET AL. 377
3.6.3. Leave Protocol
There are two types of leave, 1) Gateway Member Leave
and 2) Outer Group Controller Leave.
3.6.3.1. Gateway Member Leave
When user M3 leaves (Figure 15) the Outer group, then
the Group controller changes its private key 48569 to
98418 and outer group key is recalculated as (428,686).
After that, it broadcasts its Tree and public key value to
all users in the Outer group. Then, the new Outer group
key will be generated by the remaining users.
3.6.3.2. When an Outer Group Controller Leaves
When an Outer Group Controller Leaves (Figure 16)
from the group, then its sibling act as a New Outer
Group Controller and changes its private key value 8751
to 19478 and recalculates the group key as (681,475).
After that, it broadcast its Tree and public key value to
all users in the Outer group. Then, the new Outer group
key will be generated by the remaining users.
4. Performance Analysis
The performance of the proposed scheme is analyzed in
terms of the storage overhead, communication overhead
and the computation overhead. The storage overhead
Figure 15. User M3 leaves from the group.
Figure 16. Outer group controller leaves from the group.
represents the storage capacity needed for storing the key
information. The communication overhead corresponds
to the rekeying messages that are transmitted for group
communication. The computation overhead is the com-
putation involved in maintaining membership changes.
4.1. Storage Overhead
Storage overhead can be considered as the memory ca-
pacity required for maintaining the keys, which is di-
rectly proportional to the number of members if the key
size are same. In this section, the storage cost is formu-
lated, both at gateway member and at each member.
Thus our approach consumes very less memory when
compared to TGDH and GDH. TGDH and GDH occupy
large memory when members go on increasing. But our
Region-based Approach takes very less memory even
when the members get increased. Consider (Table 1 and
Figure 17) there are 1024 members in a group our Regi-
on-based approach consumes 10% of memory when com-
pared to GDH and 5% when compared to TGDH. The
ratio of memory occupied is very less in our approach.
Table 1. Memory cost.
Protocol Keys Public
GDH Concretely 2 N+1
Per(L,V) L+1 2N-2
TGDH Averagely [log2N]+1 2N-2
Member/Subgroup
Controller 2 X+1
Region Based
Protocol
(GECDH
&TGECDH)
Gateway
Member/Outer
group Controller
2+M X+2Y-1
Figure 17. Memory cost.
C opyright © 2010 SciRes. IJCNS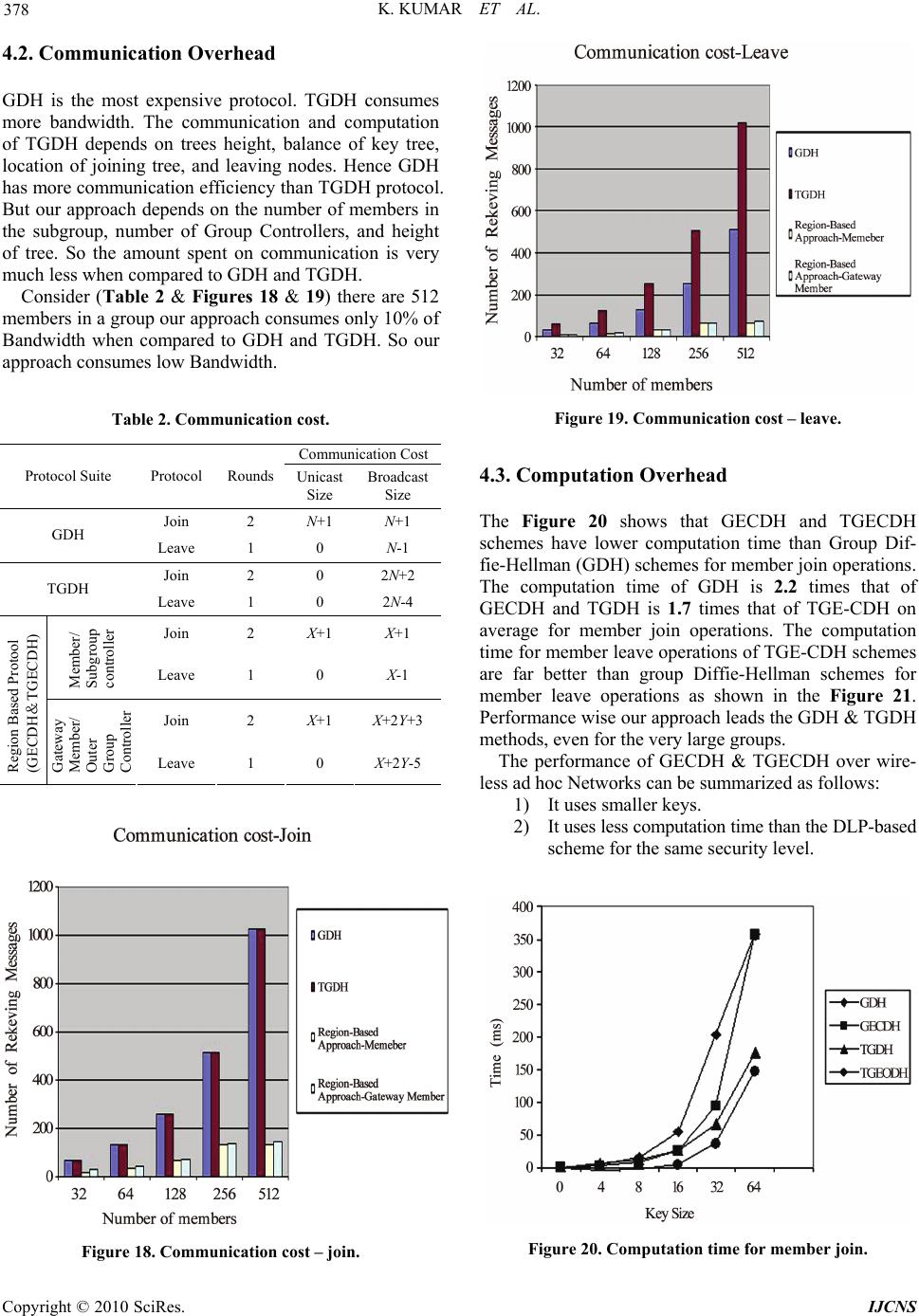

K. KUMAR ET AL. 378
4.2. Communication Overhead
GDH is the most expensive protocol. TGDH consumes
more bandwidth. The communication and computation
of TGDH depends on trees height, balance of key tree,
location of joining tree, and leaving nodes. Hence GDH
has more communication efficiency than TGDH protocol.
But our approach depends on the number of members in
the subgroup, number of Group Controllers, and height
of tree. So the amount spent on communication is very
much less when compared to GDH and TGDH.
Consider (Table 2 & Figures 18 & 19) there are 512
members in a group our approach consumes only 10% of
Bandwidth when compared to GDH and TGDH. So our
approach consumes low Bandwidth.
Table 2. Communication cost.
Communication Cost
Protocol Suite Protocol Rounds Unicast
Size
Broadcast
Size
Join 2 N+1 N+1
GDH Leave 1 0 N-1
Join 2 0 2N+2
TGDH Leave 1 0 2N-4
Join 2 X+1 X+1
Member/ Subgroup controller
Leave 1 0 X-1
Join 2 X+1 X+2Y+3
Region Based Protool (GECDH＆TGECDH) Gateway Member/ Outer Group Controller
Leave 1 0 X+2Y-5
Figure 18. Communication cost – join.
Figure 19. Communication cost – leave.
4.3. Computation Overhead
The Figure 20 shows that GECDH and TGECDH
schemes have lower computation time than Group Dif-
fie-Hellman (GDH) schemes for member join operations.
The computation time of GDH is 2.2 times that of
GECDH and TGDH is 1.7 times that of TGE-CDH on
average for member join operations. The computation
time for member leave operations of TGE-CDH schemes
are far better than group Diffie-Hellman schemes for
member leave operations as shown in the Figure 21.
Performance wise our approach leads the GDH & TGDH
methods, even for the very large groups.
The performance of GECDH & TGECDH over wire-
less ad hoc Networks can be summarized as follows:
1) It uses smaller keys.
2) It uses less computation time than the DLP-based
scheme for the same security level.
Figure 20. Computation time for member join.

K. KUMAR ET AL. 379
gion-based scheme can be efficiently distributed for mul-
tiple secure groups. Therefore, the number of rekeying
messages, computation and memory can be dramatically
reduced. Compared with other schemes, the new pro-
posed region-based scheme can significantly reduce the
storage and communication overheads in the rekeying
process, with acceptable computational overhead. It is
expected that the proposed scheme can be the practical
solution for secure group applications, especially for
battlefield scenario.
6. References
[1] Kefa Rabah, “Theory and Implementation of Elliptic
Curve Cryptography,” Journal of Applied Sciences, Vol.
5, No. 4, 2005, pp. 604-633.
Figure 21. Computation time for member leave.
3) Smaller packets are used to handle high bit error
rate Wireless links.
[2] W. Stallings, “Cryptography and Network Security Prin-
ciples and Practices,” 3rd Edition, Pearson Education.
[3] Y. Wang, B. Ramamurthy and X. K. Zou, “The Perform-
ance of Elliptic Curve Based Group Diffie-Hellman Pro-
tocols for Secure Group Communication over Ad Hoc
Networks,” IEEE International Conference on Commu-
nication, Vol. 5, 2006, pp. 2243-2248.
5. Conclusions
In this paper, a region-based key agreement scheme has
been proposed and implemented, which can enhance the
secure group communication performance by using mul-
tiple group keys. In contrast to other existing schemes
using only single key, the new proposed scheme exploits
asymmetric key, i.e. an outer group key and multiple
Subgroup keys, which are generated from the proposed
region-based key agreement algorithm. By using a set
comprising an outer group key and subgroup keys a re-
[4] Y. Amir, Y. Kim, C. Nita-Rotaru and G. Tsudik, “On the
Performance of Group Key-Agreement Protocols,” Pro-
ceedings of the 22nd IEEE International Conference on
Distributed Computing Systems, Viena, Austria, 2002.
[5] M. Steiner, G. Tsudik and M. Waidner, “Key Agreement
in Dynamic Peer Groups,” IEEE Transaction on Parallel
and Distributed Systems, Vol. 11, No. 8, 2000, pp. 769-
780.