Paper Menu >>
Journal Menu >>
 words, genetic factor has been invoked in the ABSTRACT pathogenesis of the disease. Although the Crohn's disease cannot easily be The both environmental and genetic factors have treated, it can be avoided if people at high risk change roles in the development of some diseases. Complextheir living style, such as their diet. But how can we diseases, such as Crohn's disease or Type II diabetes,tell the susceptibility of people to the disease before are caused by a combination of environmental fac-symptoms are found and help them make informed tors and mutations in multiple genes. Patients whodecisions about their health? With the development have been diagnosed with such diseases cannot eas-of DNA microarray technique, it is possible to access ily be treated. However, many diseases can be the human genetic information related to specific dis- avoided if people at high risk change their living style,eases.Assessing the association between DNA vari- one example being their diet. But how can we tell their ants and disease has been used widely to identify susceptibility to diseases before symptoms areregions of the genome and candidate genes that con- found and help them make informed decisions abouttribute to disease [2]. their health? With the development of DNA 99.9% of one individual's DNA sequences are iden- microarray technique, it is possible to access thetical to that of another person. Over 80% of this 0.1% human genetic information related to specific dis-difference will be Single Nucleotide Polymorphisms eases. This paper uses a combinatorial method to(SNP) and they promise to significantly advance our analyze the genetic data for Crohn's disease andability to understand and treat human disease. A SNP search disease-associated factors for given is a single base substitution of one nucleotide with case/control samples. An optimum random forestanother. Each individual has many single nucleotide based method has been applied to publicly availablepolymorphisms that together create a unique DNA genotype data on Crohn's disease for association pattern for that person. It is important to study SNPs study and achieved a promising result.because they represent genetic differences among human beings. Genome-wide association studies require knowledge about common genetic variations and the ability to genotype a sufficiently comprehen- sive set of variants in a large patient sample [3]. 1. INTRODUCTIONHigh-throughput SNP genotyping technologies make Crohn's disease (also known as regional enteritis) is amassive genotype data, with a large number of indi- chronic, episodic, inflammatory condition of the gas-viduals, publicly available. Accessibility of genetic trointestinal tract characterized by transmural data makes genome-wide association studies for com- inflammation (affecting the entire wall of the plex diseases possible. involved bowel) and skip lesions (areas of inflamma-Success stories when dealing with diseases caused tion with areas of normal lining in between). Crohn's by a single SNP or gene, sometimes called monogenic disease is a type of inflammatory bowel disease (IBD) diseases have been reported [4]. However, most com- and can affect any part of the gastrointestinal tract plex diseases, such as psychiatric disorders, are char- from mouth to anus. As a result, the symptoms of acterized by a non-mendelian, multifactorial genetic Crohn's disease can vary among affected individuals. contribution with a number of susceptible genes The exact cause of Crohn's disease is unknown. How-interacting with each other [5]. A fundamental issue ever, research shows that the inflammation seen inin the analysis of SNP data is to define the unit of the people with Crohn's disease involves several fac-genetic function that influences disease risk. Is it a tors: the genes the patient has inherited, the immune single SNP, a regulatory motif, an encoded protein system itself, and the environment [1]. In other subunit, a combination of SNPs in a combination of Keywords: Genetic factor; Crohn's disease; Ran- dom forest A combinatorial analysis of genetic data for Crohn's disease A combinatorial analysis of genetic data for Crohn's disease 12 Weidong Mao & Jeonghwa Lee 1 2 Department of Mathematics & Computer ScienceVirginia State UniversityPetersburg, VA 23806, USA. Department of Computer Science Shippensburg UniversityShippensburg, PA 17257, USA. Correspondence should be addressed to Weidong Mao (wmao@vsu.edu) or Jeonghwa Lee(jlee@ship.edu). J. Biomedical Science and Engineering, 2008, 1, 52-58Scientific Research Publishing JBiSE Published Online May 2008 in SciRes.http://www.srpublishing.org/journal/jbise SciRes Copyright ©2008  genes, an interacting protein complex, a metabolic or association study we described above. The Disease- a physiological pathway [6]? In general, it may beassociatedmulti-SNPcombinationfoundinassocia- impossible to associate a single SNP or gene with a tion studies can be used to predict the susceptibility disease because a disease may be caused by com-todiseases.Ontheotherside,thepredictionresults pletely different modifications of alternative path-can be used to evaluate the accuracy of the associa- ways, and each gene only makes a small contribution. tionstudies.Ahigherpredictionratemeansthe This makes the identification of genetic factors diffi-higher reliability of the association studies. cult.Multi-SNPinteractionanalysisismorereliableThe proposed method is applied to analyze the but it is computationally infeasible. An exhaustive genetic data of the Crohn's disease. We find the dis- searchamongmulti-SNPcombinationis computationallyease-associated multi-SNP combination and apply it infeasible even for a small number of SNPs. Further-to predict the susceptibility. The accuracy of the pre- more, there are no reliable tools applicable to large diction is higher than that of all previously known genome ranges that could rule out or confirm associa-methods. It can be also applied in disease prevention tionwithadisease.and control in the near future. For example, after It is important to search for informative SNPs among atraining the available case-control genome data, we hugenumberofSNPs.TheseinformativeSNPsarecan find those significant SNPs which are well asso- assumed to be associated with genetic diseases. Tag SNPsciatedwiththedisease.Whenapatientcomes,and generated by the multiple linear regression based method we obtain his/her genetic data, we don't need to check [7] are good informative SNPs, but they are reconstruc-thewholesequence,butonlydisease-associated tion-oriented instead of disease-oriented. Although the SNPs instead. This will save much money and time combinatorialsearchmethod[8]forfindingdisease-for diagnosis and can be done before the onset of dis- associated multi-SNP combinations has a better result, theeases.Therefore, treatmentcouldstartearlier to pre- exhaustivesearch is still very slow.vent or delay the occurrence of the disease. Multivariate adaptive regression spline models [9, 10] are used to detect associations between diseases 2. DISEASE ASSOCIATION SEARCH FOR and SNPs with some degree of success. However, theCROHN'S DISEASE number of selected predictors is limited, and the type In this section we first give an overview of the ran- of possible interactions must be specified in advance. dom forest tree and classification tree, then we will Multifactor dimensionality reduction methods [11, describe the genetic model. Next we propose the opti- 12] are developed specifically to find gene-gene mum random forest algorithm to search Tag SNPs. interactions among SNPs, but they are not applicable to a large set of SNPs.2.1. Classification Trees and Random Forest Random forest model has been explored in disease In machine learning, a Random Forest is a classifier association studies [13], but it was applied on simu-that consists of many classification trees. Each tree is lated case-control data in which the interacting grown as follows: model among SNPs and the number of associated 1. If the number of cases in the training set is N, SNPs are specified, thus making the association sampleN cases at random - but with replacement, model simple and the association is relatively easier from the original data. This sample will be the train- to detect. For real data, such as Crohn's disease [14],ing set for growing the tree. multi-SNP interaction is much more complex , which2. If there areM input variables, a number m<<M involves more SNPs.is specified such that at each node, m variables are In Section 2 of this paper, we propose an optimumselected randomly out of the M and the best split on random forest model for searching the disease-these m is used to split the node. The value of m is associated multi-SNP combination for given case-held constant during the forest growing. control data. In the optimum random forest model, 3. Each tree is grown to the largest extent possible. we generate a forest for each variable (e.g. SNP) There is no pruning [19]. instead of randomly selecting some variables to growA different bootstrap sample from the original data the classification tree. We can find the best classifier is used to construct a tree. Therefore, about one-third (a combination of SNPs which includes the SNP) for of the cases are left out of the bootstrap sample and each SNP, and then we may haveM classifiers if the not used in the construction of the tree. Cross- length of the genotype is M. We rank classifiers validation is not required because the one-third oob according to their prediction rate, and the SNP with a (out-of-bag)data is used to get an unbiased estimate higher prediction rates is more disease-associated.of the classification error as trees are added to the for- The association of multi-SNP combination can be est. It is also used to get estimates of variable impor- measured by the disease susceptibility prediction rate.tance.After each tree is built, we compute the In Section 3 we address the disease susceptibility pre-proximities of each terminal node. diction problem [15, 16, 17, 18]. The goal of disease In every classification tree in the forest, put down susceptibility prediction is to assess accumulatedthe oob samples and make prediction the classifica- information targeted to predicting susceptibility to tion of the oob samples. In such way we can compute complex diseases with significantly high accuracythe importance score for variables in each tree based and statistical power. The problem is based on the SciRes JBiSE Copyright ©2008 W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58 53  on the number of votes cast for the correct class. Allposedoftwohaplotypes. variables can be ranked and those important variablesThe case-control sample populations consist of N canbefoundinthisway.individuals who are represented in genotype with M Random forest is a sophisticated method in data SNPs. Each SNP attains one of the three values 0, 1, mining to solve classification problems, and it can beor 2. The sampleGis an (0, 1, 2)-valued N x M matrix, used efficiently in disease association studies to findwhere each row corresponds to an individual, each most disease-associated variables such as SNPs that columncorrespondstoaSNP. may be responsible for diseases.The sample G has 2 classes, case and control, and M variables, and each of them represents a SNP. To construct a classification tree, we split the sample S 2.2. Genetic Model into 3 child sub-samples, depending on the value (0, 1, Recent work has suggested that SNPs in human popu- 2) of the variable (SNP) on the splitting site (loci). In lation are not inherited independently; rather, sets of fact we can construct a binary tree (split sample adjacent SNPs are present on alleles in a block pat- according to homozygous or heterozygous), but there tern, so calledhaplotype. Many haplotype blocks in is no way to tell the difference between major allele human have been transmitted through many genera- (1) and minor allele (0). In order to distinguish them tions without recombination. This means although a we split the sample into 3 sub-samples instead of 2. block may contain many SNPs, it takes only a few We grow the tree to the largest possible extent. The SNPs to identify or to tag each haplotype in the block. construction of the classification tree for case- A genome-wide haplotype would comprise half of a control sample is illustrated in . In the first diploid genome, including one allele from each level, we split the sample (30 genotypes, 14 cases and allelic gene pair. The genotype is the descriptor of 16 controls) into 3 sub-samples (17, 8, 5) at loci 5 the genome which is the set of physical DNA mole-th cules inherited from the organism's parents. A pair of(the 5 SNP). In the second level, the first sub- haplotype consists of a genotype. sample splits at loci 9 and the second sub-sample SNPs are bi-allelic and can be referred as 0 forsplits at loci 7. No splitting is required for the third majority allele and 1, otherwise. If alleles on bothsub-sample because it is a terminal node with only haplotypes are the same, then the corresponding geno-one class. In the third level, the only split node splits type is homogeneous, and can be represented as 0 or 1. at loci 3. The relationship of a leaf to the tree on If the two alleles on the two haplotypes are different, which it grows can be described by the hierarchy of the genotype is heterozygous, represented as 2.splits of branches (starting from the trunk) leading to In, there are four chromosomes, wethe last branch from which the leaf hangs. The collec- assume the first two chromosomes belong to one per-tion of split site is a Multi-SNPs combination (MSC), son and the other two chromosomes belong to anotherwhich can be viewed as a classification tree. In this person. We can find on most sites the four chromo-example, MSC = {5, 9, 7, 3}and m = 4, which is a col- somes are identical, but on some sites they are differ-lection of 4 SNPs, represented as their loci. ent, nucleotides on these sites are SNP. The haplotype is the concatenation of SNPs and a genotype is com-2.3. Searching for Disease Associated Multi- SNPs To fully understand the basis of complex diseases, it Figure 2 Figure 1 Figure 1. SNP, haplotype and genotype.Figure 2. Classification tree for case-control sample. SciRes JBiSE Copyright ©2008 54W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58 Chromosome 1 Chromosome 2 Chromosome 3 Chromosome 4 SNPs SNP SNP SNP Haplotype 1 Haplotype 2 Haplotype 3 Haplotype 4 Haplotype 1 Haplotype 2 Haplotype 3 Haplotype 4 Genotype 1 Genotype 2 Split condition Number of sampless sent to child node Split site Terminal node(leaf) Split node Ccase Ccontrol  is important to identify the critical genetic factors withthehighestweight.Thecontributiontodiseases involved, which is a combination of multiple SNPs. of each SNP is quantified by its weight, but in GRF For a given sample G,S is the set of all SNPs (de-there is no way tell the difference of contribution noted by loci) for the sample, and a multi-SNPs com-among SNPs. The GRF can only tell the difference bination (MSC) is a subset of S. In disease associa-amongclassifiers(trees). tions, we need to find aMSC which consists of a com- bination of SNPs that are well associated with the dis-3. DISEASE SUSCEPTIBILITY PREDICTION ease. To find suchMSC, we need first rank all SNPs In this section we first describe the input and the out- according to their association degree (measured as put of prediction algorithms and then show how to weight) with diseases. Based on the sorting, we canapply the optimum random forest to the disease sus- find then most disease associated SNPs for a given ceptibility prediction. thresholdn.Data sets have n genotypes and each has m SNPs. Although there are many statistical methods to The input for a prediction algorithm includes: detect the most disease associated SNPs, such as odds (G1) Training genotype setg = (g ),i = 0, 1, …,n, i i,j ratio or risk rates, the result is not satisfactory. Wej =1,… m, g{0,1,2} i,j decide to use the random forest to find them.(G2) Disease status s(g {0,1}, indicating ifg,i ii = 0, 1, …, n, is in case (1) or in control (0) , and 2.4. Optimum Random Forest(G3) Testing genotype g without any disease sta- We randomly generate a group of MSCs for each SNP.t The size of theMSC should be much less than the size tus. of set S (m << M). Each MSC can be represented as aWe will refer to the parts (G1-G2) of the input as tree and all trees make the forest F.Alltrees(orthe training set and to the part (G3) as the test set. The MSCs) of the forestF(i=1, 2,…, M) must include theoutput of prediction algorithms is the disease status i th of the genotype s(g). t i SNP and the other (m-1) SNPs can be randomly cho- th We use leave-one-out cross-validation to measure sen fromS except thei SNP. In this way, theM for-the quality of the algorithm. In the leave-one-out ests cover all SNPs in S.cross-validation, the disease status of each genotype We grow a classification tree for everyMSC in in the data set is predicted while the rest of the data is each forestF. We run all the testing samples down iregarded as the training set. these trees to get the classifier for each sample in the We describe several universal prediction methods training set, then we can get a classification rate forbelow. These methods are adaptations of general com- each tree inF. TheMSC is the representative for the ii puter-intelligence classifying techniques. forestF and theMSC has the highest classificationClosest Genotype Neighbor (CN). For the test ii genotype g, find the closest (with respect to Ham- rate among all trees in F. Each member (SNP) of thet i ming distance) genotype g in the training set, and set MSC is assigned a weightw (j MSC) based on thei i i,j the statuss(g) equals tos(g). classification rate. The weights for SNPs in the same ti MSC are the same. We can find M MSCs for theM for-Support Vector Machine Algorithm (SVM). Sup- ests. If a SNP is not a member of MSC, then w = 0.port Vector Machine (SVM) is a generation learning i i,j system based on recent advances in statistical learn- The weight for each SNPW (j = 1, 2, …,M) in M is jing theory. SVMs deliver a state-of-the-art perfor- the sum of weights from allMSCs.mance in real-world applications and have been used in case/control studies [18, 20]. There are some SVM softwares available and we decide to use libsvm-2.71 [19] with the following radial basis function: In the general random forest (GRF) algorithm, the2 exp(- | u-v |) MSC is selected completely randomly and m << M. It General Random Forest (GRF). We use Leo may miss some important SNPs if they are not chosen Breiman and Adele Cutler's original implementation for anyMSC. In our optimum random forest (ORF) of RF version [19]. This version of RF handles unbal- algorithm, this scenario is avoided because we gener-anced data to predict accurately. RF tries to perform a ate at least oneMSC for each SNP. On the other hand, regression on the specified variables to produce the in GRF, the classifier (forest) consists of trees wheresuitable model. RF uses bootstrapping to produce ran- there is a correlation between any two trees in the for-dom trees and it has its own cross-validation tech- est, and the correlation will decrease the rate of thenique to validate the model for prediction/classification. classifier. But in ORF, we generate a forest by ran-Most Reliable 2 SNP Prediction (MR2) [17]. domly choosingMSC and samples for each tree andThis method chooses a pair of adjacent SNPs (site of the prediction for testing samples is in this forest only,s and s) to predict the disease status of the test which is completely independent from the other trees. i i+1 In this way, we extinguish the correlation among genotype g by voting among genotypes from the t trees. training set which have the same SNP values as g at t All SNPs are sorted according to their cumulative the chosen sitess and s. They choose the 2 adja- i i+1 weights. The most disease-associated SNP is the one (1) SciRes JBiSE Copyright ©2008 55 W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58  cent SNPs with the highest prediction rate in thetogrowmanydifferentclassificationtreesbyper- trainingset.muting the order of the splitting site (Note that the LP-based Prediction Algorithm (LP).Thistree {3, 9, 5}is different from the tree {5, 9, 3}). We method assumes that certain haplotypes are suscepti-mayusethem Tag SNPs to grow many (say, 500) ble to the disease while others are resistant to the dis-trees and choose the best tree (classifier) to predict ease.Thegenotypesusceptibilityisthenassumedtothe disease status of the testing genotype. The best be a sum of susceptibilities of its two haplotypes.treehasthehighestaveragepredictionrate(over We want to assign a positive weight to susceptible1000 trials) in the training set. Then we run the test- haplotypes and a negative weight to resistant haplotypes ing genotype down the best tree to get its disease sta- such that for any control genotype the sum of weightstus. The Optimum Random Forest algorithm is illus- of its haplotypes is negative and for any case geno-tratedin. type it is positive. We would also like to maximize the confidence of our weight assignment which can 4. RESULTS & DISCUSSION be measured by the absolute values of the genotype In this section we first describe the genetic data of the weights. In other words, we would like to maximizeCrohn's disease and then discuss our experimental the sum of absolute values of weights over all geno-results. types. This method is based on a graph X = {H, G}, where4.1. Data Set the vertices H correspond to distinct haplotypes and The genetic data is derived from the 616 kilobase the edges G correspond to genotypes connecting its region of human Chromosome 5q31 that may contain two haplotypes. The density of X is increased by drop-a genetic variant responsible for Crohn's disease by ping SNPs which do not collapse edges with an oppo-genotyping 103 SNPs for 129 trios [14]. All offspring site status. The linear program assigns weights tobelong to the case population, while almost all par- haplotypes that, for any non-diseased genotype, the ents belong to the control population. In the entire sum of weights of its haplotypes is less than 0.5 and data, there are 144 case and 243 control individuals. greater than 0.5 otherwise. We maximize the sum ofThe missing genotype data and haplotypes have been absolute values of weights over all genotypes. Theinferred using the 2SNP phasing method [21]. status of the testing genotype is predicted as sum of its endpoints [15].4.2. Measures of Prediction Quality Optimum Random Forest (ORF).In the training To measure the quality of prediction methods, we set, the optimum random forest algorithm we need to measure the deviation between the true dis- described above is used to sort all SNPs, and find out ease status and the result of predicted susceptibility, the m most disease associated SNPs for a given which can be regarded as measurement error. We will thresholdm. Them most disease associated SNPs present the basic measures used in epidemiology to (Tag SNPs) are used to build the optimum random for-quantify the accuracy of our methods. est to test the left-out sample. In leave-one-out test,The basic measures are: since the training set is different after leaving one Sensitivity: the proportion of persons who have sample out, we may have different Tag SNPs for dif-the disease and who are correctly identified as cases. ferent training sets. Themvariables (SNPs) are used Specificity: the proportion of people who do not Figure 3 Figure 3.Optimum Random Forest Algorithm. SciRes JBiSE Copyright ©2008 56W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58 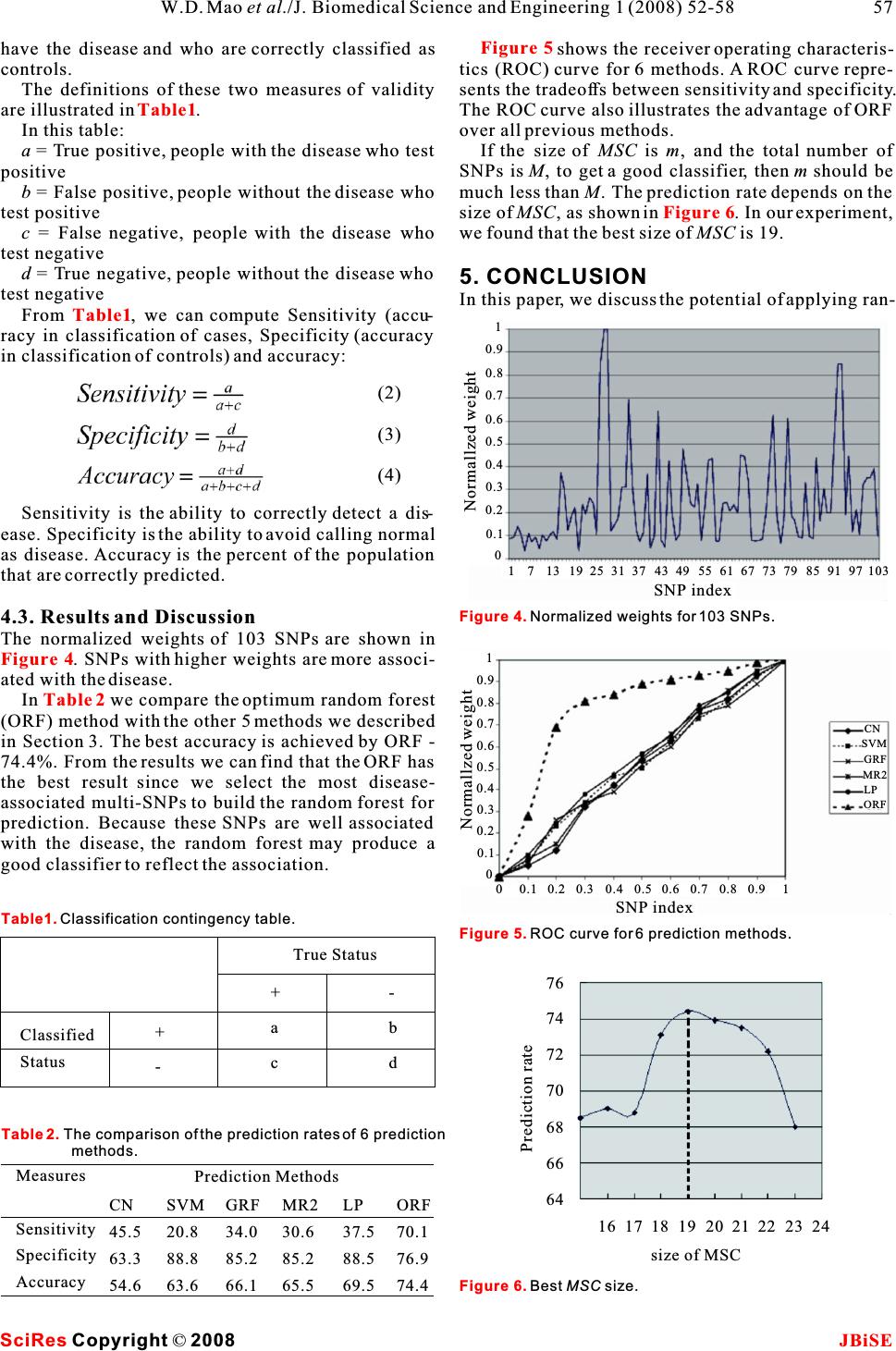 have the disease and who are correctly classified asshows the receiver operating characteris- controls. tics (ROC) curve for 6 methods. A ROC curve repre- The definitions of these two measures of validity sents the tradeoffs between sensitivity and specificity. are illustrated in.The ROC curve also illustrates the advantage of ORF In this table:over all previous methods. a= True positive, people with the disease who testIf the size of MSC is m, and the total number of positive SNPs is M, to get a good classifier, then m should be b = False positive, people without the disease who much less than M. The prediction rate depends on the test positivesize ofMSC, as shown in . In our experiment, c = False negative, people with the disease whowe found that the bestsize of MSC is 19. test negative d = True negative, people without the disease who 5. CONCLUSION test negativeIn this paper, we discuss the potential of applying ran- From, we can compute Sensitivity (accu- racy in classification of cases, Specificity (accuracy in classification of controls) and accuracy: Sensitivity is the ability to correctly detect a dis- ease. Specificity is the ability to avoid calling normal as disease. Accuracy is the percent of the population that are correctly predicted. 4.3. Results and Discussion The normalized weights of 103 SNPs are shown in . SNPs with higher weights are more associ- ated with the disease. Inwe compare the optimum random forest (ORF) method with the other 5 methods we described in Section 3. The best accuracy is achieved by ORF - 74.4%. From the results we can find that the ORF has the best result since we select the most disease- associated multi-SNPs to build the random forest for prediction. Because these SNPs are well associated with the disease, the random forest may produce a good classifier to reflect the association. Figure 5 Table1 Figure 6 Table1 Figure 4 Table 2 Prediction Methods Measures Sensitivity Specificity Accuracy CN 45.5 63.3 54.6 SVM 20.8 88.8 63.6 GRF 34.0 85.2 66.1 MR2 30.6 85.2 65.5 LP 37.5 88.5 69.5 ORF 70.1 76.9 74.4 Table 2. The comparison of the prediction rates of 6 prediction methods. Figure 5. ROC curve for 6 prediction methods. SciRes JBiSE Copyright ©2008 57 W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58 Table1. Classification contingency table. True Status - b d + - + a c Classified Status Figure 6.BestMSC size. Figure 4.Normalized weights for 103 SNPs. 1516 17 181920212223 24 size of MSC 76 74 72 70 68 66 64 Prediction rate SNP index 1 0.90.80.70.60.50.40.30.20.1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normallzed weight CN SVM GRF MR2 LP ORF SNP index 1713 19 25 31 37 4349 55 61 67 73 7985 9197 103 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normallzed weight (3) (4) (2)  Factors for Complex Diseases. Proc. IEEE International Con- dom forest on disease association studies. The pro-ference on Granular Computing 2006, pages 754-757. posed genetic susceptibility prediction method based[17]Kimmel, G. & Shamir R. A Block-Free Hidden Markov Model on the optimum random forest is shown to have afor Genotypes and Its Application to Disease Association.J. high prediction rate and the multi-SNPs being of Computational Biology 2005, 12(10): 1243-1260. [18]Listgarten, J., Damaraju, S., Poulin B., Cook, L., Dufour, J., selected to build the random forest are well associ-Driga, A., Mackey, J., Wishart, D., Greiner,R. & Zanke, B. ated with diseases. Actually the cause of complex dis-Predictive Models for Breast Cancer Susceptibility from Mul- eases is the combination of the environmental, tiple Single Nucleotide Polymorphisms. Clinical Cancer genetic factors and some other factors such as infec-Research 2004, 10:2725-2737. [19]Breiman, L. & Cutler, A.http://stat.berkeley.edu/breiman. tion and races. In our future work we are going to ana-[20]Waddell, M., Page,D., Zhan, F., Barlogie, B. & Shaughnessy, J., lyze the interactive contribution of these factors forPredicting Cancer Susceptibility from SingleNucleotide Poly- the development of complex diseases. Our next pro-morphism Data: A Case Study in Multiple Myeloma. Proc. of ject is going to find the relationship between the the 5th international workshop on Bioinformatics 2005, pages 21-28. genetic factor and race in the development of Type 2 [20]Chang, C. and Lin, C. http://www.csie.ntu.edu.tw/libsvm. Diabetes. The integrated software will be available [21]Brinza, D. & Zelikovsky, A. 2SNP: Scalable Phasing Based on soon for public use. 2-SNP Haplotypes.Bioinformatics 2006, 22(3):371-373. REFERENCE [1]National Digestive Diseases Information Clearinghouse (NDDIC), http://digestive.niddk.nih.gov/ddiseases/pubs/crohns. [2]Cardon, L.R. & Bell, J.I. Association Study Designs for Com- plex Diseases. Nature Reviews: Genetics 2001, 2:91-98. [3]Hirschhorn, J.N. & Daly, M.J. Genome-wide Association Stud- ies for Common Diseases and Complex Diseases. Nature Reviews: Genetics 2005, 6:95-108. [4]Merikangas, KR. & Risch, N. Will the Genomics Revolution Revolutionize Psychiatry.American Journal of Psychiatry, 2003, 160: 625-635. [5]Botstein, D. & Risch, N. Discovering Genotypes Underlying Human Phenotypes: Past Successes for Mendelian Disease, Future Approaches for Complex Disease.Nature Genetics 2003, 33: 228-237. [6]Clark, A.G., Boerwinkle E., Hixson J. & Sing C.F. Determi- nants of the success of whole-genome association testing. Genome Res. 2005, 15:1463-1467. [7]He, J. & Zelikovsky, A. Tag SNP Selection Based on Multivariate Linear Regression.Proc. of International Confer- ence on Computational Science 2006, LNCS 3992:750-757. [8]Brinza, D., He, J. & Zelikovsky, A. Combinatorial Search Meth- ods for Multi-SNP Disease Association.Proc. of International Conference of the IEEE Engineering in Medicine and Biology 2006, pages 5802-5805. [9]Cook N.R., Zee R.Y. & Ridker P.M. Tree and Spline Based Asso- ciation Analysis of gene-gene interaction models for ischemic stroke. Stat Med 2004, 23(9):439-453. [10]York T.P. & Eaves L.J. Common Disease Analysis using Multivariate Adaptive Regression Splines (MARS): Genetic Analysis Workshop 12 simulated sequence data. Genetic Epi- demiology 2001, 21 (S I):649-654. [11]Ritchie M.D., Hahn L.W., Roodi N., Bailey L.R., Dupont W.D., Parl F.F. & Moore J.H. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer.Am J Hum Genet. 2001, 69: 138-147. [12]Hahn L.W., Ritchie M.D. & Moore J.H. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions.Bioinformatics 2003, 19:376-382. [13]Lunetta, K., Hayward, L., Segal, J. & Van Eerdewegh, P. Screening Large-scale Association Study Data: Exploiting Interactions Using Random Forests”, BMC Genetics 2004, pages 5:32. [14]Daly, M., Rioux, J., Schaffner, S., Hudson, T. & Lander, E. High resolution haplotype structure in the human genome. Nature Genetics 2001, 29:229-232. [15]Mao, W., He, J., Brinza, D. & Zelikovsky, A. A Combinatorial Method for Predicting Genetic Susceptibility to Complex Dis- eases. Proc. International Conference of the IEEEEngineer- ing In Medicine and Biology Society 2005, pages 224-227. [16]Mao, W., Brinza, D., Hundewale, N., Gremalschi, S. & Zelikovsky,A. Genotype Susceptibility and Integrated Risk SciRes JBiSE Copyright ©2008 58W.D. Mao et al./J. Biomedical Science and Engineering 1 (2008) 52-58 |

