Journal of Service Science and Management
Vol.08 No.04(2015), Article ID:59019,11 pages
10.4236/jssm.2015.84062
Analysis Research on the Lateral Replenishment Strategy of the Chain Supermarket Fresh Agricultural Products*
Guangshu Xu, Zilong Song, Shangjun Piao
School of logistics, Beijing Wuzi University, Beijing, China
Email: guangshuxu@126.com, songzilong8@163.com, shangjunok@126.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 June 2015; accepted 15 July 2015; published 24 August 2015
ABSTRACT
The purpose of this research is to minimize the total cost of the overall system in the process of replenishment, to maximize the overall system profits. This paper regards all affiliated stores of chain supermarket as a system to do some research about the replenishment of fresh agricultural products. Then, this paper proposes the lateral replenishment strategy, analyzes its advantages, and applies the strategy thinking to the solution of the surplus or shortage of fresh agricultural products. Through the establishment of the inventory cost model, we compare the system inventory total cost between taking the lateral replenishment and deployment strategy and not using the lateral replenishment and deployment strategy, and get that there is lower total cost. Through the establishment of lateral replenishment transportation model, the optimal dispatching scheme between the surplus supermarket and the shortages supermarket is given. And then, the sensitivity analysis presents the variable range of the fresh agricultural products increment and decrement that does not affect this optimal dispatching scheme. This paper can provide a reference for the chain supermarket to deal with the shortage or surplus of fresh agricultural products so as to improve sales margins of agricultural products, to reduce the total inventory costs of the whole the chain supermarket system, and to improve the customer service levels.
Keywords:
Fresh Agricultural Products, Optimal System, Lateral Replenishment and Deployment

1. Introduction
With the improvement of living standards, there are increasingly high requirements for fresh agricultural products. People attach more importance to the quality, variety, nutritional value, and many other factors of fresh agricultural products. When consumers buy fresh agricultural products, the fresh, green, organic and healthy are the important factors to be taken into consideration. In China, the main sources of the supply of fresh agricultural products include farmers’ markets and supermarkets. Compared with farmers’ markets and others, supermarkets are more secure in fresh quality and security. Unified procurement, processing, distribution and strict checks of various aspects can meet the special requirements in the circulation with irreplaceable advantages. Therefore, chain supermarkets become the primary place for consumers to buy fresh agricultural products. However, as more and more people choose to go to the chain supermarket to buy fresh agricultural products, the uncertainty of demand for fresh produce leads to the inaccurate forecasts of supermarket for fresh agricultural products demand. Thus, to a certain extent, this causes the stockpiles or shortages of fresh agricultural products of supermarket, affects the consumer demand for fresh agricultural products, and finally causes some damage of the supermarkets interests. Therefore, researching the transverse replenishment policy of chain supermarkets fresh agricultural products can not only ensure the individual needs of consumers for fresh produce, improve customer satisfaction, but also reduce the inventory costs and improve the profits of supermarket.
Some scholars previously have done certain related researches about the shortage, surplus, replenishment of fresh agricultural products. Chaaben Kouki et al. (2015) [1] proposed inventory control model, which contributed to the literature by providing a simple and efficient algorithm to compute the best (r, Q) parameters that minimized the total cost. Yiyan Qin et al. (2014) [2] considered the pricing and lot-sizing problem for products with quality and physical quantity deteriorating simultaneously, and designed the optimal model to investigate the deterioration inventory of fresh produce and foods. Biswajit Sarkar and Sumon Sarkar (2013) [3] expanded an inventory model for deteriorating items with stock-dependent demand to determine the optimal cycle length of each product such that the expected total cost (holding, shortage, ordering, deterioration and opportunity cost) was minimized. Yu-Ping Leea and Chung-Yuan Dyeb (2012) [4] formulated a deteriorating inventory model with stock-dependent demand by allowing preservation technology cost as a decision variable in conjunction with replacement policy to find the optimal replenishment and preservation technology investment strategies while maximizing the total profit per unit time. Joaquín Siciliaa et al. (2014) [5] studied a deterministic inventory system for items with a constant deterioration rate. They considered the ordering cost, the holding cost, the backlogging cost, the deteriorating cost, and the purchasing cost in the inventory management and proposed an approach to minimize the total cost per inventory cycle. Hardik N. Soni (2013) [6] formulated a mathematical model and then some useful theoretical results had been derived to characterize the optimal solutions for non- zero and zero ending inventory system. Chih-Te Yang (2014) [7] developed an inventory model under a stock- dependent demand rate and stock-dependent holding cost rate with relaxed terminal conditions to determine the optimal order quantity and the ending inventory level such that the total profit per unit time was maximized for the retailer. Kun-Shan Wua et al. (2006) [8] considered a problem of determining the optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand. Chun-Tao Chang et al. (2010) [9] amended Wu et al.’s model by changing the objective to maximizing the total profit and set a maximum inventory level in the model to reflect the facts that most retail outlets had limited shelf space. They relaxed the restriction of the zero ending inventory when shortages were not desirable then established the theoretical results and provided an algorithm to find the optimal solution. Chia-Hsien Su (2012) [10] established a two-echelon inventory model to encourage sales the supplier offers trade credit to the retailer. And the decision variables include: replenishment cycle time, the time taken to run out of stock and the number of lots delivered from the supplier to the retailer. Parviz Fattahi et al. (2015) [11] proposed a bi-objective multi-product (r,Q) inventory model in which the inventory level was reviewed continuously. The aim of them is to find the optimal value for both order quantity and reorder point through minimizing the total cost and maximizing the service level of the proposed model simultaneously. K. Inderfurth and G. P. Kiesmüller (2015) [12] proposed two novel approaches to derive optimal and near-optimal numerical values for the critical stock level, minimizing the average holding and backorder cost for a given inflation factor. Han Zhu et al. (2015) [13] considered a single-item periodic-re- view stochastic inventory system with both minimum order quantity (MOQ) and batch ordering requirements. Ali Cheaitou et al. (2014) [14] proposed a single-product, stochastic, two-period inventory control model, which combined demand forecast updating with the flexibility of two supply sources. Gitae Kim et al. (2015) [15] presented a multi-period newsvendor model, and the problem was formulated as a multi-stage stochastic programming model with integer recourse decisions to optimize the total logistic cost for perishable products. Cinthia Pérez and Joseph Geunes (2014) [16] analyzed an inventory replenishment model with two transportation modes so as to reduce the inventory cost.
Previous scholars have made some researches on inventory management and replenishment strategy of the chain supermarket fresh agricultural products, but only focused on individual supermarkets to find the optimal strategy to achieve a certain type of supermarket inventory management and not to apply the lateral replenishment strategy to the inventory management. This paper will regard all sub supermarket stores of the chain supermarket as a system and apply the lateral replenishment strategy to the inventory management of the fresh agricultural products. And the optimal replenishment strategy of system will advance to the optimal replenishment strategy of a single-goods store. This research not only optimizes the inventory cost and restocking fee of fresh agricultural products of each store, but also lays more emphasis on the realization of the optimal inventory replenishment transfer cargo policy of the entire system. On the basis of our research, through the store inventory control and supervision, the chain supermarket can effectively minimize the whole inventory costs of fresh agricultural products and improve the profits and margins of the whole system.
2. Feasibility Analysis of Lateral Replenishment Strategy
Lateral replenishment thinking applied to the replenishment of fresh agricultural products of the chain supermarket is a relatively new approach. That conduct lateral replenishment of fresh agricultural products between supermarket stores is when there is shortage, or surplus of supermarket stores, appropriate to transport the surplus fresh agricultural products of the supermarket stores to the shortage fresh agricultural products of the supermarket stores in some period of time, thus timely and effectively solving the shortage, or surplus problems of fresh agricultural products of the supermarket stores. Through the lateral replenishment, it can have the following advantages:
1) Regard all sub supermarket stores of the chain supermarket as a system. When there is shortage or surplus of fresh agricultural products of some supermarket stores, then the shortage of the part of supermarket stores do not represent the shortage of the chain supermarket system, the surplus stock of the part of supermarket stores can not represent the surplus of the chain supermarket system. The lateral replenishment strategy can optimize inventory adjustment fresh agricultural products from the perspective of system.
2) Since all sub chain supermarket stores are unified managed by the headquarters, there is not a problem that unstable partnership occurs between the sub chain supermarket stores.
3) The replenishment price of fresh agricultural products is relatively stable, which can be controlled between the purchase price of the distribution center and the selling price of the supermarket stores. And it can be priced by headquarters to reduce the replenishment costs.
4) When the sub supermarket stores transfer fresh agricultural products from a store to another store, the distance between them should be taken into consideration. Therefore, transfer goods between stores can improve arrival rate. For the supermarket stores out of stock, the transport costs of transfering fresh agricultural products from other supermarket stores are much lower than the supply center. And for small quantities of fresh agricultural products out of stock, transfer fresh agricultural products from other sub-goods supermarket stores will be more convenient. This can help short the replenishment time, to a certain extent, improve customer service levels.
5) After adding lateral replenishment, fresh agricultural products between the supermarket stores will be allocated optimally to improve the overall profits. Also, this can reduce profits loss of the shortage situation when the supermarket stores take no notice of the shortage situation, and this can reduce profits loss of the surplus situation when the supermarket stores treat the surplus fresh agricultural products at discount prices.
In summary, the lateral replenishment has more advantages. It can be used in supermarkets fresh agricultural products replenishment, but it needs to combine the use of traditional replenishment strategy so as to play their strengths. Because it cannot exclude the situation that the inventory shortage or excess of the entire chain supermarket will occur, the lateral replenishment of fresh agricultural products between stores needs to combine traditional way to provide services of the chain supermarket.
3. The Lateral Replenishment Inventory Model and Transportation Model Design
3.1. Problem Descriptions
Because the distribution center is relatively far from the supermarket stores, or due to the certain small demand of fresh agricultural products not up to the required amount of the distribution center, the distribution center is not to carry out the distribution, resulting in the shortage situation of fresh agricultural products. Because when some supermarket stores predict the demand of fresh agricultural products, there is large deviation, which results in excessive accumulation of fresh agricultural products. For the cases above, the lateral replenishment will be applied to supermarket stores, which will be more rational to use the resources fresh agricultural products to further reduce losses and reduce costs.
The purpose of lateral replenishment of the chain supermarket fresh agricultural products is to make the optimal allocation of reasonable inventory of the supermarket fresh agricultural products, to minimize the total costs, and to get the entire optimal system. To solve the issue of the replenishment of the fresh agricultural pro- ducts between the chain supermarket stores, the lateral replenishment inventory model can be established. On the one hand, to make the whole system to the minimum inventory costs, on the other hand, to make optimal replenishment strategies of all stores to the lowest cost.
Assume that the operational status of each supermarket store is same. The demand of fresh agricultural products is independent and is in keeping with poisson distributions. The order lead time of fresh agricultural products is same and unchanged. All supermarket stores apply (s, S) storage strategy. When the stock fresh agricultural products are less than s, then they restock to S. In the case of each supermarket stores appear out of fresh agricultural products, only when the existing inventory below the safety stock quantity, there is replenishment applications from the supermarket stores, which stock stores is greater than the safety stock.
The symbols and meanings involved in the model are as follows:
1) i, j represents each chain supermarket stores, and the total number is N.
2) S0 represents the fresh agricultural products inventory of the chain supermarket system, Si represents the fresh agricultural products stocks of store i.
3) Cr represents the ordering cost of fresh agricultural products of each chain supermarket stores.
4) Ch represents the unit time fee of fresh agricultural products of each chain supermarket stores.
5) Cl represents the Shortage Costs of fresh agricultural products of each chain supermarket stores.
6) Cij represents the lateral transportation costs of fresh agricultural products of each chain supermarket stores, represents the average transportation cost of the chain supermarket stores i.
7) ai represents probability of supermarket store i meeting the demand of fresh agricultural products with its own stocks.
8) bi represents probability of supermarket store i meeting the demand of fresh agricultural products rely on lateral replenishment.
9) li represents the probability that the fresh agricultural products of supermarket store i out of stock. Because only when the fresh agricultural products of entire system is out of stock, then the fresh agricultural products of each supermarket store may is out of stock, therefore, the probability of the shortage of system fresh agricultural products: l = li.
10) e represents the expectation customer service levels of the chain supermarket system.
11) Di represents the demand of fresh agricultural products of unit time of supermarket stores i; D0 represents the demand of fresh agricultural products of system; mi represents the average demand of each supermarket store; Dij represents the replenishment quantities from store i to stores j.
12) Li represents the replenishment lead time of fresh agricultural products of each chain supermarket stores. It is the time that from the issue replenishment orders to the commodity storage.
3.2. Model Establishment
Inventory costs include order costs, storage costs, lateral transportation costs, the shortage loss costs.
Order costs CR: the order cost of fresh agricultural products can be represented a product by a single order costs and the total number of orders.
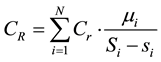 (1)
(1)
In the formula,
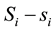 represents the actual shortage amount of each time,
represents the actual shortage amount of each time,
 represents the total num- ber of orders.
represents the total num- ber of orders.
Storage costs CH: the order cost of unit time of fresh agricultural products can be represented a product by the unit storage cost and the Average inventory quantities.
Because the model is based on the premise allowing out of stock, so the average inventory quantities do not include the demand quantities in the period of lead time. The average inventory quantities is
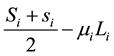
Then, get the storage costs:
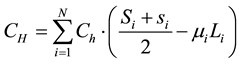 (2)
(2)
Lateral transportation costs CT: the ateral transportation costs is related with the average transportation costs, the average demand rate of fresh agricultural products and the probability of meeting the demand of fresh agricultural products through ateral transportation.
Throughout the chain supermarket system, there are three cases about the stock demand of fresh agricultural products: a) the fresh agricultural products of stores can be met through the original stock, then the probability is ai; b) the fresh agricultural products of stores can be met through lateral transportation, the probability is bi; 3) the entire supermarket system is out of stock, the fresh agricultural products cannot be met, then the probability is li. And, ai + bi + li = 1.
According to independent demand inventory model, in the period of order lead time, the demand of store i is Di Li, then:
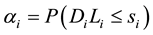 (3)
(3)
If the system is out of stock, it does not meet the conditions of lateral replenishment. Then, the store i is out of stock in the period of optimal ordering, while other stores j is in the lead time or in the period of order cycle. And the demand is always greater than the actual stocks of stores. Then, the probability is as follows:
 (4)
(4)
The lateral transportation costs of the whole chain supermarket system can be obtained from the above equation as follows:
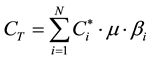 (5)
(5)
The shortage loss costs of the whole chain supermarket system are as follows:
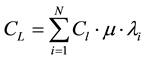 (6)
(6)
In summary, the inventory total cost model of fresh agricultural products of the chain supermarket system is as follows:
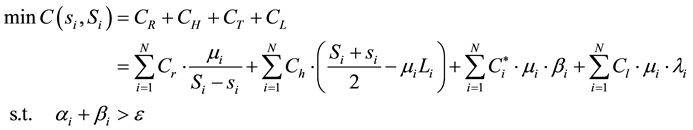 (7)
(7)
If there is no lateral transportation between supermarket store, the model becomes the follows:
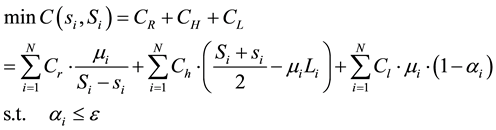 (8)
(8)
When store i has the surplus of fresh agricultural products goods stores, the surplus that has excess safety stock, needs to be transported to the stores is out of fresh agricultural products. On the contrary, when there is shortage of store i, the store i need to make replenishment application to other stores that owning more fresh agricultural products. Assume that eventually all fresh agricultural products of the chain supermarket system is distributed to all the sub stores of the chain supermarket system, the model will be the supply and demand balance transport model. m represents the stores that has Surplus, referred to as A1, A2, A3,…, Am. n represents the stores that has shortage, denoted by B1, B2, B3, …, Bn. The quantities of shortage is recorded as b1, b2, b3, …, bn. sij is the transporting capacity of the chain supermarket which is transported from store Ai owning surplus to store Bj that has shortage (i = 1, 2, 3, …, m, j = 1, 2, 3, …, n). cij represents the unit transportation costs from store Ai to store Bj. lij is the distance from store Ai to store Bj, but it will be affected by traffic in the actual transportation process. If it is considered only in distance or unit transportation costs, there will be inaccurate to the distribution program of the whole system. And the traffic situation the day is not the same in each time. rij represents traffic situation coefficients from store Ai to store Bj. pij is only in 0 - 1. The more it is closer to 1, the better the traffic situation it is. On the contrary, it is worse.
Then, the lateral replenishment transportation model is established on the basis of the traditional transportation model as follows:

 (9)
(9)
4. Example One Design
4.1. Background Description
A supermarket is a national chain supermarket and is the large-scale retail enterprises. There are a total of seven regional chain stores in Beijing. These stores are replenished by the same fresh agricultural products distribution center. In recent years, in order to increase traffic, improve the market competitiveness of industry peers, a chain supermarket increases a significant operating proportion of fresh agricultural products in supermarkets stores, and regards the fresh agricultural products as highlights and features.
Since the distribution center is relatively far from the supermarket stores, or due to the certain small demand of fresh agricultural products not up to the required amount of the distribution center, the distribution center is not to carry out the distribution, resulting in the shortage situation of fresh agricultural products. Because when some supermarket stores predict the demand of fresh agricultural products, there is large deviation, which results in excessive accumulation of fresh agricultural products. And the fresh agricultural products cannot be sold due to the rot, then the profit margins of the fresh agricultural products will be reduced. For the cases above, the lateral replenishment will be applied to A supermarket, which will be used to solve the shortage and the surplus problems of fresh agricultural products.
4.2. Data Calculation
The operational status of the seven chain stores is same. The demand of fresh agricultural products is independent and is in keeping with poisson distributions. The order lead time of fresh agricultural products is same and unchanged. All supermarket stores apply (s, S) storage strategy.
Related data are as follows:
1) The Si, si of each supermarket store, the average transportation cost:
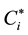 is as shown in the Table 1.
is as shown in the Table 1.
2) The single ordering cost: Cr = 1000 yuan, the inventory holding costs of a single piece of fresh produce of unit time: Ch = 5 yuan, the shortage loss costs of a single piece of fresh agricultural products: Cl = 20 yuan.
3) The demand of fresh produce stores varies every day. Criteria to the demand of a month, the average daily demand mi of the store is as shown in Table 1.
The above data are into the formula (1) and formula (2), then the order costs, storage costs can be obtained under the conditions of not allowing lateral replenishment.
 = 943 (yuan)
= 943 (yuan)
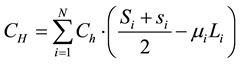 = 5887.5 (yuan)
= 5887.5 (yuan)
4) The demand of fresh agricultural products is in keeping with poisson distributions: Di ~ P(si);
Take store 1 as example, Use the Matlab 7.0 to describe demand probability distribution of the fresh agricultural products. And the demand probability distribution is shown in Figure 1, other stores are the same.
The fresh agricultural products of stores can be met through the original stock, and the probability is ai. According to the equation (3) and the probability formula of poisson distributions, the
can be got. And the results are shown in Table 2.
Table 1. Data of each sub supermarket stores.
Figure 1. The demand probability distribution of the fresh agricul- tural products of store 1.
Table 2. Probability data of store’s own inventory to meet demand.
When the chain supermarket system is out of stock, it will does not meet the conditions of lateral replenishment. Then, supermarket stores at this time needs to place an order to suppliers or distribution center, the rate of shortage is li, bi. According to Equation (4) and the formula ai + bi + li = 1, the results obtained are shown in Table 3.
5) The above data are into the formula (5) and formula (6), then the lateral transportation costs, the shortage loss costs can be obtained.


6) The order costs, storage costs can be obtained under the conditions of allowing lateral replenishment .


7) According to the inventory cost model, the total cost of inventory can be obtained under the conditions of allowing lateral replenishment.
8) When the chain supermarket system does not meet the needs of fresh agricultural products, supermarket stores at this time needs to place an order to suppliers or distribution center. Then, there will be no lateral transportation costs, and the total cost of inventory is as follows.
4.3. Results Analysis
From the two inventory costs of allowing the lateral replenishment and not allowing the lateral replenishment, it can be got that the total inventory cost of allowing the lateral replenishment is lower than the total inventory cost of not allowing the lateral replenishment.
When the supermarket adopt the lateral replenishment, even though the loss caused by shortages is much lower than ordering directly to the distribution centers, even though it needs bear the cost of transporting in the lateral transportation, and even though the storage costs are slightly higher than the cost of the replenishment adopted by distribution center or supplier, there but is a relatively small impact on the total cost of inventory. Therefore, the supermarket adopt the lateral replenishment can make the total inventory costs of the entire chain supermarket x system lower. And achieve the overall system optimization.
5. Example Two Design
5.1. Background Description
The lateral replenishment inventory model obtains the total inventory cost of allowing the lateral replenishment is lower than the total inventory cost of not allowing the lateral replenishment.
It can be provided for the chain supermarket to reduce the loss of fresh agricultural products. After the analysis and calculation of inventory cost model, we can transport the fresh agricultural products from stores owning surplus to store owning shortage. Then, the best transportation plan should be designed in order to transport the fresh agricultural products with the lowest transportation costs. And, the sensitivity analysis of the lateral replenishment inventory model should be given.
5.2. Data Calculation
Table 4 shows the distance data of stores. Table 5 shows the unit transportation data. Table 6 shows the traffic coefficient merits. Related data of all stores of a chain supermarket are as follows:
According to the lateral replenishment transport model, we use an excel to get the optimal solution. The optimal solution is as shown in Table 7. The sensitivity analysis of the transport program is shown in Table 8 and Table 9.
5.3. Results Analysis
The lateral replenishment transport model above get the optimal dispatching scheme between stores, and the sensitivity analysis of this transportation program, get the variable range of the fresh agricultural products increment and decrement that does not affect this optimal dispatching scheme. That is, within this range, the optimal dispatching scheme remains the same.
6. Conclusions
In this paper, all the sub-supermarket stores of the chain supermarket are regarded as a whole system to be researched. The goal of the research is to minimize the total inventory cost of the overall system in the process of replenishment, to maximize the overall system profits. This paper applies the lateral replenishment thinking to the replenishment of the chain supermarket, provides the solution to deal with the shortage or surplus of chain supermarket fresh agricultural products, and the shortcomings issue of traditional replenishment methods, and provides the solution to deal with the shortcomings issue of only considering the local interest of the traditional replenishment thinking. By the establishment of the lateral replenishment inventory model and the analysis of the actual examples, it can be got that the total inventory cost of allowing the lateral replenishment is lower than the total inventory cost of not allowing the lateral replenishment. Through the establishment of lateral replenishment transportation model, the optimal dispatching scheme between the surplus supermarket and the shortages supermarket is given. And then, the sensitivity analysis presents the variable range of the fresh agricultural
Table 3. Probability data of indirect replenishment to meet demand.
Table 4. Stores distance data (unit: kilometers).
Table 5. Unit shipment data.
Table 6. Traffic coefficient merits.
Table 7. Optimal solution.
Table 8. Sensitivity analysise one.
products’ increment and decrement that does not affect this optimal dispatching scheme.
This paper can provide a reference for the chain supermarket to deal with the shortage or surplus of fresh agricultural products. And, this will help the chain supermarket to improve sales margins of agricultural products, to reduce the total inventory costs of the whole the chain supermarket system, and to improve the customer
Table 9. Sensitivity analysise two.
service levels. This paper will have the certain significance for the further research of the ateral replenishment strategy of the chain supermarket fresh agricultural products.
Cite this paper
GuangshuXu,ZilongSong,ShangjunPiao, (2015) Analysis Research on the Lateral Replenishment Strategy of the Chain Supermarket Fresh Agricultural Products. Journal of Service Science and Management,08,619-630. doi: 10.4236/jssm.2015.84062
References
- 1. Kouki, C., Jemaï, Z. and Minner, S. (2015) A Lost Sales (r, Q) Inventory Control Model for Perishables with Fixed Lifetime and Lead Time. International Journal of Production Economics, 168, 143-157.
http://www.sciencedirect.com/science/article/pii/S0925527315002182
http://dx.doi.org/10.1016/j.ijpe.2015.06.010 - 2. Qin, Y.Y., Wang,
J.J. and Wei, C.M. (2014) Joint Pricing and Inventory Control for Fresh Produce and Foods with Quality and Physical Quantity
Deteriorating Simultaneously. International Journal of Production Economics, 152, 42-48.
http://www.sciencedirect.com/science/article/pii/S0925527314000073
http://dx.doi.org/10.1016/j.ijpe.2014.01.005 - 3. Sarkar, B. and Sarkar, S. (2013) An Improved Inventory Model with Partial Backlogging, Time Varying Deterioration and Stock-Dependent Demand. Economic Modelling, 30, 924-932.
http://www.sciencedirect.com/science/article/pii/S0264999312003240
http://dx.doi.org/10.1016/j.econmod.2012.09.049 - 4. Lee, Y.-P. and Dye, C.-Y. (2012) An Inventory Model for Deteriorating Items under Stock-Dependent Demand and Controllable Deterioration Rate. Computers & Industrial Engineering, 63, 474-482.
http://www.sciencedirect.com/science/article/pii/S0360835212000940
http://dx.doi.org/10.1016/j.cie.2012.04.006 - 5. Sicilia, J., González-De-la-Rosa, M., Febles-Acosta, J. and Alcaide-López-de-Pablo, D. (2014) An Inventory Model for Deteriorating Items with Shortages and Time-Varying Demand. International Journal of Production Economics, 155, 155-162.
http://www.sciencedirect.com/science/article/pii/S0925527314000383 - 6. Soni, H.N. (2013) Optimal Replenishment Policies for Non-Instantaneous Deteriorating Items with Price and Stock Sensitive Demand under Permissible Delay in Payment. International Journal of Production Economics, 146, 259-268.
http://www.sciencedirect.com/science/article/pii/S0925527313003186
http://dx.doi.org/10.1016/j.ijpe.2013.07.006 - 7. Yang, C.-T. (2014) An Inventory Model with Both Stock-Dependent Demand Rate and Stock-Dependent Holding Cost Rate. International Journal of Production Economics, 155, 214-221.
http://www.sciencedirect.com/science/article/pii/S0925527314000188
http://dx.doi.org/10.1016/j.ijpe.2014.01.016 - 8. Wu, K.-S., Ouyang,
L.-Y. and Yang, C.-T. (2006) An Optimal Replenishment Policy for Non-Instantaneous Deteriorating Items with Stock-Dependent
Demand and Partial Backlogging. International Journal of Production Economics, 101, 369-384.
http://www.sciencedirect.com/science/article/pii/S0925527305000502
http://dx.doi.org/10.1016/j.ijpe.2005.01.010 - 9. Chang, C.-T., Teng, J.-T. and Goyal, S. K. (2010) Optimal Replenishment Policies for Non-Instantaneous Deteriorating Items with Stock-Dependent Demand. International Journal of Production Economics, 123, 62-68.
http://www.sciencedirect.com/science/article/pii/S0925527309002667
http://dx.doi.org/10.1016/j.ijpe.2009.06.042 - 10. Su, C.-H. (2012) Optimal Replenishment Policy for an Integrated Inventory System with Defective Items and Allowable Shortage under Trade Credit. International Journal of Production Economics, 139, 247-256.
http://www.sciencedirect.com/science/article/pii/S0925527312001740
http://dx.doi.org/10.1016/j.ijpe.2012.05.001 - 11. Fattahi, P., Hajipour, V. and Nobari, A. (2015) A Bi-Objective Continuous Review Inventory Control Model: Pareto-Based Meta-Heuristic Algorithms. Applied Soft Computing, 32, 211-223.
http://www.sciencedirect.com/science/article/pii/S1568494615001635
http://dx.doi.org/10.1016/j.asoc.2015.02.044 - 12. Inderfurth, K. and Kiesmüller, G.P. (2015) Exact and Heuristic Linear-Inflation Policies for an Inventory Model with Random Yield and Arbitrary Lead Times. European Journal of Operational Research, 245, 109-120.
http://www.sciencedirect.com/science/article/pii/S037722171500199X
http://dx.doi.org/10.1016/j.ejor.2015.03.006 - 13. Zhu, H., Liu, X. and Chen, Y. (Frank) (2015) Effective Inventory Control Policies with a Minimum Order Quantity and batch ordering. International Journal of Production Economics, 168, 21-30.
http://www.sciencedirect.com/science/article/pii/S0925527315002169
http://dx.doi.org/10.1016/j.ijpe.2015.06.008 - 14. Cheaitou, A., van
Delft, C., Jemai, Z. and Dallery, Y. (2014) Optimal Policy Structure Characterization for a Two-Period Dual-Sourcing Inventory
Control Model with Forecast Updating. International Journal of Production Economics, 157, 238-249.
http://www.sciencedirect.com/science/article/pii/S092552731400245X
http://dx.doi.org/10.1016/j.ijpe.2014.07.028 - 15. Kim, G., Wu, K. and Huang, E. (2015) Optimal Inventory Control in a Multi-Period Newsvendor Problem with Non-Stationary Demand. Advanced Engineering Informatics, 29, 139-145.
http://www.sciencedirect.com/science/article/pii/S1474034614001128
http://dx.doi.org/10.1016/j.aei.2014.12.002 - 16. Pérez, C.
and Geunes, J. (2014) A (Q, R) Inventory Replenishment Model with Two Delivery Modes. European Journal of Operational Research,
237, 528-545.
http://www.sciencedirect.com/science/article/pii/S0377221714001842
http://dx.doi.org/10.1016/j.ejor.2014.02.049
NOTES
*Key project of Philosophy and Social Science Research in Beijing (09AbJG299); Key project of training plan of Beijing young top-notch talent (CIT&TCD201304109).








