Received 11 March 2016; accepted 10 April 2016; published 18 July 2016

ABSTRACT

The static flow resistivity is a fundamental parameter for measuring and classifying the sound absorption behavior of various types of materials. Several methods have been developed for measuring the static flow resistivity acoustically. Most of these methods cannot be implemented directly in the standard tubes which are widely used for measurements of sound absorption coefficients and impedance as defined in ISO 10534.2. The accuracy of the proposed method and the tube is verified through finite element analysis and the feasibility to determine the static flow resistivity is validated through experiments. It is validated that the accuracy of the proposed method is highly dependent on the position of the acoustic center of the measurement microphones and the accuracy can be enhanced by increasing the back cavity depth and/or decreasing the measurement frequency.

Keywords:

Static Flow Resistivity, Impedance Tube, ISO 10534.2, Sound Absorption

1. Introduction

Sound absorbing materials are essential considerations in building acoustics and noise reduction in the environment. For determining sound absorption coefficient, impedance tube is used universally. The normal sound absorption coefficient and the surface impedance of a material are often measured by an impedance tube [1] [2] . These properties include complex characteristic impedance, complex propagation constant, and random incidence absorption coefficient. The properties can be determined theoretically using the empirical prediction [3] [4] . The mechanical impedance is obtained by dividing the applied force to the particle velocity. In addition, acoustical impedance is the applied pressure divided by volume velocity [5] . Flow resistivity is determined as the real part of the ratio between the pressure drop and the flow velocity through a layer of material of unit thickness [6] . The flow resistivity plays a major role in the calculation of acoustic properties of materials like propagation constant, sound absorption and characteristic impedance. The methods for measuring the flow resistivity can be classified as direct flow method [7] and acoustical method [8] [9] . In the direct flow measurement, the pressure drop across the specimen and the flow velocity through specimen are measured separately and the ration between them is calculated. In the acoustical methods, measurements are carried out using the impedance tube with the sound generating source at one end and terminating rigid body at the other end. Microphones are placed between these two ends. There are several acoustical methods that are normally carried out in impedance tubes with a loudspeaker and several microphones at low frequency. McIntosh et al. [10] proposed to measure the sound pressure at both sides of the test specimen, and divided the sound pressure drop by the flow velocity and the specimen thickness to calculate the static flow resistivity. Woodcock et al. [11] measured the propagation constant and the characteristic impedance of the material by adopting two-cavity method and then calculated the effective flow resistivity using the inverse equation of the Delany and Bazley empirical formulae [12] . Jiancheng Tao et al. [13] found out that a thicker specimen provides more stable flow resistivity and allows a higher measurement frequency.

In this paper, a new method is proposed that can be directly applied with an impedance tube. The implementation is verified to determine the static flow resistivity and design of impedance tube. The advantage of the proposed method is that a standard impedance tube can be used directly to measure the flow resistivity. Based on the finite element model of the impedance tube, the effects of several factors can be obtained, such as position of the microphones, depth of the back cavity, measurement frequency and thickness of the specimen. The performance of the proposed method is validated by conducting experiments.

2. Theory

Noise control is essential in vehicles that carry passengers to long distances as they are confined to the same closed environment for a long range of time. Automotive companies employ various noise control materials at different locations. Generally in a car, materials like polyester, nylon, composites of carbon and aramid fibers are used. The materials are mainly placed in interior fitments, safety facilities, tire reinforcement, and carpets. They are also used for sound and thermal insulation.

Sound absorbing materials are commonly used to soften the acoustic environment of a closed volume by reducing the amplitude of the reflected waves. Absorptive materials are generally resistive in nature, either fibrous, porous or in rather special cases reactive resonators. Most of these products provide some degree of absorption at nearly all frequencies (up to 2 kHz) and performance at low frequencies typically increases with increasing material thickness. The absorption ratio and transmission loss that represent sound reflection and penetrating capability of a sample material, usually considered as the most important acoustical properties, are measured by an impedance tube.

The performance of sound absorbing materials is evaluated by the sound absorption coefficient (α). The sound propagation in a standing wave duct is assumed as stationary plane waves with zero mean flow speed propagating in air. The complex acoustic pressure p(x, t) and the particle velocity v(x, t) of the medium are given in Equations (1) and (2) [14] .

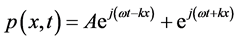(1)

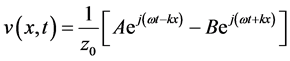(2)

where A and B are amplitudes of the incident and reflected waves, ω is the angular frequency, k is the wave number, z₀ is the characteristic impedance of the air at 20˚C, and ρ and c are the air density and speed of sound in air respectively.

3. Measurement Setup

The impedance tube is designed according to the standard impedance tube design ISO 10534.2 as shown in Figure 1. Here three microphones are kept on the side of a test specimen and at other end rigid termination is

present. The test specimen is considered to have a depth of 2 L and their back cavity depth is L which is the difference between surface of the specimen and the back termination. The loud speaker is placed at other end of the tube generating a broadband signal from 60 Hz to 1600 Hz. The sample is placed at the end of the tube on the hard termination. Two BSWA type MPA416 microphones are implemented. Since in practical applications it is hard to generate tens of frequency, the minimum frequency is kept at 100 Hz. Fortunately the static flow resistivity is not sensitive to frequency, when the measurement frequency is low [15] . The flow resistivity is acceptable when the frequency is few hundreds of Hz.

The acoustic impedance at the front surface can be determined by

(3)

where ρ is the air density, c is the speed of the sound and r is the reflection coefficient

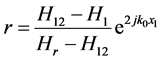(4)

where H₁₂ = p₂/p₁, Where p is the measured sound pressure at microphones 1 and 2 respectively, K₀ is the wave number, it is defined as the K₀ = 2πf/c, where f is the frequency.

Similarly the acoustic impedance can be formulated by

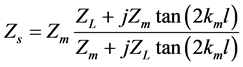(5)

where Z_m, k_m and Z_L are characteristic impedance, propagation constant and the acoustic impedance at the back surface for the specimen. Accordingly the specimen is placed at the rigid termination L = 0 and Zl ͢∞ which is obtained as [1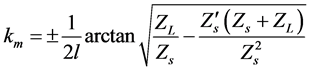6] .

(6)

For porous material, flow resistivity can be calculated using [1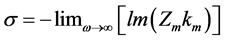7]

(7)

When the specimen thickness is rather small compared to the wavelength, it can be calculate as

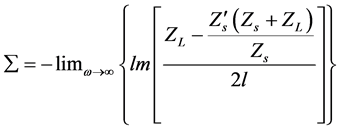(8)

In the proposed work the method involves (a) the sound absorption coefficient of porous material and non- porous material (b) the determination of static flow resistivity (c) the computation of the propagation constant and characteristic impedance, (d) Impedance measurements on the specimen when the back cavity is zero and at a random value L. It is compared to the Woodcock method and Jiancheng Tao et al method.

The modified cost impedance tube is designed as shown in Figure 2.

The impedance tube set up contains a signal source along with power amplifier section. The existing impedance tube signal characteristics is improved by modifying the signal source from generating monotone signals into one that generates white noise signals The main purpose of adding white noise is to provide a uniform reference frame in the time-frequency space [18] . Also white noise added signal permits frequencies analyze resolution of 6.25 Hz in a frequency domain of 125 - 10,000 Hz. This high resolution is necessary for the evaluation of acoustic properties using impedance tube. The noise circuitry is designed by adding the signals generated from two similar signal generators, through a resistive network. The signal is amplified using a power amplifier circuit and fed into the impedance tube through a loud speaker.

Microphones that are placed inside the tube capture the incident signal and reflected signal from the sample. These signals are too weak to be transmitted to recording devices and hence preamplifiers are used to increase a microphone signal to line-level by providing stable gain while preventing induced noise that would otherwise distort the signal. A microphone preamplifier increases the 0 to 100 microvolt range level up by 70 dB, to approximately 0 to 10 volts. A preamplifier is placed close to the microphone to reduce the effects of noise and interference. Most of the methods uses microphone, although sensors can be implemented a comprehensive review of techniques for measuring the acoustical response can be found it is important to have an accurate analytical expression for the response of a calibration object, and for this reason closed tubes are often employed, rather than cavities or open-ended tubes. The amplitude of the incident and reflected signals vary according to the sound absorption of the sample. Therefore by monitoring the amplitude variations of both signals and taking the ratio of it, the sound absorption coefficient of material is calculated. A digital storage oscilloscope, spectrum analyzer or a PC is used for storing and analyzing these signals.

4. Simulations and Discussion

In this proposed work, there are many factors that affect the measurement accuracy, such as the placement of the microphones, the rigidness of the termination and materials used for building the impedance tube. Controlling these factors in a real life experiment is not easy, and any small change in the experiment affects the outcome greatly. The extent of effects of such factors in this method is investigated through the finite element analysis of the impedance tube, which is done by using commercially available software COMSOL VERSION 5.0.

The experiment is conducted according to the ISO 10534.2. The body is composed of two parts connected by a screw mount as shown in Figure 3. A loudspeaker and three microphone ports are fixed on one side of the tube, and the right side is allocated for specimen placement. The measurement frequency range varies from 100 Hz - 1600 Hz. Measurements are made when the two microphones are placed at ports 1 and 3, and port 2 and port 3.

In the finite element analysis, the measurement frequency, static flow resistivity and thickness of the material are the preset values. The particle velocity at the left termination end is set as 1.0 m/s to generate the plane wave from the loudspeaker. The sound pressure at microphones is simulated by finite element model and the specific acoustic impedance on the front surface of the test material is determined at three instances: 1) When the back cavity depth is 0.02 m; 2) When it is 0.10 m and 3.When it is 0.15 m. Then the propagation constant, the characteristic impedance, and the static flow resistivity can be obtained by using the Equations (5)-(7).

The calculated static flow resistivity and the preset values when the measurement frequency and the specimen thickness are preset as 100 Hz and 0.00 m are shown in Table 1. It can easily be seen from the calculated results that both Equations (7) and (8) are well within the preset parameters and the maximum error is 0.19%. This shows that the proposed method can accurately measure the static flow resistivity. It should also be noted that the error of the predicted results from Equation (8) is larger than that predicted using Equation (7).

In the proposed method, the specific impedance on the specimen’s front is measured when the back cavity depth is zero and L to generate the propagation constant. We get different results with different back cavity depth L when the preset static flow resistivity, the measurement frequency, and the specimen thickness are 14,000 N/m⁴, 100 Hz, and 0.02 m, respectively. This is shown in Table 2. It can be seen that there is an increase of accuracy with the increment of the cavity depth; however this improvement is limited because of the limited length of the right hand side of a standard impedance tube (0.18 m) and the thickness of the material.

The placement of the microphone is also an important factor affecting the outcome of acoustic measurements. The measurement and the errors due to movement of the acoustic center in four configurations are shown in Table 3. In the simulation, the movement of the acoustic center of the microphone is done by changing the point of measurement of sound pressure 0.01 m farther or closer to the test material. The flow resistivity is preset at 14,000 N/m⁴, material thickness used is 0.02 m, the measurement frequency is 100 Hz and the microphones are set at ports 1 and 3.

It can be seen from Table 3 that even a ±0.01 m movement of the microphone can cause large errors of up to 18.91%, the maximum occurring when the two microphones are closest. It can also be seen that the results ob- tained by Equation (8) are less affected by the movement of microphones as compared to those calculated from Equation (7).

The calculated results with different frequencies and specimen thicknesses are presented in Table 4. The static flow resistivity is taken as 14,000 N/m⁴, the back cavity depth is 0.00 m and the two microphones are placed at ports 2 and 3, as shown in Figure 3(a). It can be seen from Table 4 that, when the specimen thickness is fixed, the error increases with the increase in the frequency and the results from Equation (8) becomes less accurate.

5. Experiments

The experiment for the proposed model for determining the static flow resistivity and measurement of sound absorption co efficient for the customized impedance tube are conducted. The side length of circular cross section of the customized impedance tube is 0.17 m, the frequency is around 100 Hz. The space between the specimen and termination is 1.06 m. Both porous and non-porous materials are used as test specimens for measuring using the customized impedance tube and standard impedance tube. The experimental setup with two 1/4 inch microphone and a digital acquisition is shown in Figure 4.

For obtaining the static flow resistivity, the sound pressure has to be measured from the front side of the specimen on the rigid termination La and Lb respectively in dB. The experiment is conducted with a test specimen in the both customized tube and a standard impedance tube. The measurement is made with the frequency range from 100 Hz to 1600 Hz which is shown in Table 4. The static flow resistivity can be obtained by using the Equation (7). The measurement of the frequency is presented in Figure 4. It is seen that thicker specimen is preferred for measurements because the results are more stable and the frequency range of measurement can be wider.

6. Conclusion

In this paper, the static flow resistivity is measured using a modified impedance tube. A standard tube is designed based on the simulation of finite element analysis of a practical impedance tube. It was found that even a small change in the movement of the acoustic centers of the microphones will result in large variations in the percentage of error. Also at lower measurement frequencies it is seen that the overall measurement error is low. The feasibility of the proposed method is validated through experiments, and it is found that a thicker specimen provides more stable flow resistivity and allows a higher measurement frequency.

Cite this paper

J. Niresh,S. Neelakrishnan,S. Subha Rani,Siddharth Shrivastava, (2016) Analysis of Static Flow Resistivity of a Modified Impedance Tube. Circuits and Systems,07,2253-2261. doi: 10.4236/cs.2016.79196

References

NOTES

^*Corresponding author.