Journal of Modern Physics
Vol.06 No.09(2015), Article ID:59029,12 pages
10.4236/jmp.2015.69137
Quantum Fractals and the Casimir-Dark Energy Duality―The Road to a Clean Quantum Energy Nano Reactor
M. S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 July 2015; accepted 21 August 2015; published 24 August 2015
ABSTRACT
Based on Witten’s T-duality and mirror symmetry we show, following earlier work, the fundamental complimentarity of the Casimir energy and dark energy. Such a conclusion opens new vistas in cold fusion technology in the wider sense of the word which we tackle via fractal nano technologies leading to some design proposals for a nano Casimir-dark energy reactor.
Keywords:
Casimir Energy, Zero Point Energy, Dark Energy, E-Infinity Theory, Quantum Set Theory, Algebraic Quantum Field, Cantorian Spacetime, Fractal Quantum Phase Space, Mirror Symmetry, Witten’s T-Duality

1. Introduction
Modern theoretical physics has a truly marvellous story to tell about its development [1] [2] and we may start the story with Newton although to make a long story short, it is advisable to start with relativity [1] - [8] . Einstein’s theory of relativity [1] - [40] was the first major modern revolution in theoretical physics since Newton and Maxwell [2] . Not only that but the work of Einstein was somehow in between relativity and the next revolution, namely quantum mechanics and that despite Einstein’s reluctance to embrace quantum entanglement [99] - [101] and the fundamental changes in our philosophy which this new theory implied [80] [81] . Ironically the present author is of a rather firm opinion that Einstein’s iconic E = mc2 is in fact the sum of two quantum parts [20] - [28] , namely that of the quantum particle energy E(O) = mc2/22 and that of the quantum wave energy E(D) = mc2 (21/22) so that Einstein did indeed hit the nail on its head, quantumly speaking [29] . It is fair to say that only a few would place the field of deterministic chaos and fractals as the next mile stone or if you want, revolution after quantum mechanics [102] -[112] . However the present author is of the opinion that the work of G. Cantor and his transfinite theory is by far the most fundamental mathematics which quantum physics requires and this fact at long last becomes known via the work of the pioneer of nonlinear dynamics, chaos and fractals, notably Lorenz, Raulle, Feigenbaum, Mandelbrot, Takens and York to mention only a few [2] [102] - [107] . However apart of the immensely important work of L. Hardy [99] - [101] , the quantum mechanics connection to chaos and fractals was another intensive effort which took much longer to bare fruit due to the genius of people like R. Feynman and the dedicated efforts of numerous scientists, particularly the quantum chaos pioneers Chirikov, Casati, Ford, Gutzwillen and Berry as well as the fractal spacetime pioneers Ord and Nottale in addition to E-infinity Cantorian spacetime theory proposed by the present author [30] - [97] . Stripped to the bare core, nonlinear dynamics is about the discovery of Cantor sets for mechanics so we are justified in asking what does fractals bring to physics in general and quantum mechanics in particular? Without going into the discussion of why we will restrict our explanation to a specific fundamental fractal, namely random Cantor set [60] [69] for which, by a well known theorem, the Hausdorff dimension is the most irrational number 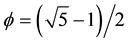 [6] [7] we will look next at one of the most important aspects of quantum mechanics, namely the Heisenberg uncertainty principle [110] . Now this principle precludes the use of one of the most powerful tools of mechanics, namely the phase space method of analysing dynamics and stability of mechanical sets [2] [108] . Needless to say the method proposed by Wiegner to overcome this limitation is not anywhere as widely used as the Hilbert space approach or as the path integral method [108] . That is where Cantor sets come to the rescue. With a Cantor set phase space, i.e. a “point less” phase space with non-standard points, there is no problem to do quantum calculations without violating the uncertainty principles [108] [110] . Of course we did similar things in the past in real spacetime and the author integrated Hilbert space into the E-infinity larger picture [98] but we think we did treat phase space a little bit step-motherly and it is time to point out our own unjustified shortcomings [117] - [119] . From here we can then point in a systematic way to the undreamed of possibilities of chaotic fractals and random Cantor set to tackle quantum physics starting from a comprehensive picture up to an exact solution [113] - [115] . This brings us to the next important point in the present discussion, namely Hardy’s quantum entanglement. Hardy was seeking an exact solution to a basic particles entanglement [99] - [101] . Using orthodox quantum mechanics in ket and bra formalism of Dirac he found the quantum probability for entanglement of two quantum particles to be about 9 percent [100] . However what he really did not suspect was what Prof. D. Mermin published a little later showing that this 9 percent was an exact value equal to ϕ to the power of five [101] . That was probably the first exact result linking without a trace of a doubt the random Cantor set with quantum mechanics and the fundamental dimensional function of von Neumann-Connes continuous and noncommutative geometry [71] of which Penrose fractal tiling [2] [6] [7] is a generic space mimicking E-infinity theory [69] [70] [73] . Remembering that Penrose tiling depends crucially upon a golden mean proportionality, we see that the hunch that this golden mean is fundamental is far more than a hunch as, as we will see in the present work, it is a fact discussed on numerous previous occasions [38] - [85] . Maybe it is at this point that we should stress the marvel hidden in a golden mean based number system and E-infinity is indeed embedded in a golden mean binary constituting de facto a golden mean computer rivalling even a transfinite version of Turing’s machine without hardware save for a modern pocket calculator on the side to perform the elementary manipulation of the adding, multiplying and dividing the golden mean and its power [41] [66] . Having solved the measure technical computational problem as well as the fundamental contradiction between the discrete and the continuous by building a method which unites both opposed concepts into a transfinite discretum which has the cardinality of the continuum, we realize that we have not only a much better understanding of the vacuum fluctuation but we found a handle on it which can be used to the extent of building mini fractal universes in the laboratory from which we can extract clean energy in the form of a Casimir energy reactor [91] . Before that however we show that ordinary energy is identical to Casimir energy and that the cosmological dark energy is the complimentary energy of the Casimir energy. For an instructive simple and exact picture of quantum spacetime, the reader is invited to examine Figure 2 of Ref. [113] . How this all fits together is the subject of the coming sections.
[6] [7] we will look next at one of the most important aspects of quantum mechanics, namely the Heisenberg uncertainty principle [110] . Now this principle precludes the use of one of the most powerful tools of mechanics, namely the phase space method of analysing dynamics and stability of mechanical sets [2] [108] . Needless to say the method proposed by Wiegner to overcome this limitation is not anywhere as widely used as the Hilbert space approach or as the path integral method [108] . That is where Cantor sets come to the rescue. With a Cantor set phase space, i.e. a “point less” phase space with non-standard points, there is no problem to do quantum calculations without violating the uncertainty principles [108] [110] . Of course we did similar things in the past in real spacetime and the author integrated Hilbert space into the E-infinity larger picture [98] but we think we did treat phase space a little bit step-motherly and it is time to point out our own unjustified shortcomings [117] - [119] . From here we can then point in a systematic way to the undreamed of possibilities of chaotic fractals and random Cantor set to tackle quantum physics starting from a comprehensive picture up to an exact solution [113] - [115] . This brings us to the next important point in the present discussion, namely Hardy’s quantum entanglement. Hardy was seeking an exact solution to a basic particles entanglement [99] - [101] . Using orthodox quantum mechanics in ket and bra formalism of Dirac he found the quantum probability for entanglement of two quantum particles to be about 9 percent [100] . However what he really did not suspect was what Prof. D. Mermin published a little later showing that this 9 percent was an exact value equal to ϕ to the power of five [101] . That was probably the first exact result linking without a trace of a doubt the random Cantor set with quantum mechanics and the fundamental dimensional function of von Neumann-Connes continuous and noncommutative geometry [71] of which Penrose fractal tiling [2] [6] [7] is a generic space mimicking E-infinity theory [69] [70] [73] . Remembering that Penrose tiling depends crucially upon a golden mean proportionality, we see that the hunch that this golden mean is fundamental is far more than a hunch as, as we will see in the present work, it is a fact discussed on numerous previous occasions [38] - [85] . Maybe it is at this point that we should stress the marvel hidden in a golden mean based number system and E-infinity is indeed embedded in a golden mean binary constituting de facto a golden mean computer rivalling even a transfinite version of Turing’s machine without hardware save for a modern pocket calculator on the side to perform the elementary manipulation of the adding, multiplying and dividing the golden mean and its power [41] [66] . Having solved the measure technical computational problem as well as the fundamental contradiction between the discrete and the continuous by building a method which unites both opposed concepts into a transfinite discretum which has the cardinality of the continuum, we realize that we have not only a much better understanding of the vacuum fluctuation but we found a handle on it which can be used to the extent of building mini fractal universes in the laboratory from which we can extract clean energy in the form of a Casimir energy reactor [91] . Before that however we show that ordinary energy is identical to Casimir energy and that the cosmological dark energy is the complimentary energy of the Casimir energy. For an instructive simple and exact picture of quantum spacetime, the reader is invited to examine Figure 2 of Ref. [113] . How this all fits together is the subject of the coming sections.
2. Building Elements of E-Infinity Diagrams
The main two elements or building blocks of E-infinity diagrams is the zero set and the empty set [64] . From these irreducibly simple set theoretical elements we can virtually build an entire spacetime and more. Thus we have [33]
(a) The zero set D(H) = ϕ
(b) The empty set D(H) = ϕ2
where D(H) is the Hausdorff dimension and . From the above we obtain the latent Casimir spacetime set representing the latent topological energy of spacetime as the difference of ϕ and ϕ2 in symbolic diagram (see Figure 1) reflecting the essence of the famous Casimir experiment with two uncharged but perfecting conducting plates [89] [91] .
. From the above we obtain the latent Casimir spacetime set representing the latent topological energy of spacetime as the difference of ϕ and ϕ2 in symbolic diagram (see Figure 1) reflecting the essence of the famous Casimir experiment with two uncharged but perfecting conducting plates [89] [91] .
From the diagrams of Figure 1 we can generalize to two limiting cases (see Figure 1 and Figure 2).
1) When the distance between the two plates of Figure 1 tends to real zero, this is then the totally empty set 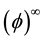 = zero. In the surrounding space we have a non-empty set with the average latent pressure everywhere equal ϕ3 while the average spacetime density is basically the fractal five dimensional average
= zero. In the surrounding space we have a non-empty set with the average latent pressure everywhere equal ϕ3 while the average spacetime density is basically the fractal five dimensional average . Consequently the density of the latent Casimir pressure is simply
. Consequently the density of the latent Casimir pressure is simply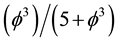 . This is exactly equal
. This is exactly equal  which is our well known ordinary measurable energy of the cosmos and in astounding agreement with cosmic measurements and observation [108] . The immediate rather profound conclusion is that the measured real energy density of the cosmos is nothing more but nothing less than the Casimir latent energy of spacetime and at this scale it is
which is our well known ordinary measurable energy of the cosmos and in astounding agreement with cosmic measurements and observation [108] . The immediate rather profound conclusion is that the measured real energy density of the cosmos is nothing more but nothing less than the Casimir latent energy of spacetime and at this scale it is
Figure 1. Symbolic representation of the E-infinity Casimir diagram for nano scales. The difference between ϕ and ϕ2 given the latent spacetime topological pressure ϕ3. The inverse of ϕ3 on the other hand is the average Hausdorff dimension of spacetime 4 + ϕ.
Figure 2. Symbolic representation of the E-infinity Casimir diagram for Hubble scales. The boundary of the holographic boundary of the universe is one sided Möbius-like so that we have no outside. In other words the outside is the totally empty set. This is the mathematical definition of the philosophical concept of non-existence or nothingness.
not related in any way to the Riemann curvature of spacetime but to the chaotic fractality of spacetime in full agreement with our picture which we adopted based on Feynman’s conjecture that gravity is similar to van der Waals fluctuation of micro spacetime frequently termed Feynman-El Naschie van der Waals quantum gravity conjecture [6] [7] [38] [69] [70] .
2) Now we look at the other extreme where the distance between the Casimir plates is equal to the diameter of our universe as shown schematically in Figure 2. The repulsive Casimir-like pressure is in this case equal  minus the latent Casimir topologic pressure ϕ3 which is working in the opposite direction so that the net repulsive topological pressure pushing the boundary of the universe outwardly is given by
minus the latent Casimir topologic pressure ϕ3 which is working in the opposite direction so that the net repulsive topological pressure pushing the boundary of the universe outwardly is given by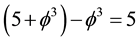 . Therefore the density of this repulsive topological pressure is
. Therefore the density of this repulsive topological pressure is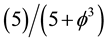 . This happens to be equal to
. This happens to be equal to  which means it is simply identical to what we calculated for the dark energy of the cosmos
which means it is simply identical to what we calculated for the dark energy of the cosmos
 . We recall that
. We recall that  was interpreted as the energy of the pre-quantum wave, i.e. the energy of the
was interpreted as the energy of the pre-quantum wave, i.e. the energy of the
empty set albeit in five dimensional Kaluza-Klein space [31] . The corresponding diagram is shown in Figure 2.
3. Determining the Exact Topological Diameter of the Universe and the Casimir Cosmic Ordinary Energy Density
We start from our exact picture of quantum spacetime [114] . This picture consists of three concentric circles. The first is the zero set of the quantum pre-particle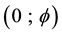 . Around this pre-particle we have a topological surface representing the empty set pre-quantum wave
. Around this pre-particle we have a topological surface representing the empty set pre-quantum wave . Finally we have the third layer which happens to be an expectation value
. Finally we have the third layer which happens to be an expectation value 

Consequently we have

where 



Second it is clear that 11 + ϕ5 is the isomorphic length of the Penrose fractal universe and therefore 22 + k = (2) (11 + ϕ5) is the corresponding diameter of the universe [30] [31] . It follows then that 22 + k is the topological diameter of our fractal M-theory like universe. We recall that this result corresponds to a super symmetric space where the isomorphic length is the result of combining intersectionally the bosonic isomorphic length 


This is the dimensionality 11 of Witten’s M-theory plus a Hardy quantum entanglement part, namely ϕ5.
4. The E-Infinity Casimir-Dark Energy Diagram for Topological Interactions in Cantorian Spacetime
Similar to the quasi probability of Wigner’s quantum mechanics in phase space [108] , our topological probability approach to quantum mechanics as enshrined in E-infinity [110] - [116] represents an alternative extremely simple fourth formulation for quantum mechanics which is not directly connected to Hilbert space, path integral nor the density matrix approach [108] . Naturally it bears a resemblance to all the afore mentioned formulations but is by no means identical and in fact it adds a few new points to our understanding of the deep mathematical structure of orthodox quantum mechanics hiding behind complex numbers and analytical continuation [2] [6] [7] [69] [70] .
The internal logic of our approach rivals that of Weyl-Wigner quantum mechanics in phase space and its logical underpinning by Groenewold and Moyal [108] . For instance as we enter into the negative dimensions regime and find that the Hausdorff dimension ϕn is getting increasingly small, it is clear that this means the “Cantor set” is becoming thinner and tending to real nothingness or the absolute empty set [6] [9] [70] . The situation is thus paralleling the density of the density matrix. Similarly when we are summing in E-infinity theory over all dimensions to reach our expectation Hausdorff dimension of the core of E-infinity spacetime 
5. The Topological Mass
For want of better words, ϕ3 was called with equal justification universal fluctuation [69] [70] [110] -[116] and since fluctuation produces “mass” it could be called “topological mass” [110] -[116] . Now mass is also an abstract word so that one could speak of mass charge as we speak of electrical charge or magnetic charge or “criminal charge”. Thus in legal language you charge someone of a property called criminality and here we have this “stuff” property that we call mass. Now for Einstein’s mass multiplied with high velocity squared is energy.
In E-infinity the topological speed of light is a velocity charge being between zero and infinity in a circular world interval where the golden mean is a topological average. Thus the topological energy is [110] -[116]

This is Hardy’s topological energy. To get “real” energy we use Newton [6] [7] [110] -[116]


This is thus what we call mass in the quantum small world. In the large cosmic world on the other hand, mass is 

Consequently we have

From the above the complimentarity of E(O) and E(D) follow:

Similar considerations apply to the Mageuijo-Smolin formula for quantum gravity energy.
6. The Mageuijo-Smolin Quantum Gravity [42]
To obtain E(O) and E(D) and visa versa we have the following transformation [42]


The same applies to a fractal de Sitter universe [2] [33]

That means ordinary energy is

and dark energy is

7. The Advantage of Being Transfinite Cantorian for Quantum Mechanics
Let us start with Heisenberg’s uncertainty [2] [110] . In E-infinity spacetime [69] [70] there is no ordinary points. It is exactly as in von Neumann’s space [6] [7] [69] [70] which he describes in jest as “pointless”. Consequently in Cantorian spacetime this fundamental principle is taken care of automatically ab initio. In fact writing ϕ3 as 

It would be a mistake to think this result is trivial. However, written in symbolic form 


or

when compared to its totally chaotic decimal expansion [102] -[107]

and find on the top of that a well known fact, namely that ϕ is the Hausdorff dimension of a random triadic Cantor set.
8. The Disadvantage of Being Transfinite Cantorian-Quantum Theory
At the risk of appearing facetious, we would like to seriously propose that in no minor measure a draw back of E-infinity Cantorian spacetime theory is that it is excessively simple. A theory should be simple but not excessively so. Being excessively simple puts a theory at risk of being called trivial as an easy shot by members of the “voluntary opposition”. In his early days working in applied mechanics, the author was in awe vis-à-vis the work of a great scholar Prof. Cliff Trusdell who coined the word rational mechanics [120] [121] . The competence of Trusdell is beyond any doubt. However his mathematical vanity was equally beyond doubt. He was able to smooth anything mathematically to the point that the author felt he was facing a superman of mechanical science. This is what impressed the author as a naïve young post graduate student until he grew out of it with the help of real engineering scientists like W.T. Koiter, J.M.T. Thompson, J. Croll, S. Nemat Nasser and A.W. Walker to mention only a few [120] [121] . There is science and there is selling science within science politics and the part related to funding is more frequently than not unrelated to science and depends on salesmanship and media more than on logic. The problem with E-infinity is that it fulfils the criteria, which says that maximal accuracy is attained in the ideal limit at maximal simplicity. When simplicity is interpreted wrongly as triviality, then it is tragic. We could find nothing better to close this section with than the wise words of a Socrates of modern science, Prof. J.A. Wheeler [69] [70] in his classic book “Information, Physics, Quantum: The Search for Links” where he wrote “Surely some day we can believe, we will grasp the central idea of it all as so simple, so beautiful, so compelling that we will say to each other, ‘Oh, how could it have been otherwise!’. How could we all have been so blind so long!”.
9. The VAK and Quantum Phase Space from the View Point of E-Infinity
In the following we show a simple deep connection between a few fundamental aspects of E-infinity and Weyl-Wigner theory [90] .
a) If we take ϕ to mean a coordinate then ϕ2 is the quasi derivative and 

b) Seen that way, then 
c) Since the VAK is a Hamiltonian “strange” attractors conjectured by Rene Thom to represent the equilibrium states of quantum mechanics [99] [100] , we see how the VAK, E-infinity and Wigner quantum phase quasi probability are intimately connected. We could proceed further to black hole information [2] and the Hawking and Beckenstein theory [2] but space limitation will not permit that.
10. Conclusion
We presented in this relatively short paper a general theory for quantum spacetime and zero point energy fluctuation based on E-infinity and related mathematical concepts. Our main results and conclusions may be summarized in the following rather important points [116] - [126] :
1) Casimir energy and ordinary energy density of the cosmos are not only identical conceptually but identical numerically.
2) Casimir energy and cosmic dark energy are complimentary in the most strict mathematical and physical meaning.
3) The difference between Casimir energy and dark energy is a difference of boundary condition where the boundary of the holographic boundary of the universe is a one sided Möbius-like manifold (see Figure 2 of Ref. [122] .
4) Using a heap of space filling fractal nano spheres, we can build in principle a mini universe and use it as an energy reactor (see Figure 1 of Ref. [116] ).
Figure 3. Universe unit circular interval (see Ref. [6] [7] [11] [39] [94] ). The point is that self similarity leading to the counter intuitive topological fact that every point in a Cantor set when “magnified” reveals itself as a complete Cantor set leads to the logical conclusion that the number of “points” in the unit interval shown as a closed ring above it is equal to the number of points in our “actual” universe. The weighted centre of “everything” in this unit circular universe is the golden mean. That is how we can reason that ϕ is the weighted speed of light which varies between zero and infinity but because of mirror symmetry and T-duality, this formally zero plus infinity divided by two leads to a finite expectation value, namely ϕ = 0.618033989 = (0.5) + (k + 1)/10 where k = 
5) The main conclusion is a natural consequence of mirror symmetry and Witten’s T-duality (see Figures 2-4 of Ref. [94] ) in addition to Dvoretzky’s theorem which explains why energy is concentrated at the edge of the universe similar to electrical charge of a Faraday cage and information of a black hole.
Acknowledgements
The author is truly indebted to the work and many discussions with the outstanding French scholar Prof. Jean-Paul Auffray. He is equally indebted to the work of Prof. L. Hardy as well as the work and advice of Nobel Laureate G. ‘tHooft. Last but not least the work of Prof. J. Mageuijo, Prof. Lee Smolin, Prof. J. Ambjorn and Prof. R. Loll were extremely important.
Cite this paper
M. S. ElNaschie, (2015) Quantum Fractals and the Casimir-Dark Energy Duality—The Road to a Clean Quantum Energy Nano Reactor. Journal of Modern Physics,06,1321-1333. doi: 10.4236/jmp.2015.69137
References
- 1. Bondi, S.H. (1964) Relativity and the Commonsense. A New Approach to Einstein. Heinemann, London.
- 2. Penrose, R. (2004) The Road to Reality. A Complete Guide to the Laws of the Universe. Jonathan Cape, London.
- 3. Okun, L.B. (2009) Energy and Mass in Relativity Theory. World Scientific, Singapore.
- 4. Rindler, W. (2004) Relativity (Special, General and Cosmological). Oxford University Press, Oxford.
- 5. El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic ‘tHooft-Veltman-Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221.
http://dx.doi.org/10.4236/wjnst.2014.44027 - 6. Helal, M.A., Marek-Crnjac, L. and He, J.-H. (20130 The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145.
- 7. Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471.
http://dx.doi.org/10.4236/ijaa.2013.34053 - 8. Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436.
http://dx.doi.org/10.4236/jmp.2014.515144 - 9. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 10. El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26.
http://dx.doi.org/10.4236/jqis.2013.31006 - 11. El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54.
http://dx.doi.org/10.4236/ijmnta.2013.21005 - 12. El Naschie, M.S. (2013) Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes From. Journal of Quantum Information Science, 3, 57-77.
http://dx.doi.org/10.4236/jqis.2013.32011 - 13. El Naschie, M.S. (2013) A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy. International Journal of Modern Nonlinear Theory and Application, 2, 107-121.
http://dx.doi.org/10.4236/ijmnta.2013.22014 - 14. El Naschie, M.S. (2013) The Hydrogen Atom Fractal Spectra, the Missing Dark Energy of the Cosmos and Their Hardy Quantum Entanglement. International Journal of Modern Nonlinear Theory and Application, 2, 167-169.
http://dx.doi.org/10.4236/ijmnta.2013.23023 - 15. El Naschie, M.S. (2013) A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493.
http://dx.doi.org/10.4236/ijaa.2013.34056 - 16. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy and Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 17. El Naschie, M.S. (2013) The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling of the Planck Scale. Open Journal of Microphysics, 3, 64-70.
http://dx.doi.org/10.4236/ojm.2013.33012 - 18. El Naschie, M.S. (2013) From Yang-Mills Photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126.
http://dx.doi.org/10.4236/jqis.2013.34016 - 19. El Naschie, M.S. (2014) Calculating the Exact Experimental Density of the Dark Energy in the Cosmos Assuming a Fractal Speed of Light. International Journal of Modern Nonlinear Theory and Application, 3, 1-5.
http://dx.doi.org/10.4236/ijmnta.2014.31001 - 20. El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156.
http://dx.doi.org/10.4236/wjm.2014.46017 - 21. El Naschie, M.S. (2014) Capillary Surface Energy Elucidation of the Cosmic Dark Energy—Ordinary Energy Duality. Open Journal of Fluid Dynamics, 4, 15-17.
http://dx.doi.org/10.4236/ojfd.2014.41002 - 22. El Naschie, M.S. (2014) Einstein’s General Relativity and Pure Gravity in a Cosserat and De Sitter-Witten Spacetime Setting as the Explanation of Dark Energy and Cosmic Accelerated Expansion. International Journal of Astronomy and Astrophysics, 4, 332-339.
http://dx.doi.org/10.4236/ijaa.2014.42027 - 23. El Naschie, M.S. (2014) Electromagnetic—Pure Gravity Connection via Hardy’s Quantum Entanglement. Journal of Electromagnetic Analysis and Applications, 6, 233-237.
http://dx.doi.org/10.4236/jemaa.2014.69023 - 24. El Naschie, M.S. (2014) Cosmic Dark Energy from ‘t Hooft’s Dimensional Regularization and Witten’s Topological Quantum Field Pure Gravity. Journal of Quantum Information Science, 4, 83-91.
http://dx.doi.org/10.4236/jqis.2014.42008 - 25. El Naschie, M.S. (2014) Entanglement of E8E8 Exceptional Lie Symmetry Group Dark Energy, Einstein’s Maximal Total Energy and the Hartle-Hawking No Boundary Proposal as the Explanation for Dark Energy. World Journal of Condensed Matter Physics, 4, 74-77.
http://dx.doi.org/10.4236/wjcmp.2014.42011 - 26. El Naschie, M.S. (2014) The Meta Energy of Dark Energy. Open Journal of Philosophy, 4, 157-159.
http://dx.doi.org/10.4236/ojpp.2014.42022 - 27. El Naschie, M.S. (2014) Pinched Material Einstein Space-Time Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90.
http://dx.doi.org/10.4236/ijaa.2014.41009 - 28. El Naschie, M.S. (2014) From Chern-Simon, Holography and Scale Relativity to Dark Energy. Journal of Applied Mathematics and Physics, 2, 634-638.
http://dx.doi.org/10.4236/jamp.2014.27069 - 29. El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, 5, 743-750.
http://dx.doi.org/10.4236/jmp.2014.59084 - 30. El Naschie, M.S. (2013) Nash Embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428.
http://dx.doi.org/10.4236/jmp.2013.410170 - 31. El Naschie, M.S. (2013) Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method. Journal of Modern Physics, 4, 757-760.
http://dx.doi.org/10.4236/jmp.2013.46103 - 32. El Naschie, M.S. (2013) The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356.
http://dx.doi.org/10.4236/jmp.2013.43049 - 33. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 34. El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
http://dx.doi.org/10.4236/jamp.2014.28088 - 35. He, J.-H. and Marek-Crnjac, L. (2013) Mohamed El Naschie’s Revision of Albert Einstein’s E = m0c2: A Definite Resolution of the Mystery of the Missing Dark Energy of the Cosmos International. Journal of Modern Nonlinear Theory and Application, 2, 55-59.
http://dx.doi.org/10.4236/ijmnta.2013.21006 - 36. El Naschie, M.S. and Marek-Crnjac, L. (2012) Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity. International Journal of Modern Nonlinear Theory and Application, 1, 118-124.
http://dx.doi.org/10.4236/ijmnta.2012.14018 - 37. El Naschie, M.S. and Helal, A. (2013) Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343.
http://dx.doi.org/10.4236/ijaa.2013.33037 - 38. Marek-Crnjac, L. and El Naschie, M.S. (2013) Chaotic Fractal Tiling for the Missing Dark Energy and Veneziano Model. Applied Mathematics, 4, 22-29.
http://dx.doi.org/10.4236/am.2013.411A2005 - 39. Marek-Crnjac, L. and El Naschie, M.S. (2013) Quantum Gravity and Dark Energy Using Fractal Planck Scaling. Journal of Modern Physics, 4, 31-38.
http://dx.doi.org/10.4236/jmp.2013.411A1005 - 40. Auffray, J.P. (2015) E-Infinity, the Zero Set, Absolute Space and Photon Spin. Journal of Modern Physics, 6, 536.
http://dx.doi.org/10.4236/jmp.2015.65058 - 41. El Naschie, M.S., Olsen, S., He, J.H., Nada, S., Marek-Crnjac, L. and Helal, A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92.
http://dx.doi.org/10.4236/ijmnta.2012.13012 - 42. El Naschie, M.S., Marek-Crnjac, L., Helal, M.A. and He, J.-H. (2014) A Topological Magueijo-Smolin Varying Speed of Light Theory, the Accelerated Cosmic Expansion and the Dark Energy of Pure Gravity. Applied Mathematics, 5, 1780-1790.
http://dx.doi.org/10.4236/am.2014.512171 - 43. El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and ‘tHooft’s 4-ε Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
http://dx.doi.org/10.11648/j.ajaa.20140203.12 - 44. El Naschie, M.S. (2014) Hardy’s Entanglement as the Ultimate Explanation for the Observed Cosmic Dark Energy and Accelerated Expansion. International Journal High Energy Physics, 1, 13-17.
http://dx.doi.org/10.11648/j.ijhep.20140102.11 - 45. El Naschie, M.S. (2014) Deriving E = mc2/22 of Einstein’s Ordinary Quantum Relativity Energy Density from the Lie Symmetry Group SO(10) of Grand Unification of All Fundamental Forces and without Quantum Mechanics. American Journal of Mechanics & Applications, 2, 6-9.
http://dx.doi.org/10.11648/j.ajma.20140202.11 - 46. El Naschie, M.S. (2014) Cosserat-Cartan Modification of Einstein-Riemann Relativity and Cosmic Dark Energy Density. American Journal of Modern Physics, 3, 82-87.
http://dx.doi.org/10.11648/j.ajmp.20140302.17 - 47. El Naschie, M.S. (2014) Asymptotically Safe Pure Gravity as the Source of Dark Energy of the Vacuum. International Journal of Astrophysics and Space Science, 2, 12-15.
http://dx.doi.org/10.11648/j.ijass.20140201.13 - 48. El Naschie, M.S. (2014) Logarithmic Running of ‘t Hooft-Polyakov Monopole to Dark Energy. International Journal of High Energy Physics, 1, 1-5.
http://dx.doi.org/10.11648/j.ijhep.20140101.11 - 49. El Naschie, M.S. (2013) Experimentally Based Theoretical Arguments that Unruh’s Temperature, Hawking’s Vacuum Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361.
http://dx.doi.org/10.11648/j.ajmp.20130206.23 - 50. Marek-Crnjac, L. (2013) Modification of Einstein’s E = mc2 to E = (1/22)mc2. American Journal of Modern Physics, 2, 255-263.
http://dx.doi.org/10.11648/j.ajmp.20130205.14 - 51. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 52. El Naschie, M.S. (2013) Determining the Missing Dark Energy Density of the Cosmos from a Light Cone Exact Relativistic Analysis. Journal of Physics, 2, 19-25.
- 53. El Naschie, M.S. (2013) The Quantum Entanglement behind the Missing Dark Energy. Journal of Modern Physics and Applications, 2, 88-96.
- 54. El Naschie, M.S. (2014) Dark Energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- 55. El Naschie, M.S. (2014) Rindler Space Derivation of Dark Energy. Journal of Modern Physics Applications, 6, 1-10.
- 56. Tan, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nano Science. Bubbfil Nanotechnology, 1, 3-12.
- 57. El Naschie, M.S. (2014) To Dark Energy Theory from a Cosserat-Like Model of Spacetime. Problems of Nonlinear Analysis in Engineering Systems, 20, 79-98.
- 58. El Naschie, M.S. (2012) Revising Einstein’s E = mc2; A Theoretical Resolution of the Mystery of Dark Energy. Proceedings of the Fourth Arab International Conference in Physics and Material Science, Alexandria, 1-3 October 2012, 1.
- 59. Ball, K.M. (1991) Volume Ratios and a Reverse Isoperimetric Inequality. Journal of London Mathematical Society, 44, 351-359.
http://dx.doi.org/10.1112/jlms/s2-44.2.351 - 60. Pisier, G. (1989) The Volume of Convex Bodies and Banach Space Geometry. Tracts in Math 94, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511662454 - 61. Kasin, B.S. (1977) The Width of Certain Finite-Dimensional Sets and Classes of Smooth Functions. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 41, 334-351. (In Russian)
- 62. Guedon, O. (2013) Concentration Phenomena in High Dimensional Geometry.
http://arxiv.org/abs/1310.1204 - 63. He, J.-H. (2013) Special Issue on Recent Developments on Dark Energy and Dark Matter. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 3, 1-2.
- 64. He, J.-H. and El Naschie, M.S. (2012) On the Monadic Nature of Quantum Gravity as a Highly Structured Golden Ring, Spaces and Spectra. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 94-98.
- 65. El Naschie, M.S. (2012) Towards a General Transfinite Set Theory for Quantum Mechanics. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 135-142.
- 66. El Naschie, M.S., He, J.-H., Nada, S., Marek-Crnjac, L. and Helal, M. (2012) Golden Mean Computer for High Energy Physics. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-92.
- 67. El Naschie, M.S. (2012) The Minus One Connection of Relativity, Quantum Mechanics and Set Theory. Journal of Fractal Spacetime & Noncommutative Geometry in Quantum and High Energy Physics, 2, 131-134.
- 68. El Naschie, M.S. (2015) Dark Energy and Its Cosmic Density from Einstein’s Relativity and Gauge Fields Renormalization Leading to the Possibility of a New ‘tHooft Quasi Particle. The Open Astronomy Journal, 8, 1-17.
http://dx.doi.org/10.2174/1874381101508010001 - 69. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
http://dx.doi.org/10.1016/S0960-0779(03)00278-9 - 70. El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.
http://dx.doi.org/10.1016/j.chaos.2008.09.059 - 71. Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego.
- 72. Krantz, S.G. and Parks, H.R. (2008) Geometric Integration Theory. Birkhauser, Boston.
http://dx.doi.org/10.1007/978-0-8176-4679-0 - 73. El Naschie, M.S. (1997) Remarks on Super Strings, Fractal Gravity, Nagasawa’s Diffusion and Cantorian Spacetime. Chaos, Solitons & Fractals, 8, 1873-1886.
http://dx.doi.org/10.1016/S0960-0779(97)00124-0 - 74. El Naschie, M.S. (1997) Introduction to Nonlinear Dynamics, General Relativity and the Quantum—The Uneven Flow of Fractal Time. Chaos, Solitons & Fractals, 8, vii-x.
http://dx.doi.org/10.1016/S0960-0779(97)88455-X - 75. El Naschie, M.S. (1999) Hyper-Dimensional Geometry and the Nature of Physical Spacetime. Chaos, Solitons & Fractals, 10, 155-158.
http://dx.doi.org/10.1016/S0960-0779(98)00235-5 - 76. El Naschie, M.S. (2012) E-Infinity—High Energy Communications Nos. 1-90. April 2010 to December 2012.
- 77. Chen, N.X. (2010) Möbius Inversion in Physics. World Scientific, Singapore.
- 78. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718.
http://dx.doi.org/10.1007/s10773-014-2123-8 - 79. El Naschie, M.S. (2001) On Twistors in Cantorian E-Infinity Space. Chaos, Solitons & Fractals, 12, 741-746.
http://dx.doi.org/10.1016/S0960-0779(00)00193-4 - 80. Rössler, O.E. (1998) Endophysics. World Scientific, Singapore.
http://dx.doi.org/10.1142/3183 - 81. El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckrey, T. and Weibel, P., Eds., Science of the Interface, Genista Verlag, Tübingen.
- 82. Li, M. (2004) A Model of Holographic Dark Energy. Physics Letters B, 603, 1-5.
http://dx.doi.org/10.1016/j.physletb.2004.10.014 - 83. El Naschie, M.S. (2006) Holographic Dimensional Reduction. Center Manifold Theorem and E-Infinity. Chaos, Solitons & Fractals, 29, 816-822.
http://dx.doi.org/10.1016/j.chaos.2006.01.013 - 84. Balachandran, A.P., Kürkcüoglu, S. and Vaidya, S. (2007) Lectures on Fuzzy and Fuzzy Susy Physics. World Scientific, Singapore.
- 85. Bahcall, J., Piran, T. and Weinberg, S., Eds. (2004) Dark Matter in the Universe. World Scientific, Singapore.
- 86. Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
- 87. Ruiz-Lapuente, P. (2010) Dark Energy, Observational and Theoretical Approaches. Cambridge University Press, Cambridge.
- 88. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and its Hidden Quantum Entangled Origin. Journal of Quantum Information Science, 4, 284-291.
http://dx.doi.org/10.4236/jqis.2014.44023 - 89. El Naschie, M.S. (2014) Casimir-Like Energy as a Double Eigenvalue of Quantumly Entangled System Leading to the Missing Dark Energy Density of the Cosmos. International Journal of High Energy Physics, 1, 55-63.
http://dx.doi.org/10.11648/j.ijhep.20140105.11 - 90. Perlmutter, S., et al., Supernova Cosmology Project Collaboration (1999) Measurements of Omega and Lambda from 42 High Redshift Supernova. Astrophysics Journal, 517, 565-585.
http://dx.doi.org/10.1086/307221 - 91. El Naschie, M.S. (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Science, 5, 313-324.
http://dx.doi.org/10.4236/ojapps.2015.57032 - 92. Kodiyalam, V. and Sunder, V.S. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, London.
- 93. El Naschie, M.S. (2005) A Few Hints and Some Theorem about Witten’s M Theory and T-Duality. Chaos, Solitons & Fractals, 25, 545-548.
http://dx.doi.org/10.1016/j.chaos.2005.01.009 - 94. Marek-Crnjac, L., El Naschie, M.S. and He, J.-H. (2013) Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology. International Journal of Modern Nonlinear Theory and Application, 2, 78-88.
http://dx.doi.org/10.4236/ijmnta.2013.21A010 - 95. Yau, S.T. and Nadis, S. (2010) The Shape of Inner Space. Basic Book, Perseus Group, New York.
- 96. Bell, J.S. (1991) Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge.
- 97. Rindler, W. (1991) Introduction to Special Relativity. Oxford Science Publications, Oxford.
- 98. El Naschie, M.S. (2007) Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness. Chaos, Solitons & Fractals, 31, 787-793.
http://dx.doi.org/10.1016/j.chaos.2006.06.003 - 99. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
http://dx.doi.org/10.4236/jqis.2011.12007 - 100. Hardy, L. (1993) Nonlocality of Two Particles without Inequalities for Almost All Entangled States. Physical Review Letters, 71, 1665-1668.
http://dx.doi.org/10.1103/PhysRevLett.71.1665 - 101. Mermin, D. (1994) Quantum Mysteries Refined. American Journal of Physics, 62, 880-887.
http://dx.doi.org/10.1119/1.17733 - 102. Addison, P.S. (1997) Fractals and Chaos: An Illustrated Course. Institute of Physics, Bristol.
http://dx.doi.org/10.1887/0750304006 - 103. Ruelle, D. (1991) Chance and Chaos. Princeton University Press, Princeton.
- 104. Graham, L. and Kantor, J.-M. (2009) Naming Infinity. The Belknap Press of Harvard University Press, Cambridge, MA and London.
- 105. Ott, E. (1993) Chaos in Dynamical Systems. Cambridge University Press, Cambridge.
- 106. Kapitaniak, T., Ed. (1992) Chaotic Oscillators (Theory and Applications). World Scientific, Singapore.
http://dx.doi.org/10.1142/9789814360258 - 107. Casati, G., Guarneri, I. and Smilansky, U. (1993) Quantum Chaos. North Holland, Amsterdam.
- 108. Kim, Y.S. and Noz, M.E. (1991) Phase Space Picture of Quantum Mechanics. World Scientific, Singapore.
http://dx.doi.org/10.1142/1197 - 109. Fried, H.M. (2014) Modern Functional Quantum Field Theory. World Scientific, Singapore.
http://dx.doi.org/10.1142/8544 - 110. El Naschie, M.S. (1995) Young Double-Slit Experiment, Heisenberg Uncertainty Principle and Correlation in Cantorian Spacetime. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 93-100.
- 111. El Naschie, M.S. (1995) Iterated Function System, Information and the Two-Slit Experiment of Quantum Mechanics. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 185-189.
- 112. El Naschie, M.S. (1995) Quantum Measurement, Information, Diffusion and Cantorian Geodesic. In: El Naschie, M.S., Rössler, O.E. and Prigogine, I., Eds., Quantum Mechanics, Diffusion and Chaotic Fractals, Pergamon Press/Elsevier, Oxford, 191-205.
- 113. El Naschie, M.S. (2015) Hubble Scale Dark Energy Meets Nano Scale Casimir Energy and the Rational of Their T-Duality and Mirror Symmetry Equivalence. World Journal of Nano Science and Engineering, 5, 57-67.
http://dx.doi.org/10.4236/wjnse.2015.53008 - 114. El Naschie, M.S. (2015) An Exact Mathematical Picture of Quantum Spacetime. Advances in Pure Mathematics, 5, 560-570.
http://dx.doi.org/10.4236/apm.2015.59052 - 115. El Naschie, M.S. (2015) From Fusion Algebra to Cold Fusion or from Pure Reason to Pragmatism. Open Journal of Philosophy, 5, 319-326.
http://dx.doi.org/10.4236/ojpp.2015.56040 - 116. El Naschie, M.S. (2015) Casimir-Dark Energy Nano Reactor Design Proposal Based on Fractals. International Journal of Innovation is Science and Mathematics, 3, 187-194.
- 117. Thom, R. (1975) Structural Stability and Morphogenesis. W.A. Benjamin Inc., London.
- 118. El Naschie, M.S. (2003) The VAK of Vacuum Fluctuation, Spontaneous Self Organization and Complexity Theory Interpretation of High Energy Particle Physics and the Mass Spectrum. Chaos, Solitons & Fractals, 18, 401-420.
http://dx.doi.org/10.1016/S0960-0779(03)00098-5 - 119. El Naschie, M.S. (2003) VAK, Vacuum Fluctuation and the Mass Spectrum of High Energy Physics. Chaos, Solitons & Fractals, 30, 579-605.
http://dx.doi.org/10.1016/j.chaos.2006.03.030 - 120. El Naschie, M.S. (1991) Stress, Stability and Chaos in Structural Engineering: An Energy Approach. McGraw Hill, London.
- 121. Thompson, J.M.T. and Hunt, G. (1973) A General Theory of Elastic Stability. John Wiley, London.
- 122. El Naschie, M.S. (2015) A Casimir Dark Energy Nano Reactor Design—Phase One. Natural Science, 7, 287-298.
http://dx.doi.org/10.4236/ns.2015.76032 - 123. El Naschie, M.S. (2016) Cosserat-Cartan and de Sitter-Witten Spacetime Setting for Dark Energy. Quantum Matter, 5, 1-4.
http://dx.doi.org/10.1166/qm.2016.1247 - 124. El Naschie, M.S. (2015) The Cantorian Monadic Plasma behind the Zero Point Vacuum Spacetime Energy. American Journal of Nano Research & Application, 3, 66-70.
- 125. El Naschie, M.S. (2015) A Nonperturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Science, 5, 313.
http://dx.doi.org/10.4236/ojapps.2015.57032 - 126. Ho, M.-W., El Naschie, M.S. and Giuseppe Vitello, M.W. (2015) Is Spacetime Fractal and Quantum Coherent in the Golden Mean? Global Journal of Science Frontier Research, 15, 61-80.




